Recycling Frank: Spontaneous emergence of homochirality in noncatalytic systems

Abstract

In this work, we introduce a prebiotically relevant protometabolic pattern corresponding to an engine of deracemization by using an external energy source. The spontaneous formation of a nonracemic mixture of chiral compounds can be observed in out-of-equilibrium systems via a symmetry-breaking phenomenon. This observation is possible thanks to chirally selective autocatalytic reactions (Frank's model) [Frank, F. C. (1953) Biochim. Biophys. Acta 11, 459–463]. We show that the use of a Frank-like model in a recycled system composed of reversible chemical reactions, rather than the classical irreversible system, allows for the emergence of a synergetic autoinduction from simple reactions, without any autocatalytic or even catalytic reaction. This model is described as a theoretical framework, based on the stereoselective reactivity of preexisting chiral monomeric building blocks (polymerization, epimerization, and depolymerization) maintained out of equilibrium by a continuous energy income, via an activation reaction. It permits the self-conversion of all monomeric subunits into a single chiral configuration. Real prebiotic systems of amino acid derivatives can be described on this basis. They are shown to be able to spontaneously reach a stable nonracemic state in a few centuries. In such systems, the presence of epimerization reactions is no more destructive, but in contrast is the central driving force of the unstabilization of the racemic state.

The emergence of homochirality is a crucial enigma in the origin of life (1): fundamental biomolecules are different from their mirror images and exist only in either the right-handed or left-handed form. For symmetry reasons, the first chiral prebiotic molecules should have been synthesized in equal amounts of both forms (2), but an initial enantiomeric excess of low value can easily exist (3), thanks to statistical fluctuation (4), asymmetry of weak forces (5), or induction by an asymmetric environment (6–9). The problem thus comes down to understanding how amplification phenomena could take place to enhance such initial deviance from symmetry, constituting a real symmetry breaking toward homochirality. Some explanations based on stereoselective polymerization are classically suggested (10, 11). However, the effect is only proportional to the initial excess and is to be destroyed in the long term by epimerization, so that these models are not sufficient as the racemic state remains stable (12).

True symmetry breaking can occur in an dynamical out-of-equilibrium chemical system, as first introduced by Frank (13), allowing the destabilization of the racemic state. Several experimental systems corresponding to such a model have been described (14–18), but as Blackmond (19) recently concluded in an analysis about such experimental models, there is still a need of “other organic transformations that could provide a closer model for how asymmetric amplification in the prebiotic world could have occurred.” To be effective, such systems need autocatalysis (so that an excess of one configuration favors its own production) and a mechanism capable of destructing the opposite configuration.

We set out to construct such a system, exclusively based on simple reactions, all realistic from the prebiotic point of view. Rather than introducing direct autocatalytic reactions (dubious in a prebiotic environment) autoinduction will be shown to emerge from a network of coupled stereoselective reactions. Moreover, as the synthesis of prebiotic material should have been an important limiting factor, a recycled system based on reversible chemical reactions is considered, rather than the classical irreversible description. The Frank-based experimentations are practically limited to materially closed systems (15, 17, 18). In the absence of recycling, they can't reach a real steady state: the evolution of the system stops with the destruction of initial reactants. This absence results in a stochastic behavior leading to a random final enantiomeric excess (16). In a closed system, the accumulation of the final products erodes the amplification process. Its elimination, for example, thanks to the establishment of a product flux by the aperture of the system, allows us to overcome this limitation (20). The recycling of materials constitutes a natural alternative to this material-consuming elimination mechanism, allowing a fully effective amplification process toward homochirality (21).

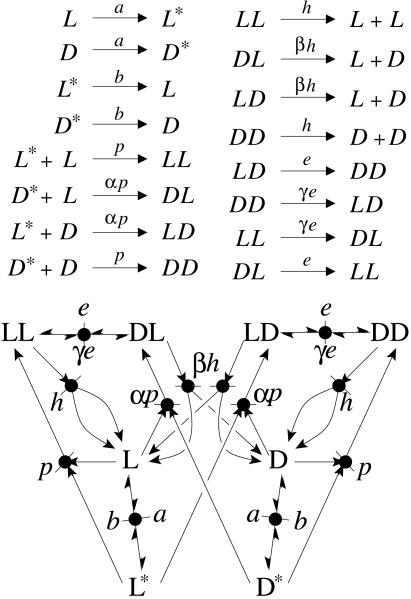
On the basis of these considerations, we describe a dynamic chemical system of reacting chiral monomers, composed of activation, polymerization, epimerization, and depolymerization (APED) reactions between deactivated monomers (L and D), activated monomers (L* and D*), and polymers (X_n, with X being either L or D, and reacting residue being, by convention, represented on the left side). For the sake of simplicity, the polymerization reactions are limited to dimerizations. The polymerizations of rates p and αp, the depolymerizations of rates h and βh, and the epimerizations of rates e and γe can be stereoselective, quantified by the parameters α, β and γ, respectively. The activation and deactivation rates are quantified by a and b, respectively (see Fig. 1). The total concentration in residues c = [L] + [D] + [L*] + [D*] + 2([LL] + [DD] + [LD] + [DL]) is a constant parameter. The APED system can be represented as an embedded Frank-like model, with no autocatalytic or catalytic reactions (see Fig. 2). The whole system is totally recycled and maintained out of equilibrium by the continuous activation of monomers.

Fig. 1.

Minimal APED system limited to dimerizations of L and D residues. (Upper) Chemical reactions. (Lower) Reaction network. a, Activation; b, deactivation; p, homochiral polymerization; αp, heterochiral polymerization; h, homochiral hydrolysis; βh, heterochiral hydrolysis; e, homochiral epimerization; γe, heterochiral epimerization.

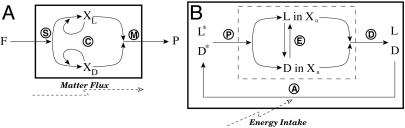
Fig. 2.

Schematic representations of Frank's model (A) and the APED model (B). (A) Circled S, synthesis of chiral compounds X_L and X_D from achiral compounds F; circled C, autocatalysis by X_L and X_D; circled M, mutual destruction of X_L and X_D to P. (B) Circled A, activation of L and D to L* and D*; circled P, polymerization from L* and D* to X_n; circled E, epimerization between polymers; circled D, depolymerization of X_n back to L and D.

If the APED model is very general, it is fully compatible with the chemistry of amino acids:

• The polymerization of amino acids can be very stereoselective, favoring the formation of homochiral peptides, namely by using N-carboxyanhydrides of α-amino acids (22, 23).

• The activation energy of the epimerization of the N-terminal residue of a peptide is much lower than that of all other residues, either in their free form or embedded in the peptide chain (24). Thus, the D/L interconversion can be restricted to the N-terminal residues of peptides, with all other inversion reactions being insignificant.

• The epimerization reaction can be very stereoselective, favoring the formation of the homochiral peptides (25).

The purpose of this work is to determine whether such a simple system can give rise to dynamic instabilities, so that homochirality can emerge. Despite the simplicity of this model, the differential equations set is still complex, as all reactions are coupled. The work was thus performed in three successive steps: an analytical study of a simplified model, a systematic numerical study of the whole system, and a numerical application describing a more realistic system of amino acid derivatives, based on literature values for the kinetic rates.

Methods

Local Stability Analysis of Fixed Points. The fixed points are calculated from the kinetic equations, in the case b = 0 s^–1 and β = γ = 0, by determining the states where the derivatives of the concentrations of all compounds equal zero. In each case, several fixed points are theoretically possible and may be reached. An absolute condition for the possibility of the fixed point is that all concentration values are positive, which implies for some cases a minimal value of c [i.e., c > 2a/(p(1 + a)) or c > a/p].

The stability of the fixed points is investigated by the linearization of the equations in the neighborhood of the fixed point. The evolution of the concentrations near a given fixed point is given by:

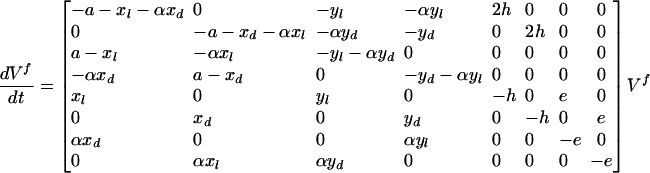with:

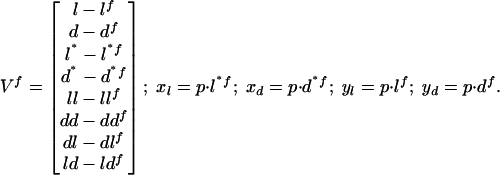l, d, l*, d*, ll, dd, ld, and dl (l ^f, d^f, l*^f, d*^f, ll^f, dd^f, ld^f, and dl^f, respectively) are the concentrations of L, D, L*, D*, LL, DD, LD, and DL, respectively, at a given time t (in the fixed point). If all of the eigenvalues (or their real part if complex) of the matrix are negative, the considered fixed point V ^f is asymptotically stable. Computer kinetic simulations were performed for particular cases to verify these analytical results. A fourth-order Runge–Kutta algorithm with adaptive stepsize control was used with xppaut software [version 5.85, written by G. B. Ermentrout et al. is free software, distributed under the GNU Public License (www.gnu.org)].

Systematic Analysis of APED Systems. A program was written in c, based on a fourth-order Runge-Kutta algorithm (26), for the automated kinetic simulation of the full APED systems (the source code is available at http://omemf.univ-montp2.fr/online/simul.c). Simulations were performed for the case a = h = e = 1 s^–1, c = 2 M, and p = 1 s^–1·M^–1, and for all values of 10^–4.5 ≤ α ≤ 10^1.5, 10^–4.5 ≤ β ≤ 10^1.5, and 10^–4.5 ≤ γ ≤ 10^1.5) by steps of 10^0.02 on a logarithmic scale. A first excess ee^init = 0.01 was introduced in an initial mixture of L and D. The calculation was performed for a fixed simulated time of reaction, and concentrations were analyzed on the last 10% time, to know whether a fixed point is reached or whether the system is unstable (corresponding to an oscillating steady state). The symmetry of the fixed point was determined thanks to the value of the global enantiomeric excess ee = (l + l* + 2ll – d – d* – 2dd)/c. The system is known to be dead if at the end of the simulation all products but the activated monomers have disappeared.

Results and Discussion

Analytical Study. We first reduced the model to the very essential reactions to perform the analytical study on a particular case. Deactivation is neglected, and the stereoselectivities of depolymerization and epimerization are considered as total (i.e., β = γ = 0). This model is obviously extreme and unrealistic, but allows a simple analytical approach of the complete model, aiming at the determination of the phenomenology to be expected in more general cases. The fixed points can be determined from the equations (see Methods). There are three possibilities:

• The symmetric state, where all species exists, all enantiomer pairs being in equal concentrations (i.e., this state is totally racemic). As can be observed, a minimal total concentration is required for fulfilling the existence of all of the compounds.

• The asymmetric state, where all residues of one absolute configurations have disappeared. This state is totally homochiral. Here again, a minimal total concentration is required.

• The “dead” state, where all concentrations are zero but for the activated species L* and D*. This state is a dead end, where no reaction can occur.

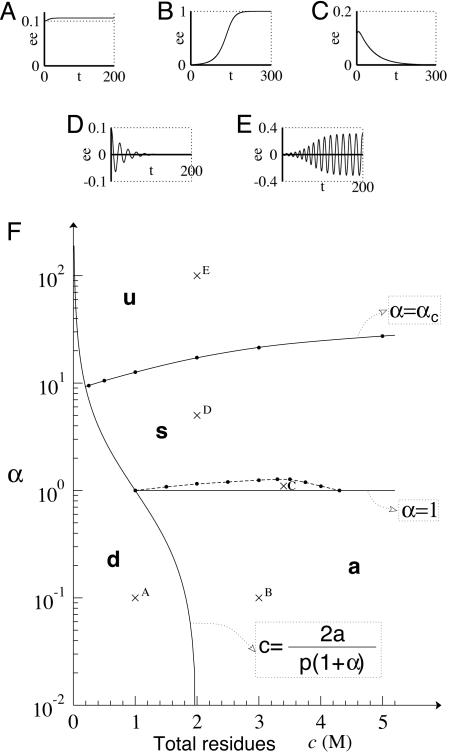
The stability of these states is investigated by the linearization of the equation sets in the neighborhood of the fixed points and the research of the eigenvalues of the corresponding matrix (see Methods). Depending on the values of c and α, four steady states can be identified (the regions of these four behaviors are represented by d, a, s, and u in Fig. 3):

Fig. 3.

The five kinds of behaviors of APED systems. (A–E) Spontaneous evolution of the enantiomeric excess of several simplified APED systems, calculated for b = 0 s^–1, a = h = e = 1 s^–1, p = 1 s^–1·M^–1, β = γ = 0 and α =0.1, c = 1M(A); α = 0.1, c = 3M(B); α = 1.1, c = 3.2M(C); α = 50, c = 2M(D); and α = 100, c = 2M(E). (F) Behavior categories of the simplified APED systems. Crosses indicate the position of the A–E system. Solid lines indicate the separations between dead (d), symmetric (s), asymmetric (a), and unstable (u) systems. The dotted line represents the separation between monotone and oscillating symmetric systems.

• In all cases, if the total concentration is too low, no dimers are formed: the only possible state is the dead one (see Fig. 3A).

• If the polymerization favors the formation of homochiral dimers (i.e., α < 1), the symmetric state is unstable, and the asymmetric state is stable. An initial racemic situation will thus spontaneously evolve to an homochiral situation: a symmetry breaking occurs, where either all L or D residues are spontaneously converted to the opposite form (see Fig. 3B).

• If the polymerization favors the formation of heterochiral dimers, and below a specific critical value (i.e., 1 < α < α_c, α_c being the critical value of α as a function of c), the symmetric state is stable, and the asymmetric state is unstable. Independently of the initial conditions, the system will evolve to the racemic state: every initial imbalance is destroyed (see Fig. 3C). Near the critical values of α, oscillations can be observed before the racemic state is reached (see Fig. 3D).

• Above the critical value of stereoselectivity (i.e., α > α_c) both symmetric and asymmetric states are unstable. As a result, the system oscillates between two opposite values of the enantiomeric excess (see Fig. 3E) and cannot reach any stable fixed point. This case seems quite surprising, but the high values required for α are probably not realistic if applied to a real chemical system.

This simple system, although based on noncatalytic reactions, is able to behave similarly as the Frank's model, with an unstabilization of the racemic state. The autocatalytic reactions (strictly necessary in the Frank's model) can thus be replaced by an autoinduction, stemming from a synergetic action of simple stereoselective reactions.

Systematic Study. Given these results, it appears that the stereoselectivity of polymerization favoring the formation of homochiral dimers (i.e., α < 1) is absolutely necessary for obtaining a symmetry breaking toward a long-term stable homochirality. To verify whether this observation is specific to this extreme model, we performed a systematic analysis of the complete model. A computer program has been written to automate the kinetic simulations and the analysis of the final state of the system as a function of α, β, and γ (see Methods).

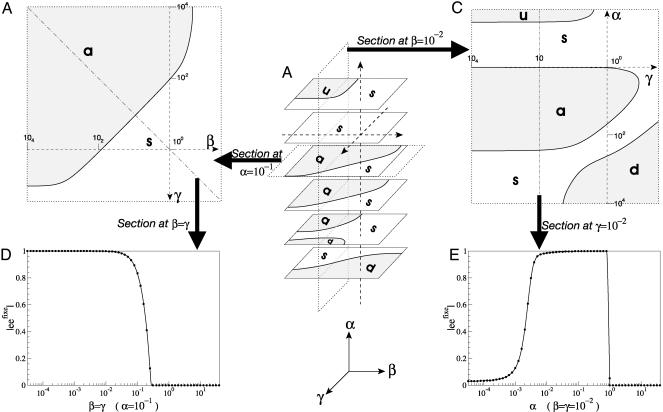
Behaviors are roughly similar as in the simple model: the systems can be symmetric, asymmetric, unstable, or dead (see Fig. 4A). Here again, a stereoselectivity of polymerization favoring the formation of homochiral dimers (α < 1), i.e., a “productive” stereoselectivity, is absolutely necessary. A strong opposite, “counterproductive,” stereoselectivity (high values of α) makes the system unstable.

Fig. 4.

Diagram of the APED states as a function of α, β, and γ, calculated for b = 0 s^–1, a = h = e = 1 s^–1, p = 1 s^–1·M^–1, and c = 1M. a: Asymmetric system; s: symmetric system; d: dead system; u: unstable system. (A) Complete αβγ diagram. The dotted axes represents the values of α, β, and γ on a logarithmic scales, from 10^–4 to 10^1.5, and intersect at α = β = γ = 1. (B) βγ Diagram for α = 10^–1 (bilogarithmic scale). (C) αγ Diagram for β = 10^–2 (bilogarithmic scale). (D) Bifurcation diagram for α = 10^–1, representing the enantiomeric excess of the stable fixed point (|ee^fixe|) as a function of β = γ (logarithmic scale). (E) Bifurcation diagram for β = γ = 10^–2, representing |ee^fixe| as a function of α (logarithmic scale).

On top of these observations, a counterintuitive behavior of the system occurs if the productive stereoselectivity is too strong (lowest values of α). Although a system with a limited stereoselectivity can reach a quasi-perfect homochirality, only incomplete homochirality is obtained with a more stereoselective polymerization: the global enantiomeric excess of the stable fixed point quickly decreases with α. The symmetry-breaking phenomenon is thus only effective for weakly stereoselective systems. In the example shown in Fig. 4 C and E, the system is asymmetric only for 10^–3 < α < 1).

The stereoselectivity of depolymerization and epimerization plays a very different role. They both have a similar influence on the system, as shown by the symmetry of the αβγ diagram. At least one of the stereoselectivities is required. Symmetry breaking is favored by the preferential epimerization of heterochiral dimers into homochiral dimers (i.e., γ < 1) and by the preferential hydrolysis of homochiral dimers rather than heterochiral dimers (i.e., β < 1). If one of these two stereoselectivities is counterproductive, the asymmetric system can still be stable if the other one is sufficiently productive (see Fig. 4 B and D).

The complete APED system is thus still efficient, although only partial homochirality is stable. It is observed that all three stereoselectivities of polymerization, epimerization, and depolymerization play a crucial role for obtaining a nonracemic system. A strong collaboration exists between these reactions, and the autoinduction phenomenon emerges from this synergy.

Real Systems. The preceding model is theoretical, but can be applied to concrete chemical systems of amino acid derivatives. In a prebiotic point of view, amino acids are known to be synthesized abiotically in many ways (27–30). However, the formation of the first prebiotic peptides is not a trivial problem, as free amino acids are poorly reactive. Some invoked prebiotic activations of stable amino acids derivatives rely on the formation of N-carboxyanhydrides of α-amino acids (NCAs) (11, 31), e.g., by the action of nitrogen oxides under mild conditions (32) or carbon monoxide in the presence of (Fe,Ni)S under drastic conditions (33). The chemistry of NCAs (34) is of great interest for building real APED systems:

• They are very reactive amino acids derivatives, which easily permit the formation of peptides in aqueous solutions (22, 35).

• The polymerization of NCAs is stereoselective (22, 23, 36, 37), favoring the formation of homochiral peptides.

• This chemistry facilitates the recycling of products, constituting a retroaction loop: peptides are hydrolyzed back to amino acids in aqueous solutions; the amino acids' reactivation into NCAs allows their reintroduction into the peptides.

The limiting factor for the loop activity is the slower reaction rate, i.e., the depolymerization rate. A wide range of possible systems can be described as a function of the environmental conditions, from slow systems with stable peptides, as in Commeyras and coworkers' model (36), to fast ones with short-life peptides, as in Wächtershäuser and colleagues' model (33).

A simulation was performed from estimated kinetic rates of peptides and NCAs reactivity in water, based on previously measured kinetic rates and other literature values. The ratios between homochiral and heterochiral coupling have been measured for several substrates. Values between 1.2 and 5.3 have been reported (37), corresponding to an average value of 0.35 for α. The difference between activation energies of epimerization of homochiral and heterochiral dipeptides has been theoretically estimated at 3 kJ·mol^–1 (25). By supposing that the preexponential parameter of Arrhenius is roughly equal for both epimerizations, γ can be estimated to:

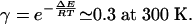Experimental measurements of γ are still in progress, but initial results tend to confirm this rough value. The rates of polymerization (fast) and peptide hydrolysis (slow) are very different in all conditions. It could be observed that the system is more effective when this difference is reduced, corresponding to low values of pH: the hydrolysis of peptides is enhanced, and the polymerization of peptides is slowed down. The rates of hydrolysis and polymerization of NCAs (37, 38) and the rate of hydrolysis of peptide (39) were thus taken for acidic conditions, corresponding to b = 5.10^–4·s^–1, p = 0.02 s^–1·M^–1, and h = 10^–7·s^–1. The epimerization rate of the N-terminal residue of peptides is of the same order as the hydrolysis rate, and the difference of activation energy between this epimerization and the one of other residues (either in free form or embedded into a peptide chain) is estimated at ≈30 kJ·mol^–1 (24). Thus, all but N-terminal residues can be neglected in epimerization, and e was taken to be equal to h. A slow activation flux a = 10^–8 s^–1 was introduced. The stereoselectivity of hydrolysis of peptide is rarely reported in the literature. An optimum value of 0.2 for β was manually found, corresponding to an hydrolysis favoring the destruction of homochiral peptides, as observed in the theoretical study.

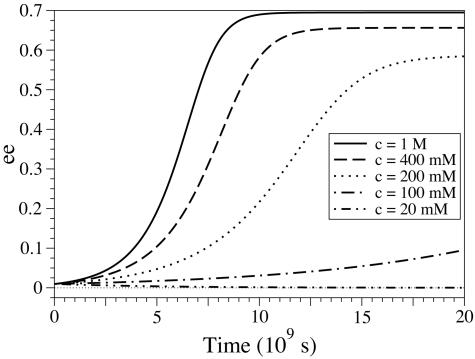
In such conditions, the racemic state can still become unstable: as long as the total concentration is sufficiently high, stable enantiomeric excess of ≈70% can be spontaneously reached in a few centuries (see Fig. 5). These conditions are globally compatible with the hypothesis of a medium getting alternatively dried and wet, with an amino acid activation involving NO_x compounds (36). The APED model appears to be possible and sensible in such environments, showing that spontaneous prebiotic homochirality can be explained without invoking any autocatalytic reactions, on the basis of simple chemical reactions.

Fig. 5.

Time evolution of the enantiomeric excess of APED systems based on experimental data, for different concentrations in residues c. Calculated for eeⁱⁿⁱ = 0.01; a = 10^–8 s^–1, b = 5·10^–4 s^–1, p = 2·10^·2 s^–1·M^–1, α = 0.35, h = 10^–7 s^–1, β = 0.2, e = 10^–7 s^–1, γ = 0.3.

Conclusion

The APED system is thus a dynamic system that can spontaneously evolve to, and remain in, a stable nonracemic state. The model described here constitutes a minimal subset of reactions, all of them being necessary for reaching symmetry breaking by the self-conversion of one of the enantiomers into the other from the racemic state. Consistently with the classical descriptions, a stereoselectivity of polymerization favoring the formation of homochiral polymers is necessary, but was shown to be insufficient. The cooperation between the epimerization of the terminal residue and the polymer hydrolysis allows the continuous conversion between L and D residues and the stabilization of the nonracemic state. If the epimerization obviously tends to the racemization of the system when it is isolated, the energetic openness of the system can, in constrast, allow the epimerization to counteract the global racemization, if either the epimerization or the depolymerization is sufficiently stereoselective, favoring the formation and the hydrolysis of homochiral polymers, respectively.

This simple model succeeds in fulfilling the two key concepts necessary for the spontaneous emergence of homochirality, as described by Blackmond (19) on the basis of the experimental system developed by Soai et al. (15):

• The synergetic action of epimerization with polymerization and depolymerization allows an emergent autoinduction phenomenon: an excess of L residues favors the inversion of D residues into L ones. Thanks to an activation reaction, this sequence of reactions constitutes a positive retroaction loop in the reaction network, which plays the same role as the direct autocatalysis of the classical Frank's model.

• Every residue is to be recycled and is likely to be epimerized. The suppression of the “wrong hand” residue (strongly required in a system of spontaneous asymmetric synthesis) is here inherent to the dynamic of a totally recycled system, allowing conversion between residues (i.e., requiring effective epimerization reactions).

As a result, this model get closer to living systems than classical models, by introducing a protometabolic pattern, i.e., describing a cyclic use of organic compounds, fed with external energy flow, rather than the common “open-flow reactor” pattern. The relevance of such a pattern in prebiotic conditions is enhanced by the fact that autocatalytic reactions are unnecessary, and that epimerization reactions are not drawbacks as often reported (40), but in contrast are the driving force of the stabilization of asymmetry.

The “bottom-up” approach, developed here, describes the emergence of a network autocatalytic system, rather than a template autocatalytic system, joining the “top-down” approach as developed by Morowitz et al. (41), who have investigated the origin of metabolism on the basis of the reductive citric acid cycle. If the prebiotic origin of a reaction network as complex as this cycle is questionable, much simpler systems may be relevant (42). Of course, the APED system does not yet constitute a metabolic pattern, but has some of its characteristics. It does not take into account the matter of creation (i.e., the formation of amino acids in the described example), but it describes the use of external energy to reproduce some properties (here, the absolute configuration of the monomers) and to increase the complexity of matter (by way of polymerization). An interesting extension to a more complex system is being investigated by others, focusing on molecular energetic use, via carboxylic-phosphoric mixed anhydrides (43).