Linkage analysis of ordinal traits for pedigree data

Abstract

Linkage analysis is used routinely to map genes for human diseases and conditions. However, the existing linkage-analysis methods require that the diseases or conditions either be dichotomized or measured by a quantitative trait, such as blood pressure for hypertension. In the latter case, normality is generally assumed for the trait. However, many diseases and conditions, such as cancer and mental and behavioral conditions, are rated on ordinal scales. The objective of this study was to establish a framework to conduct linkage analysis for ordinal traits. We propose a latent-variable, proportional-odds logistic model that relates inheritance patterns to the distribution of the ordinal trait. We use the likelihood-ratio test for testing evidence of linkage. By means of simulation studies, we find that the power of our proposed model is substantially higher than that of the binary-trait-based linkage analysis and that our test statistic is robust with regard to certain parameter misspecifications. By using our proposed method, we performed a genome scan of the hoarding phenotype in a data set with 53 nuclear families, which were collected by the Tourette Syndrome Association International Consortium for Genetics (TSAICG). Standard linkage scans using hoarding as a dichotomous trait were also performed by using genehunter and allegro. Both genehunter and allegro failed to reveal any marker significantly linked to the binary hoarding phenotypes. However, our method identified three markers at 4q34-35 (P = 0.0009), 5q35.2-35.3 (P = 0.0001), and 17q25 (P = 0.0005) that manifest significant allele sharing.

Linkage analysis has been very useful for mapping disease genes, such as the breast cancer gene BRCA1 (1, 2). Statistical methods for linkage analysis are well established for both quantitative and binary traits (3–9). However, methods for linkage analysis have not been established for ordinal traits, although many human conditions (e.g., cancer) are rated on discrete, ordinal scales. Studies have suggested genetic heritabilities for some ordinal traits (10–13). Ordinal traits are typically first dichotomized into binary traits, and then analyzed by standard linkage-analysis programs such as genehunter (8) and allegro (14).

We propose a statistical method for linkage analysis of general pedigree data with ordinal traits and demonstrate the gain of power when the ordinal, rather than dichotomized, traits are directly used. Other researchers (15) have also observed loss of power for linkage analysis due to the dichotomization of trichotomous phenotypes.

It is widely recognized that demographic and environmental factors, together with genetic mechanisms, are important determinants in most complex diseases. Thus, our model was developed to accommodate selected demographic and environmental factors.

Methods

Methods for linkage analysis include two main steps (8). The first step is to infer information about the inheritance pattern of a pedigree by means of the so-called inheritance vector. This is a unified step, regardless of the properties of a trait; hence, we adopt the same method as used in ref. 8. In the second step, the linkage of a marker to a disease locus is established if the inheritance pattern of the marker is associated with the trait because, in the absence of linkage, the inheritance pattern is expected to be independent of the trait. This second step obviously depends on the distribution of the trait, and it is the main focus of this article.

Inheritance Vector and Its Distribution. Briefly, we present the necessary notation and steps for deriving the distribution of inheritance vector (16). Given a pedigree, a founder refers to a subject whose parents are not included in the pedigree. In a nuclear family with two parents (founders) and n siblings (nonfounders), the inheritance pattern at a marker location t is described completely by an inheritance vector v(t) = (v₁, v₂, v₃, v₄,..., v_2n–1, v_2n)′, whose elements describe the outcomes of the paternal and maternal meioses transmitted to the n siblings. Specifically, v_2j–1 = 1 or 2, according to whether the grandpaternal or grandmaternal allele is transmitted in the paternal meiosis to the jth sibling. v_2j carries the similar information for the corresponding maternal meiosis, namely, v_2j = 3 or 4, according to whether the grandpaternal or grandmaternal allele was transmitted in the maternal meiosis to the jth sibling. For example, if v(t) = (1, 4, 1, 3)′, the first child received the father's paternally derived allele and the mother's maternally derived allele, and the second child received the father's paternally derived allele and the mother's paternally derived allele.

For a more complex pedigree with f founders and n nonfounders, we can index the alleles of the f founders as (1, 2), (3, 4), (5, 6),..., (2 f – 1, 2 f). Then, we can define the inheritance vector for the n nonfounders similarly. The inheritance vector completely specifies which of the 2 f distinct founders' alleles are inherited by every nonfounder. There are a total of 2²n possible inheritance vectors, which can be grouped into 2²n–f distinct configurations.

For clarity, we will use nuclear families with two founders below. The inheritance distribution is the conditional probability distribution over the possible inheritance vectors that conform the alleles observed at the marker locus t, which we denote by p{v(t) = w}for all inheritance vectors w ∈ V; here, V is the set of all possible inheritance vectors. In the absence of any genotypic information, all inheritance vectors are equally likely according to Mendel's first law, and the probability distribution is uniform (denoted as p_unif). As genotypic information is enhanced, the probability distribution becomes concentrated in certain inheritance vectors. In any case, available standard software can be used to derive the inheritance distribution for genotyped pedigrees. We used genehunter in our computation.

A Latent-Variable Model (LVM) in Linkage Analysis. To infer whether the inheritance pattern at a given marker is associated with an ordinal trait, we propose a latent-variable, proportional-odds logistic model, which is a further development of the LVM for segregation analysis (13, 17).

We consider a trait Y taking an ordinal value from 0, 1,..., K(K ≥ 1). Let x be a p-vector of covariates that is also available for every study subject. For the ith family, we assume there exist two types of latent random variables, 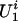and 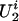, which represent (i) the common genetic or environmental factors in a family that are not observed through the covariates and (ii) the genetic susceptibility of the family founders and nonfounders, respectively. The genetic susceptibility due to a particular gene is accommodated through the inheritance vector in the pedigree as follows.

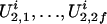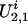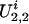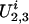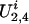Let be the genetic susceptibility of the f founders. In a simple pedigree with two founders, we have four latent variables in which and represent the genetic susceptibility associated with the two parental alleles at marker location t. Likewise, and represent the genetic susceptibility associated with the two maternal alleles at t. The genetic susceptibility is reflected through the inheritance vector v. That is, for the jth nonfounder in the ith family, his/her latent variables are 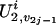and 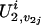. If we consider the additive susceptibility due to the gene linked to locus t, then for the jth sibling, 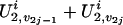for j = 1, 2,..., n, reflects the genetic susceptibility due to part of the genomes on the two chromosomes transmitted from the parents. For example, in a five-member pedigree with two parents and three offspring, if the inheritance vector of the three offspring is (1, 3, 1, 4, 2, 3), then their latent variables U₂ values are (U_2,1, U_2,3), (U_2,1, U_2,4), and (U_2,2, U_2,3).

For the latent variables introduced above, we assume that 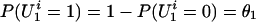, where θ₁ is an unknown parameter. Also, for a founder, 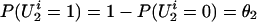, where θ₂ is an unknown parameter. This Bernoulli possibility basically assumes that there exists a single major susceptibility locus with alleles, A and a, at marker location t and that the frequency of allele A is θ₂. Furthermore, all 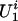values and the 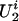values of the founders are assumed to be distributed independently and identically across families.

Conditional on all of the latent variables, denoted by Uⁱ, and inheritance vectors vⁱ, within the ith family, the traits of all nonfounders are independent and follow the following distribution:

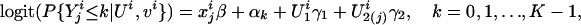[1]

where 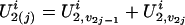, and β is a p vector of parameters, reflecting the covariate effects on the trait. The α_k variables are the trait-level-dependent intercepts, and they reflect the differences between cumulative probabilities 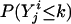. We must have α₀ ≤ α₁ ≤ ··· ≤ α_K, so that the category probabilities 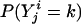are nonnegative (18). γ = (γ₁, γ₂)′ indicates the familial and genetic contributions to the trait. Without the latent variables (or γ = 0), model 1 is the commonly used proportional-odds logistic model for an ordinal response (18). In this article, individuals in category 0 are “most severely affected,” individuals in category K are “unaffected,” and individuals in other categories are between unaffected and most severely affected. Thus, we expect γ₂ > 0.

Parameter Estimates. Suppose that there are n families and n_i siblings in the ith family. If both the trait and the latent variables were observable, given a particular inheritance vector v, the complete log-likelihood function, lⁱ(α, β, γ, θ | U, v), would be equal to the following:

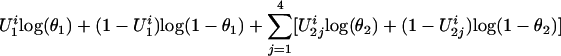[2]

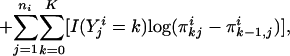where I(·) is the indicator function, and

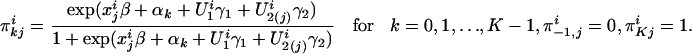The em algorithm (19) is used to find the maximum-likelihood estimation (MLE) in a similar way to Zhang et al. (13). In general, the inheritance vector v involves uncertainty at a marker location. As usual (8), we can take the expectation of the likelihood Lⁱ over the inheritance distribution inferred from the genotyped data, namely, Σ_v∈V Lⁱ(α, β, γ, θ | v)p_comp(v), where p_comp(v) is the inheritance distribution consistent with the marker information and V is the set of 2²n–f equivalent classes of inheritance vectors. Then, after the integration over the distributions of the latent variables, the likelihood becomes the following:

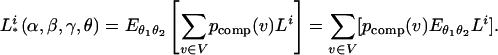[3]

After obtaining the MLEs of the parameters, we can estimate the covariance matrix of the MLEs by using an existing method (20, 21).

Logarithm of Odds (lod) Score Calculation. The likelihood-ratio statistic is used commonly in linkage analysis. The null hypothesis is that a disease gene is not in linkage with locus t. The alternative hypothesis is that locus t is linked to the disease gene. The likelihood ratio of LR = p(Y | v(t))/Σ_w∈V p(y | w)p_unif(w), where p(Y | v(t)) is the probability of the observed ordinal trait Y conditional on v(t), V is the set of 2²n–f equivalent classes of inheritance vectors, and p_unif(w) is the uniform distribution over V (i.e., the distribution in the absence of linkage). The lod score, defined as the decimal log-likelihood ratio, is commonly used (22).

In the LVM, p(Y | v(t)) is a function of parameters ω = (α, β, γ₁, θ₁) and (γ₂, θ₂). In the absence of linkage, γ₂ = 0 in model 1. Therefore, for a given θ₂,

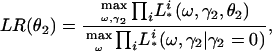[4]

and the lod score at locus t for a given θ₂ becomes lod(θ₂) = log₁₀LR(θ₂).

Based on asymptotic theory involving nonstandard conditions, the distribution of the standard likelihood-ratio statistic in our model may be complicated (13). One reason for the complication is that θ₂ is not identifiable when γ₂ = 0. In fact, this is the case for many statistical models in genetic studies. To test the presence of linkage, we follow the discussions in ref. 13 and consider the penalized log likelihood PLR(θ₂) = log LR(θ₂) + λ log[4θ₂(1 – θ₂)]. Under standard regularity conditions (13, 23), the maximum penalized log-likelihood-ratio statistic 2 max_θ2PLR(θ₂) follows 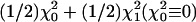. Thus, when θ₂ is not specified, 2 max_θ2PLR(θ₂) is used to determine the significance level, and the penalized lod (plod) score, defined as plod = max_θ2PLR(θ₂)/log(10), will be reported for model 1. However, for a given θ₂, we use lod(θ₂), which is a function of θ₂.

Simulation Studies

To demonstrate the promise of our model in mapping genes for ordinal traits, we report a series of simulations that are designed to examine three specific aims. First, in addition to our theoretical understanding of the asymptotic distribution of the plod score, we demonstrate numerically how the distribution appears under the null hypothesis. Second, as a critical incentive for the use of ordinal traits, we present evidence for gain of power of detecting linkage when there is a linked disease gene. The comparison is made with the use of genehunter and allegro, in which an individual's disease status is represented by a binary trait. Last, our model depends on a number of assumptions. It is important to scrutinize the robustness of our estimates when the model is misspecified.

Distribution of Likelihood-Ratio Statistic Under the Null Hypothesis. For each data set, we generated 200 five-member pedigrees with two founders and three offspring in each pedigree. One covariate, x₁, was generated from independent uniform (0, 1) distribution among all family members. Without loss of generality, we suppose that the response, Y, takes values from three ordinal levels 0, 1, and 2. In the absence of latent variable U₁, Y was simulated from an ordinal logistic model with the two logit links being –1 –0.9x₁ (for Y = 0) and –0.9x₁ (for Y ≤ 1).

For each founder in a pedigree, 20 highly polymorphic markers with 10 equally likely alleles (24), spaced 5 cM apart, were generated on one chromosome. Recombination fractions were converted to map distances without interference, and there was no linkage disequilibrium among markers (25). After the genotypes were generated for the founders, the genotypes of nonfounders were generated subsequently based on the recombination fractions.

The simulation was replicated 30,000 times (30,000 data sets). At a fixed marker locus, the empirical P values from plod scores are 0.5018, 0.1971, 0.1027, 0.0536, 0.0129, and 0.0016 when the asymptotic values are 0.5, 0.2, 0.1, 0.05, 0.01, and 0.001, respectively. Given the size of our simulation replications, the nominal and empirical P values are numerically within reasonable ranges of each other.

We also examined the number of false-positive errors when the significant linkage was declared at plod scores of >2 and >3 by using our model. When we focused on a specific locus, there were 60 of 30,000 data sets (P = 0.002) with plod scores of >2, and four with plod scores of >3 (P = 0.0001). We used Bonferroni correction to project locus-specific P values to a chromosome or the genome. For example, a plod score of 3 corresponds to ≈0.05 genomewide significance level for a typical genotypic data set of 370 microsatellite markers, as used in Application on Obsessive–Compulsive Disorder (OCD). The method given in ref. 26 could be used to explore a better approach.

Power Comparison. For the power comparison, the data sets were simulated similarly to those in the previous experiment. However, a locus between the 10th and 11th markers was set to be the disease locus, and the disease-causing allele was set at frequency 0.3. For the comparison purpose with genehunter and allegro, we do not consider any covariates in this simulation. In addition, the parameters involved in the logit link functions were set at γ₁ = 0, γ₂ = 2, α₀ = –2, and α₁ = –1. These parameters were unknown in the linkage analysis and were estimated from the data.

We conducted linkage analysis with 100 replications by using our method, genehunter, and allegro. For genehunter and allegro, the trait was dichotomized as Y = 0or Y ≥ 1. We also considered Y ≤ 1 versus Y = 2, and the results were consistent and, hence, not shown. Table 1 contrasts the results from the LVM and the nonparametric linkage (NPL) score method in genehunter and the nonparametric method (Z_lr) in allegro. Under the null hypothesis, the NPL score (8) follows a normal distribution asymptotically and, thus, can be transformed into lod score units according to the formula: NPL²/(2*log(10)) = lod. To provide numerical support to this asymptotic property, Ulgen et al. (27) carried out a simulation study of 2,400 replications of 100 nuclear families and verified that the observed distribution of (2ln10)lod fit well with 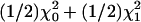under the null hypothesis. Thus, plod from our model for ordinal traits and the transformed lod score from NPL from the other software for binary traits have the same asymptotic distribution. Consequently, our plod and the NPL from genehunter could be viewed as counterparts of each other under the null hypothesis. This observation is useful to ensure the validity of the power comparison, because the type I error rates for different methods must be similar.

Table 1. Power comparison.

		Marker
Score	Method	1-3	4-6	7-9	10-11	12-14	15-17	18-20
plod >2*	LVM	54	62	74	85	80	61	57
lod >2*	GH	0	0	0	0	0	0	0
lod >2*	AL	1	0	4	5	6	2	0
plod >3*	LVM	26	31	52	66	57	34	25
lod >3*	GH	0	0	0	0	0	0	0
lod >3*	AL	0	0	1	1	1	0	0
lod >2†	LVM	49	51	66	80	74	50	47
lod >2†	GH	0	0	5	19	12	0	2
lod >3†	LVM	16	25	41	56	47	25	20
lod >3†	GH	0	0	1	0	0	0	0

Frequencies at which linkage is detected in the 100 data sets by the LVM, genehunter (GH), and allegro (AL) are shown.

^*Nonparametric lod scores converted from NPL in genehunter and Z_lr from allegro.

^†Parametric lod scores calculated by using θ₂ = 0.3 for LVM and GH.

We also compared the lod scores from the LVM with the parametric method in genehunter by specifying the disease allele frequency to be the “true” frequency of 0.3. We used the simulated model to specify the penetrances as (0.12, 0.50, 0.88), which were based on the true parameters and, hence, expected to be in favor of genehunter.

In Table 2, we used allele frequencies of 0.2 and 0.5 to examine the impact of misspecifying the allele frequency. It is evident from this table that these misspecifications have little effect on power. Therefore, the LVM is very robust in terms of power with respect to misspecification of the allele frequency, which is the only parameter to be specified after model 1 is assumed.

Table 2. Power comparison under misspecified allele frequencies.

	Specified allele frequency	Marker
Score		1-3	4-6	7-9	10-11	12-14	15-17	18-20
lod >2	0.2	40	42	57	74	71	43	40
lod >2	0.5	52	58	73	83	78	61	55
lod >3	0.2	13	21	31	44	37	20	14
lod >3	0.5	23	30	50	65	57	31	23

Frequencies at which linkage is detected in the 100 data sets are shown.

Application on Obsessive–Compulsive Disorder (OCD)

Background. OCD is a potentially disabling condition affecting nearly 5 million people in the United States (28). Patients with OCD become obsessed with unwanted worries or unpleasant images, such as persistent fears that harm may come to a loved one, an unreasonable concern with becoming contaminated, or an excessive need to do things correctly. OCD occurs in a spectrum from mild to severe, and if severe and untreated, it can destroy a person's capacity to function at work, at school, or in the home (29).

The causes of OCD have yet to be established. However, growing evidence shows that biological factors are likely to contribute to the disorder. Evidence for a genetic component in OCD comes from twin studies, family genetics studies, and segregation analyses (30).

Hoarding, as a major factor in OCD, affects 2.4 million Americans. In adults, hoarding has been defined as the gathering of articles without clear, conscious motivation or control (31). Many studies have been done on hoarding, but its etiology is not understood. Only a few studies have focused specifically on the role that genetic factors play in the transmission and expression of hoarding symptoms. One such study was undertaken by Leckman et al. (32) as part of the TSAICG. They found evidence in support of a recessive mode of transmission for the hoarding symptom dimension in families with two affected siblings with Gilles de la Tourette syndrome (GTS) (32). Zhang et al. (33) performed linkage study of hoarding in the sibling pairs in the same study sample that we used here. They found strong evidence of linkage to three different regions by using a numerical factor scale from two hoarding items as a quantitative trait. The goal of the present study is to conduct and compare genome scans by treating hoarding symptoms as either an ordinal or dichotomous trait.

The Study Sample. The study sample was obtained through GTS patients. Since Gilles de la Tourette noted in 1885 that OCD symptoms were present in GTS patients, studies have shown prevalences of obsessive–compulsive symptoms of 11–80% among individuals with GTS (34). In contrast to the prevalence of OCD of 1–3% in the general population (35), the elevated prevalence of obsessive–compulsive symptoms are found in both clinical samples composed of GTS patients and nonreferred individuals with tics and their relatives in community samples (36).

All families include at least two siblings with GTS. In the original ascertainment, families were excluded if both parents were affected with GTS or if one parent had GTS, chronic tics (CT), OCD, and/or subclinical OCD and the other parent also had CT, OCD, and/or subclinical OCD. All diagnoses were made by use of Diagnostic and Statistical Manual-III-R criteria (37). The final sample included in the genome scan consisted of 53 families, with a total of 223 individuals. No information has been collected to perform a justifiable ascertainment adjustment for hoarding, which was a limitation of this study, as it was for ref. 33.

The significant hoarding symptoms were recorded as “present” when one or both of the hoarding items on the Yale–Brown Obsessive–Compulsive Scale symptom checklist were rated as present by clinicians and as “absent” otherwise. In addition to treating hoarding as a dichotomous outcome, we also considered it as an ordinal trait; that is, we recorded 2 if both items were absent, 1 if only one item was present, and 0 if both items were present.

The panel of genotyped markers included 370 DNA markers with an average spacing of 9.1 cM in the male meiotic map on 22 autosomal chromosomes. A detailed description of the markers and map is given by TSAICG. Zhang et al. (33) presented a detailed description of the study design and data collection.

Data Analysis. Allele frequencies for the genetic markers were established by gene counting in genotyped parents. For each family, the inheritance distribution was estimated by multipoint analyses in genehunter (8) and allegro (14). In the multipoint analysis, maximum-likelihood scores (38) were computed for 3,000 different locations relative to the markers (average step size, ≈1 cM). As a standard procedure, genotype data were checked against errors before the linkage analysis.

The status of hoarding was first examined as a binary trait. Parametric and nonparametric analyses were done with genehunter and allegro. For parametric analysis, disease allele frequency was set at 0.3, and the penetrances were set at 0.125, 0.575, and 0.75 (33).

The main results reported here are from the linkage analyses of the ordinal hoarding trait. The analyses were completed by using the LVM for the nuclear families. For comparison, we obtained the likelihood-ratio statistics with an unknown θ₂ as well as a fixed value at θ₂ = 0.3.

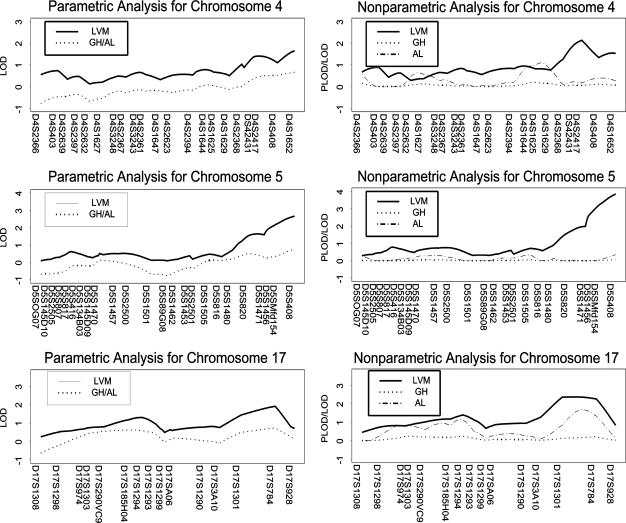
Analyses with genehunter and allegro did not reveal any evidence of linkage for this binary trait. However, the results of the analyses using the ordinal trait revealed linkage to three regions on three chromosomes (4q, 5q, and 17q). Thus, the power of detecting linkage was increased by the use of this ordinal trait in chromosomes 4 and 5. The significances of plod/lod scores are shown in Table 3. Specifically, in the region of 4q34–35, the best significance levels are .0009. In the region of 5q35.2–35.3, the best significance levels are .00001; and in the region of 17q25, the best significance level is .0005.

Table 3. Comparison of results for hoarding from LVM, genehunter, and allegro.

	P values
	Parametric, θ2 = 0.3		Nonparametric
Marker (location in cM)	LMV	GH	LMV	GH*	AL†
4q34-35
DS42431 (163.26)	0.006	0.101	0.001	0.120	0.156
D4S2417 (169.00)	0.005	0.072	0.0009	0.154	0.192
D4S408 (182.13)	0.012	0.063	0.006	0.068	0.091
D4S1652 (195.14)	0.003	0.040	0.004	0.126	0.136
5q35.2-35.3
D5S1471 (172.13)	0.003	0.122	0.001	0.560	0.563
D5S1456 (174.80)	0.002	0.139	0.0003	0.628	0.640
D5SMfd154 (182.89)	0.0006	0.095	0.00006	0.299	0.299
D5S408 (195.49)	0.0002	0.030	0.00001	0.133	0.100
17q25
D17S1301 (99.39)	0.005	0.066	0.0005	0.052	0.024
D17S784 (116.23)	0.002	0.034	0.0006	0.019	0.007

AL, allegro; GH, genehunter.

^*Based on NPL.

^†Based on Z_Ir.

Fig. 1 provides graphical comparisons of the parametric and nonparametric lod scores from genehunter and allegro, and plod/lod scores from the LVM. These values are comparable with those obtained by Zhang et al. (33) when hoarding was treated as a continuous variable derived from factor analyses. It is important to note that although Zhang et al. (33) assumed a continuous trait, the trait has only three distinct values.

Fig. 1.

LOD/PLODs produced by LMV, genehunter, and allegro on chromosomes 4, 5, and 17.

Discussion

We proposed a framework to map candidate genes for an ordinal trait by using a latent-variable, proportional-odds model. Our simulation studies clearly support the substantial gain of power by using an ordinal, as opposed to a dichotomized, trait. One may wonder whether this gain of power is at the cost of an increased type I error. Our simulations demonstrate that the locus-specific type I errors are close to the nominal level for the LVM. Using a specified allele frequency, our simplified parametric approach proves to be highly robust in detecting linkage when the specified frequency is very different from the true one. Because the severity of many health conditions are recorded on ordinal scales, our model can be employed successfully to study the genetic basis of complex traits.

Our model is very basic, and it is still in its infancy. Within our framework, it is important to investigate issues including ascertainment bias, genetic heterogeneity, inbreeding, and imprinting. Although our simulations demonstrate the great promise of our model, our experiments are still limited. Further simulation and theoretical studies of our model are warranted to understand the properties of our model.

We have used a special set of latent variables, namely, Bernoulli random variables. Preliminary evidence suggests that these latent variables work reasonably well even if the underlying latent variables are continuous (13, 17).

We applied our model to conduct a genome scan of hoarding. Significant linkage to specific loci on 4q, 5q, and 17q were found. The 4q site is in proximity to D4S1625, which was identified by the TSAICG as a region linked to the GTS phenotype. The other two regions, 5q and 17q, show the strongest evidence for linkage. Duggirala et al. (39) found strong evidence for linkage of smoking behavior to a genetic location near D5S1456. Increased allele sharing at this marker was also in pedigrees with bipolar subjects in a National Institute of Mental Health collaborative initiative for genetics of bipolar disorders (40). The region on 17q has been linked to many other diseases, including autoimmune diseases (41) and schizophrenia (42).

Overall, our results are consistent with the analysis given in ref. 33. They performed a genomewide scan of the same family data by treating the hoarding score as a quantitative trait. Normality is generally assumed for analyzing quantitative traits. In this data set, the hoarding score used in Zhang et al. (33) came from two yes–no questions, and the normality is clearly a concern. It is important that we confirmed the earlier results by the new model and a more rigorous approach.