Dynamical resonance can account for seasonality of influenza epidemics

Abstract

Influenza incidence exhibits strong seasonal fluctuations in temperate regions throughout the world, concentrating the mortality and morbidity burden of the disease into a few months each year. The cause of influenza's seasonality has remained elusive. Here we show that the large oscillations in incidence may be caused by undetectably small seasonal changes in the influenza transmission rate that are amplified by dynamical resonance.

The underlying cause of seasonal oscillations in influenza incidence (1) remains unclear despite at least 80 years of investigation (2). These oscillations are presumably due to some mechanism that causes seasonal changes in the effective transmission rate of the virus from person to person (often called seasonal forcing). But laboratory experiments and epidemiological studies have failed to establish whether these transmission changes are due to direct effects of temperature and humidity on transmission (3), to changes in mixing patterns [e.g., school terms (4) or simply more time spent indoors], or to other factors, such as increased viral production under winter conditions (evidenced by higher febrile reaction to identical influenza exposures; ref. 5). In fact, as we show here, it may be impossible to establish the underlying cause of seasonality in influenza epidemics, because the large observed oscillations in incidence can be generated by seasonal changes in the transmission rate that are too small to measure.

For an infectious disease that induces permanent immunity, simple deterministic models indicate that disease incidence has an intrinsic tendency to oscillate, even in the absence of exogenous driving factors. But these intrinsic oscillations are always damped (6). Such models are often called susceptible, infectious, recovered (SIR) models, referring to the transition of an individual between susceptible, infectious, and recovered states.

For influenza, immunity is not permanent. After recovering from one antigenic variant of the virus, a person is usually at least partially susceptible to new variants within a few years, due to gradual evolution of the virus (7). We model this process of antigenic drift by simply allowing people to lose their resistance to the circulating virus and hence to move back to the susceptible class after a few years [i.e., a SIR-susceptible (SIRS) model]. For simplicity, we do not explicitly model the exposed population but instead include people infected but not yet infectious in the “I” box. Including an exposed class yields similar results.

In a SIRS model, the intrinsic period of oscillation is approximately 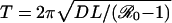, where D is the mean infectious period, and L is the average duration of immunity (4, 6). The basic reproductive number is defined as the expected number of secondary infections that a single infectious individual will cause in a wholly susceptible population.

If the period of endogenous SIRS oscillations (T) is near the period of seasonal forcing (1 year), then these two factors may resonate to produce greatly amplified oscillations in incidence (8). Appropriate parameter values for influenza (9–11), 6–10 days for D, 4–8 years for L, and 4–16 for 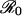, yield an endogenous oscillatory period, T, between 0.4 and 1.5 years. Therefore, the intrinsic period of oscillation for influenza is potentially close to the (annual) period of seasonal forcing, in contrast to human viral diseases that engender permanent effective immunity and typically have intrinsic interepidemic periods of 2–5 years (4).

Whereas deterministic models treat the number of people in each state as a continuous variable, in reality, individuals are discrete, and the process is more appropriately modeled as a stochastic Markov chain. The resulting demographic stochasticity causes fluctuations in disease incidence to persist (12). Demographic stochastisticity is more important if the average duration of immunity is long compared with the duration of infection (13). In the case of influenza, the ratio between these two time scales is on the order of a few years to 1–2 weeks, or ≈100.

Methods

The red curves in Fig. 1 represent solutions to the deterministic SIRS epidemic model defined by the equations

[1]

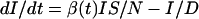[2]

where t is time in years, N is the total population size, and N-S-I gives the number of resistant (immune) individuals. The contact rate β(t) varies sinusoidally according to the formula

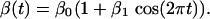[3]

In this formulation, 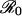equals Dβ₀. The parameter values corresponding to Fig. 1a are n = 500,000, L = 4 yr, D = 0.02 yr, β₀ = 500 per year, and β₁ = 0.02. The parameter values in Fig. 1b are n = 500,000, L = 8 yr, D = 0.025 yr, β₀ = 400 per year, and β₁ = 0.02. The blue curves in Fig. 1 represent solutions to the discrete-state continuous-time Markov chain in which events occur at the exponential rates given in Table 1.

Fig. 1.

The effect of seasonal forcing on oscillations in influenza incidence. We simulate disease dynamics in a population of 500,000 people both with (blue) and without (red) demographic stochasticity. varies sinusoidally between 9.6 and 10.4. The black curve shows the (nearly invisible) oscillations in incidence that these variations in 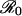would cause if disease dynamics responded instantaneously to changes in transmission, without resonance or transient fluctuations. (a) Weak resonance. The intrinsic oscillatory period is T ≈ 0.59 years (duration of infectiousness 0.02 yr, duration of immunity 4 yr). (b) Strong resonance. T ≈ 0.94 yr (duration of infectiousness 0.025 yr, duration of immunity 8 yr). When parameters are drawn at random from the ranges given for 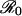, D, and L in the text, we find strong oscillations due to resonance (winter peak/summer trough >5) for 21% of parameter sets (Fig. 2).

Table 1. Markov chain transition rates.

Event	Change	Rate
Infection	(S, I) → (S - 1, I + 1)	β(t)IS/N
Recovery	(S, I) → (S, I - 1)	I/D
Immunity loss	(S, I) → (S + 1, I)	(N - S - I)/L

The Markov chain was simulated by using the standard Gillespie algorithm (14).

Results

Fig. 1 shows the effect of resonance, using simple deterministic and stochastic models of influenza dynamics in a population of 500,000 people, with very small sinusoidal forcing of the transmission rate. If resonance is weak (i.e., the endogenous period T is far from 1 year), then the resulting oscillations in incidence are much smaller than are actually observed for influenza. If resonance is strong, however, the resulting dynamics exhibit regular annual epidemics in which incidence increases by a factor of three or more from winter to summer. Fig. 2 shows the endogenous period and the resulting size of oscillations for parameters chosen at random from the plausible range for influenza. Due to resonance, large oscillations (average peak-to-trough ratio >5) occur for about one-fifth of parameter sets, even when the transmission rate varies by only a few percent.

Fig. 2.

Magnitude of observed oscillations (ratio of peak-to-trough incidence) in the stochastic forced SIRS epidemic model plotted against the approximated period of endogenous oscillations in the SIRS model , for 2,000 sets of parameters randomly chosen from the ranges given in the text (shown are the 1,560 trials where the disease persisted for at least 20 years after being started from the deterministic equilibrium). Underlying variation in transmission rate is ± 4% (i.e., β₁ = 0.04 in Eq. 3). Strong resonance occurs when the approximate endogenous period is near 1 year.

Researchers have worked to identify and measure a seasonal component of influenza transmission with the goal of explaining large annual fluctuations in incidence. But, as we have seen here using simple models, these large fluctuations may be caused by exogenous seasonal changes in transmission that are too small to detect, amplified by the endogenous population dynamics of the host–pathogen system.