Significance
Populations of sensory neurons convey information about the outside world to the brain. Postsynaptic neurons may read out their total activity or, alternatively, by focusing only on synchronous activity, they might extract specific features from the same sensory information. But does synchronous activity always encode special features of the stimulus? This question was experimentally addressed in in vivo recordings from two closely related populations of electrosensory neurons of a weakly electric fish. Despite having similar amounts of synchronous activity, only in one population of neurons did synchronous spikes carry specific information about the stimulus. A detailed spectral analysis reveals that too low levels of intrinsic noise paired with too little frequency locking of the neural oscillator destroys a synchrony code.
Keywords: synchrony, oscillations, population code, electric fish, mutual information
Abstract
Synchronous activity in populations of neurons potentially encodes special stimulus features. Selective readout of either synchronous or asynchronous activity allows formation of two streams of information processing. Theoretical work predicts that such a synchrony code is a fundamental feature of populations of spiking neurons if they operate in specific noise and stimulus regimes. Here we experimentally test the theoretical predictions by quantifying and comparing neuronal response properties in tuberous and ampullary electroreceptor afferents of the weakly electric fish Apteronotus leptorhynchus. These related systems show similar levels of synchronous activity, but only in the more irregularly firing tuberous afferents a synchrony code is established, whereas in the more regularly firing ampullary afferents it is not. The mere existence of synchronous activity is thus not sufficient for a synchrony code. Single-cell features such as the irregularity of spiking and the frequency dependence of the neuron’s transfer function determine whether synchronous spikes possess a distinct meaning for the encoding of time-dependent signals.
Neurons are the inherently noisy computing devices of the brain. Repeated stimulation with identical stimuli evokes similar but not identical neuronal responses (e.g., ref. 1). Noise from internal and external sources induces substantial variability in the number and the timing of fired action potentials (2). Because of the strong nonlinearity of the spiking threshold, neural noise can be beneficial by improving the representation of stimuli in populations of spiking neurons (3–7). Noise reduces the precision with which spikes lock to the stimulus (1). In populations of neurons that share a common input, for example by having overlapping receptive fields, noise as well as population heterogeneity has the advantage to decorrelate the responses (8, 9). That is, only those stimulus features that drive the population strongest could synchronize the response across neurons and thereby signal the presence of a particularly important stimulus.
The role of synchronous activity in the cortex is widely discussed (6, 10–12), e.g., as a possible solution for the binding problem (for review see, e.g., refs. 13 and 14), as a separate information channel to relay visual information from thalamus to visual cortex (15), as a mechanism for gain control in visual cortex (16), or as a code for odor categories in zebrafish olfactory bulb (17).
A synchrony code requires that asynchronously firing populations are synchronized or, vice versa, synchronization is escaped under certain conditions or by specific stimuli. In weakly electric fish, changes in the level of synchronization are considered an important cue for the detection of communication signals on the level of the receptor afferents (18–21) and subsequent processing in hind- and midbrain neurons (22, 23). Middleton et al. (24) demonstrated that reading out population activity of electrosensory neurons with either integrators or coincidence detectors results in two distinct representations of sensory stimuli. Integrators encode low stimulus frequencies, approximately matching frequencies characteristic of prey detection and navigation. Coincidence detectors discard low-frequency information and encode predominantly higher frequencies matching the ones of communication signals (for alternative mechanisms of such information filtering, see ref. 25). In a theoretical study the conditions for such a synchrony code have been analyzed in the limit of low signal amplitudes and exemplified for leaky integrate-and-fire neurons (26). In particular, subtle effects of intrinsic noise on the shape of peaks in the neuron’s response power spectrum have turned out to be crucial for a potential synchrony code.
We experimentally investigate the role of noise in shaping a synchrony code by comparing populations of two closely related subsystems of the electrosensory system of the weakly electric fish Apteronotus leptorhynchus. These animals use an actively generated electric field [the electric organ discharge (EOD)] to detect prey, navigate, and communicate (e.g., refs. 27–29). The tuberous electroreceptors of the active system are tuned to the frequency of their own field (30), and the most prominent type of receptor afferents, the P units, mainly encode amplitude modulations of this carrier (31–33). The second system is the passive or ampullary system that is most sensitive for low-frequency fields like those emitted by muscle activity of, e.g., prey organisms (e.g., refs. 34 and 35). The two electrosensory systems thus offer a unique opportunity to analyze the information filtering in closely related but sufficiently different populations of sensory neurons within the same species.
Our results show that similar levels of synchrony can be observed in both cell types whereas only the P units of the active system show a synchrony code consistent with the theory. To understand this difference we describe and compare characteristics of the spontaneous baseline activity as well as the encoding of dynamic stimuli. The two systems, although related, show distinct differences in various response features. In particular, the level of response variability and the strength of the resonance in the input–output correlation are much higher in the active system. It is exactly the combination of stronger noise in the P units and a more pronounced peak in its cross-spectrum with the stimulus that allows for a separation of information channels, i.e., to establish a synchrony code.
Results
Although the main type of electroreceptor afferents of the active system, the P units, have received much attention (e.g., refs. 18, 31–33, and 36) the response characteristics of the ampullary afferents of South American species of weakly electric fish have not been described in comparable detail (but see refs. 34 and 37). We thus first compare the fundamental properties of the baseline and stimulus-driven activity of both cell types and then analyze the impact of these differences on the information contained in the synchronous activity of populations of such neurons.
Baseline Activity.
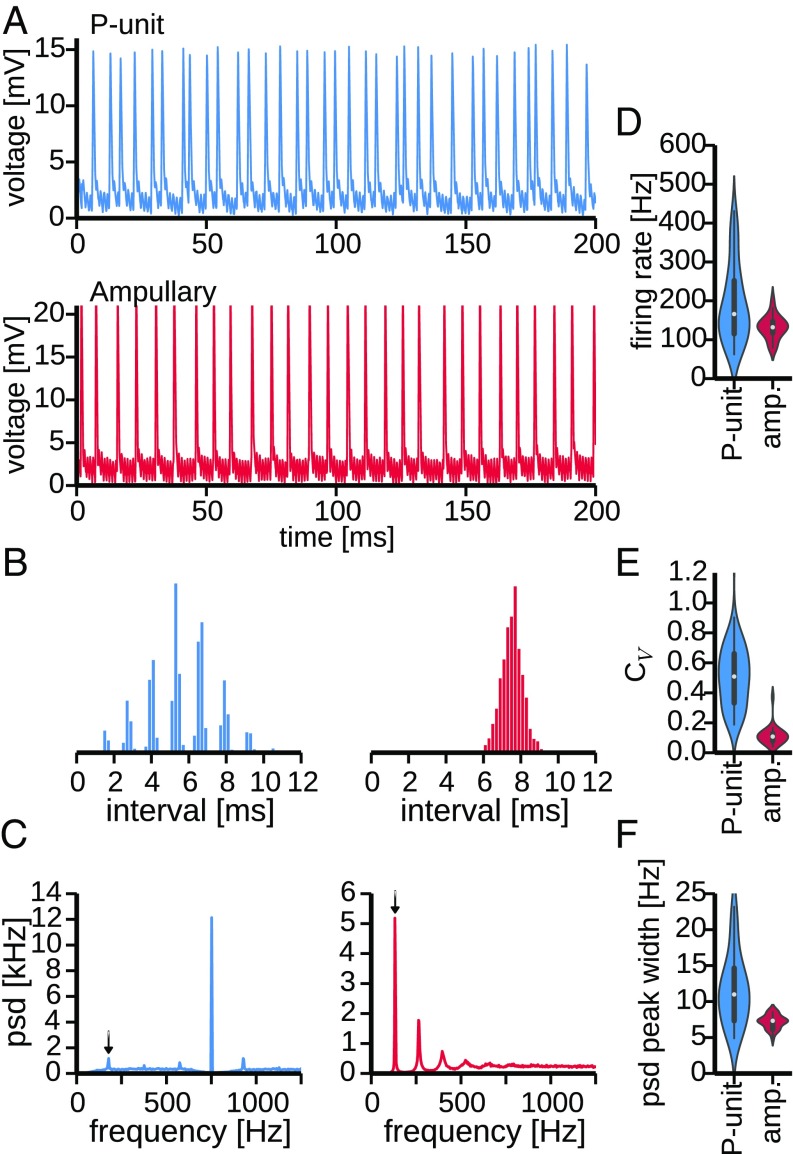
Both types of afferents are spontaneously active in the absence of an external stimulus. P units show an irregular baseline firing pattern whereas the baseline activity of ampullary afferents appears much more regular (Fig. 1A). The response regularity can be quantified by the coefficient of variation () of the interspike intervals . A of zero would indicate perfect regularity with all interspike intervals being equal, and random Poisson firing results in . The baseline activity of the depicted P unit has a broad interspike interval histogram (Fig. 1B, Left) and a coefficient of variation of (average firing rate of Hz), indicating the irregularity of the P unit’s baseline activity. For the regularly firing ampullary afferent, on the other hand, the (average baseline firing rate of Hz) is indeed close to zero, matching the narrow distribution of the interspike intervals (Fig. 1B, Right). Also, the power spectral density (PSD) of the baseline activity of both cell types differs strongly. The P-unit PSD (Fig. 1C, Left) has a peak at the baseline firing rate (arrow). The most prominent peak, however, is at the EOD frequency. This peak is a consequence of spike-time locking to the self-generated electric field, which is also the reason for the multimodal structure of the P-unit interspike-interval histogram. The EOD peak of the power spectrum is symmetrically flanked by peaks resulting from the interaction of the EOD peak and the baseline frequency. The ampullary PSD (Fig. 1C, Right), on the other hand, is dominated by peaks at the baseline firing rate and its harmonics. The strong and narrow peaks are a consequence of the regularity of the baseline firing. A peak at the fish’s EOD frequency is missing because the ampullary afferents are not driven by the EOD.
Fig. 1.
Baseline activity of P-type and ampullary electroreceptor afferents. (A, Top) Intracellular recording of spontaneous activity of a P-type electroreceptor afferent (P unit, cell 2012-03-30-ah) in the absence of an external stimulus. (A, Bottom) Spontaneous activity of an ampullary afferent (cell 2012-03-23-ad). Note that the subthreshold modulations of the membrane potential are a contamination of the recording with the fish’s own EOD. (B) Interspike interval histograms of the example cells shown above. (C) Power spectra of the baseline activity of the P unit (Left) and ampullary afferent (Right) shown above. Arrows indicate the baseline firing rates at Hz and Hz, respectively. Whereas the power spectrum of the P unit is dominated by a peak at the EOD frequency ( Hz), indicating tight locking of P-unit spikes to the fish’s own field, a respective peak is absent in the power spectrum of the ampullary afferent (EOD frequency of Hz). The power spectrum of the ampullary baseline activity, however, is dominated by the sharp peak at the firing rate. (D) Violin plots depicting the distributions of observed firing rates across all recordings of P units and ampullary afferents ( and , respectively). Width of the violin indicates density of the data points. Within the violin an abstraction of a box plot is shown, where the white circle marks the median firing rate. (E) Distributions of the observed coefficients of variation (s) of the interspike intervals across cells. (F) Distributions of the width of PSD peaks at the firing rates observed in all cells.
Differences in Population Heterogeneity.
On the population level, across all cells recorded in this study, the baseline characteristics discussed above vary to different degrees for P units () and ampullary afferents () (Fig. 1 D–F).
Whereas the medians of the observed baseline firing rates do not differ significantly (Mann–Whitney U test, ), the population heterogeneity is significantly larger in P units than in ampullary afferents (Fig. 1D, , Levene test centered on the median). P-unit firing rates are very heterogeneous; their firing rates vary from about 50 Hz to more than 450 Hz ( Hz, mean SD), similar to previously reported values (38). Ampullary afferents, on the contrary, are more homogeneous with firing rates ranging from 80 Hz to 200 Hz ( Hz, mean SD).
The s of the interspike intervals of P units are significantly higher than the ones of ampullary afferents (, Mann–Whitney U test), confirming their generally more irregular firing pattern. In addition, the P-unit population is also more heterogeneous regarding the irregularity of their baseline activity. P-unit s range from 0.33 to 0.66 whereas s of ampullary afferents are more homogeneous with values ranging from 0.08 to 0.13 (Fig. 1E, variances significantly different, , Levene test centered on median).
Reduced irregularity of the baseline activity of ampullary afferents is reflected in a smaller width of the first peak in the PSD at the baseline firing rate (arrows in Fig. 1C). On the contrary, in P units the peaks vary a lot and are on average wider than in ampullary afferents because of their more irregular firing pattern (Fig. 1F, significant difference in median , Mann–Whitney U test, Levene test yields a for the differences in variance).
Encoding of Dynamic Stimuli by Ampullary and P-Type Electroreceptor Afferents.
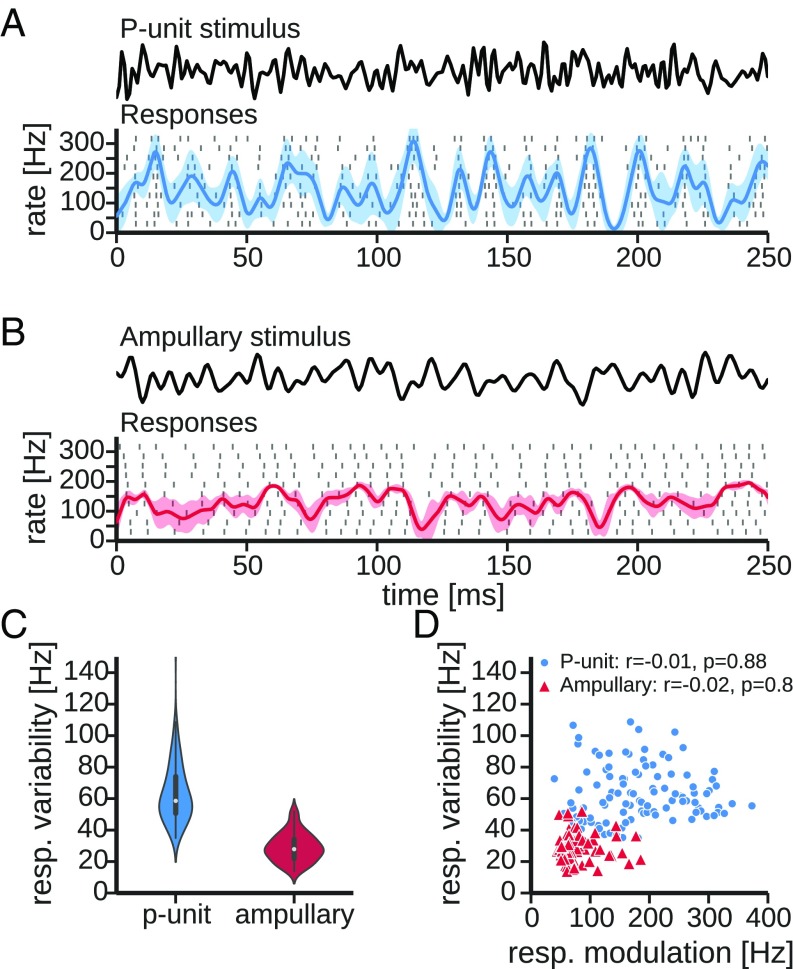
The responses to dynamic stimulation with band-limited Gaussian white noise reflect the differences in the baseline properties shown above. The cutoff frequencies of the stimuli were adjusted to cover the full coding range of the cells ( Hz and Hz for P-type and ampullary electroreceptor afferents, respectively, Fig. 2 A and B).
Fig. 2.
Encoding of dynamic stimuli in electroreceptor afferents. (A) Responses of an example P unit (cell 2010-12-07-ad, selected for the similar average firing rate). Cutoff frequency of the stimulus was at Hz, and its SD was calibrated to of the EOD amplitude. In the rasterplot each dash marks the occurrence of a spike in 10 consecutive trials (rows). Superimposed on the spike raster is the average peri-stimulus time histogram (PSTH) (solid line) and its SD (shaded area). The PSTH was estimated by convolving the spike trains with a Gaussian kernel ( ms). (B) Same as A but of an ampullary electroreceptor afferent (cell 2012-03-23-ad, same as in Fig. 1) to a band-limited white noise stimulus (Upper, cutoff at Hz). SD of the stimulus was calibrated to of the EOD amplitude. (C) Distributions of the response variability in P-type and ampullary electroreceptor afferents. Variability was estimated as the time-averaged across-trial SD of the PSTH (Eq. 5). P units show a significantly higher degree of response variability than ampullary afferents (, t test). (D) Same data as in C but the response variability is plotted as a function of the response modulation (i.e., the modulation of the PSTH, Eq. 4, a proxy of the effective stimulus intensity) for P-type (circles) and ampullary electroreceptor afferents (triangles). Correlation between the response variability and the response modulation is estimated using Pearson’s r and given in the key. The response variability is uncorrelated with response modulation. resp, response variability.
The example P unit shown in Fig. 2A has a mean firing rate of Hz and encodes the stimulus intensity with changes of its firing rate around the mean firing rate. The time-dependent firing rate was estimated by convolution with a Gaussian kernel ( ms, Eq. 3) and is referred to as the peri-stimulus time histogram (PSTH), from here on. The depth of the PSTH modulation is quantified by the response modulation (Eq. 4, i.e., SD of the PSTH over time). In this particular recording the response modulation is Hz. The ampullary afferent shown in Fig. 2B also follows the temporal pattern of the stimulus by modulating its firing rate around an average rate that is in the same range ( Hz). The response modulation is weaker ( Hz) in this example recording.
Different response modulations result from different stimulus intensities, different sensitivities of the cells, and in particular different positions and orientations of the cells relative to the stimulus (Fig. S1). For the following analysis and the comparison with predictions from theory it is, however, only relevant how strongly a cell was effectively driven by the stimulus. In the following we therefore use the response modulations as a proxy of the effective stimulus intensity.
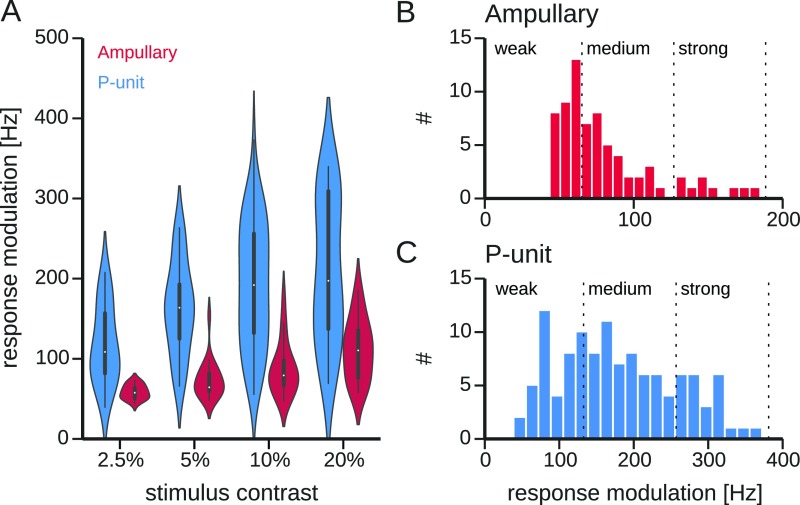
Fig. S1.
Relation of response modulation and stimulus contrast. (A) Neuronal responses of ampullary and P-unit electroreceptors were evoked by stimuli of four different contrasts, i.e., standard deviations of the random AM stimuli relative to the EOD amplitude measured by the local electrode. Violin plots show the distributions of the resulting response modulations for the different stimulus contrasts for both cell types. The response modulation, Eq. 4, is the SD of the PSTH over time. High modulations indicate a high gain with which the cell responds to the stimulus. Within the violins, a boxplot indicates median, interquartile range, and 10% and 90% percentiles. (B and C) Distributions of observed response modulations for ampullary electroreceptor afferents and P units, respectively. The full range of response modulations is divided into three categories (weak, medium, and strong responses, vertical dashed lines). Because many cells were stimulated with stimuli of different contrasts, individual cells can contribute to more than one category.
The properties of the baseline activity (Fig. 1) suggest that P-unit responses are more variable than those of ampullary afferents. The response variability (Eq. 5, i.e., SD of the PSTH over trials) illustrated as the shaded band in the PSTH in the single-cell examples (Fig. 2 A and B) suggests that the same mechanisms that cause high baseline variability in P units also affect the encoding of dynamic stimuli. In the whole population of recorded cells the P units indeed show a higher response variability than the ampullary afferents ( Hz and Hz, mean SD, , t test, Fig. 2C).
For both cell types response variability is independent of response modulation, i.e., effective stimulus intensity [Fig. 2D, Pearson’s () and (), for P-type and ampullary electroreceptor afferents, respectively]. There is very little overlap of the distributions of response variabilities even for ranges of the response modulation that are covered by both cell types (below ∼ Hz).
Thus far, we have described two populations of sensory afferents within the same sensory system in the same species that exhibit distinct differences in their response variability. In the following paragraphs we analyze how these differences affect the efficiency of a synchrony code for both populations.
Synchrony Code.
First, the synchrony code of P units (24) is reviewed in light of theoretical predictions (26), in particular its dependence on stimulus amplitude. Further, the comparison with the ampullary afferents with their less variable spike activity allows us to assess the impact of noise and other cellular properties on the efficiency or the existence of a synchrony code. The stimulus–response coherence (Eq. 8, Materials and Methods) is used to quantify how well the stimulus is represented in the responses. The coherence is a spectral measure that quantifies the (linear) correlation between stimulus and response in a frequency-resolved way. A coherence of 1 indicates a perfect linear correlation. If there is no such linear correlation, the coherence assumes values close to zero.
How presynaptic spike activity is read out potentially affects the stimulus–response coherence. Integrating all spikes (all-spike responses) yields a stronger representation of low-frequency information whereas selectively reading out synchronous spikes (synchronous responses) shifts the best frequency, the position of the coherence peak, to higher frequencies and discards low-frequency information (24).
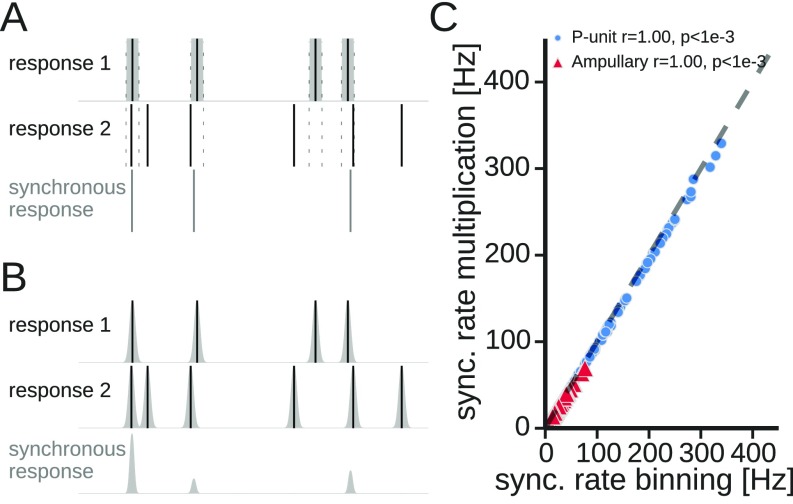
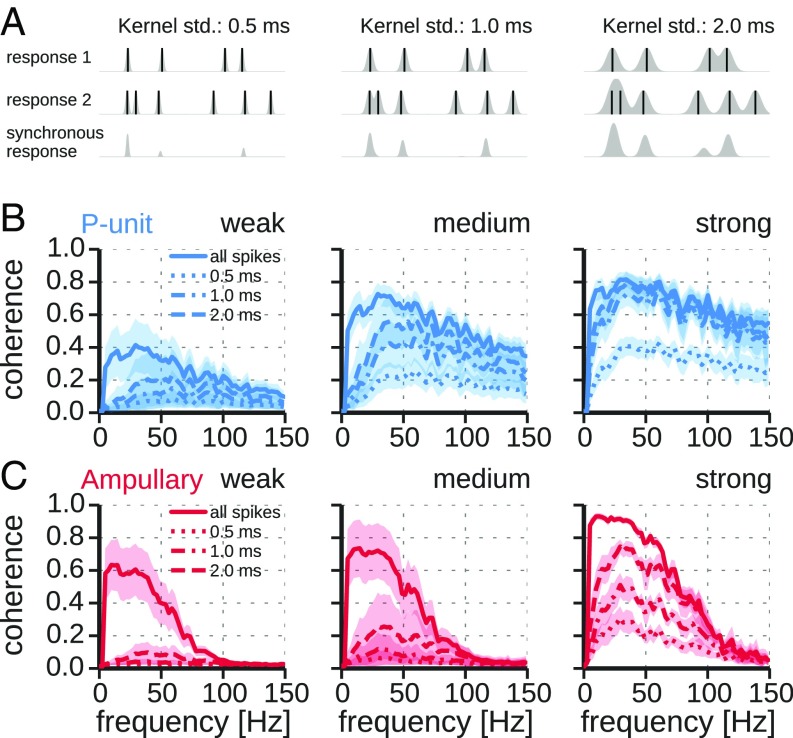
Previous studies used a “binning method” to estimate the synchronous responses (Fig. S2A). Here, synchronous responses were computed by a convolution of the individual spike trains with Gaussian kernels of different widths and subsequent multiplication of the responses (26) (Fig. 3A).
Fig. S2.
Computation of the synchronous response of pairs of responses. (A) Binning method: The spikes of response 1 (solid vertical lines indicate the occurrence of each spike) were convolved with a box kernel. If a spike of response 2 fell into the box of the first response, a spike in the synchronous response (bottom trace) was noted between the spikes of response 1 and response 2. (B) Multiplication method: Spikes of both responses were convolved with Gaussian kernels. The synchronous response is obtained by multiplying both responses. (C) Comparison of the mean synchronous response (comparable to the average rate of synchronous spikes) estimated with both methods. Data show results from both types of electroreceptors analyzed in this study. Dashed line is the bisecting line. “r” values in the key represent Pearson’s correlation coefficient. sync, synchronous.
Fig. 3.
Stimulus–response coherence for synchronous responses vs. all-spike responses in dependence on response amplitude. (A) Calculation of the synchronous response. Spike trains of pairs of responses were combined by replacing spike events (solid vertical lines) with Gaussian kernels (gray shaded). The responses were then multiplied to yield the synchronous response. Kernels with standard deviations of ms were used. For illustrative purposes kernels are scaled to their maximum in the plot. See Materials and Methods for details and Eqs. 1 and 7 for normalization of kernels. (B) Coherence spectra of P-unit responses computed from all-spike response (solid line) and synchronous response (dashed lines), using three different window sizes defining synchrony for the multiplication method as indicated. Plotted are average coherences SD for the three categories of weak, medium, and strong response modulations (compare Fig. S1). Note the elimination of low-frequency coding of synchronous spikes for weak stimuli. (C) Same as B but for responses of ampullary afferents. std, standard deviations.
Synchrony Code in P Units Is Strongest for Weak Stimuli.
For weak response modulations the shape of the stimulus–response coherences of synchronous responses qualitatively differs from the ones of all-spike responses in P units (Fig. 3B, Left). Confirming previous results (24), low-frequency information is suppressed in synchronous spikes, leading to a shift of the peak of the coherence to higher frequencies—a synchrony code is established.
However, for stronger responses, i.e., higher response modulations, the coherence of synchronous responses becomes more and more similar to the coherence of all-spike responses (Fig. 3B, Center and Right). The peak of the coherence of synchronous responses shifts to lower frequencies—the synchrony code vanishes, as predicted by Sharafi et al. (26). This is supported by a negative correlation between the position of the coherence peak and the response modulation (Fig. 4A, solid circles). In each category of response modulations we observe that the width of the synchrony window (Materials and Methods), i.e., the strictness of the synchrony detector, affects the amplitude of the coherence spectra. The coherence amplitude is reduced with smaller synchrony windows. At medium and especially at weak response modulations a stronger shifting effect can be observed with smaller synchrony windows (Fig. 3B).
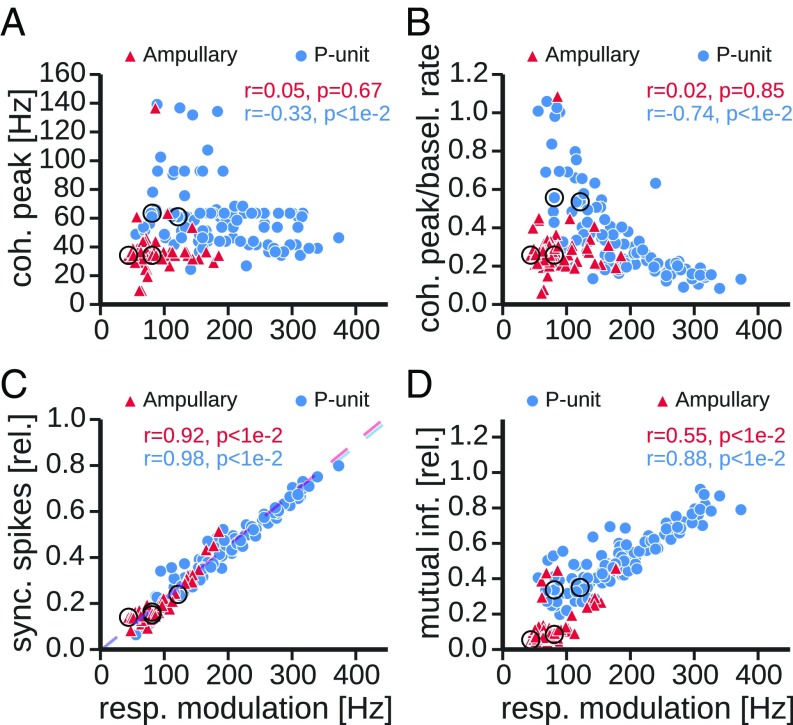
Fig. 4.
Properties of synchrony codes. Scatter plots compare properties of the coherence of synchronous spikes between ampullary (solid triangles) and P-type electroreceptor afferents (solid circles) as a function of response modulation, i.e., effective stimulus intensity. As a synchrony criterion a window of 1-ms width was used. Key in each plot indicates corresponding Pearson’s correlation coefficient and significance of the correlation. Larger circles mark the example cells shown in Fig. 5. (A) Position of the peak of the coherence of synchronous spikes. (B) Same data as in A, but the peak position of the coherence spectrum was normalized to the baseline rate of the respective cell. (C) The firing rate of synchronous spikes relative to the average firing rate during stimulation. Dashed lines are linear regressions for the two types of electroreceptor afferents. (D) Mutual information between stimulus and synchronous spikes relative to the mutual information of all-spikes responses. A lower bound of mutual information was estimated from the coherence spectra according to Eq. 10 in the frequency range from 0 Hz to 150 Hz. basel, baeline; coh, coherence; inf, information; rel, relative; resp, response; sync, synchronous.
Theoretical work predicts that the peak of the synchronous response coherence should shift toward the baseline firing frequency in the limit of weak stimuli (26). Normalizing the peak position of the coherence to the baseline firing rate shows that in P units the coherence peak indeed moves toward the baseline firing rate for weak response modulations, in accordance with the expectation (note the strong negative correlation between normalized position of coherence peak and the response modulation, Fig. 4B, solid circles).
No Synchrony Code in Ampullary Afferents Despite Similar Synchronous Activity.
In ampullary electroreceptor afferents the position of the peak of the synchronous response coherence is only slightly shifted to higher frequencies in comparison with the all-spike response coherence (Fig. 4A, solid triangles). This shift does not depend on response modulation and peak positions are far from the baseline firing rate (Fig. 4B). No synchrony code is established in ampullary afferents. In contrast to what is observed in P units, increasing the temporal precision of the synchrony estimation scales the coherence functions down, but does not affect the position of the peak.
This absence of a synchrony code cannot be explained by differences in the firing rates of the synchronous responses. For low response modulations, where we expect P units to show a synchrony code, the fraction of synchronous spikes is exactly the same for P units and ampullary afferents (Fig. 4C).
Although ampullary responses compared with P-unit responses have the same amount of synchronous spikes, synchronous spikes in ampullary afferents do not carry specific information.
Synchronous Response in Ampullary Afferents Carries Less Information.
Extracting the synchronous spikes from ampullary responses leads to a more pronounced drop in stimulus–response coherence than observed for P units (Fig. 3). Accordingly, the amount of information contained in the synchronous responses is much more reduced in ampullary than in P-type electroreceptor afferents (lower-bound estimation of the mutual information according to Eq. 10). Synchronous spikes of ampullary afferents contain only 12% (median, 9% and 19% lower and upper quartiles) of the information contained in the all-spikes response. On the other hand, synchronous responses of P units carry a significantly larger proportion (median 73%, 58% and 86% lower and upper quartiles, , Mann–Whitney U test) of the all-spikes information (Fig. 4D), despite similar fractions of synchronous spikes (Fig. 4C). In both cell types there is a positive correlation between the relative mutual information and the response modulation. The stronger the cell is driven, the less pronounced is the attenuation of the low-frequency coherence (Fig. 3 B and C, Right) and the coherence peak is less shifted (Fig. 4B). Thus, the spectra become more similar and hence synchronous and all-spike responses carry increasingly similar information.
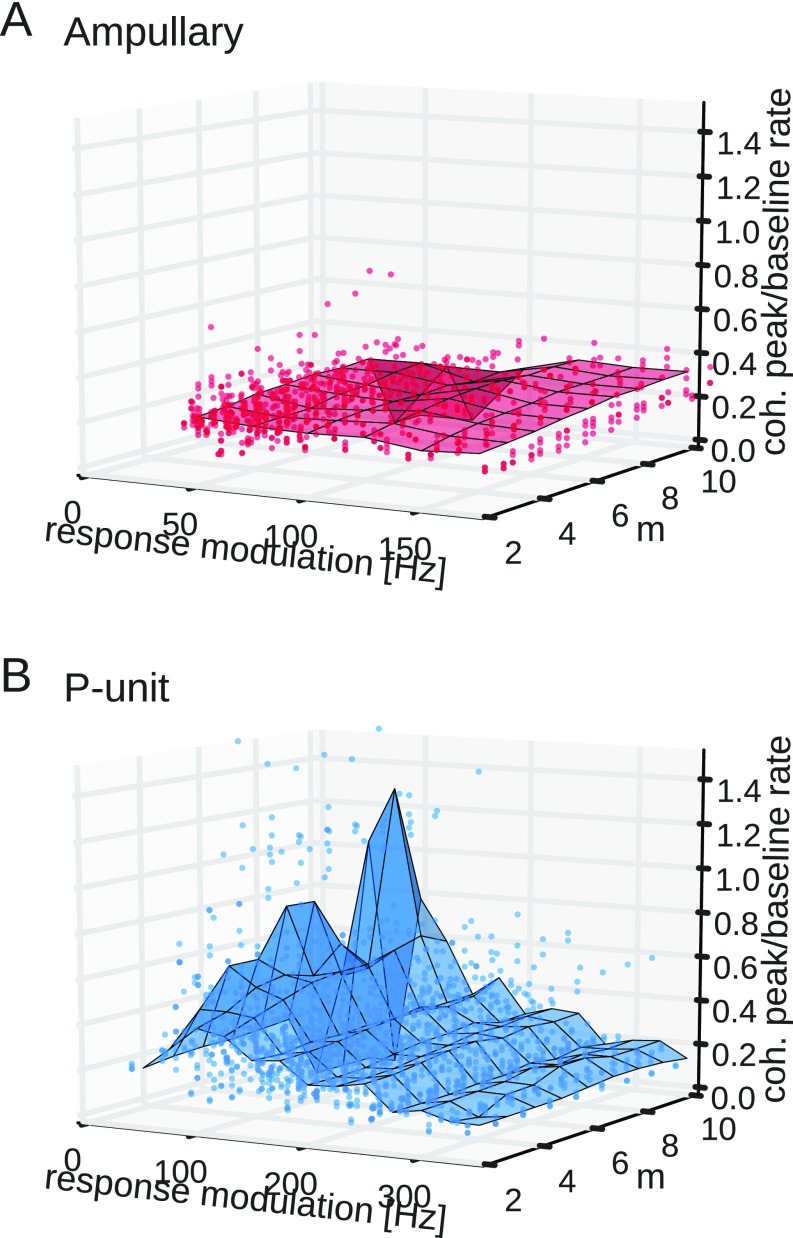
The results shown above are based on the comparison of pairs of responses but are also valid for larger populations in which spikes in m of n trials have to be synchronous (39) (Fig. S3).
Fig. S3.
Synchrony code in homogeneous populations of 10 neurons. Shown is the position of the coherence peak of synchronous spikes relative to baseline rate as a function of response modulation and number of simultaneously synchronous spikes. The peak of the stimulus–response coherence was estimated from synchronous responses where spikes from of 10 trials were required to occur simultaneously within 2 ms (Materials and Methods). The position of the coherence peak was then normalized to the baseline firing rate. Solid circles show data points for each cell, which is an average over 50 artificial populations constructed by randomly selecting 10 trials. The surface plot shows the average value in 25-Hz bins of the response modulation. (A) Independent of response modulation and number of synchronous spikes the coherence peak of ampullary afferents is only slightly shifted toward the baseline firing rate. (B) In P-unit electroreceptors a stronger synchrony criterion (higher ) results in a stronger shift of the coherence peak toward the baseline firing rate. Similar to the case of synchronous spikes in two trials (Fig. S4B) the synchrony code is more pronounced at lower response modulations. coh, coherence.
Discussion
We experimentally reproduced the previously described information filtering of synchrony detection in P-type electroreceptor afferents (24) and analyzed the preconditions of such a synchrony code in more detail. In particular, we verified the predicted dependence of a synchrony code on effective stimulus amplitude (26) and studied the influence of cellular properties, such as neural response variability, on synchrony codes by comparing our findings on P units to a related population of sensory interneurons, the ampullary afferents that exhibit less variable responses. Although they have the same fraction of synchronous spikes as the P units, the synchronous spikes in ampullary afferents do not encode different aspects of the stimulus in comparison with the information carried by all spikes.
Why P Units Allow for a Synchrony Code and Ampullary Afferents Do Not.
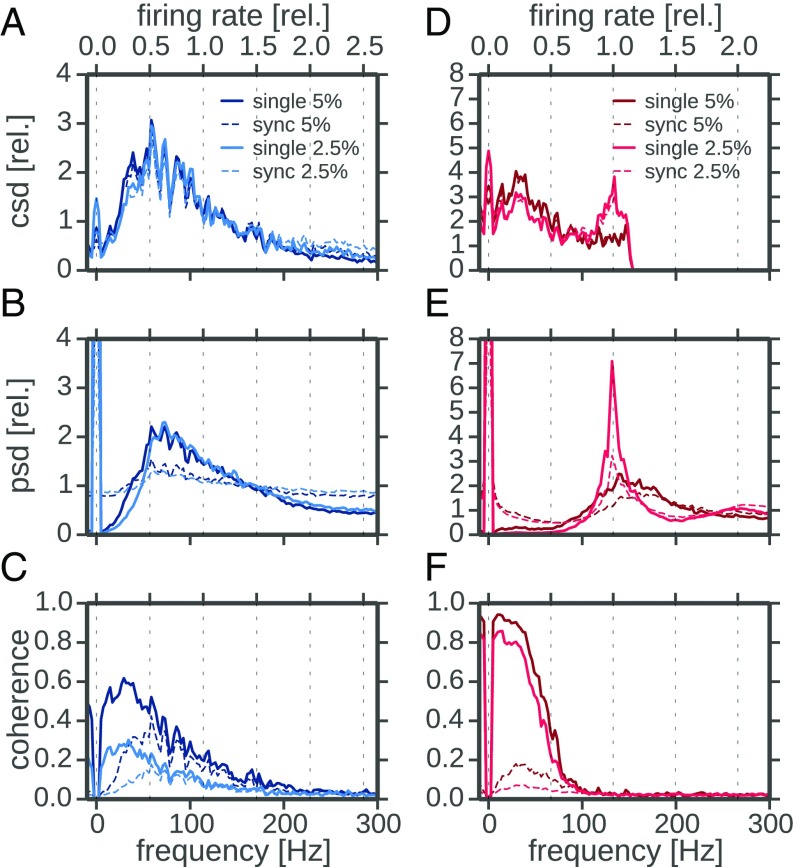
The differential effect of synchrony detection in P units and ampullary afferents can be qualitatively understood by comparing the relevant spectra. The stimulus–response coherence (Eq. 8) is essentially determined by the ratio of squared stimulus–response cross-spectrum and response power spectrum (the white stimulus does not contribute to the frequency dependence of the coherence). For two sample cells stimulated at two different levels (2.5% and 5% contrast, lighter and darker lines, respectively) we show the respective spectra for the single spike train (solid line, qualitatively similar to the all-spikes statistics shown above) and the synchronous output (dashed lines) in Fig. 5.
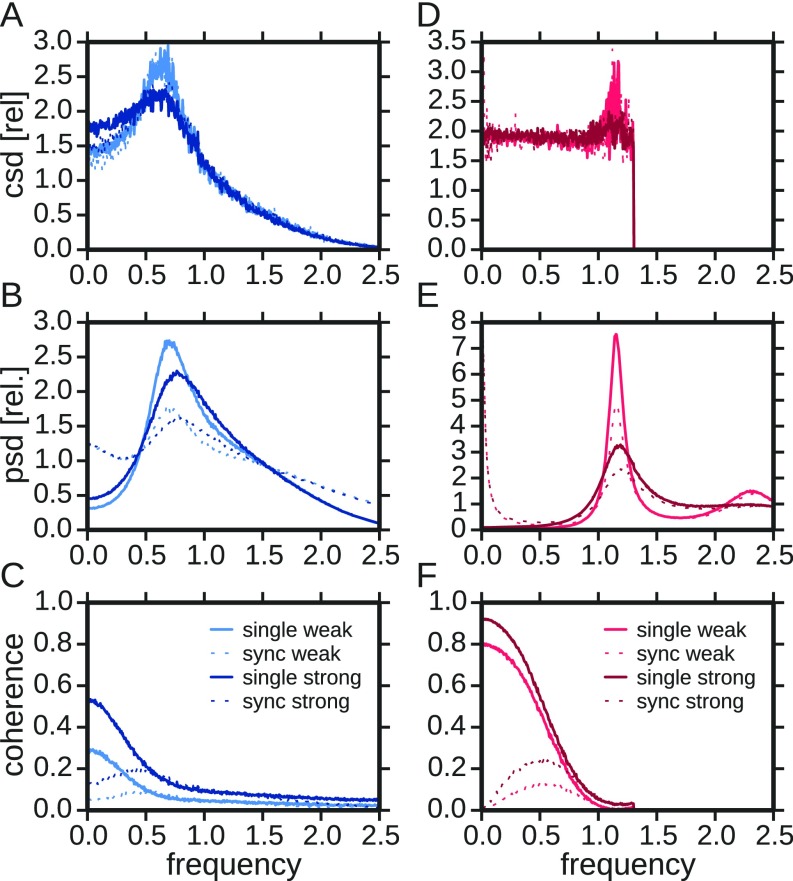
Fig. 5.
Comparison of response spectra of P-type and ampullary afferents. (A–C) Cross-, power, and coherence spectra of an example P unit (2012-03-23-ae). In each panel the respective spectra of the single trials (solid lines) and the synchronous responses (dashed lines) at two different stimulus intensities (contrast; Materials and Methods) are depicted. All spectra were calculated from response segments of 8,192 points (∼0.41 s) width with 50% overlap. Hanning windows were applied to each segment. Segments were not detrended, leading to the large 0-Hz power. Cross- and power spectra are normalized to their average in the frequency range from 10 Hz to 150 Hz for easier comparison of the shape. The second frequency axis on top is scaled according to the baseline firing rate. (D–F) Same analysis for an example ampullary afferent (2012-03-23-ad). Cells were selected to allow for a comparison at the same two stimulus intensities. csd, cross-spectral densities; psd, power-spectral densities; rel, relative.
The cross-spectra (Fig. 5 A and D) relate stimulus and response and, because of the white spectrum of the stimulus, are proportional to the transfer function. As expected from theory (26, 39), the cross-spectra are similar for the synchronous response and the single-trial response (dashed and solid lines in Fig. 5 A and D agree apart from a scaling factor). In P units they reveal a broad but pronounced peak at a frequency that is about 60% of the firing rate. This is typical for a leaky integrator cell in a mean-driven mode that is subject to a moderate amount of intrinsic noise (40, 41). The ampullary afferent on the contrary has a small peak (for small stimulus intensity) or no peak at all (for the larger stimulus intensity)—the latter behavior can be expected for a perfectly integrating cell (3, 41). The form of the small and narrow peak, however, suggests that this cell is subject to less intrinsic noise than the P unit, which is in line with the baseline activity discussed above. The differences in the cross-spectra of P units and ampullary afferents are a consequence of the level of intrinsic noise and the leakiness of the respective cell.
Turning to the power spectra, we first note that the spectra of the synchronous spikes (dashed lines in Fig. 5) differ from those of the single trials (solid lines in Fig. 5). The synchronous spikes can be approximated by multiplying the single spike trains (Fig. S2). According to the convolution theorem this multiplication translates into a convolution of the single-trial power spectrum (including its DC peak) with itself. Such a convolution flattens the power spectrum, especially when the original spectrum has a sufficiently broad peak (26). Because the single spike train power spectrum of the ampullary afferent is narrowly peaked (in particular for the lower stimulus level), this flattening is not pronounced. In contrast, the synchronous power spectrum of the P unit exhibits a rather flat shape because of the comparatively broad peak in the single spike train spectrum.
Dividing a peaked function (the squared stimulus-synchrony cross-spectrum of P units) by a flat function (the synchronous output power spectrum of P units) yields a likewise peaked function. If the power spectrum is flat, the coherence simply inherits the peak from the squared cross-spectrum. Depending on the specific level of intrinsic noise and on other biophysical parameters of the neuron, the cross-spectrum peaks in a range of 40–110% of the firing rate, which corresponds to the range of coherence peak frequencies observed in Fig. 4B. For the ampullary afferent the same mechanism cannot work because (i) there is not a pronounced peak in the cross-spectrum in the first place, and (ii) the convolved spectrum (i.e., the synchrony spectrum) is predominantly increased at low frequencies, where the single spike-train power spectrum is exceptionally small. The latter effect leads to a strong overall reduction of synchrony coherence at low frequencies compared with the single spike-train coherence (compare the strong drop from solid to dashed lines in Fig. 5F) and can thus explain the strong reduction of the information rate (Fig. 4D, red symbols).
We have tested whether a similar behavior can be found in leaky integrate-and-fire (LIF) models. By adapting the level of intrinsic noise and the value of an effective leak parameter, we were able to qualitatively reproduce the spectral features seen in the real cells (compare Fig. 5 and Fig. S4). In this picture, the P unit corresponds to an integrate-and-fire neuron with stronger leak current and higher noise level than the ampullary afferent.
Fig. S4.
Spectral analysis of model neuron. (A–C) Cross-, power, and coherence spectra of LIF neuron (Eq. S1) with , , and . (D–F) Same analysis for , , and . In each panel the respective spectra of the single trials (solid lines) and the synchronous responses (dotted lines) are shown for two different stimulus intensities (“weak”) and (“strong”). Cross- and power spectra are normalized to their average. Remaining parameters: , and width of box-kernel was chosen, such that the product of baseline firing rate and equals 0.2. Parameters were selected to qualitatively resemble experimental results in Fig. 5 of the main text. csd, cross-spectral densities; psd, power-spectral densities; rel, relative.
These results suggest that the biophysical properties of the respective cell (leak current, channel noise) might be matched to its biological function for encoding specific aspects of time-dependent sensory signals. Ampullary afferents encode low-frequency components of a stimulus in an excellent manner; however, their synchronous spikes neither encode very much nor show a very different frequency preference from the summed output. This suggests that stimulus-driven synchrony is not used in ampullary afferents. For P units the encoding performance of the summed activity of pairs of neurons is less impressive in magnitude but extends over a larger frequency band. Moreover, the higher intrinsic noise level (responsible for the lower overall coherence) permits the P units to use two codes and to encode stimulus components of different frequency bands in the summed activity and in the synchronous spikes, respectively. These effects are strongest in a regime of weak stimuli.
Behavioral Relevance of the Weak Stimulus Regime.
Behavioral observations of communication scenes in weakly electric fish of a closely related species Apteronotus rostratus in the field show that electric fish communicate at the limits of sensation (42): (i) In aggression contexts rivals are assessed and attacks are initiated at animal distances of up to more than m. At such distances the electric field intensities are extremely low (0.1 V) and therefore electroreceptor stimulation is weak. (ii) In courtship contexts the spatial distances between communication partners are low and the signals strong but a mismatch between the signal frequencies and the electroreceptor tuning again leads to weak activation of P-type afferents (20, 42, 43). (iii) During foraging prey items like the crustacean Daphnia are detected by electric signals created through muscle activity (stimulating the ampullary afferents) and the amplitude modulations induced by their resistive properties (stimulating the P units), which are in the 0.2–1 V range (44–47). The weak stimulus regime where a synchrony code is distinct from a simple population code can thus be considered a behaviorally relevant regime in which communication and prey signals need to be encoded and separated from other signals.
Readout of Electrosensory Information in the Weakly Electric Fish.
Electroreceptor afferents project to the electrosensory lateral line lobe (ELL) in the hindbrain of the fish. The P units trifurcate and synapse onto postsynaptic cells in three somatotopically organized maps, the so-called lateral, centro-lateral, and centro-medial segments [LS, CLS, and CMS, respectively (48–51)]. The target cells in the ELL are the pyramidal neurons that constitute an information bottleneck because all electrosensory information passes this stage. The coding properties of these neurons are well investigated (e.g., refs. 8 and 52–56). Across maps the spectral tuning changes from low-pass behavior in the CMS to high-pass behavior in the LS (52, 55, 56). In the context of a synchrony code this suggests that LS pyramidal cells might read out synchronous spikes only and CMS pyramidal cells integrate all their input spikes (24). Readout of synchronous spikes could be achieved by coincidence detection where the summed postsynaptic potentials (PSPs) need to cross a threshold higher than a single PSP (57). This would lead to much lower firing rates in synchrony detectors if they integrate the same number of inputs as a pyramidal cell with lower firing threshold that encodes the information contained in all input spikes (24). In fact, cells in the CMS integrate over a few tens of electroreceptor afferents only, they have small receptive fields, and they have low thresholds. On the other extreme, LS pyramidal neurons integrate over about 30 times more afferents, they receive input from large receptive fields, and they have higher thresholds (51, 58). These evidences suggest that the processing of electrosensory information in the active subsystem is split up into several processing streams, based on reading out different levels of synchrony in the P-unit population, thereby exploiting the specific information carried by synchronous spikes.
The ampullary afferents of the passive system project onto a single map only, the medial segment (MS) of the ELL (48). Little is known about the internal structure and the coding properties of the pyramidal cells in the MS of A. leptorhynchus (for Eigenmannia see ref. 37). Like the maps of the active system, the MS shows a somatotopic arrangement, rendering it unlikely that there are subpopulations of pyramidal cells that show distinct differences regarding their frequency tuning. This result would match our finding that ampullary responses do not allow the extraction of distinct information from synchronous spikes.
Low- and High-Noise Afferents in the Vestibular System.
Two anatomically distinct subpopulations of vestibular afferents in primates show characteristics that qualitatively match the properties of ampullary and P-type electroreceptor afferents. Both subpopulations show a spontaneous baseline activity that is very regular in the one and irregular in the other subpopulation. It has been concluded that the regularly firing afferents encode self-motion using a time code whereas the irregularly firing afferents use a rate code (59). We suggest that the high irregularity allows for a combined rate and time code when synchronous events in populations of afferents are taken into account.
Oscillations, Noise, and Synchrony.
Regular neuronal firing with precise locking of spike times to a driving oscillation is observed in various systems, for example, locking to pure tones in the auditory system (60, 61) and internal oscillations in electroreceptors (62) or cold receptors (63). If the periodic drive results from internal oscillations, the coding performance at this frequency is reduced (3). Accordingly, the ampullary afferents of the paddlefish show a dip in the stimulus–response coherence at this frequency (62).
The ampullary afferents recorded here have a very regular baseline firing generated by a limit-cycle oscillation (Fig. 1). Thus, the power spectrum of the response to white-noise stimuli shows a strong peak at the baseline firing rate, if the system is driven in the weak-stimulus regime (Fig. 5E). Ampullary receptor afferents need to encode low-amplitude and low-frequency signals of prey items as reliably as possible (46, 62, 64, 65). Accordingly, across species, ampullary afferents show a clear tuning to low stimulus frequencies (e.g., refs. 35, 62, and 66–68) (Fig. 3C). Because there is no need to encode stimulus frequencies beyond the firing rate, a reduced intrinsic noise level and thus a minimum response variability are beneficial.
In P units, on the other hand, the frequency range of behaviorally relevant signals is much wider. During foraging and navigation low-frequency signals dominate (e.g., refs. 29, 46, and 69) whereas in communication contexts relevant frequencies extend up to about 400 Hz (e.g., refs. 20, 42, and 43). The P-unit system must cover a much broader frequency range that exceeds the baseline firing rate. In this case, intrinsic noise improves encoding of the stimulus by escaping the entrainment of the limit-cycle oscillation (3). Indeed, P-unit responses are much more variable than the ones of ampullary afferents (Fig. 1). Such higher noise levels smear out the peak at the firing rate in the response power spectrum and as a result the stimulus–response coherence is not reduced at the firing rate (Fig. 5). The information provided by ampullary and P-type electroreceptor afferents was concluded to contribute equally to the multimodal task of prey detection (46, 64). Increased levels of noise in P units may be compensated for by the larger number of P-type electroreceptors and the integration over large receptive fields (51, 64, 70).
In addition to the limit-cycle oscillation, P units are strongly driven by the oscillating self-generated electric field, the EOD (Fig. 1C). The P-unit spikes lock to the EOD, but the intrinsic noise induces stochastic skipping of EOD cycles and in this way enables encoding of small changes in EOD amplitude (71). Stochastic skipping is also known from auditory nerve fibers (e.g., refs. 60 and 72) and cold receptors (63, 73, 74) and relies on the right amount of intrinsic noise (75). This similarity with P units suggests that in these systems a synchrony code is also possible. In cold receptors, however, temperature modulations change the frequency of the driving oscillation and thereby change the timescale on which synchronous spikes could be read out (63, 73, 74). In the auditory system, on the other hand, where auditory nerve fibers encode amplitude modulations in similar ways to P units, a synchrony code might indeed be exploited by neurons in the cochlear nucleus.
Conclusions.
The active and passive electrosensory subsystems of weakly electric fish are closely related but the electroreceptor afferents of the two systems differ in their response variability, population heterogeneity, and encoding properties. This makes them the ideal model system for analyzing the effect of response variability on a synchrony code. Differences in intrinsic noise and leakiness define whether or not a synchrony code is established. Despite similar rates of synchronous activity, information filtering by extracting synchronous spikes does not work in the ampullary afferents of the passive system. Thus, the presence of synchronous spikes is necessary but not sufficient to establish a synchrony code.
Materials and Methods
This study includes data from in vivo recordings of P units and ampullary electroreceptor afferents gathered from 44 individuals of A. leptorhynchus of either sex. Fish were obtained from a commercial fish dealer (Aquarium Glaser) and were kept in colonies of up to 20 individuals. Animals were kept in a 12-h:12-h day:night cycle, water temperatures were 26 °C to 27 °C, and water conductivity was adjusted to 180 Scm−1 to 200 Scm−1. All experimental protocols complied with national and European law and were approved by the Ethics Committees of the Ludwig-Maximilians Universität München (permit no. 55.2-1-54-2531-135-09) and the Eberhard-Karls Unversität Tübingen (permit no. ZP 1/13).
Surgery.
Before surgery animals were anesthetized by submerging them into tank water containing 150 mgL−1 MS 222 (PharmaQ) until gill movement ceased. Animals were then respirated with a constant flow of tank water provided through a piece of tubing introduced into their mouths. Respiration water contained 150 mgL−1 MS 222 to ensure anesthesia. Those parts of the skin that were to be cut were locally anesthetized by cutaneous application of liquid lidocaine hydrochloride (20 mg/ml, bela-pharm GmbH). A plastic rod was glued to the exposed bone of the skull for fixating the head. Dorsal to the operculum the lateral line nerve was exposed. After surgery fish were immobilized by intramuscular injection of from 25 L to 50 L of tubocurarine (5 mgmL−1dissolved in fish saline; Sigma-Aldrich). Respiration was then switched to normal tank water and the fish was transferred to the experimental tank. Water temperature in the experimental tank was adjusted to 26 °C. During the experimental session local anesthesia was renewed about every 2 h by carefully applying lidocaine to the skin surrounding the wounds.
Recording.
Intracellular recordings of electroreceptor afferents were done using sharp glass electrodes pulled on a P97 puller (Sutter Instruments). Electrodes had resistances in the range from 40 M to 80 M when filled with 1 molL−1 KCl. Electrode potentials were amplified (SEC-05 amplifier, operated in bridge mode; npi electronics) and low-pass filtered at 10 kHz and digitized at 20 kHz (NI-PCI 6259; National Instruments). Recordings and stimulation were controlled by the “efish” plugins of RELACS (www.relacs.net).
Measurement of Electric Fields.
The EOD of the fish was recorded in two ways. First, the so-called “global” measurement was obtained by measuring the fish’s head-to-tail EOD, using two carbon rods (8 mm diameter) placed at the head and the tail of the fish. The electrodes were placed iso-potential to the stimulus electrodes so as not to pick up the electrical stimuli applied (see below). The second measurement of the fish’s field was recorded using a dipole of silver wires (spaced at 1 cm) that was oriented perpendicular to the animal’s longitudinal axis and was placed just behind the operculum close to the body of the fish. This “local” measurement contained the fish’s own field as well as the stimulus and is taken as an estimate of the transdermal potential stimulating the electroreceptors. Global as well as local measurements were differentially amplified and bandpass filtered (DPA-2FXM, 3 Hz and 1.5 kHz lower and upper cutoffs, respectively; npi electronics). All signals were digitized at 20 kHz.
Stimulation.
Electroreceptors were stimulated with band-limited white-noise stimuli with upper cutoff frequencies of 300 Hz or 150 Hz for P-type and ampullary afferents, respectively. P units were stimulated with amplitude modulations (AMs) of the fish’s own field: the desired AM waveform was multiplied (MXS-01M; npi electronics) with the global measurement of the fish’s field. Ampullary electroreceptors were stimulated with directly applied electrical stimuli. In both cases, the stimuli were isolated from ground (ISO-02V; npi electronics) and delivered into the recording tank via two carbon rods (30 cm length, 8 mm diameter) that were placed parallel to the longitudinal axis of the fish at a distance of ∼20 cm and fully submerged in the water. Signals were calibrated relative to the local measurement (see above) of the field by proper attenuation (ATN-01M; npi electronics).
Data Analysis.
Spikes were detected online by RELACS, using the peak-detection algorithm proposed by Todd and Andrews (76). Raw data as well as spike times were stored for subsequent offline analysis. Datasets used in this study are publicly available in the open NIX data format (https://github.com/g-node/nix, ref. 77) and are publicly available (dx.doi.org/10.12751/g-node.5b08du). Data were analyzed with custom routines written in C++ and Python, using routines of matplotlib (78), numpy/scipy (79), pandas (80), and seaborn (https://web.stanford.edu/∼mwaskom/software/seaborn) packages.
Basic Spike Train Analysis.
The firing rate as a function of time, , was estimated by convolving spike responses of trial with spikes at times with a Gaussian kernel
| [1] |
with the SD of the kernel that was 0.5 ms if not otherwise stated. The single-trial firing rate then reads
| [2] |
where denotes convolution. The PSTH, , is then calculated by averaging across trials:
| [3] |
Estimating the Response Modulation as a Proxy for Effective Stimulus Amplitude.
In response to dynamic stimuli the firing rate is modulated around an average firing rate that is close to the baseline firing rate of the cell (Fig. 2 A and C). We quantified this response modulation as the SD of the PSTH over time
| [4] |
where denotes averaging over time. is the time average of the PSTH, i.e., the average firing rate.
The response modulation rather than the stimulus intensity quantifies directly the effectiveness of a stimulus to drive a particular cell (e.g., Fig. S1A). For further analyses we therefore use the response modulation as a measure for effective stimulus intensity, because we are interested in the effects a stimulus has on the neuron. Three categories of weak, medium, and strong responses were selected to separate the whole response range (zero to maximum observed response modulation) into equally large ranges irrespective of the number of neurons or trials contributing to each category (Fig. S1 B and C).
Response variability was quantified by the SD of the single-trial firing rates , Eq. 2, across trials averaged over time,
| [5] |
with the PSTH, Eq. 3.
Analysis of Synchronous and All-Spikes Response.
In line with the analyses by Middelton et al. (24) and Sharafi et al. (26), we estimated the all-spikes and synchronous-spikes responses from all pairwise combinations of repeated trials recorded in the same neuron.
The all-spikes responses were estimated by adding pairs of single-trial responses and :
| [6] |
Synchronous-spikes responses were estimated in two ways: (i) From each pair of spike trains one spike train was convolved with a box kernel of a given duration ( ms, ms, ms, ms). Whenever a spike of the second response fell into the box, a spike in the synchronous response was noted at the respective average spike time in responses 1 and 2 (Fig. S2A) (24). (ii) Single-trial responses were computed according to Eq. 2, with the SD of the Gaussian kernels (Eq. 1) matching the SD of the box kernels. Pairs of single-trial responses and were point-wise multiplied to estimate the synchronous response
| [7] |
The synchronous response is zero for times in which the kernels do not overlap and positive in overlapping epochs, indicating synchronous activity (Fig. 3A and Fig. S2B). The normalization factor ensures that perfectly overlapping spikes result in a Gaussian with integral 1 (26).
The mean response amplitudes (comparable to an average firing rate) of both methods were very similar (Fig. S2C) and all further analyses yielded similar results irrespective of the applied measure (not shown). For the rest of this work we show only results from the multiplication method (Fig. S2B).
Spectral Analysis.
To analyze the encoding of electrosensory stimuli in a frequency-resolved manner we computed the stimulus–response coherence (e.g., ref. 81)
| [8] |
between the stimulus and the neural response , i.e., single-trial spike trains or synchronous responses . Power and cross-spectra were defined in terms of the Fourier transform of a time series by the formulas
| [9] |
where ∗ denotes the complex conjugate and indicates averaging across segments. To estimate spectra and to determine the coherence, stimulus and responses were cut into segments of 8,192 data points (0.4096 s) length and a Hanning window of the same length was applied to each segment. Segments had an overlap of . As the response time series the single-trial PSTH was taken (Eq. 2, spike train convolved with a Gaussian kernel, ms).
From the coherence spectra a lower-bound estimate of the mutual information between stimulus and response was performed according to
| [10] |
with the cutoff frequency of the frequency band for which the mutual information is estimated.
Response Modulation
The response modulation rather than the stimulus contrast, its strength relative to the fish’s own field, was taken as a proxy for the stimulus intensity. To which extent a stimulus drives a particular neuron varies strongly. The observed response modulations at different stimulus contrasts strongly overlap (Fig. S1A). For several comparisons the cells were classified according to the response modulation (Fig. S1 B and C).
Detection of Synchronous Spikes
Synchronous spikes were detected by a convolution of the individual spike trains with Gaussian kernels and subsequent multiplication of the responses (26) (Fig. S2B). This approach is different from the one chosen by Middleton et al. (24) (Fig. S2A). Both approaches, however, give similar firing rates in the synchronous responses for both cell types (Fig. S2C).
Existence of Synchrony Code Does Not Depend on Population Size
In addition to the synchronous-spikes response for pairs of spike responses we estimated the synchronous responses for situations in which spikes in of trials have to be synchronous (39). Each spike train of the population is convolved with a box kernel of a certain width (height 1) and the resulting traces are summed. The synchronous response is then estimated by simply thresholding the summed spike trains and normalizing with the width of the box kernel. The selection of the threshold defines how many neurons of the population have to fire in synchrony to evoke a synchronous response. In our analysis we created 50 unique populations of spike trains of each neuron by randomly combining selected trials. For each population we estimated the synchronous response when of 10 neurons were firing synchronously in a time window of width . Chosen values were and ms.
Pyramidal neurons in ELL in the hindbrain receive information from more than two electroreceptor afferents (e.g., ref. 51). In the following analysis we therefore enlarged the population size to by randomly selecting 10 trials recorded in any recorded neuron. For a synchrony criterion we required spikes from of trials to occur simultaneously within a given time window (Materials and Methods). Requiring more spikes to be synchronous makes the synchrony criterion harder. Only if the stimulus is potent enough to drive the population sufficiently strong, is a synchronous event observed. Hence, the firing rate of the synchronous response of the population drops with increasing . Analogous to the results shown above (Fig. S4B) the position of the peak coherence was estimated relative to the baseline firing frequency. For ampullary cells the required number of synchronous spikes and the response modulation do not have a pronounced effect on the position of the coherence peak; the surface plot is almost flat (Fig. S3A). In P units, however, increasing shifts the best coding frequency (peak of the stimulus–response coherence) closer toward the baseline firing rate, resulting in a stronger synchrony code (Fig. S3B). For weak responses, i.e., weak effective stimuli, the shift is larger than for strong responses, irrespective of the number of required synchronous spikes (compare with Fig. S4B).
Spectral Effects Can Be Explained by Combinations of Leak and Noise in LIF Neurons
To better understand the spectral statistics of ampullary cells and P units (Fig. 5 in main text) and the efficiency of a synchrony code for these cell types, we simulated pairs of LIF neurons obeying the simple voltage dynamics
| [S1] |
complemented by the fire-and-reset rule: Whenever the voltage crosses the threshold , a spike is generated and the voltage is reset to the value . In Eq. S1, is the constant base current, are independent Gaussian white-noise processes with zero mean and correlation function , and is the intrinsic noise intensity. The parameter can be regarded as setting the leak conductance of the membrane. The common stimulus is modeled by broadband Gaussian white noise with cutoff frequency and noise intensity ; i.e., its power spectrum is given by for (and is zero for ).
Fig. S4 shows that we can find parameters such that the spectra of the simulated model neurons look similar to the ones of the example cells presented in Fig. 5 (main text). This similarity is achieved by changing only two parameters: The leak parameter and the intrinsic noise intensity turn out to be the key parameters to mimic the different spectral statistics of the P units and ampullary cells. An ampullary-cell–like behavior is obtained for low intrinsic noise intensity and a small leak term, resulting in a low coefficient of variation and a comparatively flat cross-spectrum (Fig. S4 D–F: ). Dynamics similar to those observed in P units are obtained by setting the intrinsic noise and leak to higher values, leading to a higher CV and a peaked cross-spectrum (Fig. S4 A–C: ).
Acknowledgments
We thank Henriette Walz and Franziska Kümpfbeck for recording parts of the data. J.B. and J.G. were funded through Bundesministerium für Bildung und Forschung (BMBF) Grant 01GQ0802 (to J.B.). A.K. and B.L. are funded through Deutsche Forschungsgemeinschaft Grant LI 1046/2-1 and BMBF Grant 01GQ1001A.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1615561114/-/DCSupplemental.
References
- 1.Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science. 1995;268(5216):1503–1506. doi: 10.1126/science.7770778. [DOI] [PubMed] [Google Scholar]
- 2.Faisal AA, Selen L, Wolpert D. Noise in the nervous system. Nature. 2008;9:292–302. doi: 10.1038/nrn2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Knight BW. Dynamics of encoding in a population of neurons. J Gen Physiol. 1972;59(6):734–766. doi: 10.1085/jgp.59.6.734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wiesenfeld K, Moss F. Stochastic resonance and the benefits of noise: From ice ages to crayfish and squids. Nature. 1995;373:33–36. doi: 10.1038/373033a0. [DOI] [PubMed] [Google Scholar]
- 5.Stocks NG, Mannella R. Generic noise-enhanced coding in neuronal arrays. Phys Rev E. 2001;64(3 Pt 1):030902. doi: 10.1103/PhysRevE.64.030902. [DOI] [PubMed] [Google Scholar]
- 6.Ermentrout GB, Galán RF, Urban NN. Reliability, synchrony and noise. Trends Neurosci. 2008;31(8):428–434. doi: 10.1016/j.tins.2008.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.McDonnell MD, Ward LM. The benefits of noise in neural systems: Bridging theory and experiment. Nat Rev Neurosci. 2011;12(7):415–426. doi: 10.1038/nrn3061. [DOI] [PubMed] [Google Scholar]
- 8.Marsat G, Maler L. Neural heterogeneity and efficient population codes for communication signals. J Neurophysiol. 2010;104(5):2543–2555. doi: 10.1152/jn.00256.2010. [DOI] [PubMed] [Google Scholar]
- 9.Marcoux CM, Clarke SE, Nesse WH, Longtin A, Maler L. Balanced ionotropic receptor dynamics support signal estimation via voltage-dependent membrane noise. J Neurophysiol. 2016;115(1):530–545. doi: 10.1152/jn.00786.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Aertsen A, Diesmann M, Gewaltig MO. Propagation of synchronous spiking activity in feedforward neural networks. J Physiol Paris. 1996;90(3-4):243–247. doi: 10.1016/s0928-4257(97)81432-5. [DOI] [PubMed] [Google Scholar]
- 11.Salinas E, Sejnowski TJ. Correlated neuronal activity and the flow of neural information. Nat Rev Neurosci. 2001;2(8):539–550. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Buzsáki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304(5679):1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- 13.Kreiter AK, Singer W. On the role of neural synchrony in the primate visual cortex. In: Aertsen A, Braitenberg V, editors. Brain Theory - Biological Basis and Computational Principles. Elsevier; Amsterdam: 1996. pp. 201–227. [Google Scholar]
- 14.Shadlen MN, Movshon JA. Synchrony unbound: A critical evaluation of the temporal binding hypothesis. Neuron. 1999;24(1):67–77. doi: 10.1016/s0896-6273(00)80822-3. [DOI] [PubMed] [Google Scholar]
- 15.Dan Y, Alonso JM, Usrey WM, Reid RC. Coding of visual information by precisely correlated spikes in the lateral geniculate nucleus. Nat Neurosci. 1998;1(6):501–507. doi: 10.1038/2217. [DOI] [PubMed] [Google Scholar]
- 16.Tiesinga PHE, Fellous JM, Salinas E, José JV, Sejnowski TJ. Synchronization as a mechanism for attentional gain modulation. Neurocomputing. 2004;58–60:641–646. doi: 10.1016/j.neucom.2004.01.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Friedrich RW, Habermann CJ, Laurent G. Multiplexing using synchrony in the zebrafish olfactory bulb. Nat Neurosci. 2004;7(8):862–871. doi: 10.1038/nn1292. [DOI] [PubMed] [Google Scholar]
- 18.Benda J, Longtin A, Maler L. Spike-frequency adaptation separates transient communication signals from background oscillations. J Neurosci. 2005;25(9):2312–2321. doi: 10.1523/JNEUROSCI.4795-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Benda J, Longtin A, Maler L. A synchronization-desynchronization code for natural communication signals. Neuron. 2006;52(2):347–358. doi: 10.1016/j.neuron.2006.08.008. [DOI] [PubMed] [Google Scholar]
- 20.Walz H, Grewe J, Benda J. Static frequency tuning accounts for changes in neural synchrony evoked by transient communication signals. J Neurophysiol. 2014;112(4):752–765. doi: 10.1152/jn.00576.2013. [DOI] [PubMed] [Google Scholar]
- 21.Stöckl A, Sinz F, Benda J, Grewe J. Encoding of social signals in all three electrosensory pathways of Eigenmannia virescens. J Neurophysiol. 2014;112(9):2076–2091. doi: 10.1152/jn.00116.2014. [DOI] [PubMed] [Google Scholar]
- 22.Marsat G, Proville RD, Maler L. Transient signals trigger synchronous bursts in an identified population of neurons. J Neurophysiol. 2009;102(2):714–723. doi: 10.1152/jn.91366.2008. [DOI] [PubMed] [Google Scholar]
- 23.Vonderschen K, Chacron MJ. Sparse and dense coding of natural stimuli by distinct midbrain neuron subpopulations in weakly electric fish. J Neurophysiol. 2011;106(6):3102–3118. doi: 10.1152/jn.00588.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Middleton JW, Longtin A, Benda J, Maler L. Postsynaptic receptive field size and spike threshold determine encoding of high-frequency information via sensitivity to synchronous presynaptic activity. J Neurophysiol. 2009;101(3):1160–1170. doi: 10.1152/jn.90814.2008. [DOI] [PubMed] [Google Scholar]
- 25.Lindner B. Mechanisms of information filtering in neural systems. IEEE Trans Mol Biol Multi-Scale Commun. 2016;2(1):5–15. [Google Scholar]
- 26.Sharafi N, Benda J, Lindner B. Information filtering by synchronous spikes in a neural population. J Comput Neurosci. 2013;34(2):285–301. doi: 10.1007/s10827-012-0421-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bullock TH, Heiligenberg W. Electroreception. Wiley; New York: 1986. [Google Scholar]
- 28.Benda J, Grewe J, Krahe R. Animal Communication and Noise. Vol 2. Springer; Berlin: 2013. Neural noise in electrocommunication: From burden to benefits; pp. 331–372. [Google Scholar]
- 29.Krahe R, Maler L. Neural maps in the electrosensory system of weakly electric fish. Curr Opin Neurobiol. 2014;24(1):13–21. doi: 10.1016/j.conb.2013.08.013. [DOI] [PubMed] [Google Scholar]
- 30.Hopkins C. Stimulus filtering and electroreception: Tuberous electroreceptors in three species of gymnotoid fish. J Comp Physiol. 1976;111(2):171–207. [Google Scholar]
- 31.Scheich H, Bullock TH, Hamstra R., Jr Coding properties of two classes of afferent nerve fibers: High-frequency electroreceptors in the electric fish, Eigenmannia. J Neurophysiol. 1973;36(1):39–60. doi: 10.1152/jn.1973.36.1.39. [DOI] [PubMed] [Google Scholar]
- 32.Bastian J. Electrolocation. J Comp Physiol. 1981;144(4):465–479. [Google Scholar]
- 33.Kreiman G, Krahe R, Metzner W, Koch C, Gabbiani F. Robustness and variability of neuronal coding by amplitude-sensitive afferents in the weakly electric fish Eigenmannia. J Neurophysiol. 2000;84(1):189–204. doi: 10.1152/jn.2000.84.1.189. [DOI] [PubMed] [Google Scholar]
- 34.Kalmijn AJ. The detection of electric fields from inanimate and animate sources other than electric organs. In: Autrum H, Jung R, Loewenstein WR, MacKay D, Teubner H, editors. Handbook of Sensory Physiology. Springer; Berlin: 1974. pp. 148–200. [Google Scholar]
- 35.Engelmann J, Gertz S, Goulet J, Schuh A, von der Emde G. Coding of stimuli by ampullary afferents in Gnathonemus petersii. J Neurophysiol. 2010;104(4):1955–1968. doi: 10.1152/jn.00503.2009. [DOI] [PubMed] [Google Scholar]
- 36.Chacron MJ, Longtin A, Maler L. Negative interspike interval correlations increase the neuronal capacity for encoding time-dependent stimuli. J Neurosci. 2001;21(14):5328–5343. doi: 10.1523/JNEUROSCI.21-14-05328.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Metzner W, Heiligenberg W. The coding of signals in the electric communication of the gymnotiform fish Eigenmannia: From electroreceptors to neurons in the torus semicircularis of the midbrain. J Comp Physiol A. 1991;169(2):135–150. doi: 10.1007/BF00215861. [DOI] [PubMed] [Google Scholar]
- 38.Gussin D, Benda J, Maler L. Limits of linear rate coding of dynamic stimuli by electroreceptor afferents. J Neurophysiol. 2007;97(4):2917–2929. doi: 10.1152/jn.01243.2006. [DOI] [PubMed] [Google Scholar]
- 39.Kruscha A, Lindner B. Partial synchronous output of a neuronal population under weak common noise: Analytical approaches to the correlation statistics. Phys Rev E. 2016;94:022422. doi: 10.1103/PhysRevE.94.022422. [DOI] [PubMed] [Google Scholar]
- 40.Lindner B, Schimansky-Geier L, Longtin A. Maximizing spike train coherence or incoherence in the leaky integrate-and-fire neuron. Phys Rev E. 2002;66(3 Pt 1):031916. doi: 10.1103/PhysRevE.66.031916. [DOI] [PubMed] [Google Scholar]
- 41.Vilela RD, Lindner B. Comparative study of different integrate-and-fire neurons: Spontaneous activity, dynamical response, and stimulus-induced correlation. Phys Rev E. 2009;80(3 Pt 1):031909. doi: 10.1103/PhysRevE.80.031909. [DOI] [PubMed] [Google Scholar]
- 42.Henninger J. PhD thesis. Universität Tübingen; Tuebingen, Germany: 2015. Social interactions in natural populations of weakly electric fish. [Google Scholar]
- 43.Stamper SA, et al. Species differences in group size and electrosensory interference in weakly electric fishes: Implications for electrosensory processing. Behav Brain Res. 2010;207(2):368–376. doi: 10.1016/j.bbr.2009.10.023. [DOI] [PubMed] [Google Scholar]
- 44.Knudsen E. Behavioral thresholds to electric signals in high frequency electric fish. J Comp Physiol. 1974;91(4):333–353. [Google Scholar]
- 45.Russell DF, Wilkens LA, Moss F. Use of behavioural stochastic resonance by paddle fish for feeding. Nature. 1999;402(6759):291–294. doi: 10.1038/46279. [DOI] [PubMed] [Google Scholar]
- 46.Nelson ME, MacIver MA. Prey capture in the weakly electric fish Apteronotus albifrons: Sensory acquisition strategies and electrosensory consequences. J Exp Biol. 1999;202(Pt 10):1195–1203. doi: 10.1242/jeb.202.10.1195. [DOI] [PubMed] [Google Scholar]
- 47.Jung SN, Longtin A, Maler L. Weak signal amplification and detection by higher-order sensory neurons. J Neurophysiol. 2016;115(4):2158–2175. doi: 10.1152/jn.00811.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Carr CE, Maler L, Sas E. Peripheral organization and central projections of the electrosensory nerves in gymnotiform fish. J Comp Neurol. 1982;211(2):139–153. doi: 10.1002/cne.902110204. [DOI] [PubMed] [Google Scholar]
- 49.Lannoo MJ, Maler L, Tinner B. Ganglion cell arrangement and axonal trajectories in the anterior lateral line nerve of the weakly electric fish Apteronotus leptorhynchus (Gymnotiformes) J Comp Neurol. 1989;280(3):331–342. doi: 10.1002/cne.902800302. [DOI] [PubMed] [Google Scholar]
- 50.Berman N, Maler L. Neural architecture of the electrosensory lateral line lobe: Adaptations for coincidence detection, a sensory searchlight and frequency-dependent adaptive filtering. J Exp Biol. 1999;202(Pt 10):1243–1253. doi: 10.1242/jeb.202.10.1243. [DOI] [PubMed] [Google Scholar]
- 51.Maler L. Receptive field organization across multiple electrosensory maps. I. Columnar organization and estimation of receptive field size. J Comp Neurol. 2009;516(5):376–393. doi: 10.1002/cne.22124. [DOI] [PubMed] [Google Scholar]
- 52.Chacron MJ, Doiron B, Maler L, Longtin A, Bastian J. Non-classical receptive field mediates switch in a sensory neuron’s frequency tuning. Nature. 2003;423(6935):77–81. doi: 10.1038/nature01590. [DOI] [PubMed] [Google Scholar]
- 53.Chacron MJ. Nonlinear information processing in a model sensory system. J Neurophysiol. 2006;95(5):2933–2946. doi: 10.1152/jn.01296.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Oswald AMM, Chacron MJ, Doiron B, Bastian J, Maler L. Parallel processing of sensory input by bursts and isolated spikes. J Neurosci. 2004;24(18):4351–4362. doi: 10.1523/JNEUROSCI.0459-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Krahe R, Bastian J, Chacron MJ. Temporal processing across multiple topographic maps in the electrosensory system. J Neurophysiol. 2008;100(2):852–867. doi: 10.1152/jn.90300.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ellis LD, et al. SK channels provide a novel mechanism for the control of frequency tuning in electrosensory neurons. J Neurosci. 2007;27(35):9491–9502. doi: 10.1523/JNEUROSCI.1106-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Softky W, Koch C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J Neurosci. 1993;13(1):334–350. doi: 10.1523/JNEUROSCI.13-01-00334.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mehaffey WH, Maler L, Turner RW. Intrinsic frequency tuning in ell pyramidal cells varies across electrosensory maps. J Neurophysiol. 2008;99(5):2641–2655. doi: 10.1152/jn.00028.2008. [DOI] [PubMed] [Google Scholar]
- 59.Sadeghi SG, Chacron MJ, Taylor MC, Cullen KE. Neural variability, detection thresholds, and information transmission in the vestibular system. J Neurosci. 2007;27(4):771–781. doi: 10.1523/JNEUROSCI.4690-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Joris P, Smith P. The volley theory and the spherical cell puzzle. Neuroscience. 2008;154(1):65–76. doi: 10.1016/j.neuroscience.2008.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.van Hemmen JL, Longtin A, Vollmayr AN. Testing resonating vector strength: Auditory system, electric fish, and noise. Chaos. 2011;21(4):047508. doi: 10.1063/1.3670512. [DOI] [PubMed] [Google Scholar]
- 62.Neiman AB, Russell DF. Sensory coding in oscillatory electroreceptors of paddlefish. Chaos. 2011;21(4):047505. doi: 10.1063/1.3669494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Longtin A, Hinzer K. Encoding with bursting, subthreshold oscillations, and noise in mammalian cold receptors. Neural Comput. 1996;8(2):21–255. doi: 10.1162/neco.1996.8.2.215. [DOI] [PubMed] [Google Scholar]
- 64.Nelson ME, MacIver MA, Coombs S. Modeling electrosensory and mechanosensory images during the predatory behavior of weakly electric fish. Brain Behav Evol. 2002;59(4):199–210. doi: 10.1159/000064907. [DOI] [PubMed] [Google Scholar]
- 65.Wilkens LA, Hofmann MH. Behavior of animals with passive, low-frequency electrosensory systems. In: Bullock T, Hopkins CD, Popper AN, Fay RR, editors. Electroreception. Springer; New York: 2005. pp. 229–263. [Google Scholar]
- 66.Montgomery J. Frequency response characteristics of primary and secondary neurons in the electrosensory system of the thornback ray. Comp Biochem Physiol A Physiol. 1984;79(1):189–195. [Google Scholar]
- 67.Weille JD. Electrosensory information processing by lateral-line lobe neurons of catfish investigated by means of white noise cross-correlation. Comp Biochem Physiol A Physiol. 1983;74(3):677–680. [Google Scholar]
- 68.Hofmann MH, Chagnaud B, Wilkens LA. Response properties of electrosensory afferent fibers and secondary brain stem neurons in the paddlefish. J Exp Biol. 2005;208(Pt 22):4213–4222. doi: 10.1242/jeb.01896. [DOI] [PubMed] [Google Scholar]
- 69.Fotowat H, Harrison RR, Krahe R. Statistics of the electrosensory input in the freely swimming weakly electric fish Apteronotus leptorhynchus. J Neurosci. 2013;33(34):13758–13772. doi: 10.1523/JNEUROSCI.0998-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Maler L. Receptive field organization across multiple electrosensory maps. II. Computational analysis of the effects of receptive field size on prey localization. J Comp Neurol. 2009;516(5):394–422. doi: 10.1002/cne.22120. [DOI] [PubMed] [Google Scholar]
- 71.Chacron MJ, Longtin A, St-Hilaire M, Maler L. Suprathreshold stochastic firing dynamics with memory in P-type electroreceptors. Phys Rev Lett. 2000;85(7):1576–1579. doi: 10.1103/PhysRevLett.85.1576. [DOI] [PubMed] [Google Scholar]
- 72.Rose J, Brugge J, Anderson D, Hind J. Phase-locked response to low frequency tones in single auditory nerve fibers of the squirrel monkey. J Neurophysiol. 1967;30:769–793. doi: 10.1152/jn.1967.30.4.769. [DOI] [PubMed] [Google Scholar]
- 73.Braun HA, Huber MT, Dewald M, Schäfer K, Voigt K. Computer simulations of neuronal signal transduction: The role of nonlinear dynamics and noise. Int J Bifurcat Chaos. 1998;08(05):881–889. [Google Scholar]
- 74.Olivares E, et al. TRPM8-dependent dynamic response in a mathematical model of cold thermoreceptor. PLoS One. 2015;10(10):1–17. doi: 10.1371/journal.pone.0139314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Longtin A. Stochastic resonance in neuron models. J Stat Phys. 1993;70(1-2):309–327. [Google Scholar]
- 76.Todd BS, Andrews DC. The identification of peaks in physiological signals. Comput Biomed Res. 1999;32(4):322–335. doi: 10.1006/cbmr.1999.1518. [DOI] [PubMed] [Google Scholar]
- 77.Stoewer A, et al. Integrating data storage and annotation in the data workflow using the nix format and libraries. Front Neurosci. 2015;9 [Google Scholar]
- 78.Hunter JD. Matplotlib: A 2d graphics environment. Comput Sci Eng. 2007;9(3):90–95. [Google Scholar]
- 79.van der Walt S, Colbert SC, Varoquaux G. The numpy array: A structure for efficient numerical computation. Comput Sci Eng. 2011;13(2):22–30. [Google Scholar]
- 80.McKinney W. 2010 Data structures for statistical computing in python. Proceedings of the 9th Python in Science Conference, eds van der Walt S, Millman J. Available at https://conference.scipy.org/proceedings/scipy2010/pdfs/mckinney.pdf. Accessed February 6, 2017.
- 81.Borst A, Theunissen F. Information theory and neural coding. Nat Neurosci. 1999;2(11):947–957. doi: 10.1038/14731. [DOI] [PubMed] [Google Scholar]