Phenotypic and genetic evidence for a unifactorial structure of spatial abilities

Significance

Spatial ability is a strong predictor of several important outcomes, including success in science, technology, engineering, and mathematics (STEM) subjects and careers. This ability is widely believed to be multifactorial, with numerous components and subdomains, such as “mental rotation,” “scanning,” and “mechanical reasoning.” This large twin study allows the genetic and environmental etiology of diverse putative spatial abilities to be explored. The results indicate that this domain is in fact unifactorial, albeit dissociable from general intelligence, suggesting that its structure is much simpler than the sprawling literature suggests. This will aid gene-hunting efforts and allow this ability and its consequences to be examined with greater precision.

Abstract

Spatial abilities encompass several skills differentiable from general cognitive ability (g). Importantly, spatial abilities have been shown to be significant predictors of many life outcomes, even after controlling for g. To date, no studies have analyzed the genetic architecture of diverse spatial abilities using a multivariate approach. We developed “gamified” measures of diverse putative spatial abilities. The battery of 10 tests was administered online to 1,367 twin pairs (age 19–21) from the UK-representative Twins Early Development Study (TEDS). We show that spatial abilities constitute a single factor, both phenotypically and genetically, even after controlling for g. This spatial ability factor is highly heritable (69%). We draw three conclusions: (i) The high heritability of spatial ability makes it a good target for gene-hunting research; (ii) some genes will be specific to spatial ability, independent of g; and (iii) these genes will be associated with all components of spatial ability.

Spatial ability is a vital skill that we use daily to understand and operate within the physical world around us. Spatial ability can be defined as the ability to produce, recall, store, and modify spatial relations among objects (1) and to visualize the transformation of these relations due to changes in perspective or other manipulations—although many competing definitions exist (1–4). Spatial ability has a unique role in predicting many life outcomes. It has been found to be a strong predictor of academic achievement and career success in science, technology, engineering, and mathematics (STEM)-related fields, even after controlling for general cognitive ability (g) (3, 5–8). STEM-related abilities are likely to become ever more important in our rapidly developing technological world, so it is important to understand this cognitive domain better. Research to date suggests that spatial ability includes several factors that are differentiable from g (intelligence). However, the structure of spatial ability is not clear (2, 9), and little is known about the genetic and environmental etiology of individual differences. The purpose of the present study is to investigate the structure and etiology of spatial ability using a genetically sensitive design.

Many components of spatial ability have been proposed, including “spatial visualization” (complex, multistage manipulations of spatial information), “mental rotation” (mentally rotating spatial forms), “spatial relations” (apprehending the relations between objects), “closure speed” (understanding spatial form in the presence of distracting content; for example, combining visual stimuli into a meaningful whole), and “closure flexibility” (searching the visual field to find a particular spatial form) as well as other related abilities, such as “spatial scanning,” “movement detection,” “mechanical reasoning,” “length estimation,” and “directional thinking,” among many others (9). However, these proposed components of spatial ability often overlap in their definitions, and there is little consensus as to the structure of this domain. This could be partly due to the fact that most spatial tests are complex, involving multiple mental processes such as apprehending and encoding spatial forms, mentally rotating them or using nonverbal reasoning (10). In addition, spatial manipulations can use 3D or 2D stimuli, and the tests may involve multiple objects (such as combining pieces to make a whole) or a single object (such as understanding and visualizing its structure) (11). These manipulations can be small scale (such as object rotation) or large scale (such as understanding the map of a building) (12). These processes have been studied in a wide variety of permutations, producing inconsistent results. It is unclear to what extent these processes are independent, rather than reflecting a single general spatial ability factor.

Even less is known about the genetic architecture of spatial ability than about its phenotypic structure. Family, twin, and adoption studies have shown that spatial ability is moderately heritable (30–50%), with heritability estimates varying depending on the particular tests used (13–20). There is evidence for partial genetic overlap between spatial ability and general intelligence (with genetic correlations around 0.60, although the estimates vary greatly depending on the measures) (21–23). However, little is known about the genetic links among different components of spatial ability. The present study uses a multivariate genetic design to investigate the genetic, as well as phenotypic, architecture among the putative components of spatial ability as well as the relationship between spatial ability and g.

We measured spatial ability using a “gamified” battery of 10 spatial tests that cover a wide range of the major putative factors across this broad domain. Specifically, we investigated three questions: (i) To what extent do genetic factors account for individual differences in spatial ability (or spatial abilities)? (ii) Is spatial ability unifactorial or multifactorial, both phenotypically and genetically? (iii) To what extent is spatial ability (or the factors of spatial ability) genetically associated with g?

Results

Phenotypic Analyses.

Our battery comprised 10 measures of spatial ability; see Fig. 1 for examples and Methods for a description, with full details in SI Appendix, Table S10. For our 10 measures of spatial ability, SI Appendix, Table S1 presents the means and SDs for the whole sample, males and females separately, and for all five sex and zygosity groups: monozygotic (MZ) males, dizygotic (DZ) males, MZ females, DZ females, and DZ opposite-sex twin pairs. Males outperformed females by an average of around half a SD (there was no significant effect of zygosity); however, ANOVA results show that sex and zygosity together explain only around 6% of variance on average. Nonetheless, for the subsequent analyses, the data were corrected for mean sex differences, as described in Methods.

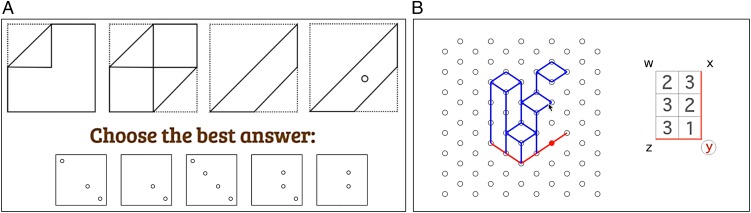
Fig. 1.

Example of the King’s Challenge spatial battery with sample stimuli for the (A) paper-folding and (B) 3D drawing subtests. Examples of all 10 subtests, together with others included in pilot work, are presented in SI Appendix, Table S10.

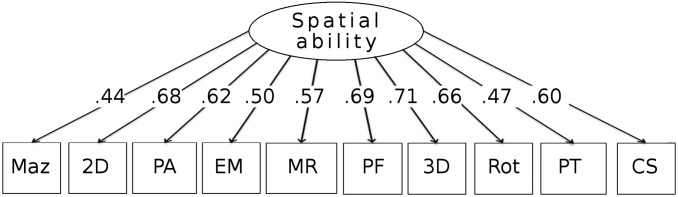
Exploratory factor analyses (EFAs) were conducted using the 10 spatial measures. One member of each twin pair was randomly selected to maintain the independence of data. (The results remained the same when the analysis was repeated after selecting the other member of the twin pair.) As shown in Fig. 2, the EFA results indicated that the 10 tests assess a single spatial ability factor, suggesting that spatial ability is unifactorial phenotypically. This single factor accounted for 42% of the variance. (See SI Appendix, Fig. S1 for the scree plot and SI Appendix, Table S2 for the correlation matrix and reproduced/residual correlation matrices.)

Fig. 2.

EFA. Shown are factor loadings for the 10 spatial tests. See Fig. 4 for test abbreviations.

Confirmatory factor analysis (CFA) was conducted to test whether the one-factor model of spatial ability fit better than a two-factor solution. CFA, as shown in Table 1, confirms that spatial ability is unifactorial phenotypically, as the unifactorial model fit significantly better than any two-factor model (three two-factor models with different compositions and constraints are presented for comparison in Table 1). All parameters such as AIC and BIC were worse for the two-factor models compared with the one-factor model of spatial ability. The root mean square error approximation was less than 0.05 for the one-factor model but was above 0.16 for most two-factor models, indicating that the one-factor model is a much better fit. A two-factor model in which the factors are allowed to correlate (model D in Table 1) fitted almost as well as the one-factor model, but the factors correlated almost at unity, again indicating that there is no meaningful dissociation within spatial ability.

Table 1.

CFA

Model	AIC	BIC	χ2	RMSEA	CFI	TLI	SRMR	r
A. 1 factor	39,450.91	39,595.71	92.47**	0.04	0.98	0.98	0.02	—
B. 2 factors, r = 0	40,235.14	40,379.94	876.70**	0.16	0.71	0.63	0.24	0.00
C. 2 factors, r = 0	40,342.06	40,486.86	983.62**	0.17	0.68	0.59	0.25	0.00
D. 2 factors	39,452.17	39,601.80	91.73**	0.04	0.98	0.97	0.02	0.99

Fit statistics for a one-factor model (model A) and three two-factor models. (Model B) The 10 spatial tests were assigned randomly to the two factors (five tests in each), and the correlation between the factors (r) was constrained to zero to force orthogonality. (Model C) The five highest loading tests in the one-factor model were assigned to one factor and the lowest five to the other; r was constrained to zero. (Model D) Like model C, but the factors were allowed to correlate. AIC, Akaike information criterion; BIC, Bayesian information criterion; CFI, Comparative Fit Index; r, Pearson’s correlation between factors; RMSEA, root mean square error of approximation; SRMR, standardized root mean square residual; TLI, Tucker–Lewis Index.

^**P < 0.01.

Because these results clearly indicate a unifactorial structure, a composite measure of spatial ability (the first principal component emerging from a principal components analysis of the 10 spatial tests) was used in subsequent analyses.

As a simple test for the possibility that the gamified administration of the tests could inflate their correlations (i.e., by method-specific variance), the main phenotypic analyses were repeated with the nongamified pilot data (Methods). The samples were too small for adequate power, but these analyses nonetheless yielded very similar results to those presented here.

CFA was also used to test the distinctiveness of spatial ability from g, as indexed by verbal and nonverbal ability measures (Methods). As expected, spatial ability has considerable overlap with g (perhaps driven by the substantial overlap with Raven’s Matrices) (24), but a two-factor model (spatial ability and g; SI Appendix, Fig. S2B) fitted the data better than a one-factor model (g; SI Appendix, Fig. S2A), indicating that spatial ability is distinct from other cognitive abilities.

Twin Analyses.

The full sex-limitation model was used to investigate possible quantitative and qualitative sex differences (Methods) for the composite spatial ability score and for the 10 spatial ability tests. We found no evidence for qualitative sex differences either for overall ability or the individual tests; in other words, the same genetic and environmental factors contributed to the variability in spatial performance for males and females. A few quantitative sex differences emerged for individual spatial ability tests; however, the differences were small when examining the ACE [genetic (A), shared environmental (C) and nonshared environmental (E) proportions of variance] estimates for males and females separately. (Full model fit statistics with nested models are presented in SI Appendix, Table S3; ACE estimates with 95% confidence intervals for males and females separately are presented in SI Appendix, Table S4.) Even with over 1,300 twin pairs, the sample size is not sufficient for sex-limitation models to reliably detect quantitative and qualitative sex differences of this small magnitude (25), so little confidence can be placed in these differences, as is evident from the wide confidence intervals around the estimates when calculated for males and females separately. For the general spatial factor, no significant quantitative or qualitative sex differences emerged (see SI Appendix, Tables S3 and S4). For these reasons and to increase power, the full sample was used in subsequent analyses, combining males and females, and same- and opposite-sex twin pairs.

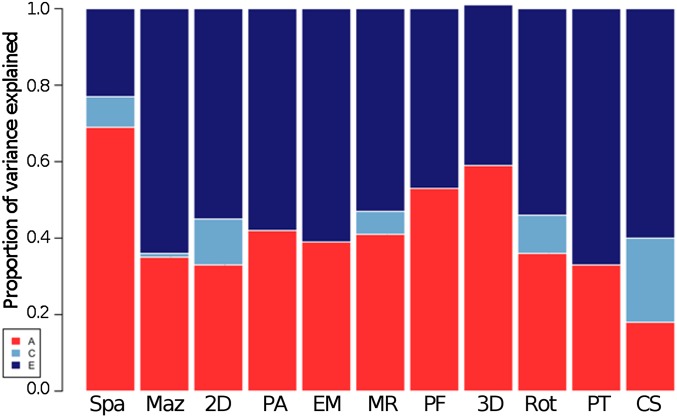
Fig. 3 presents the ACE estimates for the general spatial ability score and for the 10 spatial tests. General spatial ability was substantially heritable (69%), with a small proportion of variance explained by shared environmental factors (8%) and the rest of the variance explained by nonshared environmental factors (23%). Heritability was lower for the individual 10 tests, ranging from 18% to 59%. Twin intraclass correlations and full model fit statistics with confidence intervals are presented in SI Appendix, Table S5.

Fig. 3.

Genetic and environmental estimates for spatial tests: univariate model-fitting results. A, additive genetic components of variance; C, shared environmental components of variance; E, nonshared environmental components of variance; Spa, overall spatial ability. See Fig. 4 for test abbreviations. Confidence intervals are included in SI Appendix, Table S5.

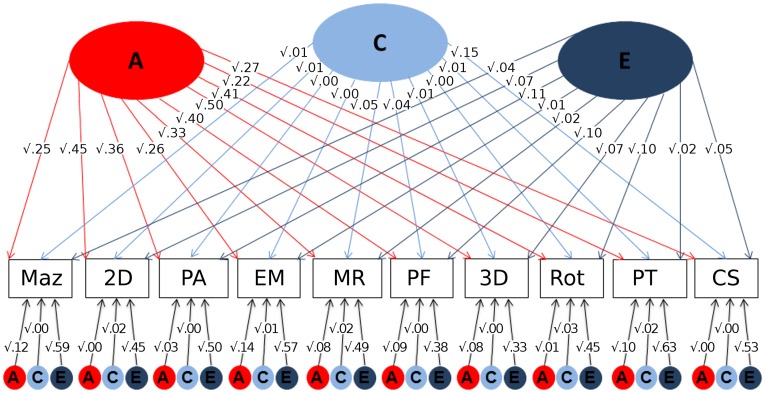
Common and independent pathway models were fitted to the data (Methods). Comparison of fit statistics between them indicated that the independent pathway model was the best fit for the data (see SI Appendix, Table S6). Fig. 4 presents the standardized squared path estimates for this model. All spatial tests loaded substantially on the common A factor, with no significant specific genetic influence remaining after controlling for the common genetic factor. On average, the common A factor accounted for 85% of the heritabilities of the 10 spatial tests [for example, the heritability of the mazes task was 37% (sum of common path 0.25 and specific path 0.12); therefore, the proportion of heritability accounted for by common factor is 0.25/0.37 = 68%]. The spatial tests are differentiated by E factors, which indicate test-specific environmental influences and measurement error specific to each test. The standardized squared path estimates with 95% confidence intervals are presented in SI Appendix, Table S7A. To test whether g could explain the unifactorial structure, SI Appendix, Fig. S3 shows the results for the same analysis after correcting the spatial scores for g. A common genetic factor still explained most of the heritability across the 10 tests, although loadings on the common A factor were reduced by about one-third. For these g-corrected scores, the common A factor accounts for 79% of the heritabilities of the 10 spatial tests on average. The standardized squared path estimates for the g-corrected model with 95% confidence intervals are presented in SI Appendix, Table S7B. The results of the common pathway model are presented in SI Appendix, Table S8 for completeness but yield the same conclusions. SI Appendix, Table S9 presents the ACE correlations between the 10 spatial tests. The genetic correlations range from 0.73 to 0.97, confirming the highly substantial pleiotropy across the spatial tests.

Fig. 4.

Independent pathway model presenting the standardized squared path estimates for the 10 spatial tests. 2D, 2D drawing; 3D, 3D drawing; A, additive genetic components of variance; C, shared environmental components of variance; CS, cross-sections; E, nonshared environmental components of variance; EM, Elithorn mazes; MR, mechanical reasoning; Maz, mazes; PA, pattern assembly; PF, paper folding; PT, perspective-taking; Rot, mental rotation.

Cholesky analysis was conducted to assess the extent to which spatial ability is distinct from verbal and nonverbal abilities. This decomposed the heritability of spatial ability (estimated at 0.70—precise estimates vary between models) into portions shared with, and unique from, verbal and nonverbal ability. Of the 0.70 heritability of spatial ability, 24% (0.17/0.70) was shared with verbal ability, an additional 33% (0.23/0.70) was shared with nonverbal ability independent of verbal ability, and 43% (0.30/0.70) was specific to spatial ability alone, independent of verbal and nonverbal ability. The environmental influences on spatial ability were similarly decomposed into shared and unique components, indicating that the small amount of shared environmental influence on spatial ability was shared with the other measures, whereas nonshared environmental factors were largely specific to each cognitive ability. Precise estimates and confidence intervals are shown in SI Appendix, Fig. S4.

We repeated the Cholesky analysis using a broader measure of intelligence (a composite g measure from ages 7–16; Methods). The results remained the same, as shown in SI Appendix, Fig. S5. The heritability of spatial ability in this model was estimated at 0.66, of which 41% (0.27/0.66) was shared with g and 59% (0.39/0.66) was specific to spatial ability independent of g.

Discussion

A gamified battery was developed to test the phenotypic and genetic structure of spatial abilities, covering a diverse range of the putative components of this cognitive domain. Our results indicate that spatial ability is unifactorial both phenotypically (Fig. 2 and Table 1) and genetically (Fig. 4). We show that performance on different spatial tests was influenced by the same genetic factors. Nonshared environmental influences, on the other hand, were largely specific to each spatial test (Fig. 4); this could be due to specific environmental influences or more likely due to test-specific measurement error.

We show that all spatial tests are moderately to substantially influenced by genetic factors (Fig. 3), with the highest heritability shown for the composite spatial factor (69%). The single spatial tests were less heritable than the composite spatial factor, suggesting that measuring spatial ability with multiple tests increases the reliability of the construct. This can also be seen from the relatively low MZ correlations for single tests compared with the composite spatial factor (SI Appendix, Table S5). Because the reliable portions of spatial ability are shared between all tests—that is, it is unifactorial, with the reliable variance in common between them—this finding suggests that using multiple tests (or perhaps a single, long test composed of many items) will capture spatial ability more reliably.

It is important to emphasize that heritability refers to the extent to which inherited differences in the DNA sequence explain the observed individual differences in a particular population, at a particular time (13). It describes what is but not what could be; in other words, it only reflects the proportion of variance attributable to genetic influences under present conditions. We found that only a modest proportion (8%) of individual differences can be accounted for by shared environmental factors, such as school and family influences, even though our sample consisted of young adults (19–21 y) who had experienced these shared family and school influences recently (Fig. 3). The rest of the individual differences were explained by nonshared environmental influences, which are environmental factors that do not contribute to similarities between twins—for example, different groups of friends or individuals’ perceptions of their environment. The estimate of nonshared environmental factors also includes any measurement error; because the magnitude of the nonshared environment component is greatly reduced for the (more highly reliable) overall spatial ability factor, in comparison with the individual tests, it seems likely that measurement error explains much of this component.

It might be reasonable to assume that the unifactorial structure of spatial ability is explained by g, but our results show that the structure is unchanged genetically after correcting for it (SI Appendix, Fig. S3). Further, the latent factor of spatial ability is a specific cognitive ability in its own right, distinguishable from intelligence not only phenotypically (SI Appendix, Fig. S2) but also genetically (SI Appendix, Figs. S4 and S5), as indicated by its significant and substantial genetic specificity (at least 40%). The unifactorial genetic structure of this spatial domain (i.e., its pleiotropy; Methods) could indicate that the same general processes contribute to all aspects of spatial ability; alternatively, because these spatial tests were administered at ages 19–21, genetic factors influencing some specific aspects may in turn drive the development of others, creating genetic correlations among them.

Research has shown that spatial ability contributes importantly to positive life outcomes, especially achievement in STEM fields (3), so we argue that it is important to clarify the structure of this domain, to make its measurement both more precise and more useful. We included all of the main putative domains of spatial ability in our test battery, with the aim of differentiating between them, but the results indicate strongly that spatial ability is unifactorial. There was no evidence of differentiation either phenotypically or genetically.

It would be a mistake to interpret weak shared environmental influence, as found in this study, as evidence that training spatial ability is not possible. These analyses only decompose the observed variance under current conditions, so the findings do not preclude successful training programs that do not currently contribute to the variance. Various interventions have been proposed, and research to date suggests that training spatial ability can be effective, with an average improvement of around 0.5 SD (11, 26). However, our findings suggest that individuals differ widely in spatial ability, in part due to genetic differences. It is possible that training will be more successful if it is tailored to these differences in ability, for example by detecting problems early in development and tailoring interventions accordingly.

The high heritability of spatial ability at ages 19–21 suggests that this phenotype is a good candidate for gene-hunting efforts attempting to identify specific genetic variants. As predicted by the “generalist genes” hypothesis (i.e., that the genetic influences on cognitive abilities are substantially pleiotropic) (27), our results show partial genetic overlap between spatial ability and g, so it is likely that as genes associated with g are identified, some of these genes will also be associated with spatial ability; however, because there is substantial genetic variance independent of g, there are also likely to be DNA differences that explain spatial ability specifically, independent of general intelligence.

Nothing would advance the field more than identifying specific genetic factors associated with cognitive abilities. However, research has shown that the heritability of complex traits, such as intelligence, is influenced by many DNA differences, possibly thousands, with each individual genetic variant having a very small effect size (28). The structure of spatial ability has important potential consequences for the success of these efforts: If this domain were multifactorial, the genetic influences on each intricate component would be considerably harder to isolate, not least because of the diverse spatial tests in common use. However, the results of the present study suggest that as genetic variants associated with spatial ability are identified, they will be related to general spatial ability, not individual subcomponents. Any study with genetic data available for any spatial test may therefore be used to identify associations with spatial ability in general. That said, a composite of diverse measures may still be preferable, to ensure that the breadth of genetic influences is captured reliably.

The limitations of the present study include the usual limitations of the twin method, described in detail elsewhere (13, 29). Another limitation is that our diverse battery of spatial testing did not include navigation abilities, such as way-finding or map-reading skills, which have been argued to be multifactorial in their own right (12). Tests of navigation abilities have been included in our ongoing research.

Given its associations with STEM outcomes, it seems likely that spatial ability will become ever more important in our increasingly technological society, but tests of this domain are of limited use if it is unclear exactly what they measure. Identifying the specific genetic and environmental influences driving this ability, and the interactions between them, may ultimately refine its measurement, but the first step is to clarify its structure. The present results offer some insight here, suggesting that spatial ability can be differentiated from g and has a much simpler phenotypic and genetic architecture than previously supposed. Clarifying the structure of this domain is an important step toward understanding its etiology, correlates, and consequences.

Methods

Participants.

Ethical approval was granted by the relevant ethics committee (Psychiatry, Nursing & Midwifery at King’s College London), and informed consent was obtained. The sample was drawn from the Twins Early Development Study (TEDS). TEDS is a large longitudinal study in the United Kingdom that recruited over 16,000 twin pairs born in England and Wales between 1994 and 1996. Although there has been some attrition, more than 10,000 twin pairs remain actively involved in the study. Importantly, TEDS is a representative sample of the UK population (30–32). Zygosity was assessed using a parent questionnaire of physical similarity, which has been shown to be over 95% accurate compared with DNA testing (33). DNA testing was conducted when zygosity was not clear from the physical similarity questionnaire criteria.

A randomly selected subsample of the older participants from the TEDS study (aged 19–21) participated in the present study, excluding individuals with major medical or psychiatric problems. After exclusions, the total number of individuals in complete twin pairs with spatial data available was 2,734 (1,367 twin pairs), of whom 543 pairs were MZ, 432 were same-sex DZ (DZss), and 392 pairs were opposite-sex DZ (DZos). When DZos data are available, the etiology of sex differences can be explored (34). The results of the full sex-limitation model fitting are presented in Results. Because little evidence was found for etiological sex differences for spatial ability, and to increase power, we used the full sample, including DZos pairs, in the genetic analyses.

Measures.

An online, gamified test battery, called the “King’s Challenge,” was used to test diverse measures of spatial ability. Examples of the test are provided in Fig. 1. A demonstration of the battery is available here: teds.ac.uk/research/collaborators-and-data/public-datasets. The King’s Challenge battery is available on request for other researchers to use. Web-based cognitive testing has been shown to be equivalent to traditional laboratory administration (35, 36).

The development of the King’s Challenge began with an extensive literature review of the various measures used to test spatial ability. We assembled all available measures of spatial abilities, including mental rotation, spatial visualization, spatial scanning, spatial reasoning, perspective-taking, and mechanical reasoning. After a series of feasibility and pilot studies, we modified the existing measures and developed new tests as appropriate, to create a preliminary battery of 27 measures, administered as paper-and-pencil tests in the first feasibility study and as a computer-based test in the second feasibility study. Based on psychometric analyses and test–retest reliability (after a 2-week period), we ultimately reduced the number of tests to 10; these represented the psychometrically best performing tests while eliminating redundancy and capturing a diverse range of proposed spatial abilities. We eliminated tests that did not show (near) normal distributions, to include only tests that were neither too easy nor too difficult for the general population; we also removed tests with low test–retest reliability (r < 0.5) and those that were redundant (correlating with each other, r > 0.65). Each of these measures is detailed in SI Appendix, Table S10, including their psychometric properties and the test–retest correlations between their paper-and-pencil and computerized administrations.

The resulting 10 spatial tests captured the major putative dimensions of spatial ability, comprising a mazes task (searching for a way through a 2D maze in a speeded task), 2D drawing (sketching a 2D layout of a 3D object from a specified viewpoint), Elithorn mazes (joining together as many dots as possible from an array), pattern assembly (visually combining pieces of objects together to make a whole), mechanical reasoning (multiple-choice naïve physics questions), paper folding (visualizing where the holes are situated after a piece of paper is folded and a hole is punched through it), 3D drawing (sketching a 3D drawing from a 2D diagram), mental rotation (mentally rotating objects), perspective-taking (visualizing objects from a different perspective), and cross-sections (visualizing cross-sections of objects). The creation of the King’s Challenge is summarized in SI Appendix, Table S10. Each test started with a practice item, for which feedback was given (unlike other items). To promote participation, the final battery was gamified with the help of IT developers, Helmes Ltd. (www.helmes.ee), meaning that the tests were embedded in a game-like narrative.

We piloted the King’s Challenge battery on 100 unrelated individuals; all measures produced reasonable test–retest reliability (r = 0.65 on average for the 10 spatial tests): pattern assembly, r = 0.56; shapes rotation, r = 0.56; paper folding, r = 0.58; cross-section, r = 0.64; perspective taking, r = 0.56; mechanical reasoning, r = 0.65; Elithorn maze, r = 0.69; 3D drawing, r = 0.63; 2D drawing, r = 0.68; maze, r = 0.46). All tests were taken using laptop or desktop computers (not smartphones or tablets) in web browsers.

Verbal and nonverbal abilities were assessed online as an index of g when the participants were 16 y old. The Mill Hill Vocabulary Scale (37) was used to assess verbal ability. The test consists of multiple-choice items. For each item, a single word is presented at the top of the screen. Participants choose an answer that is closest in meaning to the target word. Nonverbal ability was assessed using Raven’s Standard Progressive Matrices, which consists of a series of incomplete patterns (38). This test is also a multiple-choice test, in which the participant identifies the missing part of the pattern. g (intelligence) was indexed as the mean of the standardized verbal and nonverbal scores.

We also created a more robust measure of g, combining the g measures collected in TEDS longitudinally. At age 7, g was calculated as the mean of conceptual grouping (39), a Wechsler Intelligence Scale for Children (WISC) similarities test (40), a WISC vocabulary test (40), and a WISC picture completion test (40), all conducted via telephone with parents’ or guardians’ assistance. At age 9, g was calculated as the mean of a shapes test [Cognitive Abilities Test (CAT3) Figure Classification] (41), a WISC vocabulary test (41), a WISC general knowledge task (41), and a puzzle test (CAT3 Figure Analogies) (40), all collected with booklets sent to the twins by post. At age 10, the g measure was calculated as the mean of the Ravens Standard Progressive Matrices (38), a WISC vocabulary test (41), WISC picture completion (42), and a WISC general knowledge test (41), all collected via web-based testing. At age 12, g was calculated exactly as at age 10. At age 14, g was computed as the mean of Raven’s Progressive Matrices (38) and a WISC vocabulary test (40). Finally, at age 16, g was measured as described previously. The cross-age intelligence score was calculated as the mean of the g scores across the five ages for however many time points for which each individual had data.

Before genetic analyses, all measures were corrected for age and sex differences using the regression method (43) by creating standardized residual scores. This procedure was used to avoid inflation of estimates of shared environment, as both members of twin pairs are identical for age and MZ twin pairs are also identical for sex. Finally, all scores were transformed using the rank-based van der Waerden transformation (44, 45) to correct for a slight positive skew in some tests.

Analyses.

Descriptive statistics.

We compared means and variances for male and female participants and identical (MZ) and fraternal (DZ) twins for the whole sample (after exclusions). Because the present study used a twin sample, we maintained the independence of data for all phenotypic analyses (when conducting parametric tests) by randomly selecting one twin per pair. The mean differences for sex and zygosity across all of the measures, and interactions between sex and zygosity, were tested using univariate analyses of variance (ANOVA).

Factor analyses.

EFAs were conducted to assess the factor structure of spatial abilities. The factor structure was also tested by using the other half of the data (we randomly assigned members of twin pairs to two subsamples). The statistical software SPSS was used for the analyses. The factor structure was also assessed by CFAs, using the statistical software package MPlus (46).

Twin analyses.

The twin method was used to estimate the relative contribution of additive genetic (A), shared environmental (C), and nonshared environmental (E) components of variance of the spatial factor and the covariance between the spatial tests (13). The twin method offers a powerful natural experiment by comparing the similarity of scores within MZ and DZ twin pairs, as MZ twins share 100% of their DNA, whereas DZ twins share on average 50% of their segregating genes, like any other siblings. Shared environmental influences are assumed to be 1.0 and the same for MZ and DZ twin pairs growing up in the same family. The rest of the variance is attributed to nonshared environmental influence, which includes error of measurement.

ACE parameters can be estimated by comparing cross-twin correlations for MZ and DZ twins. A may be estimated approximately by doubling the difference between the MZ and DZ correlations; C is indexed by deducting the heritability estimate from the MZ correlation; and E can be assessed by deducting the MZ correlation from unity. These ACE parameters and their 95% confidence intervals were estimated more precisely using structural equation modeling. In the present study, we used the structural equation program OpenMx (47).

Univariate twin analysis of the variance of a single trait can be extended to multivariate analysis to estimate ACE parameters for the covariance between traits. Multivariate analysis also estimates additional statistics: the genetic correlation (rG), shared environmental correlation (rC), and nonshared environmental correlation (rE). Genetic correlation is an index of pleiotropy, the extent to which the same genetic variants influence multiple traits. Importantly, the genetic correlation is estimated independently of the heritabilities of the traits; that is, the heritabilities of two traits could be low, but the genetic correlation between the traits could be high. A shared environmental correlation of 1.0 indicates that the same environmental factors that make twins similar on one trait also make twins similar on another trait. Likewise, for nonshared environment (which is not shared between individuals but may influence multiple traits for each individual), a correlation of zero indicates that completely different nonshared environmental influences affect the two traits (13).

Independent pathway model.

A multivariate genetic model that allows for estimation of the extent to which the genetic and environmental influences on the traits are attributable to common latent ACE factors (48). The common factors have specific paths (standardized partial regressions) to each trait. In addition, residual paths index the extent to which the variance of the traits is not shared with other traits in the model (25, 48, 49).

Common pathway model.

A multivariate genetic model in which the etiology of all of the variables in the analysis can be reduced to a common latent factor. That is, all genetic, shared environmental, and nonshared environmental influences on all observed variables in the analyses will load onto a single latent factor. The common pathway model is considered to be more stringent than the independent pathway model, as it assumes that a single latent factor mediates the genetic, shared, and nonshared environmental effects, compared with the independent pathway model that specifies both common and specific genetic and environmental causes (25, 49, 50).

Cholesky decomposition.

A multivariate genetic analysis that is conceptually similar to hierarchical regression (29). This method estimates the extent to which the heritability of one trait is explained by the heritability of another trait. When entering a third variable in the model, it estimates the extent to which the heritability of trait 3 is explained by the heritability of trait 1 and by the heritability of trait 2 when controlling for the heritability of trait 1. In the present study, Cholesky decomposition allows for the estimation of how much heritability in spatial ability is explained by the heritability of verbal ability and how much heritability in spatial ability is explained by nonverbal ability when controlling for verbal ability.

Sex-limitation model.

When data are available for DZos as well as DZss twins, the standard univariate model can be extended to a sex-limitation model to test for differences in the ACE etiologies of sex differences, by comparing all five sex and zygosity groups: MZ males, MZ females, DZ males, DZ females, and DZ opposite-sex twin pairs (13). Differences in the magnitude of ACE estimates for males and females are called quantitative sex differences. Qualitative sex differences indicate whether different genetic or environmental factors affect males and females. Sex-limitation model-fitting was conducted by fitting a series of nested models and then testing the relative drop of the fit in the models (47). The sex-limitation model is described in detail elsewhere (34).