Significance
In allosteric proteins, binding a ligand affects activity at a distant site. The physical principles allowing for such an action at a distance are not well understood. Here we introduce a numerical scheme to evolve allosteric materials in which the number of solutions, their spatial architectures, and the correlations among them can be computed. We show that allostery in these materials uses recently discovered elastic edge modes near the active site to transmit information, and that correlations generated during evolution alone can reveal key aspects of this architecture.
Keywords: disordered materials, proteins, evolution
Abstract
We introduce a numerical scheme to evolve functional elastic materials that can accomplish a specified mechanical task. In this scheme, the number of solutions, their spatial architectures, and the correlations among them can be computed. As an example, we consider an “allosteric” task, which requires the material to respond specifically to a stimulus at a distant active site. We find that functioning materials evolve a less-constrained trumpet-shaped region connecting the stimulus and active sites, and that the amplitude of the elastic response varies nonmonotonically along the trumpet. As previously shown for some proteins, we find that correlations appearing during evolution alone are sufficient to identify key aspects of this design. Finally, we show that the success of this architecture stems from the emergence of soft edge modes recently found to appear near the surface of marginally connected materials. Overall, our in silico evolution experiment offers a window to study the relationship between structure, function, and correlations emerging during evolution.
Proteins are long polymers that can fold in a reproducible way and achieve a specific function. Often, the activity of the main functional site depends on the binding of an effector on a distant site (1, 2). Such an allosteric behavior can occur over large distances, such as 20 residues or more (3), and often involves only a sparse subset of residues in the protein (3, 4). Allosteric regulation offers an appealing target for drug design (5), and there is considerable interest in predicting allosteric pathways (6, 7). One central difficulty is that the physical mechanisms allowing such an “action at a distance” remain elusive. In some cases, allostery can be understood as the modulation of a hinge connecting two extended rigid parts of the protein (8, 9), but, often, the displacement field induced by the binding of the effector cannot be described in these terms (4, 10, 11). Another route, statistical coupling analysis (12), considers correlations within sequences of proteins of the same family to infer allosteric pathways (4, 7). The generality of this elegant approach is, however, debated (13).
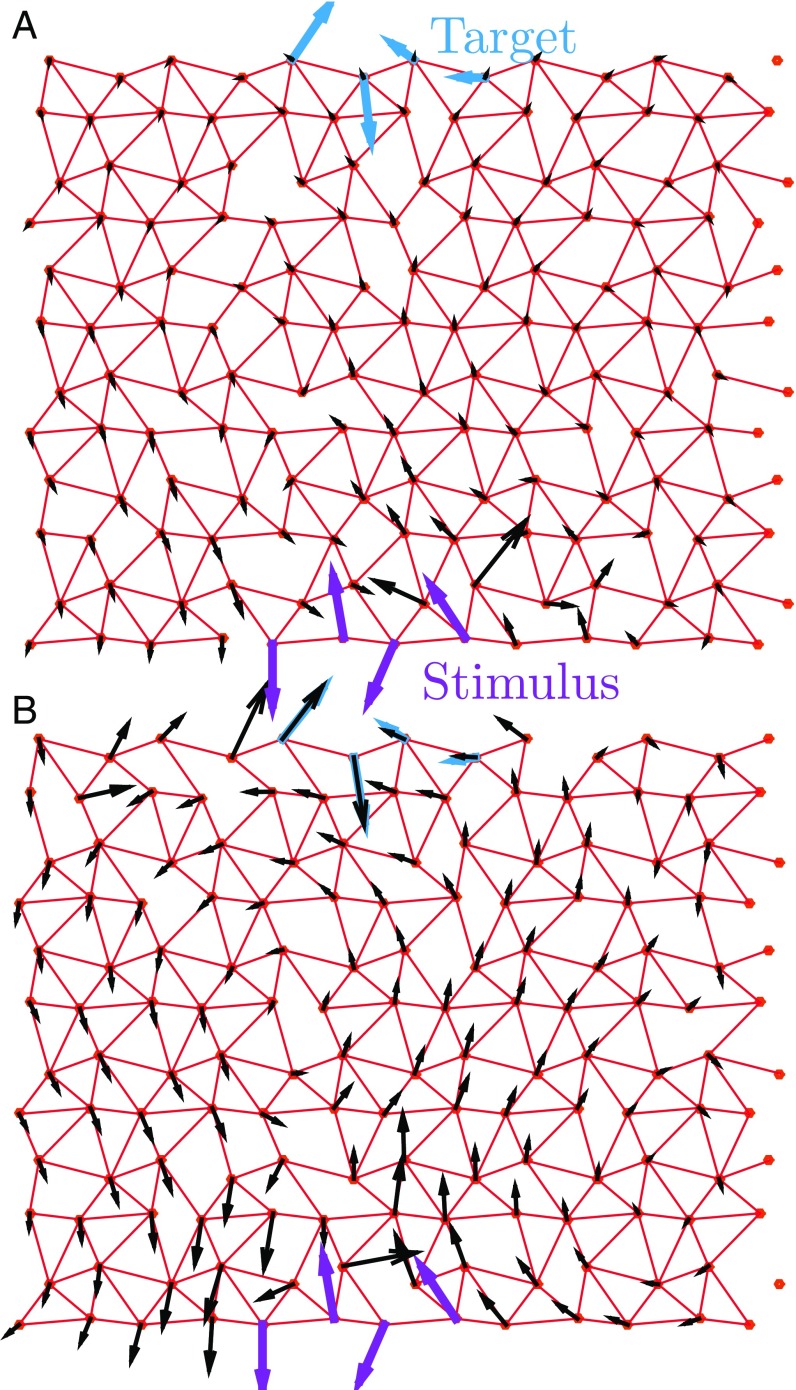
From a physical viewpoint, specific response at a distance is surprising. The structure of proteins is similar to randomly packed spheres (14). Generically, the response of such systems is nonspecific and decays rapidly in space (in a manner similar to a continuum medium) at distances larger than the particle size; this is true, except close to a critical point where the number of constraints coming from strongly interacting particles is just sufficient to match the number of degrees of freedom of the particles (15). There, the elastic response becomes heterogeneous on all scales (16, 17). This point is illustrated in Fig. 1A, showing the rapidly decaying response of a random spring network to a stimulus. However, as shown in Fig. 1B (and independently found in ref. 18 using a different algorithm), springs can be moved so that the response extends farther and specifically matches a target response on the other side of the system. This observation raises various questions, including the following: (i) Which network architectures allow for such allosteric response? (ii) Why are these architectures functional? (iii) What is the number of solutions? (iv) As we shall see, a network can be represented by a sequence; knowing only a family of sequences of solutions, can one predict which sites are important for function from their correlations alone?
Fig. 1.
Illustration of the model. A network is defined by the location of springs (in red), connecting the adjacent nodes of a distorted triangular lattice. A network has higher fitness if its response field (black arrows) to an imposed stimulus (purple arrows) reproduces a target displacement (cyan arrows) at a distant site, consisting here of four nodes. The match between the response field and the target displacement (A) is poor for a random configuration () and (B) is almost perfect for a system that has evolved by moving springs at . and .
In this work, we answer these questions by introducing a model of elastic networks that can evolve according to some fitness function , which depends on the response of the material to a well-defined stimulus. Our approach allows for considerable freedom in the choice of the fitness function. As an illustration, we impose here that a displacement of four nodes on one side of the material (the “stimulus”) elicits a given displacement of identical amplitude but different direction on four target nodes on the other side of the system. A key advantage of our scheme is that our algorithm uniformly samples the fitness landscape (we use a Monte Carlo algorithm that turns out to equilibrate rapidly), which allows us to count the number of solutions and compute the entropy , as well as to guarantee that the solutions generated are the typical (most numerous) ones. The quality of the solutions can be monitored by an “evolution temperature” that controls the fitness of the solutions probed. Our central findings are as follows. (i) There exists a transition temperature below which high-quality solutions appear and above which solutions are poor. (ii) High-quality solutions share a specific design. They present a trumpet-shaped region where the material is less constrained, which ends by a marginally connected region in the vicinity of the target. (iii) The response amplitude varies nonmonotonically between the stimulus and active sites. (iv) We rationalize this design based on a recent theory of edge modes in marginally connected disordered media (19). (v) We show that coevolution—the correlations in the structures of the family of solutions—alone is sufficient to identify the trumpet structure. Finally, this detailed characterization of the solutions also points to some of their limitations in using them in thermal environments. We discuss how the fitness function can be changed to alleviate such problems.
Description of the Evolution Model
Scalar models, where the response of a node is described by a scalar instead of a vector, have been introduced to study coevolution and allostery (20–22). Although these models can capture the rigid motion of a part of the system, they cannot address the propagation of more complex mechanical information, such as that illustrated in Fig. 1. Instead, we use elastic networks, which have been used extensively to describe the vibrational dynamics of proteins (23–25).
Specifically, we consider on-lattice models previously used to describe covalent glasses (26, 27). nodes are located on a triangular lattice (slightly distorted to avoid straight lines of nodes; see discussion in SI Appendix). harmonic springs of stiffness unity connect some of the adjacent nodes. We declare that if a spring is present in the link (as represented in red in Fig. 1), and otherwise. Thus, the network is entirely described by a connection vector whose dimension is the number of links. We define the average coordination number as . Marginally connected networks, also called “isostatic,” correspond to in two dimensions (28), and we denote .
For a given configuration , we consider the response to a ligand binding event, which we model as an imposed displacement field on a set of four adjacent nodes (the “allosteric” site) located on one free boundary of the system, as illustrated in purple in Fig. 1. After relaxing the elastic energy, such a stimulus will generate a displacement field of components in the other nodes of the system; a fast numerical calculation of this response is formulated in Methods. Here, we focus on studying networks for which the response generates a desired target displacement of identical amplitude but different direction (illustrated in cyan in Fig. 1) on an “active” site, which we also choose to consist of nodes on the other side of the system, facing the stimulus site. The case where the target is inside the system leads to similar results, as shown in SI Appendix.
Because, physically, only the strain (and not the absolute displacement) at the active site can affect catalytic properties, the target displacement is defined modulo a global translation and rotation . To rank networks in term of their allosteric ability, we define a fitness function and a cost ,
| [1] |
where label the nodes, and denotes the set of nodes belonging to the active site. Thus, corresponds to a perfect allosteric response. We restrict the networks further by imposing that all adjacent nodes in the active site are connected, and we choose a target displacement that does not stretch these bonds. The minimization of Eq. 1 can be readily performed and the fitness can be written directly in terms of and , as discussed in Methods.
Henceforth, we consider 2D networks with periodic boundaries in the direction transverse to the direction between the allosteric and active sites (this corresponds to a cylindrical geometry). As is the case for many aspects of the microscopic elasticity of amorphous materials (15), we expect our results to hold independently of the spatial dimension.
Numerical Solutions
To evolve networks, we use a Metropolis algorithm (Methods) at some evolution temperature , where springs can swap from an occupied to an unoccupied link, leaving the average coordination constant. More precisely, is the variable conjugate to the fitness, so that, once our algorithm reaches equilibrium (which it does in the range of values presented here), the probability of finding a configuration reads , where . corresponds to random networks.
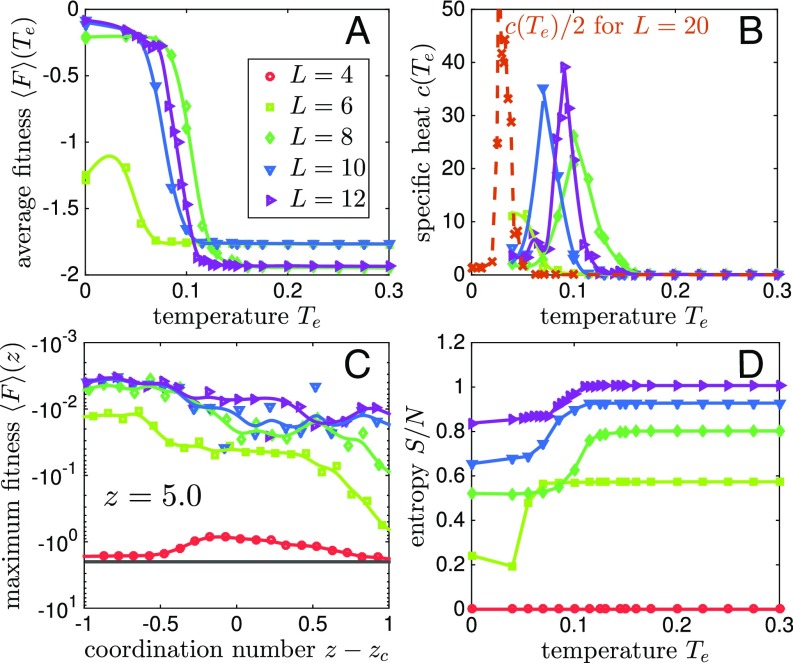
Thus, as we lower the temperature, we probe fitter and fitter networks as illustrated in Fig. 1. This point is systematically studied in Fig. 2A, showing for a given coordination, where the ensemble average is made on both Monte Carlo steps and different realizations. For , we find that this average does not depend on the time of the simulation if it is long enough, indicating that an equilibrium was reached. As decreases, we observe a transition from low to high fitness, which appears to become sharper and sharper as increases. This trend suggests some kind of transition, as we evidence further by considering the specific heat , which displays a more and more pronounced peak as increases, as shown in Fig. 2B. (Larger system sizes would be required to decide if the transition becomes sharp in the thermodynamic limit.) This result indicates that achieving an allosteric function is a collective process.
Fig. 2.
(A) Average fitness versus evolution temperature for various system sizes where . A steep change in fitness is seen near for relatively large systems. (B) Specific heat versus temperature . The maximal specific heat increases with the system size , suggesting the existence of a transition at some . (C) Fitness averaged over local maxima versus coordination number in log-linear scale. The black line shows the fitness if no mechanical response is present at the active sites. (D) Entropy density versus temperature . The entropy jump near indicates the number of degrees of freedom that must be tuned to achieve the desired response.
Below the transition, we find that the networks perform well. Their performance can be quantified by , an ensemble average of local maxima in the fitness landscape, as reported in Fig. 2C. These structures result from a pure gradient ascent in the fitness landscape. We find that, in the range of coordination we probed, the cost decreases by at least -fold with respect to random networks, i.e., the response converges very precisely toward the desired one. Thus, the system does not get stuck in local maxima of poor quality in the fitness landscape.
Finally, we can quantify the number of allosteric networks; it follows , where is the entropy. It satisfies , and is shown in Fig. 2D. For example, at , where networks perform very well, we find that their number is very large, exponential to the system size, for , but the probability to obtain such a network by chance is also exponentially low, for .
Architecture of Allosteric Networks
Hypostatic networks with are extremely floppy. It may be an interesting case to study intrinsically disordered proteins (29), but, for folded proteins, considering is more realistic. Henceforth we focus on that case and choose . In SI Appendix, our results are presented for the floppy case .
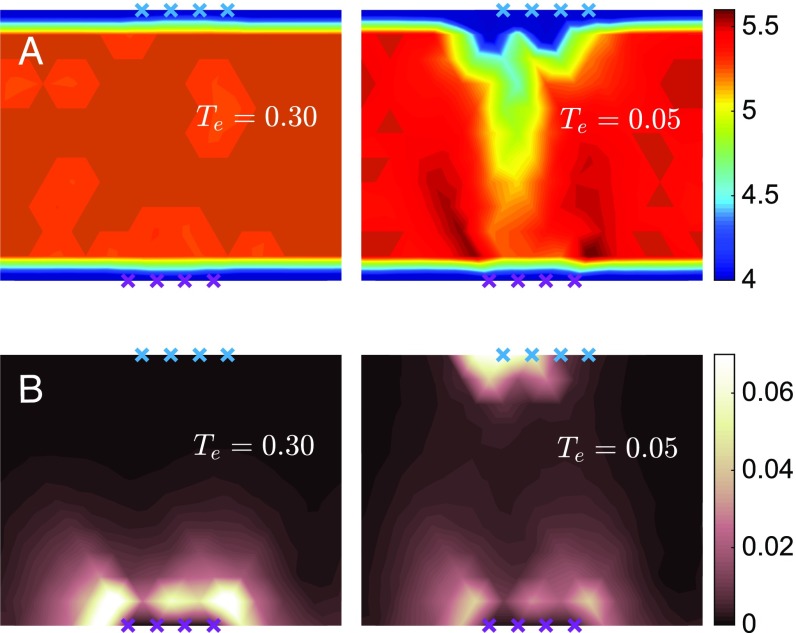
Which architecture allows for such a long-distance, specific response? A systematic design is revealed by averaging the occupancy of various solutions that our algorithm generates, as shown in Fig. 3A for (see SI Appendix for larger systems). At high temperature, the structures are essentially random and not functioning. At low temperature, a trumpet-shaped region appears that connects the allosteric and active sites. Specific features are that (i) inside the trumpet, the mean occupancy is lower than the mean, but there are no floppy modes (i.e., modes that do not deform the springs); (ii) the mean occupancy or coordination decreases monotonically from the system center to the active site; (iii) the mouthpiece of the trumpet is surrounded by two more rigid regions, which appear in dark in Fig. 3A; and (iv) the coordination number is close to its critical isostatic value in the vicinity of the active site (see Physical Processes Underlying Allostery).
Fig. 3.
(A) Map of the mean coordination number and (B) spatial distribution of the average response magnitude for configurations equilibrated at (Left) and (Right). In the functioning networks (Right), a trumpet connecting the allosteric and active sites appears in A, and the response to stimulus varies nonmonotonically inside the trumpet in B.
The trumpet-like architecture is robust: It remains qualitatively unchanged as the mean coordination number is varied, as long as . For , however, a trumpet still exists (see SI Appendix), but it is inverted: It is more coordinated than the rest of the system.
Next we study how such trumpets shape the response to a binding event, by considering the mean-squared magnitude of the normalized response at different nodes , , as shown in Fig. 3. For random networks, unsurprisingly, the response is large only close to the stimulus site. However, the response of fit networks displays a striking feature: It varies nonmonotonically between the allosteric and the active site. It almost vanishes in the bulk of the material, but reappears near the active site, where it is the strongest.
Physical Processes Underlying Allostery
The observation that fit networks develop a less-constrained region connecting the stimulus to the active site is not very surprising, because the elastic point response can remain heterogeneous on longer length scales in that case (17). This argument does not explain, however, the strong asymmetry of the trumpet, more coordinated near the stimulus and nearly marginally connected near the active site. We now argue that this design is selected for because it prevents the decay in the amplitude of the signal one expects in normal elastic materials.
Recent works have shown that marginally connected crystals can display edge modes, leading to exponentially growing response when displacements are imposed at the boundary of the system (30–32). It was very recently shown that such “explosive” modes must be present in disordered marginally connected materials as well (19). Such systems, if sufficiently constrained at some of their boundaries, can act as a lever that can amplify complex motions exponentially toward free boundaries (19).
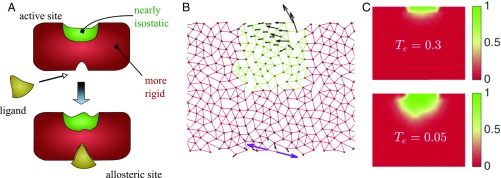
We argue that our allosteric networks are built along this principle. As sketched in Fig. 4A, their structure is approximately that of a well-connected elastic material surrounding a marginally connected network near the active site. If a stimulus is imposed on an allosteric site, the response will decay with distance in the well-connected region, leading to imposed displacements of small amplitude on the boundary of the isostatic region. As noted above, “squeezing” such systems leads to an explosive response in the direction of free boundaries, allowing the response to reach the desired amplitude on the target nodes. This explanation captures both the observation that allosteric networks are nearly isostatic near the active site and that their response varies nonmonotonically in space.
Fig. 4.
(A) Illustration of the mechanism responsible for allostery in our artificial networks. They display a nearly isostatic region in the vicinity of the active site, surrounded by a better-connected material. When the ligand binds, it induces an effective shape change at the allosteric site. This mechanical signal transmits and decays through the well-connected body of the material. It is then amplified exponentially fast in the isostatic region near the active site, leading to a large strain. (B) System made of two elastic networks with coordination (red) and (green). Its response (black arrows) to a perturbation (purple arrows) demonstrates that an isostatic network embedded in a more connected one can amplify the response near its free boundary. (C) Spatial distribution of the probability that a node is in an isostatic region connected to the active sites at and for .
To test this proposal, we build an artificial network, by embedding a random isostatic network with to a better-coordinated random network with (the details of construction are explained in Methods). As shown in Fig. 4B, the response to an imposed dipole on the open boundary of the well-connected network decays, but eventually grows rapidly toward the boundary of the isostatic region, as predicted.
As discussed in SI Appendix, we have developed an algorithm to recognize a nearly isostatic region that contains the target nodes in our evolved networks, which could be extended to real proteins using the methodology of ref. 33. In Fig. 4C, we show the probability map that a node belongs to such an isostatic network, obtained by averaging on many realizations. Fit allosteric networks indeed show a robust isostatic region attached to the active sites, which is absent for random networks.
In SI Appendix, we show that a similar architecture is found when the active site is well inside the system: The material develops a weakly connected region embedded in a more rigid one, again leading to an amplification of the response.
Beyond this central aspect of the design, detailed features of the trumpet presumably also improve function, because they are conserved. This is further demonstrated in SI Appendix, where the fitness costs of all possible “mutations” (corresponding to a change of the occupancy of a link) are computed, leading to a map that reflects the entire trumpet shape.
Conservation and Coevolution
In our model, the “sequence” of a network corresponds to the vector of zeros and ones that defines a structure. This Boolean sequence is analogous to the sequence of amino acids that defines a protein. Using our Monte Carlo at some low , we can generate a family of sequences associated with networks of high fitness. If only such a family could be observed (and assuming no knowledge on the task being performed nor on the spatial organization of the networks), would it be possible to infer which region of the system matters for function? There is evidence that such inference is useful for some protein families, if enough sequences are available (4, 7). We show that this inference also works in our model.
Key aspects of the design are more likely to stay conserved in evolution. Here we define conservation in each link as (34)
| [2] |
where is the ensemble average of the occupancy of link , and is the mean occupancy of the links. is a measure of the predictability of the occupancy of the link : It is zero when the link occupancy is random, and it is maximum when the link is always empty or always occupied. The conservation map of allosteric networks is shown in Fig. 5A. We can distinguish the trumpet pattern, but, most strikingly, the neighborhood of the active site is very conserved. This observation supports that specificity of the response is essentially controlled by the geometry of the network near the active site.
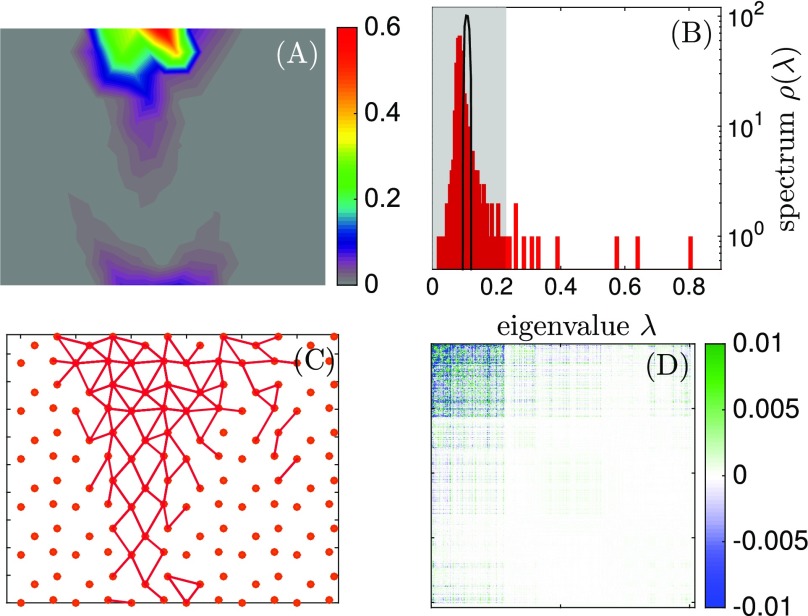
Fig. 5.
(A) Spatial distribution of conservation, as defined in Eq. 2, for and . (B) Spectrum of eigenvalues of for the high-temperature case () in black and the low-temperature case () in red. The white region indicates which eigenvalues are used to identify the springs shown in C. (C) Springs selected using the procedure explained in Conservation and Coevolution. (D) is built using the same parameters as in C. presents a clear separation in a region where the correlations are stronger, which corresponds to the trumpet shown in C. All these images are made using and .
Next, we test if an analysis of coevolution alone reveals important features of function and structure. We define the correlation matrix between the links as
| [3] |
where the • is again the ensemble average over the solutions found by the Monte Carlo algorithm. We then compute the eigenvalues of the matrix . Fig. 5B compares the spectrum of eigenvalues of a high-temperature (essentially random) network with that of allosteric networks obtained at small . In the latter case, some eigenvalues are much larger than the continuum spectrum, itself much more spread than in the random case.
To select out a “sector” (7) of links that coevolve, we (i) pick up the (other choices for the value of are documented in SI Appendix) eigenvectors with highest eigenvalues and (ii) include a given link in the sector if, for at least one of these 10 modes, . Links selected in this procedure are shown in Fig. 5C. This procedure selects precisely the links that belong to the trumpet, supporting the idea that coevolution alone can uncover key functional aspects (4, 7).
For completeness, we define a correlation matrix reconstructed from its 10 top eigenvectors,
| [4] |
is shown in Fig. 5D after reordering links in terms of the strength of their components in the top 10 modes, clearly showing a sector of links where correlations are strong in amplitude (but vary in sign).
Conclusion
We have introduced a scheme to discover materials that accomplish a specified task. The scheme allows us to characterize the architecture of the solutions, their entropy, and how correlated they are. We illustrated this approach using a specific allosteric task, where a strain imposed on an allosteric site must lead to a given strain on a distant active site. The architectures we obtain are highly anisotropic. Our analysis revealed that the physical mechanisms that enable allostery include the recently discovered presence of soft edge modes in marginally connected elastic materials (19). It would be very interesting to test if some proteins have evolved to exploit such effects by (i) measuring the displacement field induced by binding the ligand, and by checking if its magnitude varies nonmonotonically inside the protein and is amplified near the active site, as reported in Fig. 3B; and (ii) testing if the region around the active site is marginally connected, using algorithms developed in proteins to quantify connectivity and flexibility (33).
The detailed study of the architectures we found also reveals some of their limitations. Real proteins have additional constraints other than those we have considered: Among others, they are made of a chain that folds and remains relatively stable despite thermal noise. Our asymmetric structures are quite soft near the active site: As documented in SI Appendix, the thermally induced motion would be about 4 times larger there than in the other nodes also located at the system surface, which may not be desirable. Note, however, that such features will improve if alternative fitness functions are considered, which our approach allows for. This procedure could be implemented by explicitly penalizing thermal motion at the active site. An intriguing extension of our work is to reason in terms of energy, as is done, in particular, in the Monod–Wyman–Changeux model (1, 2), instead of displacement. A natural quantity to maximize is the cooperativity between two distant sites. Denoting by and the mechanical energies associated with a binding event in some site 1 and site 2, respectively, and denoting the energy of binding both, we can consider . Fitness can be large only if the two sites are strongly coupled together elastically, which, from the symmetry of the fitness, presumably corresponds to more symmetric architectures than those discovered here.
In addition, our scheme can be used to benchmark (and seek novel) methods aiming at inferring function and structure from protein sequence data alone. As an illustration, we performed a statistical coupling analysis and identified “protein sectors” from top eigenvectors of the correlation matrix. Our results support that such a method (4, 7) can indeed reveal compact regions central for function. It would be very interesting to extend this analysis to multiple and possibly time-varying tasks, and to consider how many sectors appear under these conditions. Another approach, direct coevolutionary couplings (35), identifies evolutionary interactions between amino acids. Our framework can be used to measure these interactions, and to study their relationship with elasticity, structure, and function.
Methods
Computing the Linear Response to an Imposed Displacement.
The linear response to an external force field reads
| [5] |
where the stiffness matrix depends only on connection and the link directions. Here is the entire displacement field, of dimension . Its components are noted . We use a basis for which corresponds to the stimulus nodes, whereas labels the other nodes.
To impose the stimulus at the allosteric nodes , forces must be applied on these nodes. All other nodes adapt to a new mechanical equilibrium with no net forces on them, and they follow a displacement . Thus, Eq. 5 becomes, for this choice of basis,
| [6] |
which leads to
| [7] |
with
| [8] |
When there are floppy modes in the network, is not necessarily invertible. Then, in the above formula, should be understood as the pseudoinverse. Another possibility is to regularize the problem, for example, by imposing that each node also interacts with all its next-nearest neighbors via weak springs of stiffness . Both methods lead to qualitatively identical results. Our results were computed using the second approach with the very small value .
Computing the Fitness.
Minimizing Eq. 1 with respect to the global translation and rotation leads to
| [9] |
where if .
Metropolis Algorithm.
Starting from a configuration , we consider the move toward a new configuration that differs only by the motion of a spring. The move is accepted with the probability
| [10] |
which satisfies detailed balance. Based on whether the move is accepted or not, the algorithm samples the new configuration or the original one . The next step starts from the configuration just sampled.
For each coordination number and each evolution temperature , we sample Monte Carlo sampling series with Monte Carlo steps in each, and do not consider the first half of these time series (which is sufficient to eliminate transient effects). Our results are thus averaged over configurations.
Supplementary Material
Acknowledgments
We thank B. Bialek, J.-P. Bouchaud, P. De Los Rios, E. DeGiuli, D. Malinverni, R. Monasson, O. Rivoire, and S. Zamuner for discussions and anonymous reviewers for suggestions. L.Y. was supported, in part, by the National Science Foundation (NSF) under Grant NSF PHY11-25915. M.W. thanks the Swiss National Science Foundation for support under Grant 200021-165509 and acknowledges Simons Foundation Grant 454953. This material is based upon work performed using computational resources supported by the Center for Scientific Computing at University of California, Santa Barbara and NSF Grant CNS-0960316, and by the High Performance Computing at NYU program.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1615536114/-/DCSupplemental.
References
- 1.Monod J, Wyman J, Changeux J-P. On the nature of allosteric transitions: A plausible model. J Mol Biol. 1965;12(1):88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 2.Changeux J-P, Edelstein SJ. Allosteric mechanisms of signal transduction. Science. 2005;308(5727):1424–1428. doi: 10.1126/science.1108595. [DOI] [PubMed] [Google Scholar]
- 3.Daily MD, Gray JJ. Local motions in a benchmark of allosteric proteins. Proteins. 2007;67(2):385–399. doi: 10.1002/prot.21300. [DOI] [PubMed] [Google Scholar]
- 4.McLaughlin RN, Jr, Poelwijk FJ, Raman A, Gosal WS, Ranganathan R. The spatial architecture of protein function and adaptation. Nature. 2012;491(7422):138–142. doi: 10.1038/nature11500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nussinov R, Tsai C-J. Allostery in disease and in drug discovery. Cell. 2013;153(2):293–305. doi: 10.1016/j.cell.2013.03.034. [DOI] [PubMed] [Google Scholar]
- 6.Amor BRC, Schaub MT, Yaliraki SN, Barahona M. Prediction of allosteric sites and mediating interactions through bond-to-bond propensities. Nat Commun. 2016;7:12477. doi: 10.1038/ncomms12477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Halabi N, Rivoire O, Leibler S, Ranganathan R. Protein sectors: Evolutionary units of three-dimensional structure. Cell. 2009;138(4):774–786. doi: 10.1016/j.cell.2009.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Perutz MF. Stereochemistry of cooperative effects in haemoglobin: Haem–haem interaction and the problem of allostery. Nature. 1970;228:726–734. doi: 10.1038/228726a0. [DOI] [PubMed] [Google Scholar]
- 9.Gerstein M, Lesk AM, Chothia C. Structural mechanisms for domain movements in proteins. Biochemistry. 1994;33(22):6739–6749. doi: 10.1021/bi00188a001. [DOI] [PubMed] [Google Scholar]
- 10.Goodey NM, Benkovic SJ. Allosteric regulation and catalysis emerge via a common route. Nat Chem Biol. 2008;4(8):474–482. doi: 10.1038/nchembio.98. [DOI] [PubMed] [Google Scholar]
- 11.Gandhi PS, Chen Z, Mathews FS, Di Cera E. Structural identification of the pathway of long-range communication in an allosteric enzyme. Proc Natl Acad Sci USA. 2008;105(6):1832–1837. doi: 10.1073/pnas.0710894105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lockless SW, Ranganathan R. Evolutionarily conserved pathways of energetic connectivity in protein families. Science. 1999;286(5438):295–299. doi: 10.1126/science.286.5438.295. [DOI] [PubMed] [Google Scholar]
- 13.Teşileanu T, Colwell LJ, Leibler S. Protein sectors: Statistical coupling analysis versus conservation. PLoS Comput Biol. 2015;11(2):e1004091. doi: 10.1371/journal.pcbi.1004091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liang J, Dill KA. Are proteins well-packed? Biophys J. 2001;81(2):751–766. doi: 10.1016/S0006-3495(01)75739-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liu AJ, Nagel SR, van Saarloos W, Wyart M. The Jamming Scenario: An Introduction and Outlook. Oxford Univ Press; Oxford: 2010. [Google Scholar]
- 16.Düring G, Lerner E, Wyart M. Phonon gap and localization lengths in floppy materials. Soft Matter. 2013;9(1):146–154. [Google Scholar]
- 17.Lerner E, DeGiuli E, Düring G, Wyart M. Breakdown of continuum elasticity in amorphous solids. Soft Matter. 2014;10:5085–5092. doi: 10.1039/c4sm00311j. [DOI] [PubMed] [Google Scholar]
- 18.Rocks JW, et al. 2016. Designing allostery-inspired response in mechanical networks. arXiv:1607.08562.
- 19.Yan L, Bouchaud J-P, Wyart M. 2016. Edge mode amplification in disordered elastic networks. arXiv:1608.07222.
- 20.Hemery M, Rivoire O. Evolution of sparsity and modularity in a model of protein allostery. Phys Rev E. 2015;91(4):042704. doi: 10.1103/PhysRevE.91.042704. [DOI] [PubMed] [Google Scholar]
- 21.Tlusty T, Libchaber A, Eckmann J-P. 2016. Physical model of the sequence-to-function map of proteins. arXiv:1608.03145.
- 22.Tlusty T. Self-referring DNA and protein: A remark on physical and geometrical aspects. Philos Trans A Math Phys Eng Sci. 2016;374(2063):20150070. doi: 10.1098/rsta.2015.0070. [DOI] [PubMed] [Google Scholar]
- 23.Atilgan AR, et al. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys J. 2001;80(1):505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.De Los Rios P, et al. Functional dynamics of PDZ binding domains: A normal-mode analysis. Biophys J. 2005;89(1):14–21. doi: 10.1529/biophysj.104.055004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zheng W, Brooks BR, Thirumalai D. Low-frequency normal modes that describe allosteric transitions in biological nanomachines are robust to sequence variations. Proc Natl Acad Sci USA. 2006;103(20):7664–7669. doi: 10.1073/pnas.0510426103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yan L, Wyart M. Evolution of covalent networks under cooling: Contrasting the rigidity window and jamming scenarios. Phys Rev Lett. 2014;113(21):215504. doi: 10.1103/PhysRevLett.113.215504. [DOI] [PubMed] [Google Scholar]
- 27.Yan L, Wyart M. Adaptive elastic networks as models of supercooled liquids. Phys Rev E. 2015;92(2):022310. doi: 10.1103/PhysRevE.92.022310. [DOI] [PubMed] [Google Scholar]
- 28.Maxwell JC. On the calculation of the equilibrium and stiffness of frames. Philos Mag. 1864;27(5755):294–299. [Google Scholar]
- 29.Dunker AK, et al. The unfoldomics decade: An update on intrinsically disordered proteins. BMC Genomics. 2008;9(Suppl 2):S1. doi: 10.1186/1471-2164-9-S2-S1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kane CL, Lubensky TC. Topological boundary modes in isostatic lattices. Nat Phys. 2014;10(1):39–45. [Google Scholar]
- 31.Chen BG, Upadhyaya N, Vitelli V. Nonlinear conduction via solitons in a topological mechanical insulator. Proc Natl Acad Sci USA. 2014;111(36):13004–13009. doi: 10.1073/pnas.1405969111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sussman DM, Stenull O, Lubensky TC. 2015. Topological boundary modes in jammed matter. arXiv:1512.04480.
- 33.Jacobs DJ, Rader AJ, Kuhn LA, Thorpe MF. Protein flexibility predictions using graph theory. Proteins. 2001;44(2):150–165. doi: 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
- 34.Cover TM, Thomas JA. Elements of Information Theory. 2nd Ed Wiley; New York: 2006. [Google Scholar]
- 35.Weigt M, White RA, Szurmant H, Hoch JA, Hwa T. Identification of direct residue contacts in protein–protein interaction by message passing. Proc Natl Acad Sci USA. 2009;106(1):67–72. doi: 10.1073/pnas.0805923106. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.