Designing allostery-inspired response in mechanical networks

Significance

We show that removal of a small number of bonds in a random elastic network can dramatically change its mechanical response. Our theoretical approach precisely and efficiently controls the local strain at one point in such a network in response to a strain applied elsewhere in the system. The responses we create are inspired by the long-range-correlated deformations that often characterize allostery in proteins. The ubiquity of allostery in biological molecules suggests that it is relatively easy to develop through evolution. Our nearly 100% success rate in designing these responses by removing a very small fraction of bonds shows that it is similarly easy to create these types of elastic responses in disordered mechanical networks.

Abstract

Recent advances in designing metamaterials have demonstrated that global mechanical properties of disordered spring networks can be tuned by selectively modifying only a small subset of bonds. Here, using a computationally efficient approach, we extend this idea to tune more general properties of networks. With nearly complete success, we are able to produce a strain between any two target nodes in a network in response to an applied source strain on any other pair of nodes by removing only ∼1% of the bonds. We are also able to control multiple pairs of target nodes, each with a different individual response, from a single source, and to tune multiple independent source/target responses simultaneously into a network. We have fabricated physical networks in macroscopic 2D and 3D systems that exhibit these responses. This work is inspired by the long-range coupled conformational changes that constitute allosteric function in proteins. The fact that allostery is a common means for regulation in biological molecules suggests that it is a relatively easy property to develop through evolution. In analogy, our results show that long-range coupled mechanical responses are similarly easy to achieve in disordered networks.

The ability to tune the response of mechanical networks has significant applications for designing metamaterials with unique properties. For example, the ratio $G/B$ of the shear modulus $G$ to the bulk modulus $B$ can be tuned by over 16 orders of magnitude by removing only 2% of the bonds in an ideal spring network (1). Such a pruning procedure allows one to create a network that has a Poisson ratio $\nu$ anywhere between the auxetic limit ($\nu =-\mathrm{\hspace{0.17em}1}$) and the incompressible limit [$\nu =\mathrm{\hspace{0.17em}1}/(d-1)$ in $d$ dimensions]. In another example, the average coordination number of a network controls the width of a failure zone under compression or extension (2). Both these results are specific to tuning the global responses of a material. However, many applications rely on targeting a local response to a local perturbation applied some distance away. For example, allostery in a protein is the process by which a molecule binding locally to one site affects the activity at a second distant site (3). Often this process involves the coupling of conformational changes between the two sites (4). Here we ask whether disordered networks, which generically do not exhibit this behavior, can be tuned to develop a specific allostery-inspired structural response by pruning bonds.

We introduce a formalism for calculating how each bond contributes to the mechanical response, anywhere in the network, to an arbitrary applied source strain. The formalism allows us to develop algorithms to control how the strain between two arbitrarily chosen target nodes responds to the strain applied between two arbitrary source nodes. In the simplest case, bonds are removed sequentially until the desired target strain is reached. For almost all of the initial networks studied, only a small fraction of the bonds need to be removed to achieve success. As was the case in tuning the bulk and shear moduli, we can achieve the desired response in a number of ways by pruning different bonds. We have extended our approach to manipulate multiple targets simultaneously from a single source, as well as to create multiple independent responses to different locally applied strains in the same network. Our central result is the ease and precision with which allostery-inspired conformational responses can be created with only minimal changes to the network structure.

We demonstrate the success of this method by reproducing our theoretical networks in macroscopic physical systems constructed in two dimensions by laser-cutting a planar sheet and in three dimensions by using 3D printing technology. Thus, we have created a class of mechanical metamaterials with specific allostery-inspired functions.

Theoretical Approach

Our networks are generated from random configurations of soft spheres in three dimensions or disks in two dimensions with periodic boundary conditions that have been brought to a local energy minimum using standard jamming algorithms (5, 6); the spheres overlap and are in mechanical equilibrium. We convert a jammed packing into a spring network by joining the centers of each pair of overlapping particles with an unstretched central-force spring. We chose this ensemble because it is disordered and provides initial networks with properties—such as elastic moduli—that depend on the coordination of the network in ways that are understood (1, 7, 8). We can work either with the entire system that is periodically continued in space or with a finite region with free boundaries that is cut from the initial network.

Starting with a network with $N$ nodes and $N_b$ bonds in $d$ dimensions, our aim is to tune the strain ${\epsilon }_T$ between two target nodes in response to the strain ${\epsilon }_S$ applied between two source nodes. (The two nodes comprising the source, and similarly the target, are chosen so that they are not initially connected by a bond; see Supporting Information for details.) We create a specific response in our system by tuning the strain ratio $\eta ={\epsilon }_T/{\epsilon }_S$ to a desired value ${\eta }^{\ast }$. At each step, we calculate to linear order the change in $\eta$ in response to the removal of each bond in the network using a computationally efficient linear algebra approach (Materials and Methods). We then remove the bond whose deletion minimizes the difference between $\eta$ and ${\eta }^{\ast }$ and repeat until we reach a desired tolerance.

Computational Results

We apply our tuning approach to networks with free boundaries in both two and three dimensions (Materials and Methods). We characterize the connectivity of our networks by the excess coordination number $\mathrm{\Delta }Z\equiv Z-Z_{\text{iso}}$. Here $Z$ is the average number of bonds per node and $Z_{\text{iso}}\equiv \mathrm{\hspace{0.17em}2}d-d(d+1)/N$ is the minimum number of bonds needed for rigidity in a network with free boundary conditions (9). For each trial, a pair of source nodes was chosen randomly on the network’s surface, along with a pair of target nodes located on the surface at the opposing pole. (Note that we could have chosen anywhere in the network for the location of the source and target.) In two dimensions, we chose networks that, on average, had $190$ nodes and $400$ bonds before tuning, with $\mathrm{\Delta }Z\approx 0.19$. In three dimensions, networks had, on average, $240$ nodes, $740$ bonds, and $\mathrm{\Delta }Z\approx \mathrm{\hspace{0.17em}0.18}$. Before pruning, the average strain ratio of the networks in two dimensions was $\eta \approx 0.03$ and in three dimensions was $\eta \approx 0.2$ for the system sizes and $\mathrm{\Delta }Z$ values we studied. The response of each network was tuned by sequentially removing bonds until the difference between the actual and desired strain ratios, $\eta$ and ${\eta }^{\ast }$, respectively, was less than 1%.

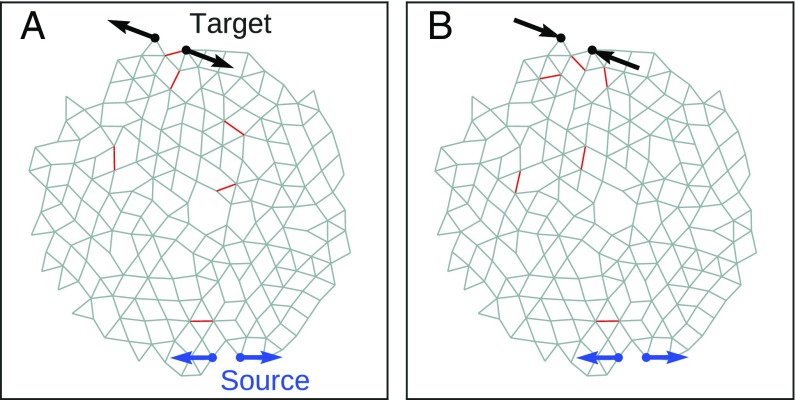
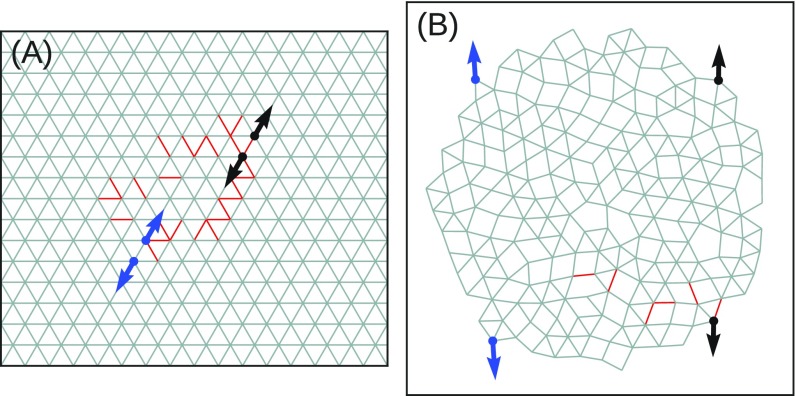
To demonstrate the ability of our approach to tune the response, we show results for $\eta =\pm 1$. Note that $\eta >\mathrm{\hspace{0.17em}0}$ ($<0$) corresponds to a larger (smaller) separation between the target nodes when the source nodes are pulled apart. Fig. 1 shows a typical result for a 2D network: in Fig. 1A, the strain ratio has been tuned to $\eta =+1$ with just 6 (out of 407) bonds removed; Fig. 1B shows the same network tuned to $\eta =-1$ with a different set of 6 removed bonds. The red lines in each figure indicate the bonds that were pruned. Animations of the full nonlinear responses of these networks are provided in Movies S1 and S2. We note that some of the removed bonds are the same for both $\eta =+1$ and $\eta =-1$.

Fig. 1.

Network with $194$ nodes, and $407$ bonds at $\mathrm{\Delta }Z=\mathrm{\hspace{0.17em}0.19}$ tuned to exhibit (A) expanding ($\eta =+1$) and (B) contracting ($\eta =-1$) responses to within 1% of the desired response. Source nodes are shown in blue, and target nodes are shown in black. Arrows indicate the sign and magnitude of the extensions of the source and target. The removed bonds are shown as red lines.

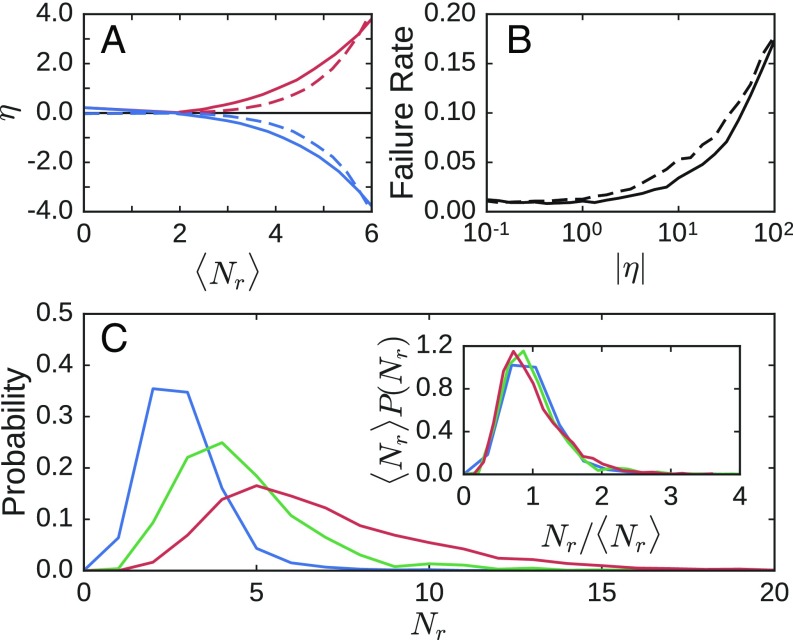
The average strain ratio versus the number of removed bonds is shown in Fig. 2A. Remarkably few bonds need to be removed to achieve strain ratios of $\eta =\pm 1$. In two dimensions, only about five bonds out of about 400 were removed, on average (∼1%); similarly, in three dimensions, only about 4 bonds out of about 740 were removed on average (∼0.5%). Fig. 2B shows the fraction of networks that cannot be tuned successfully to within 1% of a given strain ratio. The failure rate is less than 2% for strain ratios of up to $|\eta |=\mathrm{\hspace{0.17em}1}$ in two dimensions and less than 1% in three dimensions. Therefore, not only does our algorithm allow for precise control of the response, it also works the vast majority of the time. The failure rate increases significantly for $|\eta |\gg \mathrm{\hspace{0.17em}1}$, but here we are considering only the linear response of the network. Extremely large values of $\eta$ necessitate an extremely small input strain at the source and may therefore not be physically relevant.

Fig. 2.

(A) Strain ratio $\eta$ versus the number of removed bonds $N_r$ for expanding (red) and contracting (blue) responses in both 2D (solid lines) and 3D (dashed lines). For each response type and dimension, the strain ratio is averaged over 1,024 tuned networks constructed from $512$ initial systems. Networks in 2D have about $190$ nodes and $400$ bonds, on average, with an initial excess bond coordination of $\mathrm{\Delta }Z\approx 0.19$, whereas those in 3D have about $240$ nodes and $740$ bonds, on average, with $\mathrm{\Delta }Z\approx 0.18$. (B) Failure rate of tuning systems to within 1% of a specified strain ratio magnitude in 2D (dashed lines) and 3D (solid lines) averaged over contracting and expanding responses. (C) Distribution of the number of removed bonds for three different strain ratio magnitudes: $|\eta |=\mathrm{\hspace{0.17em}0.1}$ (blue), $|\eta |=\mathrm{\hspace{0.17em}1.0}$ (green), and $|\eta |=\mathrm{\hspace{0.17em}10.0}$ (red). (Inset) All three distributions collapse when scaled by the average number of removed bonds $⟨N_r⟩$.

The failure rate is insensitive to $\mathrm{\Delta }Z$ except at very small values. In the small $\mathrm{\Delta }Z$ regime, the failure rate is higher because very few bonds can be removed without compromising the rigidity of the system. If we increase the bond connectivity to $\mathrm{\Delta }Z\approx \mathrm{\hspace{0.17em}1.0}$ for networks in two dimensions, the failure rate remains very low, but bonds are removed in a thin region connecting the target and source. This narrowing of the “damage” region is reminiscent of the results of ref. 2, in which bonds above a threshold stress were broken, or of ref. 1, in which bonds that contribute the most to either the bulk or shear modulus were successively pruned. A narrow damage region is consistent with results seen in some allosteric proteins, in which strain is localized to a thin region between the source and target (10).

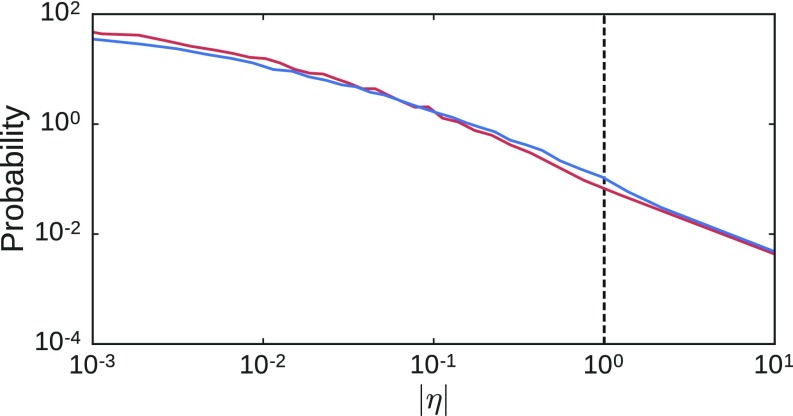
Fig. 2C shows the distribution of the number of bonds that must be removed to tune a network to within 1% of a desired strain ratio for $|\eta |=0.1$, $1$, and $10$. These distributions are broad, and the mean shifts upward as $\eta$ increases. Fig. 2C, Inset shows that the distributions collapse when normalized by the average number of removed bonds $⟨N_r⟩$. Note that we do not achieve the desired strain ratio simply by tuning the entire free surface of the network to have large strain ratios; the response of the designated target is large, whereas the strain response of other pairs of nodes is essentially unaffected by the source strain (Fig. S1).

Fig. S1.

Distribution of strain ratios for pairs of neighboring nodes on the surface (excluding the source and target pairs) of the networks before (red) and after (blue) tuning. Results are shown for 2D networks that had, on average, $190$ nodes and $400$ bonds with $\mathrm{\Delta }Z\approx \mathrm{\hspace{0.17em}0.19}$; this includes $512$ initial networks each tuned separately to a positive and negative strain ratio with magnitude $|\eta |=\mathrm{\hspace{0.17em}1.0}$ for a total of 1,024 tuned networks. Tuned networks are only included if the tuned strain ratio is within 1% of the desired strain ratio. The responses for pairs of nodes other than the source and target are essentially unaffected. The target strain ratio is shown with a vertical dashed line. All distributions include both contracting and expanding responses.

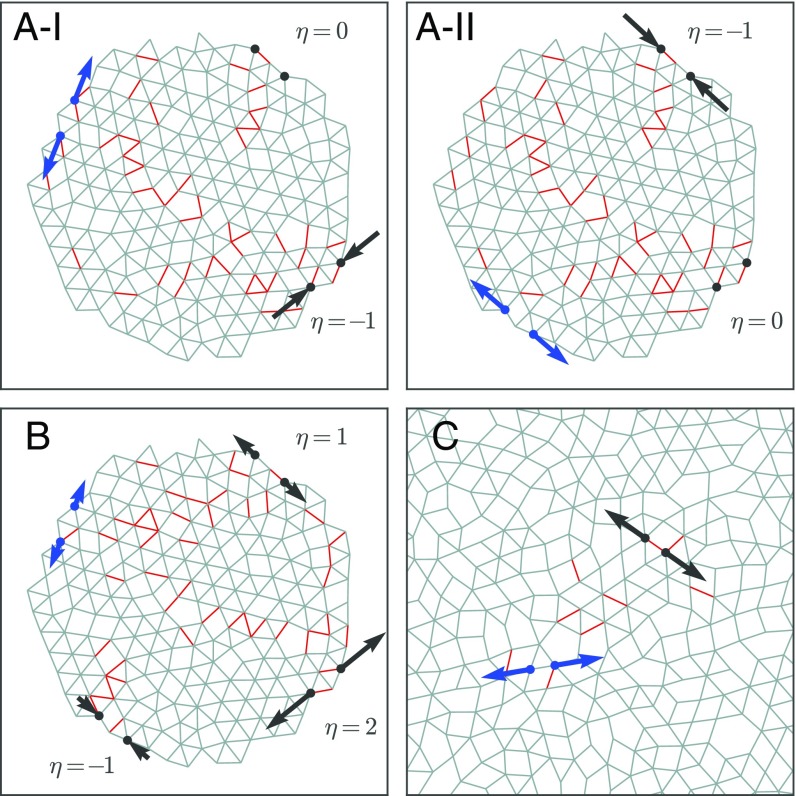
Fig. 3 demonstrates the variety of responses that we are able to create. Fig. 3A, I and II show a single network with two independent sources and targets whose responses were tuned simultaneously and independently of one another. When a strain is applied to the first pair of source nodes, its target responds strongly, whereas the other target does not respond at all. Likewise, when the strain is applied to the second pair of source nodes, its target responds, whereas the first target does not. In Fig. 3B, a network with one pair of source nodes controls three targets, each of which has been tuned to a different strain ratio. These networks have $\mathrm{\Delta }Z=\mathrm{\hspace{0.17em}1.0}$; the failure rate for creating these more complicated responses is generally higher for lower values of $\mathrm{\Delta }Z$ in two dimensions. Fig. 3C shows a periodic disordered network with one source and target, demonstrating that a network can be tuned successfully without free boundaries (see Movie S3 for an animation of the nonlinear response). We have also found that initial disorder in the network is not necessary for success (Fig. S2A), nor is close proximity of the two nodes comprising the source or the target (Fig. S2B).

Fig. 3.

(A) Network with $200$ nodes and $502$ bonds at $\mathrm{\Delta }Z=\mathrm{\hspace{0.17em}1.0}$ with two independent responses tuned simultaneously into the system. (I) One target contracts in response to a strain at the first source, whereas the other target does not respond. (II) Second target responds to a strain at the second source, whereas the first target remains unaffected. This demonstrates that separate responses can be shielded effectively from one another. (B) Same network tuned to show responses at three targets with responses of $\eta =\mathrm{\hspace{0.17em}1}$, $2$, and $-1$. All three targets are controlled by a single pair of source nodes. (C) Periodic network with $254$ nodes and $568$ bonds at $\mathrm{\Delta }Z=\mathrm{\hspace{0.17em}0.47}$ tuned to display an expanding response with $\eta =\mathrm{\hspace{0.17em}1}$, showing that open boundaries are not necessary for tuning to be successful.

Fig. S2.

(A) Periodic triangular lattice with $256$ nodes and $768$ bonds at $\mathrm{\Delta }Z=\mathrm{\hspace{0.17em}2.0}$ tuned to exhibit a strain ratio of $\eta =\mathrm{\hspace{0.17em}1.0}$. This example shows that disorder in the initial network is not necessary for a response to be tuned successfully. (B) Network with $200$ nodes and $457$ bonds with $\mathrm{\Delta }Z=\mathrm{\hspace{0.17em}0.57}$ tuned to show a strain ratio of $\eta =\mathrm{\hspace{0.17em}1.0}$. This example demonstrates that the proximity of the source nodes to each other, and similarly the target nodes, is also not necessary for success.

Experimental Results

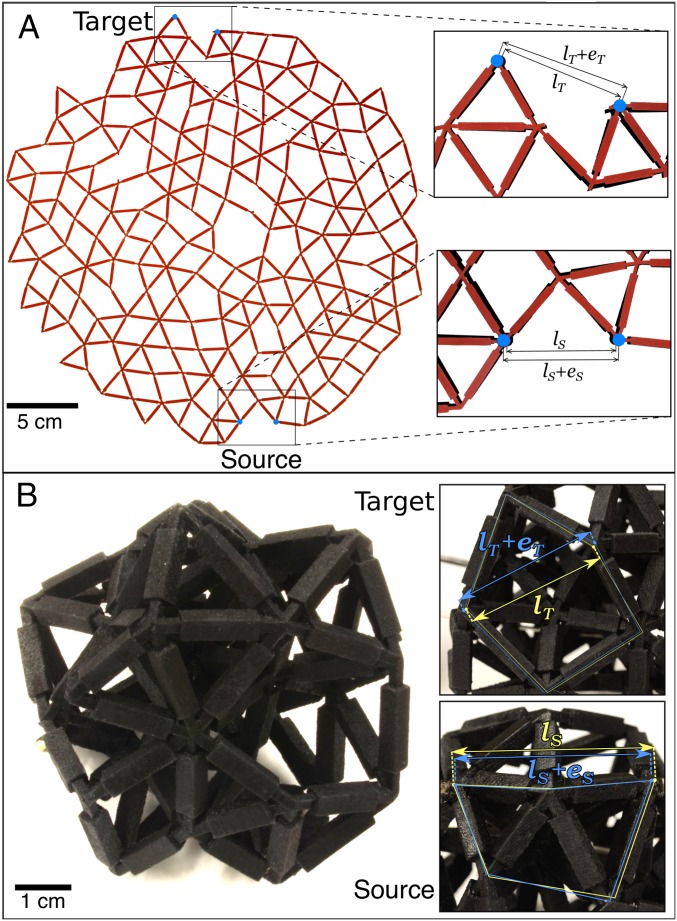
Fig. 4A shows an image of a 2D network created by laser-cutting a flat sheet. The network is the same as the simulation shown in Fig. 1A. Insets (zoomed-in areas) show the strain response at the target along with the applied strain at the source nodes. Movie S4 shows the response of a similarly designed network. Fig. 4B shows an image of a 3D network created by 3D printing. In this case, the network was designed to have a strain ratio of $\eta =-5$. Insets again show the strains of the source and target.

Fig. 4.

(A) Physical realization of the network in Fig. 1A. (Insets) Zoom-ins show the initial and final distance between the source nodes, $l_S$ and $l_S+e_S$, respectively, and between the target nodes, $l_T$ and $l_T+e_T$. The undeformed network is shown in black, and the deformed network is superimposed in red. (B) Photograph of a 3D network constructed by 3D printing with 33 nodes and 106 bonds at $\mathrm{\Delta }Z=\mathrm{\hspace{0.17em}0.42}$ tuned to exhibit a negative response ($\eta =-5.0$). (Insets) In the zoom-ins, the yellow and blue arrows show the distance between the undeformed, $l_S$ ($l_T$), and deformed, $l_S+e_S$ ($l_T+e_T$), source (target) nodes, respectively.

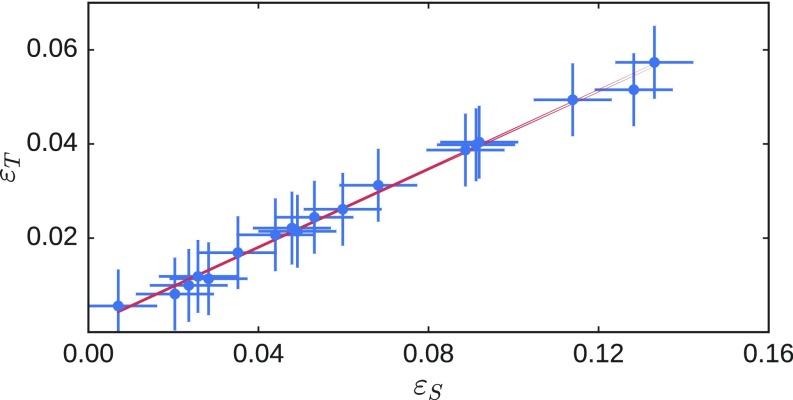
To obtain a quantitative analysis of how well the physical realizations agree with the simulated networks, we measure the strain on every bond in the 2D example when the distance between the source nodes is varied. The majority of the bonds do not change their length appreciably. We therefore focus only on the distance between nodes that were connected by bonds that were removed as the network was tuned. As one might expect, these are the most sensitive to the applied source strain. We calculate, for those changes in distances, the Pearson correlation coefficient between the experiments and the simulations,

$$C=\frac{⟨(x_i-⟨x_i⟩)(c_i-⟨c_i⟩)⟩}{{\sigma }_x{\sigma }_c}.$$ [1]

Here $x_i$ ($c_i$) is defined as the fractional change due to the source strain in the distance between nodes initially connected by bond $i$ as measured in experiments (computer simulations). The standard deviations of $x_i$ and $c_i$ are ${\sigma }_x$ and ${\sigma }_c$, respectively. We find that, when averaged over four experimental realizations of different designed networks, $C=\mathrm{\hspace{0.17em}0.98}\pm \mathrm{\hspace{0.17em}0.02}$, confirming that the experiments are very accurate realizations of the theoretical models.

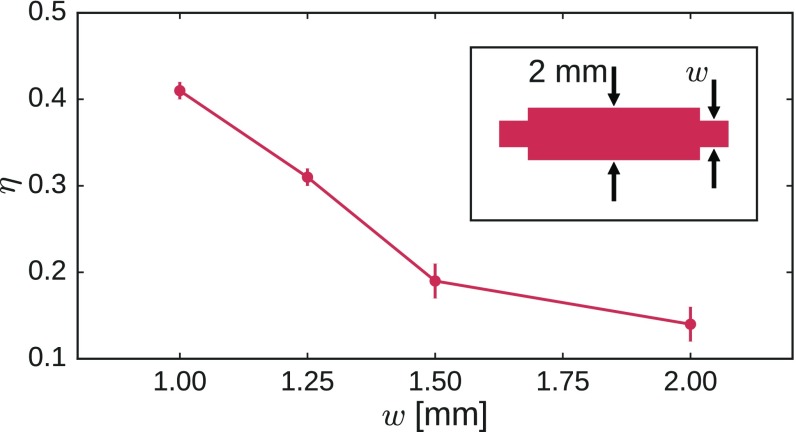
In contrast to our simulations, where junctions are connected only via central-force springs, our experimental systems have physical struts between the nodes. This introduces bond-bending forces, because the struts emerging from a node have preferred angles between them. To minimize such forces, we have manufactured the struts with a nonuniform width so that they are thinner at their ends where they attach to a node than along the rest of their length. This ensures that the struts deform preferentially near the nodes rather than buckling in their middle. Fig. 5 shows that decreasing the width of the thinnest part of the struts alleviates effects due to bond bending and monotonically increases the response. This is crucial for determining how much of the designed response survives in our physical networks.

Fig. 5.

Strain ratio $\eta$ versus $w$, the width of the struts near their ends. The responses are those of the network shown in Fig. 1A for four values of $w$. The response increases monotonically as the bonds are made thinner near the nodes. At their center, the struts have a full width of 2 mm. (Inset) The strut geometry.

Apart from bond bending, there is also a possibility of 2D networks buckling out of the plane, along with nonlinear effects that are present in real systems undergoing finite strains. All these factors can weaken the designed response. To investigate these effects, we used laser cutting to create realizations of 10 of the 2D networks produced from the computations in Fig. 2. The networks chosen were tuned successfully in the linear regime and had nonlinear responses within a factor of 2 of the linear prediction at a source strain of 5%, according to our computations. For the experimental realizations, we found that in the nonlinear regime, three of the networks demonstrated a response that was more than 10% of the designed response at a source strain of 5%. (See Fig. S3 for an example of an experimental strain measurement.)

Fig. S3.

The target strain ${\epsilon }_T$ as a function of source strain ${\epsilon }_S$ is shown in blue for a physical realization of the network depicted in Fig. 1A. The red line shows that the response is linear over a large range of input strains.

Discussion

We have shown that it is strikingly easy to tune allosteric deformation responses into an arbitrary spring network by removing only a small fraction of the bonds. Not only can we tune the strain ratio to large negative or positive values for the same network, but we achieve strain ratios of order $|\eta |\approx \mathrm{\hspace{0.17em}1}$ with almost 100% success. Our theoretical approach can also be extended to more general responses. We can control multiple pairs of target nodes simultaneously with the same pair of source nodes, and we can tune multiple independent source/target responses simultaneously into a network. We have also achieved similarly excellent results for tuning responses in periodically continued systems.

The approach we have described here performs a discrete optimization of the response. We have also tuned the response using a standard numerical optimization technique (e.g., gradient descent), by varying the stiffnesses of all of the bonds continuously. This brute force method is less efficient but equally successful in producing a desired response. Our approach can also be generalized to other types of bond manipulation such as introducing new bonds.

Our theoretical approach provides a framework for understanding and controlling the response of networks relevant to a wide range of fields. For example, networks with built-in localized, long-distance responses could be a novel way of designing architectural structures based on disordered frameworks that have added functionalities. In addition, our theoretical approach can be generalized to other problems such as origami, where one may wish to tune the fold structure so that the system folds in a specific way in response to locally applied external forces (11). This problem is similar to ours, except that folds are added instead of bonds being removed. Ref. 11 introduces an optimization technique in which fold rigidities vary continuously. This technique is computationally expensive because the network response must be recalculated with each optimization step. A generalization of our theoretical approach to origami, using language similar to that of ref. 12, could lead to a more efficient algorithm.

The network responses we create are reminiscent of the localized, long-range-correlated deformations that characterize allostery in proteins. In fact, folded proteins have long been modeled as elastic networks (13), and the response to localized forces in the resulting networks has been studied (14). Our results demonstrate the ease with which allosteric conformational changes in networks can be achieved by removing a very small set of bonds. Perhaps our finding provides a rationale for why allostery is so common in large biological molecules (15).

Similarly, our finding that networks can be tuned to have a variety of different responses may help elucidate multifunctional behavior (16) and multiple allosterically interacting sites (17) in proteins. It has also been observed that small changes in a protein’s covalent structure can often change its biochemical function (18). One might ask whether our method could be extended to develop a systematic way to determine which intraprotein interactions to modify or create new allosteric functions. It has been emphasized that the ability to control allosteric responses in folded proteins could lead to significant advances in drug design (19, 20). Although much work has focused on identifying, understanding, and controlling preexisting allosteric properties, the question of how to introduce new allosteric functions is relatively unexplored (21).

Our success in constructing experimental systems despite nonlinear and bond-bending effects suggests that results are often robust even outside the simple linear regime. However, proteins are thermal whereas our networks are athermal structures. Statistical fluctuations in the structure of proteins have been shown to play an important role in allosteric functionality (22, 23). In the linear response regime, the equilibrium response at finite temperature is equivalent to that at zero temperature, so the set of bonds that are removed and the average strain ratio are independent of temperature in the harmonic regime. However, the nonlinear response will show differences, particularly at temperatures beyond the harmonic regime. It is thus important to investigate how thermal effects can influence the ability to design a desired response in the nonlinear regime. In addition, protein contact networks generally contain prestressed bonds, as well as bond-bending and twisting constraints, whereas our theoretical networks are constructed in the absence of such effects (24–26).

Further work needs to be done to understand why removing specific bonds achieves the desired response. Our method of identifying the elements of the stress basis associated with individual bonds (Supporting Information) indicates that these stress states are fundamental to this understanding. The dependence on network size and node connectivity also needs to be understood in greater detail. The limits of our algorithm are not yet known, including the number of targets that can be controlled and the number of independent responses that can be tuned for networks of a given size and coordination. To understand experimental systems ranging from proteins to the macroscopic networks we have fabricated, we must extend the theory to include temperature, dynamics, prestress, bond-bending, and nonlinear effects due to finite strains. Our approach provides a starting point for addressing these issues.

Materials and Methods

Computed Networks and Choice of Source and Target Nodes.

To create a finite network, we choose a cutoff radius from the center of our box and remove all bonds that cross that surface. This process often creates zero-energy modes at the boundary of our network. Because we require rigid networks, we remove nodes associated with these modes. We calculate zero modes by performing a spectral decomposition of the dynamical matrix. For each zero mode calculated this way, we identify the node with the largest displacement amplitude and remove it. We then recalculate the zero modes and repeat this process until no zero modes exist. This method of removing zero modes works in any dimension and does not require an arbitrary threshold for whether a node contributes to a zero mode or not. Our final networks are approximately disk-shaped in two dimensions or ball-shaped in three dimensions with $N$ nodes and $N_b$ bonds.

We choose the pair of source nodes to lie on the exposed surface of the networks. The pair of target nodes is chosen to be on the opposing pole of the network surface. When choosing a pair of nodes, we also ensure that the nodes are not connected by a bond. This is done to avoid surface bonds whose tensions do not couple to the rest of the network. However, because our formalism relies on applying tensions and measuring the strains of bonds, we introduce a bond of zero stiffness, called a “ghost” bond, between the two nodes comprising each source or target (Supporting Information).

Further Details of Theoretical Approach.

Our approach tunes the ratio $\eta ={\epsilon }_T/{\epsilon }_S$ of the target strain ${\epsilon }_T$ to the source strain ${\epsilon }_S$ by removing bonds sequentially, one at a time. First, we define the cost function that measures the difference between the network’s response $\eta$ and the desired response ${\eta }^{\ast }$,

$${\mathrm{\Delta }}^2\equiv \sum _{j=1}^n\{\begin{array}{cc}\hfill {({\eta }_j/{\eta }_j^{\ast }-1)}^2\hfill & \hfill \text{if}\hspace{1em}{\eta }_j^{\ast }\ne 0\\ \hfill {\eta }_j^2\hfill & \hfill \text{if}\hspace{1em}{\eta }_j^{\ast }=0\end{array}\mathit{\text{,}}$$ [2]

where $j$ indexes the targets and their corresponding sources (e.g., $n=\mathrm{\hspace{0.17em}1}\mathit{\text{,}}2\mathit{\text{,}}3$ in Figs. 1 and 3 A and B, respectively). Target/source pairs may be defined for the same network response, or for separate independent responses for the same network with different applied source strains. With each step, we choose to remove the bond that creates the largest decrease in ${\mathrm{\Delta }}^2$.

To decide which bond to remove, we must calculate how the removal of each bond changes $\eta$. First, we define the vectors of bond extensions $|e⟩$ and bond tensions $|t⟩$ in response to the externally applied strain, each of length $N_b$. To access the extensions and tensions on individual bonds, we define the complete orthonormal bond basis $|i⟩$, where $i$ indexes the bonds. The extension on bond $i$ can then be found, $e_i=⟨i|e⟩$, along with the bond tension, $t_i=⟨i|t⟩$. The strain of bond $i$ is ${\epsilon }_i=e_i/l_i$, where $l_i$ is the bond’s equilibrium length. The tension and extension are related by a form of Hooke’s law,

$$|t⟩=F^{-1}|e⟩\mathit{\text{,}}$$ [3]

where the flexibility matrix is defined as $⟨i|F|j⟩={\delta }_{ij}/k_i$. Here we choose the stiffness of bond $i$ to be $k_i={\lambda }_i/l_i$, where ${\lambda }_i$ is the bond’s material modulus with units of energy per unit length.

In addition to the bond tensions and extensions, we can define the $dN$ vectors of node displacements $|u⟩$ and net forces on nodes $|f⟩$. The equilibrium matrix $Q$ relates quantities defined on the bonds to those defined on the nodes through the expressions $Q^T|u⟩=|e⟩$ and $Q|t⟩=|f⟩$ (27). In general, $Q$ is a rectangular matrix with $dN$ rows and $N_b$ columns. The total energy can then be written as

$$E=\frac{1}{2}⟨u|H|u⟩\mathit{\text{,}}$$ [4]

where the Hessian matrix $H=Q{F}^{-1}{Q}^T$ is a $dN\times dN$ matrix. In the presence of an externally applied set of tensions $|t^{\ast }⟩$, the minimum energy configuration satisfies

$$H|u⟩=Q|t^{\ast }⟩.$$ [5]

To calculate the change in the displacements if a bond were removed, the naive approach would be to set the stiffness to zero for that bond in the flexibility matrix and to solve this equation. However, performing this matrix inversion to test the removal of each bond can be prohibitively expensive, with a computational cost of $\mathcal{O}$ ($N_b{N}^3$), so we have developed a more efficient approach. Note that here we calculate the response to applied tensions, not the strains we need to calculate $\eta$. However, because we are only interested in the ratio of the target strain to the source strain and are working in the linear regime, we do not need to explicitly apply a strain nor specify the tension amplitude.

We use the equilibrium matrix $Q$ to define a convenient basis of the bond tensions and extensions. Performing a singular value decomposition of $Q$ gives access to its right singular vectors, yielding two mutually orthonormal subbases of vectors that, together, form a complete basis of size $N_b$ (28). The first subbasis comprises vectors with singular values of $Q$ that are zero, that is, tensions that do not result in net forces on the nodes. These are commonly known as the “states of self-stress” (SSS), and we denote them as $|s_{\beta }⟩$, where $\beta$ indicates the particular basis vector. These vectors can also be interpreted as incompatible extensions, or extensions that do not correspond to valid displacements. The second subbasis comprises vectors with positive singular values of $Q$: tensions that correspond to net forces on nodes, or extensions that are compatible with node displacement. We call these vectors the “states of compatible stress” (SCS) and denote them as $|c_{\alpha }⟩$, where $\alpha$ indicates the basis vector. In total, there are $N_c$ SCS basis vectors and $N_s$ SSS basis vectors, which total to $N_c+N_s=N_b$.

Using these two subbases (and rescaling the bond stiffnesses so they are identically $k$; see Supporting Information), we can calculate the discrete Green’s function

$$G=\frac{1}{k}\sum _{\alpha }|c_{\alpha }⟩⟨c_{\alpha }|\mathit{\text{,}}$$ [6]

which maps bond tensions to extensions. Using this result, we calculate the change in the bond extension vector $|e⟩$ if bond $i$ were to be removed,

$$|\mathrm{\Delta }e⟩=|C_i⟩\frac{⟨C_i|t^{\ast }⟩}{k\left(1-C_i^2\right)}\mathit{\text{,}}$$ [7]

where $|C_i⟩=kG|i⟩$ and $C_i^2\equiv ⟨C_i|C_i⟩$. From this equation, we can calculate the changes in both ${\epsilon }_T$ and ${\epsilon }_S$ and therefore the change $\eta$. This result can also be derived by inverting Eq. 5 and using the Sherman–Morrison formula to calculate the change in the inverse of the Hessian (29). Note that this calculation does not include the zero stiffnesses of the ghost bonds, which cannot be mapped to unity with the rest of the system. A generalization of Eq. 7 is needed to take this restriction into account (Supporting Information).

The next step is to calculate Eq. 7 (or its generalization found in Supporting Information) for the removal of each bond. We choose the bond that minimizes ${\mathrm{\Delta }}^2$ in Eq. 2 upon removal. One restriction is that we do not choose bonds that introduce zero modes (Supporting Information). Finally, once a bond is chosen, we recalculate the SCS and SSS subbases with the bond removed (Supporting Information).

A summary of our tuning algorithm contains the following steps:

• i)Transform to a system where all bonds initially have the same stiffnesses and add a ghost bond of zero stiffness for each pair of target and source nodes.
• ii)Use the equilibrium matrix to calculate the initial SCS and SSS bases.
• iii)Calculate the initial extensions of the source and target bonds in response to the applied tension $t^{\ast }$. Use this result to calculate the initial $\eta$.
• iv)For each bond, use the general form of Eq. 7 found in Eq. S20 to calculate the change in $\eta$ if that bond were to be removed.
• v)Remove the bond that minimizes ${\mathrm{\Delta }}^2$ in Eq. 2. Recalculate the SCS and SSS subbases with the bond removed and update the extensions of the source and target bonds.

We repeat steps iv and v until $\sqrt{{\mathrm{\Delta }}^2}<0.01$ or the process fails. The computational cost of determining and removing a bond using this algorithm is dominated by step v with a complexity of $\mathcal{O}$ ($N_b^3$), much faster than the naive approach of directly solving Eq. 5 with a complexity of $\mathcal{O}$($N_b{N}^3$).

There are three potential sources of failure represented in Fig. 2B: $\sqrt{{\mathrm{\Delta }}^2}$ cannot be lowered below $0.01$ by removing any bond, no bonds can be removed without creating zero modes, or the numerical error in ${\mathrm{\Delta }}^2$ exceeds 1%. This third source of failure arises because numerical error is introduced as bonds are removed. To ensure that our results are accurate, we compare our final value of ${\mathrm{\Delta }}^2$ to the value obtained from the solution of Eq. 5 with the given set of pruned bonds removed. If the relative error exceeds 1%, we call it a failure. Our results constitute an upper bound on the failure rate, which could potentially be reduced by using more accurate techniques to decrease numerical error or more sophisticated minimization algorithms.

Experimental Networks.

We create experimental realizations of the theoretically designed networks in both two and three dimensions. To make 2D networks, we obtain the positions of the nodes and struts from our design algorithm. Next, we laser-cut the shape of the network from a silicone rubber sheet. To reduce out-of-plane buckling, we use 1.6-mm-thick polysiloxane sheets with a Shore value of A90. The ratio of strut length to width within the plane of the network is ∼10:1. The struts are designed to be thinner at their ends to alleviate bond bending.

To make 3D networks, we determine the positions of nodes and struts from the computer simulations and fabricate the networks using 3D printing technology. The proprietary material is a mixture of rubber (simulating styrene based thermoplastic elastomers) and rigid plastic (simulating acrylonitrile butadiene styrene) with a Shore value of A85. The dimensions of each strut have a ratio of ∼1:1:11. As in our 2D networks, the struts are made thinner at their ends.

Note Added in Proof.

Yan et al. (31) present a different computational algorithm for tuning mechanical networks to generate an allosteric response.

Ghost Bonds

On the surface of our networks, there are many nodes with exactly $d$ bonds in $d$ dimensions. Any bond attached to one of these nodes is uncoupled from the rest of the network: Applying a tension to one of these bonds does not affect any tensions or extensions on any of the other bonds in the network to linear order. Likewise, no extensions can be measured on these bonds when a tension is applied elsewhere in the network. Therefore, we avoid choosing uncoupled bonds as sources or targets; this is done by ensuring that the pair of nodes comprising each source or target does not share a bond.

However, all calculations involve the bonds, so, to apply a tension or measure an extension between two nodes, it is convenient if they share a bond. To apply our approach, we introduce a ghost bond of zero stiffness between the two nodes of each source and target. These bonds do not affect our results, but they allow us to work without any direct reference to the nodes.

Creating Identical Bond Stiffnesses

To calculate the Green’s function in Eq. 6, it is necessary to work in a system where all bonds have identical stiffness. However, we do not want to be restricted to systems that satisfy this special requirement. The bonds in our experimental systems all have the same material modulus ${\lambda }_i=\lambda$, but their equilibrium lengths $l_i$ differ, resulting in bonds with nonidentical stiffnesses $k_i=\lambda /l_i$. Thus, we start with a system in which the bond stiffnesses are all different and map it onto an equivalent system in which all of the default bond stiffnesses are identical. Mapping is performed by introducing a flexibility matrix $F$ (as defined below Eq. 3) and scaling the equilibrium matrix so that $\overline{Q}=Q{F}^{-1/2}$. (Note that we can only scale out stiffnesses that are nonzero.) The energy can then be written in terms of $\overline{Q}$,

$$E=\frac{1}{2}{u}^T\overline{Q}{\overline{F}}^{-1}{\overline{Q}}^{T}u,$$ [S1]

where the scaled flexibility matrix $\overline{F}$ is proportional to the identity matrix, except for any entries that are zero. This energy is the same as that in Eq. 4, so the minimum energy configurations should have a one-to-one correspondence. Scaled extension or tension vectors are related to the unscaled versions by

$$|\overline{e}⟩=F^{-\frac{1}{2}}|e⟩$$ [S2]

$$|\overline{t}⟩=F^{\frac{1}{2}}|t⟩.$$ [S3]

Thus, we have implicitly performed all of our calculations on the scaled system and have converted back when calculating $\eta$.

Discrete Green’s Function

Using the SSS and SCS subbases, our goal is to calculate the discrete Green’s function shown in Eq. 6. We start by decomposing the bond tensions and extensions,

$$|t⟩=\sum _{\alpha }|c_{\alpha }⟩⟨c_{\alpha }|t⟩+\sum _{\beta }|s_{\beta }⟩⟨s_{\beta }|t⟩$$ [S4]

$$|e⟩=\sum _{\alpha }|c_{\alpha }⟩⟨c_{\alpha }|e⟩+\sum _{\beta }|s_{\beta }⟩⟨s_{\beta }|e⟩.$$ [S5]

Now suppose we apply some external tension to the bonds, $|t^{\ast }⟩$. The part of the external tension that projects onto the SCS basis will be balanced by tensions in the bonds, so that $⟨c_{\alpha }|t⟩=⟨c_{\alpha }|t^{\ast }⟩$. Additionally, the bond extensions that project onto the incompatible extensions, or SSS basis, should be zero because they are unphysical, $⟨s_{\beta }|e⟩=\mathrm{\hspace{0.17em}0}$. Inserting our decompositions of the tension and extension into Eq. 3, we get

$$\sum _{\alpha }|c_{\alpha }⟩⟨c_{\alpha }|t^{\ast }⟩+\sum _{\beta }|s_{\beta }⟩⟨s_{\beta }|t⟩=\sum _{\alpha }{F}^{-1}|c_{\alpha }⟩⟨c_{\alpha }|e⟩.$$ [S6]

If we project this equation onto the SCS vector $⟨c_{\alpha }\prime |$, we get a system of $N_c$ equations,

$$⟨c_{\alpha }\prime |t^{\ast }⟩=\sum _{\alpha }⟨c_{\alpha }\prime |F^{-1}|c_{\alpha }⟩⟨c_{\alpha }|e⟩=\sum _{\alpha }{K}_{\alpha \prime \alpha }⟨c_{\alpha }|e⟩,$$ [S7]

where $K_{\alpha \prime \alpha }=⟨c_{\alpha }\prime |F^{-1}|c_{\alpha }⟩$ is an $N_c\times N_c$ square matrix. If we invert this system of equations to solve for the extensions, we get

$$⟨c_{\alpha }|e⟩=\sum _{\alpha \prime }{K}_{\alpha \alpha \prime }^{-1}⟨c_{\alpha }\prime |t^{\ast }⟩.$$ [S8]

The full extension is then

$$|e⟩=\sum _{\alpha }|c_{\alpha }⟩⟨c_{\alpha }|e⟩=\sum _{\alpha ,\alpha \prime }|c_{\alpha }⟩K_{\alpha \alpha \prime }^{-1}⟨c_{\alpha }\prime |t^{\ast }⟩.$$ [S9]

In general, calculating the matrix inverse $K_{\alpha \alpha \prime }^{-1}$ is computationally intensive, because it is a square matrix of size $N_c$. To improve this, we map our system to one where all of the bond stiffnesses are identically $k$ as described in Creating Identical Bond Stiffnesses. Finally, we arrive at the Green’s function in Eq. 6,

$$G=\frac{1}{k}\sum _{\alpha }|c_{\alpha }⟩⟨c_{\alpha }|.$$ [S10]

Modifying a Single Bond

Using the Green’s function in Eq. S10, our goal is to find the change in $|e⟩$ when the stiffness of a given bond is modified. First, we define a unique SCS basis vector for bond $i$,

$$|C_i⟩=kG|i⟩.$$ [S11]

This SCS is closely related to the unique SSS defined in ref. 30. We rotate the SCS basis so that one of the SCS vectors is $|c_{\mu }⟩=|C_i⟩/\sqrt{⟨C_i|C_i⟩}$, making sure to reorthonormalize the rest of the basis with respect to this unique SCS. The benefit of this rotation is that now only the unique SCS contains a nonzero element for bond $i$. Next, we introduce a separate stiffness for bond $i$, $k_i$, which is not necessarily identical to the rest of the bonds. The matrix $K_{\alpha \alpha \prime }$ defined in Discrete Green’s Function can then be simplified to

$$K_{\alpha \alpha \prime }=\{\begin{array}{cc}\hfill k_i{C}_i^2+k\left(1-C_i^2\right)\hfill & \hfill \text{if}\hspace{0.17em}\alpha =\alpha \prime =\mu \hfill \\ \hfill k{\delta }_{\alpha \alpha \prime }\hfill & \hfill \text{otherwise}\hfill \end{array},$$ [S12]

where we have defined $C_i^2\equiv ⟨C_i|C_i⟩=⟨i|C_i⟩$. The resulting extensions are

$$|e⟩=\frac{|C_i⟩⟨C_i|t^{\ast }⟩}{C_i^2\left[k_i{C}_i^2+k\left(1-C_i^2\right)\right]}+\frac{1}{k}\sum _{\alpha \ne \mu }|c_{\alpha }⟩⟨c_{\alpha }|t^{\ast }⟩$$ [S13]

with change in extensions

$$|\mathrm{\Delta }e⟩=|C_i⟩\frac{⟨C_i|t^{\ast }⟩}{k\left(1-C_i^2\right)},$$ [S14]

where we have taken $k_i$ from an initial value of $k$ to zero.

Modifying Multiple Bonds

Here we extend Eq. S14 to allow for multiple bonds that do not have identical stiffness $k$. Suppose that all of the bond stiffnesses are identically $k_i=k$, except for a small subset of bonds that we call $\mathcal{B}$. We say a bond $i\in \mathcal{B}$ if and only if $k_i\ne k$. This set includes any ghost bonds with zero stiffness, along with bonds that are being tested for removal or modification. We typically include just three bonds in $\mathcal{B}$: the source and target ghost bonds of zero stiffness, along with the bond tested for removal.

Our goal now is to rotate our SCS subbasis $|c_{\alpha }⟩$ so that as few basis vectors as possible project onto the bonds in $\mathcal{B}$. We will denote this new rotated SCS subbasis $|{\stackrel{\sim }{c}}_{\alpha }⟩$. We define a special set of basis vectors $\mathcal{V}$ such that $\alpha \in \mathcal{V}$ if and only if $⟨i|{\stackrel{\sim }{c}}_{\alpha }⟩\ne \mathrm{\hspace{0.17em}0}$ for some $i\in \mathcal{B}$. Typically, the size of $\mathcal{B}$ will equal the size of $\mathcal{V}$. In other words, the basis vectors in $\mathcal{V}$ are the only vectors with nonzero elements for the set of bonds with nonidentical stiffnesses $\mathcal{B}$.

To calculate our rotated SCS subbasis, $|{\stackrel{\sim }{c}}_{\alpha }⟩$, we first find the unique SCS for each bond in $\mathcal{B}$, which we denote $|C_i⟩$, shown in Eq. S11. These unique SCS vectors are then orthonormalized using a modified Graham–Schmidt algorithm. The result is the set of basis vectors $\mathcal{V}$ described previously. The remainder of the rotated SCS basis is found by using the modified Graham–Schmidt algorithm to orthonormalize the original SCS basis with respect to the set of vectors $\mathcal{V}$, throwing out any vectors that are completely zeroed out. The result is our set of $N_c$ orthonormal rotated SCS vectors. However, it will be shown that only the vectors in $\mathcal{V}$ will be necessary for our solution.

Each basis vector that is not in $\mathcal{V}$ has zero projection onto bonds that are in $\mathcal{B}$, i.e., if $\alpha \notin \mathcal{V}$, then $⟨i|{\stackrel{\sim }{c}}_{\alpha }⟩=\mathrm{\hspace{0.17em}0}$ for all $i\in \mathcal{B}$. This means that if either $\alpha \notin \mathcal{V}$ or $\alpha \prime \notin \mathcal{V}$, then $|{\stackrel{\sim }{c}}_{\alpha }⟩$ and $|{\stackrel{\sim }{c}}_{\alpha }\prime ⟩$ are orthogonal over a reduced basis such that

$$⟨{\stackrel{\sim }{c}}_{\alpha }|\left(\sum _i|i⟩⟨i|\right)|{\stackrel{\sim }{c}}_{\alpha }\prime ⟩=⟨{\stackrel{\sim }{c}}_{\alpha }|\left(\sum _{i\notin \mathcal{B}}|i⟩⟨i|\right)|{\stackrel{\sim }{c}}_{\alpha }\prime ⟩.$$ [S15]

This new basis now gives us the means to rewrite $K_{\alpha \alpha \prime }$ for $\alpha \notin \mathcal{V}$ or $\alpha \prime \notin \mathcal{V}$,

$$K_{\alpha \alpha \prime }=⟨c_{\alpha }\prime |F^{-1}|c_{\alpha }⟩=⟨{\stackrel{\sim }{c}}_{\alpha }|\left(\sum _{i\in \mathcal{B}}{k}_i|i⟩⟨i\left|+\sum _{i\notin \mathcal{B}}k\right|i⟩⟨i|\right)|{\stackrel{\sim }{c}}_{\alpha }\prime ⟩$$ [S16]

$$=k\sum _{i\notin \mathcal{B}}⟨{\stackrel{\sim }{c}}_{\alpha }|i⟩⟨i|{\stackrel{\sim }{c}}_{\alpha }\prime ⟩=k⟨{\stackrel{\sim }{c}}_{\alpha }|{\stackrel{\sim }{c}}_{\alpha }\prime ⟩=k{\delta }_{\alpha \alpha \prime }.$$

The total matrix is then

$$K_{\alpha \alpha \prime }=\{\begin{array}{cc}\hfill {\stackrel{\sim }{K}}_{\alpha \alpha \prime }\hfill & \text{if}\mathcal{\hspace{1em}}\alpha ,\alpha \prime \in \mathcal{V}\hfill \\ \hfill k{\delta }_{\alpha \alpha \prime }\hfill & \text{otherwise}\hfill \end{array},$$ [S17]

where we have defined the submatrix ${\stackrel{\sim }{K}}_{\alpha \alpha \prime }=⟨c_{\alpha }\prime |F^{-1}|c_{\alpha }⟩$ for $\alpha ,\alpha \prime \in V$. We see that the matrix inversion problem is simplified to just inverting ${\stackrel{\sim }{K}}_{\alpha \alpha \prime }$.

$$K_{\alpha \alpha \prime }^{-1}=\{\begin{array}{cc}\hfill {\stackrel{\sim }{K}}_{\alpha \alpha \prime }^{-1}\hfill & \text{if}\mathcal{\hspace{1em}}\alpha ,\alpha \prime \in \mathcal{V}\hfill \\ \hfill \frac{1}{k}{\delta }_{\alpha \alpha \prime }\hfill & \text{otherwise}\hfill \end{array}.$$ [S18]

Because the size of $B$ is very small (in our case typically a set of size $3$), calculating the inverse of this matrix is very fast. The extension can now be represented as

$$|e⟩=\sum _{\alpha ,\alpha \prime \in \mathcal{V}}|{\stackrel{\sim }{c}}_{\alpha }⟩{\stackrel{\sim }{K}}_{\alpha \alpha \prime }^{-1}⟨{\stackrel{\sim }{c}}_{\alpha }\prime |t^{\ast }⟩+\sum _{\alpha \notin \mathcal{V}}\frac{1}{k}|{\stackrel{\sim }{c}}_{\alpha }⟩⟨{\stackrel{\sim }{c}}_{\alpha }|t^{\ast }⟩.$$ [S19]

The change in extension on bond $i$ when the stiffnesses are modified is then

$$|\mathrm{\Delta }e⟩=\sum _{\alpha ,\alpha \prime \in \mathcal{V}}|{\stackrel{\sim }{c}}_{\alpha }⟩\mathrm{\Delta }({\stackrel{\sim }{K}}_{\alpha \alpha \prime }^{-1})⟨{\stackrel{\sim }{c}}_{\alpha }\prime |t^{\ast }⟩.$$ [S20]

Note that the solution only depends on the basis vectors in $\mathcal{V}$; this means that only this small number of vectors must be calculated, and the rest may be neglected.

Avoiding the Introduction of Zero Modes

We impose the constraint that we do not introduce any zero-energy modes into the system when we remove bonds. We ensure the constraint by only removing bonds that contribute to the SSS subbasis. By Maxwell–Calladine counting, $N_0-N_s=dN-N_b$, where $N_0$ is the number of zero modes (27); this means that, if we remove a bond, we can either add a zero mode (increase $N_0$) or remove an SSS (decrease $N_s$). If a bond is removed that contributes to the SSS subbasis, a unique SSS will also be removed, and no zero mode will be created (30). This unique SSS, which we define as $|S_i⟩$ for bond $i$, is calculated analogously to the unique SCS, $|C_i⟩$, shown in Eq. S11. We find that

$$|S_i⟩=\sum _{\beta }|s_{\beta }⟩⟨s_{\beta }|i⟩.$$ [S21]

As long as $S_i^2\equiv ⟨S_i|S_i⟩>\mathrm{\hspace{0.17em}0}$, then bond $i$ contributes to the SSS subbasis.

Removing Bonds from SSS and SCS Subbases

When a bond $i$ is removed, we remove the corresponding unique SSS vector $|S_i⟩$ from our SSS subbasis by subtracting off its projection onto each SSS basis vector. We also remove the entries for bond $i$ from all vectors in both our SSS and SCS subbases. The two bases are then reorthonormalized using a modified Graham–Schmidt algorithm.

Animations

Videos S1 and S2 show animations of the responses of the networks in Fig. 1, and Video S3 shows the response of the network in Fig. 3C. Although our algorithm only considers and controls the linear response, we show the full nonlinear deformations in these videos so that the source and target strains are clearly visible.

To calculate the nonlinear response, we start with a tuned network and minimize the nonlinear configurational energy for increments of the source strain in a cycle from 0% to ${\epsilon }_{\text{max}}$ and back to 0%, and then to $-{\epsilon }_{\text{max}}$ and back to 0% again. The quantity ${\epsilon }_{\text{max}}$ is the maximum strain amplitude. In the network’s undeformed state, each node $i$ has an initial position vector ${𝐑}_i$. If the network is deformed in some way, then each node will have a new position

$${𝐗}_i={𝐑}_i+{𝐮}_i,$$ [S22]

where ${𝐮}_i$ is the node’s displacement vector. If two nodes share a bond, then the bond vector going from node $i$ to node $j$ is ${𝐑}_{ij}$ with magnitude $l_{ij}$, and the deformed bond vector is

$${𝐗}_{ij}={𝐗}_j-{𝐗}_i={𝐑}_j-{𝐑}_i+{𝐮}_j-{𝐮}_i={𝐑}_{ij}+\mathrm{\Delta }{𝐮}_{ij},$$ [S23]

where $\mathrm{\Delta }{𝐮}_{ij}$ is the bond extension vector. The configurational energy summed over all bonds $⟨ij⟩$ with central-force harmonic potentials is then

$$E=\sum _{⟨ij⟩}\frac{1}{2}{k}_{ij}(X_{ij}-l_{ij}),$$ [S24]

where $X_{ij}=|{𝐗}_{ij}|$, and $k_{ij}$ is the stiffness of bond $⟨ij⟩$. We minimize this energy numerically with respect to the displacementvectors ${𝐮}_i$ under the constraint that the source strain ${\epsilon }_S$ is a specified value.

Response of Experimental Networks

We measured the target strain of the physical realization of the network in Fig. 1A for a range of source strains. Fig. S3 shows that the response is a monotonic function of the source strain. Our networks, although designed in the linear regime, work well even for source strains in the nonlinear regime.