Integrated view of internal friction in unfolded proteins from single-molecule FRET, contact quenching, theory, and simulations

Significance

The dynamics of proteins, which are essential for both folding and function, are known to be strongly dependent on solvent viscosity and friction. However, an increasing number of experiments have demonstrated the importance of a contribution to protein dynamics independent of solvent friction. Such “internal friction” has recently been detected even in unfolded proteins, although they are more expanded and solvent-accessible than folded proteins. Based on two complementary experimental methods, simulations, and theory, our results provide a coherent view of internal friction in unfolded proteins and constitute an important basis for understanding the molecular origin of this phenomenon and its role for the folding of proteins and for the functional dynamics of intrinsically disordered proteins.

Abstract

Internal friction is an important contribution to protein dynamics at all stages along the folding reaction. Even in unfolded and intrinsically disordered proteins, internal friction has a large influence, as demonstrated with several experimental techniques and in simulations. However, these methods probe different facets of internal friction and have been applied to disparate molecular systems, raising questions regarding the compatibility of the results. To obtain an integrated view, we apply here the combination of two complementary experimental techniques, simulations, and theory to the same system: unfolded protein L. We use single-molecule Förster resonance energy transfer (FRET) to measure the global reconfiguration dynamics of the chain, and photoinduced electron transfer (PET), a contact-based method, to quantify the rate of loop formation between two residues. This combination enables us to probe unfolded-state dynamics on different length scales, corresponding to different parts of the intramolecular distance distribution. Both FRET and PET measurements show that internal friction dominates unfolded-state dynamics at low denaturant concentration, and the results are in remarkable agreement with recent large-scale molecular dynamics simulations using a new water model. The simulations indicate that intrachain interactions and dihedral angle rotation correlate with the presence of internal friction, and theoretical models of polymer dynamics provide a framework for interrelating the contribution of internal friction observed in the two types of experiments and in the simulations. The combined results thus provide a coherent and quantitative picture of internal friction in unfolded proteins that could not be attained from the individual techniques.

The dynamics and folding of proteins are often modeled as a diffusive process on a free-energy surface (1–3). In contrast to simpler rate processes in the condensed phase (4), however, protein dynamics are often much slower than expected from solvent friction alone. This behavior indicates that solvent molecules are not the only cause of friction, but that other sources (commonly referred to as “internal,” in contrast to the “external” action of the solvent) control protein relaxation (5–12). Internal friction has been reported for native-state dynamics (9) and folding kinetics, especially for proteins folding in the microsecond range (6, 13), but even for proteins folding in milliseconds (11), suggesting the presence of a solvent-independent frictional component in the transition-state ensemble (10, 13, 14).

The simplest mechanistic explanation for internal friction in native proteins and transition states is that in these rather compact configurations, a large fraction of the protein atoms is not fully exposed to the solvent, and is therefore dominated by collisions and interactions with other parts of the protein (9), involving predominantly small-amplitude motions, where little solvent is displaced (15). It thus came as a surprise when recent experiments and simulations demonstrated that internal friction can dominate even the dynamics of unfolded and intrinsically disordered proteins and peptides (10, 12, 16–22), which are more expanded and accessible to solvent. In both experiments (10, 12, 16, 17) and simulations (19–21), unfolded proteins often exhibit the characteristic signature of internal friction: a pronounced deviation from direct proportionality of their reconfiguration times to solvent viscosity. The underlying molecular mechanisms, however, have remained unclear. Recent single-molecule experiments indicate a correlation of internal friction with chain compaction, suggestive of attractive intrachain interactions slowing dynamics (12, 23). However, the magnitude of internal friction was found to be only weakly dependent on chain segment length and bisection of an unfolded protein, pointing to a molecular origin that is rather independent of local sequence-specific effects (12). Molecular dynamics (MD) simulations have proven particularly important for connecting experimental observations to molecular details and for investigating protein dynamics in low-viscosity regimes that are experimentally inaccessible (19–21, 24, 25). Based on these studies, different molecular contributions to internal friction have been proposed, including hydrogen bonds (19), nonnative salt bridges (14), concerted dihedral rotations involving crank-shaft motions of the polypeptide backbone (21), and differences in native-state topology (24). Deviations from direct proportionality of relaxation times and solvent viscosity can also be due to inertial effects or solvent memory in dihedral angle hopping (20, 25, 26).

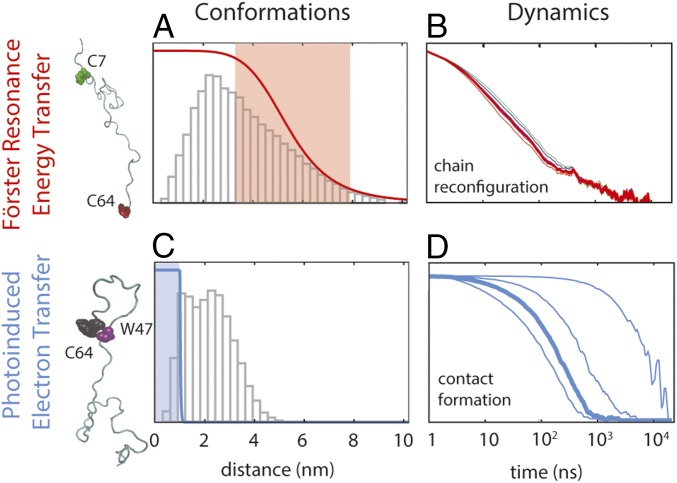
A way of testing our understanding of internal friction in unfolded proteins is the use of experimental data from complementary techniques that probe chain dynamics on different length and time scales. For instance, single-molecule experiments based on Förster resonance energy transfer (FRET) combined with nanosecond fluorescence correlation spectroscopy (nsFCS) on several unfolded proteins have revealed reconfiguration dynamics of 30- to 100-residue chain segments on time scales between about 10 ns and 100 ns (10, 12, 16, 27). In contrast, loop formation detected in contact-based measurements between Cys and Trp in a 10-residue segment within unfolded protein L was reported to occur on much slower time scales, between 1 μs and 10 μs (18). The different distance dependencies for the rates of FRET (∝1/r⁶) and contact formation (∝e^−r) and the resulting sensitivity to distance changes on different length scales provide an excellent opportunity for probing the effect of internal friction on different parts of the intramolecular distance distribution (28), corresponding to more extended versus compact conformations within the unfolded-state ensemble (Fig. 1). Comparing such experiments directly with simulations has been very challenging, both because of the high computational demands for all-atom explicit solvent simulations of unfolded proteins on the required time scales and because of the lack of force fields that provide a realistic description of the unfolded state and do not lead to overly compact chains. Recent advances in computational power (29, 30) and force field development (31–35) have started to change this situation.

Fig. 1.

Investigating the conformations and dynamics of protein L using FRET and PET. FRET is most sensitive in a range of distances close to the Förster radius (A; ∼5.4 ± 3 nm, shaded in red), whereas PET is only effective at distances smaller than the contact radius (C; <1 nm, shaded in blue). The distance dependencies of the transfer efficiency and the relative electron transfer rate are shown as red and blue lines in A and C (ranging from 1 to 0), respectively, superimposed on the distance distributions of the segments probed by FRET (C7–C64) and PET (W47–C64) from an 86-μs MD simulation of unfolded protein L (31) (gray histograms). Decays of correlations for chain reconfiguration (B) and contact formation (D) are based on the MD simulation (31). (B) Typical reconfiguration times for a sequence separation of 57 amino acids occur on a time scale of 10–100 ns and show a very weak dependence on the Förster radius (correlation curves shown for Förster radii of 5.0, 5.2, 5.4, 5.6, 5.8, and 6.0 nm, respectively). (D) In contrast, contact formation is very sensitive to the contact radius (from left to right, R_c is 1.0, 0.8, 0.6, and 0.4 nm, respectively), and therefore can differ by orders of magnitude depending on the probes used (from 100 ns to 10 μs for the 18-residue segment investigated here).

Here, we use the combination of single-molecule FRET-based and contact-based experiments on protein L and compare them with recent long-time scale atomistic simulations from Shaw and coworkers (31) and with the predictions of a polymer model that includes internal friction effects (36) to elucidate whether internal friction observed on different time and length scales can be explained with a consistent theoretical view.

Results

Conformational Ensemble of Unfolded Protein L.

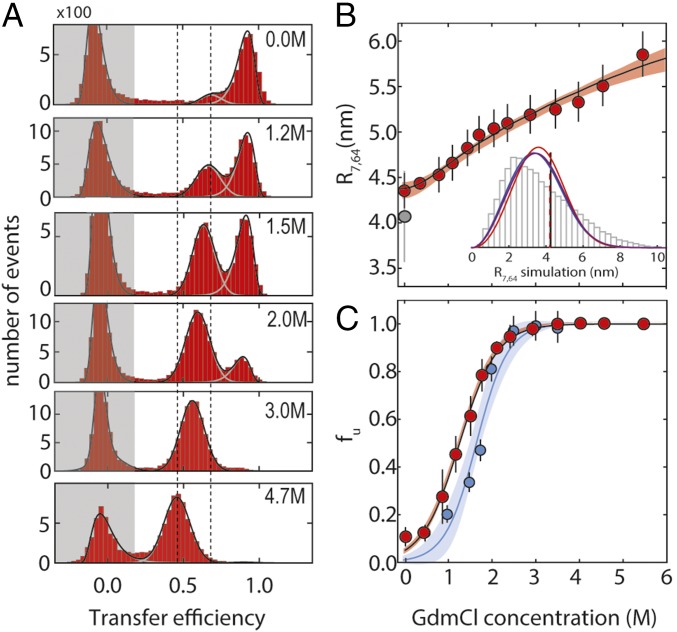
The quantitative interpretation of nanosecond relaxation times obtained by the combination of FRET with nsFCS (FRET-FCS) requires information about the conformational distribution sampled by the chain. We labeled the double-Cys variant K7CG64C of protein L with Alexa 488 and Alexa 594 as donor and acceptor fluorophores, respectively (SI Appendix and SI Appendix, Table S1; Förster radius: 5.4 nm), and used single-molecule FRET to estimate the dimensions of the unfolded state at different guanidinium chloride (GdmCl) concentrations. In the resulting FRET efficiency histograms (Fig. 2A), we observed three peaks: one at E ≈ 0.9, which corresponds to the folded state of the protein; one with E between 0.5 and 0.8, corresponding to the unfolded state; and one at a transfer efficiency of E ≈ 0, from molecules without active acceptor dye. The areas of the corresponding transfer efficiency peaks yield the relative populations of folded and unfolded states (Fig. 2C). With increasing GdmCl concentration, the unfolded state is increasingly populated, and its peak shifts from higher to lower transfer efficiency (Fig. 2B), reflecting chain expansion, as observed previously for protein L (37–39) and many other proteins (23, 40, 41).

Fig. 2.

Single-molecule FRET experiments on protein L stability and unfolded-state dimensions. (A) Examples of FRET efficiency (E) histograms at different GdmCl concentrations (folded state: high E; unfolded state: intermediate E; population with inactive acceptor dye: low E, shaded in gray). Vertical dashed lines identify the change in the mean transfer efficiency of the unfolded state between 0 and 4.7 M GdmCl. (B) RMS distance between residues 7 and 64, R_7,64, as estimated from the transfer efficiencies (SI Appendix) at different denaturant concentrations, fitted to a simple binding model (shaded area corresponds to a 90% confidence interval). Error bars represent the SD from at least two measurements at the same denaturant concentration. The gray-filled circle represents the value of R_7,64 from the MD simulation (31), with the error bar corresponding to the SD of R_7,64 when computed from 10-μs segments of the trajectory. (Inset) Distribution of distances sampled in the MD simulation between residues 7 and 64 compared with three polymer distributions [Gaussian chain (blue), worm-like chain (purple), and self-avoiding walk (red)] that correspond to the same mean transfer efficiency as computed from the MD trajectory. Vertical lines indicate the RMS distances of the distributions (virtually indistinguishable). (C) Fraction of unfolded protein, f_u, according to the relative areas of peaks corresponding to folded and unfolded states in FRET efficiency histograms (red) and f_u obtained from PET experiments (blue) (Fig. 4 and SI Appendix for comparison). Error bars represent the SD from at least two measurements at the same denaturant concentration. Shaded areas represent the 90% confidence interval of the fit.

The RMS internal distance between the labeling sites, R_7,64, in the unfolded state (Fig. 2B) and the underlying distance distribution can be inferred from the transfer efficiency by using polymer models (23) [e.g., a Gaussian chain (23, 42, 43)], a self-avoiding walk, or a worm-like chain (23) (SI Appendix). The distance distributions from the polymer models agree well with the corresponding distributions calculated from the 86-μs atomistic MD simulation of unfolded protein L in explicit solvent by Piana et al. (31) using the Amber12 force field (44) in combination with the recently developed TIP4P-D water model (31) (Fig. 2B and SI Appendix, Fig. S1). Given the similarity of the shapes of the distance distributions of the polymer models (SI Appendix, Fig. S1), we use the Gaussian chain, the simplest model, for quantifying chain dimensions over the entire range of GdmCl concentrations (Fig. 2B).

Reconfiguration Dynamics and Internal Friction from Single-Molecule FRET.

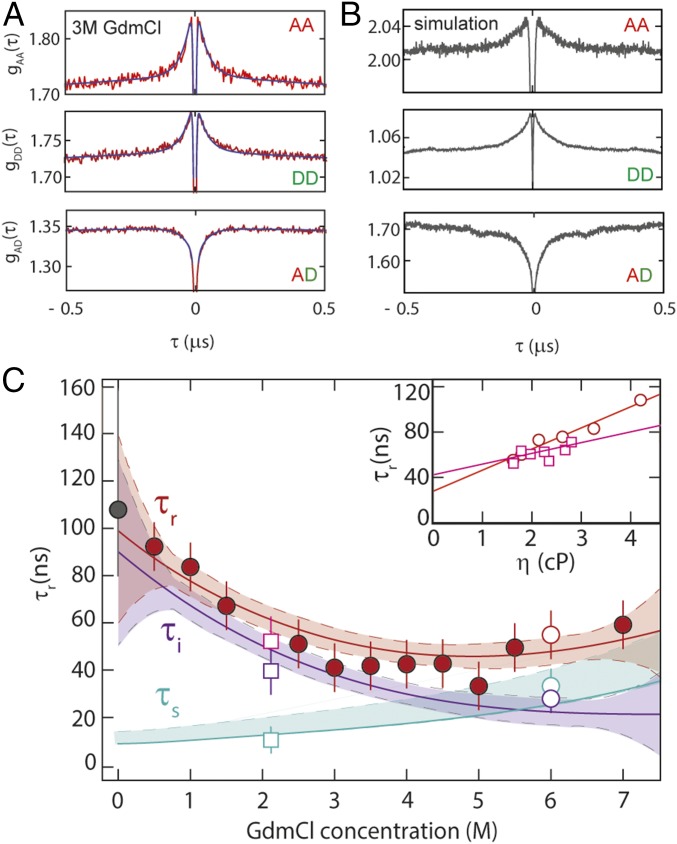
FRET-FCS reports on protein dynamics that result in distance fluctuations between the dyes (10, 12, 16, 27). The correlation curves for unfolded protein L (Fig. 3A) exhibit the characteristic correlated signal in the autocorrelation functions and anticorrelated signal in the cross-correlation function that are diagnostic of distance fluctuations between donor and acceptor (details are provided in SI Appendix). The distance relaxation time corresponding to the reconfiguration of the chain, τ_r (16) (Fig. 2C), is obtained from the fluorescence intensity relaxation time, τ_CD, by describing the chain dynamics in terms of diffusion on the potential of mean force obtained by Boltzmann inversion of the distance distribution inferred from the transfer efficiencies (Fig. 2B, Inset and SI Appendix). With increasing denaturant concentration, τ_r first decreases from 95 ± 15 ns at 0.5 M GdmCl to 45 ± 7 ns at 4 M GdmCl, and then increases again, reaching 60 ± 9 ns at 7 M GdmCl, a behavior similar to that of other proteins of comparable size and sequence composition (10, 12, 16, 27). Remarkably, τ_r calculated directly from the MD trajectory of unfolded protein L yields a value of ∼110 ns for the dominant dynamic component (Fig. 3B and SI Appendix, Fig. S2), which is very close to the experimental value, lending further support to a realistic representation of unfolded-state dynamics in the simulations using the TIP4P-D water model (31). However, the MD-based correlation function reveals residual dynamics up to time scales of several microseconds (SI Appendix, Fig. S2), indicating that complete convergence is not achieved even in this 86-μs simulation. Such slow modes in the relaxation time may reflect the population of local structural elements (hydrogen-bonded turns, bends, and extended segments) (SI Appendix, Fig. S2). Our experimental data do not provide direct evidence for dynamics on this time scale, but a low-amplitude component cannot be ruled out owing to experimental uncertainty. Based on photoinduced electron transfer (PET) experiments at low excitation rates, for which the potentially interfering triplet contribution in the microsecond range of the correlation function is particularly low (45), we estimate an upper bound of 10–15% for the contribution of microsecond dynamics, consistent with the simulations.

Fig. 3.

Probing unfolded-state dynamics by FRET-FCS. (A) Autocorrelation of acceptor fluorescence, g_AA(τ); donor fluorescence, g_DD(τ); and cross-correlation of acceptor and donor fluorescence, g_AD(τ), at 3 M GdmCl; black lines show a global fit of the three correlations, with the reconfiguration time, τ_r, as a shared fit parameter. (B) FRET-FCS correlations g_AA(τ), g_DD(τ), and g_AD(τ) based on the MD trajectory of unfolded protein L (31) (SI Appendix). (C) τ_r from the global fit of g_AA(τ), g_DD(τ), and g_AD(τ) (red-filled circles); the internal friction contribution, τ_i, (purple line), is obtained by subtracting from the polynomial interpolation curve of τ_r (red line) the solvent component, τ_s (cyan line). The gray-filled circle at 0 M GdmCl represents the reconfiguration time of the chain from the MD simulation (SI Appendix). Error bars represent an average relative error of 15%, as estimated from the SD of multiple independent measurements. Confidence intervals (90%) of the fit are represented as shaded areas of the corresponding color. (Inset) τ_r at 2.2 M (empty squares) and 6.0 M GdmCl (empty circles) as a function of solution viscosity, η; linear extrapolation to zero viscosity (Eq. 1) allows τ_s (empty cyan circle and square in main panel) and τ_i (empty purple circle and square in main panel) to be estimated.

We have previously shown that in the framework of simple polymer models, such as the Rouse model with internal friction (RIF) or Zimm model with internal friction (ZIF) (36, 46), the reconfiguration time of the chain can be decomposed into two additive components (12)

$${\tau }_r={\tau }_s+{\tau }_i.$$ [1]

[We restrict our data analysis to the RIF model; an analysis based on the ZIF model was previously shown to yield virtually indistinguishable results (12, 36).] Here, τ_s is the reconfiguration time in the absence of internal friction (described by the standard Rouse model), which is thus directly proportional to the solvent viscosity, η_s, and to the mean square interdye distance, R² (i.e., τ_s ∝ R²η_s), and τ_i is a time scale that arises from internal friction. Following a previously established procedure (10, 12), we separated τ_s and τ_i for all denaturant concentrations (Fig. 3 and SI Appendix). The resulting τ_i (Fig. 3C, purple line) increases from 28 ± 18 ns at 6 M GdmCl to ∼90 ns under native conditions. We tested the robustness of the extrapolation procedure by directly comparing τ_i with the value measured via the solvent viscosity dependence at a lower denaturant concentration. At 2 M GdmCl, the viscosity dependence of τ_r yields τ_i (2 M) ≈ 42 ± 7 ns, close to the extrapolated RIF estimate. In summary, in the absence of denaturant, the contribution of internal friction dominates the dynamics of unfolded protein L by an order of magnitude compared to the solvent friction component.

Contact Formation Dynamics from PET-FCS.

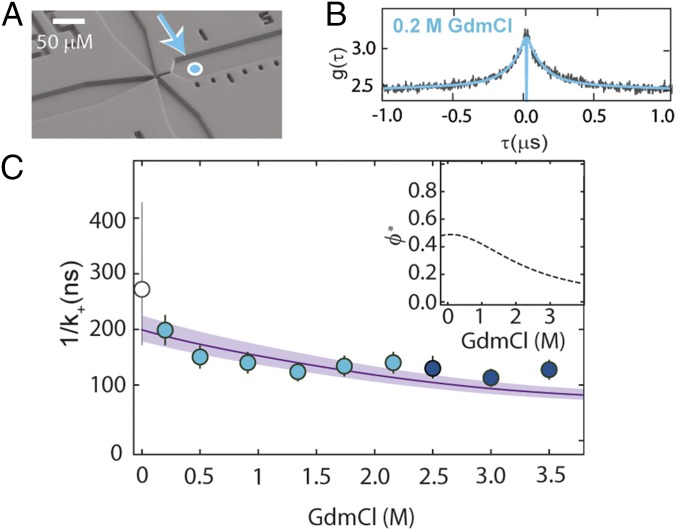
Our observations thus far are based on the long-range coupling between FRET donor and acceptor, with greatest sensitivity to distance changes in the range of the Förster radius (5.4 nm). To understand how internal friction affects dynamics as monitored by contact formation between two groups within the chain, and thus with greatest sensitivity to distance changes in the subnanometer range, we investigate loop formation (47, 48) by means of PET-FCS measurements (49, 50). Specifically, we monitor static fluorescence quenching by the formation of a nonfluorescent complex between a fluorophore (here, Oxa11) and the quencher (Trp) (49, 50) in an 18-residue segment within protein L (SI Appendix, Table S1). This process results in an approximately exponential decay in the fluorescence correlation curve, where the corresponding amplitude, c_q, and relaxation time, τ_q, are linked to the observed rate coefficients of forming and breaking the complex, k₊^obs and k₋^obs, respectively, by ${\tau }_q=1/\left(k_{+}^{obs}+k_{-}^{obs}\right)$ and $c_q=f_u{k}_{+}^{obs}/k_{-}^{obs}$, where f_u is the fraction of unfolded protein (50) (SI Appendix and SI Appendix, Fig. S3). To separate the contributions of k₊^obs and k₋^obs, it is thus necessary to quantify both c_q and τ_q, ideally under conditions where the protein is completely unfolded, so that f_u does not affect the amplitude. Here, we used a microfluidic mixing device that allows us to dilute the protein rapidly from fully denaturing (3 M GdmCl) to native conditions (0.3 M GdmCl) or intermediate GdmCl concentrations with millisecond dead time (51), enabling the observation of unfolded-state dynamics for all conditions before the protein folds. Measurements of the FRET-labeled protein in the microfluidic device confirmed that the protein was predominantly unfolded at times less than 5 ms after dilution of the denaturant (SI Appendix and SI Appendix, Fig. S4). The PET-FCS curves (Fig. 4B) exhibit a pronounced decay on the ∼100-ns time scale, which is absent in the control protein missing the Trp residue (SI Appendix, Fig. S5).

Fig. 4.

Probing unfolded-state dynamics by PET. (A) Electron micrograph of the microfluidic mixing device (51) used for transiently populating unfolded protein L at low denaturant concentrations. Fully denatured protein in 3 M GdmCl in the sample inlet (left channel) is mixed with buffer from the side inlets (top and bottom channels) to measure the dynamics of the fully unfolded protein in the right observation channel at low denaturant concentrations. The cyan-filled circle identifies the first position where complete mixing is observed, corresponding to a time after mixing of ∼4 ms. (B) PET-FCS measurement of unfolded protein L in 0.2 M GdmCl within the microfluidic device, with fit (blue line). (C) Contact formation time, obtained by correcting the observed rate, k₊^obs, for the GdmCl-dependent quenching efficiency, ϕ* (Inset). The line shows the fit with Eq. 2. Error bars represent an average relative error of 13%, as estimated from the SD of multiple measurements at a single GdmCl concentration. The corresponding value of 1/k₊ based on the MD simulation of unfolded protein L (31) with a contact radius of 0.83 ± 0.10 nm is shown as an empty circle with an error bar corresponding to a variation in the contact radius of 0.10 nm.

The diffusion-limited contact formation rate, k₊, can be obtained by correcting the observed rate, k₊^obs, for the quenching efficiency, ϕ*, which corresponds to the probability of forming the quenched state from the encounter complex (Fig. 4C, Inset and SI Appendix, Figs. S6 and S7). At denaturant concentrations approaching zero, we found a diffusion-limited contact formation time of 1/k₊ ≈ 200 ns. Notably, the formation of this contact is slower by a factor of ∼10 (taking into account the contribution of tail effects and the difference in contact radii) compared with values reported for disordered peptides of similar length [Gly-Ser or Ala-Gly-Gln repeats (48, 52, 53)], already providing an indication for the presence of internal friction in unfolded protein L. With increasing denaturant concentration, 1/k₊ decreases and approaches 100 ns at 3.5 M GdmCl (Fig. 4C). [We restricted our analysis of contact-based dynamics to below 3.5 M GdmCl, because above this concentration, the complex between Oxa11 and Trp is not sufficiently stable and, consequently, the amplitude from contact quenching becomes too small for a reliable analysis (SI Appendix and SI Appendix, Figs. S3 and S5).] This trend resembles the one observed for the reconfiguration time of the chain with FRET-FCS in the same denaturant range (Fig. 3C), but the contact formation time for this 18-residue segment is almost twofold greater than τ_r for the 57-residue segment. Can the contribution of internal friction identified in the FRET-FCS experiments explain the observed rate of loop formation?

Reconciling Reconfiguration Times and Contact Formation Times.

Our FRET-FCS data (Fig. 3C) suggest that at low denaturant concentration (<3 M GdmCl), unfolded protein L is well within the regime where internal friction dominates its global reconfiguration dynamics (i.e., τ_r ≈ τ_i). When the solvent component, τ_s, is rescaled (12, 36, 54) from the 57-residue segment probed by FRET to the 18-residue segment length probed by PET, the relative contribution of τ_i becomes even more dominant because its absolute value is independent of segment length in the RIF model, accounting for more than 90% of the reconfiguration time of this segment. In this limit, the interresidue dynamics predicted by the RIF and ZIF models reduce to the simple diffusive case, and the contact formation time can be estimated using the Szabo–Schulten–Schulten (SSS) theory (55) in terms of 1D diffusion in a potential of mean force (36),

$${\tau }_c^{IF}={\left(\frac{\pi }{6}\right)}^{0.5}\frac{R_{47,64}}{R_c}{\tau }_i,$$ [2]

where R_47,64 is the RMS distance between the quencher and the dye at equilibrium, R_c is the effective contact radius at which quenching occurs, and τ_i at the respective GdmCl concentration is taken from the analysis of the FRET-FCS experiments (Fig. 3C). R_47,64 can be estimated by rescaling the mean square distance obtained from single-molecule FRET experiments assuming Gaussian chain statistics: The resulting value of R_47,64 = 2.4 ± 0.2 nm is in very good agreement with the one from the all-atom simulation, $R_{\mathrm{47,64}}^{sim}$ = ${2.3}_{-0.3}^{+0.1}$ nm. The contact radius, R_c, depends on the specific properties of the dye-quencher pair and is used here as an adjustable parameter in the fit of the data.

Eq. 2 provides a remarkably good account of the experimental results (Fig. 4C), and the fit yields R_c = 0.83 ± 0.10 nm, which is close to previous estimates (R_c = 0.7 ± 0.3 nm) (45, 50, 56). Again, we can directly compare with the MD simulation: Using R_c from the fit of the experimental data, the contact formation time for the PET distance R_47,64 yields ${\tau }_c^{sim}(R_c=0.83)$ = ${270}_{-100}^{+150}$ ns, in agreement with the measured data. [Here, the contact is estimated as occurring between the C^α atoms of W47 and G64. Contributions from the dye linker (that is not included in the simulation), the tryptophan side chain, and related local steric hindrance affect the value of R_c. Note, however, that for the contact times between the indole ring of W47 and the C^α of G64, steric hindrance effects are negligible for large contact radii (R_c > 0.8 nm) and become significant only for small values (R_c ≤ 0.6 nm) (SI Appendix, Fig. S8).] Alternatively, we can estimate R_c by adjusting it to match the contact time from the MD simulations with the value measured at the lowest denaturant concentration, resulting in $R_c^{sim}$ = 0.9 ± 0.2 nm, again in the previously reported range (45, 50, 56). Interestingly, changing R_c from 1.0 nm [upper limit for the Oxa11-Trp pair (45)] to 0.4 nm [contact radius for the Trp-Cys pair (57)] in the analysis of the simulations leads to a roughly 100-fold increase in the relaxation time [${\tau }_c^{sim}(R_c=0.4\hspace{0.17em}\text{nm})$ = 6.8 μs]. This observation may explain, at least in part, the surprisingly slow decays previously reported for contact formation experiments in unfolded protein L (∼5 μs) based on Trp-Cys quenching (18, 30). Indeed, for the 10-residue segment studied by Waldauer et al. (18), the MD simulation (31) yields a diffusion-limited contact time for the indole ring of W47 and the C^α of T57 of 6.3 μs. The similarity of this time to the 6.8 μs obtained from the simulations for the 17-residue segment probed in our PET experiments, despite the difference in sequence length, is at variance with the prediction for a simple polymer model (Eq. 2), and is likely to reflect the pronounced sensitivity of contact formation to the detailed properties of the chain, such as local structure formation or steric accessibility (53, 58) (SI Appendix, Figs. S2, S8, and S13). We also note that our results indicate a weaker viscosity dependence than the data of Waldauer et al. (18).

In summary, the contribution of internal friction obtained from the measurement of reconfiguration times based on FRET is in agreement with the contact formation experiments using PET, and both are in accord with the all-atom simulations. However, the strong sensitivity of contact formation experiments to R_c is an important factor to be taken into account.

Discussion

There is growing consensus regarding the importance of internal friction for the dynamics of unfolded proteins and peptides both from experiments and simulations (12, 19–21, 24, 59, 60), but apparent discrepancies in the time scales observed with different experimental methods have remained (12, 16, 18), raising the question of their consistency. Here, we used two complementary single-molecule techniques, FRET and PET, which are sensitive to distance changes on very different length scales: the former near the Förster radius (∼5 ± 3 nm) and the latter in the subnanometer regime of contact formation (Fig. 1 A and C). This combination thus allows us to probe unfolded-state dynamics and the contribution of internal friction for different parts of the intramolecular distance distribution. By comparison with all-atom MD simulations and based on theoretical models that describe the contribution of internal friction either within the framework of Rouse/Zimm-type polymer dynamics or in terms of diffusion in a potential of mean force corresponding to the distance distribution (36, 55, 61), a coherent picture emerges from our results.

In the Rouse/Zimm picture of polymer dynamics, internal friction results in an additive component in the observed reconfiguration time (26, 36, 46), which we determined from FRET-FCS experiments (Fig. 3; Eq. 1). The internal friction time, τ_i, can then be incorporated in a simple model describing contact formation, the SSS approximation (55), in the limit of large internal friction (36). The resulting time scales for contact formation are in good agreement with our observations from the PET experiments (Fig. 4C). The consistency of the results based on the different experimental methods suggests that even though the two methods are sensitive to the dynamics on different length scales, simple models of polymer dynamics provide a unified description of these measurements and account for the diversity of the observed time scales.

We complement these results with a detailed analysis of a recent atomistic simulation of unfolded protein L. Availability of a long (86 μs) simulated trajectory enables a detailed comparison of FRET with contact formation experiments, which requires sufficient sampling of infrequent contact formation events. The simulations agree well with the experimentally observed dimensions and dynamics of unfolded protein L (within 10%; Figs. 2–4), but do they show evidence for the presence of internal friction? Several observations suggest that this is indeed the case. The first indication comes from a comparison with other proteins for which simulations with the same force field and water model, as well as experimental data, are available. Prothymosin α (ProTα), for example, is a highly charged, and thus very expanded, intrinsically disordered protein (62) that exhibits very low internal friction, leading to an experimentally observed reconfiguration time of 45 ± 9 ns for the C56C110 segment (12) and 24 ± 4 ns for the C1C56 segment (63). The simulations of Piana et al. (31) recapitulate the expanded chain and its rapid dynamics, yielding a reconfiguration time for both segments of ∼27 ± 20 ns. In contrast, a more compact unfolded protein for which a similarly high contribution of internal friction as for protein L was observed is the cold shock protein (Csp) from Thermotoga maritima. Again, the relatively slow dynamics from experiment (τ_r = ${116}_{-40}^{+60}$ ns) (12, 16) and simulation (τ_r = ${180}_{-90}^{+70}$ ns) agree. The experimentally observed correlation between compactness of unfolded proteins and the extent of internal friction (12) is thus also found in the simulations.

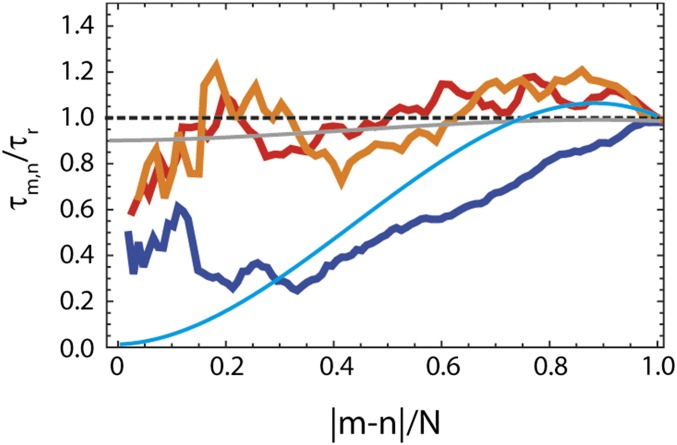
Even more revealing is the dependence of chain dynamics on the segment length of the chain. In the framework of the RIF and ZIF models, the absolute contribution of internal friction (τ_i) to the total reconfiguration time (τ_m,n) is independent of the length, |m-n|, of the chain segment probed, whereas the solvent-dominated contribution (τ_s) decreases with decreasing chain length (12, 36). As a result, the relative contribution of τ_i increases for shorter segments, and internal friction can thus be quantified from the segment length dependence of chain relaxation, which has previously been used in experiments and simulations (12, 21). Fig. 5 illustrates this behavior for the MD simulations of protein L, Csp, and ProTα: Whereas τ_m,n remains high for all segment lengths in unfolded protein L and Csp, indicating a large contribution of internal friction, τ_m,n exhibits a steady decrease with decreasing segment length in ProTα, consistent with the prediction for a chain with very low internal friction (12, 21). The behavior observed in the simulations resembles the predictions of the RIF model with a large contribution of τ_i for unfolded protein L and Csp and the prediction of the Rouse model without internal friction for ProTα (Fig. 5), further supporting a pronounced difference in internal friction in the simulations.

Fig. 5.

Dependence of the relative reconfiguration time, τ_m,n/τ_r, on the relative length of the chain segment, |m-n|/N, based on the MD simulations (31) of unfolded protein L (orange), Csp (red), and ProTα (blue). The segment length, |m-n|, (where n is either 1 or N) and the reconfiguration time, τ_mn, (averaged between the two segments of equal lengths; details are provide in SI Appendix) are normalized by the total number of amino acids, N, or for the end-to-end reconfiguration time, τ_r, of the particular protein, respectively. The gray line shows the prediction of the RIF model with the value of τ_i from nsFCS measurements of unfolded protein L extrapolated to zero denaturant (Fig. 2). For comparison, the two extreme cases of the RIF model are also shown: the Rouse chain without internal friction (cyan line) and the limit of infinite internal friction (dashed black line).

Finally, given this consistency of experiments and simulations, what can we deduce about the molecular origin of internal friction? Persistent secondary structure and tertiary contacts are virtually absent in the simulations of all three proteins (∼3–4%) (SI Appendix, Fig. S9). This finding is in agreement with the low secondary structure content of unfolded Csp under native conditions, as determined by kinetic synchrotron radiation circular dichroism experiments (43), and suggests that native-like structural elements are not required for internal friction. Short-range nonnative hydrogen bonds (sequence separation less than six residues) are similarly prevalent in all three simulations (SI Appendix, Fig. S10), and are thus also unlikely to make a large contribution. However, protein L and Csp clearly differ from ProTα in their greater abundance of transient nonnative sequence-distant hydrogen bonds, salt bridges, and hydrophobic contacts (SI Appendix, Figs. S10–S12), which is not unexpected in view of the pronounced differences in chain expansion observed in both simulations (31, 64) and experiments (12, 62) (Fig. 2). The correlation between chain dimensions, intrachain interactions, and internal friction observed in the simulations implies that intrachain interactions could also be the missing link for the experimentally observed correlation between unfolded-state compaction and internal friction (12, 23). To investigate this hypothesis further, we now turn to protein dynamics as revealed by the simulations.

Interestingly, for each of the three proteins, the respective average relaxation times are comparable for forming and breaking sequence-distant hydrogen bonds, salt bridges, and hydrophobic contacts; for dihedral angle rotations; and for the reconfiguration of short segments of approximately five residues (SI Appendix, Figs. S11–S13). This observation supports a coupling between intrachain interactions and dihedral angle rotations, which are required for large conformational rearrangements of the chain and have been implicated in internal friction based on previous simulations (20, 21, 26). However, there are marked differences between the behavior of the unfolded proteins with high and low internal friction, respectively: For unfolded protein L and Csp, all relaxation times are in the range of about 100–200 ns; for ProTα, they are almost an order of magnitude shorter, matching the difference in global chain reconfiguration times. The much faster dihedral hopping in ProTα (SI Appendix, Fig. S13) would imply that dihedral relaxation, per se, is not the dominant source of internal friction (20) but that interactions within the chain impede dihedral transitions. This conclusion is supported by the absence of internal friction in some unfolded proteins at high concentrations of denaturant (12) (at least to within experimental uncertainty), where intrachain interactions are weakened but dihedral barriers are not expected to be much different. However, even in the presence of nonnative interactions, relaxation dynamics in the vicinity of glycine residues are accelerated (SI Appendix, Fig. S13), and lowering the dihedral barriers in a compact unfolded state was found to reduce internal friction (21). It is tempting to identify the nonnative interactions between sequence-distant segments of the chain as leading to Cerf-type friction [as proposed by de Gennes (65)], as opposed to the Kuhn-type friction that results from crossing dihedral barriers (46, 65), but the coupling between dihedral dynamics and nonnative interactions suggests that the two mechanisms may not be separable. Future simulations and experiments addressing the length scaling of internal friction and the dependence of the two contributions on chain compaction may help to address this question in more detail.

How does the origin of internal friction suggested here differ from mechanisms proposed for transition states of folded proteins? As a protein approaches its native state, the influence of nonnative interactions is expected to decrease. Interestingly, however, an important contribution of nonnative salt bridges to internal friction has been identified in the folding transition state of a designed protein (14), which may resemble the charge interactions in unfolded protein L and Csp (SI Appendix, Fig. S11). Dihedral rearrangements have been implicated as a mechanism of internal friction in protein folding, especially for helical proteins, where such local transitions are particularly important for the dynamics in the transition-state region (24, 25). A lack of solvent relaxation on the time scale of dihedral barrier crossing can also result in low sensitivity of dynamics to solvent viscosity, and thus contribute to the signature commonly ascribed to internal friction (20, 25). For a fully folded protein, most of the protein atoms are excluded from the solvent, and internal friction can be assumed to result from collisions with other protein atoms instead of solvent molecules (9). The relative contributions of different interactions and mechanisms to internal friction are thus likely to depend on the progress of the folding reaction and the proximity to the native state.

In summary, the combination of two complementary single-molecule techniques with atomistic simulations provides a consistent picture of protein dynamics in the unfolded state, reveals a significant contribution of internal friction, and quantifies its magnitude. The results not only reconcile the different time scales observed in FRET and contact formation experiments but also illustrate that the recent advances in force field development now enable more realistic simulations of unfolded and intrinsically disordered proteins, in terms of both chain dimensions and dynamics. Notably, the results based on simple polymer models for the distance distributions and dynamics in the unfolded state agree well with the results using the distributions from recent all-atom simulations, supporting the use of simple models for the analysis of experimental and simulation data. The close integration of multiple experimental techniques with theory and simulations used here overcomes limitations of each individual approach. The increasing convergence of time scales in experiments and simulations and the continued improvements in force fields benchmarked with experimental data will enable an increasingly reliable interpretation of experimental observables based on molecular simulations. This synergy is an important step toward quantifying the molecular contributions to internal friction and the resulting influence on processes such as interactions of intrinsically disordered proteins and protein folding dynamics.