Identifying Future Drinkers: Behavioral Analysis of Monkeys Initiating Drinking to Intoxication is Predictive of Future Drinking Classification

Abstract

Background

The Monkey Alcohol Tissue Research Resource (MATRR) is a repository and analytics platform for detailed data derived from well‐documented nonhuman primate (NHP) alcohol self‐administration studies. This macaque model has demonstrated categorical drinking norms reflective of human drinking populations, resulting in consumption pattern classifications of very heavy drinking (VHD), heavy drinking (HD), binge drinking (BD), and low drinking (LD) individuals. Here, we expand on previous findings that suggest ethanol drinking patterns during initial drinking to intoxication can reliably predict future drinking category assignment.

Methods

The classification strategy uses a machine‐learning approach to examine an extensive set of daily drinking attributes during 90 sessions of induction across 7 cohorts of 5 to 8 monkeys for a total of 50 animals. A Random Forest classifier is employed to accurately predict categorical drinking after 12 months of self‐administration.

Results

Predictive outcome accuracy is approximately 78% when classes are aggregated into 2 groups, “LD and BD” and “HD and VHD.” A subsequent 2‐step classification model distinguishes individual LD and BD categories with 90% accuracy and between HD and VHD categories with 95% accuracy. Average 4‐category classification accuracy is 74%, and provides putative distinguishing behavioral characteristics between groupings.

Conclusions

We demonstrate that data derived from the induction phase of this ethanol self‐administration protocol have significant predictive power for future ethanol consumption patterns. Importantly, numerous predictive factors are longitudinal, measuring the change of drinking patterns through 3 stages of induction. Factors during induction that predict future heavy drinkers include being younger at the time of first intoxication and developing a shorter latency to first ethanol drink. Overall, this analysis identifies predictive characteristics in future very heavy drinkers that optimize intoxication, such as having increasingly fewer bouts with more drinks. This analysis also identifies characteristic avoidance of intoxicating topographies in future low drinkers, such as increasing number of bouts and waiting longer before the first ethanol drink.

Alcohol use disorder (AUD) is a worldwide public health concern and estimated to be the third largest preventable cause of death in the United States (Mokdad et al., 2004). Population‐based epidemiological surveys conducted in the 1990s and early 2000s estimated lifetime and past year prevalence of AUDs in the United States to be between 13 to 23% and 7.4 to 8.5%, respectively (Grant, 1997; Grant et al., 2004). However, the most recent National Epidemiologic Survey on Alcohol and Related Conditions (NESARC‐III) of adults in the United States reveals a substantial increase in AUD for both past year (13.9%) and lifetime (29.1%) outcomes. The NESARC‐III data found alarmingly higher rates in younger individuals (18‐ to 19‐year‐olds), with a 26.7% past year and 37.0% lifetime AUD. The NESARC‐III also classified AUD severity as mild, moderate, or severe, based on the number of DSM‐V criteria endorsed by respondents: mild = 2 or 3, moderate = 4 or 5, and heavy ≥ 6 (of 11 different criteria).

To model the individual differences in severity of AUDs, we developed a nonhuman primate (NHP) model of oral alcohol self‐administration (Baker et al., 2014; Grant et al., 2008). This protocol identified a range of daily ethanol intakes that encompass 4 categorical levels of drinking severity: low drinkers (LD), binge drinkers (BD), heavy drinkers (HD), and very heavy drinkers (VHD) (Baker et al., 2014). These categories are reflective of AUD severity, with HD and VHD drinking associated with signs of dependence and significant increases in pathological outcomes to the brain (Cuzon Carlson et al., 2011; Kroenke et al., 2014; Siciliano et al., 2015; Welsh et al., 2011), bone (Gaddini et al., 2015), and immune system function (Asquith et al., 2014). However, even though these categorical levels of drinking allow the uniform comparison of multiple animal cohorts to a single disease description, they do not, by themselves, identify contributing drinking topographies that contribute to risk for becoming a heavier drinker. Other animal models have addressed aspects of risk factors for acquiring AUD with outcome measures that include alcohol consumption (Lovinger and Crabbe, 2005), but few studies have captured the spectrum of chronic alcohol intakes that encompass the human diagnosis of AUD. Here, we report on an extensive set of drinking variables surrounding the initiation of daily drinking to intoxication in our NHP model that are predictive (i.e., risk factors) of chronic alcohol self‐administration. This data set allows the modeling of future categorical drinking outcomes using an extensive set of phenotypic and behavioral data.

Specifically, a wide range of data are collected and collated across individual animals and cohorts within the context of a well‐defined schedule‐induced polydipsia (SIP) protocol (Grant et al., 2008). Data include subject's drinking pattern, drinking behavior, age, and physiological response to intoxication during the induction period (see Table S1). As in previous studies, the induction period consists of 30 consecutive days of drinking 0.5 g/kg ethanol, followed by 30 days of drinking 1.0 g/kg, and finally 30 days of 1.5 g/kg for all animals. Unlike rodent studies to date, this induction phase allows researchers to associate the same dose of ethanol and resultant blood ethanol concentrations (BECs) with individual patterns of intake, such as rate and volume. The induction phase also serves as a precursor to the study of alcohol consumption under relatively unrestricted access conditions. Thus, following the induction phase all monkeys are given daily “open access” to 4% w/v of ethanol and water for 22 h/d where they can choose to drink alcohol at any time. We have used this design to consistently capture molecular and behavioral data across cohorts of monkeys in a central repository: www.matrr.com (Daunais et al., 2014).

Previously, a single cohort of 10 monkeys was used to define aspects of alcohol drinking phenotypes during the induction phase of this SIP model (Grant et al., 2008). In that study, a modified principal component analysis indicated that the largest daily volume of ethanol consumed without a 5‐minute lapse in drinking (i.e., a “bout”) during induction of the 1.5 g/kg dose was the best predictor of future categorization as either heavy or non heavy alcohol drinking. Monkeys that could finish 1.5 g/kg ethanol in a single bout were described as gulpers and went on to be heavy drinkers, and those that took many bouts of small volumes to finish the 1.5 g/kg dose were described as sippers and proceeded to be non heavy drinkers (Grant et al., 2008). The demarcation of heavy versus non heavy drinking in that initial study was an average daily ethanol intake of 3.0 g/kg ethanol over approximately 2 six‐month periods of daily open‐access drinking. As noted above, we have further evaluated these models in additional cohorts, and rather than just heavy versus non heavy categories, we now have evidence that this monkey model supports 4 distinct categorical drinking levels based on natural breaks in ethanol intake distribution combined with BEC information from 31 animals in 4 distinct cohorts, and an analysis of categorical stability over time (Baker et al., 2014).

In this study, we expand our induction phase data analyses of predictive categorical alignment using 5 times more subjects than our original study in conjunction with Decision Tree machine‐learning algorithms (Yang et al., 2010). These algorithms are particularly useful in bioinformatics because of their enhanced performance under specific adverse conditions, for example, when variables are noisy or when the number of variables is much larger than the number of observations. Decision Tree‐based algorithms are compatible in tandem with numerous optimization strategies such as bagging and gradient boosting (GB) (Lee et al., 2005). In addition, Decision Tree‐based algorithms show superior performance in problems involving the classification of data into multiple categories, and its underlying algorithm can reveal which variables contribute in the task of classification (Díaz‐Uriarte and De Andres, 2006). They have been used to discern numerous clinical patterns in adult dependence treatment (Connor et al., 2007), progression of cardiovascular disease (Melillo et al., 2015), diabetes (Huang et al., 2015), Parkinson's disease (Przybyszewski et al., 2016), and hypertension (Ramezankhani et al., 2016), among others. Indeed, the wide acceptance of decision tree approaches in clinical medicine currently has broad implications in all areas of patient management (Araújo et al., 2016; Lobach et al., 2016). This strategy suggests that variables associated with early drinking behaviors may predict the severity of future alcohol abuse.

Materials and Methods

Animals

Fifty rhesus monkeys (Macaca mulatta) from the Oregon National Primate Research Center (ONPRC) were used in this study. Animals were both male and female, derived from 7 cohorts, designated as “4,” “5,” “6a,” “6b,” “7a,” “7b,” and “10.” Table 1 displays the sex of the cohorts and their average age and weight at the beginning of 1.5 g/kg ethanol induction and after 2 consecutive 6‐month periods of open‐access drinking. Table 1 also indicates assigned drinking categories.

Table 1.

Breakdown of Cohorts Used in the Study. Weights Are Derived from the Average Age of Animals Within the Cohort

ID	N (n = 50)	Sex	Beginning of 1.5 g/kg EtOH Induction		After second 6 months of Open Access		Drinking category distribution
			Age (years)	Weight (kg)	Age (years)	Weight (kg)	LD	BD	HD	VHD
4	10	M	8.24	9.4	9.98	9.89	5	4	1	0
5	8	M	5.63	8.31	7.15	9.06	0	1	3	4
6a	6	F	3.93	4.73	5.36	5.39	0	0	0	6
6b	5	F	5.62	5.61	7.07	6.59	3	0	1	1
7a	8	M	4.18	6.89	5.7	8.27	3	1	2	2
7b	5	M	5.69	8.02	7.18	8.63	3	1	1	0
10	8	M	5.19	7.55	6.71	8.61	2	3	1	2

BD, binge drinking; HD, heavy drinking; LD, low drinking; VHD, very heavy drinking.

All animals were born into a pedigreed population and remained with their mothers in a multigenerational troop until weaning at about 2 years of age. All monkeys were continually in a social setting at ONPRC and transitioned to individual cages at least 3 months prior to the onset of ethanol self‐administration according to established protocols (Helms et al., 2014b). Subjects were not members of the cynomolgus (Macaca fascicularis) cohort that initially were defined as either heavy or non heavy drinkers using this model (Grant et al., 2008). Rhesus cohorts 4, 5, 7a, and 7b were used in the previous analyses to identify the 4 drinking categories (Baker et al., 2014) and are used in these analyses along with cohorts 6a, 6b, and 10. The age range encompasses late adolescence to early middle age of captive monkeys, and data from a subset of these monkeys addressing age as a risk factor for chronic alcohol self‐administration have been published (Helms et al., 2014b).

Monkeys were housed individually with 4 cages (1.6 × 0.8 × 0.8 m) on a single rack: 2 cages located above and 2 below. Monkeys that weighed over 10 kg were allowed access to both horizontal cages, but only 1 drinking panel was affixed to the side of the cage. Each cohort was housed in a single room, and all animals had visual and auditory access to other monkeys in the room. Male monkeys were allowed tactile access to adjacent monkeys through grooming grids inserts in the common wall of the cage, and female monkeys were allowed 2‐hour access/d to a common space by removing the horizontal barriers between the cages.

Ethanol Self‐Administration

Self‐administration data and food intake patterns were acquired through operant panels, previously described in detail (Grant et al., 2008; Vivian et al., 2001). Monkeys were induced to self‐administer 4% ethanol w/v in water using a SIP procedure (Grant et al., 2008). A key aspect of ethanol self‐administration induction is that the dose of ethanol the monkeys were required to consume each day increased every 30 days beginning with 0.5 g/kg/d, then 1.0 g/kg/d, and finally 30 days of 1.5 g/kg/d. In this manner, all monkeys drank to levels that saturated metabolic capacity and increased BEC to at least 50 mg/dl. While intoxication occurred when their BEC was >80 mg/dl (Dawson et al., 2008; Li et al., 2007), low drinkers typically will not drink beyond 50 mg/dl (Grant et al., 2008). After induction, the monkeys transitioned to 22 h/d access to ethanol (4% w/v) and open access to water. Food was supplied at least 3 times a day during meals in the form of banana‐flavored pellets (Noyes, Lancaster, NH; Bio Serv, Flemington, NJ). Meals were a minimum of 2 hours apart (2.06 ± 0.16 hours) with the first meal provided at the onset of the session. The open‐access interval analyzed was two 6‐month periods, as previously described in Grant and colleagues (2008), see Fig. 1.

Figure 1.

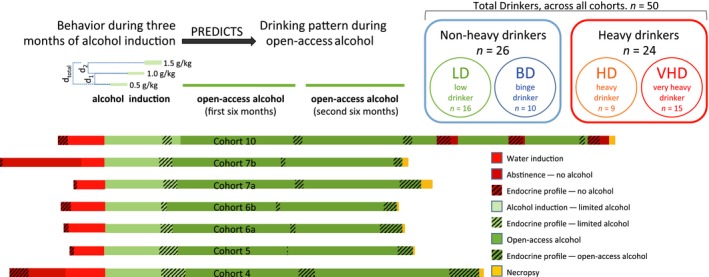
Illustration of drinking protocol, experimental paradigm, and animal category distribution. Seven rhesus cohorts participated in a common schedule‐induced polydipsia protocol. While certain aspects of the protocol were cohort specific, the behavioral observations made during the common induction phase was used to predict future drinking category classification based on common 12‐month open‐access drinking. The classification strategy for low drinking (LD), binge drinking (BD), heavy drinking (HD), and very heavy drinking (VHD) animals is described previously (Baker et al., 2014). About half of the animals in this study are either LD or BD animals (n = 26), and the other half are classified as HD or VHD (n = 24).

Computing and Statistics

All computations were executed on twin computers, each running 4 Intel Xeon E5620 processors (Intel Corporation, Santa Clara, CA) at 2.4 GHz, having 4 cores per processor, that is, a total of 16 cores per server, with 47 GB of memory. All statistical analysis and data processing were performed using Pandas, NumPy, and SciPy, which are packages for the Python programming language. Python's Scikit‐Learn package was used for all machine‐learning algorithms.

Drinking Categories

Each of the 50 animals was classified into 1 of 4 different categories (LD, BD, HD, or VHD), as previously described (Baker et al., 2014), see Fig. 1. Briefly, VHD category animals maintain an average open‐access daily ethanol intake >3 g/kg with more than 10% of days exceeding 4 g/kg. HD animals have ethanol intakes >3 g/kg for more than 20% of open‐access days. BD category animals have >2 g/kg ethanol intake for more than 55% of open‐access days and at least 1 event of >80 mg/dl BEC in a period of 12 months. LD animals make up the remaining individuals.

Drinking Behavior Attributes

This study recorded data from nearly 4,500 total sessions, approximately 1 session per day per animal, and compiled different quantitative attributes for each session, resulting in hundreds of raw and derived measurements. This high dimensional data, either derived or aggregated, was summarized into daily averages as appropriate (Grant et al., 2008). A complete list of all the attributes studied in our research can be found in Table S1.

Feature Generation

In machine learning, the attributes or variables that describe the data are known as features and are used to train classification models (Guyon et al., 2006). Features in this study are derived from raw behavioral data observed during the 90‐day ethanol induction period. Most features are used in their original format; however, others require additional processing or calculations to derive significance. To capture longitudinal trends, a feature depicting relative change within each measured attribute over a period of time is created, referred to here as a relative delta. Specifically, each attribute was measured for the first 30 days, middle 30 days, and final 30 days of ethanol induction. These effectively measure the relative change of each attribute's median value, as shown in Fig. 2 and defined in following formula:

$${\mathrm{\Delta }}_{\mathit{ij}}^{\mathrm{atrr}}=ln\left(\frac{\text{Median}(\text{Attribute}[\mathrm{stage}{}_{\mathit{i}}])}{\text{Median}(\text{Attribute}[\mathrm{stage}{}_{\mathit{j}}])}\right),$$

where i = {2,3}, j = {1,2}, and i ≠ j Furthermore, the 1.5 g/kg induction period was divided into 3 separate epochs of 10 days each, defined as p3e1, p3e2, and p3e3, respectively. In order to account for animal adaptation to stress induced by the third induction period as previously reported (Grant et al., 2008), relative deltas for these periods were are also constructed as $P{3}_{{\mathrm{\Delta }}_1}$, $P{3}_{{\mathrm{\Delta }}_2}$, and $P{3}_{{\mathrm{\Delta }}_{\mathrm{total}}}.$

Figure 2.

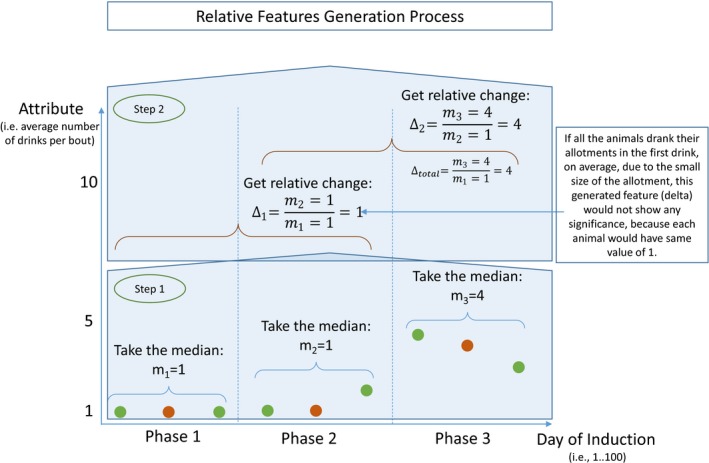
Changing drinking behaviors over time. Measuring the relative changes in behaviors over induction phases captures the longitudinal effects of changes in different drinking categories. Delta 1 (Δ₁) captures changes between the second and first induction phases, Delta 2 (Δ₂) captures changes between the third and second induction phases, and Delta total (Δ_total) represents changes between the third phase and first phase of induction. The final induction phase is likewise divided into 3 equal epochs of 10 days each, and similar deltas are calculated as $P{3}_{{\mathrm{\Delta }}_1}$, $P{3}_{{\mathrm{\Delta }}_2}$, $P{3}_{{\mathrm{\Delta }}_{\mathrm{total}}}$, respectively. These values are normalized by their natural log to represent positive or negative trends that can be used to train decision tree algorithms.

Forward Selection of Features

In addition to generating features, machine‐learning algorithms require an appropriate number of features (Barber, 2012). We used a forward selection strategy to select the most appropriate features, by testing a model iteratively, increasing the number of features at each iteration, and measuring the accuracy using a N‐fold cross‐validation (Alpaydin, 2014). Each forward selection iteration adds the feature that gives the best increase in performance in combination with existing features already in a set of chosen features.

Random Forest Classification Model

We implemented the Random Forest (RF) decision tree for prediction. RFs perform well on small data sets, resisting overfitting by penalizing data outliers without skewing the distribution of the data (Yang et al., 2010). RFs are common in bioinformatics and genomics research, where the number of features can be several orders of magnitude greater than the number of observations. An important quality of RFs is the possibility of using several distinct low‐dimensional prediction models based on small subsets of features that, together, increase classification accuracy (Yang et al., 2010). A GB classifier was used to augment the number of RFs. GB uses a regression tree for each class, for a total of n classes, fitting the negative gradient of a binomial or multinomial deviance loss function (Friedman, 2002). At each iteration, the GB algorithm draws small subsets of the data at random without replacement and creates a base learner to classify that subset of data (Friedman, 2002). It may also be internally optimized to prevent overfitting (Friedman, 2001).

A bagging technique is used to improve quality by reducing the variance of the output error, avoiding overfitting, and improving accuracy of the base classification model in spite of a limited sample size of 50 (Breiman, 1996). Bagging makes use of several training sets by uniform data sampling with replacement. Statistically, each training set is expected to contain approximately 63.2% of unique observations from the entire data set, while the rest are duplicates, creating a bootstrapped data set (Aslam et al., 2007) and pushes results toward optimal performance (Breiman, 1996).

Two‐Step Classification Model

Having multiple categories and few observations (4 categories of 50 animals, and inconsistent observations per category, see Table 1) is not an ideal classification framework, and thus, we reduced the number of categories from 4 to 2 and implement a 2‐step classification process. The first step distinguishes between 2 combined groups of similar categories: non heavy drinking group (LD and BD) versus heavy drinking group (HD and VHD). The second step differentiates the categories within groups. That is, LD and BD were separated and classified individually as subcategories of the original non heavy drinking group, and similarly, HD and VHD were separated from the heavy drinking group and classified individually using different parameters for each classification subgroup. Choosing different parameters for subcategories reduced the dimensionality of the problem and further classified animals by identifying different behavioral aspects.

Feature Interaction Interpretation

In order to understand the interaction between features, partial dependence plots (PDPs) were used to provide a visual understanding of how 2 features interact to contribute to drinking category. PDPs are 2‐dimensional color plots used to inspect the significance of the target function and a set of target features, marginalizing over the values of all other features (the complement features), produced from GB regressors.

Performance Measure and Base Case

Typically, standard accuracy is computed as the total number of correctly classified samples over the total number of samples. Here, our accuracy rate is modified to allow for a 2‐step classification model by multiplying the prior probability of a sample being in the group LD and BD or in the group HD and VHD by the standard accuracy in either of those 2 groups. Composite accuracy then is computed by multiplication with standard accuracy of the first step classification using a 10‐fold cross‐validation strategy that was averaged across 20 runs. The base case is used to determine how well the proposed methodology performs comparatively with only the naïve approach. The base case is defined as follows: let D be the list of “targets,” or the list of categories corresponding to each observation in the training data; let g (D, c) be a function over the list of targets, with the count of items in the list D that are equal to category c. Given an observation of the data, x, we define our base case as a naïve classifier:

$$NaiveClassifier(x)=arg\underset{c}{max}g(D,c).$$

A naïve classifier is an educated guess that chooses the category with strictly the greatest number of occurrences and is better than choosing at random with no prior information of the data.

Results

Derived Relative Deltas as a Representation of Longitudinal Change

Changes in observed behavioral data over the course of induction were measured as relative changes, referred to here as deltas (Δ₁, Δ₂, Δ_total, $P{3}_{{\mathrm{\Delta }}_1}$, $P{3}_{{\mathrm{\Delta }}_2}$, $P{3}_{{\mathrm{\Delta }}_{\mathrm{total}}}$). Figure 3 represents the relative changes for features associated with classifying VHD versus HD. While there are trends in deltas between drinking categories, the RF algorithm treats them as independent characteristics that do not require stringent statistical significance for them to contribute toward an overall picture of drinking behavior.

Figure 3.

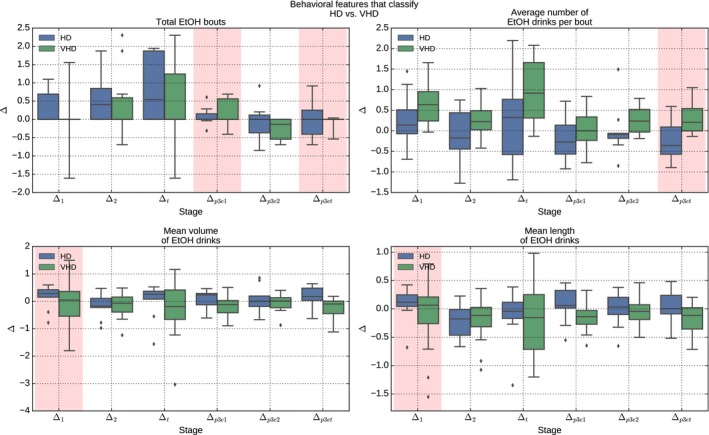
Changes in behavior over time can be represented as deltas between the induction phases. Deltas provide a robust set of features to distinguish future drinking categories. Each pair of columns represents longitudinal changes for a specific time frame between 2 categories of drinkers. Collectively, they provide a picture of how features change over time. Highlighted columns represent features automatically selected by the Random Forest classifier as contributing most toward a distinguishing classification.

Forward Selection Identifies Feature Sets that Maximize Accuracy

The forward selection strategy ranks the importance of each feature, or set of features, in order to reduce feature set dimensionality and plot classification accuracy as a function of the number of features. All combinations of shared features (Table S1) were investigated for robustness. Figure 4 illustrates how accuracy drops with an increase in the number of features. In order to maximize accuracy in the classification of “heavy” (VHD + HD) drinkers versus “non heavy” (LD + BD) drinkers, 5 features were discovered to be optimal (Fig. 4 A). Those features include sex and age at induction, the relative delta between second and third induction periods (Δ₂) for the median time between ethanol drinks, the relative delta between second and first epochs of the last induction period ($P{3}_{{\mathrm{\Delta }}_1}$) for the sequence number of the maximum ethanol bout, and the relative delta between the third and second epochs of the last induction period ($P{3}_{{\mathrm{\Delta }}_2}$) for the latency to first drink, see Table 2. In order to optimize accuracy between distinguishing LD from BD, 4 features were identified (Fig. 4 B), including the Δ₂ for the mean length of ethanol drinks and latency to first ethanol drink, and the Δ_total for mean length of ethanol drinks and the total number of bouts. Likewise, 6 separate features were determined optimal to separately classify HD and VHD drinkers (Fig. 4 C), including sex, the Δ₁ for the mean volume of ethanol drinks and the mean length of ethanol drinks, and relative changes in the third induction period for the average number of ethanol drinks per bout and total number of ethanol bouts.

Figure 4.

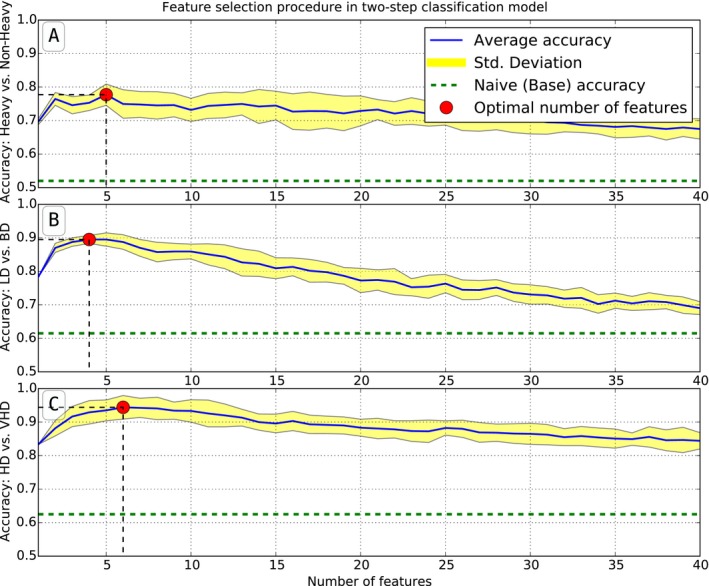
Optimal number of features chosen from forward feature selection. The horizontal axis represents the number of features chosen based on contribution. The vertical axis shows the accuracy of the drinking category classification, which could take values from [0, 1], averaged for 20 runs of 10‐fold cross‐validation, as well as the one‐sigma range of accuracy deviation. Subpanel (A) illustrates that there are 5 optimal features for the aggregated classification of LD + BD drinkers, defined as “non heavy,” versus HD + VHD groups, defined as “heavy” drinkers. Panel (B) demonstrates that there are 4 optimal features for the LD versus BD classification, and Panel (C) shows 6 features as optimal for HD and VHD category classification. The relevant features are described in Table 2.

Table 2.

Features Impacting Prediction of Drinking Categories

Feature	Period
Heavy versus non heavy (accuracy = 0.78)
Sex	Fixed
Age at ethanol induction (days)	Fixed
Median time between ethanol drinks	∆2
Sequence number of the max ethanol bout	$P{3}_{{\mathrm{\Delta }}_1}$
Latency to first ethanol drink	$P{3}_{{\mathrm{\Delta }}_2}$
LD versus BD (accuracy = 0.90)
Mean length of ethanol drinks	∆2
Latency to first ethanol drink	∆2
Mean length of ethanol drinks	∆total
Total ethanol bouts	∆total
HD versus VHD (accuracy = 0.95)
Total ethanol bouts	$P{3}_{{\mathrm{\Delta }}_1}$
Total ethanol bouts	$P{3}_{{\mathrm{\Delta }}_{\mathrm{total}}}$
Average number of ethanol drinks per bout	$P{3}_{{\mathrm{\Delta }}_{\mathrm{total}}}$
Mean volume of ethanol drinks	∆1
Mean length of ethanol drinks	∆1
Sex	Fixed

BD, binge drinking; HD, heavy drinking; LD, low drinking; VHD, very heavy drinking.

It is important to note that while the number of features and the feature content change as the classification schema changes, there are some behavioral characteristics that remain consistent (Table 2). The total number of ethanol bouts and the mean length of ethanol drinks is important to differentiate between LD versus BD drinkers and VHD versus HD drinkers, with a change occurring predominantly within the third induction period (P3_Δ) a deciding factor in VHD versus HD drinker classification.

Classification into Drinking Groups and Categories

Classification accuracy was determined based on the optimal features for distinguishing “non heavy” from “heavy” drinkers, LD from BD, and VHD from HD animals. The resulting accuracy was 78% (Fig. 4 A), 90% (Fig. 4 B), and 95% (Fig. 4 C), respectively. These values represent approximately a 3‐fold increase over naïve classification.

Total, or composite, accuracy is calculated for the entire model by determining category distribution and the accuracy rates for both the first and second steps. The prior probability of being in the non heavy group (LD and BD) and heavy group (HD and VHD) is 52% and 48%, respectively. The probability‐adjusted accuracy of being correctly classified within the non heavy and heavy drinking groups is 78%. The first step accuracy of 78% is used to find a composite average accuracy of 72% as follows:

$$\text{Composite Accuracy}=0.78\ast \left(0.52\ast 0.90+0.48\ast 0.95\right)=0.72$$

The base case for 2‐step classification is given by choosing the most likely categories during both steps. In the first step, the most likely group is the non heavy drinking group (LD and BD) with a 52% probability of being correct. In the second step, the most likely category is LD with a 62% probability of being correct. Thus, the overall accuracy for a 2‐step naive classifier is 32%. Our classification strategy represents approximately a 2.5‐fold performance improvement.

Testing Individual Cohort Accuracy

While animals studied here were clustered into separate cohorts, their common experimental protocols enable an evaluation of common behavioral features. Cohort‐centric evaluation, however, illustrates how well individual cohorts are categorized even though each cohort was independently run through the SIP protocol. Table S2 illustrates cohort‐specific accuracies, including precision and recall, when predicting whether animals will eventually aggregate with the non heavy drinking group or the heavy drinking group, and further predicting LD versus BD and HD versus VHD segregation. While several cohorts exhibit robust prediction under certain conditions (HD vs. VHD predictions for cohorts 5 = 100%, 6a = 100%, 6b = 100%, 7a = 75%, 10 = 100%), they do not fare as well under other conditions (LD vs. BD predictions for cohorts 4 = 78%, 6b = 100%, 7a = 75%, 7b = 75%, 10 = 40%). The limited cohort size makes it difficult to use intracohort predictions as the basis for broader hypothesis development or to draw conclusions about the population in total.

Partial Dependency: Pairs of Features Affecting Future Drinking Patterns

PDPs are useful to gauge complex relationships among contributing characteristics that do not follow linear constraints. Figure 5 illustrates the likelihood of all pairs of features on predicting “heavy” drinkers during the induction protocol (see detailed data in Fig. S1). The heat map colorization, where red represents high likelihood, indicates how features act independently (line graphs) and in concert with other features. For example, trends toward increased sequence number of maximum ethanol bout ($P{3}_{{\mathrm{\Delta }}_1}$) combined with trends toward decreased latency to the first ethanol drink ($P{3}_{{\mathrm{\Delta }}_2}$) indicate an increased likelihood for animals to not progress to become “heavy” drinkers. The age of ethanol induction also represents strong tendencies toward non heavy drinking at adolescence, particularly when combined with the decreased latency to the first ethanol drink ($P{3}_{{\mathrm{\Delta }}_2}$). As categorical features, such as sex, are uninformative in PDP graphs, they are omitted from PDP figures.

Figure 5.

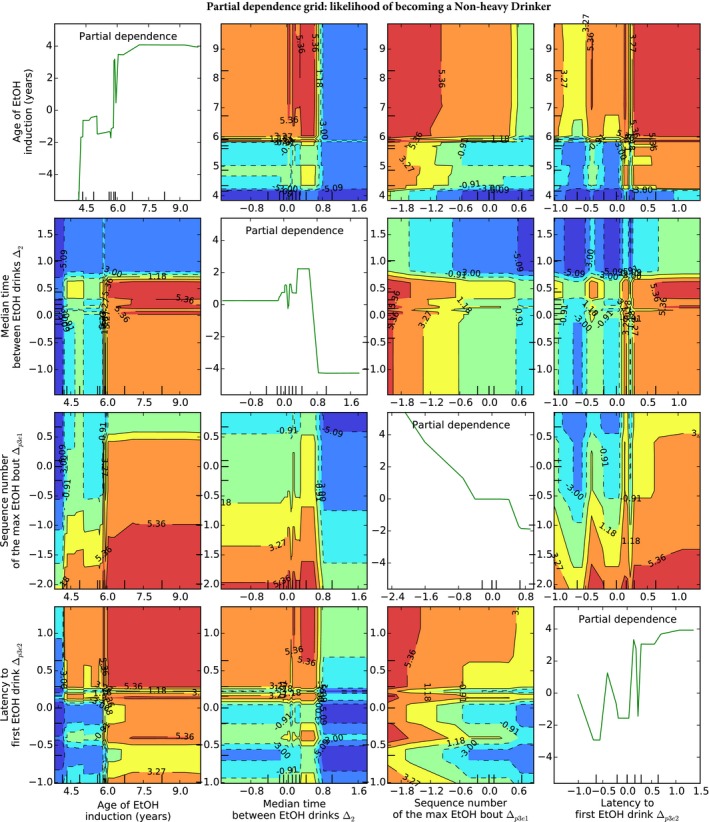
Partial dependence plot for optimal non‐heavy drinker classification features. Partial dependence plots indicate how features act independently (line graphs) and in concert with other features. The plots in this figure illustrate the likelihood of an animal remaining a non heavy drinker given the optimal features predicted. For example, trends toward increased sequence number of maximum ethanol bout ($P{3}_{{\mathrm{\Delta }}_1}$) combined with trends toward decreased latency to the first ethanol drink ($P{3}_{{\mathrm{\Delta }}_2}$) indicate an increased likelihood for animals to not progress to become “heavy” drinkers. All pairwise relationships are illustrated, with red areas indicating a greater likelihood for becoming a future heavy drinker under the combined influence of the represented features, while blue areas indicate areas of lower likelihood.

PDPs for classification of LD versus BD and HD versus VHD also represent strong relationships between features as they contribute to the classification strategy (Figs S3 and S4, respectively). For example, LD drinkers maintain mean lengths of ethanol drinks and increase the total number of ethanol bouts when compared to BD (Fig. S2) and this is reflected in PDP graphs (Fig. S3). The likelihood of becoming a LD is increased drastically as the trend in total number of ethanol bouts increases, particularly when the trend for the mean length of ethanol drinks per bout maintains or increases. Other dependency relationships are also reported, including a strong relationship for distinguishing a VHD over a HD through a strong relationship between relative changes in the third induction period, including a synergistic relationship between the change in the average number of ethanol drinks per bout ($P{3}_{{\mathrm{\Delta }}_{\mathrm{t}}}$) and the total number of ethanol bouts ($P{3}_{{\mathrm{\Delta }}_{\mathrm{t}}}$) (Fig. 3 and Fig. S4).

Discussion

Not everyone who drinks alcohol is at equal risk for developing an AUD. While risk factors can be identified in human populations, few studies examine baseline data prior to ethanol exposure, and life histories of ethanol consumption are highly subjective. In contrast, controlled animal models can play a key role in disentangling the interaction between risk factors and consequences of alcoholism. Specifically, the historical and current environmental variables of rearing, housing, nutrition, medical care, sex, age, and genetics can be controlled. NHPs provide especially useful subjects for the study of risk factors, as they display dimensions of cortical processing in cognitive tasks, experience complex social and affective processes, absorb and metabolize ethanol at similar rates as humans, and show individual differences in the self‐administration of ethanol from avoiding intoxication up to physical dependence (Cuzon Carlson et al., 2011; Grant and Bennett, 2003; Welsh et al., 2011). Translational risk factors between NHP and humans that lead to excessive alcohol drinking have been identified, including social factors (Helms et al., 2012), endocrine factors (Helms et al., 2014a), and age at the onset of drinking (Helms et al., 2014b).

The use of SIP is necessary to induce oral ethanol self‐administration in macaque monkeys and provides an experimentally rigorous, accurate, and reproducible procedure for establishing stable, chronic ethanol drinking. The induction procedure optimizes the association of drinking ethanol with the postingestive effects of intoxication. The stepwise increase in daily dose from 0.5 to 1.0 to 1.5 g/kg helps to circumvent taste aversions. Although the parameters of SIP used here are unlikely to be encountered as most humans first experience alcohol, SIP can be induced in humans (Doyle and Samson, 1988) and other schedules of reinforcement can generate other forms of adjunctive behaviors in humans such as smoking, eating, and talking (Falk, 1984, 1998). Importantly, in our model alcohol self‐administration continues after the conditions of SIP are suspended, an effect not found when rodents are food deprived and induced to drink alcohol through a SIP procedure (Falk, 1998).

Once open‐access conditions were established and ethanol self‐administration was assessed, we leveraged the previously described, categorically distinct, drinking patterns during the open‐access conditions, that is, LD, BD, HD, or VHD (Baker et al., 2014), for potential alignment to drinking behaviors that emerge during the SIP induction phases using machine‐learning classification strategies. After applying RF decision approaches with bagging and GB to enhance behavior selection, we are able to identify 5 features of drinking that are predictive of broad “heavy drinking group” and “non heavy drinking group” classifications with 78% accuracy. Using additional pattern analysis, we are able to identify 4 induction phase behaviors that subclassify the heavy drinking group into HD and VHD with 95% accuracy, and we are able to identify 3 induction phase behaviors that subclassify non heavy drinking group into BD and LD with 90% accuracy.

There are several features that contribute to the classification of future heavy drinkers group and non heavy drinkers group. It is important to remember that these features are selected as a group by the machine‐learning algorithm to optimize the categorizations, and these features may not themselves be statistically different between the categories. These features appear to work in concert and demonstrate variable impact on each other over their spectrum of influence, and many of them have been previously reported in the human literature. For example, the age of first intoxication is the age at which monkeys begin the 1.5 g/kg ethanol induction period. Although the “age at first drink” has been questioned as a predictor of future alcohol problems (Kuntsche et al., 2016), a longitudinal study on the age of “first intoxication” had a positive correlation with heavy drinking and drinking‐related problems. Our findings support the fact that an earlier age of first intoxication leads to higher likelihood of becoming a heavy drinker; however, there is a possible cohort or small number confound because only 1 cohort was older and only 1 was younger (Table 1). While sex was also found to be a predictive factor, this is a potential confound in this study because the small number of females included were biased toward heavy drinking animals. The most likely reason for the bias toward heavy drinking in the females studied to date is their age at the onset of drinking to intoxication, which was in the late‐adolescent/young adult stage. This is known to be the age of highest risk for male monkeys in our rhesus population (Helms et al., 2014a,b), and older adult females have not been characterized and added to the population base used in these studies. It is important that unlike rodent studies or even human self‐report studies, NHP studies are small by necessity. We show here that the open‐access paradigm allows us to combine data across many cohorts and many years, increasing the sample size to 50 animals. Future cohorts will continue to add to the diversity of this data set (including sex and age).

It is interesting that almost all the informative features (Table 2) are ones that operate on longitudinal scales, where observed behaviors increase or decrease during the induction period. For example, a decrease in the latency to first ethanol drink within the last (intoxicating) induction phase is a driving factor to distinguish heavy from non heavy drinkers. There is also longitudinal variability between the second and third induction phases where the heavy drinking animals increase their median time between ethanol drinks, while the non heavy maintained a longer time between drinks.

The 2‐step classification strategy implemented here provides insight into a more granular inspection of drinking categories. Specifically, as few features that distinguish heavy from non heavy drinking groups are in common with distinguishing BD from LD or VHD from HD drinkers, there is an indication that common behaviors place populations at risk of heavy drinking, but separate sets of behaviors may be responsible for extreme individuals. For example, the amount of ethanol the monkeys need to drink doubles from induction phase 1 to induction phase 2, and among the heavy drinkers, the HD appropriately increase their mean volume of ethanol drinks and mean length of ethanol drinks. However, the VHD display more variation (increasing and decreasing) in their mean volume of ethanol drinks and their mean length of ethanol drinks. Features changing during the third (intoxicating) phase of induction are especially important in distinguishing VHD from HD. The HD increase the number of ethanol bouts at the beginning of the intoxicating phase and decrease the average number of ethanol drinks per bout at the end of the intoxicating phase. The VHD maintain their total number of ethanol bouts and increase their number of ethanol drinks per bout throughout the intoxication phase of induction. As these characteristics of drinking (fewer bouts with more drinks) would collectively insure higher BECs, it appears that the VHD monkeys adapt their drinking during induction to optimize intoxication when a reliable intoxicating dose of ethanol (1.5 g/kg) is available. This topography of drinking is then maintained or exaggerated when given the opportunity to drink nearly unlimited amounts of alcohol in the 22 h/d “open‐access” sessions (see also Grant et al., 2008). On the lower end of the drinking spectrum, the LD tend to increase latency to first ethanol drink, between phases 2 and 3 of induction, perhaps to avoid intoxication in the third phase. While the LD and BD begin induction with a similar number of ethanol bouts, the LD consistently increase the number of ethanol bouts throughout the 3 phases of induction, again perhaps to avoid intoxication. The binging monkeys have a higher mean length of ethanol drinks than the LD in phase 1, but the BD decrease the length of their drinks when they reach phase 3. Thus, during the induction phases as the daily dose of ethanol increases, the BD monkeys transition to taking shorter drinks than the LD. This topography that emerges in drinking the intoxicating dose of 1.5 g/kg ethanol appears to allow for occasional days of intoxicated drinking under the open‐access conditions while keeping daily averages within the range of LD monkeys.

In conclusion, we used a machine‐learning approach to determine the most informative behaviors during alcohol induction phases to predict future categorical open‐access drinking patterns in monkeys. Our high classification accuracies and PDP analyses affirm previous findings (Grant et al., 2008), while providing greater insight into granular behavioral associations to AUDs. Interestingly, most of the predictive factors were longitudinal changes of drinking patterns associated with drinking increasing doses of ethanol over the induction phases. In particular, the difference between drinking 1.0 g/kg and 1.5 g/kg under SIP resulted in changes in the topography of intake that reflects risk for future heavy drinking. The future VHD monkeys drank in a “gulping” style (decreasing drink time while maintaining drink volume) that helps ensure intoxication. The future LD monkeys drank in a “sipping” style (longer latency to start drinking, a shorter length of ethanol drinks, and an increase in the number of bouts) that is consistent with avoiding intoxication. While the features in and of themselves may not be statistically significant, we have identified which features when taken together are highly predictive of future drinking categories. These early, predictive drinking patterns suggest a remarkable adaptation of drinking topographies that support a biological predisposition in some monkeys to seek intoxication and in other monkeys to avoid intoxication. Future genetic data from these and future cohorts will include genomic data (DNA polymorphisms), gene expression data, and epigentic data, which could identify baseline risk factors, and potential translational biomarkers, for categorical drinking. Understanding the genetic mechanisms associated with these categorical levels of drinking will help translate the risk and protective factors to the human population.

Conflict of Interest

The authors have no conflict of interest to declare.

Supporting information

Table S1. List of all attributes collected in the MATRR Database.

Table S2. Random Forest prediction results.

Fig. S1. Relative deltas for optimal heavy versus non‐heavy classification features.

Fig. S2. Relative deltas for optimal LD versus BD classification features.

Fig. S3. Partial dependency plot for optimal LD versus BD classification features.

Fig. S4. Partial dependency plot for optimal VHD versus HD classification features.