Precipitation and Crystallization Kinetics in Silica Gardens

Abstract

Silica gardens are extraordinary plant‐like structures resulting from the complex interplay of relatively simple inorganic components. Recent work has highlighted that macroscopic self‐assembly is accompanied by the spontaneous formation of considerable chemical gradients, which induce a cascade of coupled dissolution, diffusion, and precipitation processes occurring over timescales as long as several days. In the present study, this dynamic behavior was investigated for silica gardens based on iron and cobalt chloride by means of two synchrotron‐based techniques, which allow the determination of concentration profiles and time‐resolved monitoring of diffraction patterns, thus giving direct insight into the progress of dissolution and crystallization phenomena in the system. On the basis of the collected data, a kinetic model is proposed to describe the relevant reactions on a fundamental physicochemical level. The results show that the choice of the metal cations (as well as their counterions) is crucial for the development of silica gardens in both the short and long term (i.e. during tube formation and upon subsequent slow equilibration), and provide important clues for understanding the properties of related structures in geochemical and industrial environments.

1.  Introduction

Under certain conditions, precipitation of multivalent metal cations from silica‐rich solutions at high pH results in the spontaneous formation of intriguing tubular structures with plant‐like morphologies.1, 2, 3 These so‐called silica gardens arise from the coupling of chemical reaction with osmotic and buoyancy forces,4 and were shown to consist of a mixed metal (hydr)oxide/silica(te) membrane (the wall of the tubes)5, 6, 7, 8, 9, 10 that separates two solutions with fundamentally different compositions.11 Despite their purely inorganic nature, silica gardens mimic biogenic matter and thus have recurrently been the subject of discussions around the origin of life.3, 12, 13 This notion was recently refueled by the discovery of the existence of considerable electrochemical potential differences across such tubular precipitates during the early stages of evolution,11, 14 which could successfully be employed as a source of energy.15 Apart from that, related structures are known to occur in geological environments16 and industrial settings,17 and the formed membrane materials have been scrutinized with respect to their properties for application as, for example, catalysts18, 19 and reactors.20

In previous studies,11, 21 we have developed a procedure to grow single macroscopic silica‐garden tubes with well‐defined dimensions and an open end on top (Figure 1), which for the first time allowed for straightforward sampling and in situ analysis of the two solutions separated by the formed inorganic membrane. In this way, it was possible to monitor changes in pH and the concentrations of the various ionic species present in the system as a function of time. The resulting data provided detailed information on the dynamic behavior of silica gardens after completion of macroscopic growth, and revealed drastic concentration gradients across the tube walls that only slowly decayed with time. This gave fundamental insight into the complex diffusion and precipitation processes occurring in the system, which were consistent with the final composition of the membranes and furthermore explained the observed electrochemical potential differences on a quantitative level.

Figure 1.

Controlled (left) and random (right) growth of cobalt‐based silica gardens, leading to a single macroscopic tube and multiple (irregular) smaller tubes, respectively. The scale bar applies to both images. The purple and green colors in the left picture correspond to CoCl₂ (initial salt pellet) and Co₂(OH)₃Cl/Co(OH)₂ (newly formed tube wall).11

In the present work, we have continued our approach to perform time‐dependent analyses of the physicochemical characteristics of silica gardens. In particular, we used two different synchrotron‐based techniques to trace the progress of membrane mineralization from two perspectives, namely, the solution (by measuring ion concentrations) and the solid state (through diffraction on the membrane). With the obtained data, we propose a model to describe the kinetics of the coupled dissolution, precipitation, and (re)crystallization processes that take place in silica gardens based on iron and cobalt chlorides during and after tube formation.

2.  Results

The first step in our study was to measure the concentration of metal cations dissolved in the solution enclosed by the inorganic membrane, since this parameter directly reflects the interplay between dissolution and precipitation equilibria. For this purpose, we prepared single open‐tube silica gardens (as shown in Figure 1) by controlled addition of sodium silicate sol to pressed pellets of CoCl₂ ⋅6 H₂O, FeCl₂ ⋅4 H₂O, and FeCl₃ ⋅6 H₂O, according to a procedure described in detail elsewhere.11, 21 Unlike these previous studies, metal‐ion concentrations were determined by means of X‐ray absorption spectroscopy (XAS) in the present work, by using thin layers of liquid obtained by sampling small aliquots of the interior solution at different times after completed tube preparation (see Figure S1 in the Supporting Information). The resulting time‐dependent concentration data are shown in Figure 2. For all cations, a characteristic initial increase was observed up to 0.7–0.9 m (dissolution), which was followed by an exponential decrease (precipitation). In silica gardens formed with chloride salts of Co²⁺ and Fe²⁺, the metal‐ion concentration gradually approaches zero after about 7 and 30 h, respectively, whereas in the case of Fe³⁺ a constant final level of around 0.2–0.3 m is reached after about 2 h (Figure 2 C). This distinct feature is caused by progressive solidification of the interior solution, as already discussed in previous work.21 Even though the particular timescales differ, the overall progressions of metal ion concentrations are very similar in all three investigated systems, and hence the results for FeCl₂, FeCl₃, and CoCl₂ can be described by one common kinetic model (see below). Moreover, the data obtained by synchrotron‐based XAS in the present study agree well with concentration profiles measured by laboratory inductively coupled plasma (ICP) spectroscopic methods in earlier work.11, 21 We note that local concentration differences and corresponding gradients are very likely to occur in the inner solution during the early stages, in which pellet dissolution is still proceeding; however, the fact that high metal‐ion concentrations were measured near the top of the tubes right from the beginning (as well as the absence of any measurable concentration differences along the vertical direction) suggests that any such gradients play only a minor role in the overall dynamics and can be neglected in good approximation, especially in the later stages when dissolution is complete (i.e. after 1–2 h). We attribute this behavior to the comparably large dimensions of the tubes, which allow for distinct convective flows in the interior solution and hence ensure rapid local equilibration.

Figure 2.

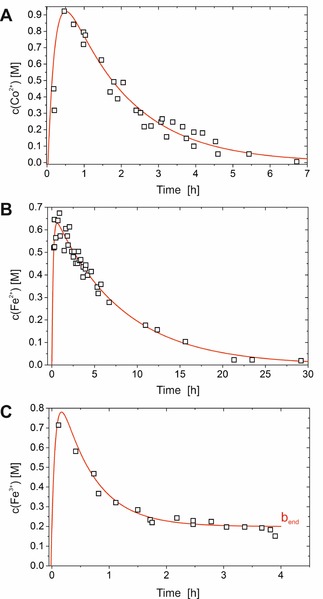
Cobalt and iron concentrations measured by XAS as a function of time inside the tubes of silica gardens grown with pellets of A) CoCl₂ ⋅6 H₂O, B) FeCl₂ ⋅4 H₂O, and C) FeCl₃ ⋅6 H₂O. Samples were taken from three independently prepared tubes for each metal salt at different times. The experimental error is estimated to ±10 % of the reported value (except for measurements prior to completion of dissolution, in which local concentration gradients are likely to cause larger errors). Red lines represent fits of the data on the basis of a kinetic model (Figure 4) that describes dissolution and precipitation processes as an irreversible consecutive reaction [according to Eqs. (1) and (2); correlation coefficients: R ²=0.909(A), 0.964 (B), 0.969 (C)]. Note that the parameter b _end in C) represents the non‐zero final concentration of metal cations detected in the FeCl₃‐based system [cf. Eq. (2)].

Having traced dissolution and precipitation phenomena in silica gardens from the solution point of view, we turn to address the characteristics of the formed solid material and corresponding changes over time. To this end, we used in‐situ XRD to monitor the degree of crystallinity and the nature of the occurring phases. First, samples aged for sufficiently long periods of time to ensure equilibration were studied in their native environment (i.e. without isolating them from the surrounding silicate sol), in order to identify the crystalline material present at the end of the process (note that no crystalline particles were detectable in the bulk of the solutions on both sides of the membrane by dynamic light scattering, that is, all detected diffraction originates from the tube walls). In line with previous observations,11, 21 cobalt hydroxide chloride (Co₂(OH)₃Cl) is formed from pellets of CoCl₂, and mixtures of Co(OH)₂ and Co₄(OH)₈ ⋅CoO_0.48(OH)_0.52NO₃ are obtained with pellets made from Co(NO₃)₂ (data not shown). In the case of iron(II), tubes grown with FeCl₂ and FeSO₄ were found to be rich in crystalline Fe₂(OH)₃Cl and Fe(OH)₂, respectively. This is in contrast to the results of our earlier work,21 in which iron(III) compounds were also predominant in the membrane grown with iron(II) salts, presumably owing to oxidation in contact with air. The present experiments show that this oxidation process occurs upon isolation of the tubes from solution, since no iron(III) species were detected by in‐situ diffraction. For both Co²⁺‐ and Fe²⁺‐based silica gardens, we cannot exclude the coexistence of amorphous phases (e.g. metal (hydr)oxides or silica) with the identified crystalline particles, although morphological analyses suggest that most of the tube wall (at least the metal (hydr)oxide component) is indeed crystalline.21 This is different for silica gardens prepared with pellets of iron(III) salts; here, no crystalline reflections could be detected for Fe(NO₃)₃ and Fe₂(SO₄)₃ (i.e. all phases in the membrane are amorphous to X‐rays), whereas relatively weak signals for FeOOH (lepidocrocite and goethite) were observed when starting with FeCl₃. Thus, the tendency for crystallization in cobalt‐ and iron‐based silica gardens seems to depend strongly on the type of metal cation used, while the nature of the forming crystalline phases appears to be influenced by the counterion; in particular, chloride salts seem to favor incorporation of the counterion into the emerging phases, which is not or less frequently the case with sulfates and nitrates.

On the basis of these findings, we performed time‐dependent XRD measurements on single open‐tube silica gardens grown with CoCl₂ (i.e. the same system as studied by XAS, cf. Figure 2 A). Due to the large dimensions of these samples (d≈3–5 mm, h≈30 mm), white X‐rays were used for the experiments to give sufficient transmission through the thick specimens (see Figure S2). The diffraction at a fixed angle was monitored with an energy‐dispersive (ED) detector and thus translated into actual diffraction patterns,22 as shown for the example of CoCl₂ in Figure S3. As expected, proceeding crystallization of Co₂(OH)₃Cl in the system leads to a continuous increase of the intensity of crystalline reflections in the diffraction patterns that allows for a quantitative analysis of the process. However, even though the used setup permits the study of large macroscopic tubes, as needed for the concentration measurements in Figure 2, it also brings about two major disadvantages. One is the limited beam size (max. 300×300 μm), which covered only a small fraction of the total area of the large tubes and hence rendered the results not necessarily representative of the entire structure. The other issue lies in the need to position the tube wall exactly at the intersection point where the virtual extension of the detector arm meets the incident X‐ray beam to obtain a proper signal. This caused repeated problems and made it difficult to acquire reproducible data with all three types of silica gardens studied.

Therefore, in an alternative setup, we prepared miniaturized tubes by placing tiny crystals of metal salt in a capillary and slowly adding sodium silicate solution, yielding filamentous structures with diameters in the range of several hundreds of micrometers (see right image in Figure 1), on which the X‐ray beam could readily be focused (see Figure S4). With this setup, reliable time‐dependent diffraction data could be collected for silica gardens grown with crystals of FeCl₃ ⋅6 H₂O, FeCl₂ ⋅4 H₂O, and CoCl₂ ⋅6 H₂O. The resulting patterns are shown as 3D representations in Figure 3 A–C. In all cases, crystallization of the phase observed at the end of the process (i.e. Co₂(OH)₃Cl, Fe₂(OH)₃Cl, and FeO(OH), respectively) starts right from the beginning after tube formation and continues over periods of several hours, as is clearly evident from the increase in the intensities of the detected crystalline reflections. To quantify these observations, the area under the peaks was integrated and converted to an apparent reaction progress α (Figure 3 D–F) representing the evolution of crystallinity in the system as a function of time (with α→1 for t→∞).23 The crystallization processes are essentially completed after about 5–10 h in silica gardens based on CoCl₂ and FeCl₂, whereas the FeCl₃ system is less prone to crystallize and develops more slowly on timescales distinctly longer than 10 h, in line with previous findings made by ex‐situ analyses after isolation of corresponding tubes.21 Furthermore, we note that the temporal evolution of diffraction patterns traced for CoCl₂ in the miniaturized setup (Figure 3 A,D) is comparable to the results obtained for single macroscopic tubes (cf. Figure S3), and that the type of crystalline phase formed is the same in macroscopic and miniaturized tubes for all three metal salts investigated (i.e. Co₂(OH)₃Cl for CoCl₂ ⋅6 H₂O, Fe₂(OH)₃Cl for FeCl₂ ⋅4 H₂O, and FeO(OH) for FeCl₃ ⋅6 H₂O; cf. Figure 3 for miniaturized tubes and the above section on the variation of counterions in macroscopic tubes). This suggests that crystallization proceeds in a similar manner in both configurations, and confirms that the XRD data shown in Figure 3 can be directly correlated with the metal‐ion concentrations in Figure 2.

Figure 3.

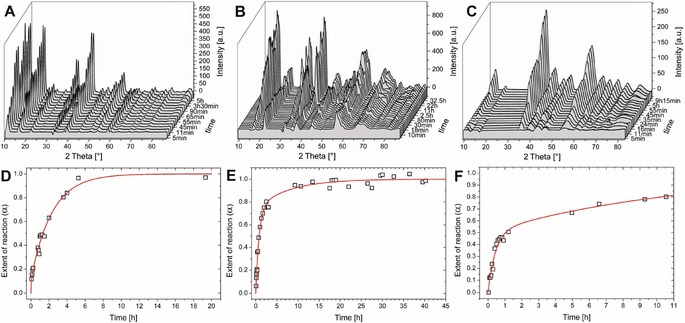
Results of in‐situ XRD measurements performed on miniaturized silica gardens grown in capillaries with crystals of CoCl₂ ⋅6 H₂O (A, D), FeCl₂ ⋅4 H₂O (B, E), and FeCl₃ ⋅6 H₂O (C, F). Top: 3D plots of diffractograms collected at different times after completed preparation. All occurring crystalline reflections can be assigned to Co₂(OH)₃Cl, Fe₂(OH)₃Cl, and FeO(OH), respectively. Bottom: Time‐dependent evolution of the reaction progress α. The red line represent fits according to the kinetic model depicted in Figure 5 [Eq. (5)].

3.  Discussion

To describe the experimental data measured in this work, we propose two kinetic models (illustrated schematically in Figures 4 and 5), which are developed step‐by‐step in the following. We emphasize that these models are simplified and do not account for the full complexity of dissolution, precipitation, and phase transformation processes occurring in these systems, which would require a much larger set of complementary experimental data. Instead, our goal was to establish a framework that allows for quantitative comparison of the different metal cations used in this work with respect to general trends in the kinetics of the relevant processes.

Figure 4.

Kinetic model used to describe dissolution and precipitation reactions occurring during the evolution of silica garden tubes, as probed by time‐dependent measurements of ion concentration in the inner solution by XAS (Figure 2).

Figure 5.

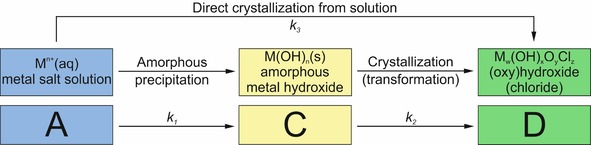
Kinetic model used to describe different precipitation pathways from dissolved metal ions to crystalline phases in the walls of silica garden tubes, as detected by in situ X‐ray diffraction (Figure 3).

The progression of metal ion concentrations (Co²⁺, Fe²⁺ or Fe³⁺) traced inside the silica garden tubes (Figure 2) is likely to result from ongoing dissolution of metal salt and parallel, as well as subsequent, precipitation of metal (hydr)oxides and/or hydroxychlorides. From a kinetic point of view, these coupled processes can be interpreted as an irreversible consecutive reaction. Starting from a solid pellet (denoted A in Figure 4), dissolution of the metal salt first leads to an increase in the concentration of free metal ions in solution (B). Subsequently, released cations are eliminated by precipitation as (oxy)hydroxides or hydroxychlorides (D). First, we consider only the situation in solution (i.e. the scenario depicted in Figure 4) and leave aside the fact that crystallization can proceed through different pathways. Under these circumstances, the time‐dependent concentration of metal ions dissolved in the inner solution b(t) should comply with the following kinetic equation [Eq. (1)]:24

$${\displaystyle b\left(t\right)=a_0\frac{k_{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{s}}}{k_{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}}-k_{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{s}}}[e^{-k_{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{s}}\left(t+t_0\right)}-e^{-k_{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}}\left(t+t_0\right)}]}$$ (1)

where a ₀ is the total analytical concentration of the metal ions and t ₀ the time period elapsed from preparation until first sampling. In the case of FeCl₃, Equation (1) must be extended by an additional term accounting for the non‐zero final concentration of the metal ions b _end [Eq. (2)]:

$${\displaystyle b\left(t\right)=b_{\mathrm{e}\mathrm{n}\mathrm{d}}{+a}_0\frac{k_{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{s}}}{k_{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}}-k_{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{s}}}[e^{-k_{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{s}}\left(t+t_0\right)}-e^{-k_{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}}\left(t+t_0\right)}]}$$ (2)

Equations (1) and (2) were used to fit the experimentally measured temporal progressions of dissolved metal ions (red lines in Figure 2), and showed reasonably good correlation for all three studied silica‐garden systems. The resulting fit parameters are summarized in Table 1. Apparently, precipitation of dissolved metal ions into the forming membranes is the overall rate‐determining step in silica gardens grown with CoCl₂ and FeCl₂ (k _Diss>k _Prec). By contrast, precipitation appears to be delimited by the rate of pellet dissolution in systems based on FeCl₃ (k _Diss<k _Prec). This finding can be explained by the dramatically lower solubility of iron(III) (hydr)oxides in aqueous media as compared to iron(II) and cobalt hydroxide,25 which causes rapid elimination of Fe³⁺ ions from solution that cannot be sustained by dissolution. On an absolute scale, precipitation is slowest in the iron(II) system, and this rationalizes why concentration gradients and electrochemical potential differences persist for the longest period of time in this case.11, 21

Table 1.

Kinetic parameters obtained by fitting time‐dependent experimental concentration data (Figure 2) in the framework of a model of an irreversible consecutive reaction [Figure 4, Eqs. (1) and (2)].

Metal salt	t 0 [min]	k Diss [10−3 s−1]	k Prec [10−4 s−1]	b end [m]	a 0 [m]
CoCl2	16	1.3±0.2	1.1±0.1	0	1.4±0.1
FeCl2	45	0.5±0.3	0.2±0.1	0	1.0±0.1
FeCl3	5	0.6±0.1	34±2	0.20±0.01	1.2±0.1

In a second step, we now consider the possibility of different routes for the formation of crystalline material in the tube walls (Figure 5). In general, the finally observed crystalline phases (hydroxychlorides for FeCl₂ and CoCl₂, oxyhydroxide for FeCl₃; Figure 5 D) can emerge either through transformation of initially precipitated amorphous material (Figure 5 C) or by direct precipitation from solution,26, 27, 28 for which dissolved metal ions (Figure 5 A) are required.

By using this model, the measured time‐resolved XRD data (Figure 3) were fitted to derive the rate constants of the two possible scenarios. For this purpose, two main assumptions were made:

1. Dissolution of solid metal salt (as traced complementarily by the concentration measurements) has been completed before the first diffraction pattern was collected (t ₀≥3 min), giving a dissolved metal ion concentration of a(t ₀) at time t ₀.

2. Compared to the amount of metal salt, a large excess of water glass is present in the system, such that the concentrations of hydroxide ions can be regarded constant throughout the process.

Under these assumptions, the relevant kinetic equations for the temporal concentrations in A, C, and D (Figure 5) can be written according to [Eqs. (3), (4), (5)]:

$${\displaystyle a\left(t\right)=a\left(t_0\right)e^{-\left(k_1+k_3\right)t}}$$ (3)

$${\displaystyle c\left(t\right)=a\left(t_0\right)\frac{k_1}{k_2-k_1-k_3}[e^{-\left(k_1+k_3\right)t}-e^{-k_{2}t}]}$$ (4)

$${\displaystyle d\left(t\right)=a\left(t_0\right)[1-e^{-\left(k_1+k_3\right)t}-\frac{k_1}{k_2-k_1-k_3}[e^{-\left(k_1+k_3\right)t}-e^{-k_{2}t}]}$$ (5)

As is evident from Figure 3 (red lines), the experimentally determined values for the progress of crystallization are reasonably well described by the proposed kinetic model. Table 2 lists the parameters resulting from the fits in Figure 3. Due to the assumption of complete dissolution prior to the first diffraction measurement, a rate constant for dissolution (like k _Diss in the model used to describe the concentration data; Figure 4) cannot be determined by this approach. Moreover, the overall rate of precipitation k _Prec discussed above is now separated into three distinct processes and corresponding rate constants, that is, precipitation of amorphous phases (k ₁), their transformation into crystalline material (k ₂), and direct crystallization (k ₃). Clearly, for all three silica garden systems k ₃ is larger than k ₂. This indicates that direct crystallization from solution (A→D) is kinetically favored over transformation of amorphous material into crystalline matter (C→D). Moreover, the initial progress of crystallization (as given by the t _α=0.5 values in Table 2) is relatively fast in the iron(II) system, despite the low overall rate of precipitation and equilibration (cf. Figure 2 and Table 1). This suggests that amorphous phases play a much less important role in this case (small k ₁), that is, tubes formed by FeCl₂ are generally more crystalline than those obtained with CoCl₂ and FeCl₃ from the beginning on. The ratio of the rate constants k ₁ and k ₃ is a direct measure for the competition in the formation of amorphous and crystalline phases (k ₁/k ₃=6.7 for Co²⁺, 0.3 for Fe²⁺, and 0.9 for Fe³⁺). These results agree with previous observations made for single macroscopic tubes by ex‐situ characterization,20 in which CoCl₂‐ and FeCl₃‐based silica gardens were found to contain significant fractions of amorphous material, whereas much higher crystallinity was detected in the case of FeCl₂. This difference was ascribed to the low porosity of iron(II) tubes, which causes slow (counter‐)diffusion of reactants and prevents the high local levels of supersaturation needed for amorphous precipitation.20 The latter feature is evident in the present in‐situ data, especially for silica gardens grown with FeCl₃ (Figure 3 C, F), for which the reaction progress α increases rapidly to values around 0.5 within the first hour, whereas a much slower evolution towards higher crystallinity is observed in the following. Indeed, crystallization was not yet completed in the iron(III) system at the end of the experiment (α≈0.8 after 10 h), in contrast to cobalt(II) and iron(II) tubes, for which α≈1 at t≥10 h. This distinct behavior is essentially due to the relative importance of amorphous iron(III) phases (large k ₁/k ₃ ratio owing to the low solubility and thus high supersaturation for iron(III) (hydr)oxides) and the slow rate of their transformation into crystalline matter (small k ₂). In the case of cobalt, the strong tendency to form amorphous species (large k ₁) is counterbalanced by equally high rates of direct crystallization (large k ₃) and amorphous‐to‐crystalline transformation (large k ₂); in view of the high k ₁/k ₃ ratio, we cannot exclude that some of the amorphous cobalt (hydr)oxide compounds remain in the final structure (i.e. after α≈1 has been reached), possibly due to kinetic stabilization by silica.29 Finally, iron(II) strongly favors direct crystallization (relatively large k ₃) and almost entirely bypasses amorphous intermediates (small k ₁ and k ₂), as already mentioned above.

Table 2.

Kinetic parameters obtained by fitting time‐dependent experimental diffraction data according to the kinetic model shown in Figure 5.

Metal salt	k 1 [10−4 s−1]	k 2 [10−4 s−1]	k 3 [10−4 s−1]	t α=0.5 [min]
CoCl2	47±7	1.2±0.2	7±7	80
FeCl2	0.8±0.2	0.4±0.2	2.7±0.2	48
FeCl3	2.9±1.3	0.3±0.4	3.2±1.8	63

4.  Conclusions

The aim of this study was to shed light on the dynamics of dissolution, precipitation, and crystallization processes in common silica garden tubes prepared with different metal salts (FeCl₃ ⋅6 H₂O, FeCl₂ ⋅4 H₂O, and CoCl₂ ⋅6 H₂O). For this purpose, synchrotron‐based X‐ray absorption spectroscopy was used to monitor the temporal progressions of metal ion concentrations inside the formed tubular structures, while in‐situ X‐ray diffraction served as a complementary technique to trace the development of crystalline material in the tube walls as a function of time. The obtained results show that in the three investigated systems, metal salt dissolution and subsequent/concurrent precipitation can be interpreted as an irreversible consecutive reaction, for which a kinetic model was proposed and applied successfully to the experimental data. As expected, the derived kinetic rate constants depend on the type of metal cation used (with chloride as counterion), essentially due to the different solubilities of the forming mineral phases, which were confirmed to be hydroxides (for all three cations), oxyhydroxides (for Fe³⁺), or hydroxychlorides (for Co²⁺ and Fe²⁺). Time‐resolved XRD measurements revealed that in all three investigated systems, crystallization commences immediately after (or even already during) macroscopic tube formation and proceeds over periods of several hours, leading to increasing total amounts of crystalline material in the inorganic membranes. While the nature of the precipitated crystalline phase seems to be influenced by the used counterion, the tendency to crystallize was again found to be mainly determined by the type of metal cation, with chloride salts of Co²⁺ and in particular Fe²⁺ giving fairly well crystallized tube walls in less than 10 h, whereas in the case of Fe³⁺ largely amorphous material was produced that only slowly transformed into crystalline particles. To describe these phenomena, a kinetic model was proposed to account for the different possible processes—direct crystallization, precipitation of amorphous (hydr)oxide phases, and transformation of amorphous into crystalline material—and to quantify their relative importance in the respective systems. The experimental diffraction data were found to comply reasonably well with the proposed model, and yielded individual rate constants that rationalize the observed behavior. Quantitative in‐situ data, such as those collected in the present work, are key to a more fundamental understanding of dynamic processes in silica gardens, which ultimately will be extrapolated to related structures known to occur in practically relevant situations such as cement hydration,30 steel corrosion,17 and rock‐fluid interactions in geological environments.16

Experimental Section

Preparation of Silica Gardens

Single macroscopic silica garden tubes were grown according to a procedure described in detail elsewhere.11, 20 In brief, the relevant metal chloride salts (FeCl₃ ⋅6 H₂O, FeCl₂ ⋅4 H₂O, and CoCl₂ ⋅6 H₂O, all obtained in p.a. grade from Merck) were pressed into pellets of 13 mm in diameter and fixed at the bottom of a plastic beaker. Subsequent addition of sodium silicate sol (1:4 (v:v) dilution of water glass from Sigma‐Aldrich, reagent grade) at a controlled rate (1–10 mL min⁻¹ depending on the type of metal salt used) produced single tubes (length: ca. 20 mm; diameter: ca. 6 mm) with an end open to the atmosphere, which allowed us to draw aliquots from the inner solution at different times. In an alternative approach (for in‐situ XRD measurements), miniaturized silica gardens were grown by placing tiny seed crystals of the aforementioned metal salts on the bottom of thin glass capillary tubes (Mark tubes from Hilgenberg; length: 85 mm, diameter: 2 mm, wall thickness: 10 μm) and slowly adding small amounts of diluted water glass (1:4) with a syringe.

X‐ray Absorption Spectroscopy

XAS measurements were performed at the material science beamline I811 of the synchrotron radiation facility MaxLab II in Lund, Sweden. 10 μL samples were extracted from the solution inside macroscopic silica garden tubes with the aid of ultrathin rectangular precision capillaries (VitroCom, inner dimensions: 0.1×2.0×50 mm, wall thickness: 100 μm, borosilicate glass), which were subsequently fixed on a holder and centered relative to the incident X‐ray beam (1 mm diameter). The concentration of Co²⁺ or Fe^2+/3+ was determined without any further dilution by measuring the height of the edge jump at the Fe_K and Co_K edges, respectively. Calibration of edge jump values to actual metal ion concentrations was achieved by measuring a series of solutions with known concentrations in the range of 0–4 m, by using a fast scanning routine (QXAS mode, −100 eV to +370 eV relative to the absorption edge, total acquisition time: 150 s). For all cations, a linear relationship was found for the height of the edge jump as a function of concentration (see Figure S1). Iron and cobalt metal foils served for energy calibration, and gave absorption energies of 7110.75 and 7708.78 eV for the Fe_K and Co_K edge, respectively. Measurements with actual samples were performed by using an extended routine in step‐scan mode (−100 to +200 eV relative to the edge, varying step width between 1 and 6 eV, with 1 s integration time per step and a total acquisition time of 600 s). All XAS experiments were done under ambient conditions in transmission mode.

In Situ XRD Experiments

Time‐resolved XRD measurements were performed in two distinct setups (macroscopic and miniaturized growth) by using two different synchrotron sources. Macroscopic silica gardens were investigated at beamline F3 of the Doris III storage ring at HASYLAB (DESY, Hamburg, Germany), which allows EDXRD experiments to be conducted with a white X‐ray beam (energy range: 6–52 keV). Therefore, thick samples (single tubes grown in Duran glass tubes with dimensions of 12×100 mm) could be analyzed without the problem of total radiation absorption. The as‐prepared samples were inserted into a specially designed thermostatted holder (see Figure S2), equipped with two windows to allow the beam to pass through the sample. The sample holder was positioned such that the center of the glass tube was exactly at the intersection point where the incident beam hits the virtual extension of the detector arm. The intensity of the incoming white beam was adjusted by a first slit system, with an effective beam area of 300×300 μm. Scattered X‐rays were detected with a Ge detector (2048 energy‐selective channels, cooled with liquid nitrogen), which was positioned at a horizontal angle of θ=7° relative to the incident X‐ray beam. A second slit system mounted on the detector arm was adjusted to an area of 100×100 μm or 200×200 μm to improve resolution. A PC coupled to a multichannel analyzer was used for data collection, and allowed automated EDXRD runs to be performed with an acquisition time of 300 s per run. Energy calibration was achieved by measuring the fluorescence peaks of a mixture of different metal powders.

Experiments with miniaturized silica gardens were carried out at beamline XRD1 of the synchrotron radiation facility ELETTRA in Trieste, Italy. Measurements were performed with a monochromatic beam (E=12.4 keV, λ=1.00 Å), which was obtained by filtering white X‐ray radiation (energy range: 4–21 keV) through an optical system including a double‐crystal Si(111) monochromator set. Since the overall beam intensity was not high enough to allow studies on thick (macroscopic) samples, silica gardens were grown in glass capillaries, as described above. The capillaries were fixed on a custom‐designed sample holder (see Figure S4) and positioned in such a way that the beam passed through the capillary slightly above the seed crystal, where the probability to hit the forming tubes was highest. XRD measurements were initiated directly after addition of silicate solution to the seed crystals, with an effective delay of about 3 min between completed preparation and the start of data collection. Subsequently, 2D diffractograms were recorded with a CCD detector (MarResearch, image diameter: 165 mm), positioned at a sample‐to‐detector distance of 60 mm, giving a final 2θ range of 0–106.2° referred to Cu_Kα1 radiation (1.54 Å). The beam size was 0.2×0.3 mm in all experiments. Acquisition times varied from 5 to 80 s, depending on the respective beam intensity, which was determined from the actual ring current. Measurements were performed repeatedly in periods ranging from 3 min at the beginning to several hours at later times. The collected 2D diffraction images were processed with Fit2D software to extract 2θ and intensity values from the raw files. Intensities were normalized to acquisition time and ring current. Subsequently, background subtraction, data smoothing, and integration of reflections were performed with a custom‐designed LabView software routine. Finally, the processed data were fitted according to the proposed kinetic models by using TableCurve 2D.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

F. Glaab, J. Rieder, R. Klein, D. Choquesillo-Lazarte, E. Melero-Garcia, J.-M. García-Ruiz, W. Kunz, M. Kellermeier, ChemPhysChem 2017, 18, 338.