Assessment of structural heterogeneity and viscosity in the cervix using shear wave elasticity imaging: initial results from a Rhesus macaque model

Abstract

Shear Wave Elasticity Imaging (SWEI) shows promise for evaluating the pregnant cervix. Changes in shear wave group velocity have been attributed exclusively to changes in stiffness. This assumes homogeneity within the region of interest and purely elastic tissue behavior. However, the cervix is structurally/microstructurally heterogeneous and viscoelastic. We therefore developed strategies to investigate these complex tissue properties. SWEI was performed ex vivo on 14 unripened and 13 misoprostol-ripened cervix specimens from Rhesus macaques. After application of tests of significant and uniform shear wave displacement, as well as reliability of estimates, group velocity decreased significantly from the distal (vaginal) to proximal (uterine) end of unripened, but not ripened, specimens. Viscosity was quantified by the slope of the phase velocity vs. frequency. Dispersion was observed in both groups (median 5.5 m/s/kHz, interquartile range: 1.5–12.0 m/s/kHz), also decreasing towards the proximal cervix. This work suggests that comprehensive assessment of complex tissues such as cervix requires consideration of structural heterogeneity and viscosity.

Introduction

During pregnancy, the cervix must prepare to allow eventual delivery of the fetus. Accordingly, dramatic remodeling of cervical microstructure causes progressive softening, shortening and dilation. This normal process appears accelerated in spontaneous preterm birth (sPTB, birth before 37 weeks gestation), which is the greatest global cause of neonatal mortality worldwide and an important risk factor for long-term health complications.(Liu et al., 2015; Shapiro-Mendoza and Lackritz, 2012; Behrman et al., 2007) The epidemiology of sPTB is complex and multifactorial (Goldenberg et al., 2008), but premature cervical change always occurs (Vink et al., 2016), making the cervix an excellent target for investigation.

Shear Wave Elasticity Imaging (SWEI) has been investigated as a noninvasive approach to quantify cervical softening (Carlson et al., 2014a; Gennisson et al., 2011; Muller et al., 2015). The parameter used most commonly is shear wave speed group velocity ( c_g, the propagation speed of the shear disturbance). Using c_g, Peralta et al. (2015a) reported an increase in cervical softness after labor induction in ewes. While compelling, mechanical and anatomical differences between sheep and humans may limit clinical applicability of the results. We use a Rhesus macaque model. Unlike sheep and other animal models used for preterm birth studies (e.g. rodents), macaques are biped/quadripeds instead of obligate quadripeds, which makes the mechanical forces on the macaque cervix more similar to humans (obligate bipeds). Also, macaques and humans share similar maternal-fetal immunology and physiology (Haluska et al., 1990; Hafez and Jaszczak, 1972). Although mechanical forces on the macaque’s cervix may not completely match those on the human’s cervix (because of climbing and jumping behavior, for example), the macaque is closer to humans in terms of ambulation than sheep or rodents.

We have used SWEI to assess the spatial distribution of stiffness within the cervix and the effects of ripening (via administration of misoprostol, a prostaglandin used clinically to soften the cervix in preparation for labor induction) in ex vivo macaque specimens (Huang et al., 2016). We noted a trend of decreasing c_g from the distal (vaginal) end to the proximal (uterine) end of the cervix, suggesting spatial variability, but measurement variation was large. We found no difference in stiffness between unripened and ripened cervices. While this could be due to a number of factors, including that there is no difference with ripening, it could be that simple c_g is not sensitive to these differences.

Our initial studies, like all studies of SWEI in the cervix to date (Carlson et al., 2014a; Gennisson et al., 2011; Muller et al., 2015; Peralta et al., 2015a), ignored two important issues: (1) potential structural/microstructural heterogeneity and (2) viscosity. Regarding the former, c_g estimation assumes that tissue is homogeneous within the analyzed ROI. While this may be true within small ROIs, no robust tests of homogeneity of shear wave propagation have been previously applied. This is an issue because cervical microstructure contains three overlapping and interwoven quasi-layers of collagen (Akins et al., 2010) and it is thus possible that inappropriate estimates have been included in reports of c_g. Another type of heterogeneity that could affect interpretation of results between individuals, and especially species, is differences in gross cervical structure. Specifically, in our previous macaque study, we assumed that c_g estimates could be compared between cervices of different sizes by simple linear scaling of fractional length, as we have successfully done in human studies (Carlson et al., 2014a). Unlike humans, however, the distal end of the Rhesus cervix is bulbous, with a tortuous central canal. Between this bulb and the internal os (where the proximal cervix ends and the uterus begins), the macaque cervix abruptly changes to resemble the human in a region we have named the transition zone; specifically, it becomes cylindrical with a relatively straight central canal. Analyzing the entire macaque cervix, including the distal bulb, likely compromised our analysis because accurate estimates most likely could not be obtained from such grossly heterogeneous tissue. Further, because humans do not share this structural feature, applicability of these results to women is compromised. Finally, and perhaps most importantly in terms of translation to the bedside, our evaluation in humans ignores the distal cervix because we have found assessment there to be less clinically relevant (regarding detection of ripening) than the mid and proximal cervix (Carlson et al., 2014b), and therefore it seems prudent to ignore the distal cervix in our macaque model as well.

The second issue is that previous estimates of c_g in the cervix have assumed that differences are defined primarily by purely elastic stiffness, with strain independent of the rate of the induced stress. However, ex vivo studies in rodents (Barone et al., 2010; Buhimschi et al., 2004) and humans (Myers et al., 2008, 2009; DeWall et al., 2010) have clearly demonstrated that the cervix behaves like a viscoelastic solid in which the magnitude of the response depends also on the rate of the applied strain (Lakes, 2009).

To overcome these potential sources of measurement imprecision, we attempted to (a) account for structural/microstructural tissue heterogeneity in a robust manner and (b) assess the viscous component of the cervix.

Three steps were required for (a). First, we analyzed only the region of the macaque cervix between the transition zone and internal os, both to reduce potential measurement inaccuracy due to extreme structural heterogeneity and to make the results more generalizable to humans. Second, we developed a test for significant and uniform shear-wave induced displacement to confirm that the region of measurement is sufficiently homogeneous for accurate evaluation. Third, we developed a test of reliability of individual measurements (e.g., rejection of spurious data).

To achieve (b), we quantified shear wave dispersion, a direct effect of viscoelasticity on shear wave propagation that results in the variation of the phase velocity c_p (the velocity of each spectral component of the wave) with shear wave frequency content (Lakes, 2009). Shear wave dispersion has been used to characterize viscoelasticity in the breast, liver, and muscle (Barry et al., 2012, 2014; Tanter et al., 2008; Muller et al., 2009; Gennisson et al., 2010). As shown by Barry et al. (2012), Deffieux et al. (2013), and Nightingale et al. (2015), the frequency dependence of c_p can be represented as a linear function of frequency defined by an intercept c₀ and a slope dc_p/df:

$$c_{\mathrm{p}}\left(f\right)=c_0+\frac{\mathrm{d}{c}_{\mathrm{p}}}{\mathrm{d}f}f.$$ (1)

Thus, an increase in the viscous response is associated with an increase in the slope dc_p/df.

We explored these two issues because comprehensive identification and quantification of key changes in the pregnant cervix should help uncover molecular mechanisms of sPTB, in turn leading to novel solutions for its prediction and prevention.

Materials and Methods

Data Acquisition

Cervical specimens were obtained from 27 Rhesus macaques from the Wisconsin National Primate Research Center through its Nonhuman Primate Biological Materials Distribution Core. All protocols were approved by the University of Wisconsin Institutional Animal Care and Use Committee.

Cervical ripening was induced in half (n=13) of the macaques via oral administration of 200 mcg of misoprostol 12 hours prior to necropsy (Huang et al., 2016). (Misoprostol is a prostaglandin routinely used to induce labor in women.) Extraction of the cervix involves incising the perineal skin around the external genitalia and removing the anterior skin, muscle, and pelvis. The fascia and connective tissue within the pelvic canal are incised and the urinary bladder and uterus (to the level of the distal vagina) are gently dissected and removed. Sharp dissection is used to remove the ovaries, uterine fundus, and the bladder. The distal uterus, intact cervix and vagina are placed in sterile saline. During experiments, we were careful to not disrupt the structure of the cervix or stretch it by handling it by the surrounding fascia. Ultrasound scanning started within one hour after extraction and lasted approximately two hours. To minimize motion artifacts, the surrounding fascia was pinned to a sound-absorbing rubber. (This procedure mirrors that used in our studies of the ex vivo human cervix (Carlson et al., 2014b), and details can be found in Huang et al. (2016).)

A Siemens S2000 system (Siemens Healthcare, Ultrasound Business Unit, Mountain View, CA, USA) was used to induce shear waves through an acoustic-radiation force impulse (ARFI) (Nightingale et al., 2002) excitation with a 9L4 linear array transducer aligned along the cervical canal from the internal os to external os (proximal/uterine to distal/vaginal cervix). ARFI was performed on a 5×5mm² region of interest (ROI) placed above the cervical canal (on both anterior and posterior cervix, in sequence). The ARFI push had a center frequency of 4MHz, a duration of 100μs, and was focused at 30mm from the transducer at f/1.5. The ROI was moved from the proximal to distal end in steps of 2.5mm. A set of reference ultrasound A-line signals were acquired for 2ms before the ARFI excitation. These reference signals were used to detect significant motion caused by the propagation of the shear wave (details below). Propagation of the shear wave was observed by acquiring A-line signals at locations further away from the ARFI excitation within the ROI. Reference and tracking signals had a center frequency of 6.16MHz, were focused at the center of the ROI with f/1.5, and were acquired at a pulse repetition frequency between 9 and 10kHz

Data Processing

All data processing was performed offline in MATLAB (Mathworks, Natick, MA, USA). Reference and post-excitation tracking signals within one ARFI acquisition were used to estimate tissue displacements caused by propagation of the shear wave using using Loupas’ cross-correlation method (Loupas et al., 1995) between the first reference signal and a later reference or post-excitation tracking signal. Low correlation (<0.98) displacement estimates were discarded. Displacements from five ARFI acquisitions were averaged to reduce noise.

Test of significant and uniform shear-wave induced displacement

Reference tissue displacements (before the application of the ARFI excitation) were used to detect regions with significant and uniform displacement (i.e., local microstructural homogeneity). Estimation of shear wave speed within an ROI (typically 5×5mm²) assumes that the wave moves at the same speed over the entire axial span. Therefore, SWS estimates in areas of marked structural inhomogeneity are vulnerable to error, making it critical to identify local areas in which uniform propagation would be expected (i.e., most homogeneous). Although this concept is universal, it is particularly relevant in complex tissues such as the cervix, and especially in the macaque because the macaque cervix is smaller than its human counterpart and it is likely that a 5×5mm² ROI would contain more than one collagen layer. To detect regions in which to accurately estimate c_g and c_p, we first determine whether the displacements produced by the shear wave are statistically significantly different from zero (no motion). If there is significant motion, we then determine uniformity of the displacement field produced by the propagation of the shear wave within the ROI.

Specifically, first, echo signals from reference tracking frames acquired before the application of the ARFI excitation were used to assess the statistics of displacement estimates when there was no shear wave propagation. These frames are typically used in vivo to estimate and compensate for bulk physiological motion.(Nightingale et al., 2015) To quantify the statistical variability of the displacement estimates in the reference frames, the time-average displacement DA(x, y) in the reference data frames (subindex “Ref”) and in the frames after the shear wave excitation (subindex “SW”) are computed as:

$${\text{DA}}_{\text{Ref}}\left(x,y\right)=\frac{1}{N_{\text{Ref}}}\sum _{n=1}^{N_{\text{Ref}}}D\left(x,y;t_{\text{Ref},n}\right)$$ (2)

$${\text{DA}}_{\text{SW}}\left(x,y\right)=\frac{1}{N_{\text{Ref}}}\sum _{n=1}^{N_{\text{Ref}}}D\left(x,y;t_n\right)$$ (3)

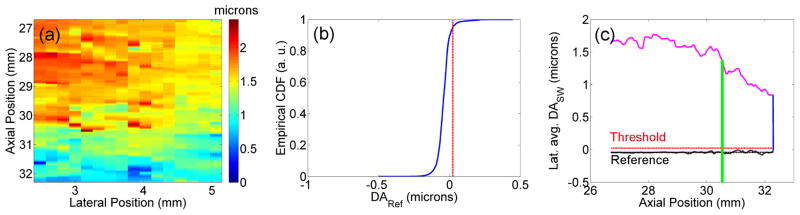
where D is the estimated displacement, x and y are the lateral and axial coordinates within the ROI, t_Ref,n and t_n are the time indices before and after the application of the ARFI excitation, respectively. N_Ref is the number of reference tracking frames. Note that the post-excitation average DA_SW includes only the first N_Ref tracking frames so that DA_SW can be compared to DA_Ref. Figure 1(a) shows an example of DA_SW in a ROI with heterogeneous displacement.

Figure 1.

Analysis of uniformity and statistical significance of shear wave motion in a ROI deemed as heterogeneous. (a) Average displacement in microns as function of the axial and lateral position. (b) Empirical cumulative distribution function (CDF) of the laterally-averaged displacement in microns in the reference frames. (c) Comparison of the laterally-averaged average displacement with the reference-based threshold.

Next, pre- and post-excitation displacements are compared. We are primarily interested in detecting heterogeneities in the axial direction because that is where we would expect them based on optical microscopy of cervical microstructure (Reusch et al., 2013)). We therefore first average DA_Ref (x, y) and DA_SW (x, y) laterally. To quantify the variability of the displacement when no shear wave is present, we obtain the empirical cumulative distribution function F_E (q) of all the DA_Ref values within the ROI. F_E (q) quantifies the probability that a value of DA_Ref is larger than q. F_E (q) is computed from a set of M values of DA_REF,m as (Georgiou and Cohen, 1998; Rosado-Mendez et al., 2016a):

$$F_{\mathrm{E}}(q)=\{\begin{array}{cc}0& q<{\text{DA}}_{\text{Ref},1}\\ m/M& {\text{DA}}_{\text{Ref},m}\le q<{\text{DA}}_{\text{Ref},m+1}\\ 1& q\ge {\text{DA}}_{\text{Ref},M}\end{array}$$ (4)

where subindex m =1, 2,…, M indicates values in increasing order. F_E (q) is used to determine a threshold value for DA_Ref above which the probability of obtaining a DA_Ref value larger than DA_SW (y) is less than 5% (arbitrary threshold). Regions within the ROI with values of DA_SW (y) above this threshold are deemed to have significant motion caused by the shear wave.

Figure 1(b) shows the empirical cumulative distribution function versus DA_Ref values. The vertical line indicates the threshold at which the probability of false motion detection is 5%. Figure 1(c) shows the laterally-averaged DA_SW (y) as a function of the axial position (magenta), the mean of the laterally-averaged DA_Ref (y) (dashed black) and the threshold for significant motion (dashed red). In this case, the DA_SW (y) line is above the threshold, indicating that the motion caused by the shear wave is statistically larger than the random motion in the reference frames.

Second, assuming significant motion, we analyze the uniformity of the displacement field by looking at the spatial distribution of DA_SW (x, y). Figures 1(a) and (c) show a case in which the lower 40% of the ROI has smaller displacements than the upper 60%. Sections with uniform displacements, such as the upper section bounded by the green line in Fig. 1(c), were chosen for further processing.

Test of estimate reliability

We combined two methods to develop a new quality metric to reject or accept data for measurement of c_g. Unlike the previous methods, which impose a minimum peak particle displacement threshold, this new criterion allows smaller displacements to be retained and thus may be appropriate for evaluation of stiffer tissues. (This was motivated in part by the finding that the macaque cervix appears much stiffer than the human (Huang et al., 2016).)

c_g was quantified using a RANdom-SAmple Consensus (RANSAC) iterative method (Wang et al., 2010). For this method, the time it takes the maximum displacement to reach the different tracking locations away from the excitation is estimated. Next, a plane is fit to the time-to-peak displacement (TTPD) as a function of the axial and lateral locations. The fit is done by maximizing the number of TTPD points lying on the fitted plane within the error of the fit. The c_g estimate is the inverse of the slope of this plane versus the lateral location. The number of TTPD inliers provides an assessment of the goodness of fit. Because this approach is non-deterministic, it must be applied several times to each data set using independent random seeds. We applied it 12 times; because of the structure of our computer cluster, it was computationally efficient to use 12 cores for parallel computing, one core for each random RANSAC seed.

We quantified the reliability of our estimates by comparing them to estimates obtained from the Radon-sum method described by Rouze et al. (2010) in which tissue displacements are averaged axially and arranged into a time vs. lateral location display. Then, displacements are summed over multiple linear projection trajectories. The c_g estimate is the inverse of the slope of the trajectory with maximum summed displacement.

Criteria for reliability (rejection of data) were a percentage of TTPD inliers from the RANSAC estimator (less than 50% inliers), and a disagreement between RANSAC and Radon-sum estimates greater than 5m/s. c_g estimates that did not meet these criteria were discarded.

Dispersion analysis

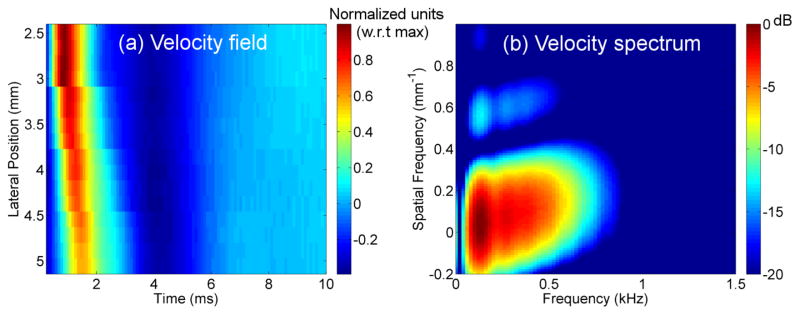
Shear wave dispersion was assessed in three sequential stages: (1) temporal bandwidth estimation, (2) model-free dispersion assessment, and (3) application of a linear model to dispersion. The first stage was to determine the useful temporal frequency bandwidth of the induced shear waves. This was done by estimating the velocity power spectrum V (f_t, f_s), i.e., the squared-magnitude of the two-dimensional Fourier transform of the particle velocity field as a function of the spatial frequency f_s and the temporal frequency f_t. Particle velocity was estimated similarly to particle displacement used in c_g estimation, except that tracking frames were considered at consecutive time points instead of reference and post-excitation tracking frames. Figures 2(a) and (b) show examples of a velocity field and the corresponding velocity spectrum, respectively.

Figure 2.

Examples of (a) Velocity field (normalized to the maximum velocity value) and (b) Velocity power spectrum.

The Maximum Velocity Power Spectrum (MVPS), V_max (f_t) was then obtained by computing at each temporal frequency the maximum value of the velocity spectrum across all spatial frequencies (Fig. 3). The high-frequency noise level was computed as the mean value of V_max (f_t) within a 0.4kHz bandwidth centered at 4kHz (1kHz below the Nyquist frequency to reduce effects of possible aliasing). The cutoff frequencies of the analysis bandwidth were determined by the lowest and highest temporal frequencies with V_max (f_t) values greater than 10dB above the high frequency noise level. Selection of cutoff frequencies is depicted in Fig. 3

Figure 3.

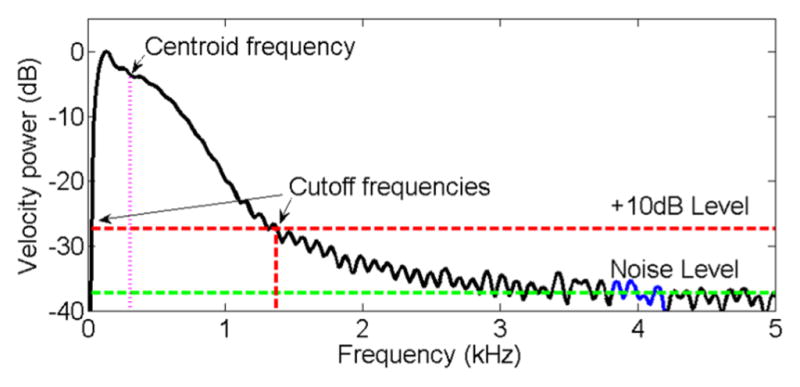
Maximum Velocity Power Spectrum (MVPS) as a function of temporal frequency. The 0.4kHz bandwidth used to determine the noise level is shown in blue. The green and red dashed lines indicate the noise level and the 10dB threshold above the noise level, respectively. Arrows indicate the cutoff frequencies for the analysis bandwidth.

The second stage utilized a model-free assessment of shear wave dispersion to determine presence of a linear relationship between c_p and temporal frequency. This was done using non-parametric estimation of c_p versus frequency based on determining spatial frequency with the maximum V (f_s, f_t) value at each temporal frequency. Details of this method are described in Nenadic et al. (2013).

The third stage employed a linear model (Eqn. 1) to estimate and interpret elastic and dispersive properties as described by Nightingale et al. (2015). To obtain values of the intercept and slope (in the linear model), “curved” projections, S, in the frequency spectrum (spatial frequency vs. temporal frequency, Fig 2(b)), were obtained to find projections of spectral peaks based on the linear model, as follows(Nightingale et al., 2015):

$$S\left(c_0,\frac{\mathrm{d}{c}_p}{\mathrm{d}{f}_t}\right)=\sum _i{V}_{max}\left(f_{s,i},f_{t,i}\right)$$ (5)

where

$$f_{s,i}\left(c_0,\frac{\mathrm{d}{c}_p}{\mathrm{d}{f}_t}\right)=\frac{f_{t,i}}{c_0+\frac{\mathrm{d}{c}_p}{\mathrm{d}{f}_t}{f}_{t,i}}$$ (6)

In this model, the values of intercept and slope that lead to the maximum S value are chosen as the estimates for further analysis. Search ranges for both parameters are determined by the spatial and temporal frequency ranges: the -6dB spatial frequency bandwidth, and temporal frequency bandwidth over which a linear dependence of the non-parametric phase velocity vs. frequency was observed (0.4–1.0kHz, as shown in the Results section). Data sets with a +10dB temporal bandwidth (determined as described in Fig. 3) smaller than 0.4–1.0kHz were excluded from the linear-model fit. Details can be found in (Nightingale et al., 2015).

The intercept c₀ is related to the stiffness of the material and the slope is related to the viscous component. We report the value of the parametric phase velocity at the median (over the entire data set) of the spectral centroid frequency (0.53kHz, as shown in the Results section), defined as the center of mass of the V_max (f_t) within the analysis bandwidth to characterize the frequency content of the shear wave.

$$f_{\mathit{Centroid}}=\frac{{\int }_{f_{t,L}}^{f_{t,H}}f\times V_{max}\left(f_t\right)}{{\int }_{f_{t,L}}^{f_{t,H}}{V}_{max}\left(f_t\right)}$$ (7)

where f_t,L =0.4kHz and f_t,H =1.0kHz. are the low and high frequency limits of the analysis bandwidth, respectively. Figure 3 also shows the centroid temporal frequency of the corresponding spectrum.

Statistical analysis

Estimates of c_g and c_p vs. frequency were analyzed to identify variations along the length of the cervix and differences between ripened and unripened specimens.

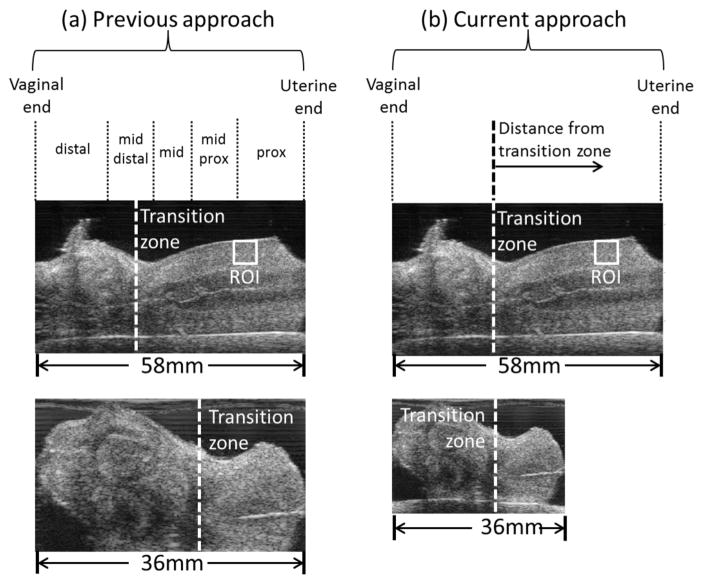
As mentioned above, our previous investigations (Carlson et al., 2014b; Huang et al., 2016) utilized a linear scaling approach to compare results between different specimens. Specifically, ROI locations for each cervix sample were grouped into five regions: distal (vaginal end), mid-distal, middle, mid-proximal, and proximal (uterine end). Each region was defined as a percentage of the length of each specimen based on the assumption that cervices of different sizes could be meaningfully compared via this scaling (Fig. 4(a)). While this worked well in the relatively large human cervix, the bulbous part of the Rhesus cervix occupies a varying percentage of the entire cervix. Thus, one region type (e.g., the mid proximal region) could include markedly structurally different regions in different cervices and thus not be comparable. We identified a common structural feature as a point of reference, specifically, the zone at which the bulbous distal cervix transforms into the cylindral proximal cervix. We denoted this as 0mm and named it the transition zone. The transition zone is indicated by the vertical dashed line in Fig. 4(a). Fig. 4(b) shows the macaque cervix proximal to the transition zone, which resembles the human cervix.

Figure 4.

Left: Analysis of the spatial variability of viscoelastic properties in (a) Huang et al. (2016) and (b) the current work. In (a) the cervix is divided into five regions with respect to its entire length (simple linear scaling). In (b) the bulbous distal cervix is disregarded, and the transition zone is taken as reference.

Identification of the transition zone was done by staff (I.R-M. and L.C.D) under guidance by an obstetrician (H.F.) by visually analyzing ultrasound B-mode images obtained during data acquisition and correlating these with low magnification microscopy images (PathScan Enabler IV, Meyer Instruments, Houston, TX) of 200 μm thick slices from each specimen. The bulbous distal cervix was excluded from analysis. SWEI parameters were studied as a function of the distance from the transition zone (0mm) to the internal os at 5mm intervals. Estimates within −2.5mm and 2.5mm from the center of each reported 5mm interval were averaged together. We report results to 10mm because of a paucity of data beyond 10mm (due primarily to cervical length). For instance, among ripened specimens we obtained 24 adequate measurements at 0mm, 19 at 5mm, and 12 at 10mm, but fewer than 6 at 15mm and beyond.

Differences in c_g, spatial gradients of c_g along the length of the cervix, c_p at 0.53kHz (centroid frequency), and the slope of the c_p vs. frequency ( dc_p/df ) were assessed with the Kruskal-Wallis non-parametric test.

Results

Group velocity

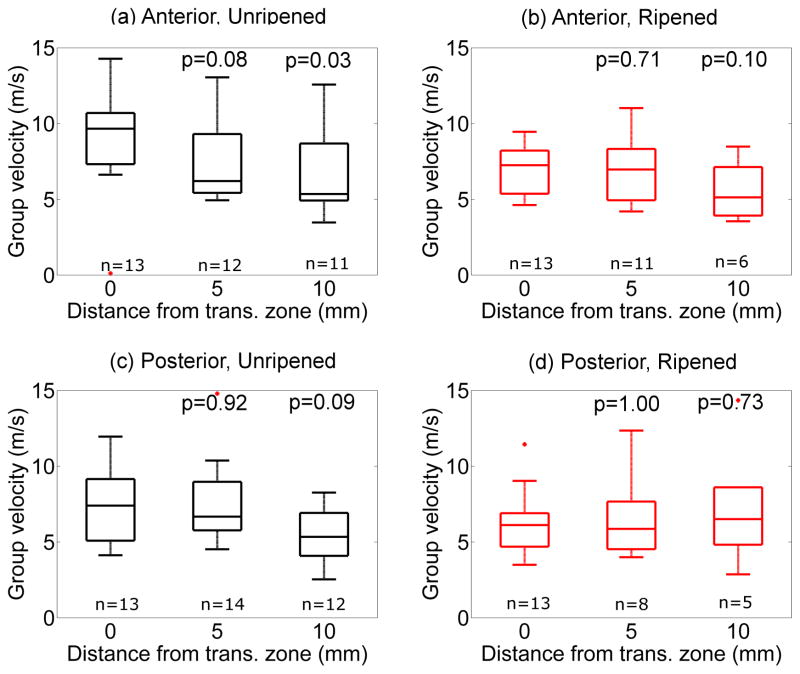
After applying the quality parameter described above to reject inappropriate data (approximately 10%), c_g was calculated for each specimen, and the results combined by group (anterior vs. posterior cervix, ripened vs. unripened specimens). c_g estimated with the RANSAC method as a function of the distance from the transition zone proximally (toward the internal os) is shown in Figure 5. The figure demonstrates that c_g generally decreased from the transition zone proximally in the unripened group, but not the ripened group, although this did not reach statistical significance in most locations. c_g estimates obtained from rejected data had a median value of 30.3m/s (interquartile range, IQR=20.3–37.8m/s). This shows that inclusion of these data would have severely biased our results. The spatial gradient of the c_g was calculated for each specimen, then averaged by group. In the unripened group, the spatial gradient was −0.3±0.3 m/s/mm (anterior) and −0.2 ±0.3 m/s/mm (posterior). In the ripened group, the spatial gradient of the c_g was 0.0 ±0.2 m/s/mm and 0.1±0.2m/s/mm for anterior and posterior, respectively. The difference in the spatial gradient of c_g between unripened and ripened groups was statistically significant (anterior p=0.04, posterior p=0.02). These findings are summarized in Table 1.

Figure 5.

Group velocity c_g as a function of distance from transition zone (proximally, toward the internal os) in unripened ((a) and (c)) and ripened ((b) and (d)) groups. Top: Anterior, Bottom: Posterior, Left: Unripened, Right: Ripened. Boxes indicate the median (middle line), the 25%ile and 75%iles (upper and lower ends), the range (whiskers), and outliers based on 1.5 times the interquartile range above the 75%ile. P values correspond to Kruskal-Wallis test with respect to the values at the transition zone (0mm).

Table 1.

RANSAC estimates of c_g at the transition zone (0mm) and 10mm proximal to the transition zone, c_g (m/s) at 0mm and 10mm proximal, and the gradient of c_g (m/s/mm).

Parameter	Anterior			Posterior
	Unripened	Ripened	p	Unripened	Ripened	p
cg, 0mm	9.5 ± 2.2	7.0 ± 1.6	0.02	7.3 ± 2.3	5.8 ± 1.5	0.21
cg, 10mm prox.	6.6 ± 2.7	5.6 ± 1.9	0.42	5.4 ± 1.9	5.4 ± 1.8	0.34
cg gradient	−0.3 ± 0.3	0.0 ± 0.2	0.04	−0.2 ± 0.3	0.1 ± 0.2	0.02

Phase velocity

Figure 6 shows the mean of the non-parametric c_p as a function of frequency at the transition zone in unripened and ripened groups. The shadowed regions indicate ± one standard deviation about the mean. Mean and standard deviations were computed after excluding outliers that were smaller than the 25%ile or larger than the 75%ile by 1.5 times the interquartile range. The c_p varied linearly with frequency between 0.25kHz and 1.25kHz. The standard deviation increased below 0.4kHz and above 1.0kHz, and therefore the Radon-sum-like linear model was applied between 0.4kHz and 1.0kHz. Values of slope and intercept in the unripened group were 9.7m/s/kHz and 4.1m/s ( R ₂ = 0.98 ), respectively, and 9.2m/s/kHz and 4.2m/s ( R ₂ = 0.98 ) in the ripened group.

Figure 6.

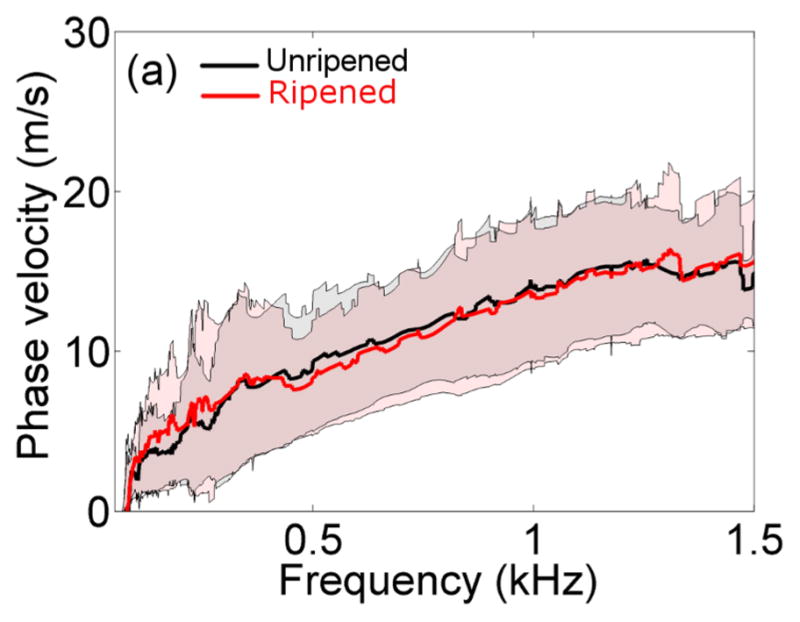
Non-parametric estimates of the phase velocity as a function of the frequency at the transition zone in the unripened (black) vs. ripened (red) groups. The thick lines indicate the mean between specimens, and shadowed areas indicate ± one standard deviation.

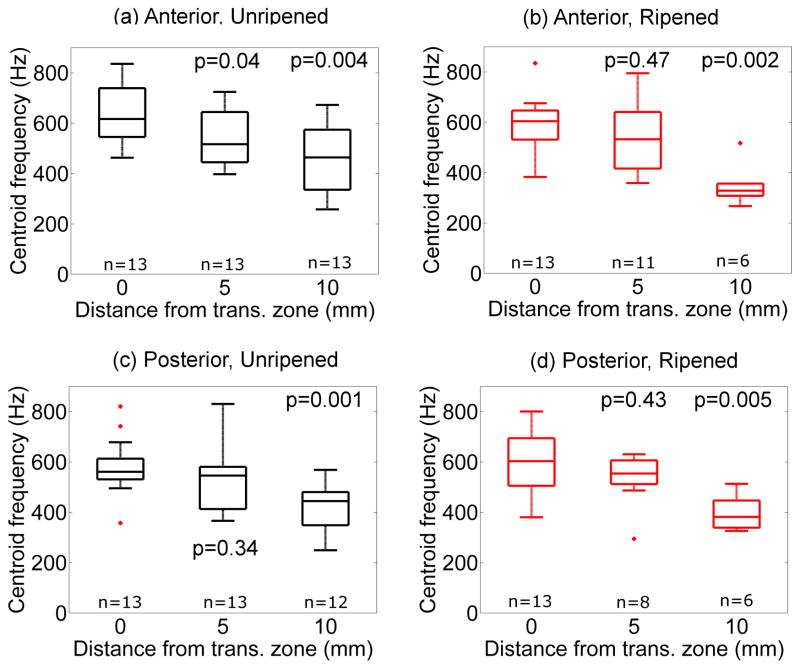
Figure 7 shows the spectral centroid frequency as a function of the distance from the transition zone in the same arrangement as Fig. 5. Values of centroid frequency and its spatial gradient along the cervix were similar for all specimens. In unripened and ripened specimens, centroid frequency decreased from 0.59 ±0.03 kHz at the transition zone to 0.40 ±0.03 kHz at 10mm. After combining estimates for all samples and all locations, the median value was 0.53kHz. Thus the linear-model’s phase velocity at 0.53kHz was used as an independent assessment of stiffness.

Figure 7.

Spectral centroid frequency as a function of distance from transition zone in unripened (a) and (c) vs. ripened (b) and (d) groups. Top: Anterior, Bottom: Posterior, Left: Unripened, Right: Ripened. Note that the higher frequency content of the shear waves agrees with the observation that shear wave speed is higher closer to the transition zone. P values correspond to Kruskal-Wallis test with respect to the values at the transition zone (0mm).

Figure 8 shows the phase velocity c_p from the linear model at 0.53kHz along the cervical canal as a function of distance from transition zone in the same arrangement as Fig. 7. As with c_g, the c_p at 0.53kHz decreases proximal to the transition zone, albeit at a lower rate that is not significantly different between ripened and unripened groups.

Figure 8.

Parametric c_p,LM at 0.53kHz as a function of distance from the transition zone. Top: Anterior, Bottom: Posterior, Left: Unripened, Right: Ripened. P values correspond to Kruskal-Wallis test with respect to the values at the transition zone (0mm).

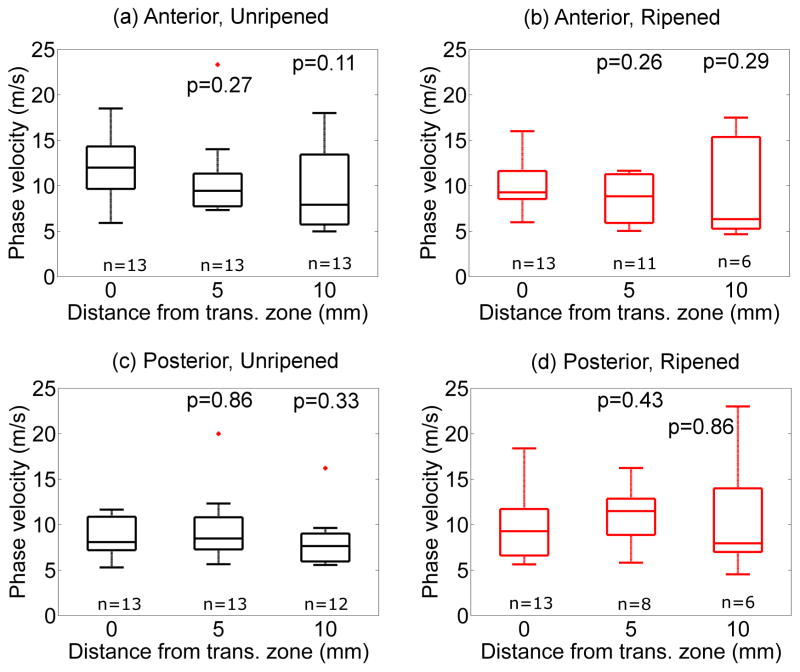
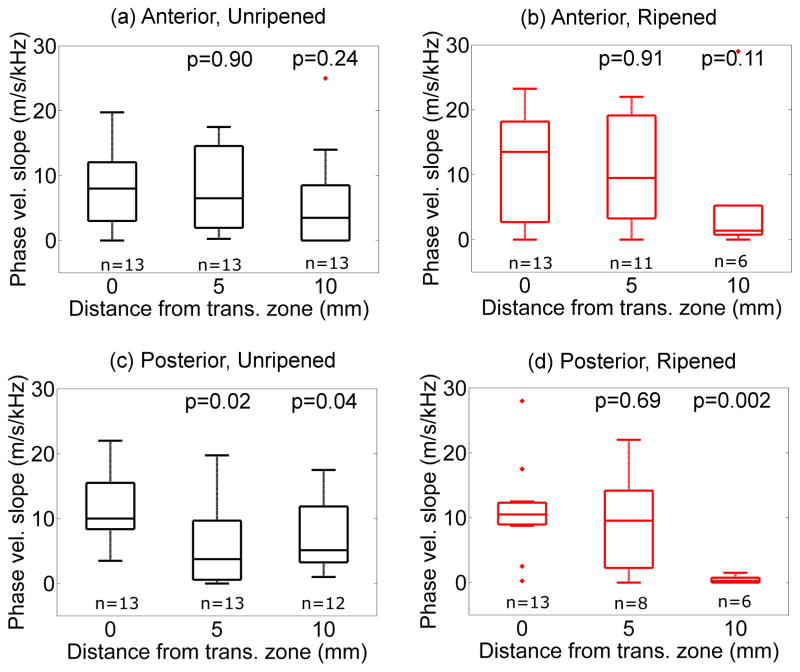
Figure 9 shows variation of the slope of the c_p vs. frequency (dc_p/df ) as a function of distance proximal to the transition zone. In the unripened group, dc_p/df decreased slightly from the transition zone at a rate of −0.5 ±0.2 m/s/kHz/mm (anterior) and −0.6 ±0.3m/s/kHz/mm (posterior). In the ripened group, the dc_p/df decreased at a rate of −0.2 ±0.3 m/s/kHz/mm (anterior) and −0.4 ±0.2 m/s/kHz/mm (posterior). No significant differences were found between groups (anterior vs. posterior, unripened vs. ripened).

Figure 9.

Slope of the phase velocity vs. frequency as a function of the distance from the transition zone. Top: Anterior, Bottom: Posterior, Left: Unripened, Right: Ripened. P values correspond to Kruskal-Wallis test with respect to the values at the transition zone (0mm).

Discussion

Cervical ripening during pregnancy is complex and poorly understood. Cervical microstructure is comprised of quasi-aligned layers of collagen within an extracellular matrix (ECM) that also includes proteoglycans (PGs), elastin, cells (fibroblasts and immune cells), and water. Modifications to the ECM in the pregnant cervix result in softening, shortening and dilation of the cervix in preparation for delivery. These changes appear accelerated in preterm delivery. Most investigation has focused on collagen, but PGs such as decorin are abundant in the cervix (House et al., 2009), and in fact are a known source of viscosity (Buhimschi et al., 2004). As delivery nears and prostaglandin production increases, collagen fibers become thicker (Kuc and Scott, 1997) and the proportion of decorin increases relative to collagen (Kokenyesi and Woessner, 1990). Both structural/microstructural properties and viscosity might be expected to cause dispersion in the cervix, and thereby affect c_g estimates. As discussed in the Introduction, this was the motivation for the current investigation.

Application of our novel tests to account for structural/microstructural heterogeneity and reliability allowed better resolution of the spatial gradient than in our previous study. Specifically, we observed a reduction in group shear wave speed ( c_g ) between unripened and ripened groups (−2.6 ± 2.7m/s and −1.5 ± 2.8m/s at the transition zone of the anterior and posterior cervix, respectively), a much greater reduction than in our previous estimates in the same specimens (Huang et al., 2016). Unlike before, we found a significant difference in the spatial gradient of c_g in the unripened vs. the ripened group. In fact, we observed no gradient in the ripened group. Although our numbers are much too small to draw confident conclusions, these findings may suggest that cervical tissue becomes more homogeneous with ripening, which would be consistent with prevailing theories.

Interestingly, in non-ripened samples, the spatial gradient of the group velocity trended opposite in the NHP cervix (softer proximally) compared to the ex vivo human cervix (softer distally).(Carlson et al., 2014b) Our veterinary pathologist (HAS) attributes this difference (as well as the overall increased stiffness of the NHP cervix) to evolutionary adaptations to different biomechanical forces; specifically, humans are obligate bipeds, while NHPs are both bi- and quadriped, with daily locomotion involving climbing and jumping, both arboreally (between trees) as well as to and from the ground. Regardless, what is important to the current study is that exogenous induction of ripening resulted in a reduction in spatial gradients in both species.(Carlson et al., 2014b)

Of note, c_g measurements reported here were obtained using shear particle displacement estimates, but we also investigated the use of particle velocity estimates from the differential displacement between two consecutive tracking time points (Rouze et al., 2015). This comparison between velocity- and displacement-based c_g estimates, c_g,vel and c_g,disp, can be used to evaluate dispersion. Because velocity data are biased toward a higher frequency part of the shear wave spectrum than displacement data, the estimation of particle velocity effectively acts as a high pass filter applied to the displacement data. This is inconsequential in non- or low-dispersive tissue because phase velocity does not change significantly with frequency, and thus c_g,vel/c_g,disp would be close to unity. However, in highly dispersive media, c_g,vel is expected to be greater than c_g,disp. Fig. 10 depicts c_g,vel/c_g,disp as a function of dc_p/df. Each solid point and its error bars indicate the mean and the standard error from grouping the values of both parameters from all specimens for a particular position along the cervix. The figure suggests dispersion because c_g,vel/c_g,disp increases as a function of dc_p/df. In other words, our results are consistent with high dispersion. The median dc_p/df among all specimens and all ROI locations is 5.5 m/s/kHz, with an interquartile range of 1.5–12.0 m/s/kHz. A detailed analysis of the discrepancy between c_g,vel and c_g,disp and its relationship with spatial gradients in dispersion in the cervix is subject of current research.

Figure 10.

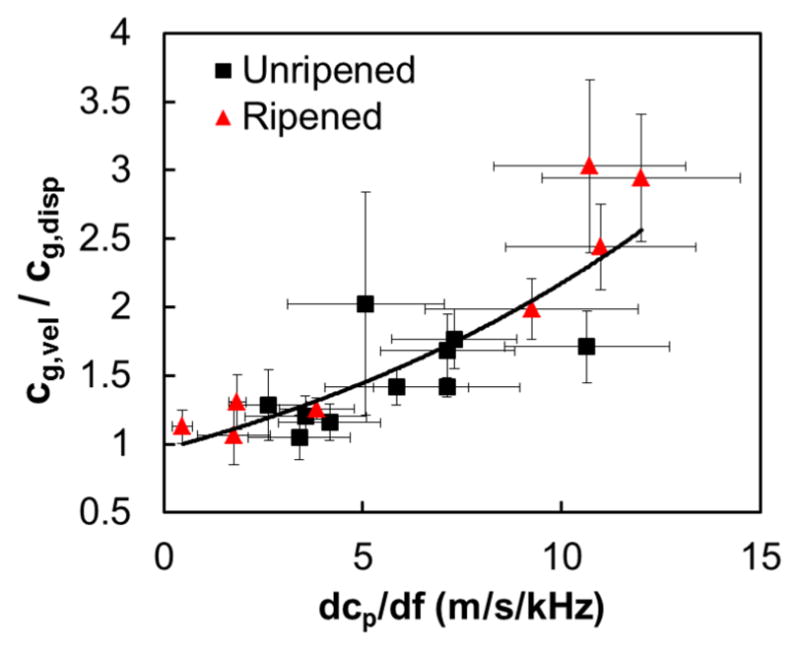
Ratio of the velocity-based and the displacement-based group velocities as a function of the phase velocity slope vs. frequency in unripened (black) and ripened (red) samples.

To our knowledge, this is the first report of dispersion in cervical tissue. That said, the results are consistent with a simulation study of cervical ECM ripening via varying spatial arrangements and abundance of collagen, PGs, elastin, cells and water (Peralta et al., 2015c). In this simulation, softening and increased viscosity was observed with increasing collagen fiber thickness as the wave propagates parallel to the fibers. A study in the ex vivo rat cervix corroborate these findings. Specifically, using stress-relaxation tests, Barone et al. (Barone et al., 2010) confirmed viscoelasticity before and during pregnancy in the rat cervix. They also found the proximal cervix to be less viscous than the distal, which is consistent with our findings of decreased dispersion proximally in the macaque cervix (Fig. 9). It is important to consider, however, that viscosity is not necessarily the sole contributor to the dispersion we observed.

For instance, microstructural heterogeneity may play a role in the differences between the macaque and human cervix. Our previous studies suggest that the macaque cervix is about 4 times stiffer than the human (Huang et al., 2016; Carlson et al., 2014a, b); in the anterior unripened macaque cervix, c_g was 2.6 ± 1.0 times larger (anterior), and 2.1 ± 1.0 times larger (posterior) than in the human cervix. However, this may be misleading. As discussed in the Introduction, for the purposes of SWEI analysis, previous studies have considered the cervix an homogeneous, isotropic elastic solid. However, the wavelength of the induced shear wave is on the order of 1cm, which is about the same size, or larger (especially in the macaque), than the thickness of each layer. This principle can be elucidated by imaging cervical microstructure as a stack of transverse isotropic plates, and its relevance is demonstrated by a study in the Achilles tendon, another tissue containing quasi-aligned collagen with transverse isotropy. Aubry et al. (2013) found that when the shear wave propagates parallel to the fibers, c_g is about three times larger than when it propagates perpendicularly. In a related study, Brum et al. (2014) reported a change of 9.5 ± 6.4m/s/kHz and 2.5 ± 1.7m/s/kHz in c_p vs. frequency between 0.3kHz and 0.7kHz when the wave propagates parallel and perpendicular to the fibers, respectively. Via a theoretical model based on Lamb waves, they demonstrated that shear wave dispersion assessed in the parallel condition is determined only by the guided wave effect, not viscosity. The similarity of these results with ours at the transition zone suggests that layers with collagen fibers running parallel to the cervical canal might have contributed to the larger c_g values and shear wave dispersion (on the order of 10m/s/kHz) in the macaque cervix compared to the human. In fact, this might also explain our limited sensitivity to changes in viscosity expected from exogenous prostaglandin administration.

This principle highlights a limitation of this study, specifically that inaccurate measurement may have occurred due to thin layers (compared to shear wavelength). Although we made an effort to evaluate SWEI only within regions of homogeneous wave propagation, we did not consider the potential for guided wave effects. We are currently studying this with simulations based on finite-element analysis. In addition, our study was limited to the sagittal view of the cervix because of its clinical relevance (this is the plane that is used clinically for intravaginal scans). Because of this, the same plane was also chosen in our previous ex vivo studies in humans. As a result, the analysis of shear wave propagation was mostly restricted to the plane parallel to collagen fibers aligned with the cervical canal. In the transverse plane, the small radius of the cervix (5.8 ± 1.1mm) restricts the shear wave tracking length. Future studies should address this limitation to expand the characterization of the cervix to address its anisotropy. We are currently exploring other techniques, such as backscatter-based Quantitative Ultrasound, to gain insight into this phenomenon.(Guerrero et al., 2016)

Another limitation is that we studied ex vivo tissue and therefore cannot translate the absolute values of the parameter estimates to the in vivo cervix. Our initial assessment of the in vivo NHP cervix showed that c_g in the non-pregnant NHP cervix is about half the values obtained ex vivo. The difference can be attributed to the experimental conditions (room temperature vs. body temperature) and to the lack of turgidity and perfusion. Furthermore, shear wave speed estimation in stiffer media is associated with increased variance in shear wave speed estimates.(Wang et al., 2013) This resulted in limited statistical power of changes induced by exogenous ripening (0.88 and 0.47 for c_g at the transition zone in the anterior and posterior side, respectively; 0.82 for the spatial gradient of c_g in both the anterior and posterior sides). Therefore, effects of ripening reported here should be interpreted with caution. That said, this study elucidates effects of structural/microstructural heterogeneity and shear wave dispersion on the interpretation of c_g which is certainly relevant to in vivo study. We are currently applying this insight to our longitudinal in vivo studies of pregnant macaques and women.

The linear model used to parametrize the dependence of c_p vs. frequency is only an intermediate step in a comprehensive description of the mechanical properties of a tissue. Comprehensive study requires estimating frequency-dependent storage and loss moduli, an approach that is usually simplified by applying a rheological model, e.g. Maxwell’s, Voigt’s, or Zener’s. After comparing high-frequency simulated dispersion analysis, Peralta et al.(Peralta et al., 2015b) found that Zener’s three-parameter model better described simulated material properties than either Maxwell’s or Voigt’s two-parameter models. Further, each models goodness-of-fit to the simulated dispersion curve varied within the analyzed frequency bandwidth, suggesting that higher-order models might be more useful for representing different viscoelastic components of tissue, each of which have different relaxation times. One of these models, the Prony series model, was recently used in a compression test of the ex vivo human cervix (Yao et al., 2014). The development of an appropriate model for inversion strategies tailored to cervical tissue and its changes during pregnancy is currently under investigation.

The proposed methods for testing for significant motion and heterogeneities in tissue displacements are currently being improved in several ways. First, shear-wave induced displacements were quantified following a multi-tracking location (MTL) approach. This method is sensitive to speckle-related noise, i.e., variations in the estimated time of arrival of the shear wave at two tracking locations due to differences in the speckle patterns.(McAleavey et al., 2015)These effects, which are expected to worsen in viscous materials, can be overcome with a single-tracking location (STL) approach, i.e., fixing the tracking location and computing the difference in the time of arrival of shear waves produced at two different locations.(Elegbe and McAleavey, 2013) Second, time-averaging of post-push displacements in the test for significant motion was done over the first t_n time samples after the ARFI excitation. This approach has the risk of missing the arrival of the shear wave at the most distant tracking locations from the push. In this study, this issue is not significant due to the relatively large c_g values, resulting in the wave traveling through the ROI within the 2ms averaging-time span. This is further reduced by the lateral average of time-averaged displacements presented in Fig. 1(c). However, we acknowledge this can be an issue in softer materials, such as the in vivo cervix. This can be overcome by centering the time-averaging window at the maximum displacement. Third, the selection of homogeneous motion was performed manually. We are exploring way to automate this task. Finally, the selection of 5m/s as a threshold for discrepancy between the two group velocity estimators was arbitrary. We are currently performing a systematic analysis of tradeoffs between the goodness of fit and the discrepancy between the estimators. Our goal is to design a tissue-independent quality metric that objectively quantifies the reliability of group velocity estimates.(Rosado-Mendez et al., 2016b, c)

Conclusions

In summary, unlike previous studies, our results suggest a difference in the spatial gradient of shear wave speed estimates between the ripened and unripened ex vivo Rhesus macaque cervices after application of our new techniques for assessing adequacy of data. However, effects of ripening should be interpreted with caution due to the large variance of the estimated parameters. Most importantly, we found the Rhesus macaque cervix is highly dispersive. While it is too early to draw conclusions about what might be occurring at the microstructural level during cervical ripening, this work suggests that comprehensive SWEI evaluation of the cervix (and other complex tissues) should take into account structural/microstructural heterogeneity and viscosity. Our novel approach provides a means to study the cervix in vivo, and we are currently applying it to longitudinal studies of pregnant macaques and women.