Observation of discrete time-crystalline order in a disordered dipolar many-body system

Abstract

Understanding quantum dynamics away from equilibrium is an outstanding challenge in the modern physical sciences. It is well known that out-of-equilibrium systems can display a rich array of phenomena, ranging from self-organized synchronization to dynamical phase transitions^1,2. More recently, advances in the controlled manipulation of isolated many-body systems have enabled detailed studies of non-equilibrium phases in strongly interacting quantum matter^3–6. As a particularly striking example, the interplay of periodic driving, disorder, and strong interactions has recently been predicted to result in exotic “time-crystalline” phases⁷, which spontaneously break the discrete time-translation symmetry of the underlying drive^8–11. Here, we report the experimental observation of such discrete time-crystalline order in a driven, disordered ensemble of ~ 10⁶ dipolar spin impurities in diamond at room-temperature^12–14. We observe long-lived temporal correlations at integer multiples of the fundamental driving period, experimentally identify the phase boundary and find that the temporal order is protected by strong interactions; this order is remarkably stable against perturbations, even in the presence of slow thermalization^15,16. Our work opens the door to exploring dynamical phases of matter and controlling interacting, disordered many-body systems^17–19.

Conventional wisdom holds that the periodic driving of isolated, interacting systems inevitably leads to heating and the loss of quantum coherence. In certain cases, however, fine-tuned driving can actually decouple quantum degrees of freedom from both their local environment¹³ and from each other²⁰. Recently, it has been shown that strong disorder, leading to many-body localization (MBL)^21,22, allows a system to retain memory of its initial state for long times, enabling the observation of novel, out-of-equilibrium quantum phases^3,5,23. One example is the discrete time crystal (DTC)^8–11, a phase which is nominally forbidden in equilibrium^24,25. The essence of the DTC phase is an emergent, collective, subharmonic temporal response. While this phenomenon resembles the coherent revivals associated with dynamical decoupling¹², its nature is fundamentally different as it is induced and protected by interactions rather than fine-tuned control fields. It is especially intriguing to investigate the possibility of DTC order in systems that are not obviously localized²⁶. This is the case for dipolar spins in three dimensions, where the interplay between interactions and disorder can lead to critical sub-diffusive dynamics^16,27.

We experimentally investigate the formation of discrete time-crystalline order in an ensemble of nitrogen vacancy (NV) spin impurities in diamond. Each NV center has an electronic S = 1 spin, from which we isolate an effective two level system by applying an external magnetic field. These isolated spin states can be optically initialized/detected and manipulated via microwave radiation^12,14 (see Fig. 1a and Methods). Our sample has a high concentration (45 ppm) of NV centers, giving rise to strong long-range magnetic dipolar interactions¹⁶. The spins are also subject to multiple sources of disorder owing to lattice strain, paramagnetic impurities and the random positioning of NV centers. A strong, resonant microwave field is used to control spin orientations, resulting in an effective Hamiltonian (in the rotating frame),¹⁶

$$H\left(t\right)={\displaystyle \sum _i{\Omega }_x\left(t\right)}{S}_i^x+{\Omega }_y\left(t\right)S_i^y+{\Delta }_i{S}_i^z+{\displaystyle \sum _{ij}\left(J_{ij}/r_{ij}^3\right)}\left(S_i^x{S}_j^x+S_i^y{S}_j^y-S_i^z{S}_j^z\right).$$ (1)

Here, $S_i^{\mu }\left(\mu \in \left\{x,y,z\right\}\right)$ are Pauli spin-1/2 operators acting on the effective two-level system spanned by the spin states |m_s = 0〉 and |m_s = −1〉, Ω_x(y) is the Rabi frequency of the microwave driving, Δ_i is a disordered on-site field with approximate standard deviation W = 2π × 4.0 MHz, r_ij is the distance between spins i and j (average nearest-neighbor separation r₀ ~ 8 nm), and J_ij are the orientation dependent coefficients of the dipolar interaction. We note that the average interaction, $J_{ij}/r_0^3\sim 2\pi \times 105\text{kHz}$¹⁶, is significantly faster than typical spin coherence times¹⁴.

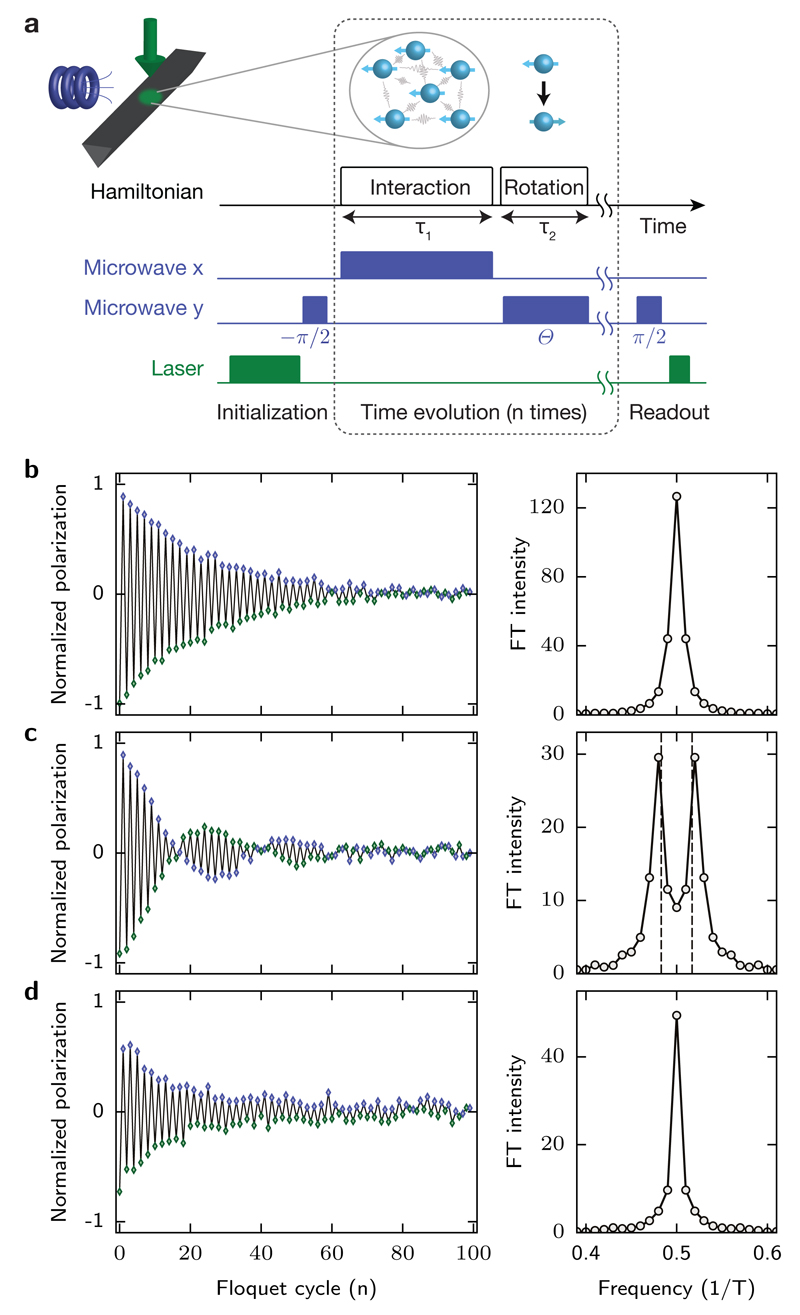
Fig. 1. Experimental setup for observing time-crystalline order.

a, NV centers in a nanobeam fabricated from black diamond are illuminated by a focused green laser beam and irradiated by a microwave source. Spins are prepared in the $(|m_s=0\rangle +|m_s=-1\rangle )/\sqrt{2}$ state using a microwave (−π/2)-pulse along the $\widehat{y}$ axis. Subsequently, within one Floquet cycle, the spins evolve under a dipolar interaction and microwave field Ω_x aligned along the $\widehat{x}$ axis for duration τ₁, immediately followed by a global microwave θ-pulse along the $\widehat{y}$ axis. After n repetitions of the Floquet cycle, the spin polarization the $\widehat{x}$ axis is read out. We choose τ₁ as an integer multiple of 2π/Ω_x to minimize accidental dynamical decoupling¹³. b-d, Representative time traces of the normalized spin polarization P(nT) and respective Fourier spectra, |S(ν)|², for different values of interaction time τ₁ and θ: (b) τ₁ = 92 ns, θ = π, (c) τ₁ = 92 ns, θ = 1.034π, and (d) τ₁ = 989 ns, θ = 1.034π. Dashed lines in c indicate ν = 1/2 ± (θ − π)/2π. Data are averaged over more than 2 ⋅10⁴ measurements.

In order to probe the existence of time-crystalline order, we monitor the spin dynamics of an initial state polarized along the +$\widehat{x}$ direction. We begin by applying continuous microwave driving (spin locking) along $\widehat{x}$ with Rabi frequency Ω_x = 2π × 54.6 MHz for a duration τ₁ (Fig. 1a). Next, we rotate the spin ensemble by an angle θ around the $\widehat{y}$ axis using a strong microwave pulse with Ω_y = 2π × 41.7 MHz for duration τ₂ = θ/Ω_y ≪ τ₁. This two-step sequence defines a Floquet unitary with a total period T = τ₁ + τ₂ and is repeated n times, before the polarization P(nT) along the $\widehat{x}$ axis is measured. The resulting polarization dynamics are analyzed in both the time and frequency domain. Repeating these measurements with various values of τ₁ and θ allows us to independently explore the effect of interactions and global rotations.

Figure 1b-d depict representative time traces and the corresponding Fourier spectra, $S\left(\nu \right)\equiv {\displaystyle {\sum }_{n}P\left(nT\right)e^{i2\pi nv},}$ for various values of τ₁ and θ. For relatively short interaction time τ₁ = 92 ns and nearly perfect π-pulses (θ ≈ π), we observe that the spin polarization P(nT) alternates between positive and negative values, resulting in a sub-harmonic peak at ν = 1/2 (Fig. 1b). In our experiment, the microwave pulses have an intrinsic uncertainty 0.9% stemming from a combination of spatial inhomogeneity in the microwave fields, on-site potential disorder, and the effect of dipolar interactions (see Methods). These eventually cause the oscillations to decay after ~ 50 periods. While such temporal oscillations nominally break discrete time-translation symmetry, their physical origin is trivial. To see this, we note that for sufficiently strong microwave driving, ${\Omega }_x\gg W,J_{ij}/r_0^3,$ the dynamics during τ1 are governed by an effective polarization-conserving Hamiltonian¹⁶, $H_{\text{eff}}\approx {\displaystyle {\sum }_i{\Omega }_x{S}_i^x+{\displaystyle {\sum }_{ij}\left(J_{ij}/r_{ij}^3\right)S_i^x{S}_j^x.}}$ During τ₂, the evolution can be approximated as $R_y^{\theta }\approx e^{-i\theta {\displaystyle {\sum }_i{S}_i^y}}.$ When θ = π, this pulse simply flips the sign of the $\widehat{x}$ polarization during each Floquet cycle, resulting in the ν = 1/2 peak. However, this 2T-periodic response originates from the fine tuning of θ and should not be robust against perturbations. Indeed, a systematic change in the average rotation angle to θ = 1.034π causes the 2T-periodicity to completely disappear, resulting in a modulated, decaying signal with two incommensurate Fourier peaks at ν = 1/2 ± (θ − π)/2π(Fig. 1c). Remarkably, we find that a rigid 2T-periodic response is restored when interactions are enhanced by increasing τ₁ to 989 ns, suggesting that the ν = 1/2 peak is stabilized by interactions. In this case, we observe a sharp peak in the spectrum at ν = 1/2 and the oscillations in P(nT) continue beyond n ~ 100 (Fig. 1d), indicating persistent subharmonic temporal response.

The robustness of this apparent periodic order is further explored in Fig. 2. With an interaction time τ₁ = 790 ns and θ = 1.034π, the polarization exhibits an initial decay followed by persistent oscillations over the entire time window of our experimental observations (Fig. 2a). We perform a Fourier transform on sub-sections of the time-trace with a sweeping window of size m = 20 (Fig. 2a) and extract the intensity of the ν = 1/2 peak as a function of the sweep position, n_sweep (Fig. 2b). The ν = 1/2 peak intensity clearly exhibits two distinct decay timescales. At short times, we observe a rapid initial decay corresponding to non-universal dephasing dynamics, while at late times, we observe a slow decay. Only near the phase boundary (θ = 1.086π), the lifetime is significantly decreased. We fit the slow decay to an exponential to extract a lifetime for the periodic order. As shown in Fig. 2c, for θ = 1.034π, this lifetime increases with the interaction time (τ₁) and eventually approaches the independently measured spin depolarization time $T_1^{\rho }\sim 60\mu \text{s}.$ This demonstrates that for sufficiently long interaction times, the observed periodic order is only limited by coupling to the environment²⁷. We associate this with DTC order^8–11. Remarkably, within the DTC phase, the lifetime is essentially independent of θ, indicating exceptional robustness (Fig. 2d).

Fig. 2. Long-time behavior of time-crystalline order.

a Representative time trace of the normalized spin polarization P (nT) in the crystalline phase (τ₁ = 790 ns and θ = 1.034π). The time-dependent intensity of the ν = 1/2 peak is extracted from a short-time Fourier transformation with a time window of length m = 20 shifted from the origin by n_sweep. b Peak height at ν = 1/2 as a function of n_sweep for different pulse imperfections at τ₁ = 790 ns. Lines indicate fits to the data using a phenomenological double exponential function. The noise floor corresponds to 0.017, extracted from the mean value plus the standard deviation of ∑_ν|S(ν)|² excluding the ν = 1/2 peak. c Extracted lifetime of the time-crystalline order as a function of the interaction time τ₁, for θ = 1.034π. Shaded region indicates the spin life-time $T_1^{\rho }=60\pm 2\mu s$ (extracted from a stretched exponential²⁷) due to coupling with the external environment. d Extracted decay rate of the time-crystalline order as a function of θ for different interaction times, τ₁ = 385 ns (circle), 586 ns (square) and 788 ns (triangle). Only very weak dependence on θ − π is observed within the DTC, contrary to a dephasing model (Methods). In c, d, vertical error bars display the statistical error (s. d.) from the fit and empty symbols mark data near the time-crystalline phase boundary.

We carefully examined if the observed periodic order could arise from an accidental XY sequence¹³ or from inhomogeneous dephasing resulting from the effective single-particle disorder in the dressed state basis. To avoid the former, τ₁ is always choosen as an integer multiple of 2π/Ω_x. For the latter, while it was shown that disorder alone is insufficient for stabilizing DTC in the absence of interactions^8–11, we verified this experimentally; implementing a rotary echo sequence that reduces such dephasing, we find no change in the DTC lifetime and actually an enhancement in the DTC fraction (see Methods and Extended Data Fig. 1). In principle, fast Markovian dephasing could also lead to apparent periodic order at extremely small values of θ − π by eliminating coherences along both $\widehat{y}$ and $\widehat{z}$, leaving only $\widehat{x}$ polarization dynamics. In such a case, the decay rate of periodic order should increase quadratically with θ − π. However, this explanation is inconsistent with the observed robustness of DTC lifetime for a range of θ − π (Fig. 2d) and the independently measured dephasing rate (see Methods).

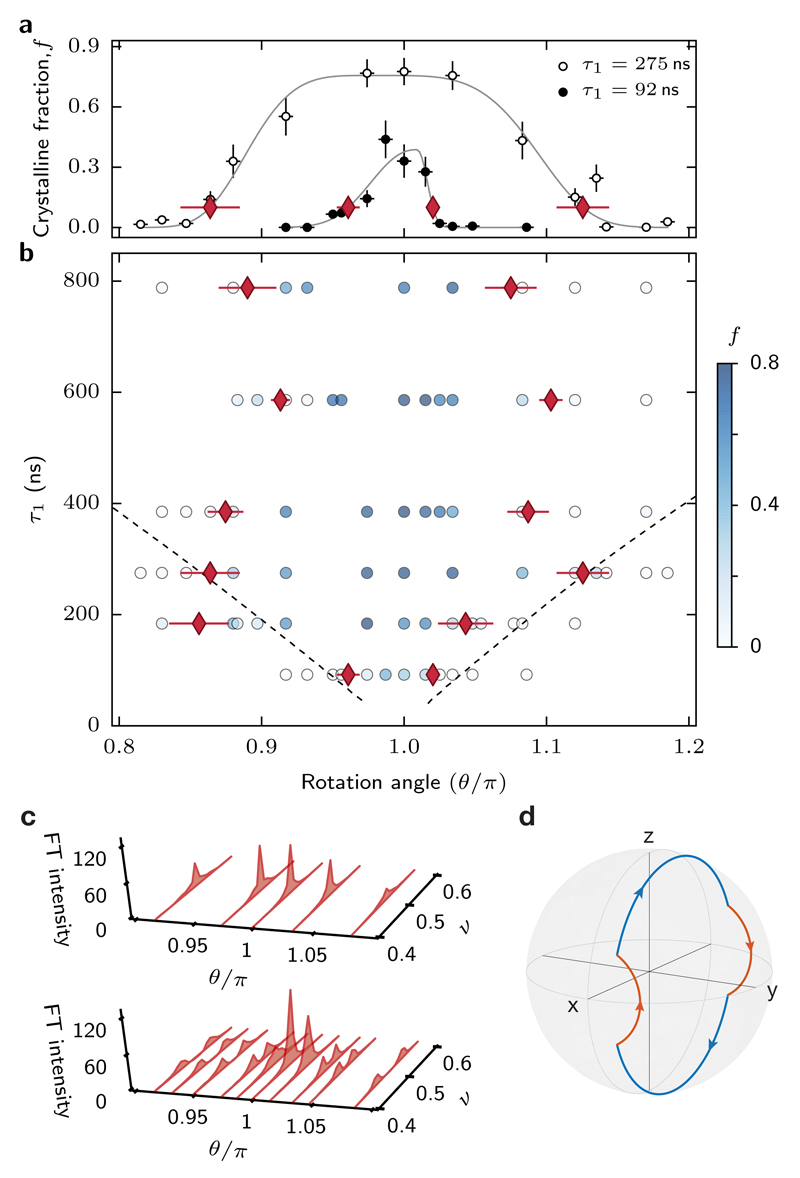
To experimentally determine the DTC phase boundary, we focus on the long-time behavior of the polarization time traces (50 < n ≤ 100) and compute the “crystalline fraction” defined as the ratio of the ν = 1/2 peak intensity to the total spectral power, $f={\left|S\left(v=\frac{1}{2}\right)\right|}^2/{\displaystyle {\sum }_v{\left|S(v)\right|}^2}$ (see Methods). Figure 3a shows f as a function of θ for two different interaction times. For weak interactions (τ₁ = 92 ns), f has a maximum at θ = π but rapidly decreases as θ deviates by ~ 0.02π. However, for stronger interactions (τ₁ = 275 ns), we observe a robust DTC phase which manifests as a large crystalline fraction over a wide range 0.86π < θ < 1.13π. We associate a phenomenological phase boundary with f = 10% and observe that the boundary enlarges with τ₁, eventually saturating at τ₁ ≈ 400 ns (Fig. 3b). The phase boundary can also be visualized as the vanishing of the ν = 1/2 peak and the simultaneous emergence of two incommensurate peaks (Fig. 3c).

Fig. 3. Phase diagram and transition.

a Crystalline fraction f as a function of θ obtained from a Fourier transform at late times (50 < n ≤ 100). Vertical error bars are limited by the noise floor (see Methods), horizontal error bars indicate the pulse uncertainty of 1%. Grey lines denote a super-Gaussian fit to extract the phase boundary (see Methods). In a, b, red diamonds mark the phenomenological phase boundary, identified as a 10% crystalline fraction. Horizontal error bars denote the statistical error (s. d.) from the fit. The colors of the round data points in b represent the extracted crystalline fraction at the associated parameter set. The dashed line corresponds to a disorder-averaged theoretical prediction for the phase boundary. Asymmetry in the boundary arises from an asymmetric distribution of rotation angles (see Methods). c Evolution of the Fourier spectra as a function of θ for two different interaction times, τ₁ = 385 ns (top) and τ₁ = 92 ns (bottom). d Bloch sphere indicating a single spin trajectory of the 2T-periodic evolution under the long-range dipolar Hamiltonian (red) and global rotation (blue).

The rigidity of the ν = 1/2 peak can be qualitatively understood by constructing effective eigenstates of 2T Floquet cycles, including spin-spin interaction. We approximate the unitary time evolution over a single period as $U_T=R_y^{\theta }{e}^{-i{H}_{\text{eff}}{\tau }_1}$ and solve for a self-consistent evolution using product states as a variational ansatz. To this end, we consider the situation where a typical spin returns to its initial state after 2T: |ψ(0)〉 ∝ |ψ(2T)〉 = e^−iθSy e^iϕ_iSx e^−iθSy e^−iϕ_iSx |ψ(0)〉, and self-consistently determine the interaction-induced rotation angle ${\varphi }_i\equiv {\displaystyle {\sum }_j{J}_{ij}}/r_{ij}^3\langle S_j^x\rangle {\tau }_1\approx {\overline{J}}_i{\tau }_1\langle \psi (0)\left|S^x\right|\psi \left(0\right)\rangle ,$ where |ψ(0)〉 is the initial spin state and ${\overline{J}}_i={\displaystyle {\sum }_j{J}_{ij}/r_{ij}^3}$ (see Methods). One expects ϕ_i to change sign after each Floquet cycle, since the average polarization 〈ψ(0)|S^x|ψ(0)〉 should be flipped. Intuitively, the self-consistent solution can be visualized as a closed path on the Bloch sphere (Fig. 3d), where each of the four arcs corresponds to one portion of the 2T periodic evolution. When θ = π, such a solution always exists. More surprisingly, even when θ ≠ π, a closed path can still be found for sufficiently strong interactions, |J̄_iτ₁| > 2|θ_i − π|; in such cases, the deviation in θ away from π is compensated by the dipolar interactions (Fig. 3d). We obtain a theoretical phase boundary by numerically averaging the self-consistent solution over both disordered spin positions and local fields. The resultant phase boundary is in reasonable agreement with the experimental observations for short to moderate interaction times τ₁, but overestimates the boundary at large τ₁ (dashed line, Fig. 3b, see Methods).

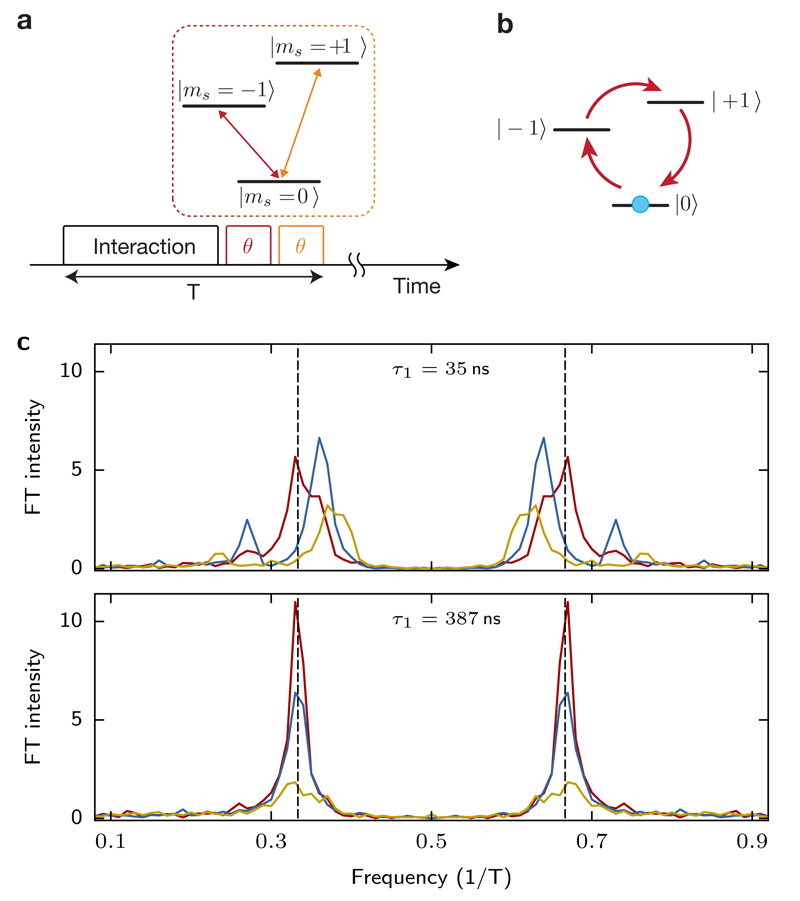
Finally, Fig. 4 demonstrates that the discrete time-translation symmetry can be further broken down to ℤ₃^9–11,28, resulting in DTC order at ν = 1/3. Here, we utilize all three spin states of the NV center. We begin with all spins polarized in the |m_s = 0〉 state and evolve under the bare dipolar Hamiltonian for a duration τ₁ (see Methods). Next, we apply two resonant microwave pulses, each of duration τ₂, first on the transition |m_s = 0) → |m_s = −1〉 and then on the transition |m_s = 0〉 → |m_s = +1〉. In combination, this sequence of operations defines a single Floquet cycle with period T = τ₁ + 2τ₂. As before, we measure the polarization, P(nT), defined as the population difference between the |m_s = 0〉 and |m_s = −1〉 states (Fig. 4a). When each of the applied microwaves corresponds to an ideal π-pulse, this sequence realizes a cyclic transition with ℤ₃ symmetry (Fig. 4b), which is explicitly broken by any change in the pulse duration. The Fourier spectra of P(nT) for various pulse durations and two different values of τ₁ are shown in Fig. 4c. With weak interactions (τ₁ = 35 ns), the position of the peaks is extremely sensitive to perturbations, but with sufficiently strong interactions (τ₁ = 387 ns) the peaks are pinned to a rigid value of ν = 1/3 despite large perturbations, indicating the observation of ν = 1/3 DTC. The lifetime of the observed ν = 1/3 DTC is shorter than that of the ν = 1/2 DTC, consistent with the presence of additional dynamics in the full dipolar Hamiltonian (see Methods). The ability for our system to exhibit stable period-tripling distinguishes it from bifurcations in driven, classical systems where period-tripling typically implies chaos²⁹.

Fig. 4. ℤ₃ time-crystalline order.

a Experimental sequence to demonstrate a 3T-periodic discrete time-crystalline order. A single Floquet cycle is composed of three operations: time evolution under long-range dipolar Hamiltonian and rapid microwave pulses for two different transitions. b Visualization of the 3T-periodicity in the polarization dynamics for the case of θ = π. c Fourier spectra of the polarization dynamics for two different interaction times and for three different rotation angles θ: 1.00π (red), 1.086π (blue) and 1.17π (yellow). Dashed lines indicate ν = 1/3, 2/3.

Our observation of DTC order cannot be simply explained within current theoretical frameworks based upon either localization^8–11 or pre-thermalization^23,26. In particular, the present system with long-range dipolar interactions is not expected to be localized in either the static or driven case. In the static case, it has been previously demonstrated that our system exhibits slow thermalization associated with critical dynamics¹⁶. In the driven case, the long-time evolution is governed by the average Hamiltonian $D\approx {\displaystyle {\sum }_i\left(J_{ij}/r_{ij}^3\right)S_i^x{S}_j^x+\left(\theta -\pi \right)/T{\displaystyle {\sum }_i{S}_i^y},}$ which likewise does not yield localized dynamics^15,30. We further note that the effective Hamiltonian of the ℤ₃ DTC includes not only Ising-type interactions but also spin exchange interactions, providing additional channels for thermalization (see Methods).

In principle, even in the absence of localization, time-crystalline order can persist for a long, but finite, pre-thermal time-scale^23,26. Within this time-scale, the spin system relaxes to a pre-thermalized state, defined as the thermal ensemble of D with a temperature determined by the energy density of the initial state. Since our initially polarized state is effectively at infinite temperature with respect to D (owing to the anisotropy of the dipolar couplings), one does not expect to observe pre-thermal DTC order. This is in contrast to our actual observations, which show that the DTC lifetime is limited by the depolarization time $T_1^{\rho }$ due to coupling with the environment²⁷ (Fig. 2c). We have explicitly verified that the DTC order is not significantly affected by varying the initial polarization (see Methods). One possible explanation is that due to slow critical thermalization¹⁶, the spins in our system do not reach even a pre-thermal state. Finally, the interplay between coherent interactions and dephasing in open systems at long times could also play a role. Detailed understanding of such mechanisms requires further theoretical investigation.

A number of remarkable phenomena in quantum dynamics have recently been observed in engineered many-body systems consisting of ten to a few hundred particles^3–6.Our present observations indicate that robust DTC order can occur in large systems without fine-tuned interactions and disorder, even in the regime where localization is nominally not expected to occur. Our work raises important questions about the role of localization, long-range interactions and coupling to the environment in driven systems and opens up several new avenues for fundamental studies and potential applications. In particular, it should be possible to extend these studies to realize novel dynamical phases in more complex driven Hamiltonians, and to explore if such novel phases can be used to create and stabilize coherent quantum superposition states for applications such as quantum metrology^17–19.

Methods

A. Experimental details

Our sample and experimental setup have been previously described¹⁶. We utilize a diamond sample containing a high concentration (~ 45 ppm) of NV centers, corresponding to an average NV-NV separation of 5 nm. For a single crystalline orientation of NV centers, selected by applying an external magnetic field, this corresponds to an average separation of 8 nm, resulting in a typical dipolar interaction strength of 2π × 105 kHz. The system furthermore exhibits strong on-site energy disorder, owing to the effects of lattice strain, the random position of NV centers as well as the presence of scattered paramagnetic impurities (consisting mainly of P1 centers and ¹³C nuclear spins). For each NV, the effective random field Δ_i is therefore a function of its local environment, including interaction effects of neighboring NV centers. This results in an approximately Gaussian distribution with standard deviation W = 2π × 4.0 MHz. We extract W by measuring the linewidth of an ESR spectrum with sufficiently weak microwave driving strength to avoid power broadening. In order to control the experimental probe volume, we fabricate a diamond nanobeam structure (~ 300 nm × 300 nm × 20 µm) and confocally address a region of ~ 300 nm diameter using a green laser (532 nm). This realizes an effective three dimensional excitation volume containing ~ 10⁶ NV centers. By applying an external magnetic field along one of the diamond crystal axes, we spectrally isolate one group of NV centers and selectively address an effective two-level system between the |m_s = −1〉 and |m_s = 0〉 spin states via coherent microwave radiation. The addition of a microwave IQ-mixer allows for arbitrary rotations around any linear combination $\widehat{x}$ and $\widehat{y}$.

B. Experimental sequence

Initial polarization of NV centers into |m_s = 0〉 is performed via laser illumination at a wavelength of 532 nm, a power of 50 µW and a duration of 100 µs. Subsequent application of a microwave (−π/2)-pulse along the $\widehat{y}$ axis is used to coherently rotate the spin ensemble into $|+\rangle =\left(\left|m_s=0\rangle +\right|m_s=-1\rangle \right)/\sqrt{2}.$ The spins are then subjected to continuous driving at a Rabi frequency 2π × 54.6 MHz along the $\widehat{x}$ axis for a duration τ₁. This so-called spin-locking technique suppresses two-spin (flip-flip and flop-flop) processes due to energy conservation as well as to decouple spins from their environment¹⁶. In our sample, this technique leads to spin lifetimes of $T_1^{\rho }\sim 60\mu s$²⁷. Finally, we apply a short microwave pulse along the $\widehat{y}$ axis over an angle θ ~ π. We repeat this Floquet cycle with various values of θ, controlled by changing the Rabi driving strength as well as the pulse duration. The imperfection in microwave manipulations (for initialization into |+〉 as well as rotation angles θ) amounts to 0.9%, arising from a combination of spatial inhomogeneity of the driving field (0.8%) as well as on-site potential disorder (0.6%). Following a coherent time evolution, the spin state of the NV ensemble is optically detected by applying a final (π/2)-pulse along the $\widehat{y}$ axis and measuring the population difference in the |m_s = 0〉 and |m_s = −1〉 basis. The polarization is defined as P = 𝓟₀ − 𝓟₋₁ with 𝓟_a denoting the population in spin state a, by calibrating the NV fluorescence using a Rabi oscillation contrast measurement. To avoid heating of the sample, resulting in drifts in the Rabi frequency, a waiting time of 600–900 µs is implemented before the sequence is repeated. The minimum spacing between microwave pulses is maintained at 1 ns.

To understand the effect of different initial states on the DTC phase, we replaced the initial (−π/2)-pulse with a (−π/3)-pulse. This results in the preparation of a global spin state, which is rotated from the $\widehat{x}$ axis by π/6. Despite this change, the measured DTC lifetime (47.6 ± 2.4 µs) agrees well with that of the polarized spin state (49.2 ± 3.3 µs), demonstrating that DTC order is insensitive to the initial state.

C. Experimental identification of phase boundary

To identify the position of the phase boundary in our experiment, we define the crystalline fraction f as $f={\left|S\left(v=\frac{1}{2}\right)\right|}^2/{\displaystyle {\sum }_v{\left|S(v)\right|}^2}.$ Error bars in f are calculated via error propagation in consideration of the noise floor in the Fourier spectrum; each measured spectrum contains a background noise level σ_n, resulting in a variation of f as,

$$\delta f=f\sqrt{{\left({\sigma }_n/{\left|S\left(v=\frac{1}{2}\right)\right|}^2\right)}^2+{\left(N{\sigma }_n/{\displaystyle \sum _v{\left|S\left(v\right)\right|}^2}\right)}^2-2N{\sigma }_n^2/\left({\left|S\left(v=\frac{1}{2}\right)\right|}^2{\displaystyle \sum _v{\left|S\left(v\right)\right|}^2}\right),}$$ (2)

where N = 50 is the number of points in the Fourier spectrum. This gives rise to an uncertainty in the DTC fraction: f ∈ [f − δf, f + δf ] (Fig. 3a). To extract the phase boundary, we use a phenomenological, super-Gaussian function

$$F_{{\tau }_1}\left(\theta \right)=\{\begin{array}{c}{f}_{{\tau }_1}^{\max }\exp \left[-\frac{1}{2}{\left(\frac{\left|\theta -{\theta }_0\right|}{{\sigma }_{-}}\right)}^p\right],\theta \le {\theta }_0\\ f_{{\tau }_1}^{\max }\exp \left[-\frac{1}{2}{\left(\frac{\left|\theta -{\theta }_0\right|}{{\sigma }_{+}}\right)}^p\right],\theta \ge {\theta }_0\end{array}$$ (3)

where σ_±, θ₀, p are the characteristic width, central position and the power of the super-Gaussian fit, and $f_{{\tau }_1}^{\max }$ max is the maximum value of the DTC fraction for a given duration τ₁. The proposed function naturally captures the observed asymmetry in the phase boundary. We define the phase boundary as the rotation angle θ_± where $F_{{\tau }_1}\left({\theta }_{\pm }\right)=0.1,\text{i}.\text{e}.{\theta }_{\pm }={\theta }_0\pm {\sigma }_{\pm }{\left[2\ln \left(f_{{\tau }_1}^{\max }/0.1\right)\right]}^{\frac{1}{p}}.$ Errors in the phase boundary are derived from the fit uncertainties.

D. Theoretical description

As a variational ansatz, we consider the time evolution of a homogeneous product state of the form |Ψ〉 = |ψ₀〉^⊗N with |ψ₀〉 = cos(θ₀/2)|+〉 +sin(θ₀/2)e^iϕ₀|−〉, where $|+\rangle =\left(\left|m_s=0\rangle \pm \right|m_s=-1\rangle \right)/\sqrt{2}.$ The qualitative behavior does not change even if we allow spins to be oriented in different directions. An approximate eigenstate for the time evolution over two periods is obtained by solving the equation for a single spin, |ψ₀〉 = e^−iθSy e^iϕ_iSx e^−iθSy e^−iϕ_iSx |ψ₀〉 with a self-consistently determined ϕ_i = J̄_i〈ψ₀|S^x|ψ₀〉 where ${\overline{J}}_i={\displaystyle {\sum }_j{J}_{ij}/r_{ij}^3}$ is the total strength at site i. The sign of ϕ_i is flipped in the second evolution as the spin polarization along the $\widehat{x}$ direction alternates in each cycle. Note that we have ignored the effects of the on-site disorder potential Δ_i, interactions during global rotations and rotations induced by Ω_x. This is justified due to the high microwave driving strength Ω_x(y) ≫ W and Ω_xτ₁ being integer multiples of 2π. (The effects of on-site disorder are fully included in the numerical computations.) A non-trivial solution (θ₀ ≠ ±π) is obtained if the first two rotations result in a vector that is rotated by π along the $\widehat{y}$ axis (Fig. 3d), which is satisfied when ϕ₀ = mπ − ϕ_i/2 with m ∈ ℤ and cot θ₀ = −(−1)^m tan(θ/2) sin(ϕ_i/2). Solving for cos² θ₀ yields

$${\cos }^2{\theta }_0=\frac{{\tan }^2\left(\theta /2\right){\sin }^2\left({\varphi }_i/2\right)}{1+{\tan }^2\left(\theta /2\right){\sin }^2\left({\varphi }_i/2\right)}.$$ (4)

Using ϕ_i = J̄_iτ₁ cos θ₀, one can show that a solution exists only when | tan (θ/2)J̄_iτ₁/4| > 1, implying that |θ − π| < |J̄_iτ₁/2| in the vicinity of θ ≈ π. The linear dependence of the phase boundary is consistent with the phase diagram provided in Ref.11. As long as a solution exists, small variations in θ correspond to a smooth deformation of the closed trajectory. Therefore, the existence of such a closed path stabilizes the time-crystalline phase. We emphasize that such a 2T-periodic path is a consequence of interactions; without the change of sign in ϕ_i, the eigenstates of the unitary evolution over one or two periods coincide, and therefore, unless the rotation angle is fine-tuned, T-periodic motion cannot be broken into a 2T period. The eigenstates of unitary evolution over one period can be obtained as even and odd linear combinations, $\left(\left|\Psi \rangle \pm e^{-i{\in }_i}{U}_1\right|\Psi \rangle \right)/\sqrt{2},$ where $U_1={\otimes }_i\left(e^{-i\theta S_i^y}{e}^{-i{\varphi }_i{S}_i^x}\right),$ and the quasi-energy eigenvalue is given by e^i2ϵ_i = 〈Ψ|(U₁)²|Ψ〉.

To estimate the phase boundary, we numerically solve the self-consistency equation. Here, we include the effects of on-site disorder potential Δ_i in all four rotations as well as the disorder in J̄_i arising from the random positions of NV centers. The distribution of J̄_i is simulated for 1000 spins, randomly distributed in three dimensions with an average separation r₀ and minimum cutoff distance r_min = 3 nm (limited by NV-NV electron tunneling²⁷). Instead of cos(θ₀), we solve for a self-consistent distribution for cos(θ₀), where 〈S^x〉 is defined as the mean of the distribution. The average order parameter 〈cos² θ₀〉 is computed for various values of τ₁ and θ and compared with a threshold value of 0.1 in order to identify the phase boundary. The experimental and numerical phase boundaries are asymmetric about θ = π. We attribute this to the inherently asymmetric distribution of the effective rotation angle, ${\theta }_i\approx {\tau }_2\sqrt{{\Omega }_y^2+{\Delta }_i^2+{\overline{J}}_i^2},$ which causes the transition to occur earlier for positive deviations θ − π.

While we assumed ϕ_i to be a classical variable in this analysis, the interaction induced rotation angle is an operator $\widehat{\varphi }$ that exhibits quantum fluctuations and leads to non-trivial quantum dynamics. Under such dynamics, spins get entangled, resulting in mixed state density matrices. These effects cannot be ignored in the case of long interaction times, effectively limiting the present description. We believe that the diminished range of θ in the experimentally obtained phase diagram (Fig. 3b) is related to this effect.

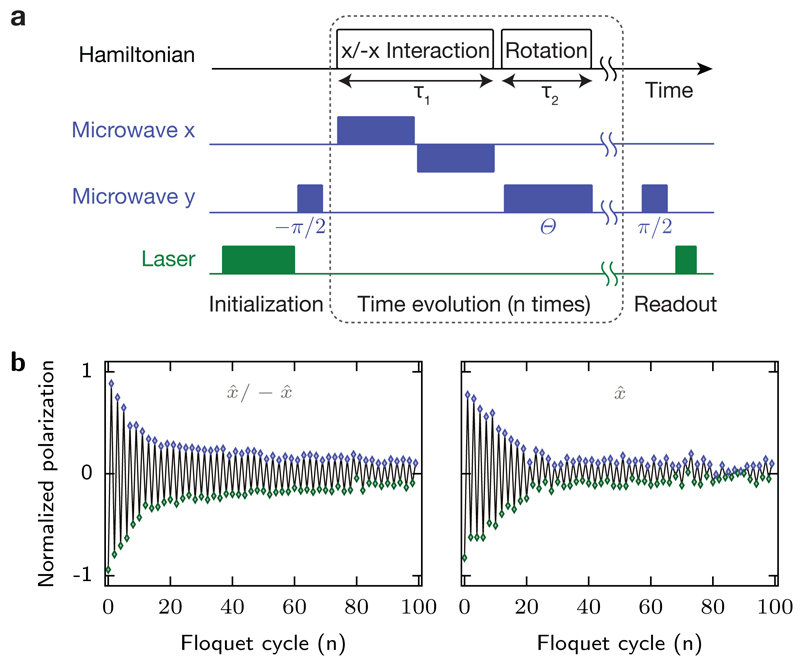
E. Rotary echo sequence

Certain features of DTC order could potentially arise from spatially inhomogeneous microwave driving along the $\widehat{x}$ axis during the spin-locking sequence. This leads to variations in the effective, single-particle disorder in the dressed state basis, which could give rise to an effective self-correcting dynamical decoupling that might resemble DTC order¹³. In particular, in the spin-locking sequence, spins precess along the axis (Ω_x(r_i) + J̄_i)$\widehat{x}$ + Δ_iẑ, with effective Rabi frequency ${\Omega }_{x,i}^{\text{eff}}=\sqrt{{\left({\Omega }_x\left(r_i\right)+{\overline{J}}_i\right)}^2+{\Delta }_i^2},$ where Ω_x(r_i) is the spatially inhomogeneous Rabi frequency, J̄_i is the mean-field Ising interaction, and Δ_i characterizes the quasi-static on-site disorder. In the case of strong driving (Ω_x ≫ Δ_i, J̄_i), this precession axis is determined by Ω_x and spins undergo dephasing dominated by global microwave inhomogeneities. If the net rotation during one spin-locking cycle is an odd integer multiple of π, this could accidentally lead to an XY-sequence¹³ that may result in 2T-periodicity. In our measurements, we always choose τ₁ as an integer multiple of 2π/Ω_x to minimize such effects.

While it has been shown theoretically that disorder alone is insufficient (in the absence of interactions) for stabilizing DTC order^8–11, to experimentally demonstrate that the accidental decoupling is not responsible for the observed DTC ordering, we implement a so-called “rotary echo” sequence, where after half the interaction time τ₁, the microwave driving is flipped from Ω_x to −Ω_x (Extended Data Fig. 1a). In the limit of strong driving, such a sequence eliminates the phase acquired between the two dressed states for each spin, regardless of the exact value of Ω_x. As shown in Extended Data Fig. 1b, the DTC lifetimes at late times are nearly identical between the cases of the rotary echo and continuous +$\widehat{x}$ driving. Moreover, the rotary echo spin polarization maintains a larger amplitude at late times, excluding the possibility of self-correcting dynamical decoupling as the origin of the observed DTC.

F. Markovian dephasing effects on discrete time crystalline order

The presence of the sub-harmonic peak at ν = 1/2 at small values of θ − π can, in principle, also be explained based on fast Markovian dephasing in the dressed state basis. Indeed, for sufficiently fast dephasing, coherences along both $\widehat{y}$ and $\widehat{z}$ will be eliminated after each rotation, $R_y^{\theta }.$ Thus, the only evolution that remains is the population dynamics along $\widehat{x}$, which exhibits 2T-periodicity from the alternating sign. Microscopically, such strong dephasing could potentially originate from either dipolar interactions between the spins or from coupling to an external (Markovian) environment.

Intuitively, the result of such dephasing can be understood as an “effective” projective measurement of polarization along $\widehat{x}$ in each Floquet cycle, reminiscent of the quantum Zeno effect. In order to quantify and distinguish such dephasing-induced sub-harmonic rigidity, we consider the dynamics (over one Floquet period) of a single spin undergoing Markovian dephasing, with super-operator $\widehat{𝒟}[\rho ]=-\frac{\gamma }{2}(\rho -4S^x\rho S^x)$ and dephasing rate γ. Assuming θ − π ≪ 1, evolution falls into two well known limits. In the under-damped limit (weak dephasing), S(ν) exhibits two Lorentzian peaks at ν = ±η with a linewidth set by γτ₁, where τ₁ is the spin-locking duration and cos(2πη) = cos θ(1 + e^γτ₁)/2. In the over-damped limit (strong dephasing), S(ν) (at late times) exhibits a peak at ν = 1/2 with a linewidth (in Floquet units)

$$\Gamma \approx \frac{{(\theta -\pi )}^2}{2\text{tanh}(\gamma {\tau }_1/2)}.$$ (5)

These over-damped oscillations of the spin polarization exhibit sign flips between the even and odd cycles, leading to a sub-harmonic Fourier response reminiscent of DTC.

While strong Markovian dephasing can indeed result in a ν = 1/2 sub-harmonic peak, we observe three distinct experimental signatures clearly showing that our observations are not governed by this effect. First, the linewidth, Γ (Eq. 5), of the sub-harmonic peak should be quadratically sensitive to the deviation of θ from π. This is in stark contrast with our experimental observations shown in Fig. 2d, where this linewidth Γ is essentially independent of θ within the DTC phase. Second, according to the dephasing model (Eq. 5), the lifetime of the 3T-periodic DTC is expected to be longer than that of the 2T-periodic DTC due to enhanced dephasing (from a lack of spin-locking) in the bare basis²⁷. However, we observe the exact opposite behavior. Finally, Markovian dephasing requires an effective environment with a relatively fast sub-µs correlation time. This is also inconsistent with our experimental observations. In particular, we performed Rabi oscillation decay measurements with a rotary echo sequence, resulting in a lower bound of 1.5 µs on the Markovian dephasing time T₂. This time scale still includes contributions from static on-site disorder and interactions, and thus the Markovian dephasing rate is, in fact, significantly slower than this. Indeed, we have independently extracted the typical timescales of disorder fluctuations in our system¹⁶, and we find that they are similar (60 µs) to depolarization timescale under spin-locking dynamics. Effects resulting from such slow dephasing should be completely negligible within a typical Floquet period. Thus, we conclude that fast dephasing alone does not explain the observed DTC order.

At the same time, in the time crystalline order description based on interacting spin models^8–11, the time crystalline order is expected to be robust and is not expected to exhibit any functional dependence on the angle θ, in complete agreement with experimental observations. This is also the case for our self-consistent description. We finally note that the interplay between coherent interactions and dephasing could potentially play a role in stabilizing DTC order at longer interaction times. Detailed understanding of such mechanisms require further theoretical investigation.

G. Derivation of Effective Hamiltonian for ℤ₃ symmetry breaking phase

Using microwave driving resonant with two different transitions (Fig. 4a), we realize dynamics involving all three spin states and observe a robust 3T-periodic time-crystalline order. The unitary matrix of the time evolution during the fundamental period T is given as

$$U_3=e^{-i{\Sigma }_i({\sigma }_{-1,0}^i+{\sigma }_{0,-1}^i)\theta /2}{e}^{-i{\Sigma }_i({\sigma }_{+1,0}^i+{\sigma }_{0,+1}^i)\theta /2}{e}^{-i{H}_2\tau },$$ (6)

where ${\sigma }_{a,b}^i\equiv |m_s=a\rangle \langle m_s=b|$ for spin-i and H₂ = H_dis + H_int is the effective Hamiltonian of NV centers for all three spin states including on-site disorder potentials $H_{\text{dis}}={\displaystyle {\sum }_i{\Delta }_i^{+}{\sigma }_{+1,+1}^i}+{\Delta }_i^{-}{\sigma }_{-1,-1}^i$and dipolar interactions for spin-1 particles¹⁶

$$H_{\text{int}}={\displaystyle \sum _{ij}\frac{J_{ij}}{r_{ij}^3}}\left[-\frac{{\sigma }_{+1,0}^i{\sigma }_{0,+1}^j+{\sigma }_{-1,0}^i{\sigma }_{0,-1}^j+h.c.}{2}+({\sigma }_{+1,+1}^i-{\sigma }_{-1,-1}^i)({\sigma }_{+1,+1}^j-{\sigma }_{-1,-1}^j)\right].$$ (7)

We note that this Hamiltonian is obtained in the rotating frame under the secular approximation. The Hamiltonian H₂ conserves the total population in any of the three spin states, ${𝒫}_a={\displaystyle {\sum }_i{\sigma }_{aa}^i}$ with a ∈ {0,±1}. If each microwave pulse realizes a π-pulse (θ = π), their combination results in a cyclic transition $R_3^{\pi }:|m_s=+1\rangle \mapsto -|m_s=-1\rangle \mapsto i|m_s=0\rangle \mapsto |m_s=+1\rangle ,$ and the population 𝓟_a becomes periodic over three periods. Under such evolution, the effective Hamiltonian over three periods is given by $D_3^{\pi }=[H_2+{(R_3^{\pi })}^{-1}{H}_2{R}_3^{\pi }+{(R_3^{\pi })}^{-2}{H}_2{(R_3^{\pi })}^2]/3,$ in which on-site disorders average to zero, and the interactions are modified to

$$D_3^{\pi }={\displaystyle \sum _{ij}\frac{J_{ij}}{r_{ij}^3}}\left[{\displaystyle \sum _a{\sigma }_{aa}^i{\sigma }_{aa}^j}-\frac{1}{3}{\displaystyle \sum _{a\ne b}{\sigma }_{ab}^i{\sigma }_{ba}^j}\right].$$ (8)

The first term describes Ising-like interactions that shift energy when any pair of spins are in the same state, and the second term corresponds to spin-exchange interactions that allow polarization transport. These additional exchange interactions may lead to a shorter DTC lifetime as compared to the ν = 1/2 DTC. For small perturbations in the microwave pulse angle ϵ = θ − π, the effective dynamics, to leading order, are governed by

$$D_3^{\pi +ϵ}\approx D_3^{\pi }+\frac{ϵ}{3\tau }{\displaystyle \sum _j({\sigma }_{+1,0}^j+{\sigma }_{-1,0}^j+i{\sigma }_{+1,-1}^j+h.c.}),$$ (9)

which explicitly breaks the conservation laws for 𝓟_a.

Extended Data

Extended Data Figure 1. Effect of rotary echo sequence.

a Experimental sequence: during the interaction interval τ₁, the phase of the microwave driving along x̂ is inverted after τ₁/2. b Comparison of time traces of P(nT) in the presence (left) and absence (right) of an x̂/-x̂ rotary echo sequence at similar τ₁ and θ (left: τ₁ = 379 ns, θ = 0.979π; right: τ₁ = 384 ns, θ = 0.974π). The rotary echo leads to more pronounced 2T-periodic oscillations at long time. Microwave frequencies used in the rotary echo sequence: Ω_x = 2π × 52.9 MHz, Ω_y = 2π × 42.3 MHz.