Effects of Visual Feedback and Memory on Unintentional Drifts in Performance During Finger Pressing Tasks

Abstract

This study tested two hypotheses on the nature of unintentional force drifts elicited by removing visual feedback during accurate force production tasks. The role of working memory (memory hypothesis) was explored in tasks with continuous force production, intermittent force production, and rest intervals over the same time interval. The assumption of unintentional drifts in referent coordinate for the fingertips was tested using manipulations of visual feedback: Young healthy subjects performed accurate steady-state force production tasks by pressing with the two index fingers on individual force sensors with visual feedback on the total force, sharing ratio, both, or none. Predictions based on the memory hypothesis have been falsified. In particular, we observed consistent force drifts to lower force values during continuous force production trials only. No force drift or drifts to higher forces were observed during intermittent force production trials and following rest intervals. The hypotheses based on the idea of drifts in referent finger coordinates have been confirmed. In particular, we observed superposition of two drift processes: A drift of total force to lower magnitudes and a drift of the sharing ratio to 50:50. When visual feedback on total force only was provided, the two finger forces showed drifts in opposite directions. We interpret the findings as evidence for the control of motor actions with changes in referent coordinates for participating effectors. Unintentional drifts in performance are viewed as natural relaxation processes in the involved systems; their typical time reflects stability in the direction of the drift. The magnitude of the drift was higher in the right (dominant) hand, which is consistent with the dynamic dominance hypothesis.

Introduction

When a person produces an accurate force level in isometric conditions with the help of visual feedback on the force magnitude, removing visual feedback typically leads to a slow drifts of the force toward lower values without the subject being aware of this drift (Slifkin et al. 2000; Vaillancourt and Russell 2002; Shapkova et al. 2008). Several studies invoked the notion of working memory limitations to interpret the unintentional force drift (Slifkin et al. 2000, Vaillancourt and Russell 2002). This hypothesis (we will address it as “the memory hypothesis”) received indirect support in studies of brain electrical and metabolic activity (Vaillancourt et al. 2003; Coombes et al. 2011; Poon et al. 2012) and in a study of patients with Parkinson's disease who are known to display working memory problems (Vaillancourt et al. 2001).

A conceptually different explanation of unintentional force drifts has been suggested recently based on the idea of control with referent coordinates (RC) for salient variables (Zhou et al. 2014; Ambike et al. 2015). Within this approach (reviewed in Latash 2010; Feldman 2015), the neural control of force is associated with setting a value of RC for the effector (e.g., a fingertip); the difference between the fixed actual coordinate (AC) of the fingertip and its RC leads to the force (F) production: F = k(AC−RC), where k is a coefficient called apparent stiffness (Latash and Zatsiorsky 1993). If AC cannot be changed (in isometric conditions), the natural tendency of all physical systems to move to a minimum of potential energy results in a drift of RC (and possibly also of k, Ambike et al. 2016b) toward AC leading to a drop in force. This hypothesis has received support in several recent studies of multi-finger force/moment production tasks (Ambike et al. 2016a,b,c; Parsa et al. 2016a,b).

Most earlier studies reported force drift toward lower magnitudes, except for very low initial force values (Vaillancourt and Russell 2002; Ambike et al. 2015). All these studies explored force production by a single effector. When a certain force magnitude is produced by an abundant set of effectors, there is a solution space (the uncontrolled manifold, UCM, Scholz and Schöner 1999). Subjects typically prefer certain patterns of force sharing (Li et al. 1998) without exploring the whole UCM. This preference has been formalized using the idea of optimization (Terekhov et al. 2010; Park et al. 2010; Parsa et al. 2016b). Based earlier studies (Ambike et al. 2015; Parsa et al. 2016b), we hypothesized that force drift in tasks involving a few effectors would be due to two factors: the aforementioned RC drift leading to a drop in total force (F_TOT) and a drift toward a preferred sharing pattern.

Two types of unintentional drifts in performance, fast (with typical times of 1-2 s) and slow (with typical times of 10 s or more) have been reported. The former were reported in studies with external perturbations (Wilhelm et al. 2013; Zhou et al. 2014; Reschechtko et al. 2014) and with quick purposeful force changes (Ambike et al. 2016a). The latter have been described in all the aforementioned continuous force production studies. The UCM hypothesis assumes that any task by an abundant system of effectors is associated with a UCM (where salient performance variables stay unchanged) and the orthogonal to the UCM space (ORT) where salient performance variables change. Processes within the UCM are expected to show low stability and, correspondingly, long times of natural relaxation. In contrast, processes within ORT are more stable and, correspondingly, faster. So, fast force drifts were expected to originate in ORT while slower drifts – in the UCM. Note that, while UCM and ORT are mathematically orthogonal, this does not mean that they are independent. Hence, drifts in one of the two spaces may be reflected in drifts in the other space. The task of constant F_TOT production by two fingers is associated with the UCM, along which SR changes while F_TOT stays constant, and ORT, along which F_TOT changes. Since all our tasks were steady-state ones, we expected slow drifts only along both UCM and ORT for F_TOT depending on the available feedback.

The main goal of the current study was to compare the two hypotheses, i.e., the memory hypothesis and the RC-based hypothesis, directly in two-finger accurate force production tasks. The following specific hypotheses were tested:

• H1: Based on the memory hypothesis, we predicted that the force drift to lower values would be largest in the rest condition and smallest in the continuous force production condition. This hypothesis is based on the fact that turning visual feedback off leaves the natural somatosensory feedback unchanged; this feedback may be expected to help the subject avoid excessive changes in the produced force. If the memory hypothesis is indeed correct, we expected to see larger force drift when natural somatosensory feedback was also made unavailable, and the subjects had to rely on memory alone to produce the required force level.

• H2: We expected to see both a drift of F_TOT toward lower values and a drift of sharing ratio (SR) toward the 50:50 pattern. This was expected to lead to an unintentional increase in the force produced by the finger with the initially lower share of F_TOT. This hypothesis is based on recent studies in somewhat different experimental conditions documenting force and sharing drifts (Ambike et al. 2015, 2016c; Parsa et al. 2016b). None of those studies documented an increase in the force of a finger with the lower initial share.

• H3: In the condition with visual feedback on F_TOT only (no feedback on SR), we expected no drift in F_TOT but a consistent slow drift in the individual finger forces in opposite directions leading to drift in SR. This predictions follows hypothesis H2 and the idea of control with RC. Indeed, without visual feedback on SR, a drift of SR toward 50:50 was expected. Since F_TOT feedback was present, no change in F_TOT was expected. This naturally leads to the prediction of counter-directional changes in the forces produced by the two fingers.

To test H1, we compared the force drifts in three conditions. First, we used the traditional condition with continuous force production test (continuous force production test). Second, we asked the subjects to rest for a comparable time interval before reproducing the memorized force level (continuous memory task). Third, we interrupted the same time interval with several episodes of rest followed by force production based on memory (intermittent memory task); the brief episodes of force production were expected to remind the subject of the required force level via somatosensory feedback.

Hypotheses H2 and H3 were tested in the continuous force production task when the subjects were required to use both typical (close to 50:50) and atypical patterns of sharing F_TOT between the two fingers. We modified visual feedback and compared the force drift characteristics across conditions with visual feedback on only one of the two main variables (F_TOT or SR) and with no visual feedback on either variable.

Methods

Subjects

Twelve subjects (7 males and 5 females; age 24.6 ± 5.0 years, body mass = 62.5 ± 9.7 kg, body height = 1.71 ± 0.07 m, mean ± standard deviation) were recruited for the study. All subjects were right-handed according to their hand use during writing. The subjects were healthy and free of any neuromuscular disorders or injuries that would interfere with the pressing task. The hand length, measured from the distal wrist crease to the tip of the longest finger, was 18.3 ± 0.6 cm. The hand width, measured at the metacarpal level, was 8.8 ± 0.7 cm. Each subject gave written informed consent form according to the procedures approved by the Pennsylvania State University Institutional Review Board.

Equipment

Two six-component force sensors (Nano-17, ATI Industrial Automation, Apex, NC) were used to measure normal forces generated by the left and right index fingers. The interface surfaces of both sensors were covered with sandpaper (300 grit) to prevent slipping of the fingers. The force sensors were attached to the aluminum panel with their centers separated by 9 cm. The aluminum panel was firmly fixed to the table in front of the subjects. Finger force signals were sampled at 100 Hz using 16-bit AD board (NI PCI-6225, National Instruments, Austin, TX). A customized Lab VIEW program (Lab VIEW 2012, National Instruments, Austin, TX) was used to display a real-time force data, and experimental task on a computer screen (22-inch diagonal, 1920 × 1080 pixels) placed 0.75 m in front of the subject. Force sensors were zeroed before each trial with the fingertips resting on the sensors.

Experimental procedure

Maximal voluntary contraction (MVC) task

Before the main parts of the experiment, we determined the maximum voluntary contraction force (MVC) by asking subjects to press on force sensors with both index fingers as hard as they could for 3 s. The MVC trials were repeated three times, with 30-s rest intervals in-between. The highest force value across the three trials was selected as MVC force. To avoid effects of fatigue, subjects were given 3-min rest after the MVC task.

Main part of the experiment

The subjects sat comfortably at the table in front of the computer monitor. Their forearms rested on the table with the left and right index fingertips placed on the force sensors.

Throughout the three main tasks (see below), subjects performed all trials with both index fingers pressing in a natural fashion to produce two task variables: the total force (F_TOT) and force sharing ratio (SR). The task variables were computed on-line as:

$$F_{\mathit{\text{TOT}}}=F_L+F_R$$ (1)

$$\mathit{\text{SR}}=(F_R/F_{\mathit{\text{TOT}}})•100\%$$ (2)

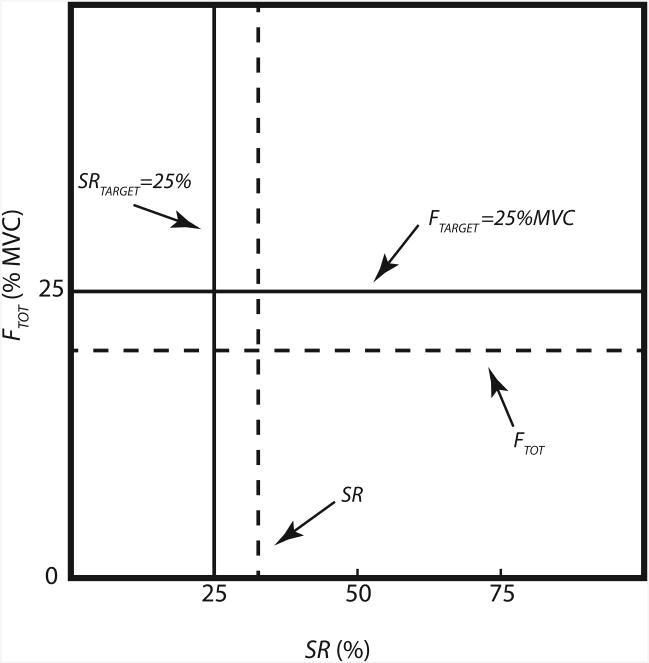
where F_L and F_R are the normal forces of the left and right index fingers, respectively. The subjects were given visual feedback on F_TOT and/or SR values on the monitor screen (Figure 1). A horizontal dashed line moved up and down with the F_TOT magnitude. SR was shown with a vertical dashed line that moved horizontally. For example, equal force sharing by both fingers (SR=50%) corresponded to the position of the vertical dashed line in the middle of the screen, while an increased contribution of the right index force moved the dashed vertical line to the right (SR>50%). The target values of the total force (F_TARGET) and sharing ratio (SR_TARGET) were shown on the screen as fixed solid horizontal and vertical lines, respectively. The force variables, F_TOT and F_TARGET, were expressed as a percentage of MVC force. Each subject performed three different tasks during the experimental session: 1) continuous pressing task; 2) continuous memory task; and 3) intermittent memory task. The order of the three tasks was randomized.

Figure 1.

Organization of the visual feedback on the monitor screen. A horizontal dashed line moved up and down with the total force (F_TOT) magnitude. The force sharing ratio (SR) was shown with a vertical dashed line that moved horizontally. The target values of the total force (F_TARGET) and sharing ratio (SR_TARGET) were shown on the screen as fixed solid horizontal and vertical lines, respectively. In the current example, sharing ratio target was set to 25% (SR₂₅). The force variables, F_TOT and F_TARGET, were normalized to the subject's MVC and expressed as MVC percentage.

Task 1: Continuous pressing task

In the continuous pressing task, two factors were modified: 1) sharing ratio; and 2) visual feedback. SR_TARGET values could be 25%, 50%, and 75% (SR₂₅, SR₅₀, and SR₇₅, respectively). Across all SR conditions, F_TARGET was 25%MVC. This value was selected based on previous studies as leading to consistent force drift toward lower magnitudes and not associated with fatigue (Ambike et al. 2015; Parsa et al. 2016a).

Four different types of visual feedback were used: 1) on both F_TOT and SR (ALL_ON), 2) on F_TOT only (SR_OFF), 3) on SR only (F_OFF), and 4) on neither F_TOT nor SR (ALL_OFF). When visual feedback was not provided for a variable, the associated dashed line was not moving.

In total, there were 12 conditions (three SR × four visual feedback), and each condition was repeated three times in a row. Each trial started with subjects moving the horizontal (F_TOT) and vertical (SR) dashed lines to match the F_TARGET and SR_TARGET solid horizontal and vertical lines. After reaching the target, the subjects were required to maintain the position of the dashed lines as steady as possible for 6 s. Then, the visual feedback was modified to match one of the four visual feedback conditions. The subjects were instructed to continue producing the same finger forces for the next 24 s. The exact time of the visual feedback change (t₀) was stored for off-line analysis. After each trial, 30-s rest was given. The order of trials was block randomized across the SR_TARGET and visual feedback conditions.

Task 2: Continuous memory task

The same F_TARGET of 25%MVC and three values of SR_TARGET: SR₂₅, SR₅₀, and SR₇₅ were used. At the beginning of each trial, we provided feedback on both F_TOT and SR (ALL_ON) and asked subjects to match and keep SR_TARGET and F_TARGET for 6 s. During this initial phase, subjects were instructed to remember the finger forces they were exerting on force sensors at that time. After the initial 6 s, all visual feedback was turned off (ALL_OFF), and subjects were asked to relax for the next 15 s while keeping their fingertips on the force sensors. Then, the subjects were asked to press on the force sensors for 3 s more and accurately reproduce the memorized finger forces. Each condition was repeated three times with 30-s rest interval. The order of trials was block randomized across the SR_TARGET.

Task 3: Intermittent memory task

The same sharing ratio targets (SR₂₅, SR₅₀, and SR₇₅) and F_TARGET = 25% MVC were used. Similar to the continuous memory task, we provided ALL_ON visual feedback during the first 6 s of the trial and asked subjects to remember the finger forces they were generating. Then, visual feedback was turned off (ALL_OFF) and the subjects were asked to relax for 4 s while keeping the fingertips on the force sensors. After 4 s of rest, subjects pressed for 3 s on the force sensors and tried to accurately reproduce the memorized finger forces. This was again followed by 4 s of rest and 3 s of force production. Subjects were asked to repeat these relaxation/force-matching cycles four times in a row. Each condition was repeated three times with 30-s rest breaks, and the order of trials was block randomized across the SR_TARGET.

Data analysis

The data analysis was performed off-line using a custom Python code (Python 3.0, Python Software Foundation) and run within the interactive IPython integrated development environment (Pérez and Granger 2007). Prior to data analysis, all recorded forces were low-pass filtered at 10 Hz with the fourth-order, zero-lag Butterworth filter. The finger force time series over the three repetitions under the same condition were averaged before further data analysis.

Analysis of effects of visual feedback on task variables (F_TOT and SR)

The temporal changes of the task variables F_TOT and SR were computed from the continuous pressing task, using data recorded from t₀ (time of visual feedback change) till the end of the trial. The temporal changes in the task variables were quantified in two ways. First, the time profiles of F_TOT and SR were fitted with an exponential function:

$$y(t)=a{e}^{-t/\tau }+c$$ (3)

where y is either F_TOT or SR, t is time, τ is the time constant representing the rate of change, and a and c are constants (we selected the exponential fit based on an earlier study, Ambike et al. 2015). The exponential function was fitted to the F_TOT and SR time profiles averaged across subjects for each SR_TARGET and visual feedback condition. The goodness of fit of the exponential functions was estimated with coefficients of determination R².

Second, we computed the difference between the final and initial values of SR and F_TOT. Initial SR and F_TOT values were assumed to be equal to the required F_TARGET and SR_TARGET before time t₀ (i.e., under full visual feedback), while final SR an F_TOT values were estimated as averages over the last 0.5 s of the trial. The resultant differences ΔF_TOT and ΔSR (for F_TOT and SR, respectively) were negative when signals drifted toward lower values.

Analysis of changes in individual finger forces (F_R and F_L)

We also quantified drifts in the right and left finger forces (ΔF_R and ΔF_L, respectively) during the continuous pressing task, computed as the difference between the final and initial values of F_R and F_L. Initial F_R an F_L values were estimated as averages over the 0.5 s window prior to t₀ (i.e., with full visual feedback), while to final F_R and F_L values were estimated as averages over the last 0.5 s of the trial.

Analysis of effects of memory on task variables

In the continuous memory tasks, ΔF_TOT and ΔSR were computed as the difference between the average values over a 0.5-s plateau at the end of the force matching interval and the average values over a 0.5-s window prior to time t₀. In the intermittent memory tasks, the ΔF_TOT and ΔSR were computed as the difference between the average values over a 0.5-s plateau during the last force matching cycle and the average values over a 0.5-s window prior to time t₀.

Statistics

All descriptive statistics are reported in the text and figures as means and standard errors unless stated otherwise.

To address specific hypotheses H1-H2, three-way repeated-measures ANOVAs tested the effects of Visual Conditions (two levels: ALL_OFF and F_OFF for F_TOT, and ALL_OFF and SR_OFF for SR), SR_TARGET (three levels: SR₂₅, SR₅₀, SR₇₅) and Time (two levels: Pre and Post) on ΔF_TOT and ASR in the continuous pressing task. Two-way repeated-measures ANOVAs were used to test the effects of SR_TARGET(three levels: SR₂₅, SR₅₀, SR₇₅) and Time (two levels: Pre and Post) on ΔF_TOT and ASR in the continuous memory and intermittent memory tasks.

To test specific hypothesis H3, we explored the changes in individual finger forces. A three-way repeated-measures ANOVA tested effects of Finger (two levels: F_R and F_L), Visual Conditions (three levels: ALL_OFF, F_OFF and SR_OFF) and SR_TARGET (three levels: SR₂₅, SR₅₀, SR₇₅) in the continuous pressing task, and two three-way ANOVAs with Finger (two levels: F_R and F_L), Time (two levels: Pre and Post) and SR_TARGET (three levels: SR₂₅, SR₅₀, SR₇₅) factors were used in the continuous memory and intermittent memory tasks.

We validated the assumption of sphericity by Mauchly's test. When the assumption was violated, the p -value after correction using Greenhouse-Geisser epsilon is reported instead. Post-hoc tests with Tukey's p -value adjustment for multiple comparisons were run to analyze significant effects. All statistical tests were performed with R (R Core Team 2013, version 3.2.2) software with the significance level set at 0.05.

Results

Overall, subjects were able to successfully finish all the experimental tasks. None of the subjects reported any signs of fatigue or discomfort.

Testing the memory hypothesis (specific hypothesis H1)

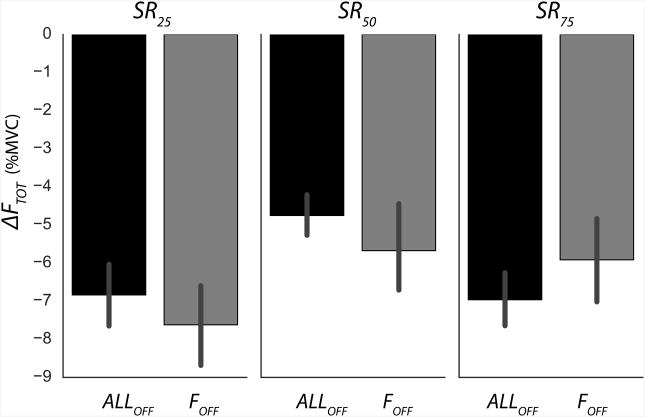
During the continuous pressing task, F_TOT dropped throughout the trial and ΔF_TOT values were consistently negative across all conditions without visual feedback on F_TOT (Figure 2), and the main effect of Time was significant (F_(1,11) = 74.26, p < 0.001). The ΔF_TOT magnitudes were smaller for the SR₅₀ condition (−5.2 ± 0.6, all ΔF values are in percent of MVC) than for the SR₂₅ (−7.2 ± 0.7) and SR₇₅ (−6.4 ± 0.7) conditions, confirmed by the significant interaction SR_TARGET × Time (F_(2,22) = 8.72, p < 0.005). The post-hoc tests revealed that, at the end of the trial, ΔF_TOT were significantly different only between the SR₂₅ and SR₅₀ targets. ΔF_TOT values for ALL_OFF and F_OFF conditions were similar (−6.2 ± 0.4 vs. −6.4 ± 0.6, respectively); no other effects on ΔF_TOT were significant.

Figure 2.

The magnitudes of changes in the total force (ΔF_TOT) averaged across subjects with standard error bars, for different visual feedback conditions and sharing ratio targets (SR_TARGET). Visual feedback conditions were: On F_TOT only (SR_OFF); on SR only (F_OFF); and on neither F_TOT nor SR (ALL_OFF). The sharing ratio targets were 25%, 50%, and 75% (SR₂₅, SR₅₀, and SR₇₅, respectively).

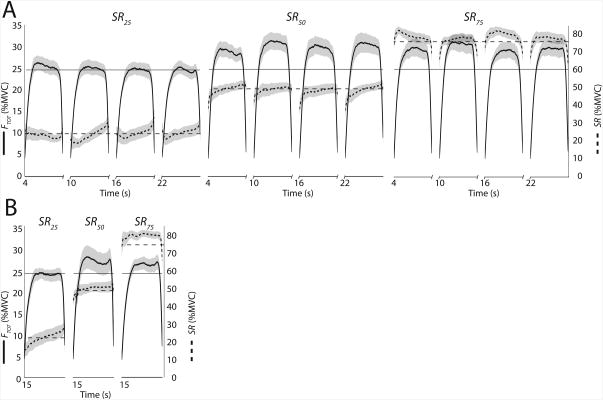
None of the trials with reproduction of finger forces based on memory (continuous memory and intermittent memory tasks) showed a drift of forces toward lower values. Figure 3 shows the F_TOT, and SR time profiles from the intermittent memory (A) and continuous memory (B) tasks, averaged across subjects for each SR_TARGET. Each panel shows the data when the subjects attempted to match the memorized finger forces.

Figure 3.

The sharing ratio (SR, dashed traces) and total force (F_TOT, solid traces) time profiles from the intermittent memory (A) and continuous memory (B) tasks, averaged across subjects with standard error shades, for each SR_TARGET. The sharing ratio targets were 25%, 50%, and 75% (SR₂₅, SR₅₀, and SR₇₅, respectively). Each panel shows the data when the subjects attempted to match the memorized finger forces, when neither F_TOT nor SR feedback was provided. Solid horizontal thin lines represent target total force, while horizontal dashed lines show sharing ratio targets.

In the intermittent memory task, subjects overestimated the required SR targets, i.e. they tended to produce larger percentage of F_TOT by the right finger: ΔSR averaged across the SR_TARGET conditions was 5.7 ± 1.7, with significant effect of Time (F_(1,11) = 8.63; p < 0.01). The amount of SR overshoot was similar for SR₂₅ (4.9 ± 3.8%) and SR₅₀ (5.1 ± 2.7%), and slightly higher for SR₇₅ (7.1 ± 2.7%). The effect of SR_TARGET was not significant (p = 0.83). F_TOT increased in the intermittent memory tasks: ΔF_TOT averaged across the SR_TARGET conditions was 5.2 ± 1.2, and the effect Time was significant (F_(1,11) = 10.49, p < 0.01). ΔF_TOT values were 1.2 ± 1.6, 7.5 ± 2.4, and 6.9 ± 1.8%MVC for SR₂₅, SR₅₀, and SR₇₅, respectively (Time × SR_TARGET interaction was statistically significant; F_(2,22) = 5.97; p < 0.01). Post-hoc tests that ΔF_TOT values in SR₂₅ < SR₅₀, SR₇₅ conditions. For SR₂₅ the effect of Time on ΔF_TOT was not significant.

On average, the individual finger forces increased by 2.9 ± 0.6 %MVC in the intermittent memory task, which was confirmed by the significant effect of Time (F_(1,11) = 13.88; p < 0.01). The amount of force drift for the right finger was somewhat larger than for the left, but this difference was not significant (ΔF_R = 1.8 ± 0.9 and ΔF_L = 1.12 ± 0.7, p = 0.23). Individual finger forces drifted less when the left finger contributed to the task more (0.5 ± 0.8%, 2.1 ± 0.9%, and 1.9 ± 1.1% for SR₂₅, SR₅₀ and SR₇₅, respectively). There was a significant Time × Target × Finger interaction effect. This three-way interaction reflected the fact that, for the left finger, none of the main effects was significant, while for the right finger there were significant Time (F_(1,11) = 6.39; p < 0.05), Target (F_(2,22) = 3.71; p < 0.05), and Time × Target (F_(2,22) = 7.87, p < 0.05) effects. The additional post-hoc test showed that only SR₂₅ significantly differed from SR₅₀ and SR₇₅ during the last force matching cycle.

In the continuous memory tasks, subjects also typically increased the SR values: ΔSR averaged across SR_TARGET was 8.2±1.8, with significant effect of Time (F_(1,11) = 20.18, p < 0.001). The ΔSR values were very similar for SR₂₅ (6.5 ± 3.7) and SR₅₀ (6.1 ± 3.2), and somewhat higher for SR₇₅ (12.1 ± 2.3), but neither the effect of SR_TARGET nor Time × SR_TARGET interaction effect on ΔSR were significant (p = 0.32). Overall, F_TOT was also slightly overestimated in the continuous memory tasks. ΔF_TOT averaged across SR_TARGET was 2.9 ± 1.1, but the effect of Time was not significant (p = 0.07). This overshoot was mostly observed in SR₅₀ (5.3 ± 2.7) and SR₇₅ (3.5 ± 1.5) conditions; the amount of ΔF_TOT in SR₂₅ condition was minimal (0.1 ± 1.3). However, no effects were significant.

In the continuous memory tasks, the average increase in individual finger forces was 1.9 ± 0.5%MVC, and this drift over Time was significant (F_(1,11) = 6.24; p = 0.05). The amount of force drift for the right finger was larger than for the left finger; however, the difference was not significant (ΔF_R = 1.4 ± 0.8 and ΔF_L = 0.5 ± 0.6, p = 0.12). No other significant effects were found.

Drifts of total force and sharing ratio (specific hypothesis H2)

During the tasks with continuous force production, both main task variables, F_TOT and SR, showed drifts after the visual feedback was turned off (ALL_OFF condition). When visual feedback was turned off for one of the task variables only, that variable showed a drift while the other variable (with continuing feedback) stayed unchanged. Typically, F_TOT drifted toward lower magnitudes, while SR drifted toward a 50:50 sharing pattern.

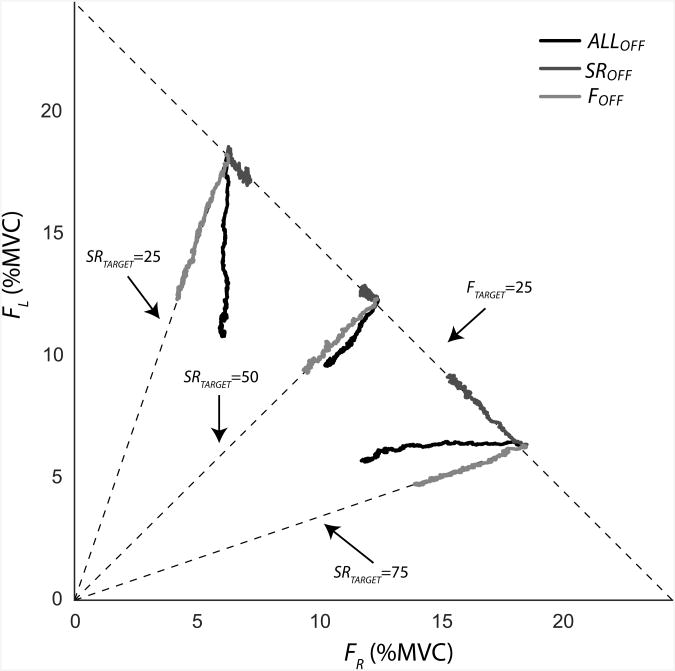
Figure 4 shows F_TOT and SR plotted in the finger force space. Thick traces represent data averaged across subjects for the three SR targets (SR₂₅, SR₅₀, and SR₇₅) and three visual feedback conditions (ALL_OFF, SR_OFF, F_OFF), while the intersections of the dashed lines show the {SR; F_TOT} targets. No error shades are shown to prevent cluttering of the plot. Note that F_TOT consistently drifted toward lower values (toward the origin of coordinates), while the direction of SR drift depended on the initial SR value.

Figure 4.

The total force (F_TOT, dashed line with negative slope) and sharing ratio (SR, dashed lines with positive slopes) represented in the finger force space (F_L and F_R, left and right finger forces, respectively). The solid traces represent data averaged across subjects for the three sharing ratio targets (SR_TARGET: 25%, 50%, and 75%) and three visual feedback conditions: On F_TOT only (SR_OFF); on SR only (F_OFF); and on neither F_TOT nor SR (ALL_OFF). No error shades are shown to prevent cluttering of the plot. Note that F_TOT consistently drifted toward lower values, while the direction of SR drift depended on the initial SR value.

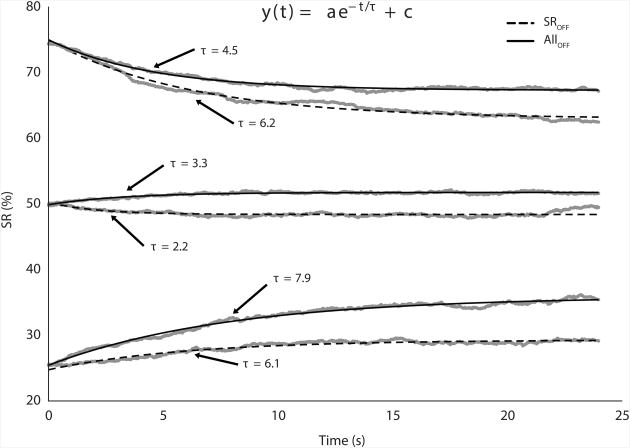
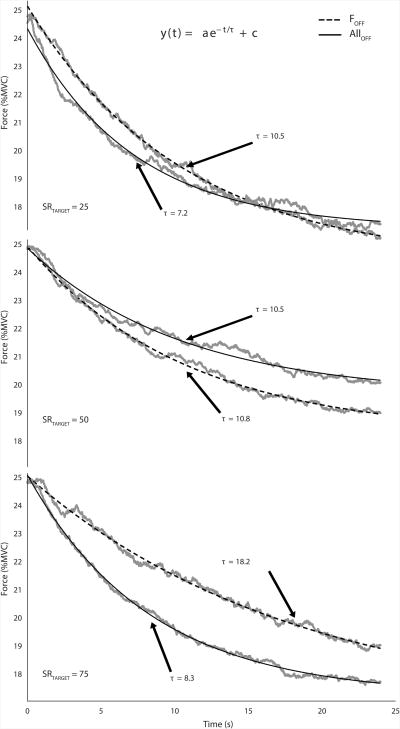
Figures 5 and 6 show the time profiles of SR and F_TOT, averaged across subjects, with the drifts approximated using exponential functions. The median R² values for F_TOT and SR fits were 0.99 and 0.96, respectively. The fitted SR time profiles show that the drifts were more pronounced for the SR₂₅ and SR₇₅ targets (Figure 5, bottom and top pairs of traces). In contrast, under the SR₅₀ condition, the SR drift was relatively small and inconsistent across subjects (Figure 5, middle traces). The time constants for the fitted SR drifts under the SR₂₅ and SR₇₅ conditions ranged between 4.5 and 8 s. The F_TOT time profiles showed consistent, unidirectional drifts toward lower values in both ALL_OFF and F_OFF conditions. The time constant for the fitted F_TOT drifts ranged between 7 and 18 s. This descriptive analysis was performed on averaged across subjects' data only because of the high within-subject variability of the drift time profiles.

Figure 5.

Time profiles of the force sharing ratio (SR) during the pressing task, averaged across subjects (gray traces), with the drifts approximated using exponential functions (black lines). Dashed lines showed data for the visual feedback on the total force only (SR_OFF), and solid lines show data from the conditions with visual feedback on neither total force nor sharing ratio (ALL_OFF).

Figure 6.

Time profiles of the total force (F_TOT) during the pressing task, averaged across subjects (gray traces), with the drifts approximated using exponential functions (black lines). Dashed lines showed data for the visual feedback on the sharing ratio only (F_OFF), and solid lines show data for the conditions with visual feedback on neither total force nor sharing ratio (ALL_OFF). No error shades are shown to prevent cluttering of the plot.

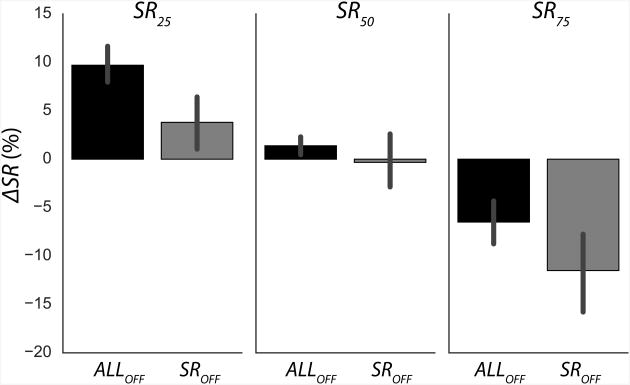
The magnitudes of changes in the two task-related variables (ΔSR and ΔF_TOT) across different visual feedback and SR_TARGET conditions are illustrated in Figures 7 and 8. Typically, ΔSR values were positive for the SR₂₅ condition (6.7 ± 1.76%), negative for the SR₇₅ condition (−8.9 ± 2.4%), and close to zero for the SR₅₀ condition (0.5 ± 1.5%). The main effect of Time on ΔSR was not significant (p = 0.73), but there was a significant SR_TARGET × Time interaction effect (F_(2,22) = 19.4; p < 0.001). Post-hoc tests revealed that only ΔSR for SR₂₅ and SR₅₀ were not significantly different from each other (although close to the significance level, p = 0.057).

Figure 7.

The magnitudes of changes in the sharing ratio (ΔSR), averaged across subjects with standard error bars, for different visual feedback conditions and sharing ratio targets (SR_TARGET). Visual feedback conditions were: On F_TOT only (SR_OFF); on SR only (F_OFF); and on neither F_TOT nor SR (ALL_OFF). The sharing ratio targets were 25%, 50%, and 75% (SR₂₅, SR₅₀, and SR₇₅, respectively).

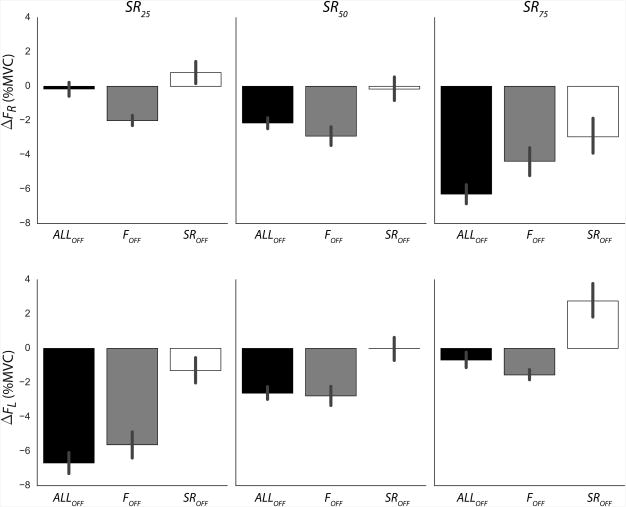
Figure 8.

The magnitudes of drifts of individual right and left finger forces (ΔF_R and ΔF_L), averaged across subjects with standard error bars, for different visual feedback conditions and sharing ratio targets. Visual feedback conditions were: On F_TOT only (SR_OFF); on SR only (F_OFF); and on neither F_TOT nor SR (ALL_OFF). The sharing ratio targets were 25%, 50%, and 75% (SR₂₅, SR₅₀, and SR₇₅, respectively). Note the predominantly negative values of ΔF_R and ΔF_L; note also positive ΔF values for the SR_OFF condition and unequal initial force sharing (SR₂₅ and SR₇₅).

Drifts of individual finger forces (specific hypotheses H2 and H3)

Figure 8 shows the magnitudes of drifts of individual finger forces (ΔF_R and ΔFL) during the continuous pressing task, averaged across subjects for different visual feedback and SR_TARGET conditions. Overall, there was no significant difference between the left and right finger; however, the finger that contributed more to the task showed larger force decrease. Individual finger forces drifted towards lower values when visual feedback on F_TOT was not provided (i.e., ALL_OFF and F_OFF conditions). In contrast, drifts toward higher forces could be observed in the SR_OFF condition with uneven initial sharing. This was reflected in a significant main effect of Visual Feedback on force drifts (F_(2,22) = 36.93, p < 0.001); post-hoc tests confirmed that SR_OFF differed from both ALL_OFF and F_OFF conditions. In particular, when a task started with the right finger contributing more to F_TOT (SR₇₅), F_R decreased over time in the SR_OFF condition (negative ΔF_R values), while F_L increased over time (positive ΔF_L values). This observation was confirmed by a significant Finger × Target interaction (F_{(2, 22)} = 59.95; p < 0.001).

The individual finger forces drifted towards higher values only when a finger generated 25% of F_TOT (e.g., left finger in the SR₇₅ condition) and visual feedback on F_TOT but not SR was provided (SR_OFF condition). The drift of individual finger forces under the SR_OFF condition was minimal when the trials started with equal contribution to the task (SR₅₀). However, the Visual Feedback × Target interaction was under the level of statistical significance (p = 0.08).

Discussion

Results of our study speak against the memory hypothesis (Slifkin et al. 2000; Vaillancourt and Russell 2002) and in favor of the hypothesis assuming that unintentional force drifts represent relaxation processes in the physical-physiological system involved in force production (Ambike et al. 2015; reviewed in Latash 2016a,b). In particular, specific hypothesis H1 predicted, based on the memory hypothesis, that the force drift to lower force magnitudes would be smallest in the continuous pressing task, larger in the intermittent memory task, and largest in the continuous memory task. These predictions were falsified. Indeed, the continuous pressing task was the only one to show a consistent drop in the pressing force, while the other two tasks showed no force change or an increase in the force. Two other specific hypotheses were based on the idea of control with referent spatial coordinates (RCs, Latash 2010; Feldman 2015). Both have been confirmed in the experiment. In particular, we saw drifts of total force (F_TOT) toward lower magnitudes and of the sharing ratio (SR) toward 50:50 across conditions as well as an increase in the force produced by the finger with the initially lower share of F_TOT under visual feedback on F_TOT only (as predicted by specific hypothesis H2). In the condition with visual feedback on F_TOT only (no feedback on SR), we observed the most unusual pattern involving balanced counter-directional slow drifts in the individual finger forces that kept F_TOT constant (specific hypothesis H3). Note that all these changes happened despite the instruction to the subjects to keep both finger forces unchanged over the duration of each trial. Further in this section, we discuss implications of these observations for such topics as the neural control of the action with shifts in RCs, optimization in actions by abundant systems, the role of sensory feedback in avoiding force drifts, and the origins of unintentional drifts in performance.

Physical approach to the neural control of movement

Our approach to the neural control of movement is based on the idea of control with parameters of appropriate laws of nature (Latash 2010, 2016, 2017; Feldman 2015). Laws of nature (physics) link salient variables with the help of parameters. In classical physics of inanimate systems, it is typically assumed that parameters stay unchanged or change slowly as compared to typical changes in the variables. As a result, control of an inanimate system, for example of a robot or a prosthetic device, is typically built on prescribing patterns of peripheral variables with the help of powerful actuators and quick-acting feedback loops. In contrast, during voluntary movements, changes in parameters produce changes in variables linked by the corresponding laws of nature. Changes in parameters may be very fast, commonly faster than the induced changes in variables (Latash and Gottlieb 1991; Latash 1992).

Within the idea of hierarchical control of movements, parameters at different hierarchical levels are associated with spatial RCs (Latash 2010, 2016b; Feldman 2015). At the top, task-related, level, a low-dimensional set of RCs for the end-effector or the whole-body are defined. These are later mapped on RCs for individual effectors such as limbs, digits, joints, and muscles. For example, at the joint level, RCs are equivalent to the reciprocal and coactivation commands ({r, c} commands) as defined within the equilibrium-point hypothesis (Feldman 1966, 1980, 1986). At the muscle level, RC is equivalent to the threshold of the tonic stretch reflex (λ). The physiological meaning of RCs at all levels is subthreshold depolarization of appropriate neuronal pools (reviewed in Feldman 2015).

The described hierarchical scheme involves a sequence of few-to-many mappings: It starts with a relatively low-dimensional RC at the task level, which ultimately leads to a high-dimensional set of λs for the involved muscles. According to the principle of abundance (Gelfand and Latash 1998; Latash 2012), these transformations do not pose computational problems for the central nervous system (they are not problems of motor redundancy, cf. Bernstein 1967). Instead, they allow synergic organizations that ensure desired stability properties of salient performance variables (reviewed in Latash 2008).

Within the described hierarchical scheme of control with RCs, three types of movement are possible. First, involuntary movements happen when no change in the RC at the task level takes place, and movement is caused by changes in the external force field. Second, if RC is changed intentionally by the actor, an intentional voluntary movement takes place. There is also a third class of movements that occur when the subject does not intend to change the RC but such a change happens without the subject's awareness. Such movements have been addressed as voluntary unintentional (reviewed in Latash 2016a). In our experiment, we described such movements at the level of task-related variables (such as total force and share, F_TOT and SR), as well as at the level of individual finger forces (F_R and F_L). While unintentional force drifts have been described in several studies involving a single effector (Slifkin et al. 2000; Vaillancourt and Russell 2002; Shapkova et al. 2008; Ambike et al. 2015), only a handful of recent studies explored unintentional movements within a two-level hierarchical system (Ambike et al. 2015; Parsa 2016a,b). As discussed later, our observations allow drawing important conclusions on the origin of unintentional voluntary movements and the role of visual information in unintentional force drifts.

Optimization in abundant systems

Two characteristics of abundant mappings have been commonly used, average sharing and covariation (Li et al. 1998; reviewed in Latash 2008). The former characteristic reflects average contributions of individual elements to the task. The issue of sharing a task across a set of elements has been commonly addressed using optimization approaches (reviewed in Prilutsky and Zatsiorsky 2002). The main idea of optimization is that the neural controller facilitates solutions to apparently redundant problems that minimize a cost function. Typically, cost functions are unknown and guessed by researchers based on intuitive considerations and experience (for an example of using an analytical approach to compute a cost function based on experimental observation see Terekhov et al. 2010). In our experiment, sharing of F_TOT between the two fingers was prescribed. As a result, the task could be viewed as marginally redundant (Latash et al. 2001). This term means that the number of elements is equal to the number of constraints so that formally a single solution exists satisfying the constraints. However, each constraint is not absolute (allowing for a margin of error), and, as a result, an infinite number of solutions are available that solve the problem within some acceptable level of accuracy.

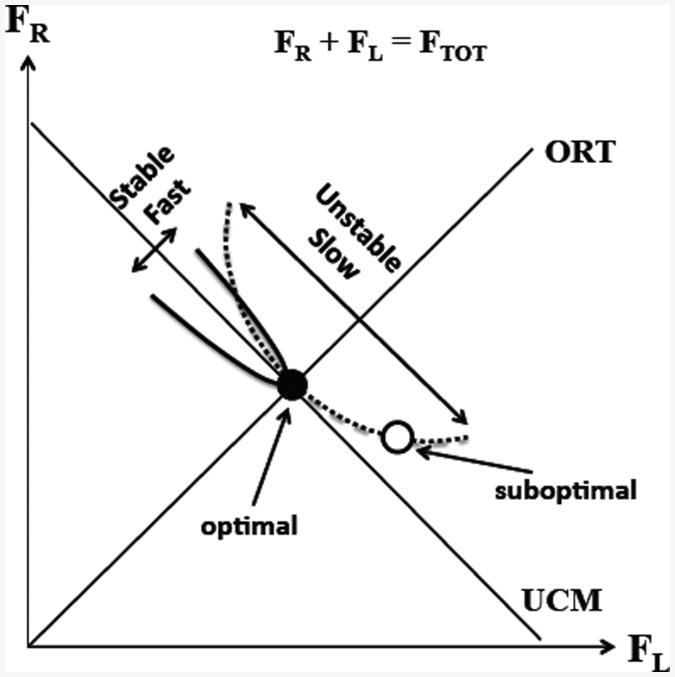
Figure 9 illustrates the task in the space of two finger forces. The dashed slanted line is the uncontrolled manifold (UCM; Scholz and Schöner 1999) for a given F_TOT magnitude. The idea of optimization assumes that there is a preferred point on the UCM corresponding to a minimum of some cost function. A number of studies with accurate two-finger force production have shown that, across repetitive trials, the data show substantial scatter and form an ellipse elongated along the UCM (Latash et al. 2001; reviewed in Latash 2008). This implies that the cost function imposes a relatively mild constraint on the sharing, so that solutions along the UCM can vary across trials more than the F_TOT variation. This is illustrated in Fig. 9 with a relatively shallow potential field providing for stability of the preferred sharing. If a person is asked to perform the task with a sharing different from the preferred one, the natural tendency of all physical systems to move toward states with lower potential energy is expected to cause an unintentional drift along the UCM leading to a drop in the force of one of the fingers and an increase in the force of the other finger (see Figures 4 and 8). This process is expected to be relatively slow corresponding to the low stability of the preferred sharing along the UCM. We observed such a drift of SR in our experiment leading to the predicted pattern: A drop in the force of one of the fingers accompanied by an increase in the force of the other finger. These observations provide direct evidence in favor of the existence of an optimal sharing magnitude, consistent across trials and characterized by relatively low stability.

Figure 9.

An illustration of constant total force (F_TOT) production task in the space of two finger forces, F_R and F_L. The slanted line with a negative slope is the uncontrolled manifold (UCM) for a given F_TOT magnitude. A preferred solution (black point) on the UCM corresponds to a minimum of a cost function. Other solutions (e.g., open circle) deviate from the optimal one and lead to a slow drift toward the optimal solution. The plot shows a relatively shallow potential field along the UCM providing for low stability of the preferred sharing and slow drift processes. The orthogonal direction (ORT) is characterized by high stability (steep potential field) and fast processes.

Origins of unintentional drifts in performance

One of the goals of our experiment was to test the memory hypothesis of the unintentional force drift phenomenon. This hypothesis has been supported in a number of physiological studies (Vaillancourt et al. 2003; Coombes et al. 2011; Poon et al. 2012). They are also compatible with animal brain studies (Goldman-Rakic 1988; Selemon and Goldman-Rakic 1988). Our results tend to speak against this hypothesis (see in more detail below). This evidence, however, cannot be viewed as conclusive, primarily because “memory” is not well defined. For example, an unintentional drift of a parameter within a control system (such as RC) may be interpreted as the controller forgetting the required magnitude of that parameter. Such a definition of memory, in our opinion, would be too broad. For example, it would allow invoking memory when a hot teapot cools down.

Earlier arguments against the memory hypothesis (Ambike et al. 2015) included a claim that, if a magnitude of a variable is forgotten, both lower and higher magnitudes may be expected with about equal chances. This was shown to be false: Consistent unidirectional force drifts have been reported in several studies with only a few examples of force increase when the initial force value was very low. Those atypical observations have been interpreted as resulting from a completely different mechanism, properties of slow-adapting sensory receptors (Ambike et al. 2015). In our experiment, drifts of finger force to higher values were observed in specific conditions when the initial force values were not very low. These observations suggest that the unintentional force drifts reflect an interaction of several factors within the physical (physiological) system involved in action production. Here we offer a comprehensive interpretation of the observed phenomena.

Within the scheme of control with RCs, producing force by an effector is viewed as a consequence of a difference between RC and the actual effector coordinate (AC) scaled with an apparent stiffness coefficient, k: F = k(RC − AC). If the effector is free to move, AC will move to RC, where the system would reach a state of minimal potential energy. This direct coupling between RC and AC is expected to be associated with relatively fast processes with time delays typical of conduction and electromechanical delays (on the order of 0.1 s). In earlier studies (Zhou et al. 2014, 2015; Ambike et al. 2015), we hypothesized an additional mechanism, termed RC-back-coupling, involving motion of RC toward AC, which also contributes to a drop in the difference (RC − AC). Experimental data, so far, suggest that RC-back-coupling is much slower compared to direct coupling with characteristic times ranging from 1-2 s to 10-20 s (Zhou et al. 2014; Reschechtko et al. 2014; Ambike et al. 2015, 2016c).

This scheme is applicable to several effectors producing force in parallel assuming that, at the task level, RC_TASK is defined. Further, RC_TASK is mapped on RCs for the individual effectors. This mapping is expected to be abundant unless additional constraints are introduced. In our experiment, the mapping RC_TASK => {RC_R, RC_L} was marginally abundant given the prescribed sharing of the total force; this mapping led to only very small deviations of F_TOT and SR from the task values translating into small deviations from the required combinations of F_R and F_L. However, as soon as one of the salient feedbacks was turned off, one of the constraints was lifted, and we observed consistent finger force drifts constrained by the remaining visual feedback. Turning visual feedback on F_TOT off led to predictable consequences, a drift of F_TOT (and also of F_R and F_L) to lower magnitudes (as in Vaillancourt and Russell 2002; Ambike et al. 2015). This phenomenon fits the described scheme based on RC-back-coupling. Turning visual feedback on SR off, however, led to less predictable results. The subjects showed drifts of SR toward more equal sharing patterns (in the direction of 50:50; cf. Parsa et al. 2016b). If F_TOT feedback was available, no visible drift in F_TOT took place leading to counter-directional changes in F_R and F_L caused by the SR drift. We interpret these results as a consequence of a complementary mechanism to RC-back-coupling: A tendency of an abundant system to drift toward a preferred (optimal) sharing pattern. Such a tendency may be viewed analogous to minimization of potential energy, although the role of potential field is played by a cost function, which may not have a comparably clear physical interpretation (illustrated as the shallow potential field along the UCM in Fig. 9). Turning both feedbacks off produced a superposition of the two effects (see Figure 4). Overall, at the level of individual fingers, force drifts could be seen in different directions depending on the available feedback. We do not see how these results could be interpreted within the memory hypothesis while they seem to be a natural consequence of the idea of control with RCs.

Role of salient sensory information

Why did the force drifts disappear (or even reverse the sign!) in our memory trials? We believe that two major factors defined these behaviors. The first is salient sensory information used to set the task. In our case, the tasks were set using visual information, and this factor could diminish potential role of somatosensory information in informing subjects that they produced major errors in the required force values. The second in the idea of RC re-setting, which requires a more detailed explanation.

The idea of RC-back-coupling assumes that RC drifts happen at all times as long as RC differs from AC. The effects of these drifts are corrected if adequate sensory information is available. Large effects can be seen if relevant sensory information is unavailable. Crucial role of sensory information for stability of motor actions has been known for many years since the old observations of motor problems in patients with tabes dorsalis (Mauritz and Dietz 1980) as well as those with advanced stages of diabetes (Lord et al. 1993; Van Deursen and Simoneau 1999) and large-fiber peripheral neuropathy (Sanes et al. 1984; Tunik et al. 2003). In all those cases, performance of even relatively simple tasks is possible only under continuous visual control. Note that the hypothesized mechanism of the effects of RC-back-coupling is independent of potential effects of memory. Its effects are expected even if the subject remembers the required force very well. When the subjects relaxed during our memory tests, RC = AC, and no RC drift was expected leading to no major force errors, as observed in the experiments. The brief episodes of force production in the intermittent memory test were short enough not to produce visible force drifts by themselves (recall that those drifts were relatively slow). During the relaxation phases, RC was reset based on memory without major mistakes.

The relatively small but significant force increase after episodes of inaction remains so far unexplained. It is possible that peripheral factors such as properties of pressure-sensitive receptors (cf. Iggo and Muir 1969) and muscle mechanics (cf. De Ruiter et al. 1998) could play a role. Note that there could be two strategies for reproducing force: Reproducing RC based on memory or attending to sensory information and adjusting RC to match the memorized perception of force. The former strategy is not expected to lead to force change unless there are problems with memory and/or changes in muscle mechanics. Given the consistent force change to higher magnitudes, in contrast to all the earlier studies, we feel reluctant invoking the memory hypothesis for this phenomenon. Muscle mechanics is complex and is known to show history effects including hysteresis (Zatsiorsky and Prilutsky 2012). So, its contribution to the force errors is possible.

Another finding, however, suggests that there may be one more factor related to hand dominance that defined the force increase characteristics. Namely, the force increase was consistently larger when the right hand produced higher percentage of F_TOT (Figure 3). For the SR₇₅ condition, i.e., when the right hand produced higher proportion of F_TOT, there was a trend for SR to overshoot the initial value. This trend was much smaller or not seen in the SR₂₅ condition. These observations are compatible with the idea that the non-dominant hand has an advantage in performing steady-state tasks that require high stability (such as holding a nail when the right hand moves the hammer). This idea has been developed within the dynamic dominance hypothesis (Sainburg 2002, 2005) and received support in a few recent studies of multi-finger synergies stabilizing total force during pressing tasks (Park et al. 2012; Parsa et al. 2016a,b).

Concluding Comments

The ideas of control with RC and RC-back-coupling offer a rich framework for analysis of both intentional and unintentional actions. We see no other hypothesis able to account for the data presented in this study (unless, of course, one assumes that the brain purposefully pre-computes and generates signals leading to erroneous forces with consistent deviations from the desired magnitudes.) We would like to acknowledge that our analysis was based on a number of simplifications. In particular, we have not considered possible drifts in the apparent stiffness coefficient k. A recent study has shown that the typical slow drift in force in single-finger pressing tasks is associated with a consistent drift in the finger RC while changes in k were variable across subjects (Ambike et al. 2016b). While these results justify focusing attention on RC drifts, still drifts in k remain a possibility to be explored in more detail.