Abstract
Two different bifurcation scenarios of firing patterns with decreasing extracellular calcium concentrations were observed in identical sciatic nerve fibers of a chronic constriction injury (CCI) model when the extracellular 4-aminopyridine concentrations were fixed at two different levels. Both processes proceeded from period-1 bursting to period-1 spiking via complex or simple processes. Multiple typical experimental examples manifested dynamics closely matching those simulated in a recently proposed 4-dimensional model to describe the nonlinear dynamics of the CCI model, which included most cases of the bifurcation scenarios. As the extracellular 4-aminopyridine concentrations is increased, the structure of the bifurcation scenario becomes more complex. The results provide a basic framework for identifying the relationships between different neural firing patterns and different bifurcation scenarios and for revealing the complex nonlinear dynamics of neural firing patterns. The potential roles of the basic bifurcation structures in identifying the information process mechanism are discussed.
Keywords: Bifurcation, Neural firing pattern, Bursting, Spiking, Chronic constriction injury model
Introduction
Neural firing patterns play important roles in the neural coding mechanism and the integrated behavior of a nervous system such as synchronization behaviors (Thomas et al. 1994; Braun et al. 1994; Ivancevic et al. 2009). Identification of nonlinear dynamics in a single neuron has attracted much attention in both experimental and theoretical investigations (Gu et al. 2014; Gu and Pan 2015; Liu et al. 2016; Brette 2008; Xu and Wang 2014; Ma et al. 2015; Lv and Ma 2016). Biological experiments have been performed on axons, somatosensory cortex neurons, cold sensory neurons, Purkinje cells, hypothalamus neurons, sciatic nerve fibers of CCI models(Mandelblat et al. 2001; Braun et al. 2011; Yang et al. 2009), and chronically compressed dorsal root ganglion (CCD) (Xie et al. 2011). In physiology, the neural information is thought to be encoded in the firing frequency. However, the firing frequency of temperature receptor in dogfish first increased and then decreased as temperature increased (Braun et al. 1994). Different firing patterns were observed at different levels of temperature and suggested to encode the temperature. In the CCD model that is also a pathological pain model, changes of firing frequency as well as the firing patterns were observed when riluzole that is a block of the persistent sodium current was used, which means that changes of the neuropathic pain information (Xie et al. 2011). Mathematical models, such as the Hodgkin–Huxley model, the FitzHugh–Nagmo model, the Hindmarsh–Rose (HR) model, and the Chay model have been widely studied to identify the different firing patterns and bifurcations of neural firing patterns (Hindmarsh and Rose 1984; Fan and Holden 1992; Chay 1985; González-Miranda 2012; Innocenti et al. 2007; Duan et al. 2008; Shilnikov and Kolomiets 2008; Innocenti and Genesio 2009; Rech 2011). Many complex or novel nonlinear behaviors related to chaos or bifurcations have been investigated in the theoretical models, which are helpful for the progresses of nonlinear dynamics in neuroscience (González-Miranda 2005, 2012; Barrio and Shilnikov 2011; Barrio et al. 2015, 2014; Zheng and Tonnelier 2009; Yamada and Kashimori 2013; Wei et al. 2014; Lv et al. 2016; Ma and Tang 2015).
As suggested in Braun et al. (1994), the transition of firing patterns may participate the neural information coding. Different transitions or bifurcation scenarios from period-1 bursting to period-1 spiking were simulated in the HR and Chay models; this was thought to be a universal regularity of biological rhythms (Holden and Fan 1992; Fan and Holden 1992, 1993; Fan and Chay 1994; Chay 1985; Chay et al. 1995; Duan and Lu 2006; Barrio and Shilnikov 2011). Recently, these bifurcations have been observed in the biological experiments on the sciatic nerve fibers of a CCI model, with adjustment of extracellular potassium or calcium concentration (Li et al. 2004; Gu 2013b; Gu et al. 2014; Gu and Pan 2015), which provided more information than former investigations, wherein only local parts of the bifurcation scenarios—such as period-doubling to chaos, period-adding bifurcation with chaos, and period-adding bifurcation without chaos in bursting patterns—were reported (Jia et al. 2012; Gu and Chen 2014). If noise was introduced, the period-adding bifurcation without chaos was changed into period-adding bifurcation with stochastic bursting, which was observed in the experiment (Gu et al. 2003, 2014; Yang et al. 2009). The bifurcation structures of neural firing patterns in a two-dimensional parameter space simulated in the HR model and the Chay model,—within which each bifurcation scenario is from period-1 bursting to period-1 spiking,—provide a framework for identifying different firing patterns.
Compared with experimental observations of different bifurcation scenarios in which one parameter was adjusted (Mandelblat et al. 2001; Gu et al. 2003, 2014; Li et al. 2004; Yang et al. 2009; Braun et al. 2011; Jia et al. 2012; Gu and Pan 2015), there are far fewer bifurcation scenarios that involve adjusting two parameters (Wu et al. 2008; Zheng et al. 2009; Gu et al. 2013; Gu 2013a). Of the two bifurcation scenarios from period-1 bursting to period-1 spiking, one manifested a complex process and the other a simple process; these were observed in an identical CCI model as the extracellular calcium concentration ([) decreased and extracellular cesium concentration was fixed at two different levels (Wu et al. 2008). Recently, six cases of two different bifurcation scenarios with decreasing [ were observed in identical CCI models when the extracellular potassium concentrations were fixed at two different levels (Gu 2013a). Most of the experimental bifurcations comprise only a part of the bifurcation scenario from period-1 bursting to period-1 spiking. The basic framework of bifurcation structures in a 2-dimensional parameter space simulated in the theoretical models has not yet been demonstrated in the experimental model.
In the present study, multiple examples of two different bifurcation scenarios with decreasing [ were observed in identical CCI models when the extracellular 4-aminopyridine concentration ([4-AP]) was fixed at two different levels. Different from previous investigation (Gu 2013a), all bifurcation scenarios proceed from period-1 bursting to period-1 spiking via complex or simple processes, and form a basic framework for identifying relationships between different bifurcation scenarios and firing patterns. These bifurcations match those simulated in a recently built four-dimensional model (Gu and Pan 2015) to describe the nonlinear dynamics of the CCI model.
Experimental and theoretical models
Experimental model
An animal model of chronic constriction injury (CCI) to the rat sciatic nerve (Bennett and Xie 1988) created by Bennet and Xie was adopted in the present paper. This model appears to reproduce many features of neuropathic pain disorders, which has been widely used in studies of neuropathic pain (Bennett and Xie 1988; Tal and Eliav 1996). After injury, the sodium, potassium, and calcium ion channels were reassembled at the membranes of axons of the injured site, and was capable of generating various spontaneous neural firing patterns (Tal and Eliav 1996). In a series of previous studies, the CCI model was used to investigate the bifurcations of spontaneous neural firing patterns recorded in myelinated primary afferent axons connected to the injured site (Gu et al. 2003, 2013, 2014; Li et al. 2004; Yang et al. 2006; Wu et al. 2008; Yang et al. 2009; Zheng et al. 2009; Jia et al. 2012; Jia and Gu 2012; Gu and Pan 2015). In this context, the model is used as an experimental neural pacemaker. The University Biomedical Research Ethics Committee approved all experiments.
A surgical operation reported in Bennett and Xie (1988) was performed to produce a neural pacemaker. Adult male Sprague-Dawley rats (150–300 g) were injured using chronic ligatures. After 6–14 days, the injury site was exposed and perfused continuously with 34 C Kerb’s solution in which the control [ was 1.2 mmol/L (mM) and the control extracellular [4-AP] was 0 mM. 4-AP is capable of blocking the potassium channel. The spike trains of spontaneous firing patterns generated in the membrane of the injured site were recorded from the individual fibers ending at the injured site with a Powerlab system (Australia). The sampling frequency was 10.0 kHz. The time intervals between the maximal values of the successive spikes were calculated as interspike interval (ISI) series.
A neural pacemaker often generates period-1 bursting under control conditions. Various bifurcation scenarios of firing patterns beginning from period-1 bursting were observed in the experimental model as [ decreased. In the present study, [ was chosen as the bifurcation parameter and [4-AP] was chosen as the conditional parameter. The experimental procedures were as follows (Zheng et al. 2009): first, [4-AP] was set at 0 mM and [ was adjusted from 1.2 to 0 mM to produce a bifurcation scenario in the experimental neural pacemaker. This was bifurcation scenario 1. Second, [ was readjusted from 0 to 1.2 mM to restore the firing pattern. After at least 10 min of accommodation, [4-AP] was changed to and then set at 0.25 mM. If the firing pattern remained unchanged, then [ was adjusted from 1.2 to 0 mM (during which time [4-AP] remained unchanged) to induce another transition procedure. This was bifurcation scenario 2. Scenarios 1 and 2 took place in otherwise identical pacemakers.
In the present experiment, [ was adjusted by replacing the solution. After the replacement, the dynamics of the membrane of the neural pacemaker changed slowly enough to exhibit a transition procedure, but quickly enough to produce a firing pattern different from that of the initial one within a finite time span. This type of the replacement to induce gradual change has often been employed in the exploration of bifurcation scenarios of neural firing patterns (Mandelblat et al. 2001; Braun et al. 2011; Gu and Pan 2015), restricted by the constraints of the experiments.
Deterministic theoretical model
A recently built four-dimensional neuronal model (Gu and Pan 2015) for describing the complex nonlinear dynamics of the firing patterns observed in the CCI model was adopted in the present paper and was described as follows:
| 1 |
| 2 |
| 3 |
| 4 |
where t is time, V is membrane potential, n is the probability of potassium channel activation, is the dimensionless intracellular calcium ion concentration ([) of the cytosol, and is dimensionless luminal calcium concentration. The , , , and in the right side of Eq. (1) are the current of the mixed Na channel, voltage-dependent K channel, calcium-dependent K channel, and leakage ionic channel, respectively.
Equation (2) describes the changes in the dynamics of n.
The third equation includes four parts. The first part is the rise of [ that is induced by the influx of ions through calcium channels in the plasma membrane; the second part describes the fall in [ that is stimulated by the efflux of intracellular ions; the third part describes the release of luminal to enhance [ through the calcium release channel (CRC); and the last part is the sequestration of intracellular into endoplasmic reticulum (ER) stores, which leads to the decrease of [.
Equation (4) describes the dynamics of . The parameters , , , and , describe the reversal potentials for K, mixed Na, leakage ions, and , respectively. In addition, , , , and are the maximum conductance divided by the membrane capacitance, respectively, and , is the relaxation time of the voltage-gated K channel. describes the rate constant for the efflux of intracellular ions. is the pump activity of in the calcium store. In addition, is the steady-state value of n, and and are the probabilities of activation and inactivation of the mixed channel, respectively.
is described as follows:
| 5 |
where and are the release rate of and the dissociation constant of , respectively.
In this study, mV, 75 mV, mV, pS, pS, pS, , , and is chosen as the conditional parameter, corresponding to [4-AP], and is the bifurcation parameter, corresponding to [. The higher the [4-AP], the lower the value. The lower the [, the lower the value.
Stochastic model
A Gaussian white noise, , is used to simulate the effects of noise in the real nervous system. Adding to the right of Eq. (1) and with Eqs. (2–4) unchanged forms the stochastic model. The statistical properties of are and , where D is the noise intensity, and is the Dirac -function.
Integration method
The deterministic and stochastic four-dimensional models are solved using a Mannella numerical integration method (Mannella and Palleschi 1989) with an integration time step of 0.001 s. An action potential occurs when the voltage increases and crosses a value of −25.0 mV.
Simulation results
Four cases of bifurcation scenarios in the deterministic model
When , different firing patterns are simulated in the 4-dimensional model when different values of are chosen. For example, period-1 bursting, period-2 bursting, bursting with multiple spikes, and period-1 spiking occur when , 153, 76.9, and 25.9 mV, respectively (Fig. 1). As is decreased, a bifurcation scenario from period-1 bursting to period-1 spiking is simulated and proceeds from period-adding bifurcation without chaos (Fig. 2a), which is called case-1 in the present paper. For example, the period-1 bursting is changed into period-2 bursting as is changed from 155.4 to 155.3 mV. The bursting with multiple spikes per burst changes to spiking via a sharp decrease of ISI, which is called “shrinkage” (Gu 2013b), and at last to period-1 spiking.
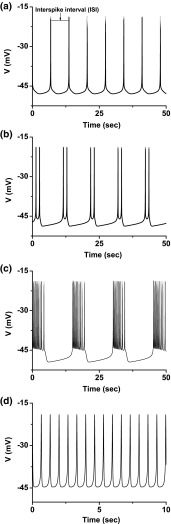
Fig. 1.
Firing patterns in the 4-dimensional model to describe nonlinear dynamics of sciatic nerve fibers of chronic constriction injury model when . a Period-1 bursting when ; b period-2 bursting when ; c bursting with multiple spikes per burst when ; d period-1 spiking when
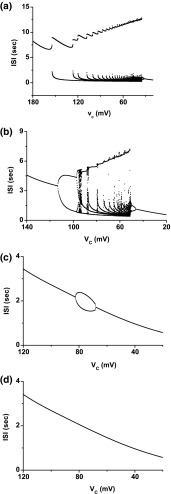
Fig. 2.
Four bifurcation scenarios with decreasing in the 4-dimensional model when different values are chosen for . a Case-1: a bifurcation scenario proceeds from period-adding bifurcation without chaos to bursting with multiple spikes, to spiking via the shrinkage of ISI, and at last to period-1 spiking when ; b Case-2: a bifurcation scenario proceeds from a period-adding bifurcation with chaos or from a period-doubling bifurcation to chaos, to bursting with multiple spikes, to spiking via shrinkage, and at last to period-1 spiking when ; c Case-3: Period-1 bursting changes to period-2 firing, then to period-1 spiking when ; d Case-4: period-1 bursting changes directly to period-1 spiking when
When , a bifurcation scenario different from case-1 is simulated, transitioning from a period-adding bifurcation with chaos or period-doubling bifurcation to chaos, to bursting with multiple spikes, to spiking via “shrinkage”, and at last to period-1 spiking (Fig. 2b), which is named case-2 in the present paper. The chaotic firing patterns may play important roles in two aspects. One is that the chaotic bursting may play roles in detecting external stimulus because of the effect of “critical sensitivity”, as proposed in a previous investigation (Yang et al. 2006). The other is that the firing patterns may encode the neuropathic pain information, as suggested by Xie et al. (2011).
When , a bifurcation scenario with a simple process from period-1 bursting to period-2 firing and to period-1 spiking is simulated (Fig. 2c), which is called case-3. No chaotic firing patterns are found within this bifurcation scenario.
When , period-1 bursting changes to period-1 spiking directly with decreasing , labeled case-4 (Fig. 2d).
For each of the four cases of the bifurcation scenario, the firing frequency increases with decreasing . As suggested by Braun et al. (1994) and Xie et al. (2011), different firing patterns lying in bifurcation scenarios may encode different neuropathic pain information, which should be further studied in future.
Four cases of bifurcation scenarios in the stochastic model
When noise is introduced, the period-adding bifurcation without chaos of case-1 bifurcation scenario changes into period-adding bifurcation with stochastic bursting, as shown in Fig. 3a, which has been reported in many previous studies (Gu et al. 2003; Yang et al. 2009; Gu and Chen 2014; Gu and Pan 2015). The stochastic bursting is induced by noise near the bifurcation point. For example, period-1 bursting () in the deterministic model is changed into stochastic bursting in the stochastic model (), as shown in Fig. 4b. The behavior of the stochastic bursting exhibits stochastic transitions between period-1 burst and period-2 burst. Such a stochastic firing pattern may play important roles in enhancing signal to noise ratio, as proposed in the previous investigation (Gu et al. 2003). However, the behavior far from the bifurcation point remains unchanged in the the stochastic model. For example, the behavior is still period-1 bursting for and period-2 bursting for , as shown in Fig. 4a, b, respectively. In the stochastic model, the process of period-adding bifurcation with a lower number spikes per burst remains unchanged and periodic bursting with a lower period number can be identified, as shown in Fig. 3a. However, the periodic bursting pattern with a larger period number changes to a nonperiodic bursting pattern which is a mixture of multiple bursting patterns. In addition, the firing patterns near the “shrinkage” are disturbed by the noise to a certain extent, however, the “shrinkage” phenomenon remains. Above all, although noise disturbed the ISIs or firing patterns, the basic process of case-1 bifurcation scenario remains unchanged in the stochastic model. More details about the stochastic dynamics of the case-1 bifurcation scenario were reported in Gu and Pan (2015). We do not present more details about the stochastic bursting and period-adding bifurcation scenario with stochastic bursting to avoid repetition.
Fig. 3.
Firing patterns in the stochastic model with and . a Period-1 bursting when ; b stochastic bursting lying between period-1 bursting and period-2 bursting when ; c period-2 bursting when
Fig. 4.
Four bifurcation scenarios with decreasing in the 4-dimensional stochastic model when different values are chosen for . a Case-1: the bifurcation scenario when and ; b Case-2: the bifurcation scenario when and ; c Case-3: period-1 bursting changes to period-2 firing, then to period-1 spiking when and ; d Case-4: period-1 bursting changes directly to period-1 spiking when and
For case-2, although the ISIs, especially the firing patterns near the shrinkage, are disturbed by the noise, the basic process remains unchanged in the stochastic model, as shown in Fig. 3b (). More details of the bifurcation scenario simulated in the stochastic model were reported in Gu and Pan (2015) and are not present here to avoid repetition.
In the stochastic model, the basic process of the case-3 and case-4 bifurcation scenarios remains unchanged and the ISIs are disturbed by the noise, as shown in Fig. 3c, d (). It shows that the influence of noise on the bifurcation scenario with simple structures is small.
Framework of bifurcation scenarios in both deterministic and stochastic models
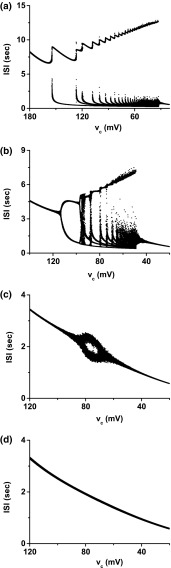
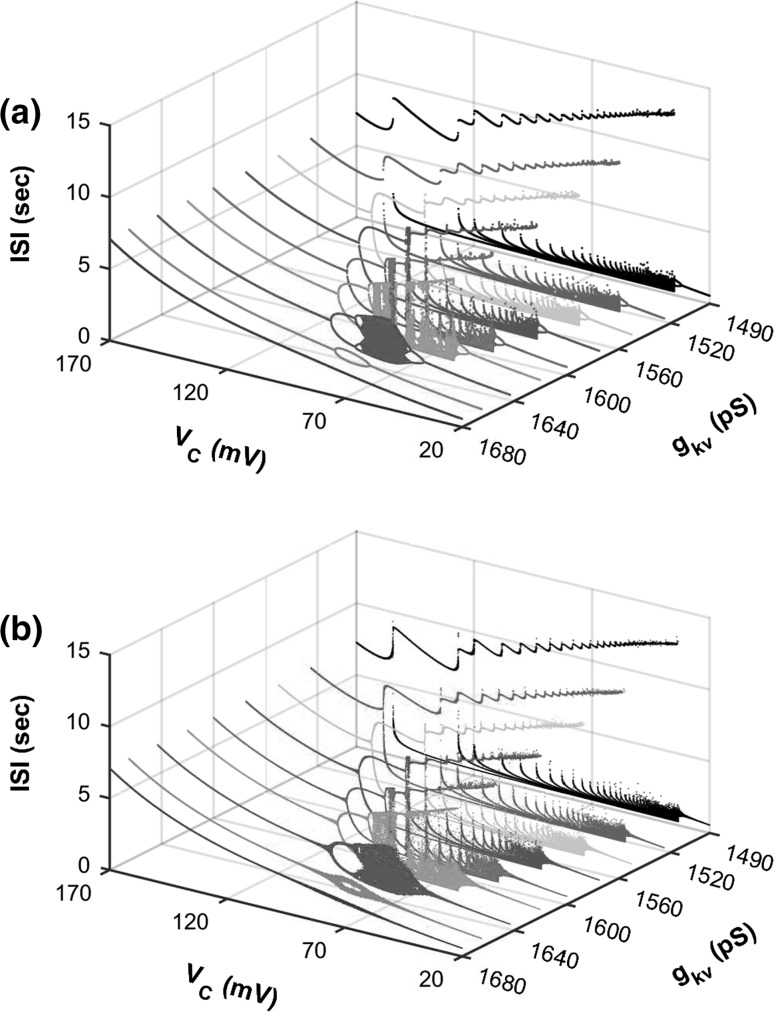
When different values are chosen for , different bifurcation scenarios with decreasing are simulated in the 4-dimensional model (Fig. 5a), which forms a framework for identifying relationships between different firing patterns and different bifurcation scenarios. In the stochastic model, except the bifurcation points and firing patterns with multiple spikes per burst of case-1, the basic structure of the framework changes little, although the ISIs are disturbed by noise, as shown in Fig. 5b (). As can be seen in Fig. 5a, b, the value increases from case-1 to case-4, or from relatively simple to complex bifurcation scenarios. It can be inferred that if the potassium channel is blocked, the bifurcation scenario changes from a higher number to a lower number; in other words, the bifurcation process scenario becomes more complex.
Fig. 5.
Bifurcation structures of neural firing patterns in a 2-dimensional parameter space (, ). a Deterministic model; b stochastic model with
Experimental results
Overview of the experimental results
Fixing [4-AP] at two different levels and adjusting [ from 1.2 to 0 mM at each [4-AP] level produced qualitatively different bifurcation scenarios, bifurcation scenarios 1 and 2. These two scenarios were observed in 326 neural pacemakers. Most bifurcations were just a part of the bifurcation scenario from period-1 bursting to period-1 spiking. In the present study, six examples of two different bifurcation scenarios from period-1 bursting to period-1 spiking observed in identical CCI models are provided as representative results. The detailed processes of these bifurcation scenarios are explained as follows.
Six examples
Example 1
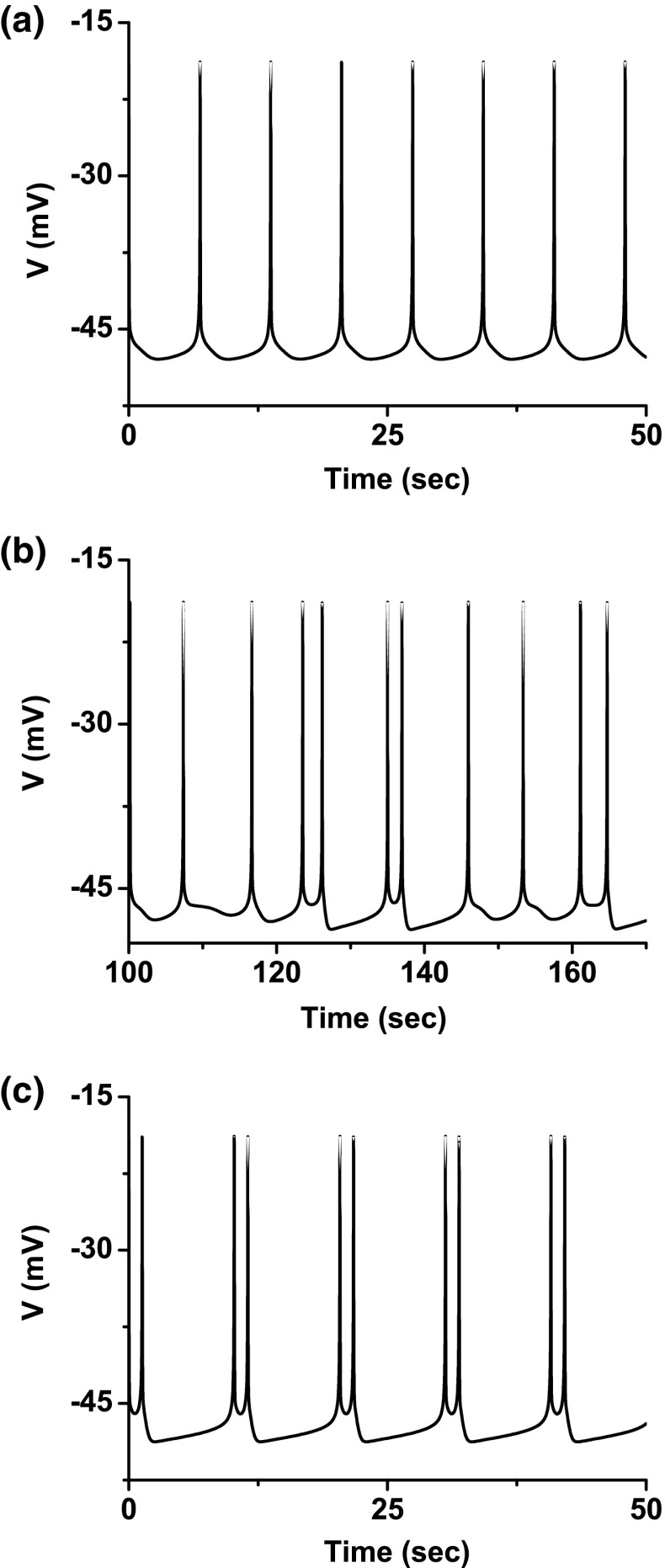
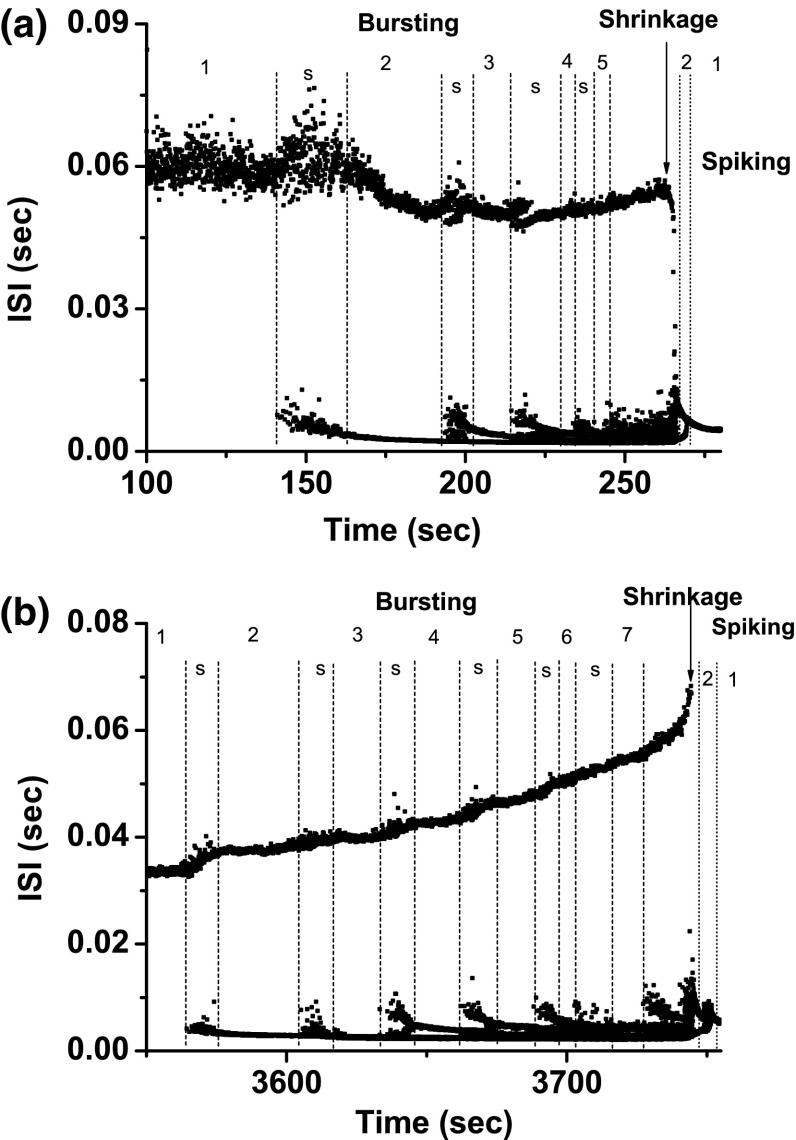
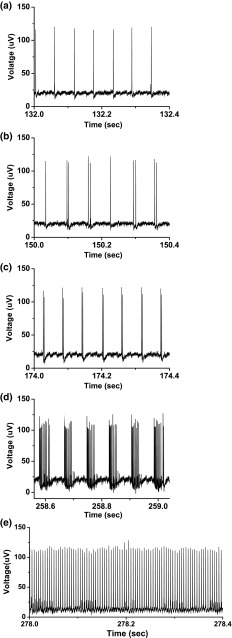
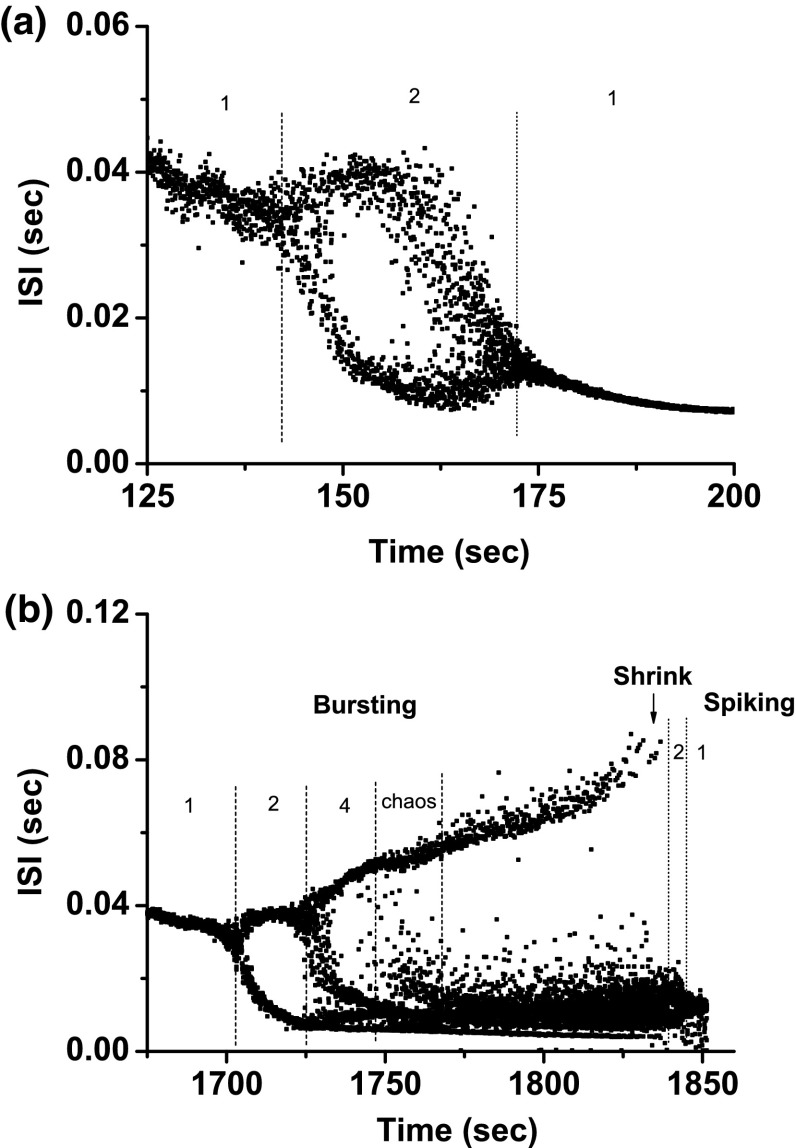
Both bifurcation scenarios 1 and 2 manifested processes corresponding to case-4 bifurcation scenario. Both processes began from period-adding bifurcation with stochastic bursting, as shown in Fig. 6a, b. After shrinkage, the bursting pattern changed to a spiking pattern, and at last to period-1 spiking. Scenario 2 exhibited a more complex process than scenario 1. The period-1 bursting, stochastic bursting between the period-1 and period-2 bursting patterns, period-2 bursting, bursting with multiple spikes per burst, and period-1 spiking located within scenario 1 closely match those simulated in the theoretical model (Fig. 1 and Fig. 3), as shown in Fig. 7. The behavior of the stochastic bursting pattern between the period-k and period-() bursting patterns involved stochastic transition between period-k and period-() bursts (, and 5 for scenario 1, and and 6 for scenario 2), as shown in Fig. 7b.
Fig. 6.
Example 1 of different bifurcation scenarios with decreasing [ for different [4-AP]. a Bifurcation scenario 1 corresponding to case-1 at 0 mM [4-AP]; b bifurcation scenario 2 corresponding to case-1 at 0.25 mM [4-AP]. Period-1 bursting changed to period-1 spiking via a process beginning from period-adding bifurcation with stochastic bursting, which corresponds to the case-1 bifurcation scenario. The number and the character “s” represent the spikes per burst and stochastic bursting, respectively
Fig. 7.
Different firing patterns lying within bifurcation scenario 1 of example 1. a Period-1 bursting; b stochastic bursting lying between period-1 and period-2 bursting patterns; c period-2 bursting; d bursting with multiple spikes per burst; e period-1 spiking
Example 2
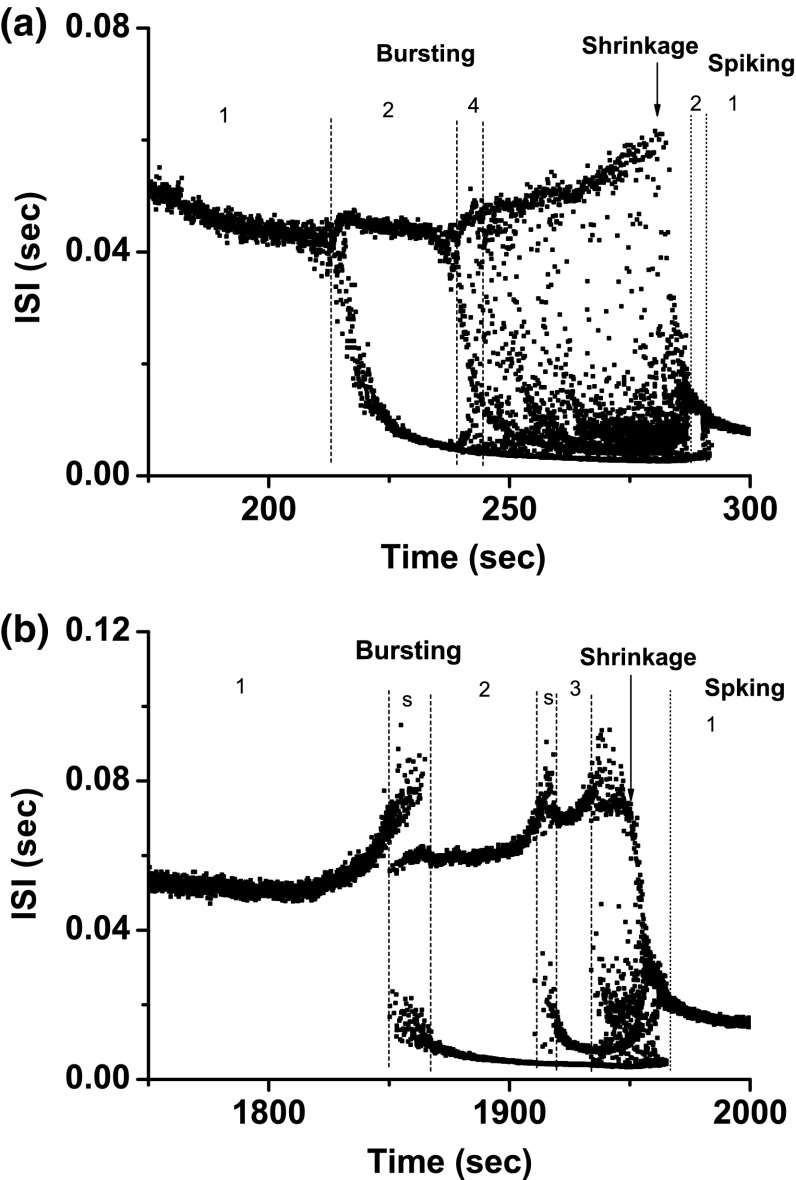
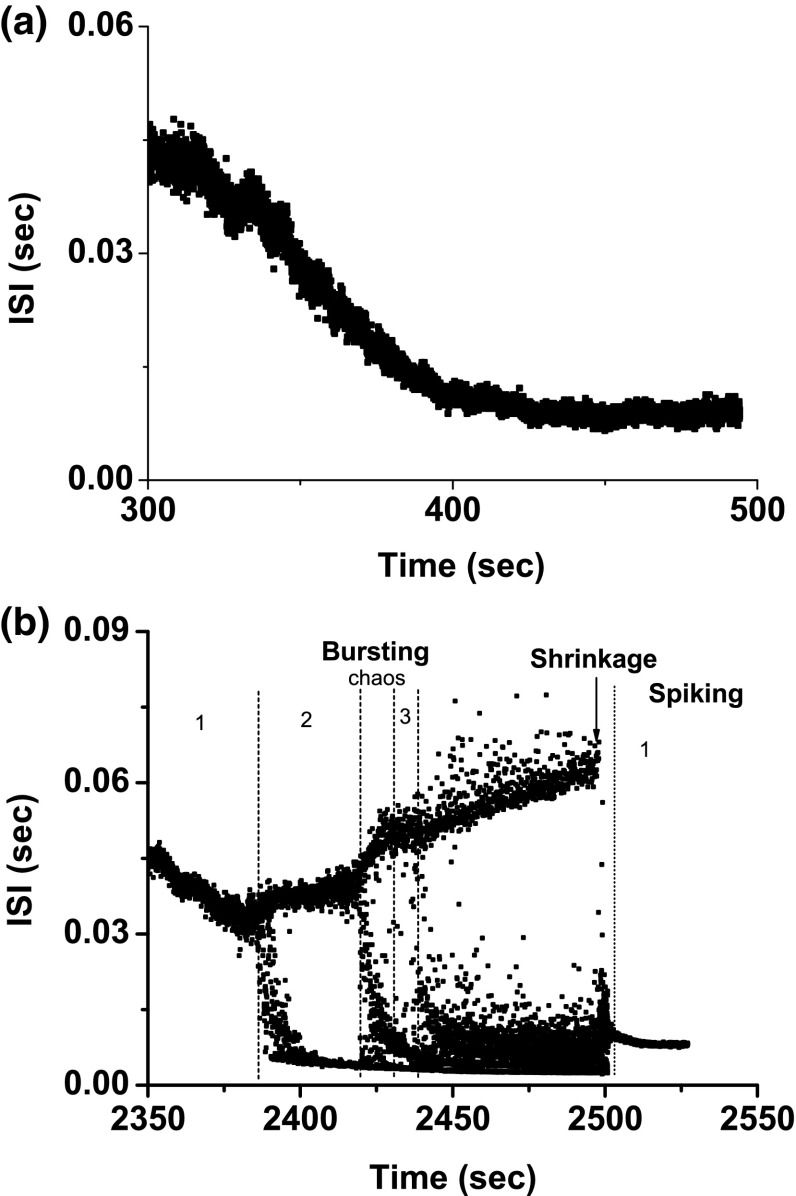
Bifurcation scenario 1 exhibited a process from period-1 bursting to period-1 spiking corresponding to case-2 (Fig. 8a), shifting from period-doubling bifurcation to chaos. After “shrinkage”, a complex bursting pattern with multiple spikes per burst changed to a spiking pattern.
Fig. 8.
Example 2 of different bifurcation scenarios with decreasing [ for different [4-AP]. a Bifurcation scenario 1 corresponding to case-2 at 0 mM [4-AP]. Period-1 bursting changed to period-1 spiking via a process from period-doubling bifurcation to chaos; b bifurcation scenario 2 corresponding to case-1 at 0.25 mM [4-AP]. Period-1 bursting changed to period-1 spiking via a process beginning from period-adding bifurcation. The number and the character “s” represent the spikes per burst and stochastic bursting, respectively
Bifurcation scenario 2 manifested a transition process from period-1 bursting, to stochastic bursting, to period-2 bursting, to stochastic bursting, to period-3 bursting, to complex bursting, to spiking via “shrinkage”, and at last to period-1 spiking (Fig. 8b), which corresponds to case-1.
Example 3
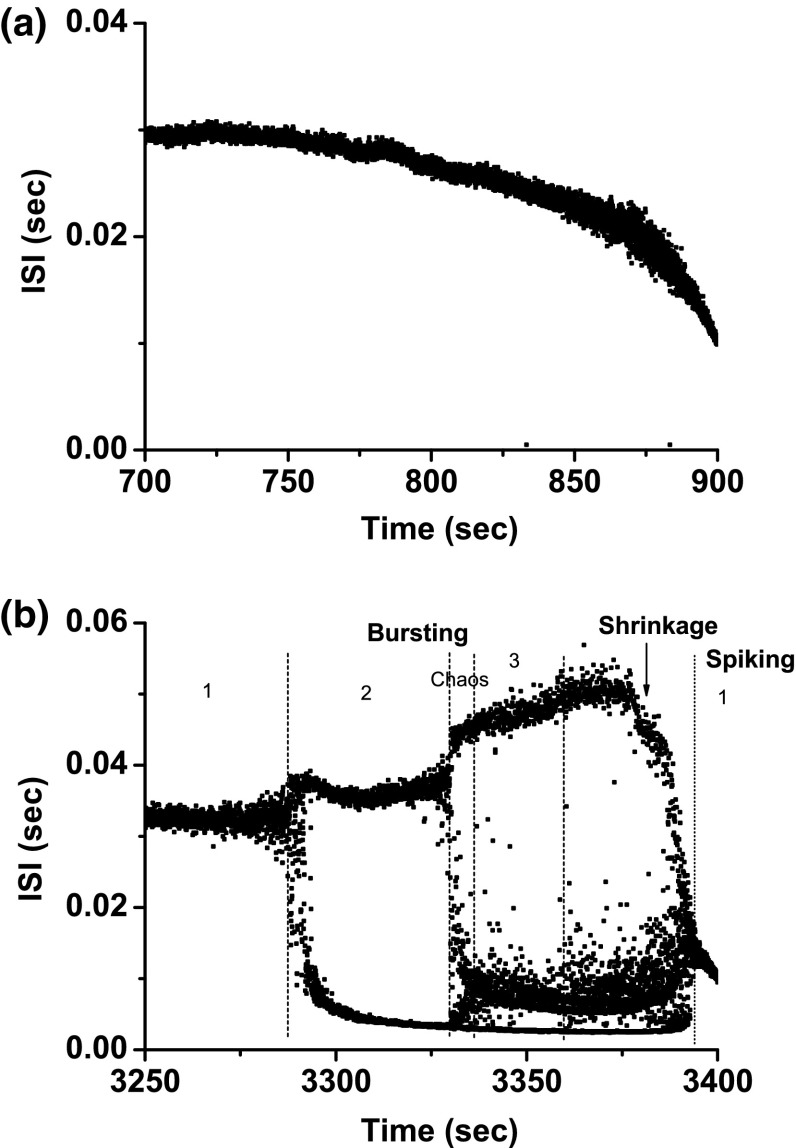
Figure 9a depicts scenario 1, involving a shift from period-1 bursting, to period-2 firing, at last to period-1 spiking, which corresponds to case-3.
Fig. 9.
Example 3 of different bifurcation scenarios with decreasing [ for different [4-AP]. a Bifurcation scenario 1 corresponding to case-3 at 0 mM [4-AP]. Period-1 bursting changed to period-2 firing and to period-1 spiking; b bifurcation scenario 2 corresponding to case-2 at 0.25 mM [4-AP]. Period-1 bursting changed to period-1 spiking via a process from period-doubling bifurcation to chaos. The number represents the spikes per burst
Bifurcation scenario 2 exhibited a complex process (Fig. 9b). After period-1 bursting, the firing pattern changed to period-2 bursting, to period-4 bursting, to chaotic bursting, to a complex firing patterns with a long ISI, to a spiking pattern via “shrinkage”, to period-2 spiking, and at last to period-1 spiking. Such a scenario corresponds to case-2, which begins from period-adding bifurcation with chaos.
Example 4
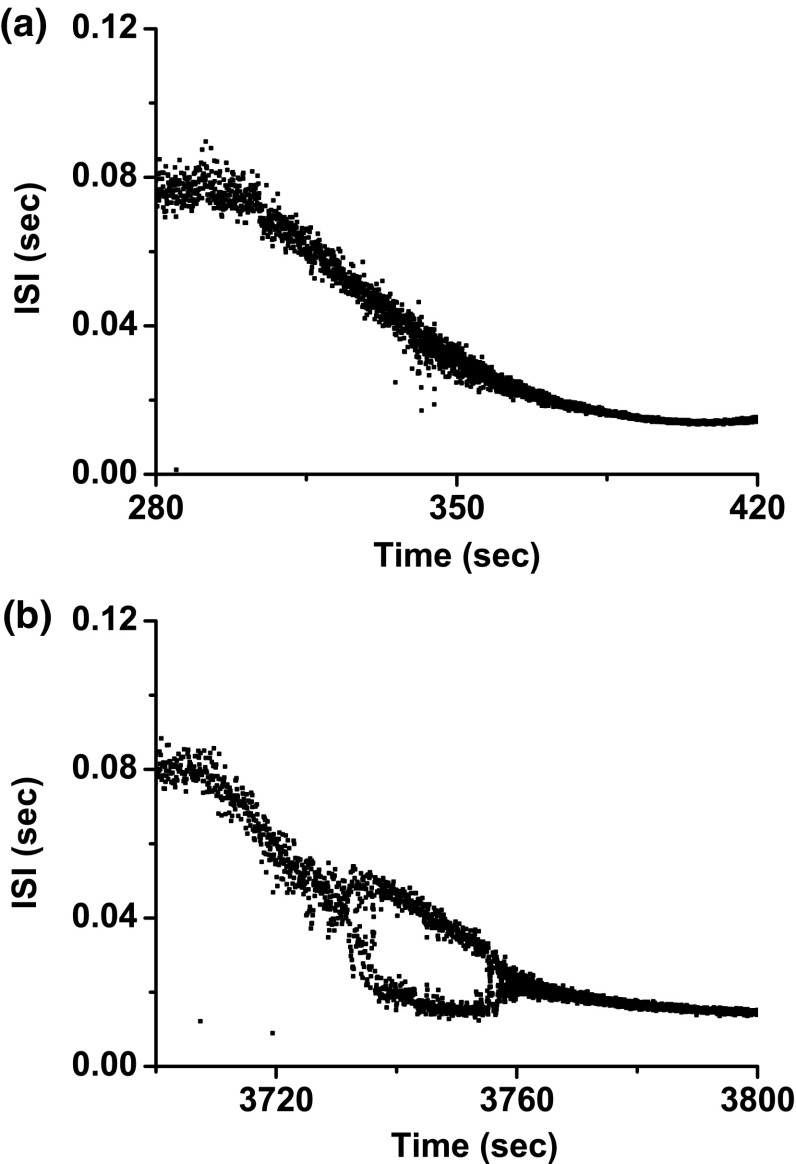
In bifurcation scenario 1, the process transitioned directly from period-1 bursting to period-1 spiking, corresponding to case-4 (Fig. 10a).
Fig. 10.
Example 4 of different bifurcation scenarios with decreasing [ for different [4-AP]. a Bifurcation scenario 1 corresponding to case-4 at 0 mM [4-AP]. Period-1 bursting directly changed to period-1 spiking; b bifurcation scenario 2 corresponding to case-2 at 0.25 mM [4-AP]. Period-1 bursting changed to period-1 spiking via a process beginning from period-adding bifurcation with chaos. The number represents the spikes per burst
Bifurcation scenario 2 exhibited a process from period-1 bursting, to period-2 bursting, to chaotic bursting, to period-3 bursting, to complex bursting, to spiking via “shrinkage”, and at last to period-1 spiking (Fig. 10b), corresponding to case-2.
Example 5
Bifurcation scenario 1 manifested a simple, direct process from period-1 bursting to period-1 spiking (Fig. 11a), which corresponds to case-4.
Fig. 11.
Example 5 of different bifurcation scenarios with decreasing [ for different [4-AP]. a Bifurcation scenario 1 corresponding to case-4 at 0 mM [4-AP]. Period-1 bursting changed directly to period-1 spiking; b bifurcation scenario 2 corresponding to case-2 at 0.25 mM [4-AP]. Period-1 bursting changed to period-1 spiking via a process beginning from period-adding bifurcation with chaos. The number represents the spikes per burst
Bifurcation scenario 2 exhibited a process beginning from period-adding bifurcation and proceeding from period-1 bursting, to period-2 bursting, to chaotic bursting, to period-3 bursting, to complex firing, and at last to period-1 spiking (Fig. 11b), which corresponds to case-2.
Example 6
Bifurcation scenario 1 proceeded directly from period-1 bursting to period-1 spiking, corresponding to case-4 (Fig. 12a).
Fig. 12.
Example 6 of different bifurcation scenarios with decreasing [ for different [4-AP]. a Bifurcation scenario 1 corresponding to case-4 at 0 mM [4-AP]. Period-1 bursting changed directly to period-1 spiking; b bifurcation scenario 2 corresponding to case-3 at 0.25 mM [4-AP]. Period-1 bursting changed to period-2 firing, and then to period-1 spiking
Bifurcation scenario 2 manifested a process from period-1 bursting, to period-2 firing, to period-1 spiking (Fig. 12b), which corresponds to case-3.
Summary of the experiment results
The bifurcation scenarios of the 6 examples are summarized in Table 1. The bifurcation scenarios also formed a basic framework that is consistent with those shown in Fig. 5. The [4-AP] was increased, corresponding to the decrease of , which means that the bifurcation scenario can be changed from a higher-number case to a lower-number case, or the bifurcation scenario becomes more complex. In addition, for each of the bifurcation scenario, the firing frequency increases with decreasing [, and the neuropathic pain information is enhanced with decreasing [, as suggested by Xie et al. (2011).
Table 1.
Summary of bifurcation scenarios of 6 examples
| Bifurcation scenario | Case | Structure |
|---|---|---|
| Scenario 1 of example 1 | 1 | Relatively simple |
| Scenario 2 of example 1 | 1 | Relatively complex |
| Scenario 1 of example 2 | 2 | Relatively simple |
| Scenario 2 of example 2 | 1 | Relatively complex |
| Scenario 1 of example 3 | 3 | Relatively simple |
| Scenario 2 of example 3 | 2 | Relatively complex |
| Scenario 1 of example 4 | 4 | Relatively simple |
| Scenario 2 of example 4 | 2 | Relatively complex |
| Scenario 1 of example 5 | 4 | Relatively simple |
| Scenario 2 of example 5 | 2 | Relatively complex |
| Scenario 1 of example 6 | 4 | Relatively simple |
| Scenario 2 of example 6 | 3 | Relatively complex |
Discussion and conclusion
Different bifurcation scenarios of firing patterns were observed in different CCI models, which were induced by adjusting two physiological parameters. These bifurcation scenarios included patterns of transition from period-1 bursting to period-1 spiking via complex processes which included shifting from period-doubling bifurcation to chaos, period-adding bifurcation with chaos, and period-adding bifurcation with stochastic burstings or via simple processes. The results provide strong evidence that an individual neuron is capable of generating different bifurcation scenarios, which forms a framework for identifying the relationships between different firing patterns and different bifurcation scenarios in an isolated CCI model. The results of the present paper and other investigations (González-Miranda 2012; Barrio and Shilnikov 2011; Barrio et al. 2015, 2014) provide deep and comprehensive insight into the nonlinear dynamics or bifurcations of neural firing patterns in a two-dimensional parameter space.
Earlier studies observed bifurcation and chaos in neural firing patterns on axons and neurons stimulated by external signals (Hayashi et al. 1982; Aihara et al. 1984). Without external stimuli, biological experiments have been performed on somatosensory cortex neurons, cold sensory neurons, Purkinje cells, hypothalamus neurons, and CCI models (Mandelblat et al. 2001; Braun et al. 2011; Jia et al. 2012; Gu and Chen 2014). Bifurcation scenarios from period-1 bursting to period-1 spiking that involved adjusting one parameter were observed in different CCI models (Li et al. 2004; Gu 2013b; Gu et al. 2014; Gu and Pan 2015). Recently, different bifurcation scenarios that involved adjusting two parameters were observed in different individual neural pacemakers (Gu 2013a). The bifurcation parameter is [ and the conditional parameter is extracellular potassium concentration. However, the processes of most bifurcations exhibited part of the scenarios from period-1 bursting to period-1 spiking. The results of the present paper present different bifurcation scenarios from period-1 bursting to period-1 spiking, which is an important advance for identifying the dynamics of the firing patterns observed in the biological experiment.
The CCI model has been widely used to investigate many features of neuropathic pain disorders and spontaneous firing patterns induced by injury (Bennett and Xie 1988; Tal and Eliav 1996). These neural firing patterns are involved in pathological pain and central sensitization, which has been proposed as the key step for many sensory abnormalities (Yamamoto and Sakashita 1998; Dib-Hajj et al. 1999; Djouhri et al. 2006). The responses of chaotic bursting to external electronic stimulation have been reported as “critical sensitivity” (Yang et al. 2006) and the stochastic firing patterns were related to the coherence resonance (CR), which implies that noise plays an important role in information processing (Gu et al. 2003, 2014; Yang et al. 2009). The neural firing patterns in one-dimensional parameter space were identified as playing important roles in neural information processing in single electro-sensory afferents of a fish to detect temperature (Braun et al. 1994). For each of the bifurcation scenario, the neuropathic pain information is enhanced with decreasing [, as suggested by Xie et al. (2011). The bifurcation structures of firing patterns in two-dimensional parameter space are also helpful for identifying neural information coding mechanisms. For example, in physiological contexts, the effects of neurotransmitters and neuromodulators on a neuron usually influence more than one physiological parameter (Newpher and Ehlers 2008) to induce changes in firing patterns within parameter spaces, which is related to the transfer of information between neurons. Understanding the diversity of bifurcation scenarios in firing patterns and the framework of bifurcation structures in the parameter space generated by individual neurons will be beneficial for identifying the neural information process mechanisms.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant Nos. 11572225, 11402055 and 11372224.
References
- Aihara K, Matsumoto G, Ikegaya Y. Periodic and nonperiodic response of a periodically forced Hodgkin–Huxley oscillator. J Theor Biol. 1984;109:249–269. doi: 10.1016/S0022-5193(84)80005-3. [DOI] [PubMed] [Google Scholar]
- Barrio R, Shilnikov A. Parameter-sweeping techniques for temporal dynamics of neuronal systems: case study of Hindmarsh–Rose model. J Math Neurosci. 2011;1:6. doi: 10.1186/2190-8567-1-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrio R, Martínez MA, Serrano S, et al. Macro- and micro-chaotic structures in the Hindmarsh–Rose model of bursting neurons. Chaos. 2014;24:023128. doi: 10.1063/1.4882171. [DOI] [PubMed] [Google Scholar]
- Barrio R, Lefranc M, Martínez MA, et al. Symbolic dynamical unfolding of spike-adding bifurcations in chaotic neuron models. EPL. 2015;109:20002. doi: 10.1209/0295-5075/109/20002. [DOI] [Google Scholar]
- Bennett GJ, Xie YK. A peripheral mononeuropathy in rat produces disorders of pain sensation like those seen in man. Pain. 1988;33:87–107. doi: 10.1016/0304-3959(88)90209-6. [DOI] [PubMed] [Google Scholar]
- Braun HA, Wissing H, Schäfer K, Hirsch MC. Oscillation and noise determine signal transduction in shark multimodal sensory cells. Nature. 1994;367:270–273. doi: 10.1038/367270a0. [DOI] [PubMed] [Google Scholar]
- Braun HA, Schwabedal J, Dewald M, et al. Noise-induced precursors of tonic-to-bursting transitions in hypothalamic neurons and in a conductance-based model. Chaos. 2011;21:047509. doi: 10.1063/1.3671326. [DOI] [PubMed] [Google Scholar]
- Brette R. The Cauchy problem for one-dimensional spiking neuron models. Cogn Neurodyn. 2008;2:21–27. doi: 10.1007/s11571-007-9032-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chay TR. Chaos in a three-variable model of an excitable cell. Phys D. 1985;16:233–242. doi: 10.1016/0167-2789(85)90060-0. [DOI] [Google Scholar]
- Chay TR, Fan YS, Lee YS. Bursting, spiking, chaos, fractals and universality in biological rhythms. Int J Bifurc Chaos. 1995;5:595–635. doi: 10.1142/S0218127495000491. [DOI] [Google Scholar]
- Dib-Hajj SD, Fjell J, Cummins TR, Zheng Z, Fried K, LaMotte R, Black JA, Waxman SG. Plasticity of sodium channel expression in DRG neurons in the chronic constriction injury model of neuropathic pain. Pain. 1999;83:591–600. doi: 10.1016/S0304-3959(99)00169-4. [DOI] [PubMed] [Google Scholar]
- Djouhri L, Koutsikou S, Fang X, McMullan S, Lawson SN. Spontaneous pain, both neuropathic and inflammatory, is related to frequency of spontaneous firing in intact C-fiber nociceptors. J Neurosci. 2006;26:1281–1292. doi: 10.1523/JNEUROSCI.3388-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan LX, Lu QS. Codimension-two bifurcation analysis on firing activities in Chay neuron model. Chaos Solitons Fractals. 2006;30:1172–1179. doi: 10.1016/j.chaos.2005.08.179. [DOI] [Google Scholar]
- Duan LX, Lu QS, Wang QY. Two-parameter bifurcation analysis of firing activities in the Chay neuronal model. Neurocomputing. 2008;72:341–351. doi: 10.1016/j.neucom.2008.01.019. [DOI] [Google Scholar]
- Fan YS, Holden AV. From simple to complex bursting oscillatory behaviour via intermittent chaos in the Hindmarsh–Rose model for neuronal activity. Chaos Solitons Fractals. 1992;2:349–369. doi: 10.1016/0960-0779(92)90012-C. [DOI] [Google Scholar]
- Fan YS, Holden AV. Bifurcations, burstings, chaos and crises in the Rose–Hindmarsh model for neuronal activity. Chaos Solitons Fractals. 1993;3:439–449. doi: 10.1016/0960-0779(93)90029-Z. [DOI] [Google Scholar]
- Fan YS, Chay TR. Generation of periodic and chaotic bursting in an excitable cell model. Biol Cybern. 1994;71:417–431. doi: 10.1007/BF00198918. [DOI] [PubMed] [Google Scholar]
- González-Miranda JM. Block structured dynamics and neuronal coding. Phys Rev E. 2005;72:051922. doi: 10.1103/PhysRevE.72.051922. [DOI] [PubMed] [Google Scholar]
- González-Miranda JM. Nonlinear dynamics of the membrane potential of a bursting pacemaker cell. Chaos. 2012;22:013123. doi: 10.1063/1.3687017. [DOI] [PubMed] [Google Scholar]
- Gu HG. Different bifurcation scenarios of neural firing pattern in identical pacemakers. Int J Bifurc Chaos. 2013;23:1350195. doi: 10.1142/S0218127413501952. [DOI] [Google Scholar]
- Gu HG. Experimental observation of transition from chaotic bursting to chaotic spiking in a neural pacemaker. Chaos. 2013;23(2):023126. doi: 10.1063/1.4810932. [DOI] [PubMed] [Google Scholar]
- Gu HG, Chen SG. Potassium-induced bifurcations and chaos in neural firing patterns observed from a biological experiment on a neural pacemaker. Sci Chin Technol Sci. 2014;57:864–871. doi: 10.1007/s11431-014-5526-0. [DOI] [Google Scholar]
- Gu HG, Pan BB. A four-dimensional neuronal model to describe the complex nonlinear dynamics observed in the firing patterns of a sciatic nerve chronic constriction injury model. Nonlinear Dyn. 2015;81:2107–2126. doi: 10.1007/s11071-015-2129-7. [DOI] [Google Scholar]
- Gu HG, Yang MH, Li L, et al. Dynamics of autonomous stochastic resonance in neural period-adding bifurcation scenarios. Phys Lett A. 2003;319:89–96. doi: 10.1016/j.physleta.2003.09.077. [DOI] [Google Scholar]
- Gu HG, Jia B, Chen GR. Experimental evidence of a chaotic region in a neural pacemaker. Phys Lett A. 2013;377:718–720. doi: 10.1016/j.physleta.2013.01.015. [DOI] [Google Scholar]
- Gu HG, Pan BB, Chen GR, Duan LX. Biological experimental demonstration of bifurcations from bursting to spiking predicted by theoretical models. Nonlinear Dyn. 2014;78:391–407. doi: 10.1007/s11071-014-1447-5. [DOI] [Google Scholar]
- Hayashi H, Ishzuka S, Ohta M, Hirakawa K. Chaotic behavior in the onchidium giant neuron. Phys Lett A. 1982;88:435–438. doi: 10.1016/0375-9601(82)90674-0. [DOI] [Google Scholar]
- Hindmarsh JL, Rose RM. A model of neuronal bursting using three coupled first order differential equations. Proc R Soc Lond B Biol sci. 1984;221:87–102. doi: 10.1098/rspb.1984.0024. [DOI] [PubMed] [Google Scholar]
- Holden AV, Fan YS. From simple to simple bursting oscillatory behaviour via chaos in the Hindmarsh–Rose model for neuronal activity. Chaos Solitons Fractals. 1992;2:221–236. doi: 10.1016/0960-0779(92)90032-I. [DOI] [Google Scholar]
- Innocenti G, Genesio R. On the dynamics of chaotic spiking-bursting transition in the Hindmarsh–Rose neuron. Chaos. 2009;19:023124. doi: 10.1063/1.3156650. [DOI] [PubMed] [Google Scholar]
- Innocenti G, Morelli A, Genesio R, Torcini A. Dynamical phases of the Hindmarsh–Rose neuronal model studies of the transition from bursting to spiking chaos. Chaos. 2007;17:043128. doi: 10.1063/1.2818153. [DOI] [PubMed] [Google Scholar]
- Ivancevic T, Jain L, Pattison J, Hariz A. Nonlinear dynamics and chaos methods in neurodynamics and complex data analysis. Nonlin Dyn. 2009;56:23–44. doi: 10.1007/s11071-008-9376-9. [DOI] [Google Scholar]
- Jia B, Gu HG. Identifying type I excitability using dynamics of stochastic neural firing patterns. Cogn Neurodyn. 2012;6:485–497. doi: 10.1007/s11571-012-9209-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia B, Gu HG, Li L, et al. Dynamics of period doubling bifurcation to chaos discovered in the spontaneous neural firing patterns. Cogn Neurodyn. 2012;6:89–106. doi: 10.1007/s11571-011-9184-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L, Gu HG, Liu ZQ, et al. A series of bifurcation scenarios in the firing pattern transitions in an experimental neural pacemaker. Int J Bifurc Chaos. 2004;14:1813–1817. doi: 10.1142/S0218127404010114. [DOI] [Google Scholar]
- Liu YW, Li SS, Liu ZR, Wang RQ. High codimensional bifurcation analysis to a six-neuron BAM neural network. Cogn Neurodyn. 2016;10:149–164. doi: 10.1007/s11571-015-9364-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lv M, Ma J. Multiple modes of electrical activities in a new neuron model under electromagnetic radiation. Neurocomputing. 2016;205:375–381. doi: 10.1016/j.neucom.2016.05.004. [DOI] [Google Scholar]
- Lv M, Wang CN, Ren GD, et al. Model of electrical activity in a neuron under magnetic flow effect. Nonlinear Dyn. 2016;85:1479–1490. doi: 10.1007/s11071-016-2773-6. [DOI] [Google Scholar]
- Ma J, Tang J. A review for dynamics of collective behaviors of network of neurons. Sci China Technol Sci. 2015;58:2038–2045. doi: 10.1007/s11431-015-5961-6. [DOI] [Google Scholar]
- Ma J, Qin HX, Song XL, et al. Pattern selection in neuronal network driven by electric autapses with diversity in time delays. Int J Mod Phys B. 2015;29:1450239. doi: 10.1142/S0217979214502397. [DOI] [Google Scholar]
- Mandelblat Y, Etzion Y, Grossman Y, et al. Period doubling of calcium spike firing in a model of a purkinje cell dendrite. J Comput Neurosci. 2001;11:43–62. doi: 10.1023/A:1011252730249. [DOI] [PubMed] [Google Scholar]
- Mannella R, Palleschi V. Fast and precise algorithm for compute simulation of stochastic differential equations. Phys Rev A. 1989;40:3381–3386. doi: 10.1103/PhysRevA.40.3381. [DOI] [PubMed] [Google Scholar]
- Newpher TM, Ehlers MD. Glutamate receptor dynamics in dendritic microdomains. Neuron. 2008;58:472–497. doi: 10.1016/j.neuron.2008.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rech PC. Dynamics of a neuron model in different two-dimensional parameter-spaces. Phys Lett A. 2011;375:1461–1464. doi: 10.1016/j.physleta.2011.02.037. [DOI] [Google Scholar]
- Shilnikov AL, Kolomiets ML. Methods of the qualitative theory for the Hindmarsh–Rose model: a case study—a tutorial. Int J Bifurc Chaos. 2008;18:2141–2168. doi: 10.1142/S0218127408021634. [DOI] [Google Scholar]
- Tal M, Eliav E. Abnormal discharge originates at the site of nerve injury in experimental constriction neuropathy (CCI) in the rat. Pain. 1996;64:511–518. doi: 10.1016/0304-3959(95)00175-1. [DOI] [PubMed] [Google Scholar]
- Thomas E, William JR, Zbigniew JK, et al. Chaos and physiology: deterministic chaos in excitable cell assemblies. Physiol Rev. 1994;74:1–47. doi: 10.1152/physrev.1994.74.1.1. [DOI] [PubMed] [Google Scholar]
- Wei XL, Chen YH, Lu ML, et al. An ephaptic transmission model of CA3 pyramidal cells: an investigation into electric field effects. Cogn Neurodyn. 2014;8:177–197. doi: 10.1007/s11571-013-9269-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu XB, Mo J, Yang MH, et al. Two different bifurcation scenarios in neural firing rhythms discovered in biological experiments by adjusting two parameters. Chin Phys Lett. 2008;25:2799–2802. doi: 10.1088/0256-307X/25/8/018. [DOI] [Google Scholar]
- Xie RG, Zheng DW, Xing JL, et al. Blockade of persistent sodium currents contributes to the riluzole-induced inhibition of spontaneous activity and oscillations in injured DRG neurons. PLoS ONE. 2011;6:e18681. doi: 10.1371/journal.pone.0018681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu XY, Wang RB. Neurodynamics of up and down transitions in a single neuron. Cogn Neurodyn. 2014;8:509–515. doi: 10.1007/s11571-014-9298-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada Y, Kashimori Y. Neural mechanism of dynamic responses of neurons in inferior temporal cortex in face perception. Cogn Neurodyn. 2013;7:23–38. doi: 10.1007/s11571-012-9212-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto Y, Sakashita Y. Differential effects of intrathecally administered N-type and P-type sensitive calcium chaanel blockers upon two models of experimental mononeuropathy in the rat. Brain Res. 1998;794:329–332. doi: 10.1016/S0006-8993(98)00306-0. [DOI] [PubMed] [Google Scholar]
- Yang J, Duan YB, Xing JL, et al. Responsiveness of a neural pacemaker near the bifurcation point. Neurosci Lett. 2006;392:105–109. doi: 10.1016/j.neulet.2005.09.007. [DOI] [PubMed] [Google Scholar]
- Yang MH, Liu ZQ, Li L, et al. Identifying distinct stochastic dynamics from chaos: a study on multimodal neural firing patterns. Int J Bifurc Chaos. 2009;19:453–485. doi: 10.1142/S0218127409023135. [DOI] [Google Scholar]
- Zheng QH, Liu ZQ, Yang MH, et al. Qualitatively different bifurcation scenarios observed in the firing of identical nerve fibers. Phys Lett A. 2009;373:540–545. doi: 10.1016/j.physleta.2008.12.027. [DOI] [Google Scholar]
- Zheng G, Tonnelier A. Chaotic solutions in the quadratic integrate-and-fire neuron with adaptation. Cogn Neurodyn. 2009;3:197–204. doi: 10.1007/s11571-008-9069-6. [DOI] [PMC free article] [PubMed] [Google Scholar]