Proximal-distal differences in movement smoothness reflect differences in biomechanics

This article presents the first thorough characterization of the smoothness of wrist rotations (flexion-extension and radial-ulnar deviation) and comparison with the smoothness of reaching (shoulder-elbow) movements. We found wrist rotations to be significantly less smooth than reaching movements and determined that this difference reflects proximal-distal differences in biomechanics: the greater impedance (inertia, damping, stiffness) of the shoulder-elbow filters noise in the command signal more than the impedance of the wrist.

Abstract

Smoothness is a hallmark of healthy movement. Past research indicates that smoothness may be a side product of a control strategy that minimizes error. However, this is not the only reason for smooth movements. Our musculoskeletal system itself contributes to movement smoothness: the mechanical impedance (inertia, damping, and stiffness) of our limbs and joints resists sudden change, resulting in a natural smoothing effect. How the biomechanics and neural control interact to result in an observed level of smoothness is not clear. The purpose of this study is to 1) characterize the smoothness of wrist rotations, 2) compare it with the smoothness of planar shoulder-elbow (reaching) movements, and 3) determine the cause of observed differences in smoothness. Ten healthy subjects performed wrist and reaching movements involving different targets, directions, and speeds. We found wrist movements to be significantly less smooth than reaching movements and to vary in smoothness with movement direction. To identify the causes underlying these observations, we tested a number of hypotheses involving differences in bandwidth, signal-dependent noise, speed, impedance anisotropy, and movement duration. Our simulations revealed that proximal-distal differences in smoothness reflect proximal-distal differences in biomechanics: the greater impedance of the shoulder-elbow filters neural noise more than the wrist. In contrast, differences in signal-dependent noise and speed were not sufficiently large to recreate the observed differences in smoothness. We also found that the variation in wrist movement smoothness with direction appear to be caused by, or at least correlated with, differences in movement duration, not impedance anisotropy.

NEW & NOTEWORTHY This article presents the first thorough characterization of the smoothness of wrist rotations (flexion-extension and radial-ulnar deviation) and comparison with the smoothness of reaching (shoulder-elbow) movements. We found wrist rotations to be significantly less smooth than reaching movements and determined that this difference reflects proximal-distal differences in biomechanics: the greater impedance (inertia, damping, stiffness) of the shoulder-elbow filters noise in the command signal more than the impedance of the wrist.

smoothness is a hallmark of healthy movement and likely has both neural and biomechanical origins. Many studies have characterized the smoothness of fast eye and reaching movements and found them to be remarkably smooth, meaning that their speed profiles were generally unimodal and symmetric (Atkeson and Hollerbach 1985; Harris and Wolpert 1998; Morasso 1981), and that the jerkiness¹ of these movements was low (close to the theoretical minimum) (Flash 1987; Flash and Hogan 1985). This finding was remarkable because it suggested that humans may control their movements so as to maximize smoothness, at least under certain conditions. Harris and Wolpert (1998) later proposed a fundamental motivation for maximizing movement smoothness: smooth movements are advantageous because they minimize the negative effects of signal-dependent noise² (SDN), resulting in more precise movements (see also Faisal et al. 2008). Thus the observed smoothness of many movements may be a side product of a control strategy that minimizes movement error. However, this is not the only reason for movement smoothness. Our musculoskeletal system itself contributes to movement smoothness: the mechanical impedance³ (inertia, damping, and stiffness) of our limbs and joints resists sudden change, resulting in a natural smoothing (low-pass filtering⁴) from the control signal to the resulting movement. Sharp action potentials create rounded muscle twitches, and rounded muscle twitches create gradual movement (by comparison), each smoother than the former. How the biomechanics and neural control interact to result in an observed level of smoothness is not clear, particularly for different degrees of freedom (DOF).

Despite the essential role of distal upper-limb movements in daily life, few studies have investigated the smoothness of movements involving distal DOF even though there are known proximal-distal differences in factors that could affect smoothness. For example, for a given joint torque, distal DOF (wrist and fingers) have more SDN than proximal DOF (shoulder and elbow) (Hamilton et al. 2004). This noise corrupting the control signal could make the resulting distal movements less smooth than proximal movements. Also, the dynamics of proximal DOF involve large inertias, whereas the dynamics of distal DOF are dominated by stiffness effects, not inertia (Charles and Hogan 2011; Deshpande et al. 2012; Peaden and Charles 2014). To illustrate, rotating the wrist at a comfortable pace requires roughly 10 times more torque to overcome the passive stiffness of the wrist than the inertia of the hand (Charles and Hogan 2011). Since inertia and stiffness contribute differently to the low-pass filtering effect of a system⁵, this proximal-distal shift in the dominance of inertia vs. stiffness could result in different levels of smoothness.

Understanding the smoothness of movements involving distal DOF is also important because it can potentially be used as a marker for movement disorders and rehabilitation. To clarify, movement disorders often result in a decrease in movement smoothness. For example, stroke patients’ reaching movements are associated with a decrease in movement smoothness (Rohrer et al. 2002), while rehabilitation is accompanied by an increase in movement smoothness (Dipietro et al. 2009; Rohrer et al. 2002; Rohrer et al. 2004). Using smoothness as a marker of disorder and recovery is especially attractive in the context of robotic rehabilitation since the robot can easily measure movement smoothness. However, despite the development and implementation of a large number of rehabilitation robots for distal upper-limb DOF (Maciejasz et al. 2014), the smoothness of movements involving the distal upper limb has not been thoroughly characterized; in the absence of an unimpaired baseline, using smoothness as a marker is not currently possible.

The purpose of this study is to 1) characterize the smoothness of wrist rotations (flexion-extension and radial-ulnar deviation), 2) compare it to the smoothness of planar reaching movements (horizontal shoulder abduction-adduction and elbow flexion-extension), and 3) determine the cause of differences in smoothness between wrist and reaching movements. We found that wrist rotations were significantly less smooth than reaching movements (P < 0.002) and exhibited a pattern of smoothness that varied between targets and outbound/inbound (center-out/out-center) directions (P < 0.0001). To understand why wrist rotations were less smooth than reaching movements, we investigated if this phenomenon was caused by differences in the low-pass filtering properties of the DOF, the amount of SDN, or the requirements of the task. We found that the bandwidth⁶ of the shoulder-elbow system is considerably smaller than that of the wrist and therefore low-pass filters noise in the neural signal more than the wrist, resulting in smoother movements. In contrast, differences in SDN and task requirements do not appear large enough to produce the observed differences in smoothness. To understand why wrist movement smoothness varied between targets and movement directions, we tested the effect of anisotropy in the mechanical impedance of the wrist and found that it does not cause the observed pattern. Instead, differences in movement duration with target and direction exhibited the same pattern as differences in movement smoothness. Since smoothness decreases with movement duration, the differences in smoothness are likely caused by, or at least correlated with, differences in movement duration.

METHODS

Experiment

Subjects.

Ten healthy human subjects participated in this study [5 men and 5 women; age 23 ± 3 (means ± SD) years, range 18–26]. All subjects were right-handed and reported being free of injuries or disorders affecting upper-limb movement. After procedures approved by Brigham Young University’s Institutional Review Board, informed consent was obtained from all subjects.

Experimental setup.

Each subject participated in sessions involving wrist rotations and sessions involving reaching movements.

wrist rotation experiment.

Subjects were seated in a chair with the right arm in the parasagittal plane. The shoulder was in ~45° of flexion and 0° of abduction and humeral rotation, and the elbow was in ~45° of flexion. The forearm rested on a support to their side and was prevented from pronating or supinating by a custom-built apparatus that fixed the distal forearm at three bony landmarks, constraining the forearm midway between pronation and supination. This method was successfully applied in previous studies (Charles and Hogan 2010, 2011) and resulted in “a snug squeezing sensation on the ventral and dorsal aspects of the distal forearm that largely eliminated pro-sup but did not interfere with wrist rotations” (Charles and Hogan 2010). Preventing pronation-supination allowed us to focus on the 2 DOF of the wrist and compare with reaching movements, which also involve 2 DOF.

In subjects’ right hand was placed a lightweight handle to which an electromagnetic motion sensor (trakSTAR by Ascension Technology, Shelburne, VT) was rigidly attached (Fig. 1A). This sensor has a static angular resolution and accuracy of 0.021° and 0.5°, respectively, and measured the orientation of the handle at a sampling frequency of ~333 Hz. On a screen in front of the subject were eight peripheral targets equally distributed around a center target, as well as a cursor that moved with wrist flexion-extension (FE) and radial-ulnar deviation (RUD), as detailed below. The radius of the targets was 1/10 of the radius of the circle on which the peripheral targets resided (chosen to fit the screen), and the radius of the cursor was 1/4 of the radius of the targets. FE and RUD were defined as Euler angles according to the recommendation by the International Society of Biomechanics (Wu et al. 2005), modified for in vivo use with a handle as follows. The wrist was in neutral FE when the center of the sensor (mounted on top of the handle in the subject’s hand), the wrist joint center, and the elbow joint center (assumed halfway between the lateral and medial epicondyles) were in the same parasagittal plane. The wrist was in neutral RUD when the head of the third metacarpal, the wrist joint center, and the lateral epicondyle were in the same horizontal plane.

Fig. 1.

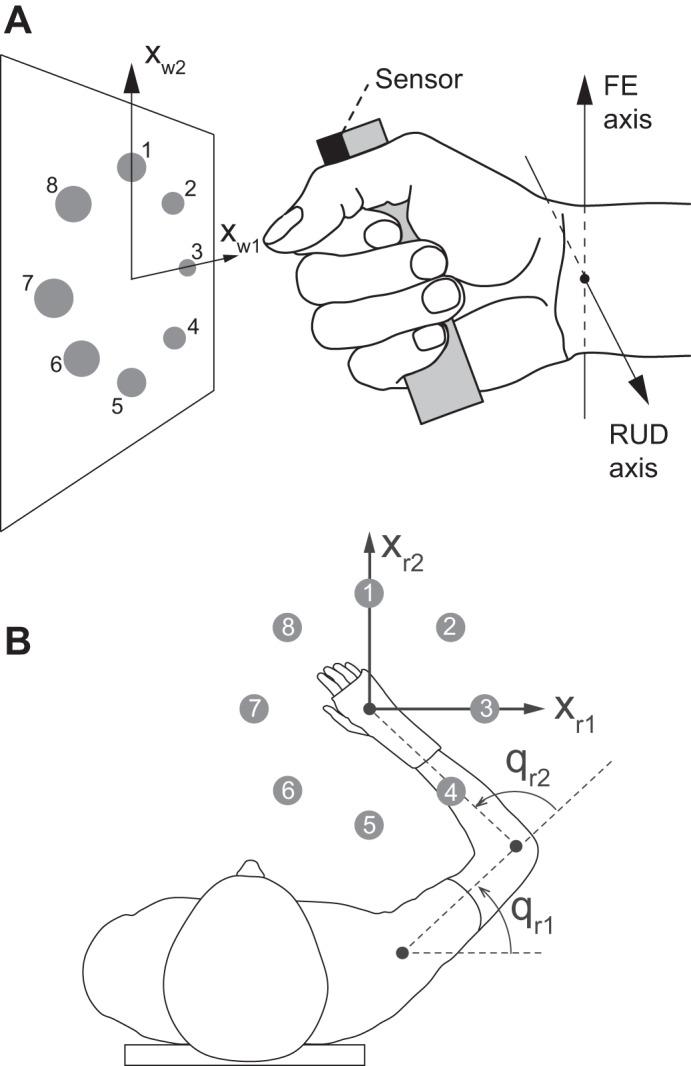
Experimental setup for wrist movements (A) and reaching movements (B). A. Subjects rotated their wrist in combinations of flexion-extension (FE) and radial-ulnar deviation (RUD) to point to targets on a screen. Each movement required 15° of wrist rotation. B: subjects also made planar shoulder-elbow (reaching) movements toward targets. Each movement required 14 cm of displacement of the hand. Both wrist and reaching movements included fast, medium, and slow movements (durations of 300, 550, and 900 ms, respectively).

The cursor represented the orientation of the hand as follows (Charles and Hogan 2010). The hand was represented as a unit vector whose orientation was defined by q_w = [q_w1, q_w2]^T, where q_w1 and q_w2 are Euler angles representing flexion and ulnar deviation, respectively (with negative values denoting extension and radial deviation). The position of the cursor, x_w = [x_w1, x_w2]^T, was equal to the planar components of this unit vector, resulting in the following relationship between x_w and q_w: x_w1 = −sin q_w1 cos, and x_w2 = −sin q_w2 (the negative signs simply indicate that the cursor position was defined as positive to the right and upward, whereas the wrist angles were positive in flexion and ulnar deviation). Note that for the moderate rotation sizes used in this study (15°, see below), this relationship is virtually the same as x_w1 = −q_w1 and x_w2 = −q_w2. At the center target, this approximation is exact, i.e., x_w = [0,0]^T when q_w = [0,0]^T. At the peripheral targets, where the difference between | x_w | and | q_w | is the largest, the maximum difference was only 0.21°, which is less than the accuracy of our motion capture system. In other words, except for a simple scaling factor used to fit the targets onto the screen, the position of the cursor was indistinguishable from the orientation of the wrist joint.

reaching experiment.

Subjects were seated in a height adjustable chair, fastened with shoulder straps to minimize trunk movement. Each subject’s right forearm was placed in a sling suspended ~2 m from the ceiling to hold the arm and forearm approximately in the horizontal plane. The forearm was oriented midway between pronation and supination (i.e., the palm faced downward), and the wrist was placed in a splint to prevent wrist rotation. Subjects held in their fist an electromagnetic motion sensor (see above) which recorded the position of the hand. This sensor has a static linear resolution and accuracy of ~0.5 mm and 1.4 mm RMS, respectively, and measured the position of the hand in all three translational DOFs at a sampling frequency of ~333 Hz. On a screen in front of the subject was the same graphical user interface described above (also scaled to fit the screen), but the cursor moved in proportion to the translation of the hand, x_r = [x_r1, x_r2]^T (Fig. 1). The cursor position was calibrated to be at the center target when the orientation of the arm, q_r = [q_r1, q_r2]^T, was in neutral position, defined as q_r = [45°, 90°]^T, where q_r1 and q_r2 represent horizontal shoulder abduction and elbow flexion, respectively.

Protocol.

Each subject participated in three wrist rotation and three reaching sessions involving different movement durations, which resulted in different movement speeds (fast, medium, and slow) since the movement amplitudes were held constant. The six sessions were presented in random order, with a 3-min break between sessions.

In each session, subjects were required to make either 15° wrist or 14-cm reaching movements to move the cursor between the center target and one of the eight peripheral targets as prompted by a visual cue (changing target color). The area covered by the targets is in the middle of the range of motion of wrist and reaching movements and represents roughly the same proportion of the total range of motion of reaching and wrist movements (~15%). Each prompt was designed to elicit a discrete movement by requiring that the subject come to a complete stop on the target and wait at least 0.6 s before the next target was displayed. Subjects were prompted to move to targets in random order for a total of 160 one-way moves per test (10 round trip moves to each of the 8 targets). In the beginning of the study, subjects were instructed to make “continuous and straight movements,” but no instructions were given regarding movement smoothness.

To characterize the effect of movement speed on smoothness, all sessions required the same movement amplitude (15° or 14 cm) but had different requirements on movement duration. Fast, medium, and slow sessions required movements lasting 300 ± 75, 550 ± 100, and 900 ± 150 ms, respectively. After each movement, subjects received visual feedback on the screen indicating if the movement was too fast or too slow. The duration of a movement was measured from the moment the cursor left the original target to the moment it entered the destination target. Longer movements were given larger ranges because pilot experiments showed that reaching the target in a given amount of time was more difficult for longer movement durations.

In each session, subjects began with 32 practice moves and then continued until they had made 10 successful movements to each target and from each target, where a movement was defined as successful if its duration was inside the acceptable range. Therefore, over the course of the experiment, each subject made a minimum of 10 two-way movements to eight targets at three different speeds with both the shoulder-elbow and wrist, for a total of over 960 movements.

Data processing.

The data were resampled at 333 Hz, which was necessary because the data were originally sampled at a nonconstant rate (around 333 Hz). We differentiated the data repeatedly to obtain velocity, acceleration, and jerk, low-pass filtering after each differentiation using a sixth-order Butterworth filter with 15-Hz cutoff frequency and zero phase lag using Matlab’s filtfilt function (the effect of low-pass filtering on measures of movement smoothness is addressed below). The cutoff frequency was chosen to be above the range of voluntary movement (Mann et al. 1989) and above the bandwidths of the shoulder-elbow and wrist (see results). The data were then parsed into discrete movements, and the unsuccessful movements (with duration outside of the acceptable range) were excluded from further analysis. We computed speed as the magnitude of velocity and trimmed the remaining, successful movements to start at the moment the speed exceeded 10% of the maximum speed (s_max) for the last time before reaching s_max, and end the moment the speed first dropped below 10% of s_max after reaching s_max.

Measures of smoothness.

For each movement, we calculated two measures of smoothness: jerk ratio and the number of maxima in the speed profile (NumMax).

jerk ratio.

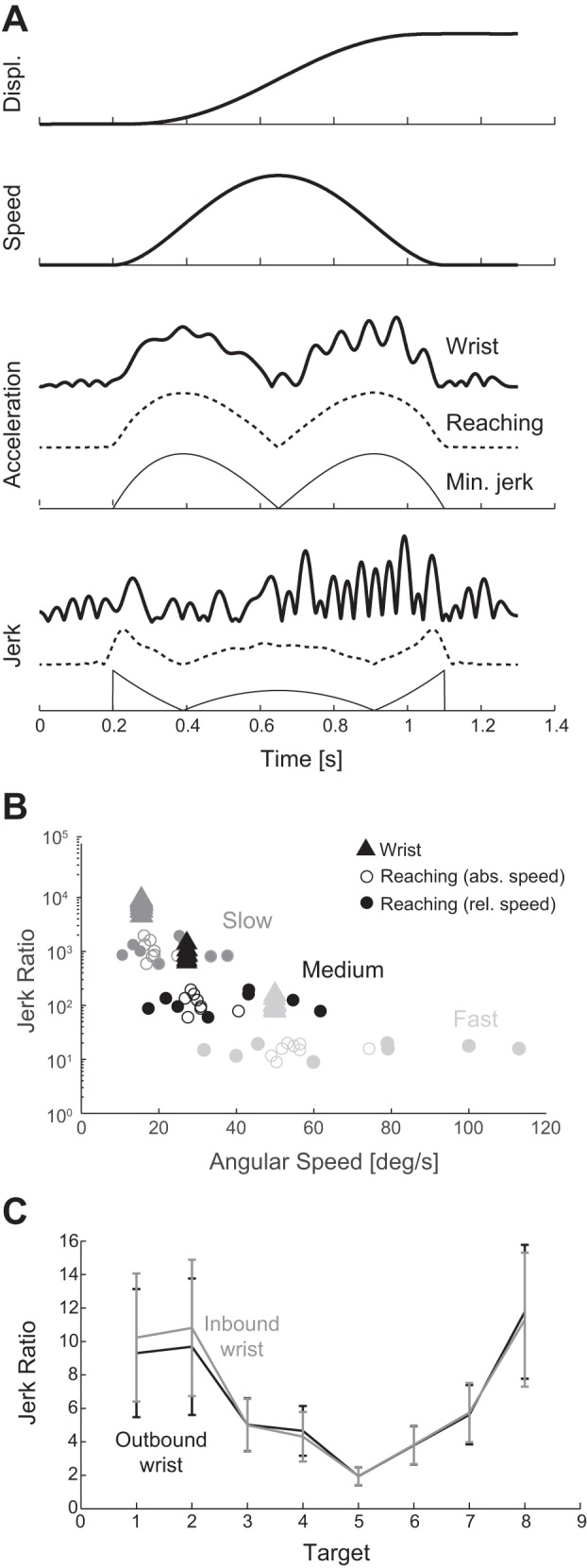
Jerk ratio was calculated as the integrated squared jerk (ISJ) of a movement and was normalized by the ISJ of the equivalent minimum-jerk trajectory (MJT) to allow comparison between wrist and reaching movements. The ISJ was defined as $\int \left({\stackrel{⃛}{q}}_{w1}{}^2+{\stackrel{⃛}{q}}_{w2}{}^2\right)dt$ for wrist movements and $\int \left({\stackrel{⃛}{x}}_{r1}{}^2+{\stackrel{⃛}{x}}_{r2}{}^2\right)dt$ for reaching movements, integrated over the duration of the movement. The equivalent MJT was defined as the MJT that shares the same starting position, ending position, duration, and threshold condition (starting and ending at 10% of its maximum speed) as the real data. By definition, the jerk ratio is equal or greater than 1, with 1 signifying a real movement that is as smooth as possible.

nummax.

The number of maxima in the speed profile, NumMax, has been used as a measure of smoothness in previous studies (Brooks et al. 1973; Fetters and Todd 1987; Hoffman and Strick 1986). Speed was defined as $\Vert {\dot{\mathit{q}}}_{\mathit{w}}\Vert =\sqrt{{\dot{q}}_{w1}{}^2+{\dot{q}}_{w2}{}^2}$ for wrist rotations and $\Vert {\dot{\mathit{x}}}_{\mathit{r}}\Vert =\sqrt{{\dot{x}}_{r1}{}^2+{\dot{x}}_{r2}{}^2}$ for reaching movements. Maxima were identified using peakdet (Billauer 2015), a public-domain peak detection algorithm that requires local maxima to be greater than surrounding minima (or start or end points) by a parameter delta. We set delta to 0.0001 to detect even very small maxima. NumMax is an integer greater than or equal to 1, with larger values of NumMax indicating lower smoothness.

Statistical analysis.

Our experiment included four factors: DOF (shoulder-elbow vs. wrist), target (1–8), outbound/inbound direction (center-out vs. out-center), and speed (fast, medium, and slow). To determine differences in movement smoothness between wrist and reaching movements, we performed separately for each measure (jerk ratio and NumMax) a five-way mixed model ANOVA with DOF, target, direction, and speed as fixed factors and subject as a random factor. To characterize spatial variations in the smoothness of wrist rotations, we conducted for the wrist measures alone four-way mixed model ANOVA tests with target, direction, and speed as fixed factors and subject as a random factor. All post hoc analyses were performed using the Tukey-Kramer method. Jerk ratio varied over several orders of magnitude between factors, so we transformed the measures to log10 before the ANOVA tests. For plotting purposes, jerk ratio values were transformed back to their original values and plotted on a logarithmic scale.

Low-pass filtering the data (see Data processing) was necessary to remove nonphysiological high-frequency content amplified by each differentiation, but it clearly affected our measures of movement smoothness. However, filtering may leave the relative magnitude of the measures between factors unchanged. To determine the sensitivity of the relative magnitudes to low-pass filtering, we recalculated all jerk ratio and NumMax values and repeated the statistical analyses above for five additional filters: sixth-order Butterworth filters with cutoff frequencies at 5, 10, 20, and 25 Hz, and a second-order Butterworth filter with cutoff frequency at 15 Hz.

Simulation and Comparison

To understand the causes underlying any observed differences in smoothness between wrist and reaching movements or spatial variations in wrist rotation smoothness, we used models of wrist and reaching movements to test a number of hypotheses.

Models of wrist and reaching dynamics.

We modeled both wrist and reaching movements according to (Tee et al. 2004), which included feedforward and feedback control (Fig. 2). The feedforward controller modeled the passive dynamics of the system. The feedback controller implemented proportional+derivative control, with proportional and derivative gains equal to active joint stiffness and damping, respectively.

Fig. 2.

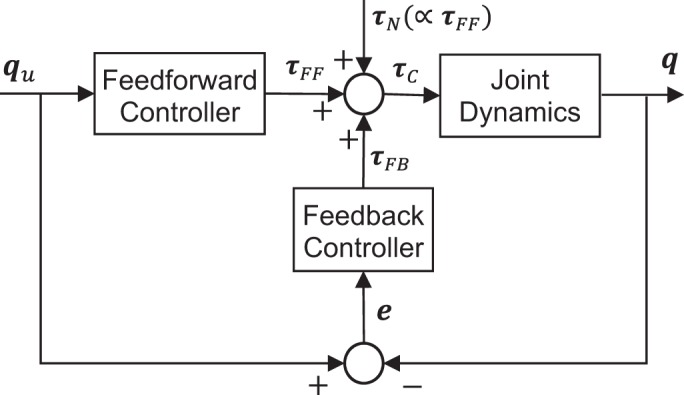
To understand the effect of signal-dependent noise on movement smoothness, we modeled wrist and reaching movements using feedforward and feedback control according to (Tee et al. 2004). Variables q_u and q represent the desired and actual joint trajectories, with error e representing the difference. The feedforward torque τ_FF, feedback torque τ_FB, and signal-dependent noise torque τ_N sum to the control torque τ_C.

wrist dynamics.

Model structure: The dynamics of the wrist were modeled as $I_w{\ddot{\mathit{q}}}_{\mathit{w}}+D_w{\dot{\mathit{q}}}_{\mathit{w}}+K_w{\mathit{q}}_{\mathit{w}}-{\mathit{G}}_{\mathit{w}}={\mathit{\tau }}_{\mathit{w}}$, where ${\mathit{q}}_{\mathit{w}}={\left[\begin{array}{cc}{q}_{w1}& q_{w2}\end{array}\right]}^T$ represents angular displacement in flexion (q_w1) and ulnar deviation (q_w2); I_w, D_w, and K_w are 2-by-2 matrices representing the inertia, passive damping, and passive stiffness of the wrist joint, respectively (passive meaning in the absence of muscle activity); G_w = [0 m_wr_wg]^T is the gravitational torque acting about the wrist, with m_w, r_w, and g denoting the mass of the hand, distance from the wrist to the center of mass of the hand, and gravitational acceleration, respectively; and τ_w = [τ_w1 τ_w2]^T represents the input torque in q_w. For the moderately sized rotations investigated in this study (15° from neutral position), this linear model is an excellent approximation (mean error in maximum torque: 0.8%) of the nonlinear model of the wrist as a universal joint with nonintersecting axes (Charles and Hogan 2011) and has been successfully used to explain the curvature of wrist rotations (Charles and Hogan 2012).

Passive impedance parameters: Parameter values were estimated from prior studies. Importantly, in addition to choosing default values (described here), we tested the robustness of our conclusions to changes in parameter values (see Sensitivity Analysis). The moments of inertia of the hand about the wrist joint in FE and RUD were estimated from (de Leva 1996) using average weight and height for men and women. The products of inertia (the off-diagonal terms) were assumed to be zero since the moments of inertia are similar, resulting in $I_w=\left[\begin{array}{cc}0.0023& 0\\ 0& 0.0026\end{array}\right]kg{m}^2$. The mass of the hand and distance from the wrist to the center of mass of the hand were calculated in the same way, resulting in m_w = 0.41 kg and r_w = 0.061 m.

The passive stiffness of the wrist has been measured in FE, RUD, and combinations, resulting in a 2-by-2 stiffness matrix (Formica et al. 2012; Pando et al. 2014). This matrix was found to be quite proportionate between subjects⁷, with a mean value (averaged across ± 15° from neutral position in each direction in 5 male and 5 female subjects) of $K_w=\left[\begin{array}{cc}1.28& -0.178\\ -0.178& 1.74\end{array}\right]Nm/rad$ (Formica et al. 2012). Although prior studies have reported passive damping in FE alone, no values have been published for passive damping in both DOF of the wrist. However, because both stiffness and damping are predominantly caused by muscle stretch (at least close to the center of the ROM of a joint), they have been found to be—and are often modeled as being—roughly proportional [see Charles and Hogan (2012) for more details]. The constant of proportionality can be calculated by assuming a damping ratio. Perreault et al. (2004) showed the damping ratio for the shoulder-elbow system to be remarkably constant around 0.26, relatively independent of joint torque. Here we assumed this same damping ratio to estimate the wrist passive damping matrix D_w by scaling K_w such that the resulting damping ratio in FE⁸, $D_w^{11}/\left(2\sqrt{K_w^{11}{I}_w^{11}}\right)$, was 0.26 (superscripts denote the matrix element), yielding $D_w=\left[\begin{array}{cc}0.028& -0.0039\\ -0.0039& 0.038\end{array}\right]Nms\hspace{0.17em}/rad$. The resulting damping in FE (0.028 Nms/rad) falls in the middle of prior measurements of passive damping in FE (range 0.014–0.09 Nms/rad, mean 0.038 Nms/rad) (Gielen and Houk 1984; Klomp et al. 2014; Lakie et al. 1984; Park et al. 2011).

Feedback gains: The proportional and derivative gains of the feedback controller represent active stiffness and damping (i.e., in the presence of muscle activity). The active stiffness of the wrist has been measured under various displacement conditions (short and long range) and loading conditions (torque or co-contraction), but only in FE (de Vlugt et al. 2011; Halaki et al. 2006; Klomp et al. 2014; Milner and Cloutier 1993; 1998; Schouten et al. 2006; Sinkjaer and Hayashi 1989). A measurement of long-range stiffness during production of a modest flexor torque (15% of the maximum voluntary contraction of the flexor carpi radialis) (Halaki et al. 2006) was deemed most appropriate for our simulation (see discussion) and used as the stiffness in FE. This value (5.9 Nm/rad) is similar to other long-range measurements made during modest torque production [5 Nm/rad with 0.9 Nm torque (de Vlugt et al. 2011), and 6.1 Nm/rad with 1 Nm torque (Klomp et al. 2014)]. To obtain an estimate of the entire stiffness matrix, we scaled the passive stiffness matrix K_w so the element representing stiffness in FE would equal 5.9 Nm/rad, resulting in $K_{FB,w}=\left[\begin{array}{cc}5.9& -0.82\\ -0.82& 8.03\end{array}\right]Nm\hspace{0.17em}/rad$. As for passive damping, we estimated the active damping matrix by assuming a damping ratio in FE, $D_{FB,w}^{11}\hspace{0.17em}/\left(2\sqrt{K_{FB,w}^{11}\hspace{0.17em}{I}_w^{11}}\right)$, of 0.26, resulting in $D_{FB,w}=\left[\begin{array}{cc}0.061& -0.0084\\ -0.0084& 0.082\end{array}\right]Nms\hspace{0.17em}/rad$. The resulting active damping in FE (0.061 Nms/rad) falls in the middle of prior measurements of active damping in FE (range 0.01–0.11 Nms/rad, mean 0.069 Nms/rad) (Halaki et al. 2006; Klomp et al. 2014; Milner and Cloutier 1993, 1998; Ridderikhoff et al. 2004; Schouten et al. 2006).

reaching dynamics.

Model structure: The dynamics of reaching were modeled according to (Tee et al. 2004) as $H_r\hspace{0.17em}\left({\mathit{q}}_{\mathit{r}}\right){\ddot{\mathit{q}}}_{\mathit{r}}+C_r\mathit{\left(}{\mathit{q}}_{\mathit{r}}\mathit{,}\hspace{0.17em}{\dot{\mathit{q}}}_{\mathit{r}}\mathit{\right)}{\dot{\mathit{q}}}_{\mathit{r}}\mathit{=}{\mathit{\tau }}_{\mathit{r}}$, where q_r = [q_r1 q_r2]^T represents horizontal shoulder adduction and elbow flexion (Fig. 1); H_r is a 2-by-2 matrix representing the configuration-dependent inertia, and C_r is a 2-by-2 configuration- and velocity-dependent matrix representing Coriolis and centrifugal effects; and τ_r = [τ_r1 τ_r2]^T is the input torque in q_r.

Passive impedance parameters: Passive stiffness and damping were excluded according to (Tee et al. 2004), because, unlike wrist movements (Charles and Hogan 2011), their contribution to the passive dynamics of reaching is believed to be small (active stiffness and damping were included through feedback—see below). Parameters for H_r and C_r were taken from (Tee et al. 2004) and calculated according to Eq. 6.3 in Burdet et al. (2013).

Feedback gains: As for the wrist model, the proportional and derivative gains of the feedback controller associated with reaching movements represent active stiffness and damping. Active stiffness was estimated according to (Tee et al. 2004) as a function of joint torque: $K_{FB,r}=\left[\begin{array}{cc}10.8+3.18\left|{\tau }_{r1}\right|& 2.83+2.15\left|{\tau }_{r2}\right|\\ 2.51+2.34\left|{\tau }_{r2}\right|& 8.67+6.18\left|{\tau }_{r2}\right|\end{array}\right]Nm\hspace{0.17em}/rad$ (Gomi and Osu 1998). The damping matrix was assumed proportional to the stiffness matrix K_FB,r such that the damping ratio in q_r1 was 0.26, a value observed experimentally for the shoulder and elbow (Perreault et al. 2004; Tsuji et al. 1995), resulting in $D_{FB,r}\left(1,1\right)=2\zeta \sqrt{K_{FB,r}\hspace{0.17em}\left(1,1\right)H_r\hspace{0.17em}\left(1,1\right)}$, where ζ= 0.26. The resulting damping ratio in q_r2 was slightly different than 0.26 because H_r is not proportional to K_FB,r. We chose this estimate of damping instead of the estimate used in (Tee et al. 2004) because this estimate results in an experimentally validated damping ratio. Note that we repeated the tests with different parameters to determine the sensitivity of our findings on our choice of model parameters (see discussion).

Hypotheses underlying differences in smoothness between wrist and reaching movements.

We hypothesized that differences in movement smoothness between wrist and reaching movements were caused by differences in the mechanical low-pass filtering properties of the DOF (Hypothesis 1), the amount of neuromuscular noise (Hypothesis 2), or the speeds required by the task (Hypothesis 3).

hypothesis 1: differences in low-pass filtering properties.

Assuming similar amounts of high-frequency content in the neural (input) signals generating wrist and reaching movements, differences in the low-pass filtering properties of the DOF (system) could produce differences in the smoothness of wrist and reaching movements (output signals) (Krylow and Rymer 1997). The low-pass filtering properties of a system are given by the system’s frequency response, which can be calculated from a model of the system’s dynamics following basic linear systems theory⁹ (Palm 2014). The aspects of the frequency response relevant to this study are captured in the system’s bandwidth. Note that a system’s bandwidth depends on its stiffness, damping, and inertia, so any differences in stiffness, damping, and/or inertia between the shoulder-elbow and wrist may result in differences in low-pass filtering between the two systems. To test the hypothesis that differences in low-pass filtering properties caused the differences in movement smoothness, we determined the bandwidth of the shoulder-elbow and wrist systems (represented by Dynamics in Fig. 2) from their transfer functions. To determine the systems’ transfer functions, we linearized the dynamics of the wrist, which eliminated the gravitational torque. Likewise, we linearized the dynamics of reaching about the neutral position (q_r = [45° 90°]^T), which eliminated the $C_r{\dot{\mathit{q}}}_{\mathit{r}}$ term representing nonlinear interaction torques. Re-arranging the control diagram yielded the following transfer functions for wrist and shoulder-elbow dynamics:

$$T{F}_w=\frac{1}{I_w{s}^2+\left(D_w+D_{FB,w}\right)s+\left(K_w+K_{FB,w}\right)}\mathrm{and}\hspace{0.17em}T{F}_r=\frac{1}{H_r{s}^2+D_{FB,r}s+K_{FB,r}}\mathrm{.}$$

We calculated the bandwidth of each system using Matlab’s bandwidth function, which defined the bandwidth as the first frequency where M drops below −3 dB (this occurs approximately at s) of its DC-value (M (ω = 0)). The joint stiffness of reaching movements depends on joint torque, so we calculated the mean magnitude of shoulder and elbow torques needed to simulate the reaching movements in the experiment (14-cm movements to 8 targets) following a MJT, resulting in |τ_r| = [2.9 0.85]^T, [0.86 0.25]^T, and [0.32 0.095]^T Nm for 300, 500, and 900-ms movements, respectively.

For comparison, we also determined the frequency content of the actual movements and of equivalent MJT. The frequency content of the actual movements was determined by computing the power spectrum of the displacement in each DOF. Subjects’ movement data during a single session (e.g., fast wrist rotations) were trimmed to the shortest length of data of all subjects and transformed into the frequency domain using Welch’s method with Matlab’s pwelch function. The power spectra for a session were then averaged across subjects, resulting in a mean power spectrum for each of the six sessions. The frequency content of the equivalent MJT represents the minimum bandwidth needed to complete each session and was determined as for the real movements, but with a train of MJT instead of the sequence of real movements. Each MJT in the train matched its real-movement counterpart in terms of origin/destination targets and duration and was strung together with 0.6-s rest periods between neighboring MJT (the minimum duration of the rest periods in the experiment).

hypothesis 2: differences in neuromuscular noise.

Differences in the amount of neuromuscular noise associated with wrist vs. reaching movements could produce differences in movement smoothness. Muscle contraction is always associated with noise or variability (Faisal et al. 2008) due to the orderly recruitment and variation in firing rate found in the motor neuron pool innervating muscles (Jones et al. 2002). The variability in the resulting muscle force is known to increase linearly with the mean of the muscle force (Schmidt et al. 1979), resulting in a constant coefficient of variation (CV), defined as the standard deviation of a signal divided by its mean (Hamilton et al. 2004). The CV differs among muscles in the upper limb; distal muscles are known to have more variability than proximal muscles when producing the same amount of force (Hamilton et al. 2004). However, it is unclear if this greater variability in distal muscles could be responsible for reducing the smoothness of distal movements because movements involving distal DOF presumably require lower force.

To test if the difference in CV between proximal and distal DOF could be responsible for the observed difference in movement smoothness, we injected SDN τ_N proportional to the feedforward signal as a disturbance into the system (Fig. 2). The noise was taken from a normally distributed random signal with zero mean, scaled so that the CV of τ_FF + τ_N was equal to experimentally measured values of CV [0.013 for wrist rotations and 0.005 for reaching movements (Hamilton et al. 2004)]. To isolate the effect of this noise and place wrist and reaching movements on equal footing, we assumed the desired trajectory to be a maximally smooth (i.e., minimum-jerk) trajectory. Movements were simulated at 1,000 Hz and differentiated to obtain velocity, acceleration, and jerk. As in the experiment (see Data processing), we filtered after each numerical differentiation with a sixth-order Butterworth filter with 15-Hz cutoff frequency and zero phase lag (using Matlab’s filtfilt function). To avoid introducing transients during filtering, 0.2 s of nonmoving data were added to the beginning and end of the data set before filtering. We repeated the process on five movements to each target and direction (80 total trajectories) and calculated for each simulated movement the measures of smoothness (jerk ratio and NumMax) as described above.

hypothesis 3: differences in required speed.

Although the parameters of the experimental protocol were chosen to compare wrist and reaching movements on an equal basis, it is possible that any differences in smoothness were due to differences in task requirements. To clarify, the wrist and reaching movements tested here each involved two DOF and equal numbers of targets and movements to each target, but the required movement amplitudes and speeds were not directly comparable since the task required angular displacement of the wrist but linear displacement of the hand. Because movement speed is known to affect smoothness, any differences in the required speed could have created differences in smoothness. In other words, if the speed of fast wrist movements were actually comparable to the speed of medium-paced reaching movements, and if the speed of medium-paced wrist movements were actually comparable to the speed of slow reaching movements, the differences in the jerk ratio between wrist and reaching movements would vanish (Fig. 5).

Fig. 5.

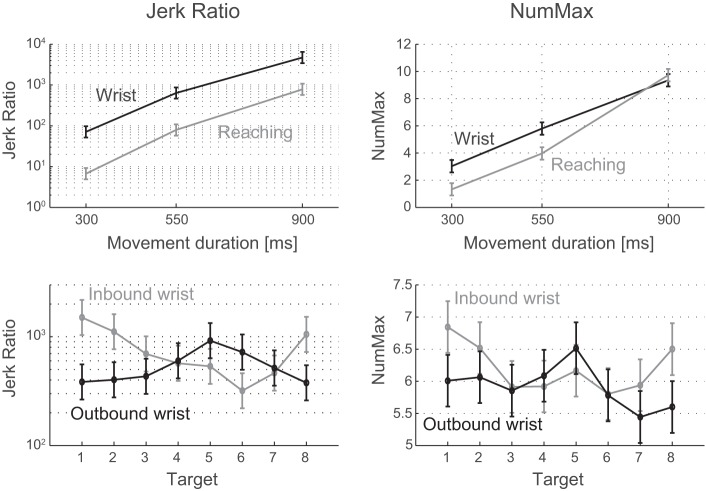
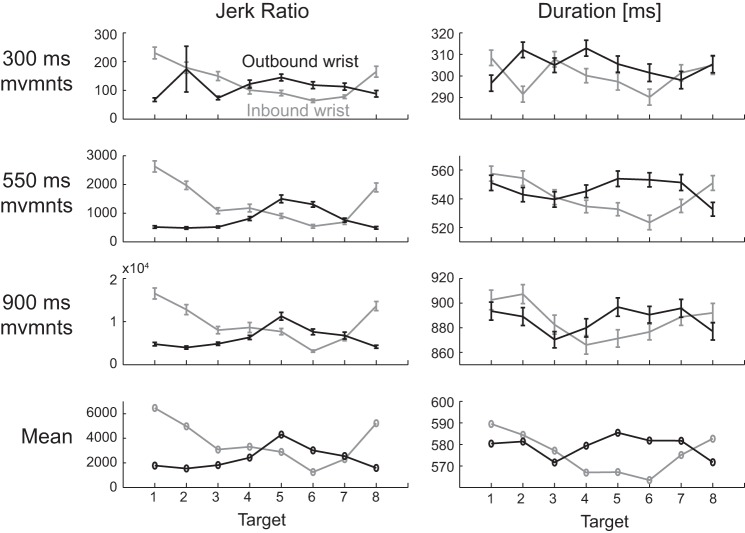
Measures of movement smoothness: Jerk ratio (left) and NumMax (right). Row at top: both measures showed that reaching movements were smoother than wrist movements, and that fast movements were smoother than slow movements. Row at bottom: the smoothness of wrist rotations varied with target and whether the movement was outbound (center-out) or inbound (out-center). Target numbers are explained in Fig. 1.

To test this hypothesis, we compared the angular speed at the shoulder and elbow to the angular speed at the wrist (this is preferred over comparing linear speeds because the choice of moment arm for wrist rotations is arbitrary). More specifically, we determined the mean angular speed of equivalent MJT to each target. We used the MJT (as opposed to actual movements) to compare task requirements instead of subjects’ response to the requirements. Wrist speed was calculated as the magnitude of the vector sum of the velocity in each DOF: $\sqrt{{\dot{q}}_{w1}{}^2+{\dot{q}}_{w2}{}^2}$. The angular speeds of the shoulder and elbow were calculated from a MJT of the hand, and the angular speed associated with movement to a given target was defined as the average of the speeds in each DOF $\left(\frac{\left|{\dot{q}}_{r1}\right|+\left|{\dot{q}}_{r2}\right|}{2}\right)$. For comparison, we also calculated the average of the absolute speeds in each DOF: $\left(\frac{\left|{\dot{q}}_{r1}\right|+\left|{\dot{q}}_{r1}+{\dot{q}}_{r2}\right|}{2}\right)$.

Hypotheses underlying differences in wrist movement smoothness between directions.

We hypothesized that differences in wrist movement smoothness between targets (1–8) and directions (outbound/inbound) were caused by differences in musculoskeletal mechanics (Hypothesis 1) or movement speed (Hypothesis 2).

hypothesis 1: differences in musculoskeletal mechanics.

Any anisotropy in movement smoothness may have been caused by an anisotropy in musculoskeletal mechanics. The mechanics of the wrist are known to be anisotropic (Formica et al. 2012; Pando et al. 2014), which is the likely cause underlying an observed anisotropy in movement curvature (Charles and Hogan 2012), suggesting that it might also be the cause of anisotropy in other kinematic measures such as smoothness. To clarify, the torque required to rotate the wrist in a given direction depends on the direction because the stiffness, damping, and gravitational torques are different in different directions (the inertia of wrist rotations is relatively isotropic). Because noise is signal dependent, differences in torque with direction result in differences in noise with direction and may therefore cause differences in movement smoothness.

To test this hypothesis, we modeled wrist rotations as above and focused on differences in smoothness between directions. Since wrist rotations are known to be underdamped (Halaki et al. 2006), we also simulated wrist rotations resulting from step inputs in torque to investigate the effects of overshoot on movement smoothness. Although a step input in torque is a rough approximation of the torque input observed in real movements (Hoffman and Strick 1999), it has been used successfully to understand other kinematic wrist behaviors (Charles and Hogan 2012). The measures of smoothness (jerk ratio and NumMax) were calculated for each simulated movement as described above for the real movements.

hypothesis 2: differences in movement speed.

Since slower movements are known to be considerably less smooth than fast movements (Doeringer and Hogan 1998; Vallbo and Wessberg 1993), any difference in smoothness between directions could conceivably be caused by slight differences in movement speed within the acceptable range in movement duration (±75, 100, and 150 ms for fast, medium, and slow movements, respectively). We investigated if directions with lower movement smoothness had longer movement durations.

Sensitivity Analysis

To test the robustness of our conclusions, we repeated our wrist and reaching simulations using a variety of model parameter values. More specifically, we determined the range in bandwidths for (passive and active) stiffness and inertia values ranging from half to twice our original values. As a function of stiffness and inertia (see above), damping was affected secondarily. We also repeated our simulations of SDN, increasing the CV of the noise until the resulting jerk ratio matched the observed jerk ratio.

RESULTS

Experiment

To characterize the smoothness of wrist movements and compare it to the smoothness of reaching movements, we asked subjects to make separate wrist and reaching movements at fast, medium, and slow speeds (specified by duration). The raw displacement data were differentiated and filtered to obtain velocity, acceleration, and jerk (Fig. 3 and Fig. 4). We calculated two measures of smoothness: jerk ratio and the number of maxima in the speed profile (NumMax), as shown in Fig. 5.

Fig. 3.

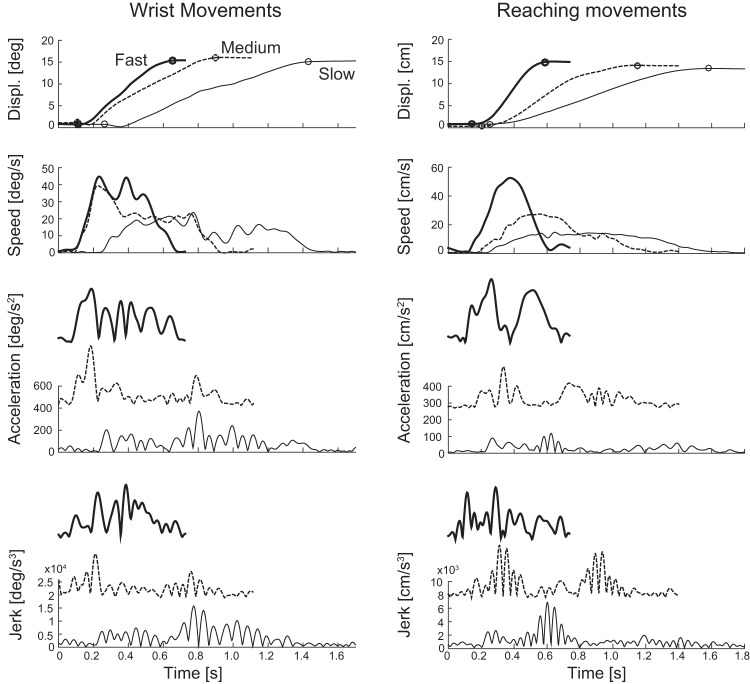
Examples of fast, medium, and slow wrist and reaching movements. Shown are the magnitude of the displacement, velocity, acceleration, and jerk vectors. The difference in smoothness is most easily seen in the speed profiles. All movements are outbound movements to target 1 (Fig. 1) made by the same subject. The circles in the top row indicate the start and stop of the movement based on 10% of maximum speed. To allow for better comparison of fast, medium, and slow acceleration and jerk, we added vertically offset versions as insets (each triad was scaled together).

Fig. 4.

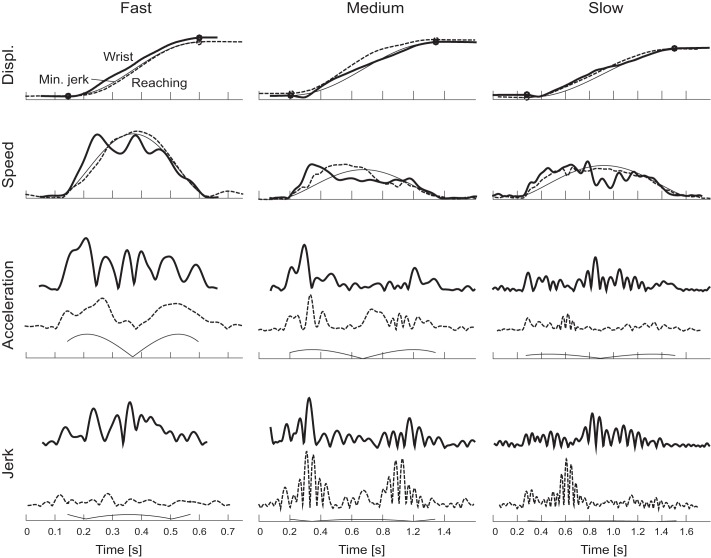
Direct comparison of wrist (thick solid line) and reaching (dashed line), with equivalent minimum-jerk trajectories (thin solid line) for reference. Wrist and reaching movements are scaled in magnitude to have matching equivalent minimum-jerk trajectories. All movements are outbound movements to target 1 (Fig. 1) made by the same subject (same movements as in Fig. 3). The circles in the top row indicate the start and stop of the movement based on 10% of maximum speed.

Our statistical analysis compared both measures between DOF (wrist, reaching), targets (1–8), directions (outbound, inbound), and speeds (fast, medium, slow). Wrist rotations were found to have significantly greater jerk ratio (P < 0.0001) and number of maxima (P = 0.016) than reaching movements (Table 1). We also found significant differences in wrist movement smoothness between targets (P < 0.0001 for jerk ratio and NumMax) and outbound/inbound direction (P = 0.0004 for jerk ratio and 0.0014 for NumMax). More specifically, jerk ratio varied between targets in a roughly sinusoidal pattern, with outbound and inbound smoothness ~180° out of phase (Fig. 5). The pattern for NumMax showed a similar trend but was less marked than the pattern in jerk ratio. We also found that wrist movement smoothness decreased significantly with movement duration (P < 0.0001 for jerk ratio and NumMax), consistent with similar findings for reaching [this study and Doeringer and Hogan (1998)] and finger movements (Vallbo and Wessberg 1993).

Table 1.

Results of statistical analysis

Data	Effect	Num DF/Den DF	F-Value Jerk Ratio	F-Value NumMax	P Value Jerk Ratio	P Value NumMax
Reach and wrist	joint	1/9	120	19.8	<0.0001	0.0016
Wrist	target	7/63	5.75	6.64	<0.0001	<0.0001
Wrist	direction	1/9	30.6	20.6	0.0004	0.0014
Wrist	speed	2/18	723	506	<0.0001	<0.0001
Wrist	target*direction	7/63	33.0	6.89	<0.0001	<0.0001

Simulation and Comparison

Differences in smoothness between wrist and reaching.

hypothesis 1: differences in low-pass filtering properties.

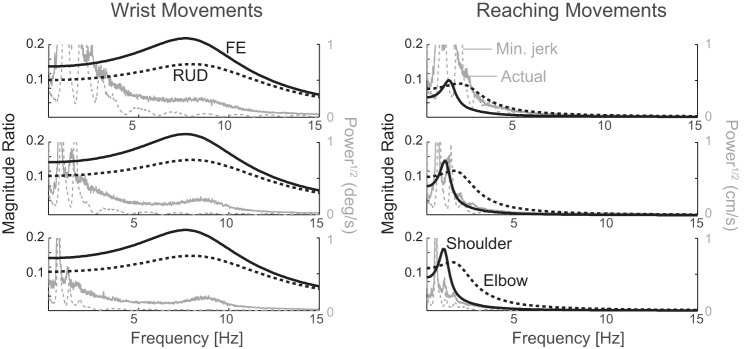
The wrist has a greater bandwidth than the shoulder-elbow system (Fig. 6), indicating that shoulder and elbow dynamics are capable of smoothing noise in the input (joint torque) more than wrist dynamics. More specifically, the bandwidth of the dynamics of the wrist was 12.5 Hz in FE and 13.4 Hz in RUD, whereas the bandwidth of the dynamics of the shoulder and elbow was 1.92 and 3.16 Hz for 300-ms movements, 1.58 and 2.67 Hz for 550-ms movements, and 1.47 and 2.52 Hz for 900-ms movements. Also shown is the mean power spectrum of subjects’ movements and the power spectrum of the equivalent MJTs, the latter representing the minimum bandwidth required to complete the tasks if subjects moved as smoothly as possible. Consistent with the greater bandwidth of wrist dynamics, wrist movements exhibit considerable power above 3 Hz not seen in reaching movements. Since this power is not required by the task (compare with the power in the MJTs), it represents noise and appears to decrease sharply at the end of the bandwidth of the wrist (around 10 Hz), consistent with the hypothesis that this is noise that is not filtered out by the dynamics of the wrist. Note that the absence of significant power in reaching movements above 3 Hz may be because noise in the input was filtered out by the dynamics of the shoulder and elbow, or because there was no significant noise in the input to the shoulder and elbow above 3 Hz (or a combination of the two). Note also that the decrease in the power of reaching and wrist movements, which occurs around 3 and 10 Hz, respectively, cannot be due to the low-pass filtering performed during the data processing because the cutoff frequency of the filter was at 15 Hz; its magnitude ratio at 10 Hz is −0.032 dB, corresponding to only a 0.37% decrease.

Fig. 6.

Magnitude ratio (measure of how much different frequencies in the torque input appear in the displacement output) of wrist and reaching movements of 300, 550, and 900 ms durations (top, middle, and bottom row, respectively). The range in frequencies over which the magnitude ratio stays high (bandwidth) is larger for the wrist (red lines in left column) than for the shoulder-elbow (red in right column), allowing more high-frequency noise (>2–3 Hz) to pass from the wrist torque to wrist displacement, resulting in jerkier wrist movements. Shown for comparison in gray are the power spectra of actual movements (solid) and equivalent minimum-jerk trajectories (dashed). The power spectra of actual movements show that wrist movements contained more power at higher frequencies (another indicator of greater jerkiness) than reaching movements even though the minimum power required to complete the task (shown by the power spectra of the minimum-jerk trajectories) was similar for wrist and reaching movements.

hypothesis 2: differences in neuromuscular noise.

Adding noise proportional to the feedforward torque had little effect on the simulated trajectories (Fig. 7A). The simulated speed profiles closely resembled a MJT and did not exhibit the multiple large peaks observed in real movements (Fig. 3 and Fig. 4). The mean jerk ratio and NumMax for simulated noisy 900-ms movements were 8.0 ± 5.4 and 1.2 ± 0.41 for the wrist (compared with 4,723 and 9.3 in the experiment) and 1.02 ± 0.0083 and 1 ± 0 for reaching (compared with 785 and 9.7). For the simulated jerk ratio to reach that observed in the experiment would require an ~40-fold increase in CV for the wrist and a 2,500-fold increase in CV for reaching. Therefore, although adding noise reduced the smoothness of wrist movements more than reaching movements, the reduction was far too small to account for the lack of smoothness observed in real movements.

Fig. 7.

A: simulated 900-ms wrist and reaching movements with signal-dependent noise (SDN), compared with the equivalent minimum-jerk trajectory. The displacement and speed of simulated wrist (thick solid line), reaching (dashed), and minimum-jerk (thin solid) trajectories are indistinguishable, indicating that SDN is not sufficiently large to produce the jerkiness observed experimentally (compare with Fig. 4). Wrist and reaching trajectories were scaled so their minimum-jerk trajectories matched, as in Fig. 4. The acceleration and jerk profiles are offset for a clearer view. B: to compare the smoothness of wrist and reaching movements as a function of movement speed instead of duration (Fig. 5), we plotted jerk ratio vs. mean angular speed for wrist movements (filled triangles) and reaching movements (solid and empty circles). Light gray, black, and dark gray markers represent 300-, 550-, and 900-ms movements, respectively. The mean angular speed for wrist movements within a duration category (300, 550, 900 ms) were very similar because amplitude and duration were constant, but for reaching movements, angular speed depended on target and relative vs. absolute speed (filled and empty circles, respectively). C: simulated 900-ms wrist movements with SDN, plotted as a function of target (explained in Fig. 1). This and other simulations of wrist rotations with SDN did produce differences in smoothness between targets, but the smoothness of outbound and inbound movements were in phase, unlike what we observed experimentally (compare with bottom-left subplot in Fig. 5), suggesting that factors not included in our model must be responsible for the observed differences in smoothness between targets.

hypothesis 3: differences in required speeds.

When compared on the basis of angular speed, wrist rotations are still less smooth than reaching movements (Fig. 7B). Jerk ratio decreases with an increase in angular speed for both wrist and reaching movements, but compared at a given speed, wrist movements have more jerk ratio than most of the reaching movements.

Spatial variations in wrist movement smoothness.

The variation in jerk ratio with target exhibited a clear sinusoidal pattern, accentuated by the fact that outbound and inbound patterns were 180° out of phase. We tested two hypothesized causes underlying this pattern.

hypothesis 1: differences in musculoskeletal mechanics.

The anisotropy in mechanical impedance and gravity (i.e., differences in stiffness, damping, inertia, and gravity with direction) did create an anisotropy in movement smoothness (Fig. 7C), but the pattern of smoothness did not match the observed pattern (Fig. 5). Although the simulated pattern was approximately sinusoidal and close to the right phase for inbound movements, the outbound pattern was completely in phase with the inbound pattern (instead of 180° out of phase), and the magnitude of the jerk ratio was too low by two orders of magnitude. After a thorough investigation, we found that the simulated pattern (Fig. 7C) resulted from the combined effects of gravity and stiffness (whether isotropic or anisotropic). To clarify, all outbound movements require the same amount of torque initially (at the center target), but as the movements progress toward the peripheral targets, movements involving radial deviation require more torque to overcome gravity and stiffness compared with movements involving ulnar deviation, where gravity produces some of the torque required to overcome stiffness. The torques required to overcome joint inertia and damping are small compared with those required to overcome stiffness and gravity, so the total torque required to rotate the wrist is essentially a function of joint angle. Consequently, the torques required for inbound movements are virtually the same as those required for outbound movements (but in reverse with respect to time), resulting in very similar amounts of noise accumulated in the input signal over the duration of the movement. Therefore, the smoothness of simulated outbound and inbound movements involving the same target is similar, and the simulated outbound and inbound patterns are in phase.

Simulating movements with a step input in torque instead of a desired trajectory in the form of a MJT also created differences in movement smoothness between directions (not shown), but the resulting pattern was also different from the observed pattern. The simulated pattern was periodic but had roughly twice the period of the observed pattern, inbound and outbound patterns were in phase, and the magnitude of the jerk ratio was again too low by two orders of magnitude. In addition, the trajectories resulting from step inputs varied greatly from the observed trajectories. These findings suggest that the observed differences in smoothness with direction are unlikely due to differences in musculoskeletal mechanics with direction.

hypothesis 2: differences in movement duration.

Slight differences in the duration of subjects’ movements with direction (within the allowable range) did roughly match the differences in movement smoothness in terms of both frequency and phase (Fig. 8), suggesting that the pattern in smoothness is related to the pattern in duration. Larger movement durations (slower movements) are associated with greater jerk ratios, as expected from the observed differences in smoothness between speeds described above. Although the match is not perfect (especially for outbound movements to targets 1 and 2), the overall pattern agrees quite well; outbound and inbound patterns in duration are roughly 180° out of phase and approximately match the phase of the outbound and inbound patterns in smoothness, respectively. The mean jerk ratio values correlated with duration for outbound and inbound movements (correlation coefficients of 0.67 and 0.89, respectively). In contrast, correlating outbound jerk ratio to inbound duration and vice versa yielded negative correlation coefficients (−0.76 and −0.27) indicating out of phase relationships. While this finding suggests that the slight differences in movement smoothness with direction may have been caused by slight differences in duration, it is possible that both findings are correlated phenomena caused by a yet unknown cause.

Fig. 8.

Differences in wrist movement smoothness (jerk ratio, left column) with target (1–8) and direction (outbound vs. inbound) match the differences in duration (right column) with target and direction, indicating that the observed differences in smoothness between targets are likely caused by—or at least correlated with—differences in movement duration (which are known to cause differences in smoothness). Outbound and inbound values are plotted in black and gray, respectively.

Sensitivity Analysis

Effect of filtering on measures.

We investigated the effect of filtering after each differentiation on our smoothness measures. More specifically, we determined the effect of filter cutoff frequency and order on the measures and the statistical significance of the main comparisons, compared with the baseline filter (6th-order Butterworth filter with cutoff frequency at 15 Hz). As expected, the jerk ratio increased significantly as the cutoff frequency of the filter was increased from 5 to 25 Hz, but it increased systematically across factors such that the main results remained unaffected. The only significant result that became insignificant was for the factor target at 5-Hz cutoff frequency, but the sinusoidal variation and 180° phase shift between inbound and outbound were clearly visible. Accordingly, the target-by-direction interaction remained significant (P < 0.0001) for all cutoff frequencies.

NumMax also increased with the cutoff frequency of the filter, but it did so in a manner that affected some of the statistical results. At cutoff frequencies of 20 and 25 Hz, NumMax was significantly larger for reaching movements than for wrist rotations (P = 0.0011 and P < 0.0001 for 20 and 25 Hz, respectively). Also, the pattern of variation in NumMax between targets and outbound/inbound directions broke down at 20 and 25 Hz. The sensitivity of differences in NumMax between factors to the cutoff frequency is likely caused by the fact that this measure does not distinguish between large and small peaks. As the cutoff frequency increases, the number of small peaks increases at a greater rate than the number of large peaks, but an additional large peak reduces movement smoothness more than an additional small peak. Therefore, the NumMax measure is not reliable at higher frequencies.

The order of the filter, which affects the slope of the roll-off, did not have a large effect on our statistical results. Decreasing the order from 6 to 2 caused only one change in significance: the P value for comparing NumMax between reaching and wrist went from 0.0016 to 0.058. However, the P value for the jerk ratio, which is a more robust measure, remained <0.0001 independent of filter order.

Effect of changes in parameters.

Halving stiffness and doubling inertia produced the minimum bandwidth, and doubling stiffness and halving inertia created the maximum bandwidth. In these cases damping remained unchanged since it scaled by $1\hspace{0.17em}/\hspace{0.17em}\sqrt{KI}$ (see methods) and bandwidth scaled with natural frequency ($\sqrt{K\hspace{0.17em}/\hspace{0.17em}I}$), so halving stiffness and doubling inertia halved the bandwidth, etc. The range in bandwidths for stiffness and inertia values ranging from half to twice our original values was 6–25 and 7–27 Hz for wrist FE and RUD, and 0.8–3.8 and 1.3–6.3 Hz for the shoulder and elbow, respectively. For reaching, stiffness depended on movement speed, so we calculated the lower end of the bandwidth range by halving the lowest stiffness (during slow movements), and we calculated the upper end of the bandwidth range by doubling the highest stiffness (during fast movements).

We also determined the increase in SDN required for the jerk ratio of our simulated movements to match the jerk ratio of actual movements. The experimentally measured coefficients of variation of SDN (Hamilton et al. 2004) would have to be increased by factors of 40 and 2,500 for wrist and reaching, respectively.

DISCUSSION

The purpose of this study was to 1) characterize the smoothness of wrist rotations, 2) compare it to the smoothness of planar reaching (shoulder-elbow) movements, and 3) determine the cause of differences in smoothness between wrist and reaching movements. Subjects performed separate wrist and reaching movements at multiple speeds. For each movement, we calculated two measures of smoothness (jerk ratio and the number of maxima in the speed profile, NumMax). We used these measures to compare smoothness between wrist and reaching movements, and to characterize wrist movement smoothness in terms of speed, target, and direction (outbound/inbound). Finally, we used models of the dynamics and control of wrist and shoulder-elbow movements to determine the cause of observed differences in smoothness.

Wrist Movements Were Significantly Less Smooth than Reaching Movements

We found wrist rotations to be significantly less smooth than reaching movements (Fig. 5) and determined that this difference reflects differences in the biomechanics of the shoulder-elbow vs. the wrist: the greater impedance (inertia, damping, stiffness) of the shoulder-elbow filters noise in the command signal more than the impedance of the wrist. In contrast, differences in SDN and the requirements of our experiment were not sufficiently large to recreate the observed differences in smoothness.

Observed differences in smoothness.

The difference in smoothness between wrist and reaching movements was quite robust. The mean jerk ratio for wrist movements was greater than the mean jerk ratio for reaching movements at all movement speeds (fast, medium, slow) and filter orders (2 and 6) and cutoff frequencies tested (5, 10, 15, 20, and 25 Hz). NumMax exhibited the same trend for fast and medium-paced movements filtered with a lower cutoff frequency (5, 10, 15 Hz) but reversed the trend for higher cutoff frequencies, presumably because this measure does not distinguish between large and small peaks in speed. Nevertheless, the NumMax measure is useful at lower filter cutoff frequencies because it is more intuitive than the jerk ratio. In addition to the results involving jerk ratio and NumMax, the difference in smoothness between wrist and reaching movements is perhaps seen most clearly in the difference in the power spectra (Fig. 6): wrist movements have considerably more power than reaching movements above 3 Hz (see below).

Hypothesis 1.

We found strong evidence that the difference in smoothness could be caused by differences in the low-pass filtering properties of the musculoskeletal dynamics. The bandwidth of the shoulder-elbow is much lower than the bandwidth of the wrist (Fig. 6) and therefore filters high-frequency noise (>2–3 Hz) more than the wrist. The simulated bandwidths are relatively robust against variations in model parameters (see below) and consistent with prior measurements for wrist (Halaki et al. 2006; Sinkjaer and Hayashi 1989) and reaching movements (Bennett 1993; Bennett et al. 1992; MacKay et al. 1986; Piovesan et al. 2012, 2013). Subjects’ wrist movements had considerable power beyond the spectrum of the corresponding MJTs, indicating that this power was not necessary to complete the task and therefore considered noise. The spectrum of this noise extended up to the end of the bandwidth of the wrist (~10 Hz), above which higher frequency noise in the torque input would have been filtered out. In contrast, reaching movements did not exhibit appreciable power above the bandwidth of the shoulder and elbow (~3 Hz). The lack of power above 3 Hz could reflect the low-pass filtering properties of the shoulder and elbow or a lack of noise in the input torque above 3 Hz. However, the former possibility is more likely since the tests of the latter (discussed next) did not match the observed behavior.

Hypothesis 2.

We did not find compelling evidence supporting the hypothesis that the differences in smoothness were due to greater noise in the torque of distal muscles. To clarify, the coefficient of variation of joint torque (CV, defined as the standard deviation of a signal divided by its mean) increases from proximal to distal, but presumably distal movements require less torque, so it was not clear if distal joint torque contained more or less noise. In our simulations with noise, wrist rotations were less smooth than reaching movements, but the jerk ratio and number of maxima were one to three orders of magnitude smaller than those observed experimentally, suggesting that the differences in smoothness were not likely caused by differences in CV. For the simulated movements to exhibit the same jerk ratio and number of maxima as the experimentally observed movements would require improbably large errors in CV (see results) or our impedance parameters (see below). In addition, we found upon further investigation that at least part of the difference in smoothness between simulated wrist and reaching movements was due to the difference in bandwidth, not CV. To clarify, because wrist rotations have a greater bandwidth, equal amounts of noise in joint torque will make wrist rotations less smooth than reaching movements. The amount of noise in torque is proportional to the CV and the torque itself. The wrist has a 2.6-times greater CV than reaching movements, but reaching movements require more torque. For example, medium-paced reaching movements required roughly 3 times more torque than medium-paced wrist rotations, resulting in roughly equal amounts of noise in torque. That simulated medium-paced wrist rotations were less smooth than reaching movements must therefore be due to the difference in bandwidth. We conclude that although SDN contributes to the difference in smoothness between wrist and reaching movements, its contribution is small.

Hypothesis 3.

The evidence supporting the hypothesis that the observed differences in smoothness were caused by different requirements placed on the wrist and reaching movements is weak. Since wrist movements are rotations and reaching movements focus on translating the hand, it is not clear how to make sure the requirements are equal. Although there exist several reasonable bases on which to compare wrist and reaching movements, there is not a single best way, so we compared wrist and reaching movements on multiple bases. The only reasonable basis for comparison of which we are aware that goes against the conclusion that wrist movements are noisier than reaching movements has to do with subjects’ self-chosen interpretations of speed categories. In a prior study (Charles and Hogan 2010), subjects were asked to make 15° wrist movements and 14-cm reaching movements (same amplitudes as in this study) at two speed instructions: “as fast as possible” and “at a comfortable pace.” On average, subjects’ fast and comfortably paced wrist rotations had considerably lower durations than the corresponding reaching movements (wrist: 281 and 652 ms; reaching: 403 and 934 ms), suggesting that the medium-paced reaching movements studied here (550-ms duration) may have appeared fast to subjects, and the slow reaching movements studied here (900-ms duration) may have appeared medium-paced to subjects. Comparing 300-ms wrist movements to 550-ms reaching movements and 550-ms wrist movements to 900-ms reaching movements, any difference in jerk ratio vanishes (Fig. 5), indicating that wrist and reaching movements are equally smooth.

However, multiple other reasonable bases for comparison support the conclusion that wrist movements are less smooth than reaching movements. The first and most compelling piece of evidence is that the power spectra of subjects’ wrist movements contained considerable power not necessary for the task (i.e., noise), whereas the power spectra of subjects’ reaching movements did not (Fig. 6). Second, wrist rotations show a greater amount of jerk ratio when compared on the basis of joint speed (Fig. 7B). Third, the jerk ratios of reaching movements within the same duration category (fast, medium, slow) are similar despite large differences in joint speed (Fig. 7B), suggesting that changes in movement smoothness may have been caused by changes in duration, not speed (whether this is true for wrist rotations is unclear because the required joint speeds were the same for all targets). In other words, comparing wrist and reaching movements on the basis of movement duration, as in this study, may be more important than slight differences in movement amplitude. Fourth, the wrist and reaching movements studied here are equivalent on the basis of their amplitude compared with the range of motion. The targets were placed in the center of the ROM of the wrist and reaching and occupy roughly the same proportion of the total ROM of the wrist and reaching (~15%).

Proprioception.

It is possible that the observed difference in smoothness between wrist and reaching movements could have been caused by differences in proprioception. However, although there is a higher density of muscle spindles per muscle weight in muscles involved in fine movements, higher spindle densities do not appear to be associated with greater proprioceptive sensitivity; consequently, “there is no evidence indicating a superior acuity for detecting movements and changes in limb position as one goes from proximal to distal joints” (Jones and Lederman 2006).

What is the source of the observed discontinuities?

We have shown that the wrist DOF suppresses any discontinuities in muscle force to a lesser degree than the shoulder and elbow, but what is the source of discontinuities in muscle force if not SDN? This question has been studied extensively for finger movements. Vallbo and Wessberg (1993) observed that finger movements appeared to be implemented by a series of force pulses at a frequency of 8–10 Hz, which produced discontinuities in velocity at the same frequency. This observation was robust, appearing in a large variety of conditions, including movements of varying amplitudes and speeds; movements involving one or all fingers (2–5) and the preferred or nonpreferred hand; movements by subjects with varying levels of motor skills; and movements with and without vision, a constant torque load, or prior explanation of the experiment or its intent.

Early hypotheses regarding the source of these discontinuities included the motor cortex, the spinal cord, the stretch reflex, and mechanical resonance. However, there is evidence against the stretch reflex (Wessberg and Vallbo 1996) and mechanical resonance (Vallbo and Wessberg 1993), and more recent studies have demonstrated that the “pulsatile velocity changes of slow finger movements are directly correlated to oscillatory activity in the motor cortex, which is sustained by cerebellar drive through thalamus and premotor cortex”, suggesting that “oscillatory activity in the cerebello-thalamo-cortical loop represents the neural mechanism for the intermittent control of continuous movements” (Gross et al. 2002). Importantly, such studies have determined directionality of signals in addition to correlation, providing direct evidence that these movement discontinuities have a central origin, indicating that continuous finger movements are implemented as a series of repeated micromovements (Schnitzler and Gross 2005).

Some studies have extended similar findings to the wrist, showing that wrist movements were associated with significant coherence around 6–12 Hz between acceleration and motor units (Kakuda et al. 1999), between motor units (Kakuda et al. 1999), and between muscle activity (EMG) and the motor cortex (Conway et al. 2004). Indeed, it appears that the entire motor system may be organized by a 10-Hz clock (Lisman 2015) that enables “coordinated communication between spatially distributed local networks in the brain” (Schnitzler and Gross 2005). This would suggest that all movements of significant duration (longer than 100 ms) are fundamentally discontinuous (Lisman 2015), but that these discontinuities (according to the current study) are suppressed to different extents by the low-pass filtering properties of the musculoskeletal dynamics of different DOF.

Wrist Rotation Smoothness Varied with Target and Direction

We found that the smoothness of wrist rotations varied sinusoidally between targets, and that the variation in outbound movements was ~180° out of phase with the variation of inbound movements. We found compelling evidence that this pattern was correlated with (if not caused by) differences in movement duration (Fig. 8). In contrast, differences in stiffness, damping, inertia, and/or gravity between directions are not likely causes of the pattern.

Although the match between the variations in jerk ratio and duration is not perfect, the fact that the patterns match for outbound and inbound, which are 180° out of phase, is relatively strong evidence of a mechanistic relationship. Although it is possible that the variation in movement duration caused the variation in smoothness, it is also possible that both variations are caused by another cause. Why movements in different directions had different durations is unknown. Our simulations showed that the variation in mechanical impedance (inertia, damping, stiffness) and gravitational torque with target did cause a variation in movement smoothness, but it was far too small in magnitude and did not match the observed variation, indicating that the variation in smoothness was not likely due to biomechanics. Likewise, it is unlikely that the known variations in impedance and gravitational torques caused the observed variation in movement duration (and secondarily the observed variation in smoothness) because they do not match the observed variation in duration either.

Sensitivity Analysis

General considerations.

The difference in bandwidths between wrist and reaching movements is large and quite robust to errors in parameter values. Our parameter values would have to be off by a factor of 2 in the worst possible combination (wrist stiffness twofold too large and inertia twofold too small, and vice versa for the shoulder and elbow) for the higher bandwidth for reaching movements (elbow) of 300-ms duration (the duration with the highest bandwidth) to be comparable to the lower bandwidth for the wrist (FE). Even then, the bandwidth of the shoulder would still be much lower than that of the wrist in RUD. Likewise, the difference between the experimentally observed smoothness measures and those estimated with SDN was large and unlikely to be due to errors in parameter values; the coefficients of variation for wrist and reaching muscles would have to be 40 and 2,500 times greater, respectively, than the experimentally measured coefficients (Hamilton et al. 2004) to yield smoothness measures similar to those measured in our experiment.

Stiffness.

Our simulations included estimates of joint stiffness during movement, which are notoriously difficult to measure. Although we based our estimates in the center of a relatively large number of past studies, it is conceivable that errors in our stiffness estimates could have resulted in flawed conclusions. However, further investigation showed the conclusions to be remarkably robust to changes in stiffness estimates.

classification of joint stiffness.

To clarify, it is helpful to classify past measurements of joint stiffness into categories based on the range of motion over which the measurement was made (short range vs. long range) and the amount of muscle activity during the measurement (passive vs. active). Short-range stiffness (SRS), which is measured by using small perturbations and is thought to reflect the stretching of actin-myosin cross-bridges before they break, is greater than long-range stiffness (LRS), which is measured by using larger perturbations and presumably involves cycling of the cross-bridges (Halaki et al. 2006; Hu et al. 2011; Rack and Westbury 1974). Passive and active joint stiffness are measured in the absence and presence of muscle activity, respectively, and can both be divided into measurements of SRS and LRS. It is important to further subdivide measurements of active joint stiffness into measurements performed 1) while the subject was trying to maintain a static posture or the subject’s joint was moved by a motor and 2) during voluntary movement. Measurements performed during posture maintenance or while being moved by a robot have shown that increasing muscle activity (by applying a torque bias or co-contracting) increases both SRS and LRS (de Vlugt et al. 2011; Gomi and Osu 1998; Klomp et al. 2014; Perreault et al. 2001), presumably because increased muscle activity engages more contractile filaments. In contrast, some studies have shown that stiffness decreases during voluntary movement compared with posture maintenance (Bennett et al. 1992; Ludvig and Perreault 2014) despite the increase in muscle activity necessary to make a movement, perhaps because of the transition from SRS to LRS.

stiffness in reaching model.

Our model of stiffness used to simulate reaching movements followed (Tee et al. 2004), which was based on measured changes in stiffness with joint torque during posture maintenance, not movement (Gomi and Osu 1998). Therefore, although this model is able to predict measurements of stiffness during movement quite well (Tee et al. 2004), it may have overestimated the active stiffness in our simulations of reaching movements. We repeated our reaching simulations with active stiffness that was reduced to passive stiffness. We found that decreasing active stiffness only lowered the simulated bandwidth, separating it farther from the bandwidth of wrist rotations. Likewise, reducing active stiffness had a negligible impact on the jerk ratio and number of maxima simulated with SDN (compared with the observed measures).

passive stiffness in wrist model.

Our simulation of wrist movements included estimates of both passive stiffness (forward dynamics) and active stiffness (proportional gain). The estimate of passive stiffness excluded SRS and was measured while the wrist was rotated by a motor (Formica et al. 2012). It is therefore likely a relatively accurate estimate of passive stiffness during voluntary movement.

magnitude of active stiffness in wrist model.

Active wrist stiffness likely varies with joint torque, but, unlike active shoulder-elbow stiffness, there do not currently exist reports of how active wrist stiffness varies with torque. We therefore used an estimate of active wrist stiffness at a constant joint torque and then determined the sensitivity of our conclusions on that choice of stiffness. Our estimate of active wrist stiffness was taken while subjects exerted a torque bias of 15% of the maximum voluntary contraction of the flexor carpi radialis (Halaki et al. 2006). The measurement value was similar to values made during production of 0.9–1 Nm torques (de Vlugt et al. 2011; Klomp et al. 2014), which is greater than the torques needed for fast wrist rotations [~0.1–0.2 Nm (Charles and Hogan 2011)]. Therefore, we likely overestimated active stiffness in our simulations of wrist movements. We performed additional simulations in which we reduced active stiffness to the point where it equaled the mean of prior measurements of passive SRS (Axelson and Hagbarth 2001; De Serres and Milner 1991; Klomp et al. 2014; Leger and Milner 2000) (40% of its original value). However, this reduction was still not sufficient to close the gap between wrist and reaching movements; it reduced the bandwidth of wrist FE and RUD from 12.5 and 13.4 Hz to 8.8 and 9.4 Hz (compared with the highest shoulder and elbow bandwidths of 1.9 and 3.2 Hz) and did not have any statistically significant effect on the jerk ratio or number of maxima simulated with SDN. In summary, varying active wrist stiffness from values that were too high (estimated with torque greater than that needed for fast wrist rotations) to values that were quite low (only passive SRS) did not change the main conclusions of this paper.

shape of active stiffness in wrist model.

The active wrist stiffness matrix was assumed to be a scaled version of the passive stiffness matrix, but it is possible that the stiffness in FE and RUD scale by different factors. This would result in an active stiffness ellipse with a different shape (aspect ratio) than the passive stiffness ellipse. To test the effect of different scaling factors on the results, we repeated our simulations with two additional active stiffness matrices whose stiffness ellipses had the same area (overall stiffness) but different shape than the default active stiffness matrix. The first matrix was scaled more in FE than in RUD compared with the passive stiffness matrix, resulting in an isotropic stiffness ellipse (circle). The second matrix was scaled more in RUD than FE compared with the passive stiffness matrix, resulting in a highly anisotropic stiffness ellipse with twice the aspect ratio as the default ellipse. These two conditions represent a relatively large range in the ratio of the scaling factors for FE and RUD, from 0.59 (isotropic) to 1.36 (anisotropic). However, the effect of these changes was small, with changes in bandwidth of less than 15% and negligible changes in the measures simulated with SDN (compared with the difference between simulated and observed measures). In summary, our conclusions are robust to relatively large (factor of 2), uniform and nonuniform scaling in active reaching stiffness.

Gravity.

In our experiment, we compared reaching movements performed with gravity support to wrist movements performed without gravity support. We chose these paradigms because they require roughly similar amounts of effort. Supporting the weight of the arm is much more difficult than supporting the weight of the hand, and supporting the weight of the arm for the required minimum of 480 movements would have led to significantly more fatigue (which itself can affect smoothness) than supporting the weight of the hand. Nevertheless, this difference in experimental conditions could have produced the observed differences in smoothness and begs the question: how does the smoothness of reaching movements compare with the smoothness of wrist movements when they are evaluated on an equal “gravitational footing” (either both with gravity or both without gravity)?

considerations from the literature.

It makes sense that gravity could affect the smoothness of movements: gravity alters the amount of torque required to accelerate or decelerate movements or simply hold a posture. Furthermore, changes in torque can affect joint stiffness and the amount of SDN, both of which affect movement smoothness. Gravity is known to affect other characteristics of movement, including the curvature, acceleration peak, and acceleration time of reaching movements in the sagittal plane (Gaveau et al. 2014), and the range over which individuals can control the direction of their shoulder and elbow stiffness (Hu et al. 2012). However, whether or how gravity affects movement smoothness is unknown since it has not been quantified and there are competing effects. For example, moving against gravity, as in the wrist movements from the center target to target 1 (Fig. 1A), requires additional torque to accelerate but less torque to decelerate. Despite many prior studies reporting on the smoothness of horizontal and vertical reaching movements, there is no indication of any difference in movement smoothness between horizontal and vertical reaching. Early studies emphasized the smooth, bell-shaped speed profile of reaching movements in both the horizontal plane (Flash and Hogan 1985; Morasso 1981) and the vertical plane (Atkeson and Hollerbach 1985). Furthermore, although no studies have quantitatively assessed the effect of gravity on movement smoothness, several studies provide qualitative observations that gravity does not affect smoothness. For example, Nilsen et al. (2003) reported smooth, bell-shaped velocity profiles regardless of the orientation of the body relative to gravity.

additional simulations.

Nevertheless, to further investigate if gravity affects movement smoothness, we repeated our simulations under different gravitational conditions. Our original wrist simulations included gravity (to match the experiment), so we repeated them without gravity to estimate the effect of gravity. Our original reaching simulations did not include gravity since subjects received support against gravity in the experiment. Simulating horizontal reaching movements with gravity is difficult because the additional torque required to support the arm against gravity acts about a different axis than the torques required to reach in the horizontal plane. Although some muscles are involved in both tasks (e.g., anterior and posterior deltoid), the extent to which the additional activity in these muscles required to overcome gravity affects the torque about a perpendicular axis needed for reaching is unclear. Instead, we simulated reaching movements in the sagittal plane and repeated the simulations with and without gravity (this is equivalent to reaching in the horizontal plane with gravity acting in the direction of x_r1—see Fig. 1B).

results of additional simulations.

Because our estimate of active wrist stiffness was independent of torque, removing gravity did not affect the bandwidth. In reality reducing torque would reduce active wrist stiffness, but the decrease is expected to be small because the gravitational torque (0.2 Nm) is relatively small compared with the torques that were required (0.1–2.1 Nm) in the studies used to estimate our active stiffness value (de Vlugt et al. 2011; Halaki et al. 2006; Klomp et al. 2014; Sinkjaer and Hayashi 1989). In other words, we expect the bandwidth of the wrist is relatively insensitive to gravity. In contrast, the gravitational torque required for reaching in the vertical plane is large and increased active stiffness two- to threefold (depending on movement duration) compared with our simulations without gravity. That said, even this large increase in stiffness only increased the bandwidth of the shoulder and elbow to 2.5 and 4.0 Hz, which is still small compared with the bandwidth of the wrist (12.5 and 13.4 Hz). Finally, the simulations with SDN were only slightly dependent on gravity. Removing gravity from the wrist simulations decreased the jerk ratio by 15%, and adding gravity to the reaching simulations increased jerk ratio by 4%, but these changes are negligible compared with the 40-fold and 2,500-fold increases in noise necessary to match the experimentally observed jerk. In summary, comparing wrist and reaching on an equal gravitational footing (both with or without gravity) did not alter our conclusions.

Limitations

Visual differences.

There were two differences in visual feedback between wrist and reaching movements. First, because the cursor represented the angle of the wrist during wrist movements but the position of the hand during reaching movements, it was not possible to make the visual gains between actual movement and cursor displacement (degrees to pixels or length to pixels) identical for wrist and reaching movements. The visual gains were chosen such that the peripheral targets (placed at 15° or 14 cm from the center target for wrist rotations and reaching movements, respectively) filled the screen. Second, during wrist rotations, the wrist and cursor moved in the same direction, whereas during reaching movements, the hand moved in the horizontal (transverse) plane but the cursor representing the hand moved in the vertical (frontal) plane. These differences in visual feedback could have caused the observed differences in smoothness. For example, the visual gain would be expected to affect the amplitude of visual-based corrections, and such corrections could directly influence movement smoothness. An additional experiment without visual feedback would be necessary to conclusively rule out this possibility.

However, in the absence of such an experiment, there are several reasons suggesting that it is unlikely that the differences in visual feedback contributed significantly to the observed differences in smoothness. First, the degree of smoothness observed in reaching movements has been shown to be largely independent of visual feedback (Doeringer and Hogan 1998). Second, our data processing focused on the ballistic portion of movements (see methods), removing or reducing the corrective movements that rely heavily on visual feedback. Third, although the amplitudes of wrist rotations and reaching movements are not directly comparable, the angular displacements at the shoulder and elbow required for the reaching movements are similar to the angular displacements at the wrist: the absolute angular displacement was 18° for the shoulder and 16° for the elbow (averaged over all targets), compared with 15° for the wrist. In other words, the visual gain from angular displacement to cursor movement was similar for the two tasks. Fourth, the mapping from horizontal hand movement to vertical cursor movement is trivial for healthy subjects, who have “learned this mapping in their previous experience with computer ‘mousing.’” (Shadmehr and Wise 2005). Indeed, many studies of visuomotor adaptation use this setup as the starting point to which perturbations are added (Galea et al. 2011; Kagerer et al. 1997; Krakauer et al. 2000, 2005). Accordingly, we were unable to find any prior studies that measured how long it takes for subjects to adapt to the mapping from hand movement in the horizontal plane to cursor movement in the vertical plane, perhaps because subjects have already adapted through years of prior experience of using a computer mouse. Fifth, for reaching movements to targets 3 and 7 (Fig. 1B), the hand and cursor did move in the same direction, but the smoothness in these directions was similar to the smoothness in the other directions (Fig. 7B).

Mechanical differences.

There were several mechanical differences between the wrist and reaching tasks that could have caused the observed differences in movement smoothness. 1) The wrist movement task required torque to compensate for gravity, whereas during the reaching movement task the arm was supported against gravity with a sling. 2) The sling resulted in indirect effects on reaching movements not present during wrist rotations. 3) Although each subject’s trunk was constrained with shoulder straps during reaching movements, the straps did not fully eliminate motion of the scapula or the center of rotation of the glenohumeral joint. Unintended motion of the scapula resulted in inertial interaction torques (on the upper limb) not included in the wrist movements (the forearm was more grounded than the scapula) or in our simulation of reaching movements. To quantify the effect of these differences on movement smoothness, one could perform an additional experiment comparing movements in a single proximal DOF to movements in a single distal DOF, both performed in the same plane to allow equal gravitational exposure. Simultaneously recording the motion of the glenohumeral joint would enable one to calculate the inertial interaction torques on the upper arm.

In the absence of such an experiment, we find it unlikely that these mechanical differences contributed significantly to the observed differences in smoothness. 1) As described above (Sensitivity Analysis—Gravity), a review of past studies and performance of additional simulations to compare wrist and reaching movements on an equal footing revealed that differences in gravitational support were likely too small to account for the observed differences in smoothness. 2) During reaching movements the arm was suspended by a 2-m sling and was therefore not perfectly constrained to the horizontal plane. For the 14-cm reaching movements, the maximum angle subtended by the sling was 4.0°, resulting in a maximize rise of the forearm of 4.9 mm. This rise in the forearm as the hand approached the peripheral targets produced a resistive force pointing back toward the center target, requiring additional torque at the shoulder and elbow. Postsimulation calculations confirmed our expectation that the additional torque was small for fast movements (6 and 4% of the shoulder and elbow torque, respectively). However, for comfortably paced and slow movements, which do not require much torque to accelerate and decelerate the arm, the additional torque due to the sling was 22 and 14% of the shoulder and elbow torque for comfortably paced movements and 64 and 39% of the shoulder and elbow torque for slow movements. In other words, although the sling eliminated the shoulder and elbow torques required to directly support the arm against gravity, which would have been much larger (by 1–2 orders of magnitude), the sling indirectly modified the torques required to move the arm in the horizontal plane, and we did not include this effect in our simulations. Because increasing torque indirectly increases both bandwidth and SDN, including this increase in our simulations would have moved the bandwidth of the shoulder-elbow closer to that of the wrist and moved the simulated jerk closer to the observed jerk. However, the changes are negligible compared with the differences. Increasing shoulder and elbow torque by 64 and 39%, respectively, resulted in an increase in bandwidth on the order of 2%, two orders of magnitude smaller than the roughly sixfold increase needed to match the bandwidth of the wrist. Likewise, increasing shoulder and elbow torque by 64 and 39% is much less than the 2,500-fold increase in noise required for our reaching simulations with noise to match our observations. 3) Measurements of reaching movements performed in different laboratories with varying amounts of trunk constraint (Atkeson and Hollerbach 1985; Flash and Hogan 1985; Gaveau et al. 2014; Morasso 1981; Nilsen et al. 2003) yielded smooth speed profiles, suggesting that the amount of trunk immobilization had little effect on the smoothness of reaching movements.

Other considerations.

measures of smoothness.

There are other measures of movement smoothness that could have been used to characterize wrist movement smoothness and compare with the smoothness of reaching movements (Balasubramanian et al. 2012; Rohrer et al. 2002). Our main measure, jerk ratio, is dimensionless, allowing direct comparison between wrist and reaching movements, and unlike dimensionless jerk (Hogan and Sternad 2009), has an intuitive interpretation (how many times less smooth than the smoothest possible movement). Although the number of maxima in the speed profile is less robust, we included it because it is commonly used and very intuitive.

hypotheses.

A limited number of hypotheses and models were used to investigate the causes underlying our observations. We chose simple models to capture first-order phenomena and reduce the sensitivity of our results on large numbers of parameters. Additional experiments could be used to further test our conclusions. To determine if a decrease in bandwidth of wrist dynamics would result in smoother movements, one could add inertia to the wrist, although such movements would require greater torque, which would increase the SDN.

Data filtering.

Although filtering the data after each differentiation was necessary to remove nonphysiological high-frequency content and obtain reasonable estimates of higher order derivatives, it clearly affected the measures. We dealt with this issue by testing whether the properties of the filter (cutoff frequency and order) altered the relative differences in smoothness observed between wrist and reaching movements, targets, directions, and speeds, and would therefore alter the main conclusions of the paper. We found that jerk ratio was robust against changes in cutoff frequency (5–25 Hz) and filter order (2 and 6), whereas differences in the number of maxima in the speed changed at higher cutoff frequencies, likely because this measure does not distinguish between large and small peaks. Note that the difference in the power spectra of subjects’ wrist and reaching movement is completely independent of filtering (since we performed the power spectrum estimation on unfiltered position data) and provides important evidence that wrist movements are less smooth than reaching movements.

Conclusion

This study provides the first thorough characterization of the smoothness of wrist movements in two DOFs of which we are aware, compares it to the baseline of reaching movements, and explores potential causes underlying observed patterns in movement smoothness. The finding that proximal-distal differences in the low-pass filtering properties of DOF are the likely cause for the observed differences in movement smoothness underline the importance of understanding biomechanical contributions to motor control. That distal movements are less smooth than proximal movements can feel counterintuitive since distal DOF are used for fine manipulation and are considered more dexterous than proximal DOF. However, if dexterity includes agility (the ability to move quickly and easily), then greater dexterity implies less smoothness: the same bandwidth that allows agile (i.e., high-frequency) movements also passes more high-frequency noise. Thus agility and jerkiness are two sides of the same coin. Accordingly, we predict that fingers, whose large bandwidth [on the order of 25 Hz (Vallbo and Wessberg 1993)] allows them to represent the epitome of agility, have the jerkiest of all upper-limb movements. Although the smoothness of finger movements has been thoroughly characterized (see above), we are not aware of any comparison of finger movement smoothness to other joints.

The characterization of wrist movement smoothness as a function of movement direction and speed can be used as a baseline for evaluations of the severity of movement disorders. Such evaluations could be made through the use of robotic rehabilitation devices, motion capture sensors, or wearable activity sensors capable of measuring displacement or one of its derivatives across the wrist. This opportunity to use movement smoothness as a measure of impairment and recovery (Dipietro et al. 2009; Rohrer et al. 2002, 2004) is especially relevant to wrist movements because they tend to remain impaired longer and, being less smooth even in unimpaired subjects, could potentially provide a more sensitive measure of recovery than shoulder/elbow movements.

AUTHOR CONTRIBUTIONS

L.H.S. performed experiments; L.H.S., A.D.D., and S.K.C. analyzed data; L.H.S., A.D.D., and S.K.C. interpreted results of experiments; L.H.S., A.D.D., and S.K.C. prepared figures; L.H.S. and S.K.C. drafted manuscript; L.H.S., A.D.D., and S.K.C. edited and revised manuscript; S.K.C. conceived and designed research; S.K.C. approved final version of manuscript.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).