Vagal baroreflex latency in circulatory control

In the recent paper by Eckberg et al. (2016) the issue of baroreflex latency resurfaces, and in particular how this latency turns up in recordings of blood pressure and heart rate: at resting heart rates, does the vagal branch of the baroreflex exert its feedback mainly within one heartbeat (our view; DeBoer et al. 1987), or is most of the feedback effect to be expected one beat later (Eckberg et al.)?

In the paper by Eckberg et al. (2016), it is stated that our group assumes that frequency domain and time domain analyses give different results. We will elucidate this point by comparing different analysis techniques for heart rate and blood pressure variability data.

In their paper, Eckberg et al. tackle the question of vagal baroreflex latency by a combination of time and frequency domain analyses of available recordings. To do so, they construct a continuous R–R interval signal by assigning the value of the past interval to the moments of occurrence of QRS complexes and fitting a cubic spline to these data points. A continuous systolic pressure signal is constructed in the same fashion (Fig. 1). The details of this procedure are not given in the cited paper, but have been described in Cooke et al. (1999). To mimic Fig. 4C in Eckberg et al. we constructed Fig. 1 A for a theoretical signal, sinusoidally varying at 0.25 Hz. Figure 1 B shows the delay of the maximum in the R–R interval signal to be equal to the distance between the occurrence of the finger systolic pressure to the R‐peak in the ECG. Under resting circumstances, at a heart rate of 60 bpm, this is around 0.6 s. The phase difference in the figure is around −54 deg. One should keep in mind that for baroreflex effects on the R–R interval the physiologically relevant period is from the occurrence of the pulse wave upstroke at the level of the baroreceptors to the beginning of the ECG P‐wave.

Figure 1. Different representations of fluctuations in systolic pressure and R–R interval.

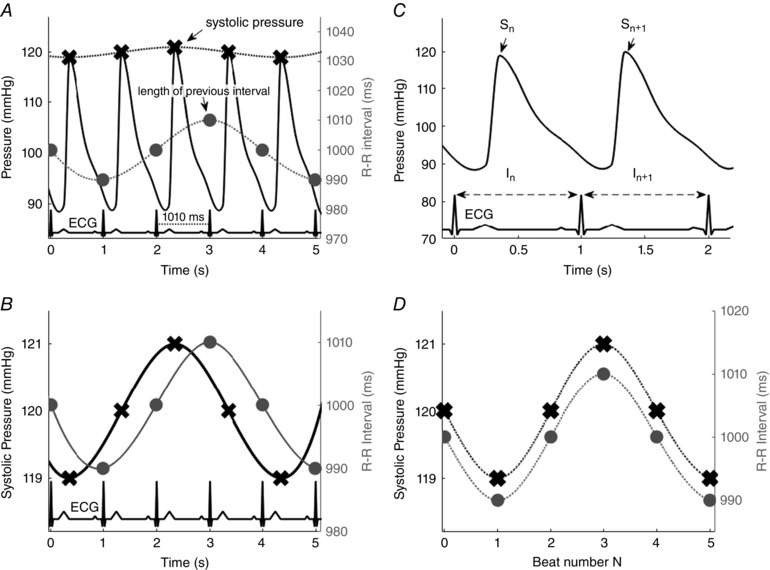
A and B, the transformation of the beat‐to‐beat variation in successive systolic pressures (crosses) and R–R intervals (circles) into a continuous signal by spline interpolation of the point values. Note the different vertical scales. C and D, alternatively, the variations can be represented as successive values per beat number. Both representations are equally useful, but they result in relevant differences in the apparent phase between interval and pressure fluctuations.

In our research, we assign all data which occur between two QRS complexes to the same row of the data matrix (Fig. 1 C) and we apply a fast Fourier transform to the dataset, the average heart rate serving as the sample rate. We have proven that this method gives virtually identical spectral results to the more rigid non‐interpolating algorithms like the spectrum of counts (DeBoer et al. 1984). Consequently, when the data from Fig. 1 A are put on this number scale, they look like Fig. 1 D: pressure and interval changes are in phase. In the cross‐spectrum this shows up as a phase difference of 0 deg, of course not implying that there is no vagal baroreflex latency. In general, our method finds a phase difference between systolic pressure and R–R interval variations of around –60 deg at 0.1 Hz (i.e. pressure changes leading), decreasing to around 0 deg at 0.25 Hz (DeBoer et al. 1987). Eckberg et al. find similar results, taking the differences in methods into account.

However, Eckberg et al. state that the short phase shift/time delay of 0.4 s at their highest used respiratory rate of 0.25 Hz can only be the result of some feed‐forward central respiratory sinus arrhythmia. They consider the measured latency of less than 0.5 s, as found by mechanical (Seidel et al. 1997) or electrical stimulation (Borst & Karemaker, 1983) of the baroreflex too short for what happens in spontaneous variability. Moreover, that sort of stimulation would be unphysiologically strong and the induced earliest effect too small. Therefore, the ‘real’ latency would be at least the 1.35 s, which they found for 0.1 Hz oscillations, both for spontaneous and paced breathing. This interpretation is too easy. For one, changes in systolic pressure during a phenylephrine test (the gold standard for baroreflex sensitivity measurement) correlate best with the durations of the ongoing heartbeat, as long as heart rate is below 75 bpm, only jumping to the next interval at higher heart rates (Pickering & Davies, 1973). Heart rates in the study by Eckberg et al. are well below this value. The latency measurements by neck cuff suction may, indeed, be unpleasant for the test subjects, but the patients with an implanted stimulator of the carotid sinus nerves did sometimes not even notice the stimulation.

Finally, in blood pressure and heart rate oscillations in the range 0.05–0.25 Hz, the slow sympathetic baroreflex response to one cycle is mixed into the next cycle. Hence, the phase difference between pressure and interval at 0.1 Hz can well be explained by this sympathetic contribution, shifting the latency from pressure to heart rate to much longer values (DeBoer et al. 1987). Due to this sympathetic contribution, at higher respiratory frequencies the interval values can even appear to lead pressure (DeBoer, 1985, p. 157).

In conclusion, variations in systolic pressure are immediately translated into changes in cardiac vagal bursts by the baroreflex. In this way, the next diastolic pressure is stabilized, whereby blood pressure stability is bought at the expense of heart rate variability.