Control of a two-dimensional movement signal by a noninvasive brain-computer interface in humans

Abstract

Brain-computer interfaces (BCIs) can provide communication and control to people who are totally paralyzed. BCIs can use noninvasive or invasive methods for recording the brain signals that convey the user's commands. Whereas noninvasive BCIs are already in use for simple applications, it has been widely assumed that only invasive BCIs, which use electrodes implanted in the brain, can provide multidimensional movement control of a robotic arm or a neuroprosthesis. We now show that a noninvasive BCI that uses scalp-recorded electroencephalographic activity and an adaptive algorithm can provide humans, including people with spinal cord injuries, with multidimensional point-to-point movement control that falls within the range of that reported with invasive methods in monkeys. In movement time, precision, and accuracy, the results are comparable to those with invasive BCIs. The adaptive algorithm used in this noninvasive BCI identifies and focuses on the electroencephalographic features that the person is best able to control and encourages further improvement in that control. The results suggest that people with severe motor disabilities could use brain signals to operate a robotic arm or a neuroprosthesis without needing to have electrodes implanted in their brains.

Brain activity produces electrical signals that can be detected from the scalp, from the cortical surface, or within the brain. Brain-computer interfaces (BCIs) change these signals from mere reflections of brain activity into outputs that convey the user's intent to the outside world (1). Because they do not depend on nerves and muscles, BCIs can provide communication and control to people with severe neuromuscular disorders such as amyotrophic lateral sclerosis (ALS), brainstem stroke, cerebral palsy, and spinal cord injury. The primary goal of BCI research is to enable these users, who may be completely paralyzed (“locked in,” unable even to breathe or to move their eyes), to express their wishes to caregivers, operate word-processing programs, or even control multidimensional movements of a robotic arm or a neuroprosthesis.

BCIs can be noninvasive or invasive. Noninvasive BCIs, which derive the user's intent from scalp-recorded electroencephalographic (EEG) activity, are already in use for basic communication and control (2, 3). Invasive BCIs, which derive the user's intent from neuronal action potentials or local field potentials recorded within the brain, are being studied mainly in nonhuman primates (4-12). These invasive BCIs face substantial technical difficulties and entail significant clinical risks: they require that recording electrodes be implanted in the cortex and function well for long periods, and they risk infection and other damage to the brain. The efforts to develop them, despite these disadvantages, are based on the widespread belief (13-17) that only invasive BCIs will be able to provide users with real-time multidimensional control of a robotic arm or a neuroprosthesis. The study presented here shows in humans that a noninvasive BCI, using sensorimotor rhythms recorded from the scalp, can provide multidimensional control that is within the range reported for invasive BCI studies in monkeys. These results suggest that people with severe motor disabilities might control complex movements without having electrodes implanted in their brains.

Methods

Human Subjects. Four people [a man age 41 (user A), a woman age 27 (user B), a man age 31 (user C), and a man age 23 (user D)] were the BCI users in this study. User A had a complete midthoracic (T7) spinal cord injury 26 years before the study. User D had an incomplete midcervical (C6) spinal cord injury 7 years before the study. Both had normal arm function, had little or no leg function, and used wheelchairs. Users B and C had no disabilities. These users varied widely in their prior BCI experience. User A had participated in several studies of one-dimensional cursor control (228 sessions; 91 h of performance) (18), and user B had participated in one such study (28 sessions; 11 h of performance). User C had no previous experience. User D had participated in a one-dimensional study (47 sessions; 19 h of performance) 4-5 years earlier and had no BCI experience in the 4 years since. The study was approved by the New York State Department of Health Institutional Review Board, and each user gave informed consent.

Study Protocol. During BCI operation, the user sat facing a video screen (19, 20). EEG activity was recorded from 64 standard electrode locations distributed over the entire scalp (21). All 64 channels were referenced to the right ear, amplified 20,000× (bandpass 0.1-60 Hz), digitized at 160 Hz, and stored. A small subset of channels controlled cursor movement online (see below).

A trial began when a target appeared at one of eight locations on the periphery of the screen (Fig. 1A). A target location was block-randomized (i.e., each occurred once every eight trials). One second later, the cursor appeared in the middle of the screen and began to move in two dimensions with its movement controlled by the user's EEG activity as described below. If the cursor reached the target within 10 s, the target flashed as a reward. If it failed to reach the target within 10 s, the cursor and the target simply disappeared. In either case, the screen was blank for 1 s, and then the next trial began.

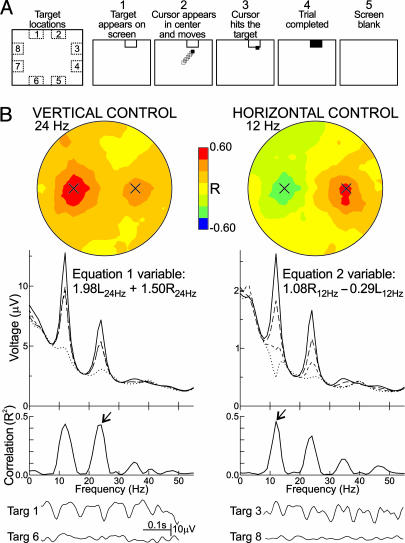
Fig. 1.

The protocol and the EEG control it achieves. (A) Protocol. The screen at Left shows the eight possible target locations. The other screens show the sequence of events in one trial. 1, a target appears; 2, 1 s later the cursor appears and moves in two dimensions controlled by the user's EEG activity as described in Methods; 3, the cursor reaches the target; 4, the target flashes for 1 s; 5, the screen is blank for 1 s and then the next trial begins. (Step 2 lasts up to 10 s. If the cursor does not reach the target in this time, the trial jumps to step 5.) (B) Topographical and spectral properties of user A's EEG control. In this user, vertical movement was controlled by a 24-Hz beta rhythm and horizontal movement by a 12-Hz mu rhythm. (Top) Scalp topographies (nose at top) of the correlations of the 24-Hz and 12-Hz rhythms with vertical and horizontal target levels, respectively. The sites of the left- and right-side scalp electrodes [locations C3 and C4 over sensorimotor cortex (21)] that controlled the cursor are marked. Vertical correlation is greater on the left side, whereas horizontal correlation is greater on the right side. The topographies are for R rather than R² to show the opposite (i.e., positive and negative, respectively) correlations of right and left sides with horizontal target level. (Middle) Voltage spectra (i.e., the weighted combinations of right-side and left-side spectra) from which were derived the vertical and horizontal variables and their corresponding R² spectra. Voltage spectra are shown for the four vertical target levels [targets 1 and 2 (solid), 3 and 8 (long dash), 4 and 7 (short dash), and 5 and 6 (dotted)] and for the four horizontal target levels [targets 3 and 4 (solid), 2 and 5 (long dash), 1 and 6 (short dash), and 7 and 8 (dotted)], respectively. For the R² spectra, the arrows point to the frequency bands used for the vertical and horizontal variables, respectively. (Bottom) Samples of EEG activity from single trials. On the Left are traces from electrode C3 (i.e., the major contributor to the vertical variable) for trials in which the target was at the top (target 1 in Fig. 1 A) or bottom (target 6) screen edge. On the Right are traces from electrode C4 (the major contributor to the horizontal variable) for trials in which the target was at the right (target 3) or left (target 8) edge. They illustrate the sensorimotor rhythm control that enabled the user to move the cursor to the target.

A daily session consisted of eight 3-min runs separated by 1-min breaks. Users A-D completed 68, 22, 40, and 25 sessions, respectively, at a rate of 2-4 per week. In each user's initial sessions, the transition from one-dimensional to two-dimensional control was accomplished by gradually increasing the magnitude of movement in the second dimension and/or by alternating between one-dimensional runs in the vertical and horizontal dimensions and then switching to two-dimensional runs.

Control of Cursor Movement. Each dimension of cursor movement (Fig. 1A, screen 2) was controlled by a linear equation in which the independent variable was a weighted combination of the amplitudes in a mu (8-12 Hz) or beta (18-26 Hz) rhythm frequency band over the right and left sensorimotor cortices. The weights in this variable were updated after each trial by an adaptive algorithm to optimize the translation of the user's EEG control into cursor control.

During the cursor movement period, the cursor moved every 50 ms and was controlled as follows. The last 400 ms of spatially filtered EEG activity [large Laplacian filter (22) from two locations over sensorimotor cortex (C4 on the right and C3 on the left) (21)] underwent autoregressive frequency analysis (23) to determine the amplitudes in specific mu-rhythm and beta-rhythm frequency bands. The selection of mu- and/or beta-rhythm bands was based on the characteristics of each user's previously developed one-dimensional control; the form of their combination was based on initial studies of two-dimensional control (1, 18, 24). To determine vertical cursor movement (M_V), one right-side amplitude (R_V) and one left-side amplitude (L_V) were each multiplied by a weight (w_RV and w_LV, respectively), and the results were added to give the “vertical variable,” the independent variable in a linear equation that specified a vertical cursor movement in pixels:

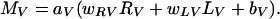1

To determine horizontal cursor movement (M_H), one right-side amplitude (R_H) and one left-side amplitude (L_H) were each multiplied by a weight (w_RH and w_LH, respectively), and the results were added to give the “horizontal variable,” the independent variable in a second linear equation that specified a horizontal cursor movement in pixels:

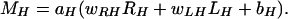2

The terms a_V, a_H, b_V, and b_H in these equations were controlled online as described in refs. 19 and 25. Positive and negative values of M_V moved the cursor up and down, respectively. Positive and negative values of M_H moved it right and left, respectively.

Throughout data collection, full topographical and spectral analyses (19, 26) (e.g., Fig. 1B) showed that the users' cursor control was due to actual sensorimotor rhythm control rather than to non-EEG artifacts.

The Adaptive Algorithm. Initially, the Eq. 1 weights were both +1.0, and the Eq. 2 weights were +1.0 and -1.0. Thus, vertical movement was initially controlled by the sum of R_V and L_V, and horizontal movement was controlled by the difference between R_H and L_H, as in an earlier study (24). From then on, after each trial, the weights were automatically adapted on the basis of past trials to optimize, for subsequent trials, the translation of the user's EEG control into cursor movement control. For this adaptation, each of the eight possible target locations was first expressed as one of the four possible vertical levels and one of the four possible horizontal levels (Fig. 1 A). Then, the least-mean-square (LMS) algorithm (27) was used to adjust the weights to minimize for past trials the difference between the actual target location and the target location predicted by Eqs. 1 and 2. (That is, the LMS algorithm determined the weights for the linear functions that would have given the best results had they actually been used for past trials.) Thus, to the extent that the user's past EEG control predicted future EEG control, this adaptation optimized the online translation of EEG control into cursor control. Furthermore, it took advantage of, and thereby encouraged, improvements in the user's EEG control. For example, if the correlation with vertical target level increased for L_V and not for R_V, the magnitude of w_LV in Eq. 1 increased and the magnitude of w_RV decreased.

Ancillary Studies. Additional sessions addressed two important ancillary issues: (i) users' ability to move the cursor to targets at novel locations and (ii) whether users used covert muscle contractions to control sensorimotor rhythms. To determine how well users could move the cursor to novel locations, targets were presented at 16 possible locations consisting of the original 8 (Fig. 1 A) and 8 more that were on the periphery between the original 8 and did not overlap with them. Target location was block-randomized (i.e., each occurred once in 16 trials). We compared the average movement times to the original and novel locations.

To confirm previous evidence (28) that BCI users do not use limb muscle contractions to control sensorimotor rhythms, we recorded electromyographic (EMG) activity from forearm flexor and extensor muscle groups during a standard session. These muscle groups were selected because they are strongly represented in the areas of sensorimotor cortex over which EEG control was focused (e.g., Fig. 1B). EMG activity was recorded (amplification 5,000; filter 1-400 Hz) from two electrode pairs (each pair oriented longitudinally with a 2-cm interelectrode distance), one pair on the flexor and one pair on the extensor surface of the forearm midway between wrist and elbow. From these data, we calculated EMG activity (average amplitude of rectified signal as a percent of value for maximum voluntary contraction) during cursor movement for each direction of each dimension of target location and also calculated the correlations (measured as R²) between EMG activity and the vertical and horizontal levels of target location.

Results

For each user, performance gradually improved over the training sessions as he or she gradually gained better control over the rhythm amplitudes that controlled the cursor and as the adaptive algorithm gradually adjusted the weights so as to vest control of cursor movement in those amplitudes that the user was best able to control. As described in refs. 1, 18, and 24, users tended to employ motor imagery to control the cursor, particularly early in training. The data presented here are those of each user's final three sessions, comprising 742 trials for user A, 521 for user B, 528 for user C, and 717 for user D. From these data we assessed both EEG control and the cursor movement control that it provided. A video of this performance is Movie 1, which is published as supporting information on the PNAS web site.

We assessed EEG control by spectral and topographical analysis of the correlations (measured as R²) (18, 24, 29) between target location and the average values for the trial of the vertical and horizontal variables (Eqs. 1 and 2), respectively. For each user, each variable correlated strongly with its own dimension of target location and did not correlate with the other variable's dimension (Table 1). Thus, each user developed two independent control signals: one for vertical movement and one for horizontal movement.

Table 1. Correlations of the vertical and horizontal variables with their appropriate and inappropriate dimensions of target location.

	R2
Correlation	User A	User B	User C	User D
Vertical variable with vertical target level	0.44	0.31	0.40	0.54
Vertical variable with horizontal target level	0.00	0.00	0.01	0.01
Horizontal variable with horizontal target level	0.48	0.29	0.27	0.54
Horizontal variable with vertical target level	0.00	0.00	0.01	0.01

To assess further the independence of the vertical and horizontal variables, we evaluated the individual movements, which occurred every 50 ms, to determine whether a vertical (or horizontal) movement that was correct (i.e., toward the target) affected the probability that the simultaneous horizontal (or vertical) movement was also correct. For each user, the probability that a correct movement in one dimension was accompanied by a correct movement in the other dimension was almost identical to the probability predicted by simply multiplying the fraction of all vertical movements that were correct by the fraction of all horizontal movements that were correct (i.e., 103%, 99%, 107%, and 104% of expected for users A-D, respectively). Thus, vertical and horizontal control did not appear to interfere with each other; users controlled movements in both dimensions simultaneously.

Fig. 1B shows the topographical and spectral properties of user A's control. Vertical movement was controlled by 24-Hz beta activity and horizontal movement by 12-Hz mu activity. At Top are scalp topographies (nose at top) of the correlations of the 24-Hz and 12-Hz rhythms with vertical and horizontal target levels, respectively. The sites of the left and right scalp electrodes (C3 and C4 over sensorimotor cortex) (21) that controlled the cursor are marked. [The topographies are for R rather than R² to show the opposite (i.e., positive and negative, respectively) correlations of right and left sides with horizontal target level.] In Fig. 1B Middle, for the four vertical and the four horizontal target levels, the voltage spectra are shown from which the vertical and horizontal variables (Eqs. 1 and 2), respectively, were derived with their corresponding R² spectra. The arrows point to the frequency bands used in these variables. The weights in the variables show that vertical movement was determined more by 24-Hz amplitude on the left, whereas horizontal movement was determined mainly by 12-Hz amplitude on the right. These weights are consistent with the relative magnitudes of the correlations seen in the topographies. In Fig. 1B Bottom are samples of EEG activity from electrodes that contributed to the vertical and horizontal variables for trials in which the target was at the top or bottom or at the right or left screen edge. They illustrate the strong sensorimotor rhythm control that the user employed to move the cursor to the target. Whereas mu and beta rhythms each changed with both dimensions of target location (e.g., Fig. 1B spectra and traces), the adaptive algorithm's focus on beta for vertical control and mu for horizontal control gave independent vertical and horizontal variables.

The EEG control summarized in Table 1 and illustrated in Fig. 1B gave each user effective cursor movement control. Users A-D reached the target within the 10 s allowed in 89%, 70%, 78%, and 92% of the trials, respectively, and their average movement times for these trials were 1.9, 3.9, 3.3, and 1.9 s, respectively. [Furthermore, the first of the eight possible target locations reached by the cursor correlated with the actual target location (P < 0.001 for each user), indicating that cursor movement was not random.] To evaluate the trajectories of cursor movement, we determined for each user the cursor's average path to each of the eight target locations and the timing of its movement along this path. Fig. 2 shows the results. User A moved most quickly along an axis from location 2 to location 6. He reached the other six locations by curved paths (convex upward) that took somewhat longer. His paths to locations 4 and 7 are particularly interesting: the cursor moved rapidly across the screen and then slowed as it turned down to the target. He stated that he tried to go above these targets and then drop down on them. User B, who was less skilled, started in one of three directions (i.e., upper left, upper right, or lower left) and then diverged to the individual targets. User C showed more early precision than user B and less than user A. User D diverged in eight different directions quite early and then followed a straight or slightly curved path to each location.

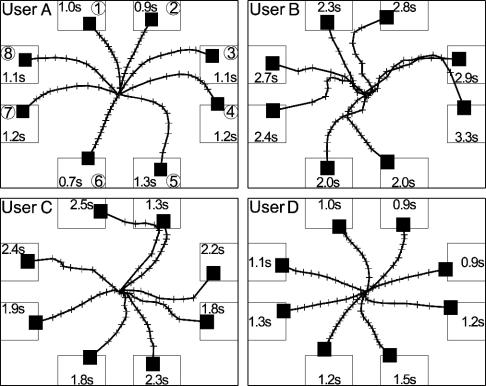
Fig. 2.

Cursor trajectories. Each user's average cursor path to each target for all trials in which the cursor reached the target within 2 s for user A, 5 s for user B, 4 s for user C, and 2 s for user D (i.e., the fastest 53-75% of the user's target hits, so as to best reveal the movement path and timing). Each path is divided by crosses into tenths of the time taken to reach the target, and the average time is shown in the target. The circled numbers are the target locations as in Fig. 1 A. A video of user A's real-time performance is shown in Movie 1.

Users A, C, and D each completed eight additional sessions in which targets appeared at 16 possible locations [8 original (Fig. 1 A) and 8 novel]. In the first of these sessions, movement time averaged 10% more for the novel locations than for the original locations. For the next seven sessions, it averaged 5% more. For none of the users was this slight difference significant (P > 0.05 for each user by F test).

In these same users, EMG activity was recorded from forearm flexor and extensor muscle groups. Fig. 3 summarizes (A) and illustrates (B) the data. EMG amplitude during cursor movement for each direction of each dimension of target location was low, usually averaging <10% of maximum voluntary contraction. Most important, for each muscle group of each user, the correlations between EMG amplitude and the vertical and horizontal levels of target location were extremely low (i.e., all R² values were <0.03). Thus, the users' sensorimotor rhythm-based cursor control did not depend on covert contractions of muscle groups strongly represented in the areas of sensorimotor cortex producing the rhythms.

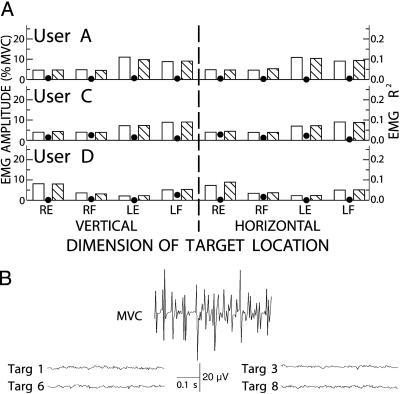
Fig. 3.

EMG activity during cursor control. (A) EMG amplitudes [in percent of maximum voluntary contraction (MVC)] during cursor movement for each direction (top or left, open bars; bottom or right, hatched bars) of each dimension (vertical or horizontal) of target location and its corresponding R² value (filled circle) for right and left forearm flexor (RF and LF) and extensor (RE and LE) muscle groups of users A, B, and D. EMG amplitudes are low, and (as the R² values show) EMG is not correlated with target direction in either dimension of target location. (B) Samples of right forearm extensor EMG activity from user D. The top trace shows a MVC. The other traces are from trials in which the target was at the top (Fig. 1 A, target 1), bottom (target 6), right (target 3), or left (target 8) screen edge. As they illustrate, EMG activity during cursor control was very low and was not correlated with target location.

Discussion

The results show that people can learn to use scalp-recorded EEG rhythms to control rapid and accurate movement of a cursor in two dimensions. Control develops gradually over training sessions as the user gradually acquires better EEG control and as the BCI system gradually focuses on those rhythm amplitudes that the user is best able to control. Thus, the two-dimensional movement control demonstrated in this study is a skill that the user and the system gradually master together. As cursor control improves, the motor imagery users employ early in training tends to become less important and performance becomes more automatic.

A user's previous one-dimensional experience, which as noted above was extensive for user A, limited for user B, absent for user C, and in the distant past for user D, appeared to have little impact on two-dimensional performance (Table 1 and Fig. 2). On the other hand, users A and D, who had spinal cord injuries, achieved substantially better performance than users B and C, who were not disabled. If future studies show this to be a consistent finding, it could reflect motivational differences and/or sensorimotor cortex plasticity associated with spinal cord injury (30).

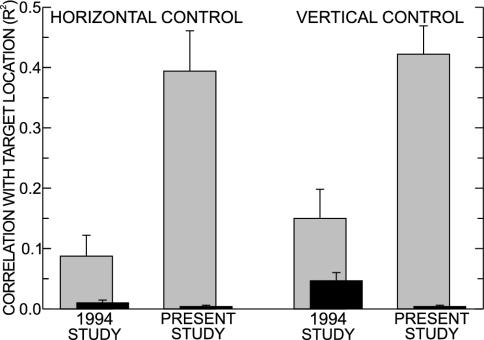
Comparisons with Previous Noninvasive Control. The multidimensional control achieved here is particularly striking when compared with the weak phenomenon described in our first effort to achieve such control (24). Fig. 4 compares the 1994 study (24) and the present study in terms of their correlations (measured as R²) between the vertical and horizontal variables and the vertical and horizontal dimensions of target location. [The very brief description of a second early study by Kostov and Pollock (31) does not give sufficient information for inclusion in this comparison. It appears to describe a low level of control like that of our 1994 study (24).] For each control variable (i.e., horizontal or vertical), correlation with its dimension of target location is several times higher for the present study than for our early study. Furthermore, correlation with the other (i.e., the wrong) dimension, which for the vertical variable was substantial in the early study, is almost entirely absent in the present study. Correlation with the wrong dimension produces a bias in cursor control: movement to targets near either of two opposite corners (e.g., upper right and lower left) is easy, whereas movement to targets near the other two corners is difficult or impossible.

Fig. 4.

Comparison with previous noninvasive control. Average (±SE) correlations (measured as R²) between the vertical and horizontal variables and the vertical and horizontal dimensions of target location for our initial (1994) study of multidimensional EEG control (24) and for the present study. Gray bars, correlations with the appropriate dimension of target location; black bars, correlations with the inappropriate dimension. The present study achieves much higher correlations with the appropriate dimension and avoids correlations with the inappropriate dimension. The R² values of the 1994 study (24) are from its table 1 (i.e., average R² for the appropriate dimension for the four users who achieved two-dimensional control) and its figure 3 (i.e., average R² for the inappropriate dimension. The R² values for the present study are averages from Table 1.

The much stronger and more independent control shown here is the product of two critical advances. The first comprises changes in signal processing (e.g., autoregressive frequency bands, multiple frequency bands, and spatial filtering) (18, 22, 25) that increase the correlation between the user's intent (i.e., which way to move the cursor) and the EEG features (i.e., sensorimotor rhythm amplitudes) that convey that intent. The second advance is the adaptive algorithm that focuses on those features the user is best able to control and encourages further improvement in control. The present study applies these advances to EEG-based multidimensional control. As Fig. 4 and Table 1 show, and as Fig. 2 illustrates, they give vertical and horizontal variables that are each strongly correlated with its appropriate dimension and uncorrelated with the other dimension (thereby making all locations on the screen equally accessible to the user). These advances transform EEG-based multidimensional control from a weak phenomenon of little practical value into a strong control technology with practical implications for people with severe motor disabilities. The present study's confirmation of previous data (28) indicating that EEG-based control does not depend on muscle contractions further supports the potential value for people who are paralyzed.

Comparison with Invasive Studies. Whereas this study uses a noninvasive method for recording brain signals, other current efforts to develop BCI control of multidimensional movement use invasive methods in which electrodes implanted in the brain record action potentials of single cortical neurons (5-9) or local field potentials (10, 11). All of these invasive multidimensional studies have to date been confined to nonhuman primates, and most have been limited to observation (i.e., to showing that the activity recorded by these electrodes during or immediately before a normal muscle-controlled limb movement can provide a good picture of that movement). Actual BCI operation, in which the monkey uses its brain signals (rather than its limb muscles) to control multidimensional movement, has been described in studies from three laboratories, those of Donoghue [Serruya et al. (6)], Schwartz [Taylor et al. (7)], and Nicolelis [Carmena et al. (9)]. Although the protocols and objectives of these three invasive studies differ in some respects from each other and from the present noninvasive study, all four share the goal of controlling multidimensional point-to-point movement and, thus, they can be compared in terms of their success in achieving this goal.

Performance on a point-to-point movement task can be summarized in three measures: movement time (i.e., the lower the better); movement precision (i.e., target size as percentage of workspace; the smaller the better); and hit rate (percent of targets reached in the time allotted; the higher the better). Table 2 presents these measures for the three invasive studies and the present noninvasive study. The values given are those of each study's best user (whether monkey or human).

Table 2. Comparison of point-to-point movement control achieved in invasive BCI studies in monkeys and in the present noninvasive BCI study in humans.

Study	Movement time, s	Movement precision, target size as % of workspace	Hit rate, %
Serruya et al. (6)	1.5	2.3	?
Taylor et al. (7)	1.5	1.3	86
Carmena et al. (9)	2.2	7.7	89
Present study	1.9	4.9	92

The values of each study's best user (monkey or human) are shown. Movement precisions are calculated from the dimensions of the targets, the cursors, and the workspaces. The values for Serruya et al. (6) (except for hit rate, which is not stated in the paper) are taken from that paper's text and its figure 1, a and d. The values for Taylor et al. (7) are derived from that paper's text and its table 2 (Monkey M, 2.0-cm targets). For Carmena et al. (9), movement time and hit rate are derived from sessions 19-21 of Monkey 2 as displayed in that study's figure 1C and the target, cursor, and workspace dimensions needed to calculate movement precision, which are not stated in the paper, are derived from its figure 1B (Task 1). The resulting value for target size was confirmed by the magnitude of movement evident in individual trials in the paper's figure 6G during the g phase (in which the cursor must remain in the target).

Movement times are similar across the studies (and are 2-3 times what would be expected for hand-operated joystick cursor control). Hit rates are also similar. Target size varies more, with the smallest targets those of Taylor et al. (7) and Serruya et al. (6), the largest target that of Carmena et al. (9), and the target of the present noninvasive study falling in between. This quantitative comparison indicates that the noninvasive BCI described here supports point-to-point movement control that falls in the range reported for invasive BCIs that use electrodes implanted in the cortex. Furthermore, the finding that movements to novel target locations entailed only a slight, statistically insignificant increase in movement time shows that the users' control is not limited to movements that have been practiced but rather can be readily applied to reach new target locations. Although the present study does not assess other aspects of movement control (e.g., moving the cursor to a location and then holding it in place), a recent study of one-dimensional control indicates that such aspects are within the capacities of a noninvasive BCI (32). Together with these results, the impressive noninvasive multidimensional control achieved in the present study suggests that a noninvasive BCI could support clinically useful operation of a robotic arm, a motorized wheelchair, or a neuroprosthesis.

Potential Improvements. Movement control by this noninvasive BCI could be further improved in speed and accuracy (and extended to three dimensions) in several ways: by expanding the adaptive algorithm to include additional EEG recording locations, additional frequency bands, and/or time-domain EEG features; by refining the user training protocol; and by improving the translation of EEG features into cursor movements (18). Furthermore, recent studies (33, 34) suggest that the EEG-based BCI methods described here could be even more effective if they were applied to activity recorded from the cortical surface [i.e., electrocorticographic (ECoG) activity], which has greater spatial resolution and frequency range than scalp EEG activity and does not require that electrodes be implanted within the brain. The present methods applied to ECoG activity could constitute a minimally invasive BCI technology that might ultimately yield the best results: excellent movement control without the level of technical difficulty and clinical risk associated with inserting electrodes into the brain.

Conclusions. This study extends the possible applications of noninvasive BCI technology to include real-time multidimensional movement control. The results suggest that it may not be necessary to implant electrodes in the brain to achieve multidimensional control, and they thereby increase the probability that BCIs will eventually become an important communication and control option for people with severe motor disabilities.