Determination of Phenotypic Resistance Cutoffs From Routine Clinical Data

Supplemental Digital Content is Available in the Text.

Abstract

Background:

HIV-1 drug resistance can be measured with phenotypic drug-resistance tests. However, the output of these tests, the resistance factor (RF), requires interpretation with respect to the in vivo activity of the tested variant. Specifically, the dynamic range of the RF for each drug has to be divided into a suitable number of clinically meaningful intervals.

Methods:

We calculated a susceptible-to-intermediate and an intermediate-to-resistant cutoff per drug for RFs predicted by geno2pheno_[resistance]. Probability densities for therapeutic success and failure were estimated from 10,444 treatment episodes. The density estimation procedure corrects for the activity of the backbone drug compounds and for therapy failure without drug resistance. For estimating the probability of therapeutic success given an RF, we fit a sigmoid function. The cutoffs are given by the roots of the third derivative of the sigmoid function.

Results:

For performance assessment, we used geno2pheno_[resistance] RF predictions and the cutoffs for predicting therapeutic success in 2 independent sets of therapy episodes. HIVdb was used for performance comparison. On one test set (n = 807), our cutoffs and HIVdb performed equally well receiver operating characteristic curve [(ROC)–area under the curve (AUC): 0.68]. On the other test set (n = 917), our cutoffs (ROC–AUC: 0.63) and HIVdb (ROC–AUC: 0.65) performed comparatively well.

Conclusions:

Our method can be used for calculating clinically relevant cutoffs for (predicted) RFs. The method corrects for the activity of the backbone drug compounds and for therapy failure without drug resistance. Our method's performance is comparable with that of HIVdb. RF cutoffs for the latest version of geno2pheno_[resistance] have been estimated with this method.

INTRODUCTION

Drug resistance of HIV type 1 (HIV) can be measured in vitro with phenotypic resistance tests.^1–3 The output of these tests is the fold-change in the median inhibitory concentration between a certain HIV variant and a reference strain. This quantity is called the resistance factor (RF) and is also referred to as phenotype, in this context. Statistical models trained on genotype–phenotype pairs afford accurate prediction of the RF, given a genotype.^4,5 The utility of phenotypes in optimizing cART has been established.^6–9 However, phenotypes require interpretation with respect to the in vivo activity of the tested variant, ie, the range of possible RFs for a drug (dynamic range) has to be divided into a suitable number of clinically meaningful intervals.^8–13 These intervals are drug dependent and defined in cutoffs of the RF. Historically, refinement of the interpretation of the RF has undergone several iterations. Initially, a cutoff per drug was defined in terms of the reproducibility of the phenotypic tests (technical cutoffs).¹⁴ Later, the distribution of RFs of (samples from) therapy-naive patients was used for defining a susceptible-to-resistant RF cutoff for each drug (biological cutoffs).^15,16 Finally, it was recognized that the RF, an in vitro measurement, requires explicit transformation for its intended in vivo application, the prediction of the suppression of the viral load (VL). Efforts in defining clinically relevant cutoffs (short: clinical cutoffs) gave rise to the notion of the division of the dynamic range into the idealized categories susceptible, intermediate, and resistant (SIR), using 2 cutoffs per drug. Susceptible indicates full drug activity, intermediate decreased drug activity, and resistant no drug activity.^8,11,14 Although drug compounds in cART act in concert, the RF quantifies the activity of a drug in vitro and in isolation. Thus, RF cutoff determination with clinical data requires correcting for the activity of the backbone compounds.^8,11 This correction can be achieved using hard-to-obtain data from (pseudo-) monotherapies for cutoff determination. In pseudo-monotherapies, an examined drug compound is added to a failing regimen. This allows for observing the activity of the drug with reduced influence of the backbone.^8,9,17 Correction for the backbone activity can be also achieved mathematically.^12,18,19 However, no methodology exists for calculating cutoffs that produce clinically meaningful SIR categories without requiring the expert selection of thresholds for drug activity.

In this analysis, we establish a novel methodology for calculating clinically relevant phenotypic resistance cutoffs from routine clinical data. Although drug resistance is a continuum, we aim at calculating cutoffs with which the dynamic range can be divided into intervals that best approximate the SIR categories, as defined above. We correct for the activity of the backbone compounds mathematically, as well as for lack of therapeutic success despite full susceptibility to the drug compounds in a cART, as measured in a phenotypic test or predicted by a genotypic interpretation system.

MATERIALS AND METHODS

Drugs Considered in This Study

The following antiretroviral drugs are considered in this work: lamivudine (3TC), abacavir (ABC), zidovudine (AZT), stavudine (d4T), didanosine (ddI), emtricitabine (FTC), tenofovir (TDF), efavirenz (EFV), nevirapine (NVP), amprenavir (APV), atazanavir (ATV), darunavir (DRV), fosamprenavir (FPV), indinavir (IDV), lopinavir (LPV), nelfinavir (NFV), saquinavir (SQV), and tipranavir (TPV). Other antiretroviral drugs were excluded because of insufficient representation in the EuResist Integrated Database (EIDB²⁰) or lack of a model for genotypic drug-resistance interpretation in geno2pheno_[resistance] (g2p; http://www.geno2pheno.org; see Ref. 4).

Data Sources

A total of 36,744 protease and reverse-transcriptase sequences from treatment-naive patients were obtained from the Los Alamos National Laboratory Sequence Database (LANLSD²¹; http://www.hiv.lanl.gov/; downloaded on March 31, 2015).

HIV data from routine clinical practice were obtained from 2 sources: the EIDB (http://www.euresist.org; downloaded April 11, 2014) and the HIVdb treatment-change episode (TCE) repository²² (http://hivdb.stanford.edu; downloaded November 21, 2013). The EIDB contains data from 66,254 patients, including HIV genotypes, VL measurements, CD4 counts, and compounds used in antiretroviral therapies. The HIVdb TCE repository stores 1527 TCEs from 4 data sources, including 58 TCEs from the EuResist database. In the context of the HIVdb TCE repository, a TCE documents relevant clinical parameters concerning a change in the drug compounds of cART.

Distribution of Fold-Change for Therapy-Naive Patients

Nucleotide sequences from LANLSD were aligned, translated, and interpreted with g2p v. 3.4, a data-driven genotypic drug-resistance interpretation system that predicts the RF from the genotype for various protease inhibitors (PIs) and reverse-transcriptase inhibitors (RTIs). Sequences resulting in an alignment error or producing a warning due to missing important sequence regions were discarded. Because we require an RF distribution for susceptible virus variants, sequences containing at least one major drug-resistance mutation²³ were excluded as well, as therapy-naive patients may carry drug-resistant variants.^24,25 The remaining sequences were used for calculating a therapy-naive RF distribution for the drugs considered in this study.

Calculation of Probabilities of Susceptibility (POS)

g2p is a genotypic drug-resistance interpretation system that predicts RFs for PIs and RTIs, given a nucleotide sequence of the protease and reverse-transcriptase genes. The number of genotype-phenotype pairs per drug on which g2p v. 3.4 is trained is given in Table 1, Supplemental Digital Content, http://links.lww.com/QAI/A934. Using g2p v. 3.4, all nucleotide sequences in EIDB were aligned. Sequences resulting in an alignment error or producing a warning due to missing important sequence regions were discarded. The remaining protease and reverse-transcriptase sequences were translated and interpreted. The resulting RF predictions were used for fitting a sigmoid function for approximating the POS given a predicted RF, as described before (probability of resistance⁴). Briefly, a 2-component Gaussian-mixture model is fitted to the RF predictions for each drug. These 2 Gaussians represent the susceptible and resistant viral populations, respectively. A sigmoid function is then fitted to approximate the probability of resistance, given an RF, that can be calculated with these 2 Gaussians. We define the POS as one minus the probability of resistance.

TABLE 1.

Therapy Characteristics

Definition of Treatment Episode (TE)

TEs differ from TCEs in that no treatment change is required, ie, TEs encompass first-line therapies as well. In this analysis, a TE consists of a baseline protease and reverse-transcriptase genotype, a list of drug compounds used in therapy, a follow-up VL and, optionally, a baseline VL. The baseline genotype and the baseline VL must have been obtained no earlier than 90 days before treatment initiation, in line with previously developed definitions of the standard datum.^20,26 However, baseline genotypes for first-line therapies are exempt from this requirement, as the virus has not been subject to selective pressure by drug therapy. In the presence of multiple data points, baseline measurements obtained at a date closest to therapy initiation are preferred. Follow-up VLs must have been obtained between 4 and 12 weeks after therapy initiation, preferring VL measurements whose measurement date is closest to 8 weeks after therapy start. TEs with a VL below 400 HIV-1 RNA copies per milliliter of blood serum (short: cp/mL) or presenting at least 100-fold reduction in the VL are labeled as successes. TEs for which a baseline VL is available, the follow-up VL is above 400 copies per milliliter, and the VL reduction is less than 100-fold are labeled as failures.^20,26 TEs containing drugs not considered in this analysis or with unboosted PIs (except for nelfinavir) do not satisfy the TE definition.

Definition of Treatment-Failure Episode (TFE)

TEs with baseline sequences predicted by g2p to have high RFs for some of the therapy's drug compounds are rare in EIDB. Therefore, we resort to nucleotide sequences measured during therapy, which imply therapeutic failure, as a certain degree of viral replication is required for sequencing. Toward this end, we define a TFE as follows. A TFE consists of a list of drugs used during therapy and an HIV sequence obtained during the therapy. The therapy is required to have lasted at least 4 weeks, and the genotype is required to have been obtained no earlier than 4 weeks before therapy stop. In TFEs, we assume that the treating clinician changed the therapy based on the results of the genotypic drug-resistance test. TFEs-containing drugs not considered in this analysis or with unboosted PIs (except for nelfinavir) do not satisfy the TFE definition.

Calculation of Probabilities of Success

After application of the TE definition to the EIDB, approximately 10% of the resulting TEs were selected at random and set aside for testing purposes. The remaining TEs were merged with TFE obtained from EIDB, labeled as failures. The resulting data set was used for estimating RF-conditional probabilities of success for each drug (see Methods, Supplemental Digital Content, http://links.lww.com/QAI/A934). Summarizing, TE baseline genotypes were interpreted with g2p, resulting in predicted RFs for the drugs in each TE. For each drug considered in this analysis, RF-conditional success and failure probability densities were estimated using weighted kernel density estimation ²⁷. When estimating the success density, we correct for the activity of the backbone compounds of therapy by down-weighting RFs from success-labeled TEs with the POS of the backbone compounds. When estimating the failure density, we correct for lack of success in the absence of resistance by down-weighting failures with the POS of their drug compounds. The resulting success and failure densities were used for calculating empirical probabilities of success. Aiming at noise reduction and analytical determination of cutoffs, we fit the following sigmoid function to the probabilities of success. Let 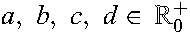be the parameters of the sigmoid function.

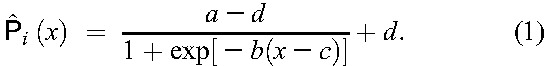For determining the susceptible-to-intermediate (lower) and the intermediate-to-resistant (upper) cutoffs, we use the roots of the third derivative of the right-hand side of Equation 1, as these are located at the extrema of the curvature of 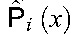. Thus, they are located at RF values at which the probability of success is significantly reduced or marginal, respectively. Cutoff determination for each drug was performed with 1000 bootstrap replicates²⁸ of each subset of TEs including that drug. However, for some drugs, this procedure selected the lower cutoff at an RF below the 95th percentile of the RF distribution of therapy-naive patients. To avoid what could be interpreted as overcalling of intermediate resistance, the lower cutoff for a drug was selected either at the smaller root of the third derivative of the right-hand side of Equation 1 or at the 95th percentile of the RF distribution of therapy-naive patients for that drug, whichever is larger.¹⁷

Performance Assessment and Comparison

We assess the performance of the cutoffs calculated with the procedures we used on 2 test data sets. The first test data set includes TEs from the EIDB which were not used for cutoff determination (approximately 10% of the total). The second test data set contains TEs extracted from the HIVdb TCE Repository by applying the TE definition to it. For each TE, a genetic susceptibility score (GSS) was calculated. Specifically, RFs predicted for the drug compounds in the TEs were obtained with g2p, subsequently producing SIR labels through the cutoffs. Each drug was assigned an integer score, depending on its SIR label: S → 1, I → 0.5, R → 0. The GSS for a TE amounted to the sum of its integer scores. Performance of the GSS in predicting therapeutic success was calculated in terms of area under the receiver operating characteristic curve (AUC²⁹). For performance comparison, the baseline genotypes of the TEs in the test data sets were interpreted with HIVdb v.6.0.6,³⁰ resulting in SIR labels for the drug compounds in the TEs. GSS was calculated as described above, and the performance of the GSS in predicting therapeutic success was quantified in terms of area under the curve (AUC) as well. P-values were calculated with a 2-sided Wilcoxon signed-rank test.³¹ Whenever multiple testing was performed, P values were corrected using the Benjamini–Hochberg method.³²

RESULTS

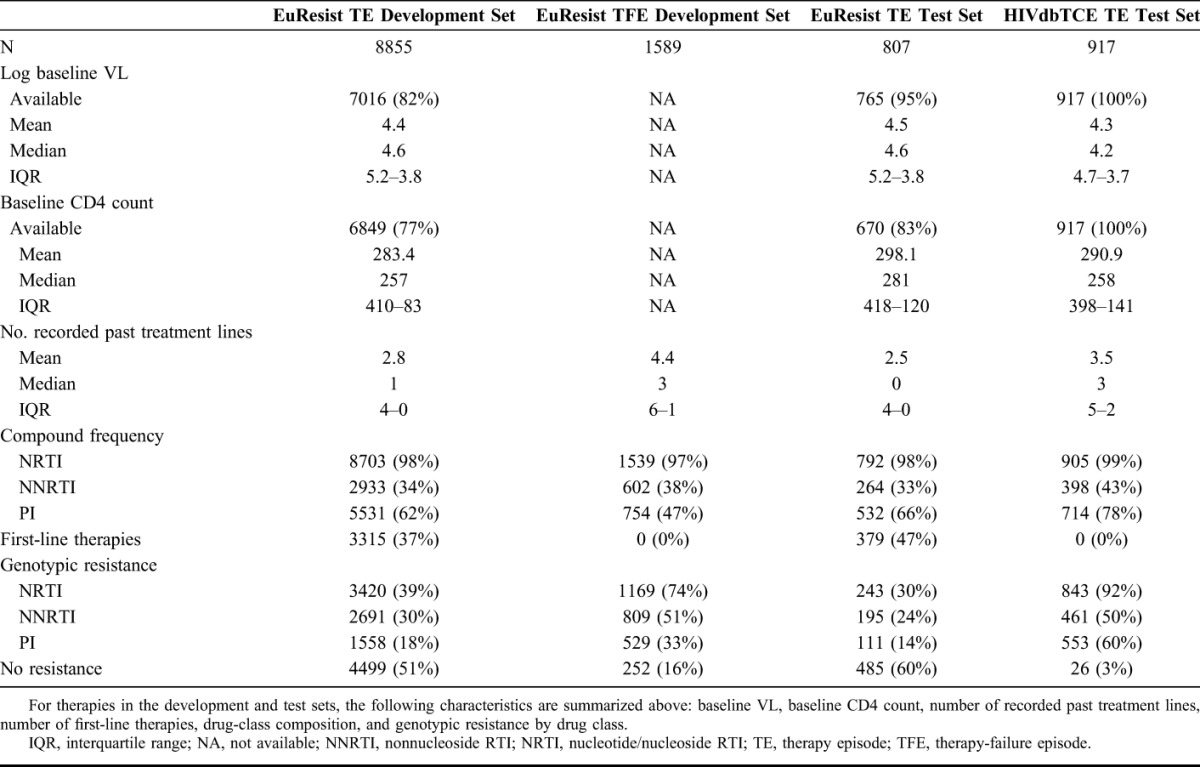
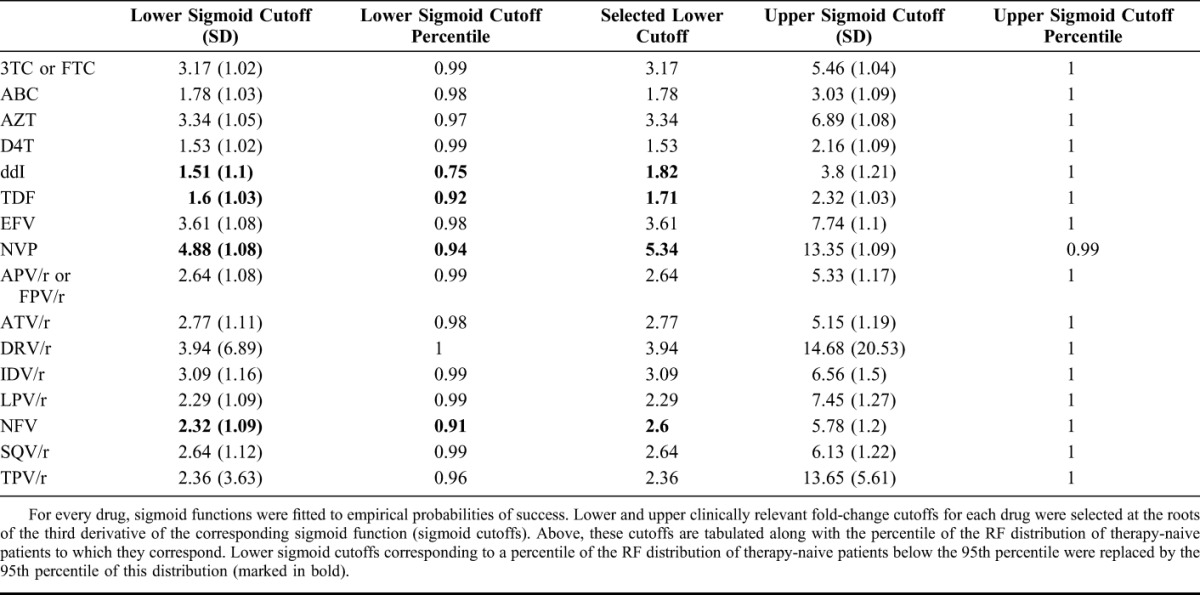
Among 36,744 nucleotide sequences of the protease and reverse-transcriptase genes downloaded from LANLSD, 43 (<1%) protease and 75 (<1%) reverse-transcriptase sequences were discarded because of alignment problems or sequence-quality warnings. Furthermore, 860 (2.3%) protease and 680 (1.8%) reverse-transcriptase sequences were discarded because they contained some major drug-resistance mutations. In addition, a total of 74,764 nucleotide sequences from EIDB were submitted to g2p for interpretation, some of which did not correspond to either the protease or reverse-transcriptase genes. Of these, 21,199 (28%) were discarded because of alignment problems or because they triggered a sequence-quality warning. RF percentiles for the resulting RF distributions for therapy-naive patients, along with the corresponding POS, can be found in Table 2, Supplemental Digital Content, http://links.lww.com/QAI/A934. On average, RFs at the 95th percentile of the RF distribution of therapy-naive patients have a POS of 0.87 with a SD of 0.13. Baseline characteristics for the TEs and TFEs extracted from EIDB and the HIVdb TCE repository are shown in Table 1, whereas the drug-compound distribution for these data sets is shown in Table 2. On average (SD), follow-up VLs used for labeling TEs were obtained 7.04 (2.48) weeks after treatment initiation, with a median time of 7 weeks after treatment initiation (interquartile range: 9–5 (Figure 1, Supplemental Digital Content, http://links.lww.com/QAI/A934)). Successes accounted for 79% or 83%, respectively, of TEs that were labeled using a follow-up VL obtained 4 or 12 weeks after treatment initiation, respectively. Upper and lower RF cutoffs obtained with the procedure described in Methods are displayed in Table 3. Lower cutoffs for the drugs ddI, TDF, NVP, and NFV were replaced by the 95th percentile of the RF distribution of therapy-naive patients, as they were smaller than this percentile. For performance assessment and comparison, GSS for the TEs in 2 test sets were computed with predicted RFs, discretized with the obtained cutoffs, as well as with HIVdb discrete predictions. On the EIDB test set, our method and HIVdb performed equally well (AUC = 0.68). However, our method (μ = 2.55; σ = 0.88) produced lower GSS than HIVdb (μ = 2.66; σ = 0.75; P < 10⁻¹⁶). Our method's integer scores for NRTIs (μ = 0.83; σ = 0.35; vs. μ = 0.86; σ = 0.30), NNRTIs (μ = 0.92; σ = 0.24; vs. μ = 0.95; σ = 0.20), and PIs (μ = 0.88; σ = 0.30; vs. μ = 0.92; σ = 0.23) were lower than those produced with HIVdb (corrected P < 0.0043). On the HIVdbTCE test set, our method (AUC = 0.63) and HIVdb (AUC = 0.65) performed comparably well. On average, our method (μ = 1.82; σ = 0.97) produced lower GSS than HIVdb (μ = 2.18; σ = 0.88; P < 10⁻¹⁶) on the HIVdbTCE test set. Integer scores of our method for NRTIs (μ = 0.16; σ = 0.33; vs. μ = 0.21; σ = 0.37), NNRTIs (μ = 0.19; σ = 0.39; vs. μ = 0.19; σ = 0.39), and PIs (μ = 0.06; σ = 0.23; vs. μ = 0.07; σ = 0.24) were also lower than those produced with HIVdb (corrected P < 0.043).

TABLE 2.

Drug-Compound Distributions

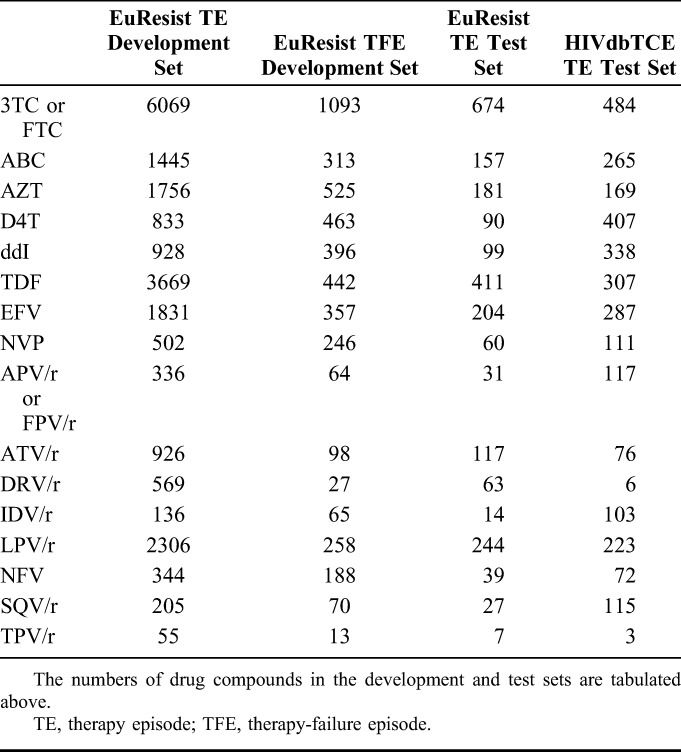
FIGURE 1.

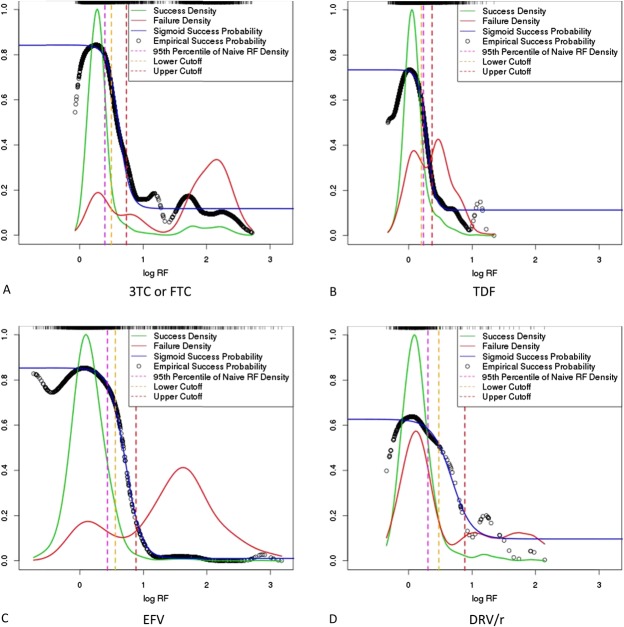
Density and probability plots (selected compounds). Weighted kernel density estimation was used for estimating a success and a failure density for each drug compound. These densities were used for calculating RF-dependent empirical success probabilities, to which a sigmoid function was fitted. A lower and an upper RF cutoff were chosen at the roots of the third derivative of the sigmoid function. However, the lower cutoff was replaced by the 95th percentile of the RF distribution of therapy-naive patients, if it was lower than this percentile. Success and failure densities, as well as empirical and sigmoid success probabilities are plotted above for the drug compounds 3TC or FTC (A), TDF (B), EFV (C), and DRV/r (D). Ninety-fifth percentiles of the RF factor distribution, as well as lower and upper cutoffs determined with the roots of the third derivative are indicated by vertical dashed lines. Resistance-factor density is also depicted as a rug plot at the top of each individual plot. Note that for producing these joint depictions of probabilities of success and of success and failure densities, success and failure densities were rescaled to the interval between zero and one. This was accomplished by dividing the values of the densities by the largest value of both densities.

TABLE 3.

Clinically Relevant Phenotypic Resistance Cutoffs

DISCUSSION

In this work, we present a method for calculating clinically relevant cutoffs for the RF that does not depend on expert interpretation. Our method offers the following advantages. (1) The cutoffs produced with this method are tightly coupled with the clinically meaningful definition of lower and upper RF cutoffs for producing SIR categories (see Introduction). We achieve this by translating this definition into an adequate mathematical counterpart. Specifically, our method chooses cutoffs at the curvature extrema of a sigmoid function approximating the probability of success (Fig. 1). By doing so, we circumvent the need for manual selection of (arbitrary) drug activity thresholds.¹² Nevertheless, cutoffs can be chosen manually based on other geometric features of the sigmoid function (see Figure 2 and Table 3, Supplemental Digital Content, http://links.lww.com/QAI/A934) or at specific probabilities of success. (2) Our method corrects for the activity of backbone drug compounds, but does not achieve this using coarse, discrete weights, as with GSS. Instead, we correct for backbone activity in success-labeled TEs with fine-grained RF weights that depend on the POS of all therapy compounds. (3) In failure-labeled TEs, we correct for failures not associated with resistance, which is especially important because we use data from routine clinical practice for calculating the cutoffs.

FIGURE 2.

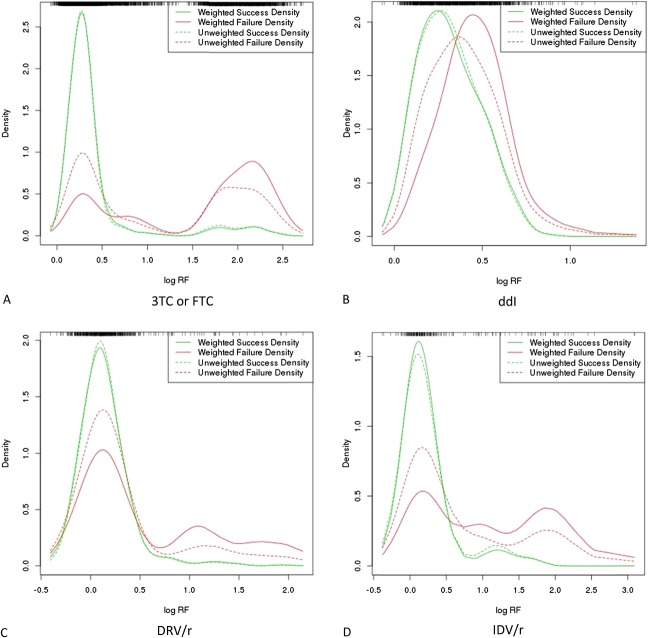
Comparison of weighted and unweighted densities (selected compounds). Empirical success and failure densities were estimated with weighted kernel density estimation, as described in Methods. Above, the weighted densities for the drug compounds 3TC or FTC (A), ddI (B), DRV/r (C), and IDV/r (D) are plotted along with their unweighted versions. Resistance-factor density is also depicted as a rug plot at the top of each individual plot.

We have observed that empirical probabilities of success decrease as log RF values reach their lower limit (Fig. 1). This artifact results from the use of the probability density functions of the normal distribution for estimating success and failure densities (see Methods, Supplemental Digital Content, http://links.lww.com/QAI/A934). However, this artifact is corrected for by subsequent fitting of sigmoid functions to the empirical probabilities of success (Fig. 1).

We exemplify the computation of RF weights for an antiretroviral therapy with 3 drug compounds (see Table 4, Supplemental Digital Content, http://links.lww.com/QAI/A934). For failure-labeled TEs, weights decrease with the sum of the POS for all compounds in the therapy. The maximum weight, 1, is awarded to RFs from TEs for which the sum of POS is equal to 0. Thus, the influence of RFs from failure-labeled TEs is greater the less the susceptibility of the virus to the administered drug compounds, which corrects for failure in the absence of resistance. In contrast, for calculating RF weights for success-labeled TEs, the POS of the drug in question is subtracted from the sum of POS for the backbone drug compounds. The maximum weight, 1, is awarded to RFs of the drug in question indicating full drug susceptibility, whereas the virus is not susceptible to the backbone drug compounds. Hence, RFs from success-labeled TEs have a greater influence, the higher the susceptibility of the drug in question and the lower the susceptibility of the backbone drug compounds. This corrects for the activity of the backbone compounds. For selected drug compounds, a comparison of the densities obtained with and without RF weighting, respectively, is shown in Figure 2. When weighted failure densities are compared with their unweighted counterparts, one can observe a shift of the probability mass from lower RF ranges to higher ones. This effect is especially pronounced in the failure densities of ddI and IDV because their side-effect profiles are less favorable than those of 3TC/FTC and DRV.^33–37 Thus, for cutoff calculation, our method downweights therapy failures that are not caused by drug resistance. Comparative examination of the weighted and unweighted success densities for ddI and IDV makes the effects of the weighting procedure apparent. Specifically, the weighting procedure compensates for the effect of the backbone drug compounds by down weighting the success densities at higher RF values.

The definition of SIR categories takes the activity of a drug into account, and (intentionally) does not account for the differential capacities of antiretroviral drugs to elicit virological success. For instance, at the same probability of success, the virus may be classified as susceptible to one drug whereas it is classified as intermediate for another drug. Taking this into consideration, cutoff determination through mathematical optimization is hampered by the difficulty of finding an adequate objective function for optimization that is universal for all drugs. In the past, cutoff calculation has been attempted by maximizing the AUC quantifying the performance of prediction of therapeutic success.¹⁹ Briefly, cutoffs are iteratively optimized by producing a GSS with a given set of cutoffs and subsequently modifying these cutoffs such that there is an increase in the AUC. This procedure involves the calculation of cutoffs for all drugs in the data set simultaneously, and may be less effective in separating the effects of individual drugs. Furthermore, the use of such an objective function is bound to maximize predictive performance in the GSS while producing inconsistencies of the applied SIR categories. We avoid this undesired effect by estimating cutoffs for each drug separately. Nonetheless, the separation of the contributions of individual drugs to therapeutic success remains challenging, as antiretroviral drugs may interact with each other.^38,39

Except for DRV/r and TPV/r, the SD of the calculated cutoffs is at most 1.5. The higher variability of the cutoffs for DRV/r can be explained by the drug's comparatively high barrier to resistance.³³ Our data set contains only few DRV/r-containing TEs with an RF above the upper cutoff (Fig. 1). Therefore, significantly different numbers of TEs with a high resistance to DRV/r at baseline will be selected across bootstrap replicates, which results in increased variability. The increased variability for the cutoffs for TPV/r is due to the low numbers of TEs containing this drug (Table 2). We tested the calculated cutoffs on 2 test sets. The performance of cutoffs was equal or comparable with that of HIVdb. However, the GSS calculated with the cutoffs were significantly smaller than those calculated with HIVdb. Therefore, our cutoffs have a higher tendency to label an RF with nonsusceptible SIR categories than HIVdb. We interpret this to be a result of the strict adherence to SIR categories in the cutoff estimation procedure. Specifically, genotypic drug-resistance interpretation systems produced by experts may take the propensities of individual drugs to elicit therapeutic success into account more strongly. This results in fewer resistant predictions for drugs with a high potency and a high barrier to resistance.

In this work, we present a method for calculating clinically relevant cutoffs for (predicted) RFs. The method corrects for the activity of the backbone drug compounds and for therapy failure without drug resistance. A sigmoid function is used for estimating the probability of therapeutic success, given an RF. Therefore, RF cutoff selection can be based on geometric features of the sigmoid function or on thresholds of the probability of success. Validation with 2 clinical data sets showed that the performance of our method was comparable with that of a popular rules-based drug-resistance interpretation method. The method has been applied for estimating RF cutoffs for the latest version of g2p, v. 3.4.