Abstract
Motivated by analysis of gene expression data measured in different tissues or disease states, we consider joint estimation of multiple precision matrices to effectively utilize the partially shared graphical structures of the corresponding graphs. The procedure is based on a weighted constrained ℓ∞/ℓ1 minimization, which can be effectively implemented by a second-order cone programming. Compared to separate estimation methods, the proposed joint estimation method leads to estimators converging to the true precision matrices faster. Under certain regularity conditions, the proposed procedure leads to an exact graph structure recovery with a probability tending to 1. Simulation studies show that the proposed joint estimation methods outperform other methods in graph structure recovery. The method is illustrated through an analysis of an ovarian cancer gene expression data. The results indicate that the patients with poor prognostic subtype lack some important links among the genes in the apoptosis pathway.
Keywords: Constrained optimization, Convergence rate, Graph recovery, Precision matrices, Second-order cone programming, Sparsity
1. INTRODUCTION
Gaussian graphical models provide a natural tool for modeling the conditional independence relationships among a set of random variables (Lauritzen (1996); Whittaker (1990)). They have been successfully applied to infer relationships between genes at transcriptional level (Schäfer and Strimmer (2005); Li and Gui (2006); Li, Hsu, Peng et al. (2013)). Gaussian graphical models are tightly linked to precision matrices. Suppose X = (X1,…, Xp)′ follows a multivariate Gaussian distribution Np(μ, Σ). The precision matrix Ω = Σ−1 describes the graphical structure of its corresponding Gaussian graph. If the (i, j)-th entry of the precision matrix ωij is equal to zero, then Xi and Xj are independent conditioning on all other variables Xk, k ≠ i, j. Correspondingly, no edge exists between Xi and variable Xj in the graphical structure of Gaussian graphical model. If ωij ≠ 0, then Xi and Xj are conditionally dependent and they are therefore connected in the graphical structure. Define the support of Ω by , which is also the set of edges in the Gaussian graphical model. If the maximum degree of Ω, is relatively small, we call Ω sparse. Since the expression variation of a gene can usually be explained by a small subset of other genes, the precision matrix for gene expression data of a set of genes is expected to be sparse.
Many methods for estimating high-dimensional precision matrix or its Gaussian graphical model have been developed in the past decade. Meinshausen and Bühlmann (2006) introduced a neighborhood selection approach by regressing all other variables on each variable with an ℓ1 penalty. The method consistently estimates the set of non-zero elements of the precision matrix. Efficient algorithms for exact maximization of the ℓ1-penalized log-likelihood have also been proposed. Yuan and Lin (2007), Banerjee, Ghaoui and d’Aspremont (2008) and Dahl, Vandenberghe and Roychowdhury (2008) adopted an interior point optimization method to solve this problem. Based on the work of Banerjee, Ghaoui and d’Aspremont (2008) and a block-wise coordinate descent algorithm, Friedman, Hastie and Tibshirani (2008) developed the graphical Lasso (GLASSO) for sparse precision matrix estimation; it is computationally efficient even when the dimension is greater than the sample size. Yuan (2010) developed a linear programming procedure and obtained oracle inequalities for the estimation error in term of matrix operator norm. Cai, Liu and Luo (2011) developed a constrained ℓ1 minimization approach (CLIME) to estimate sparse precision matrix. All of these methods addressed the problem of estimating a single precision matrix or a single Gaussian graphical model.
In many applications, the problem of estimating multiple precision matrices arises when data are collected among multiple groups. For example, gene expression levels are often measured over multiple groups (tissues, environments, or subpopulations). Their precision matrices and the corresponding graphical structures imply gene regulatory mechanisms and are of great biological interest. Since the gene regulatory networks in different groups are often similar to each other, the graphical structures share many common edges. Estimating a single precision matrix group by group ignores the partial homogeneity in their graphical structures, which often leads to low power. To effectively utilize the shared graphical structures and to increase the estimation precision, it is important to estimate multiple precision matrices jointly.
Previous attempts to jointly estimate multiple precision matrices include Guo, Levina, Michailidis et al. (2011) and Danaher, Wang and Witten (2014). Guo, Levina, Michailidis et al. (2011) proposed a hierarchical penalized model to perserve the common graphical structure while allowing differences across groups. Their method achieves Frobenius norm convergence when p log(p)/n goes to zero, where p is the number of variables, and n is the total sample size. Unfortunately, for genomic applications, the number of genes often exceeds the total sample size and, as a result, invalidates the theoretical justification in Guo, Levina, Michailidis et al. (2011). Danaher, Wang and Witten (2014) proposed two algorithms of joint graphical lasso (FGL and GGL) to estimate precision matrices that share common edges. Their approach is based upon maximizing a penalized log likelihood with a fused Lasso or group Lasso penalty. The paper did not provide any theoretical justification on the statistical convergence rate of their estimators.
In this paper, we propose a weighted constrained ℓ∞/ℓ1 minimization method to estimate K sparse precision matrices (MPE) jointly. Different from Guo, Levina, Michailidis et al. (2011) and Danaher, Wang and Witten (2014), the proposed estimators converge to the true precision matrices even when p = O{exp(na)}, for some 0 < a < 1. In addition, when K is sufficiently large, compared to the estimators from separate estimation methods, our proposed estimators converge to the true precision matrices (under the entry-wise ℓ∞ norm loss) faster. An additional thresholding step on the estimators with a carefully chosen threshold yields thresholded estimators with additional theoretical properties. The thresholded estimators from our method converge to the true precision matrices under the matrix ℓ1 norm. Finally, when the graphical structures across groups are the same, our method leads to the exact recovery of the graph structures with a probability tending to 1.
The rest of the paper is organized as follows. Section 2 presents the estimation method and the optimization algorithm. Theoretical properties of the proposed method and accuracy of the graph structure recovery are studied in Section 3. Section 4 investigates the numerical performance of the method through a simulation study. The proposed method is compared with other competing methods. The method is also illustrated by an analysis of an epithelial ovarian cancer gene expression study in Section 5. A brief discussion is given in Section 6 and proofs are presented in the Appendix.
2. METHODOLOGY
The following notations are used in the paper. For a vector a = (a1,…, ap)T ∈ ℝp, define and . The vector a−i is the vector of a without the i-th entry. The support of a is defined as supp(a) = {i : ai ≠ 0}. For a matrix A = (aij) ∈ ℝ p×q, its entrywise ℓ∞ norm is denoted by |A|∞ = maxi,j |aij|. Its matrix ℓ1-norm is denoted by , and its spectral norm is denoted by ║A║2. The sub-matrix A−i,−i is the matrix of A without the i-th row and the i-th column. Denote by λmax(A) and λmin(A) the largest and smallest eigenvalues of A, respectively. For two sequences of real numbers {an} and {bn}, write an = O(bn) if there exists a constant C such that |an| ≤ C|bn| holds for all sufficiently large n, write an = o(bn) if limn→∞ an/bn = 0. If an = O(bn) and bn = O(an), then an ⩆ bn.
2.1 The Joint Estimation Method
We introduce an estimation method to jointly estimate K precision matrices with partial homogeneity in their graphical structures. The method uses a constrained ℓ1 minimization approach, that has been successfully applied to high dimensional regression problems (Donoho, Elad and Temlyakov (2006); Candés and Tao (2007)) and signal precision matrix estimation problem (Cai, Liu and Luo (2011)) to recover the sparse vector or matrix.
For 1 ≤ k ≤ K, let X(k) ∼ N(μ(k), Σ(k)) be a p-dimensional random vector. The precision matrix of X(k), denoted by , is the inverse of the covariance matrix Σ(k). Suppose there are nk identically and independently distributed random samples of . The sample covariance matrix for the k-th group is
where . Denote by n = Σk nk the total sample size and wk = nk/n the weight of the k-th group. We estimate for k = 1, …, K by the constrained optimization
| (1) |
where λn = C(log p/n)1/2 is a tuning parameter. The ℓ∞/ℓ1 objective function is used to encourage the sparsity of all K precision matrices. The constraint is imposed on the maximum of the element-wise group ℓ2 norm to encourage the groups to share a common graphical structure.
Denote by the solution to (1). They are not symmetric in general. To make the solution symmetric, the estimator is constructed by comparing and and assigning the one with a smaller magnitude at both entries,
This symmetrizing procedure is not ad-hoc. The procedure assures that the final estimator achieves the same entry-wise ℓ∞ estimation error as . The details are discussed in Section 3.
2.2 Computational algorithm
The convex optimization problem (1) involves estimating K p × p precision matrices. To reduce the computation complexity, it can be further decomposed into p sub-problems that involve estimating K p × 1 sparse vectors:
| (2) |
for 1 ≤ j ≤ p, where ej ∈ ℝp is the unit vector with j-th element 1 and other elements 0. A lemma shows that solving (2) is equivalent to solving (1).
Lemma 1
Suppose is the solution to (1) and , where is the solution to (2). Then for 1 ≤ k ≤ K.
Problem (2) can be solve by a second-order cone programming. The existing packages to solve (2) include the SDTP3 and the SeDuMi package in Matlab, and the CLSOCP package in R. CLSOCP uses a one-step smoothing Newton method of Liang, He and Hu (2009). This algorithm has good precision but works relatively slowly for high dimensional problems. SeDuMi and SDTP3 adopt the primal-dual infeasible-interior point algorithm (Newsterov and Todd (1998)). The most time-consuming part of the algorithm is to solve the Schur complement equation, which involves Cholesky factorization. The sparsity and the size of the Schur complement matrix are two factors that affect efficiency. SDTP3 is able to divide a high dimensional optimization problem into sparse blocks and uses the sparse solver for Cholesky factorizations. It is therefore faster than SeDuMi in solving (2). In this paper, we used the SDTP3 package for all the computations. For a problem with p = 200, nk = 150 and K = 3, it takes a dual-core 2.7 GHz Intel Core i7 laptop approximately 11 minutes to solve (1).
2.3 Tuning Parameter Selection
Choosing the tuning parameters in regularized estimation is in general a difficult problem. For linear regression models, Chen and Chen (2008); Wang, Li and Leng (2009); Wang and Zhu (2011) studied how to consistently choose the tuning parameters when p = O(na) for some a > 0. Recently, Fan and Tang (2013) proposed a general information criterion (GIC) for choosing the tuning parameter for estimating the generalized linear model in ultra-high dimensional settings, p = O(exp(na)) for some a > 0. The GIC criterion adopts a novel penalty on the degree freedom of the model so that it consistently chooses the proper tuning parameter under mild conditions. Unfortunately, the Gaussian graphical model is different from the generalized linear model, and therefore the justification of GIC does not apply to our problem. We propose a tuning parameter selection method based on BIC and a re-fitted precision matrix on the restricted model.
Since follows a multivariate Gaussian distribution Np(μ(k), Σ(k)), we have
| (3) |
where . The regression coefficients satisfy (Anderson (2003))
| (4) |
Based on these results, we propose a tuning parameter selection procedure:
For a given λ, calculate the estimator . Based on the support of , use least squares and neighborhood selection to re-fit the precision matrix estimator .
Define , the set of non-zero off-diagonal elements of the i-th row of .
- Repeat Step 3 for i = 1,…, p and k = 1,…, K. The resulting matrices , k = 1,…, K are not symmetric. We symmetrize by the same procedure:
We use , k = 1,…, K as the estimators corresponding to the tuning parameter λ. The optimal tuning parameter can be selected by Bayesian information criterion (BIC),
| (6) |
where . We obtain the solution to our method over a wide range of tuning parameters and choose that minimizes BIC(λ).
Since the refitted estimator can potentially reduce some bias introduced in the optimization due to the penalty term, using it in BIC (6) improves the tuning parameter selection in the numerical studies. However, using as an estimator of Ω(l) is not recommended because when is large, the re-fitted estimator might lead to overfitting. Overfitting does not severely affect the tuning parameter selection, because BIC puts penalties on complicated models that are less likely to be chosen.
3. THEORETICAL PROPERTIES
3.1 Estimation Error Bound
We investigate the properties of the proposed estimator by considering the convergence rates of , including estimation error bounds and graph structure recovery. We assume the following conditions:
-
(C1)There exists some constant a > 0, such that
-
(C2)
sup1≤k≤K {λmax (Ω(k))/λmin(Ω(k))} ≤ M0 for some bounded constant M0 > 0.
-
(C3)
If eij = I(i = j), , and the largest eigenvalue of Cov(Zij) is λmax,ij, supij λmax,ij ≤ M1.
-
(C4)
n1 ⩆ n2 ⩆ ⋯ ⩆nK ⩆ n/K.
Condition (C1) allows p to grow exponentially fast as n. It also allows the number of groups K to grow slowly with p and n. For example, when log p = O(nr) and K = O(nb) for r + 2b < 1 and 3b < r, (C1) holds. Condition (C3) allows X(k) to be dependent across groups. When X(k) are independent, Cov(Yij) = IK, and thus maxij λmax,ij = 1.
Let be the maximum matrix ℓ1 norms of the K matrices. A theorem establishes the convergence rate of the precision matrix estimates under the element-wise ℓ∞ norm.
Theorem 1
Let λn = C0 (log p/n)1/2 for some constant . If (C1)–(C4) hold,
| (7) |
with a high probability converging to 1 and C1 = 2C0.
Remark 1: The value of C0 depends on M0. In practice, M0 is often unknown. However, we can use the tuning parameter selection method, such as BIC in (6), to choose λn. The details are discussed in Section 2.3.
Remark 2: Theorem 1 (and Theorems 2 and 3) does not require the true precision matrices Ω(k) to have identical graphical structures. Both the values and locations of non-zero entries can differ across Ω(k), k = 1,…, K.
Define
Proposition 1
Let be the set of estimators , where only depends on the k-th sample . Assume the samples are independent across K groups. Under (C4), there exists a constant α > 0, such that
for sufficiently large n.
Theorem 1 shows that the convergence rate of from our joint estimation method is less than or equal to C1 Mn (log K log p/n)1/2 with a probability tending to 1. When K is bounded, Proposition 1 shows that with a non-vanishing probability αK, the minimax convergence rate of any separate estimation method is at least αMn(K log p/n)1/2. For bounded but sufficiently large K, C1 (log K)1/2 ≤ αK1/2. Therefore, the convergence upper bound in (7) for the joint estimation method is less than the convergence lower bound in Proposition 1 for the separate estimation method. In other words, compared to separate estimation methods, our joint estimation method leads to estimators with a faster convergence.
An additional thresholding step on the estimators with a careful chosen threshold leads to new estimators, that converge to the true precision matrices under the matrix operator norm. Define the thresholded estimator as follows,
with C1 the constant defined in (7). Let and . Define as the union sparsity.
Theorem 2
Suppose that (C1)–(C4) hold. Then with a high probability converging to 1,
| (8) |
The convergence rates of depend on the union sparsity level s0(p). When the precision matrices share the same graphical structure, for all k = 1,…, K. When the number of shared edges in the graphical structures increases, the union sparsity s0(p) decreases, and consequently converges to Ω(k) faster.
Let . Matrix  = (âij)p×p measures the overall estimation errors among the entries of and Ω(k) for k = 1,…, K.
Corollary 1
Suppose that the conditions in Theorem 2 hold. Then with a high probability converging to 1,
3.2 Graphical Structure Recovery
Theoretical analysis for graphical structure recovery is very complicated when the graphical structures of the precision matrices are different across the K groups since the results depend on the structures of the shared edges. Here we focus on the case in which the K precision matrices have a common support. Let be the support for the k-th precision matrix, and the common support be . When , , k = 1,…, K, by Theorem 1 we estimate by
where C1 is a constant given in Theorem 1. Let
We have a result on support recovery.
Theorem 3
Suppose that the conditions in Theorem 1 hold. Assume that
| (9) |
Then with a high probability converging to 1.
When the graphical structures are the same across all K groups, the lower bound condition (9) is weaker than the lower bound condition needed for graphical structure recovery by separate estimation methods. Based on Proposition 1 and its proof, to fully recover the shared graphical structure by separate estimation methods, a necessary condition is
When K is sufficiently large, this condition is stronger than (9).
4. SIMULATION STUDIES
4.1 Data generation
We evaluated the numerical performance of the proposed method and other competitive methods, including the separate precision matrix estimation procedures proposed by Friedman, Hastie and Tibshirani (2008) and Cai, Liu and Luo (2011) and the joint estimation method proposed by Guo, Levina, Michailidis et al. (2011) and Danaher, Wang and Witten (2014). The separate precision matrix estimation methods were applied to each group, and therefore ignored the partial homogeneity in graphical structures among groups. In all numerical studies, we set p = 200, K = 3 and (n1, n2, n3) = (80, 120, 150). The simulated observations were generated in each group independently from a multivariate Gaussian distribution N{0, (Ω(k))−1}, where Ω(k) is the precision matrix in the k-th group. For each model, 100 replications were performed.
We present results for two different types of graphical models: the Erdös and Rényi (ER) model (Erdös and Rényi (1960)) and the Watts-Strogatz (WS) model (Watts and Strogatz (1998)). For the ER model, the graph contains p vertices and each pair of vertices are connected with a probability 0.05. For the WS model, first a ring lattice of p vertex is created; one vertex is connected with its neighbors within order distance of 15, and then the edges of the lattice are rewired uniformly and randomly with a probability 0.01. These graph models have several topological properties such as sparcity and a “small world” property often observed in true biological gene regulatory networks. See Fell and Wagner (2000); Jeong, Tombor, Albert et al. (2000); Vendrascolo, Dokholyan, Paci et al. (2002); Greene and Higman (2003).
Based on the ER model or the WS model, a common graph structure was generated. Let M be the number of edges in the common graph structure. Then, ⎿ρM⏌ random edges were added to the common graph structure to generate graph structures for each group, where the parameter ρ was the ratio between the number of group-specific edges and common edges. We considered ρ = 0, 1/4, and 1. The first setting represents the scenario where the precision matrices in all groups share the same graph structure. After the graph structure of each group was determined, the values of non-zero off-diagonal entries were generated independently as uniform in [−1, −0.5] ∪ [0.5, 1]. The diagonal values were assigned to a constant so that the condition number of each precision matrix was equal to p.
4.2 Simulation results
Each method was evaluated for a range of tuning parameters under each model. The optimal tuning parameter was chosen by BIC (6). Several measures are used to compare the performances of these estimators. The estimation error was evaluated in terms of average matrix ℓ1 norm, ℓ2 norm (spectral norm), and Frobenius norm:
The graph structure recovery results were evaluated by average sensitivity (SEN), specificity (SPE), and Matthews correlation coefficient (MCC). For a true precision matrix Ω0 = (ω0,ij) with support set , suppose its estimator has the support set . Then the measures with respect to Ω0 and are defined as follows:
Here, TP, TN, FP, and FN are the numbers of true positives, true negatives, false positives and false negatives:
We compared and and report the average sensitivities (SEN), specificities (SPE), and Matthews correlation coefficient (MCC) among K groups.
The comparisons of the results for the four graphical models are shown in Tables 1 and 2. It shows that when ρ = 0, the true graph structures are the same across all three groups, joint estimation methods perform much better than the separate estimation methods. As ρ increases, the structures across different groups become more different, and the joint estimation methods gradually lose their advantages. Our method has the best performance in graph structure recovery among all the methods. Even when ρ = 1, it still performs significantly better than the separate estimation methods. Our method has the best performance in graph structure recovery and it achieves the highest Matthews correlation coefficient. Its estimation error measured under the matrix ℓ1, ℓ2, and the Frobenius norm are comparable to other joint estimation methods.
Table 1.
Simulation results for data generated based on the Erdös and Rényi graph with different ratios of the number of individual-specific edges to the number of shared edges. Results are based on 100 replications. The numbers in the brackets are standard errors. CLIME: method of Cai, Liu and Luo (2011); GLASSO: graphical Lasso; JEMGM: method of Guo, Levina, Michailidis et al. (2011); fgland GGL: methods of Danaher, Wang and Witten (2014); MPE: proposed method.
| Model(ρ) | Method | Performance | |||||
|---|---|---|---|---|---|---|---|
| L1 | L2 | LF | SEN | SPE | MCC | ||
| ER(0) | CLIME | 19.62(0.32) | 7.72(0.08) | 49.48(0.83) | 0.25(0.01) | 0.99(0.00) | 0.34(0.01) |
| GLASSO | 20.57(0.38) | 7.91(0.12) | 46.81(0.68) | 0.03(0.02) | 1.00(0.00) | 0.11(0.02) | |
| JEMGM | 16.21(0.47) | 6.82(0.05) | 39.24(0.20) | 0.31(0.01) | 0.99(0.00) | 0.46(0.01) | |
| FGL | 20.26(0.72) | 7.89(0.09) | 46.89(0.62) | 0.05(0.02) | 1.00(0.00) | 0.12(0.02) | |
| GGL | 20.15(0.83) | 7.87(0.10) | 46.42(0.64) | 0.05(0.03) | 1.00(0.00) | 0.13(0.02) | |
| MPE | 18.33(0.38) | 7.32(0.10) | 48.27(0.98) | 0.47(0.02) | 1.00(0.00) | 0.63(0.01) | |
| ER(1/4) | CLIME | 20.60(0.27) | 8.62(0.09) | 57.13(0.86) | 0.20(0.02) | 0.98(0.00) | 0.27(0.01) |
| GLASSO | 21.48(0.56) | 8.22(0.19) | 51.82(1.47) | 0.17(0.05) | 0.97(0.01) | 0.19(0.03) | |
| JEMGM | 19.17(0.42) | 7.65(0.06) | 47.07(0.21) | 0.25(0.01) | 0.99(0.00) | 0.37(0.01) | |
| FGL | 21.72(0.59) | 8.51(0.05) | 54.21(0.39) | 0.11(0.01) | 0.98(0.00) | 0.16(0.01) | |
| GGL | 21.28(0.36) | 8.56(0.09) | 54.37(0.65) | 0.10(0.03) | 0.99(0.00) | 0.16(0.03) | |
| MPE | 19.47(0.29) | 8.36(0.10) | 55.93(0.88) | 0.32(0.01) | 0.99(0.00) | 0.49(0.01) | |
| ER(1) | CLIME | 28.73(0.30) | 10.86(0.17) | 72.98(1.68) | 0.11(0.03) | 0.98(0.01) | 0.17(0.01) |
| GLASSO | 35.47(48.52) | 11.40(10.62) | 74.19(75.65) | 0.11(0.08) | 0.97(0.08) | 0.13(0.02) | |
| JEMGM | 28.25(0.62) | 9.91(0.07) | 62.74(0.19) | 0.12(0.00) | 0.99(0.00) | 0.22(0.01) | |
| FGL | 29.96(0.56) | 10.56(0.08) | 68.89(0.67) | 0.05(0.02) | 0.99(0.00) | 0.09(0.01) | |
| GGL | 30.25(0.66) | 10.58(0.06) | 68.71(0.51) | 0.05(0.01) | 0.99(0.00) | 0.09(0.01) | |
| MPE | 28.43(0.32) | 10.60(0.09) | 70.83(0.85) | 0.19(0.01) | 0.99(0.00) | 0.34(0.01) |
Table 2.
Simulation results for data generated based on the Watt-Strogatz graph with different ratios of the number of individual-specific edges to the number of shared edges. Results are based on 100 replications. The numbers in the brackets are standard errors. CLIME: method of Cai, Liu and Luo (2011); GLASSO: graphical Lasso; JEMGM: method of Guo, Levina, Michailidis et al. (2011); fgland GGL: methods of Danaher, Wang and Witten (2014); MPE: proposed method.
| Model(ρ) | Method | Performance | |||||
|---|---|---|---|---|---|---|---|
| L1 | L2 | LF | SEN | SPE | MCC | ||
| WS(0) | CLIME | 29.80(0.23) | 13.05(0.19) | 87.71(1.96) | 0.11(0.03) | 0.99(0.00) | 0.25(0.02) |
| GLASSO | 29.55(0.25) | 12.35(0.08) | 79.20(0.47) | 0.08(0.01) | 0.99(0.00) | 0.20(0.01) | |
| JEMGM | 29.59(0.46) | 11.89(0.27) | 74.32(2.50) | 0.11(0.04) | 1.00(0.00) | 0.27(0.03) | |
| FGL | 29.45(0.33) | 12.43(0.13) | 80.10(1.22) | 0.10(0.02) | 0.99(0.00) | 0.23(0.03) | |
| GGL | 29.65(0.23) | 12.65(0.11) | 80.53(0.67) | 0.08(0.02) | 1.00(0.00) | 0.22(0.02) | |
| MPE | 28.99(0.22) | 12.72(0.12) | 84.35(1.11) | 0.16(0.01) | 1.00(0.00) | 0.34(0.01) | |
| WS(1/4) | CLIME | 42.70(0.35) | 14.80(0.19) | 102.03(2.08) | 0.08(0.02) | 0.98(0.01) | 0.15(0.01) |
| GLASSO | 42.79(0.58) | 14.25(0.07) | 95.38(0.49) | 0.04(0.00) | 0.99(0.00) | 0.09(0.00) | |
| JEMGM | 43.06(0.60) | 13.44(0.17) | 84.35(1.75) | 0.12(0.02) | 0.98(0.00) | 0.21(0.01) | |
| FGL | 43.33(0.59) | 14.31(0.06) | 96.24(0.49) | 0.06(0.01) | 0.98(0.00) | 0.11(0.01) | |
| GGL | 42.84(0.54) | 14.30(0.11) | 95.95(0.95) | 0.05(0.01) | 0.99(0.00) | 0.11(0.01) | |
| MPE | 42.15(0.39) | 14.60(0.11) | 100.13(1.16) | 0.10(0.00) | 0.99(0.00) | 0.23(0.01) | |
| WS(1) | CLIME | 63.27(0.35) | 18.64(0.19) | 128.83(1.94) | 0.04(0.01) | 0.99(0.00) | 0.08(0.01) |
| GLASSO | 62.94(0.31) | 17.85(0.11) | 120.11(1.01) | 0.02(0.01) | 0.99(0.00) | 0.04(0.01) | |
| JEMGM | 63.67(0.85) | 16.82(0.23) | 107.53(2.20) | 0.07(0.01) | 0.98(0.00) | 0.12(0.01) | |
| FGL | 63.11(0.28) | 17.86(0.07) | 120.82(0.66) | 0.02(0.00) | 0.99(0.00) | 0.04(0.00) | |
| GGL | 63.13(0.35) | 17.87(0.12) | 120.31(1.05) | 0.03(0.01) | 0.99(0.01) | 0.04(0.01) | |
| MPE | 62.89(2.57) | 18.18(0.47) | 123.98(2.71) | 0.08(0.09) | 0.98(0.09) | 0.15(0.01) |
Since the tuning parameter selection may affect the performance of the methods, we plot in Figure 1 the receiver operating characteristic (ROC) curves averaged over 100 repetitions with the false positive rate controlled under 10%. The methods proposed by Danaher, Wang and Witten (2014) have two tuning parameters. For each sparsity tuning parameter, we first chose an optimal similarity tuning parameter from a grid of candidates by BIC and then plotted the ROC curves based on a sequence of sparsity tuning parameters and their corresponding optimal similarity tuning parameters. Because these methods involve choosing two tuning parameters, they are slower than our method in computation (The computation of FGL and GGL is based on the R package “JGL” contributed by Danaher (2013)). Figure 1 shows that our method consistently outperforms the other methods in graph structure recovery.
Figure 1.
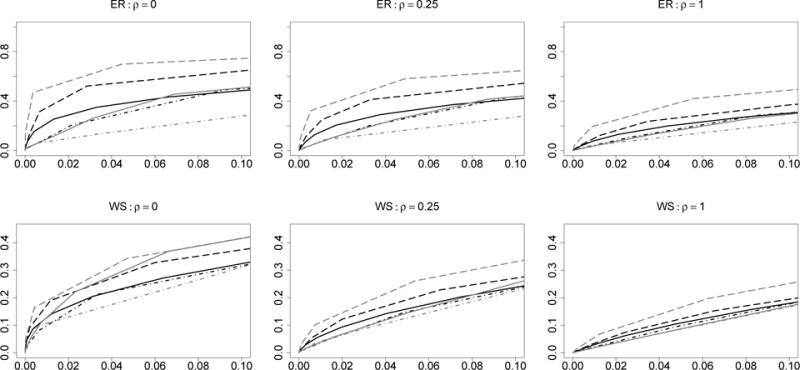
Receiver operator characteristic curves for graph structure recovery for the simulated Erdős and Rényi graphs (the first row), and the Watts-Strogatz graphs (the second row). The x-axis and y-axis of each panel are average false positive rate and average sensitivity across K = 3 groups. Black solid line: CLIME; black dot-dashed line: GLASSO; black long-dashed line: JEMGM; grey solid line: FGL; grey dot-dashed line: GGL; grey long-dashed line: MPE.
5. EPITHELIAL OVARIAN CANCER DATA ANALYSIS
Epithelial ovarian cancer is a molecularly diverse cancer that lacks effective personalized therapy. Tothill, Tinker, George et al. (2008) identified six molecular subtypes of ovarian cancer, labeled as C1–C6, where the C1 subtype was characterized by significant differential expressions of genes associated with stromal and immune cell types. The patients in C1 subtype group have shown to have a lower survival rate compared to the patients from other subtypes. The data set includes RNA expression data collected from n = 78 patients of C1 subtype and n = 113 patients from the other subtypes. We are interested to see how the wiring (conditional dependency) of the genes at the transcription levels differs among molecular subgroups of ovarian cancer. We focus on the apoptosis pathway from the KEGG database (Orgata, Goto, Sato et al. (1999); Kanehisa, Goto, Sato et al. (2012)) to see whether the genes related to this pathway (p = 87) are differentially wired between the C1 and other subtypes.
To stabilize the graph structure selection, we bootstraped the samples 100 times within each group. At each time, Iik was sampled uniformly taking values in i = {1,…, nk}, with k = 1, 2. Let , where is the p-dimensional gene expression data for the Iik-th patient in the kth subtype group. The bootstrap sample is , with k = 1, 2. We then applied our proposed method and its competitors to each of the bootstrapped samples to obtain the estimators of the two precision matrices , k = 1, 2. The supports of the estimators were recorded so that . We then added up for all bootstrap samples and got the final frequency of each edge being selected. Those edges that were selected in more than 50 of the 100 bootstrap samples were finally selected as important edges. This type of bootstrap aggregation methods has been commonly used in recovering the sparse graphical structures (Meinshausen and Bühlmann (2010); Li, Hsu, Peng et al. (2013)), which often leads to better selection stability for sparse precision matrix.
Table 3 lists the number of edges selected by the bootstrap aggregation of our proposed method and its competitors. The separate estimation methods (CLIME and GLASSO) resulted in graphs that share fewer edges in the precision matrices of the two cancer subtype groups. JEMGM resulted in most shared edges, followed by GGL and our method (MPE). Overall, FGL and GGL selected a lot more linked genes than other methods. Figure 2 shows the Gaussian graphs estimated by these six methods. FGL, GGL and MPE selected more unique edges among the gene expression levels for the C2–C6 subtype cancer than those for the C1 subtype. This suggests that the patients with poor prognostic subtype (C1) lack some important links among the Apoptosis genes.
Table 3.
Number of edges selected by the proposed method and its competitors. “C1 unique” counts the number of edges that only appear in the precision matrix of the gene expression levels in C1 cancer subtype; “Other unique” counts the number of edges that only appear in C2–C6 cancer subtypes; and “Common” counts the number of edges shared by both precision matrices.
| Method | C1 unique | Other unique | Common |
|---|---|---|---|
| CLIME | 40 | 43 | 20 |
| GLASSO | 11 | 11 | 7 |
| JEMGM | 23 | 22 | 77 |
| FGL | 8 | 112 | 23 |
| GGL | 14 | 148 | 44 |
| MPE | 13 | 38 | 42 |
Figure 2.
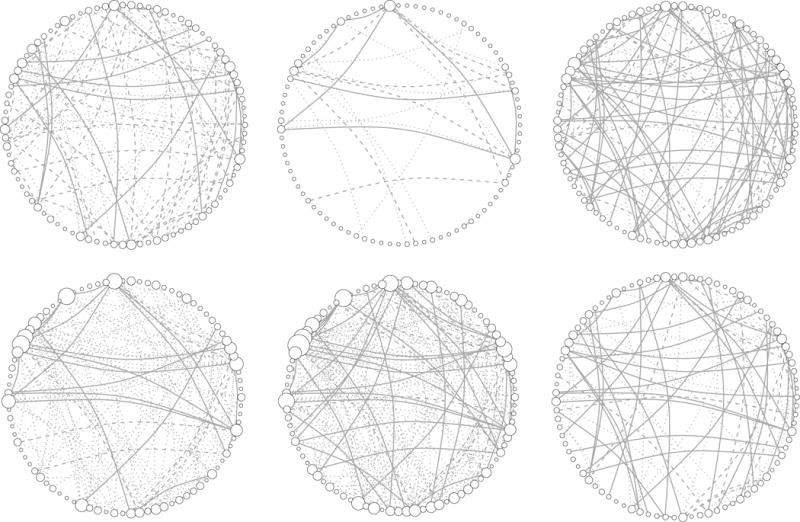
Estimated Gaussian Graphs by the proposed method and its competitors. The dashed edges are links unique to the precision matrix estimator of the C1 subtype, the dotted edges are unique to that of other subtypes, and the solid edges are shared by both estimators. The size of node is a linear function of its degree. Upper left panel: CLIME; upper middle panel: GLASSO; upper right panel: JEMGM; bottom left panel: FGL; bottom middle panel: GGL; bottom right panel: MPE.
We further defined the nodes with degrees equal or larger than five based on the union of the estimated graphs of two subtypes as the hub nodes. FGL and GGL yielded estimators with most of the hub nodes completely unlinked in the estimated graph for C1 cancer subtype. The estimators by MPE had several edges between the hub nodes shared by both subtype groups, while also displaying some links unique to each group. The hub nodes identified by MPE were FASLG, CASP10, CSF2RB, IL1B, MYD88, NFKB1, NFKBIA, PIK3CA, IKBKG, and PIK3R5. Among these, CASP10, PIK3CA, IL1B, and NFKb1 have been implicated in ovarian cancer risk or progression. In particular, PIK3CA has been implicated as an oncogene in ovarian cancer (Shayesteh, Lu, Kuo et al. (1999)), indicating the importance of these hub genes in ovarian cancer progression.
6. DISCUSSION
It is of interest to discuss the connection and difference between the problem considered in this paper and the problem of estimating matrix graphical models (Leng and Tang (2012); Yin and Li (2012); Zhou (2014)). Matrix graphical models consider the random matrix variate X following the distribution MNp×q(M; U, V) with the probability density function (pdf)
Here M ∈ ℝ p×q is the mean matrix, U ∈ ℝ p×p is the row covariance matrix, and V ∈ ℝ q×q is the column covariance matrix. Thus, each row and each column of X share the same covariance matrices U and V. This distribution implies that vec(X) follows a vector multivariate Gaussian distribution Npq(vec(M), U ⊗ V), where “vec” is the vectorization operator and “⊗” is the Kronecker product.
Our model assumes X(k) follows the vector multivariate Gaussian distribution Np(μ, Σ(k)). If n = n1 =… = nK, X = (X(1),…, X(K)) ∈ ℝ p×K is a random matrix variate. However, each column of X has its own covariance matrix Σ(k), and each row of X may also have its own. Therefore, the covariance matrix of vec(X) cannot be expressed as the Kronecker product of two positive definite matrices. In general, the degree of freedom of Cov(vec(X)) is larger than that of U ⊗ V mentioned above.
Supplementary Material
Acknowledgments
T. Tony Cai’s research was supported in part by NSF Grants DMS-1208982 and DMS-1403708, and NIH Grant R01 CA127334. Hongzhe Li’s research was supported in part by NHI Grants R01 CA127334 and R01 GM097505. Weidong Liu’s research was supported in part by NSFC, Grants No. 11201298, No. 11322107, the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning Shanghai Pujiang Program, Shanghai Shuguang Program and 973 Program (2015CBB56004). Jichun Xie’s research was supported in part by NIH Grant UL1 TR001117.
We thank the Editor, an associate editor and the reviewers for their insightful comments and suggestions that have helped us substantially improve the quality of the paper.
The research was supported in part by NSF FRG Grant DMS-0854973, NSF MRI Grant No. CNS-09-58854, NIH grants CA127334, GM097505. Weidong Liu’s research was also supported by NSFC Grant No.11201298 and No.11322107, the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, Shanghai Pujiang Program, Foundation for the Author of National Excellent Doctoral Dissertation of PR China and Program for New Century Excellent Talents in University.
Footnotes
SUPPLEMENTARY MATERIAL
In the supplementary material, we provide additional simulation studies to compare the proposed methods and other competitive methods. We also include the proofs of the theorems.
Contributor Information
T. Tony Cai, Professor of Statistics, Department of Statistics, The Wharton School, University of Pennsylvania, Philadelphia, PA 19104.
Hongzhe Li, Professor of Biostatistics, University of Pennsylvania Perelman School of Medicine, Philadelphia, PA 19104.
Weidong Liu, Professor, Department of Mathematics, Institute of Natural Sciences and MOE-LSC, Shanghai Jiao Tong University, Shanghai, China.
Jichun Xie, Assistant Professor, Department of Biostatistics and Bioinformatics, Duke University School of Medicine, Durham, NC 27707.
References
- Anderson TW. An introduction to multivariate statistical analysis. Wiley-Interscience; 2003. [Google Scholar]
- Banerjee O, Ghaoui LE, d’Aspremont A. Model selection through sparse maximum likelihood estimation for multivariate gaussian or binary data. J Machine Learning Research. 2008;9:485–516. [Google Scholar]
- Cai T, Liu W, Luo X. A constrained ℓ1 minimization approach to sparse precision matrix estimation. Journal of American Statistical Association. 2011;106:594–607. [Google Scholar]
- Candés E, Tao T. The dantzig selector: Statistical estimation when p is much larger than n. The Annals of Statistics. 2007;35:2313–2351. [Google Scholar]
- Chen J, Chen Z. Extended bayesian information criterion for model selection with large model space. Biometrika. 2008;95:232–253. [Google Scholar]
- Dahl J, Vandenberghe L, Roychowdhury V. Covariance selection for non-chordal graphs via chordal embedding. Optimization Methods and Software. 2008;23:501–420. [Google Scholar]
- Danaher P. JGL: Performs the Joint Graphical Lasso for sparse inverse covariance estimation on multiple classes. R package version 2.3. 2013 doi: 10.1111/rssb.12033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danaher P, Wang P, Witten D. The joint graphical lasso for inverse covariance estimation across multiple classes. Journal of the Royal Statistical Society, Series B. 2014:76–2. doi: 10.1111/rssb.12033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoho D, Elad M, Temlyakov V. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Transactions on Information Theory. 2006;52:6–18. [Google Scholar]
- Erdös P, Rényi A. On the evolution of random graphs. Publications of the Mathematical Institute of the Hungarian Academy of Sciences. 1960;5:17–61. [Google Scholar]
- Fan Y, Tang C. Tuning parameter selection in high dimensional penalized likelihood. Journal of the Royal Statistical Society. 2013;75:531–552. [Google Scholar]
- Fell D, Wagner A. The small world of metabolism. Nature Biotechnology. 2000:18–11. doi: 10.1038/81025. [DOI] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2008;9:432–441. doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greene L, Higman V. Uncovering network systems within protein structures. Journal of Molecular Biology. 2003;334:781–791. doi: 10.1016/j.jmb.2003.08.061. [DOI] [PubMed] [Google Scholar]
- Guo J, Levina E, Michailidis G, Zhu J. Joint estimation of mulitple graphical models. Biometrika. 2011;98:1–15. doi: 10.1093/biomet/asq060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong H, Tombor B, Albert R, Oltvai Z, Barabási A. The large-scale organization of metabolic networks. Nature. 2000:407–6804. doi: 10.1038/35036627. [DOI] [PubMed] [Google Scholar]
- Kanehisa M, Goto S, Sato Y, Furumichi M, Tanabe M. KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Research. 2012;40:D109–D114. doi: 10.1093/nar/gkr988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauritzen SL. Graphical Models. Clarendon Press; Oxford: 1996. [Google Scholar]
- Leng C, Tang C. Sparse matrix graphical models. Journal of American Statistical Association. 2012:107–499. [Google Scholar]
- Li H, Gui J. Gradient directed regularization for sparse gaussian concentration graphs, with applications to inference of genetic networks. Biostatistics. 2006;7:302–317. doi: 10.1093/biostatistics/kxj008. [DOI] [PubMed] [Google Scholar]
- Li S, Hsu L, Peng J, Wang P. Bootstrap inference for network construction with an application to a breast cancer microarray study. The Annals of Applied Statistics. 2013:7–1. doi: 10.1214/12-AOAS589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang F, He G, Hu Y. A new smoothing Newton-type method for second-order cone programming problems. Applied Mathematics and Compuation. 2009;215:1020–1029. [Google Scholar]
- Meinshausen N, Bühlmann P. High-dimensional graphs and variable selection with the lasso. Annals of Statistics. 2006;34:1436–1462. [Google Scholar]
- Meinshausen N, Bühlmann P. Stability selection. Journal of Royal Statistics Society, Series B. 2010;72:417–473. [Google Scholar]
- Newsterov Y, Todd M. Primal-dual interior-point methods for self-scaled cones. SIAM Journal on Optimization. 1998;8:324–364. [Google Scholar]
- Orgata H, Goto S, Sato K, Fujibuchi W, Bono H, Kanehisa M. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Research. 1999;27:29–34. doi: 10.1093/nar/27.1.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer J, Strimmer K. An empirical bayes approach to inferring large-scale gene association networks. Bioinformatics. 2005;21:754–764. doi: 10.1093/bioinformatics/bti062. [DOI] [PubMed] [Google Scholar]
- Shayesteh L, Lu Y, Kuo W, Baldocchi R, Godfrey T, Collins C, Pinkel D, Powell B, Mills G, Gray J. Pik3ca is implicated as an oncogene in ovarian cancer. Nature Genetics. 1999;21:99–102. doi: 10.1038/5042. [DOI] [PubMed] [Google Scholar]
- Tothill R, Tinker A, George J, Brown R, Fox S, Lade S, Johnson D, Trivett J, Etemadmoghadam D, Locandro B, Traficante N, Fereday S, Hung J, Chiew Y, Haviv I, Group A. O. C. S. Gertig D, deFazio A, Bowtell D. Novel molecular subtypes of serous and endometrioid ovarian cancer linked to clinical outcome. Clinical Cancer Research. 2008;14:5198–5208. doi: 10.1158/1078-0432.CCR-08-0196. [DOI] [PubMed] [Google Scholar]
- Vendrascolo M, Dokholyan N, Paci E, Karplus M. Small-world view of the amino acids that play a key role in protein folding. Physical Review E. 2002;65 doi: 10.1103/PhysRevE.65.061910. [DOI] [PubMed] [Google Scholar]
- Wang H, Li B, Leng C. Shrinkage tuning parameter selection with a diverging number of parameters. Journal of Royal Statistical Society, Series B. 2009;71:671–683. [Google Scholar]
- Wang T, Zhu L. Consistent tuning parameter selection in high dimensional sparse linear regression. Journal of Multivariate Analysis. 2011;102:1141–1151. [Google Scholar]
- Watts D, Strogatz S. Collective dynamics of “small world” networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Whittaker J. Graphical Models in Applied Multivariate Analysis. Wiley; 1990. [Google Scholar]
- Yin J, Li H. Model selection and estimation in the matrix normal graphical model. Journal of Multivariate Analysis. 2012;107:119–140. doi: 10.1016/j.jmva.2012.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M. Sparse inverse covariance matrix estimation via linear programming. Journal of Machine Learning Research. 2010;11:2261–2286. [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in the gaussian graphical model. Biometrika. 2007;94:19–35. [Google Scholar]
- Zhou S. Gemini: Graph estimation with matrix variate normal instances. Annals of Statistics. 2014;42:532–562. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


