Skip to main content
PMC home page
Elsevier Sponsored Documents logoLink to Elsevier Sponsored Documents
. 2016 Sep;13:35–43. doi: 10.1016/j.wace.2016.07.001

Comparing regional precipitation and temperature extremes in climate model and reanalysis products

Oliver Angélil a,⁎, Sarah Perkins-Kirkpatrick a, Lisa V Alexander a, Dáithí Stone b, Markus G Donat a, Michael Wehner b, Hideo Shiogama c, Andrew Ciavarella d, Nikolaos Christidis d
PMCID: PMC5351813  PMID: 28344929

Abstract

A growing field of research aims to characterise the contribution of anthropogenic emissions to the likelihood of extreme weather and climate events. These analyses can be sensitive to the shapes of the tails of simulated distributions. If tails are found to be unrealistically short or long, the anthropogenic signal emerges more or less clearly, respectively, from the noise of possible weather. Here we compare the chance of daily land-surface precipitation and near-surface temperature extremes generated by three Atmospheric Global Climate Models typically used for event attribution, with distributions from six reanalysis products. The likelihoods of extremes are compared for area-averages over grid cell and regional sized spatial domains. Results suggest a bias favouring overly strong attribution estimates for hot and cold events over many regions of Africa and Australia, and a bias favouring overly weak attribution estimates over regions of North America and Asia. For rainfall, results are more sensitive to geographic location. Although the three models show similar results over many regions, they do disagree over others. Equally, results highlight the discrepancy amongst reanalyses products. This emphasises the importance of using multiple reanalysis and/or observation products, as well as multiple models in event attribution studies.

Keywords: Extremes, Evaluation, Event attribution, CAM5.1, MIROC5, HadGEM3-A-N216

1. Introduction

As the climate continues to change under the influence of anthropogenic emissions, there has been a growing interest in how the occurrence of extreme weather events fit within the climate change context (Seneviratne et al., 2012). A common method of characterising the anthropogenic contribution to extreme weather is to analyse the relative probabilities of exceeding an extreme threshold in two simulated distributions (Stone and Allen, 2005, Stott et al., 2004, Stott et al., 2013). These distributions can be constructed from two large ensembles of simulations generated by a dynamical climate model, each run under a different climate scenario: a historical ‘real world’ (RW) representative of recent observed climate, and a counter-factual ‘natural world’ (NAT) representative of a climate without human interference in the climate system. Purpose-built model evaluation should underpin the probabilistic event attribution framework used in these studies, whereby the probabilities of extremes are compared across the historical model output and a number of observation and/or reanalysis products. This is necessary as attribution statements are highly sensitive to the shapes of the tails from which they are calculated (Angélil et al., 2014b, Fischer and Knutti, 2015, Jeon et al., 2016). For example, the use of simulated RW and NAT distributions with shorter tails than those of observed distributions lead to exaggerated attribution statements – the shorter tails increase the relative strength of the anthropogenic signal from the noise of natural variability (Bellprat and Doblas-Reyes, 2016). In such an evaluation the use of multiple observation and/or reanalysis products must be considered, as their representation of extremes can differ remarkably (Donat et al., 2014).

Many event attribution studies however typically fail to incorporate multiple observation and/or reanalysis products to evaluate the extreme tails of simulated distributions (Stott et al., 2004, Pall et al., 2011, Peterson et al., 2012, Peterson et al., 2013, Herring et al., 2014, Herring et al., 2015). One possible reason for the paucity of such evaluation is the lack of long (∼50 years) historical simulations, and long spatially and temporally complete observational records required for the evaluation of extremes. For example, evaluating one-in-ten-year extremes with datasets ten years in length is both challenging and unreliable.

Using datasets 35 years in length (1979–2013), we evaluate the likelihood of exceeding (or falling below for cold events) one-in-one- and one-in-ten-year daily temperature and precipitation thresholds (defined according to a reference product) over land regions of the world, in ensembles of historical simulations generated by three Atmospheric Global Climate Models (AGCMs). The primary aim of this study is to explore observational uncertainties in model evaluation relevant for extreme event attribution, at the regional scale.

2. Data

2.1. Atmospheric Global Climate Model data

Output was generated by three AGCMs as part of the C20C+ Detection and Attribution Project (see http://portal.nersc.gov/c20c for more information, Folland et al. 2014). Since Pall et al. (2011) numerous event attribution studies have been published utilising output from AGCMs in order to produce the large ensembles needed to accurately resolve the statistics of rare weather events. Here we use CAM5.1, MIROC5 and HadGEM3-A-N216 (‘HadGEM3’ hereinafter), the first three AGCMs to have a sufficient number of simulations submitted to the C20C+ archive. As there are 10 ensemble members generated by MIROC5 (run at ∼1.4°) which span a number of decades, we use the first 10 historical ensemble members from CAM5.1 and HadGEM3, run at ∼1° and ∼0.5° resolution respectively. The members in each ensemble differ from each other only in their initial conditions. Simulations from all AGCMs are roughly 50 years in length but have been trimmed to match availability of the AGCM and reanalyses products used.

The AGCMs are forced under observed boundary conditions. These boundary conditions include greenhouse gases, tropospheric aerosols, volcanic aerosols, ozone concentrations, solar luminosity, sea surface temperature (SST), sea ice coverage (SIC), and land cover. In CAM5.1, prescribed SSTs up to 1982 are an adjusted version of the HadISST1 dataset (Rayner et al., 2003), after which the NOAA-OI.v2 dataset is used (Hurrell et al., 2008). The HadGEM3 (Christidis et al., 2013) and MIROC5 (Shiogama et al., 2013, Shiogama et al., 2014) prescribed monthly SST and SIC were taken from the HadISST1 dataset.

2.2. Reanalyses

We compare the probabilities of daily extremes in the three AGCMs with four reanalysis products (results using two additional reanalyses products can be found in the Supplementary Material). We firstly examine the ECMWF Interim Reanalysis (ERA-Interim, Dee et al. (2011)) as it has been found that temperature extremes in ERA-Interim correlate more strongly with gridded observations than a selection of other reanalysis products (Donat et al., 2014). Because there is some uncertainty in the representation of extreme weather between observations and reanalyses products (Donat et al., 2014), we complement ERA-Interim with three additional products from the current state-of-the-art generation (Rienecker et al., 2011). These are: NCEP Climate Forecast System Reanalysis (CFSR, Saha et al., (2010)); National Aeronautics and Space Administration (NASA)'s Modern-Era Retrospective Analysis for Research and Applications (MERRA, Rienecker et al., (2011)); and most recently available, the Japanese 55-year Reanalysis (JRA-55, Kobayashi et al. (2015)).

As they are still widely used products, results using the National Centers for Environmental Prediction/National Centre for Atmospheric Research (NCEP/NCAR) Reanalysis 1 (NCEP1, Kalnay et al., (1996)) and NCEP Department of Energy (DOE) Reanalysis 2 (NCEP2, Kanamitsu and Ebisuzaki, (2002)) are included in the Supplementary Material. Despite NCEP1 being shown to perform poorly relative to other reanalyses and observation products for temperature extremes (Donat et al., 2014), it has been widely used in recent event attribution studies (Herring et al., 2014, Herring et al., 2015).

HadGHCND (Caesar et al., 2006) – the only quasi-global long-running in situ-based observation product consisting of daily temperature fields, was excluded from this study not only because it is spatially and temporally incomplete, but also as it is developed at coarse resolution (3.75°×2.5°) relative to other products in this study. As all data in this study are remapped to the resolution of the coarsest product, we have opted for high resolution analysis over using HadGHCND. All AGCM and reanalysis data have been interpolated to the NCEP1/NCEP2 grid (192×94 grid; 1.9°), using a first-order conservative remapping technique (Jones, 1999).

Since reanalyses are different from observations as they are essentially an assimilation of observations through an atmospheric model, we use gridded observations of daily temperature and precipitation over Australia, from the Australian Water Availability Project (AWAP, Jones et al., (2009)). Observations over only Australia are used because existing gridded observations of daily temperature and precipitation are spatially incomplete. Hot, cold, and wet extremes over three Australian regions are compared between AWAP and ERA-Interim (see Fig. S7).

It should be noted however, that caution should be taken when comparing gridded observations with models due to the “issue of scale” (Avila et al., 2015), which leads to a mismatch between the two types of products. Gridded observations represent regularly spaced values derived from point locations, while output from models represent area averages. There is an additional issue at play in gridded observations such as HadEX2 and GHCNDEX: the order of operations applied to calculate extremes differ from products that provide daily grids of temperature and precipitation, such as climate models and reanalyses. Extremes are first calculated at point locations and then gridded, while in models, extremes are calculated from the gridbox average. This creates a systematic bias where the difference in hot and cold extremes in models are smaller than those found in GHCNDEX and HadEX2.

3. Method

For the evaluation of extremes, thresholds of one-in-one-year (1365 chance of occurrence) and one-in-ten-year (13650 chance of occurrence) hot, cold, and wet days occurring at the grid and regional scales have been defined from daily anomalies in ERA-Interim, with the base period being the 1979–2013 climatology at each grid cell or region. ERA-Interim serves as our reference product in order to clearly demonstrate differences amongst all AGCMs and reanalyses products. Although perhaps less relevant for extreme event attribution, the selection of the one-in-one-year thresholds allows us to examine extreme anomalies for which sampling should not be problematic considering the length of the period examined. When the desired percentile was between two data points, the nearest point to a linearly interpolated value between the two points was chosen.

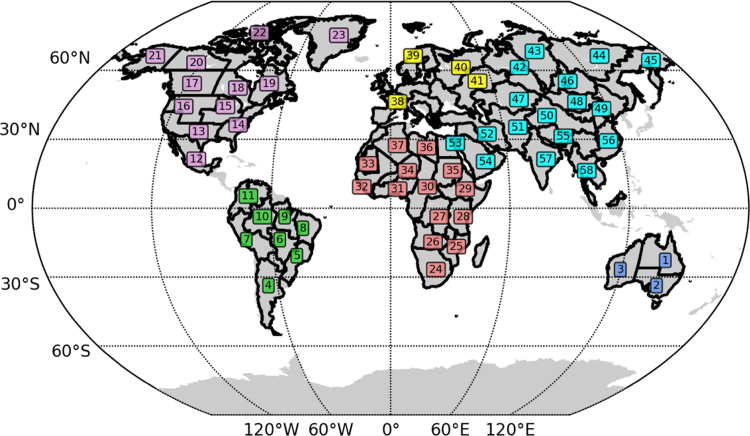
The regions used are demarcated by the 58 regions (see Fig. 1 and Angélil et al., (2014b)) in the Weather Risk Attribution Forecast (WRAF, http://web.csag.uct.ac.za/~daithi/forecast/). Each region, roughly 2·106km2, is based on political-economic borders, and omits regions dominated by small islands (for which the statistical characteristics of extreme atmospheric weather will be strongly constrained under imposed-ocean conditions).

Fig. 1.

Fig. 1

Open in a new tab

Weather Risk Attribution Forecast regions colour-coded according to their continents. Each region is roughly 2·106km2.

Before we calculate the probability of exceeding the thresholds defined from ERA-Interim in the AGCMs and reanalyses, we convert the raw data at every grid cell/region to daily anomalies based on the 1979–2013 climatologies. We do this instead of calculating anomalies based on seasonal climatology, as we are mostly interested in extremes occurring anytime within the annual cycle – those being typically hazardous to humans and their built environments. Correcting for mean bias is an essential step before comparing the shapes of the distributions, as the raw values between products can differ substantially. This procedure is performed separately for each reanalysis product and ensemble member.

4. Results

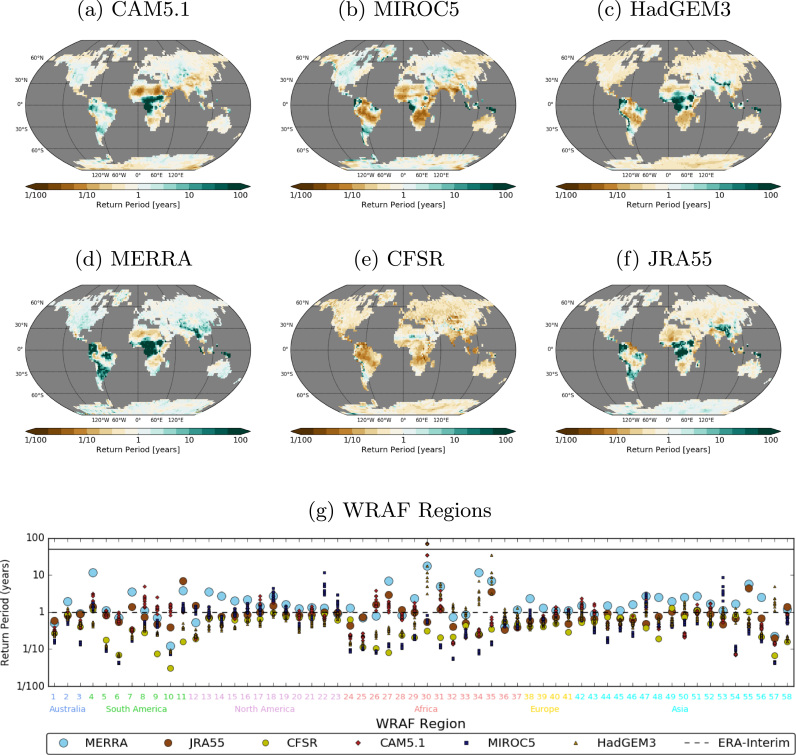
Return period curves are first shown for selected regions (Fig. 2). Next, the probabilities of exceeding (or falling below for extremely cold events) the one-in-one- and one-in-ten-year thresholds (defined in ERA-Interim) in the datasets, are plotted as return periods. For the maps (panels (a) to (f) in Fig. 3, Fig. 4, Fig. 5), the resulting return periods from the CAM5.1, MIROC5, and HadGEM3 ensembles, are averaged in order to gauge the mean exceedance in the entire ensemble. For the panels (panels ‘g′ in Fig. 3, Fig. 4, Fig. 5) comparing the probabilities of extremes occurring over the WRAF regions, results from the ensemble members are plotted separately such that spread within the ensemble can be visualised.

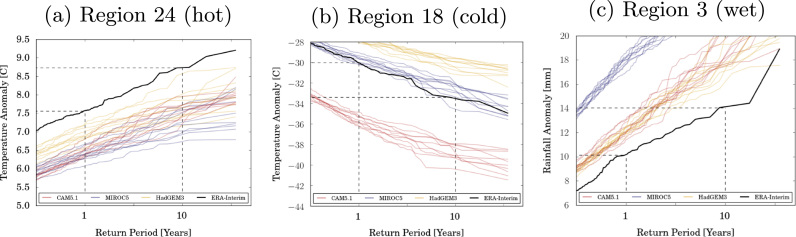
Fig. 2.

Fig. 2

Open in a new tab

Return Periods of hot (a), cold (b), and wet (c) average daily near-surface temperature / precipitation anomalies over regions 24 (southern Africa), 18 (central Canada), and 3 (western Australia) respectively. Red, blue, and yellow lines are from the 10 MIROC5, CAM5.1 and HadGEM3 simulations respectively, while the black line is from ERA-Interim. Each distribution covers the 1979–2013 period. Dashed lines show the return values for events having a one-in-one- and one-in-ten-year return period in the reference product, ERA-interim.

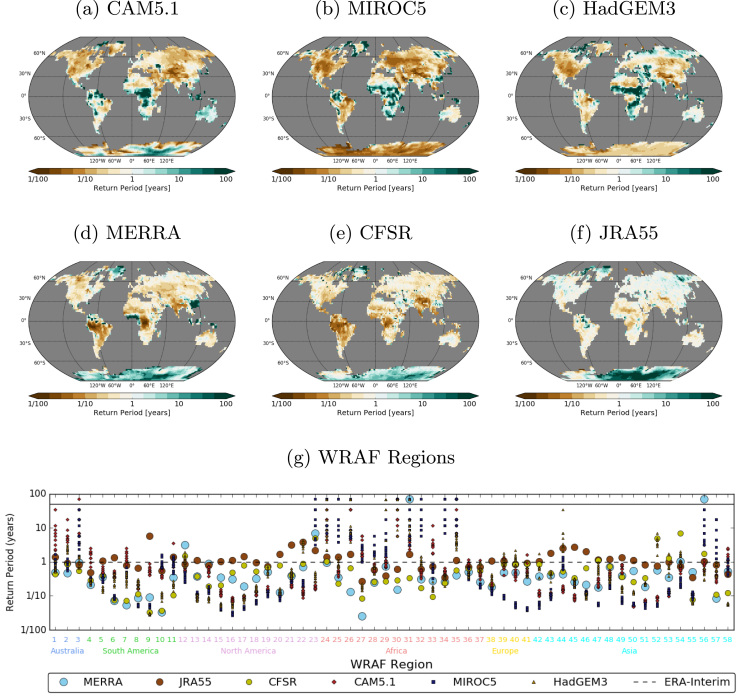
Fig. 3.

Fig. 3

Open in a new tab

Return periods of one-in-one-year hot days defined from ERA-Interim. To account for mean bias, before calculating return periods, anomalies were calculated based on 1979–2013 means at every grid cell. Data for the 1979–2013 period have been used to calculate return periods. Panels shown are CAM5.1 (a), MIROC5 (b), HadGEM3 (c), MERRA (d), CFSR (e) and JRA-55 (f). Panel g shows the same but for hot extremes occurring over the Weather Risk Attribution Forecast regions. Numbers and colours on the x-axis refer to regions and continents in Fig. 1 respectively. Markers above the solid line have a return period of infinity, i.e. the event did not occur in the dataset. The dashed line represents the return period of the reference (ERA-Interim).

Fig. 4.

Fig. 4

Open in a new tab

Same as Fig. 3 but for one-in-one-year cold days.

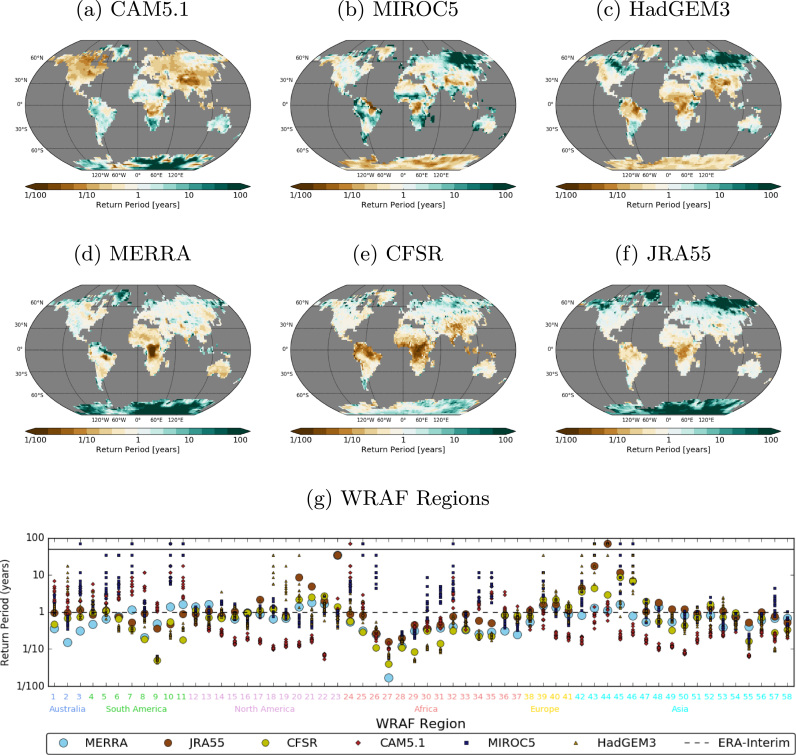
Fig. 5.

Fig. 5

Open in a new tab

Same as Fig. 3 but for one-in-one-year wet days.

Fig. 2 shows return periods curves of 1979–2013 daily mean temperature/precipitation anomalies from ERA-Interim and every member in each of the AGCMs, over three WRAF regions. Panels a, b, and c are for hot, cold, and wet weather over southern Africa, central Canada and western Australia respectively. Relative to ERA-interim, all AGCMs underestimate the probability of hot extremes over southern Africa; CAM5.1 and HadGEM3 under- and overestimate the probability of cold extremes over central Canada respectively; and all AGCMs overestimate the probability of wet extremes over western Australia.

While these biases from the AGCMs appear fairly large, the question remains as to how they compare against possible biases in the reanalyses. We can get some indication of this by comparing against other reanalyses. Fig. 2 highlights the spread of return periods for two different return values based on one-in-one- and one-in-ten-year anomalies in ERA-interim. Fig. 3, Fig. 4, Fig. 5 show return periods that one-in-one-year extremes defined in ERA-Interim have of occurring in CAM5.1, MIROC5, HadGEM3, MERRA, CFSR, and JRA-55, over grid cells and all WRAF regions (results for one-in-ten-year extremes, NCEP1, and NCEP2 can be found in the Supplementary Information). In the maps, cyan colours (high return periods) indicate the chance of exceeding (falling below for cold events) the threshold is lower than in ERA-Interim, while golds (low return periods) indicate the chance of exceeding/falling below the threshold is greater. Panel (g) in Fig. 3, Fig. 4, Fig. 5 depict return periods for extremes occurring over the regions demarcated in Fig. 1 – with the colours and numbers along the x-axis representing continents and WRAF regions respectively. For example, as in Fig. 2a, Fig. 3g shows high return periods for the AGCMs over region 24, relative to ERA-interim (represented by the dashed line).

In all panels of Fig. 3, Fig. 4, Fig. 5, return periods can vary considerably between regions and/or continents. It therefore makes sense to avoid drawing conclusions about a product as a whole, but rather to judge AGCM performance according to regions. If we weigh each reanalysis equally we can take a consensual approach to gauge the agreement/credibility of the reanalyses. The greater the agreement between reanalyses the more suitable they are to gauge AGCM performance at simulating the frequency of extremes. Before looking at comparisons between the reanalyses and AGCMs in more detail, the reader is directed to figure S7. Here we test ERA-Interim against gridded observations from the Australian Water Availability Project (AWAP). The hot, cold, and wet tails of distributions of daily temperature and rainfall are compared over regions 1 (Northeastern Australia), 2 (Southeastern Australia), and 3 (Western Australia) as demarcated in Fig. 1. The tails of the distributions align well (differences in the return periods for one-in-one-year return levels from ERA-Interim, are less than one month in all panels) – such a result is not unexpected as these are regions that are well sampled with in situ observations. Reanalyses performance are however expected to be reduced over regions which are poorly sampled with in situ observations.

The spatial distribution of return periods relative to the reference product for hot extremes in Fig. 3 looks similar to those for one-in-ten-year extremes in Fig. S1, the latter exhibiting amplified values of the former (markers tend away from the reference). Such a result is expected as a shift in focus to more extreme anomalies means the count of days beyond these thresholds is fewer, rendering our results more sensitive to differences between ERA-Interim and the other datasets. This can additionally be seen between the cold and wet pairs of figures, and agrees with results found by Fischer and Knutti (2015). Since extreme event attribution studies typically examine extremes occurring less frequently than once a year, the results pertaining to one-in-ten-year extremes, although less accurate by definition, may have more relevance.

In Fig. 3, over much of Australia, CAM5.1 underestimates the frequency of hot days relative to the reanalyses (from here onwards the reader should assume all statements regarding the ‘under-simulation’ or ‘over-simulation’ of the frequency of extremes in the AGCMs to be relative to the reanalyses). The relevant markers in panels g of Figs. 3 and S1 show large spread amongst the CAM5.1 ensemble members. This characteristic can again be explained by a shift (of the threshold) further out into the tails of the ensemble mean. As a consequence of poor AGCM sampling in this case, fewer counts beyond the threshold return increasingly sensitive results to slight variations in those counts – the reason the spread amongst CAM5.1 simulations over Australia is greater than that of the MIROC5 and HadGEM3 simulations. Equally, the frequency of hot extremes over much of the tropics in all AGCMs are underestimated (in many cases occur roughly 10 times less frequently in the AGCMs than in reanalyses), while the frequency of hot extremes over most of the Northern Hemisphere are overestimated relative to ERA-interim and JRA-55 (roughly 10 times more frequent in the AGCMs), and moderately relative to MERRA and CFSR. Over WRAF regions 31 (West Africa) and 56 (South-east China) no events in MERRA exceed a one-in-one-year hot event in ERA-Interim. NCEP1 stands out from the other reanalyses as being the product with the highest occurrence of infinity high return periods for hot days over the WRAF regions (Fig. S4).

For cold extremes (Fig. 4) the AGCMs underestimate the frequency of cold extremes over much of Australia, Southern Africa, and South America (return periods tend to be anywhere between 1 and 10 times higher in the AGCMs). Over Western Europe return periods correspond relatively well with the reanalysis, while over Northern North America, Eastern Europe and most of Asia, MIROC5 and HadGEM3 perform well but CAM5.1 overestimate the frequency of extremes by roughly a factor of 5. In JRA-55 over region 44 (Eastern Russia), no events fall below the one-in-one-year cold thresholds defined in ERA-Interim. In Fig. S5 we again see more occurrences of return periods of infinity in NCEP1 than in any other product. Where exactly it under-performs is however highly contextual.

The spread amongst the different datasets is less in the results for precipitation (Fig. 5) than for temperature. The spread between return periods for one-in-one-year wet events lie within an order of magnitude between the datasets over Northern Asia, Europe, and much of North America. Less agreement is generally found in tropical regions (particularly of South America, Africa, and Southern Asia). In the maps and panel g, CFSR stands out as having a tendency to simulate the chance of wet extremes more often than the other datasets. MERRA on the contrary underestimates the frequency of wet extremes relative to the AGCMs and other reanalyses. We see increased uncertainty in results for one-in-ten-year events (Fig. S3) due to poorer sampling because we are examining one-in-ten-year extremes in a series 35-years in length. Fig. S6 depicts NCEP1 as having strikingly different results from the other datasets over regions of Africa and South America.

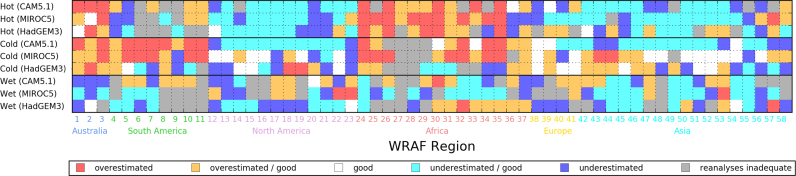
For their simulation of hot, cold, and wet events over each region, each AGCM is, in two summary figures (Fig. 6 for one-in-one-year events and Fig. 7 for one-in-ten-year events), assigned one of six statements suggesting attribution statements to be either “overestimated”, “overestimated/good”, “good”, “underestimated/good”, “underestimated”, or “reanalyses inadequate”. Statements are assigned as follows. A z-score is calculated for each reanalysis, i.e. the number of standard deviations its exceedance probability lies from the mean of the distribution of exceedance probabilities, assuming Gaussianity amongst the probabilities – one value for each of the 10 ensemble members (note that a Gaussian is not fit to distributions of rainfall or temperature, but rather to the exceedance probabilities from the 10 ensemble members). Z-scores are converted to p-values before a trinomial value is assigned to each p-value. 2 or 0 is assigned for p-values less than 0.01 or greater than 0.99, respectively. Unity is assigned to all remaining p-values. The colour of each square in Fig. 6, Fig. 7 is ultimately assigned according to the combination of four (one per reanalyses) trinomial values. “0000″ suggests the AGCM has underestimated the frequency, suggesting an “overestimated” attribution statement; “0001″, “0011″, or “0111″ is assigned “overestimated/good”; “1111″ is assigned “good”; “1112″, “1122″, or “1222″, or is assigned “underestimated/good”; “2222″ is assigned “underestimated”, and lastly all remaining combinations, which by definition have the highest standard deviations, are assigned “reanalyses inadequate”.

Fig. 6.

Fig. 6

Open in a new tab

Summary figure illustrating whether the three AGCMs are likely to underestimate, overestimate, or accurately estimate (see text for explanation of definitions) attribution statements for hot, cold, and wet one-in-one-year events, over each of the 58 WRAF regions. Grey colours denote AGCM results that fall within a large spread of reanalyses – uncertainty is deemed too large to make a statement regarding AGCM performance.

Fig. 7.

Fig. 7

Open in a new tab

Same as Fig. 6 but for one-in-ten-year events.

Fig. 6 summarises the panels (g) from Fig. 3, Fig. 4, Fig. 5. Reds, blues and whites suggest overestimated, underestimated, and reliable attribution statements respectively, while greys suggest large discrepancy amongst reanalyses products rendering them inadequate for evaluation. For hot and cold events we see clustering of similar colours across continents or neighbouring regions. For example results suggest a bias towards stronger attribution statements for hot and cold events over Australia, South America and Africa, while these events are more likely to be underestimated over North America and Asia. Such a characteristic over large spatial domains is less prominent for wet events. Also noteworthy is that the AGCMs rarely exhibit strongly opposing results over individual regions, i.e. there are few cases where one AGCM is “overestimated” while another is “underestimated” or vice versa. Therefore, if only one of the three AGCMs is used in an event attribution study, there is more chance than not that the other two would show a similar tendency in its bias.

We notice that the AGCMs generally tend to underestimate the frequency one-in-ten-year events (Fig. 7), suggesting a greater chance of overestimating attribution statements, consistent with Bellprat and Doblas-Reyes (2016). While results between neighbouring regions or even across continents tend to be similar (particularly for hot and cold events), it is evidently possible for them to vary significantly. This characteristic should caution scientists to avoid drawing generalisations about whether attribution statements are overly strong or weak. While there may be a slight bias for attribution statements pertaining to one-in-ten-year events to be overly strong, in agreement with Bellprat and Doblas-Reyes (2016), our results suggest that there is still bias favouring overly weak attribution statements over many regions of the world, for example for hot extremes over most of North America and Asia (Fig. 7). Bellprat and Doblas-Reyes (2016) draw from other studies that simulated distributions from the current generation of climate models are characterised by having ensemble spreads that are too narrow (Weisheimer and Palmer, 2014). It is however possible for models to be under-dispersive (characterised by U-shaped rank histograms) but have tails which are longer than those of observations or reanalyses. Such cases would result in a bias favouring overly weak attribution statements. This study however only compares variability between the AGCMs and reanalyses in distributions covering a 35-year period. Biased attribution statements can also result from: errors in the trend, which would incorrectly position the distribution given a particular sub-period analysed (van Oldenborgh et al., 2013); as well an incorrect response to ocean forcing during the period and over the region of the event being attributed.

5. Discussion and conclusions

The results presented in Fig. 6, Fig. 7 are only a guideline, suggesting underestimated, overestimated or accurate attribution statements. In addition to the other potential errors in models (leading to biased attribution statements when looking at real extreme events rather than spread over a 35-year period), as mentioned in the previous section, probabilistically-derived attribution statements can also be influenced by response bias, i.e. the difference between the means of the historically and naturally forced distributions, which has not been explored in this study.

The spread of ensemble members and their proximity to reanalyses can provide information about uncertainties in model evaluation relevant for event attribution. Attribution statements calculated over a particular region (for a particular variable), over which the AGCM-derived return periods fall within a large spread of return periods obtained from reanalyses, should be taken with caution. These cases are therefore greyed out in the summary figures. Over these regions it may currently be best practise to avoid publishing any attribution statement, as disagreement amongst reanalyses begs the question “toward which reanalysis/observation product should one scale? ”. Answering this question would require further analysis in order to weight different observation/reanalyses products.

If simulated extremes are found to have a low chance of occurrence over a region relative to reanalyses (higher return periods), then since the tails are “too short”, any attribution statement calculated for an extreme over the region and AGCM under investigation, is likely be overestimated. The use of an “overestimated attribution statement” refers to an unrealistically high quantification of anthropogenic responsibility. This is because the signal-to-noise ratios between the historical and natural distributions would be greater than otherwise suggested by reanalyses. The opposite would hold for regions over which extremes are simulated “too frequently” by the AGCMs.

Generally, the rarer the event examined, the greater the small-scale variability in results, i.e. neighbouring grid cells can exhibit increasingly different return periods (see the figures for one-in-ten-year events in the Supplementary Material). This characteristic is not necessarily a consequence of poor sampling as shown by Angélil et al., (2014a). Rather, the exact magnitude of an event may be increasingly sensitive to topography the rarer the event.

Differences between the AGCMs may be partially due to CAM5.1 using prescribed aerosol burdens, while MIROC5 and HadGEM3 simulate aerosol distributions from prescribed aerosol emissions. The MIROC5 and HadGEM3 experimental setups therefore allow for interactions between the simulated weather and atmospheric chemistry, while in CAM5.1 the absence of this interaction may prevent the occurrence of feed-backs relevant in the simulation of extremes.

The final panels (g) from Fig. 3, Fig. 4, Fig. 5, S1, S2, S3, S4, S5, and S6 depict actual return periods, while Fig. 6, Fig. 6 offer a summary highlighting how AGCM-reanalyses differences bias attribution statements. One weakness of the summary figures is that results are slightly more arbitrary: the threshold (0.01 and 0.99) used to define boundaries between definitions could easily be adjusted. Our approach however only assigns clear-cut labels (“overestimated”, “good” or “underestimated”) when the evidence is either that the reanalyses are mutually consistent enough to be considered robust, or when all reanalyses lie far from the AGCM distribution.

In cases where attribution statements are found to be “overestimated” or “underestimated”, an artificial adjustment of the extreme threshold used to calculate exceedance probabilities in the model runs is advised (Jeon et al., 2016). Jeon et al. (2016) detail a basic procedure to ensure the exceedance probability in the historical model runs and the observations are the same. For example, our results suggest a bias towards overly strong attribution statements for hot extremes over Africa (shorter tails lead to unrealistically high signal to noise ratios). Here, the observed threshold used to calculated exceedance probabilities would be shifted towards the mean of the distribution. Attribution statements can now be calculated using the adjusted threshold. The method is desirable not only because it is straightforward, but as it reduces biases in a physically consistent way.

Sippel et al. (2016) demonstrate a resampling procedure to alleviate observation-model biases, which also preserves physical consistencies. If output from multiple models are available, their approach can be expanded to account for a counter-factual world had human activity not inferred with the climate system. Here, the ratio of runs used from each model which collectively reduce biases in the ‘real world’ scenario, should be applied to form a subset of runs in the counter-factual world.

Our results draw attention to the large discrepancies amongst commonly used reanalysis products, and agree with results found by Sillmann et al. (2013) and Donat et al. (2014). These discrepancies should expose the danger of using one or even two reanalysis/observation products for evaluation. The results of this analysis highlight the importance for attribution studies targeting specific extremes to evaluate the shapes of the tails of distributions with a number of products, ideally using a combination of reanalysis and observations if the period under evaluation and the length of the extreme permits. Additionally, although different AGCMs can be similar in their biases, we encourage the use of multiple AGCMs when performing event attribution, as AGCM results can still vary considerably.

Acknowledgements

OA, SP-K, LVA and MGD were supported by the Australian Research Council under Grant CE110001028. In addition SP-K was supported by DECRA grant DE140100952 and MGD DECRA grant DE150100456. DS and MW were supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research, under contract number DE-AC02- 05CH11231. HS was supported by the Program for Risk Information on Climate Change. AC and NC were supported by the Joint UK DECC/Defra Met Office Hadley Centre Climate Programme (GA01101) and by the EUCLEIA Project funded by the European Union's Seventh Framework Programme [FP7/20072013] under grant agreement number 607085.

Footnotes

Appendix A

Supplementary data associated with this article can be found in the online version at doi:10.1016/j.wace.2016.07.001.

Appendix A. Supplementary data

Application 1
mmc1.pdf (2.7MB, pdf)

.

References

  1. Angélil O., Stone D.A., Pall P. Attributing the probability of South African weather extremes to anthropogenic greenhouse gas emissions: Spatial characteristics. Geophys. Res. Lett. 2014;41(9):3238–3243. [Google Scholar]
  2. Angélil O., Stone D.A., Tadross M., Tummon F., Wehner M.F., Knutti R. Attribution of extreme weather to anthropogenic greenhouse gas emissions: sensitivity to spatial and temporal scales. Geophys. Res. Lett. 2014;41(6):2150–2155. [Google Scholar]
  3. Avila F.B., Dong S., Menang K.P., Rajczak J., Renom M., Donat M.G., Alexander L.V. Systematic investigation of gridding-related scaling effects on annual statistics of daily temperature and precipitation maxima: a case study for south-east Australia. Weather Clim. Extrem. 2015;9:6–16. [Google Scholar]
  4. Bellprat O., Doblas-Reyes F. Unreliable climate simulations overestimate attributable risk of extreme weather and climate events. Geophys. Res. Lett. 2016 (n/a–n/a) [Google Scholar]
  5. Caesar J., Alexander L., Vose R. Large-scale changes in observe daily maximum and minimum temperatures: creation and analysis of a new gridded data set. J. Geophys. Res.: Atmos. 2006;111(5):1–10. [Google Scholar]
  6. Christidis N., Stott P.A., Scaife A.A., Arribas A., Jones G.S., Copsey D., Knight J.R., Tennant W.J. A new HadGEM3-A-based system for attribution of weather- and climate-related extreme events. J. Clim. 2013;26:2756–2783. [Google Scholar]
  7. Dee D.P., Uppala S.M., Simmons a.J., Berrisford P., Poli P., Kobayashi S., Andrae U., Balmaseda M.a., Balsamo G., Bauer P., Bechtold P., Beljaars a.C.M., van de Berg L., Bidlot J., Bormann N., Delsol C., Dragani R., Fuentes M., Geer a.J., Haimberger L., Healy S.B., Hersbach H., Hólm E.V., Isaksen L., Kållberg P., Köhler M., Matricardi M., Mcnally a.P., Monge-Sanz B.M., Morcrette J.J., Park B.K., Peubey C., de Rosnay P., Tavolato C., Thépaut J.N., Vitart F. The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011;137(656):553–597. [Google Scholar]
  8. Donat M.G., Sillmann J., Wild S., Alexander L., Lippmann T., Zwiers F.W. Consistency of temperature and precipitation extremes across various global gridded in situ and reanalysis datasets. J. Clim. 2014;27(13):5019–5035. [Google Scholar]
  9. Fischer E.M., Knutti R. Anthropogenic contribution to global occurrence of heavy-precipitation and high-temperature extremes. Nat. Clim. Change. 2015;5:1–6. URL 〈 http://www.nature.com/doifinder/10.1038/nclimate2617〉. [Google Scholar]
  10. Folland, C., Stone, D.A., Frederiksen, C., Karoly, D.J., Kinter, J., 2014. The International CLIVAR Climate of the 20th Century Plus (C20C +) Project : Report of the Sixth Workshop. Clivar Exchanges, 19 (65), pp. 57–59.
  11. Herring S.C., Hoerling M.P., Peterson T.C., Stott P.A. Explaining extreme events of 2013 from a climate perspective. Bull. Am. Meteorol. Soc. 2014;95(9):S1–S96. [Google Scholar]
  12. Herring, S.C., Hoerling, M.P., Kossin, J.P., Peterson, T.C., A., S.P., 2015. Extreme Events of 2014. Bulletin of the American Meteorological Society, 96 (12).
  13. Hurrell J.W., Hack J.J., Shea D., Caron J.M., Rosinski J. A new sea surface temperature and sea ice boundary dataset for the community atmosphere model. J. Clim. 2008;21(19):5145–5153. [Google Scholar]
  14. Jeon S., Paciorek C.J., Wehner M.F. Quantile-based bias correction and uncertainty quantification of extreme event attribution statements. Weather Clim. Extrem. 2016;12:24–32. URL 〈 http://linkinghub.elsevier.com/retrieve/pii/S2212094715300220〉. [Google Scholar]
  15. Jones D.A., Wang W., Fawcett R. High-quality spatial climate data-sets for Australia. Aust. Meteorol. Oceanogr. J. 2009;58(4):233–248. [Google Scholar]
  16. Jones P.W. First- and second-order conservative remapping schemes for grids in spherical coordinates. Mon. Weather Rev. 1999;127(9):2204–2210. [Google Scholar]
  17. Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, G., Woollen, J., Zhu, Y., Chelliah, M., Ebisuzaki, W., Higgins, W., Janowiak, J., Mo, K. C., Ropelewski, C., Wang, J., Leetmaa, a., Reynolds, R., Jenne, R., Joseph, D., 1996. The NCEP/NCAR 40-Year Reanalysis Project.
  18. Kanamitsu M., Ebisuzaki W., Woollen J., Yang S.-K., Hnilo J.J., Fiorino M., Potter G.L. NCEPDOE AMIP-II reanalysis (R-2) Bull. Am. Meteorol. Soc. 2002;83(11):1631–1643. URL 〈 http://journals.ametsoc.org/doi/abs/10.1175/BAMS-83-11-1631〉. [Google Scholar]
  19. Kobayashi S., Ota Y., Harada Y., Ebita A., Moriya M., Onoda H., Onogi K., Kamahori H., Kobayashi C., Endo H., Miyaoka K., Takahashi K. The JRA-55 reanalysis: general specications and basic 498 characteristics. J. Meteorol. Soc. Jpn. Ser. II. 2015;93(1):5–48. URL 〈 https://www.jstage.jst.go.jp/article/jmsj/93/1/93_2015-001/_article〉. [Google Scholar]
  20. Pall P., Aina T., Stone D.A., Stott P.a., Nozawa T., Hilberts A.G.J., Lohmann D., Allen M.R. Anthropogenic greenhouse gas contribution to flood risk in England and Wales in autumn 2000. Nature. 2011;470(7334):382–385. doi: 10.1038/nature09762. [DOI] [PubMed] [Google Scholar]
  21. Peterson T.C., Stott P.a., Herring S.C. Explaining extreme events of 2011 from a climate perspective. Bull. Am. Meteorol. Soc. 2012;93(7):1041–1067. [Google Scholar]
  22. Peterson T.C., Hoerling M.P., Stott P.a., Herring S.C. Explaining extreme events of 2012 from a climate perspective. Bull. Am. Meteorol. Soc. 2013;94(9):S1–S74. [Google Scholar]
  23. Rayner N., Parker D., Horton E., Folland C., Alexander L., Rowell D., Kent E., Kaplan A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res.: Atmos. 2003;108(D14) [Google Scholar]
  24. Rienecker M.M., Suarez M.J., Gelaro R., Todling R., Bacmeister J., Liu E., Bosilovich M.G., Schubert S.D., Takacs L., Kim G.K., Bloom S., Chen J., Collins D., Conaty A., Da Silva A., Gu W., Joiner J., Koster R.D., Lucchesi R., Molod A., Owens T., Pawson S., Pegion P., Redder C.R., Reichle R., Robertson F.R., Ruddick A.G., Sienkiewicz M., Woollen J. MERRA: NASA's modern-era retrospective analysis for research and applications. J. Clim. 2011;24(14):3624–3648. [Google Scholar]
  25. Saha S., Moorthi S., Pan H.L., Wu X., Wang J., Nadiga S., Tripp P., Kistler R., Woollen J., Behringer D., Liu H., Stokes D., Grumbine R., Gayno G., Wang J., Hou Y.T., Chuang H.Y., Juang H.M.H., Sela J., Iredell M., Treadon R., Kleist D., Van Delst P., Keyser D., Derber J., Ek M., Meng J., Wei H., Yang R., Lord S., Van Den Dool H., Kumar A., Wang W., Long C., Chelliah M., Xue Y., Huang B., Schemm J.K., Ebisuzaki W., Lin R., Xie P., Chen M., Zhou S., Higgins W., Zou C.Z., Liu Q., Chen Y., Han Y., Cucurull L., Reynolds R.W., Rutledge G., Goldberg M. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010;91(8):1015–1057. [Google Scholar]
  26. Seneviratne, S., Nicholls, N., Easterling, D.R., Goodess, C., Kanae, S., Kossin, J., Luo, Y., Marengo, J., McInnes, K., Rahimi, M., Reichstein, M., Sorteberg, A., Vera, C., Zhang, X., 2012. Changes in climate extremes and their impacts on the natural physical environment. Managing the Risk of Extreme Events and Disasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the IPCC, Annex IIanaging the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation, pp. 109–230.
  27. Shiogama H., Watanabe M., Imada Y., Mori M., Ishii M., Kimoto M. An event attribution of the 2010 drought in the South Amazon region using the MIROC5 model. Atmos. Sci. Lett. 2013;14:170–175. [Google Scholar]
  28. Shiogama H., Watanabe M., Imada Y., Mori M., Kamae Y., Ishii M., Kimoto M. Attribution of the June-July 2013 heat wave in the Southwestern United States. Sola. 2014;10(0):122–126. URL 〈 http://jlc.jst.go.jp/DN/JST.JSTAGE/sola/2014-025?lang=en&from=CrossRef&type=abstract〉. [Google Scholar]
  29. Sillmann J., Kharin V.V., Zhang X., Zwiers F.W., Bronaugh D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. model evaluation in the present climate. J. Geophys. Res.: Atmospheres. 2013;118(4):1716–1733. [Google Scholar]
  30. Sippel S., Otto F.E.L., Forkel M., Allen M.R., Guillod B.P., Heimann M., Reichstein M., Seneviratne S.I., Thonicke K., Mahecha M.D. A novel bias correction methodology for climate impact simulations. Earth Syst. Dyn. 2016;7(1):71–88. [Google Scholar]
  31. Stone D.A., Allen M.R. The end-to-end attribution problem: from emissions to impacts. Clim. Change. 2005;71(3):303–318. [Google Scholar]
  32. Stott P.A., Stone D.A., Allen M.R. Human contribution to the European heatwave of 2003. Nature. 2004;432(7017):610–614. doi: 10.1038/nature03089. [DOI] [PubMed] [Google Scholar]
  33. Stott, P.A., Allen, M.R., Christidis, N., Dole, R., Hoerling, M.P., Huntingford, C., Pall, P., Perlwitz, J., Stone, D.A., 2013. Attribution of Weather and Climate-Related Extreme Events. In Monograph: “Climate Science for Serving Society: Research, Modelling and Prediction Priorities”, pp. 1–44.
  34. van Oldenborgh G.J., Doblas Reyes F.J., Drijfhout S.S., Hawkins E. Reliability of regional climate model trends. Environ. Res. Lett. 2013;8(1):014055. URL 〈 http://stacks.iop.org/1748–9326/8/i=1/a=014055?key=crossref.2aa3fd77fc365abd77e9d8773bb66738〉. [Google Scholar]
  35. Weisheimer A., Palmer T.N. On the reliability of seasonal climate forecasts. J. R. Soc. 2014:1–10. doi: 10.1098/rsif.2013.1162. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Application 1
mmc1.pdf (2.7MB, pdf)

RESOURCES