Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Mar 15;7:44070. doi: 10.1038/srep44070

Rotational Effects of Nanoparticles for Cooling down Ultracold Neutrons

Xiaoqing Tu 1, Guangai Sun 1, Jian Gong 1, Lijuan Liu 1, Yong Ren 1,2, Penglin Gao 1, Wenzhao Wang 1, H Yan 1,a
PMCID: PMC5353586  PMID: 28294116

Abstract

Due to quantum coherence, nanoparticles have very large cross sections when scattering with very cold or Ultracold Neutrons (UCN). By calculating the scattering cross section quantum mechanically at first, then treating the nanoparticles as classical objects when including the rotational effects, we can derive the associated energy transfer. We find that rotational effects could play an important role in slowing down UCN. In consequence, the slowing down efficiency can be improved by as much as ~40%. Since thermalization of neutrons with the moderator requires typically hundreds of collisions between them, a ~40% increase of the efficiency per collision could have a significant effect. Other possible applications, such as neutrons scattering with nano shells and magnetic particles,and reducing the systematics induced by the geometric phase effect using nanoparticles in the neutron Electric Dipole Moment (nEDM), are also discussed in this paper.

Slowing down neutrons is a crucial problem in both fundamental physics and condensed matter physics. For fundamental neutron physics, the slower the neutrons, the longer the measurement time. Therefore more precise measurements can be made for the slower neutrons. Neutrons with energy lower than 10−7 eV are classified as Ultracold Neutrons(UCN) which can be confined by gravity and form quantum bound states1. UCN experiments can help us know more about the fundamental physical laws in many ways. For example, by precisely measuring the gravitational quantum states of neutrons, constraints can be imposed on the coupling between the hypothetical chameleon fields and ordinary matters2,3. Moreover, the study of neutron lifetime can further our understanding of weak interaction between hadrons4,5,6,7, the measurement of nEDM can help in solving the CP violation problem8, the neutron β-decay experiment can be implemented to measure the Axial-Vector weak coupling constant9, and the spin precession of UCN has already been used to test the Lorentz invariance10. In condensed matter physics and other interdisciplinary field, UCN have been used in studying the slow kinetic process of macromolecule, fundamental biological science, biomedicine and biopharming. The length scale that the neutron can probe depends on its wavelength. The larger the wavelength, the larger the neutron probing scale. Small Angle Neutron Scatter(SANS), Ultra Small Angle Neutron Scattering(USANS) and Spin Echo Small Angle Neutron Scattering(SESAME) have been developed to probe large scale structures of various samples by measuring small angle scattering precisely. How to obtain more UCN is important in fundamental science, practical engineering, and industrial applications11,12,13,14,15,16, etc. Slowing down neutrons effectively is the key problem since the day when neutron was discovered.

For typical thermal neutron sources, the percentage of UCN is extremely small. At neutron temperature of 300 K, the population ratio of UCN is ~10−11, and it can only be increased to ~10−9 when the neutron temperature is cooled down to 20 K. Obviously, obtaining UCN by directly selecting it from a wide energy spectrum is not efficient. There are other methods such as using gravity or reflection from a moving surface to decelerate a beam of neutrons17. However all these methods can not increase the original phase density in the primary moderator18.

Nesvizhevsky et al. have proposed a novel moderator scheme for UCN using nanoparticles19, in which nano spheres made by low neutron-absorption materials are immersed in the liquid helium at temperature close to 0 K. The nanoparticles are in thermal equilibrium with the superfluid helium. Hence there is no friction and the nanoparticles can move freely and scatter with UCN intensively in the moderator, which we will illustrate later by a detailed example. Nesvizhevsky et al. first calculated the neutron scattering cross section quantum mechanically. During that process, the neutron energy can be transferred to the translational movement of the nanoparticles. The energy loss of the neutron to the nanoparticle was obtained by using the principle of energy-momentum conservation. It was found that under some specific experimental conditions, this method might increase the ultracold neutron density by several orders of magnitude19,20. In comparison with other methods in which UCN are obtained by selecting neutrons within a very narrow fraction of the whole energy spectrum, this new method can increase the phase space density of UCN.

However, rotational effects are neglected in the previous study19. Intuitively, rotational degrees of freedom of nanoparticles could play a non-negligible role. In this paper, we try to further this interesting idea by including rotational effects, and the same conditions assumed in ref. 19 are followed, i.e., free nanoparticles are in thermal equilibrium with superfluid helium at 0 K, no internal degrees of freedom of nanoparticles are excited for the neutron energy under consideration, etc. Thus the limitations of applicability in the previous study in ref. 19 are also the same in our work. The remainder of this article is organized as follows. We first illustrate quantum coherence effect for neutron scattering by a simple example. Then we present our methods and results in which the rotational effects of nanoparticles are included. Other possible applications are also discussed, such as neutron scattering with nano shells and magnetized nanoparticles, and reducing the geometric phase effect which is one of the most important systematics of the nEDM experiment. Finally, we present the conclusion of this work.

Quantum Coherence

Due to the similarity between the neutron wavelength and the nanoparticle size, cold neutrons and UCN interact strongly with nanoparticles because of quantum coherence. Simple cases are illustrated here. First, we suppose the slow neutrons described by a plane wave are scattered by a single nucleus fixed at the origin. Then the scattered neutron wave can be expressed as follows during this low energy process18,21,22,23,24:

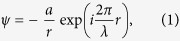graphic file with name srep44070-m1.jpg

where a is the scattering length of neutrons in the nucleus, λ denotes the de Broglie wavelength of the incident neutron, and r is the distance from the origin. It is easy to obtain the total scattering cross section:

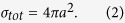graphic file with name srep44070-m2.jpg

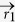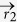Then we come to another situation, in which two nucleus of the same type fixed at different positions Inline graphic and Inline graphic are scattered by neutrons. The scattered wave is:

graphic file with name srep44070-m5.jpg

Since the wavelength of UCN is much larger than the distance between the nucleus, i.e., 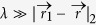Inline graphic, the scattered wave can be approximated as:

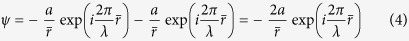graphic file with name srep44070-m7.jpg

where Inline graphic is the average of r1 and r2. The total scattering cross section in this case is given by:

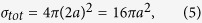graphic file with name srep44070-m9.jpg

which is four times of that associated with single nucleus. In short, due to the very large wavelength of UCN compared with nano-sized particles, quantum coherence plays a crucial role. It produces a quadric increment for the total scattering cross section as the nucleus number of the nanoparticle increases. For instance, if a C60 atom is scattered by UCN, its total scattering cross section is 3600 rather than 60 times of that of a single carbon atom.

Based on these facts, UCN will be scattered strongly by the nano-sized particle immersed in the low temperature superfluid helium moderator. Therefore neutrons can be moderated by these nanoparticles.

Mean Energy Loss per Collision between a Neutron and a nanoparticle

In ref. 19, the total cross section of a neutron scattered by a fixed nanoparticle was calculated quantum mechanically using the first order Born approximation. During the collision, the neutron energy is transferred to the translational movement of the nanoparticles. The energy loss of the neutron to the nanoparticles is obtained classically by simply applying the energy-momentum conservation. The simplicity and elegance of the method are inspiring. We try to include the rotational effects of the nanoparticles in a similar manner, i.e., first calculating the scattering cross section quantum mechanically, then studying the rotational effects of the nanoparticles classically.

We first calculate the cross section of neutrons scattering with nanoparticles by using the first order Born approximation. Note although a more precise calculation of the total scattering cross section by using the partial wave method has been done in ref. 25, only a ~10% difference from the Born approximation is observed. Next, to obtain the energy carried away by the rotational degrees of nanoparticles, we treat the latter as classic objects. As illustrated in Fig. 1, an incoming neutron with impact parameter b is scattered by a nano sphere of radius R. Classically, only if the impact parameter is within the range of the particle size, can a collision occur. The energy, momentum and angular momentum will be redistributed between the two objects. Since the translational energy transfer was already solved, here we only consider the results due to the rotational degrees of freedom.

Figure 1. neutron wave scattered by a nanoparticle.

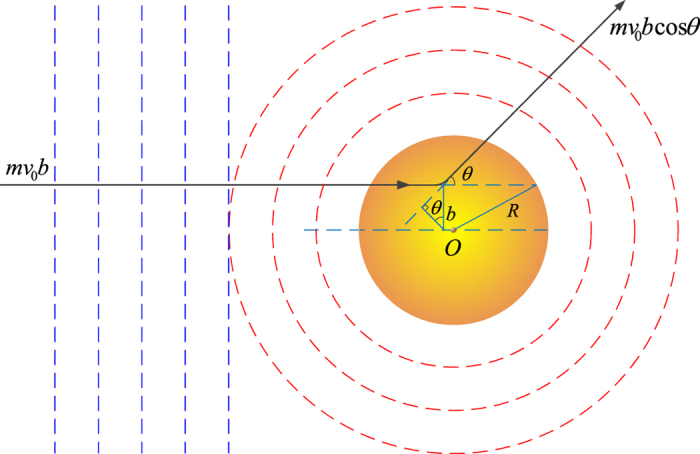
Figure 1

Open in a new tab

According to the law of angular momentum conservation,

graphic file with name srep44070-m10.jpg

where J is the momentum of inertia, m the neutron mass, v0 the incident neutron velocity, ω the angular velocity of the nano sphere, and θ the scattering angle. Applying the law of energy conservation, the rotational energy carried by the sphere is expressed as:

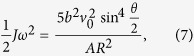graphic file with name srep44070-m11.jpg

where A is the nano sphere mass in units of neutron mass. The ratio of rotational energy transfer is easily obtained:

graphic file with name srep44070-m12.jpg

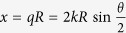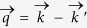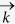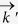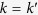where Inline graphic, Inline graphic is the scattering wave vector, Inline graphic is the incident wave vector, and Inline graphic is the final wave vector. The collision is elastic in the center-of-mass frame, so we have Inline graphic.

Substituting the scattering amplitude into Eqn. (8), the mean energy loss due to rotational degrees can be derived as:

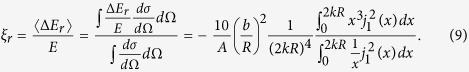graphic file with name srep44070-m18.jpg

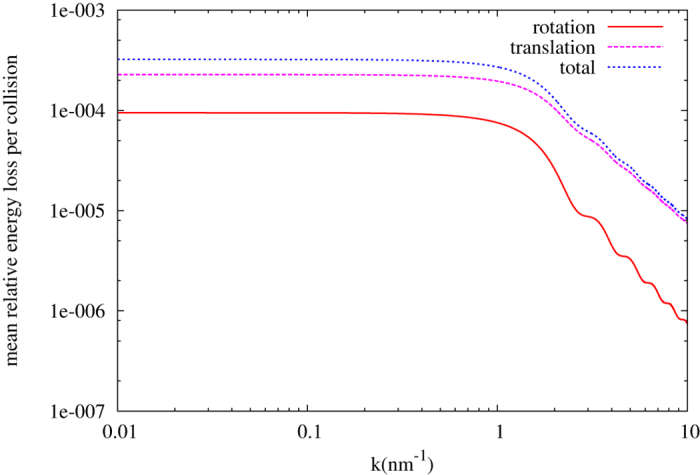
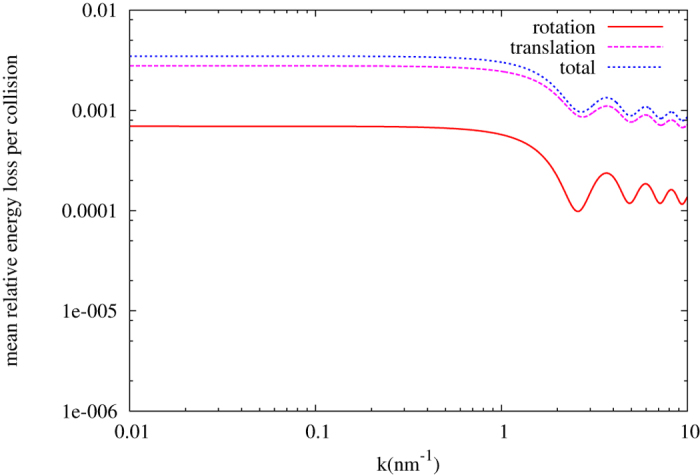
where j1(x) is the first order spherical Bessel function. We calculate the above integrals numerically by using the Simpson’s method26. When calculating the rotational-degree-caused energy transfer, the problem is considered classically, in which the neutron is considered as a point-like particle. Only if the impact parameter is within the radius of the nanoparticle, will a collision happen. In this classical situation, the average impact parameter is obviously 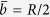Inline graphic for incident neutrons when collisions occur. The total energy loss is the sum of the energy loss due to the translation and rotation movements. We present the behavior of the energy loss ratio due to rotational effects in Fig. 2 for a diamond nanoparticle with radius of 1 nm.

Figure 2. Translation, rotation, and total relative mean energy loss per collision, as a function of neutron wave vector, for the diamond nanoparticle with radius of 1 nm.

Figure 2

Open in a new tab

When the incident neutron wave vector is much smaller than the nanoparticle size, i.e., 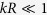Inline graphic:

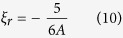graphic file with name srep44070-m21.jpg

while in this case the translational energy transfer rate is:

graphic file with name srep44070-m22.jpg

It is easy to see that under long wavelength limit, rotational degrees of freedom of the nanoparticles carry as much as 5/12, i.e. ~40% amount of energy as the translational degrees of freedom. As we can see from Fig. 3, when the rotational effects are taken into account, the energy transfer efficiency is increased by as much as 40%. To slow down neutrons as much as possible, it is important to increase the energy transfer efficiency for each collision between neutrons and the moderator. Typically, hundreds or even thousands of collisions are required for neutrons to be in thermal equilibrium with the moderator, so a 40% increase of the efficiency per collision can be significant.

Figure 3. The ratio of energy loss due to rotation degrees of freedom to translation of the 1 nm dimond nano sphere.

Figure 3

Open in a new tab

Neutrons Scattered by a Nano Shell

The average relative energy loss is inversely proportional to the mass of nanoparticles. Higher moderating efficiency is expected when the mass of the scatterer becomes smaller. Therefore, we turn to consider the nano shell, of which the mass is much smaller than that of the nanoparticle in the same volume. Here we calculate the associated moderating efficiency. For simplicity, we only consider single layer shells. The phenomenological potential for the interaction of a neutron with a nano shell can be express as:

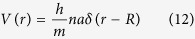graphic file with name srep44070-m23.jpg

where h is the Planck’s constant, n the neutron surface density of the shell and R the shell radius.

Using the first order Born approximation, the total scattering cross section is found to be:

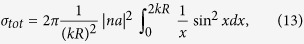graphic file with name srep44070-m24.jpg

The total mean relative energy loss per collision is derived as

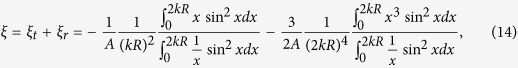graphic file with name srep44070-m25.jpg

where A is the mass of nano shell, again in units of the neutron mass. As a shell has a relatively larger initial momentum than a sphere since the former concentrates its mass on surface, we expect that rotational effects are less efficient. In fact, if we take long wavelength limit, the ratio is

graphic file with name srep44070-m26.jpg

which is ~17% less than the sphere case.

For practical purposes, we consider using C60, of which the radius is 0.71 nm, to moderate UCN. By applying Eqn. (13), we found that the total scattering cross section of C60 is 3600 times of a single carbon nucleus. The derived energy loss per collision of C60 is shown in Fig. 4.

Figure 4. Translation, rotation, and total relative mean energy loss per collision, as a function of neutron velocity, for C60.

Figure 4

Open in a new tab

Though mean energy loss per collision is proportional to 1/A, i.e., inversely proportional to the total nucleus number in the nanoparticle, the neutron scattering cross section is in quadratic relation to the nucleus number. If we only take the scattering effects into consideration, higher neutron cooling efficiency is expected for larger nanoparticles. However, the neutron absorption cross section increases linearly with the nucleus number. It will be an optimization problem to balance all these factors.

Neutrons Scattered by a Magnetized nanoparticle

It is known that neutrons can interact with magnetic particles since they have a magnetic moment. Hence it is natural to consider the magnetic effects for some specific nanoparticles. According to ref. 21, magnetic scattering has no interference with the nuclear scattering. The magnetic scattering cross section includes spin states transitions and for the elastic case it can be expressed as:

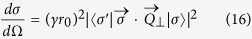graphic file with name srep44070-m27.jpg

where r0 is the classical radius of electrons, and γ is the gyromagnetic ratio of neutrons, 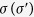Inline graphic refers to the spin state, 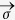Inline graphic are the Pauli matrices and:

graphic file with name srep44070-m30.jpg

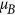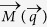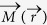where Inline graphic the magnetic moment of electrons, Inline graphic is the Fourier transformation of the nano sphere magnetization Inline graphic.

Using Eqn. (16), the total cross section of a neutron scattered by a magnetized nanoparticle is found to be:

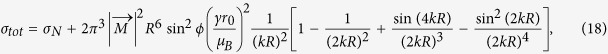graphic file with name srep44070-m34.jpg

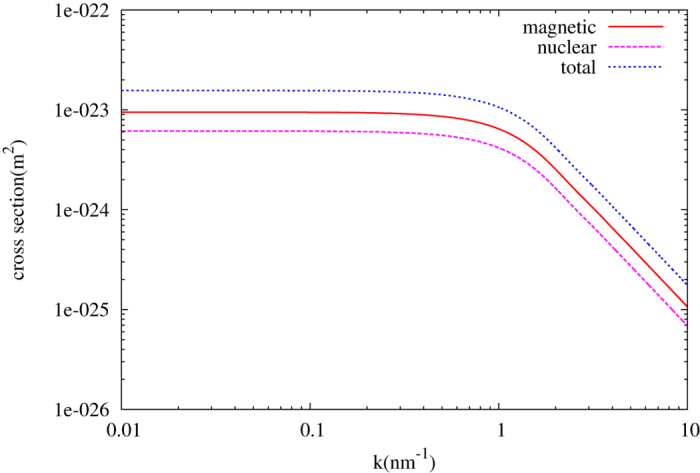
where σN is the nuclear scattering cross section of the nanoparticle, ϕ the angle between the scattering wave vector and the magnetization. For atoms with strong magnetism, we expect that the magnetic scattering might be important. For example, the magnetic scattering length of the Co atom is even larger than its nuclear scattering length, then its magnetism may also serve to slow down neutrons. The magnetic, nuclear and total cross sections are shown in Fig. 5.

Figure 5. Nuclear, magnetic and the total scattering cross sections of Co nanoparticle with radius of 1 nm.

Figure 5

Open in a new tab

Possible Application in the nEDM Experiments

There are other possible applications of nanoparticles in fundamental neutron physics. In the nEDM experiment, the geometric phase effect is considered to be a major systematic error27, which is due to the correlation between the velocity and the position time series of the UCN28. When using 3He atoms as the co-magnetometer, it was found that this geometric phase effect get suppressed due to randomizations caused by collisions between 3He atoms and liquid 4He. It was also noticed that the diffusive reflections of UCN by the wall can reduce this effect28. However, this effect can not bring great benefits here since the neutron has a negligible cross section when scattering with 4He. If we introduce nanoparticles into the liquid 4He, not only the neutrons can be further slowed down, but also the geometric phase effect caused by scattering neutrons is reduced.

Conclusion and Discussion

Due to quantum coherence, nano-sized particles have very large cross sections when scattered with very cold and ultracold neutrons. Neutrons with large wavelength will strongly interact with the nanoparticles immersed in the superfluid helium, which consequently take away energy of the incident neutrons. Based on this fact, neutrons could be slowed down if the temperature of nanoparticles is lower than that of neutrons. Previously, only translational energy is considered within this new moderating mechanism. By taking into account of the rotational effects, we find that neutron-moderating efficiency might be increased by as much as 40% accordingly. One of the most important advantages of this moderator scheme is its simplicity. For the superthermal liquid helium UCN moderator used by several nEDM experiments29,30,31, if their operating temperature can be lowered down to ~mK, the moderator scheme discussed in this paper could be realized simply by adding some nanoparticles. Since many tests and experiments have been done for the superthermal UCN sources operating at temperatures of a few hundreds mK, we would expect the main technology difficulty might be cooling the liquid helium inside the moderator down to ~mK. The temperature required is just the practical lower limit of the commercially available dilution refrigerators. Practically, it would be difficult to realize the new moderator scheme but it is not impossible. We further derive the scattering cross section and moderating efficiency of neutrons scattered by a nano shell made by C60 as an example. We also consider using the magnetic nanoparticles to slow down neutrons, and give the associated scattering cross section. We find that nanoparticles could be applied to the nEDM experiment not only to slow down neutrons but also reduce a systematic error.

Additional Information

How to cite this article: Tu, X. et al. Rotational Effects of Nanoparticles for Cooling down Ultracold Neutrons. Sci. Rep. 7, 44070; doi: 10.1038/srep44070 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Acknowledgments

This work was supported by National Key Program for Research and Development(Grant 2016YFA0401500 /1/2/3/4).

Footnotes

The authors declare no competing financial interests.

Author Contributions H.Y. proposed the idea. X.T. and H.Y. performed the calculations, G.S., J.G., Y.R., checked the results. All authors reviewed the manuscript.

References

  1. Nesvizhevsky V. V. et al. Quantum states of neutrons in the Earth’s gravitational field. Nature 415, 297–299 (2002). [DOI] [PubMed] [Google Scholar]
  2. Schmiedmayer J. & Abele H. Probing the dark side. Science 349, 786–787 (2015). [DOI] [PubMed] [Google Scholar]
  3. Jenke T. et al. Gravity resonance spectroscopy constrains dark energy and dark matter scenarios. Phys. Rev. Lett. 112, 151105 (2014). [DOI] [PubMed] [Google Scholar]
  4. Yue A. T. et al. Improved determination of the neutron lifetime. Phys. Rev. Lett. 111(22), 222501 (2013). [DOI] [PubMed] [Google Scholar]
  5. Wietfeldt F. E. & Greene G. L. Colloquium: The neutron lifetime. Rev. Mod. Phys. 83(4), 1173–1192 (2011). [Google Scholar]
  6. Alarcon R. Fundamental physics with cold and ultracold neutrons. Revista Mexicana De Fisica 53, 125–127 (2007). [Google Scholar]
  7. Arzumanov S. et al. A new project to measure the neutron lifetime using storage of ultracold neutrons and detection of inelastically scattered neutrons. Nuclear Instruments and Methods in Physics Research A 611(2-3), 186–188 (2009). [Google Scholar]
  8. Serebrov A. P. Solid deuterium and UCN factory: application to the neutron electric dipole moment measurement. Nuclear Instruments and methods in Physics Research A. 440(3), 653–657 (2000). [Google Scholar]
  9. Liu J. et al. Determination of the axial-vector weak coupling constant with ultracold neutrons. Phys. Rev. Lett. 105(18), e107708 (2010). [DOI] [PubMed] [Google Scholar]
  10. Altarev I. et al. Test of Lorentz invariance with spin precession of ultracold neutrons. Phys. Rev. Lett. 103(8), 081602–081605 (2009). [DOI] [PubMed] [Google Scholar]
  11. Nesvizhevsky V. V. et al. Neutron whispering gallery. Nature Physics 6(2), 114–117 (2010). [Google Scholar]
  12. Dubbers D. & Schmidt M. G. The neutron and its role in cosmology and particle physics. Rev. Mod. Phys. 83(4), 1111–1171 (2011). [Google Scholar]
  13. Trkov A. Nuclear reactions and physical models for neutron activation analysis. Journal of Radioanalytical and Nuclear Chemistry 304(2), 763–778 (2015). [Google Scholar]
  14. Nesvizhevsky V. V. Experiments with ultracold neutrons. Physics Letters B 34(4), 293–295 (2011). [Google Scholar]
  15. Pokotilovskii Yu. N. & Gareeva G. F. A method for high-resolution and high-efficiency spectroscopy of ultracold neutrons at a small energy transfer and low scattering probabilities. Instruments and Experimental Techniques 46(1), 13–18 (2003). [Google Scholar]
  16. Nesvizhevsky V. V. et al. Study of levitating nanoparticles using ultracold neutrons. New J. Phys. 14(9), 1–5 (2012). [Google Scholar]
  17. Thomsen K. Conceptual proposal for compound moderators with preferential emission directions. Physics Procedia 60, 278–293 (2014). [Google Scholar]
  18. Golub R., Richardson D. & Lamoreaux S. K. Ultra-Cold Neutrons, (Adam Hilger. 1991). [Google Scholar]
  19. Nesvizhevsky V. V., Pignol G. & Protasovb K. V. Nanoparticles as a possible moderator for an ultracold neutron source, International Journal of Nanoscience 6(06), 485–499, (2007). [Google Scholar]
  20. Nesvizhevskya V. V., Pignola G. & Protasovb K. V. Thermalization of neutrons by ultracold nanoparticles 24th International Conference on Low Temperature Physics 1679–1681 (2006). [Google Scholar]
  21. Squires G. L. Introduction to the theory of thermal neutron scattering. (Dover Publications, Inc. 1996). [Google Scholar]
  22. Sakurai J. J. Modern Quantum Mechanics. (Addison-Wesley Publishing Company, Inc. 1994). [Google Scholar]
  23. Messiah A. Quantum Mechanics(Dover Publications, INC. 2013). [Google Scholar]
  24. Lefmann K. Neutron Scattering: Theory, Instrumentation and Simulation 83, 023402 (2011). [Google Scholar]
  25. Artem’ev V. A., Nezvano A. Yu. & Nesvizhevsky V. V. Precise calculations in simulations of the interaction of low energy neutrons with nano-dispersed media. Crystallography Reports. 61(1), 84–88 (2016). [Google Scholar]
  26. Press W. H. et al. Numerical Recipes(Cambridge University Press, 1989). [Google Scholar]
  27. Golub R. & Lamoreaux S. K. Neutron electric-dipole moment, ultracold neutrons and polarized 3He. Phys. Rep. 237(1), 1–62 (1994). [Google Scholar]
  28. Yan H. & Plaster B. Impact of motion along the field direction on geometric-phase-induced false electric dipole moment signals. NIMA 642, 84 (2011). [Google Scholar]
  29. Ito’ T. M. et al. An apparatus for studying electrical breakdown in liquid helium at 0.4 K and testing electrode materials for the neutron electric dipole moment experiment at the spallation neutron source. Rev. Sci. Instrum. 87, 045113 (2016). [DOI] [PubMed] [Google Scholar]
  30. Masuda Y. et al. Spallation UCN production for nEDM. Physics Procedia 51, 89–92 (2013). [Google Scholar]
  31. Schmidt-Wellenburg P. A. Development and Tests of a Superthermal Helium-4 Source for the Production of Ultra Cold Neutrons(Technische Universität München, 2005) [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES