Cooperative extraction of membrane nanotubes by molecular motors

Abstract

In eukaryotic cells, nanotubes represent a substantial fraction of transport intermediates between organelles. They are extracted from membranes by molecular motors walking along microtubules. We previously showed that kinesins fixed on giant unilamellar vesicles in contact with microtubules are sufficient to form nanotubes in vitro. Motors were attached to the membrane through beads, thus facilitating cooperative effects. Koster et al. [Koster, G., VanDuijn, M., Hofs, B. & Dogterom, M. (2003) Proc. Natl. Acad. Sci. USA 100, 15583–15588] proposed that motors could dynamically cluster at the tip of tubes when they are individually attached to the membrane. We demonstrate, in a recently designed experimental system, the existence of an accumulation of motors allowing tube extraction. We determine the motor density along a tube by using fluorescence intensity measurements. We also perform a theoretical analysis describing the dynamics of motors and tube growth. The only adjustable parameter is the motor binding rate onto microtubules, which we measure to be 4.7 ± 2.4 s^–1. In addition, we quantitatively determine, for a given membrane tension, the existence of a threshold in motor density on the vesicle above which nanotubes can be formed. We find that the number of motors pulling a tube can range from four at threshold to a few tens away from it. The threshold in motor density (or in membrane tension at constant motor density) could be important for the understanding of membrane traffic regulation in cells.

Membrane nanotubes play an important role in intracellular traffic, in particular for lipid and protein exchange between various compartments in eukaryotic cells. Several works have shown the existence of dynamic membrane tube networks in living cells (1–3). In vitro assays using purified organelles and cellular extracts have led to the formation of similar membrane networks and showed that microtubules (MTs) and molecular motors are necessary (4–7). Because membrane and cytosol compositions are complex, it was not possible to identify the minimal components required to pull tethers until recently. In ref. 8, we showed that these membrane networks could be formed simply by fixing kinesins on giant liposomes in contact with immobilized MTs. This minimal system provided clear evidence that molecular motors were able to pull tubes in the absence of any other protein. For typical values of membrane bending rigidity and membrane tension, the force necessary to pull a tube is ≳15 pN (9). However, the maximum force that a kinesin motor can exert (stall force) is ≈6 pN (10), implying that more than a single motor is required to pull tubes. This finding suggests that the force is distributed over a few motors. In ref. 8, motors were permanently attached to small beads and, typically, between 15 and 30 motors were estimated to be in contact with MTs and able to pull on the membrane simultaneously. More recently, by using a similar minimal system, Koster et al. (11) succeeded to form tethers when motors were individually attached to membrane lipids. They proposed that clusters of motors could be formed dynamically at the tip of a growing tube. However, these motor clusters had not yet been observed. In this work, we present a direct observation and quantitative characterization of the dynamic accumulation of motors at the tip of tubes. We designed a specific fluorescent probe to label the binding sites to which motors are attached individually and, by using a recently developed protocol, we were able to quantify the fluorescence distribution along the tube that exactly follows the motor distribution.

We also develop a theoretical analysis describing the dynamics of motors on both vesicle and tube surfaces. We analytically determine the conditions leading to tube extraction and show the existence of an initial minimal surface density of motors on the vesicle below which no tubes can be pulled, in agreement with our experimental observations. Moreover, we determine the motor density profile along the tube and discuss the existence of a steady state for tube growth.

From the comparison between theory and experiments, we determine the binding rate of kinesins onto MTs in a geometry close to the in vivo situation. We also estimate the number of motors needed to pull a membrane tube.

Materials and Methods

Reagents. Egg phosphatidylcholine and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl) were purchased from Avanti-Polar Lipids. β-BODIPY 530/550 C₅-hexadecanoyl phosphatidylcholine (BODIPY PC) and streptavidin–FITC were purchased from Molecular Probes. Rhodamin–biotin dihexadecanoyl-phosphatidylethanolamine (DHPE-Biot-Rhod) lipids were synthesized as described by Jolimaitre et al. (ref. 26; see chemical structure in Fig. 5, which is published as supporting information on the PNAS web site). Streptavidin was purchased from Pierce Biotechnology. All chemicals, including casein and poly(l-lysine), were purchased from Sigma, except ATP and GTP, which were purchased from Roche Molecular Biochemicals. Catalase and glucose oxidase (Aspergillus niger) were purchased from Calbiochem. Streptavidin-coated polystyrene beads (100-nm diameter) were purchased from Bangs Laboratories (Carmel, IN).

Giant Unilamellar Vesicles (GUVs). GUVs were prepared by the electroformation technique (12). They were essentially composed of egg phosphatidylcholine lipids and various concentrations of DHPE-Biot-Rhod, 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl) (nonfluorescent), or BODIPY PC, depending on the type of experiment.

Microtubules and Kinesins. Tubulin was purified according to standard procedures to a final concentration of 3 mg/ml. GTP at a final concentration of 1 mM and 10% glycerol were added. Tubulin solution was left for 45 min at 37°C to polymerize. Fifteen minutes before the end of incubation, 20 μM taxol was added to stop depolymerization of MTs. Biotinylated hemagglutinin–kinesin (a gift from F. Nédélec, European Molecular Biology Laboratory, Heidelberg) was purified as described in ref. 13.

Tube Assays. Tube assays were conducted as follows. (i) A coverslip was incubated for 1 min in a poly(l-lysine) solution (0.01% wt/vol), then rinsed in water and dried under a nitrogen flux. A flow chamber was built as in ref. 8. The total volume was ≈12 μl. (ii) MTs were injected into the chamber and incubated for 3 min. (iii) The chamber was rinsed with 20 μl IMI buffer (50 mM imidazole, pH 6.7/50 mM NaCl/2 mM EGTA/1 mM MgCl₂) and then with 20 μl of 5 mg/ml casein diluted in IMI buffer. After a 5-min incubation, the chamber was rinsed with 20 μl of IMI buffer. (iv) During steps ii and iii, biotinylated kinesins were incubated with a large excess of streptavidin (2 × 10^–12 mol kinesin in contrast to 2 × 10^–11 mol streptavidin). (v) Streptavidin–kinesin complexes were injected in the chamber and incubated for 10 min; the chamber was rinsed again with IMI buffer. All free streptavidins or nonactive motors were removed from the chamber after this step. (vi) The chamber was rinsed with a motility buffer (IMI buffer with 1 mM ATP) mixed with 0.18 mg/ml catalase, 0.37 mg/ml glucose oxydase, 25 mM glucose, and 5 mM DTT as an oxygen scavenger to avoid photobleaching. The final osmolarity was 200 milliosmolar. In the presence of ATP, kinesins move along MTs and eventually detach. (vii) Finally, a few vesicles (typically 50) were injected into the chamber. Because of the excess of streptavidin–kinesin complexes, all attachment sites of biotinylated lipids were occupied and there were complexes left in the solution. The final state consisted in kinesin-coated vesicles sedimented on a MT network in presence of ATP.

Bead Assays. We injected kinesin-coated beads (100-nm diameter) in a chamber similar to that of tube assays (see above), as described in ref. 14. Beads bound MTs and moved. A homemade software for bead tracking gave the kinesin average velocity at zero load.

Image Acquisition and Analysis. Epifluorescence images were acquired on an inverted videomicroscopy setup [Leica, Micromax video camera from Princeton Instruments (Trenton, NJ)] with an acquisition rate of one image every second by using a short exposure (typically 200 ms) to limit photobleaching. The resulting movie was analyzed with homemade software giving the distribution of fluorescence intensity along the membrane tube as a function of time. The spatial resolution was 134 nm/pixel.

Diffusion Constant Measured by Fluorescence Recovery After Photobleaching. We used a confocal inverted microscope (Zeiss Axiovert 200) with an argon laser. We studied biotinylated vesicles coated with kinesin/FITC–streptavidin complexes. We analyzed the fluorescence recovery after photobleaching of a disk (≈3 μm²) at the bottom of vesicles. The diffusion constant of biotinylated lipid–streptavidin–kinesin complexes in the membrane of a GUV was obtained from the fit of the fluorescence recovery curve according to Soumpasis (15).

Observation

Our minimal system consisted of a partly biotinylated GUV, coated with biotinylated kinesins through streptavidin molecules. The vesicle played the role of a membrane reservoir. This vesicle sedimented onto a taxol-stabilized MT network in presence of 1 mM ATP. The ATP concentration was chosen in such a way that the motor velocity was close to maximum, whereas motors stayed sufficiently attached to MTs (10). In our assay, the number of kinesins was directly controlled by fixing the biotinylated lipid concentration in the membrane. The protocol (see Materials and Methods) was set up so that one kinesin molecule binds to one biotinylated lipid. First, during the preincubation step, kinesin and streptavidin concentrations were adjusted so that, at most, one kinesin binds to one streptavidin, because of the large excess of streptavidin compared to kinesin. Then, by immobilizing streptavidin–kinesin complexes on the MTs before vesicle injection, we could thoroughly rinse the chamber and get rid of free streptavidins and nonactive motors in solution. Because the total number of biotinylated lipids in the vesicle was much lower than the number of available streptavidin–kinesin complexes (by at least 1 order of magnitude), every binding site for motors was occupied because of the high affinity of streptavidin for biotin. This site saturation was achieved faster than the time required to pull the first tube (1 min). The number of motors attached to the membrane is therefore equal to the number of biotinylated lipids. Moreover, for concentrations >0.01 mol% DHPE-Biot-Rhod, we have also checked that the number of streptavidin molecules per biotinylated lipids remains constant when varying the DHPE-Biot-Rhod concentration (Fig. 6, which is published as supporting information on the PNAS web site). Besides, we have verified that the quantity of streptavidin–kinesin complexes attached to the lipids through nonspecific interactions can be neglected for concentrations of DHPE-Biot-Rhod >0.001 mol% (data not shown).

It is not possible to label kinesins directly by using a fluorescent antibody, which would bind the hemagglutinin-tag on the head of the motor, because it would inhibit completely kinesin motion (13). As a consequence, to detect the quantity of motors, we synthesized a lipid with both a biotin function and a fluorophore on the head group (DHPE-Biot-Rhod; see Materials and Methods and ref. 26). The measurement of fluorescence intensity of DHPE-Biot-Rhod along the tube gives the motor distribution as our protocol has been adjusted to have one motor per DHPE-Biot-Rhod.

Various parameters can be tuned in our assay. The initial concentration of motors on the vesicle surface, called ρ_∞ in the theory section below, can be modified by changing the concentration of biotinylated lipids. The vesicle tension, σ, can be adjusted by changing the osmolarity of the solution inside the vesicle. By optimizing these parameters, it was possible to obtain either very dense networks of membrane tubes with many bifurcations and bundles as in ref. 11 (Fig. 7, which is published as supporting information on the PNAS web site), or sparse ones with only one or two tubes per vesicle (Fig. 1A). The last case corresponds to high vesicle tensions and low motor concentrations, and is more suitable for a proper comparison to the theory.

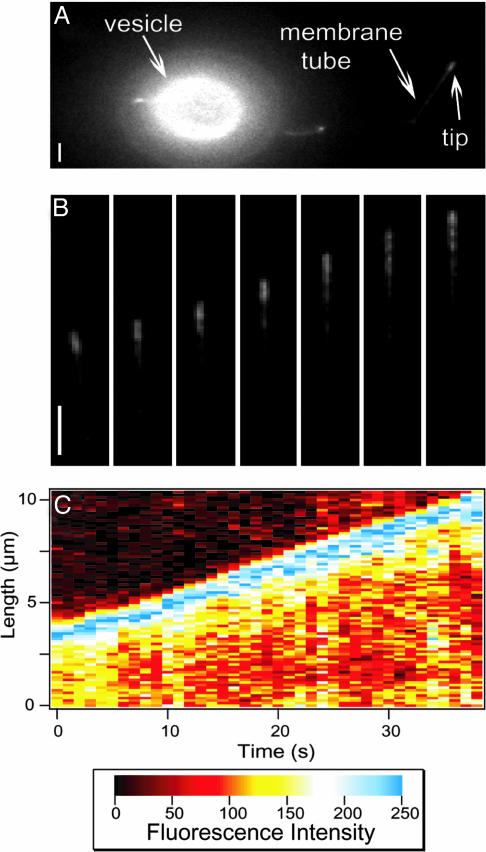
Fig. 1.

Membrane tube growth. (A) Fluorescence image showing a vesicle, a tube, and the accumulation of motors at its tip. The vesicle contains 0.1 mol% DHPE-Biot-Rhod. (Bar, 2 μm.) (B) Time sequence images of a growing tube (one image per 5 s). It corresponds to the membrane tube in A. The tube grows along a MT with a velocity of ≃0.16 μm/s. (Bar, 2 μm.) (C) Fluorescence intensity plot as a function of position along the tube path and time, for the same tube as in B.

By applying an osmotic pressure in the bulk 10% lower than in the vesicle, it was possible to impose a initial tension σ = Δ∏R/2 on the membrane. Taking an average vesicle radius R of 10 μm and an osmotic pressure difference Δ∏ of 20 milliosmolar gives σ ≃ (2.5 ± 1.3) × 10^–4 N/m. We further checked this tension value by directly measuring the force needed to pull a tube, 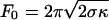(9), by using optical tweezers. The obtained value F₀ ≃ 27.5 ± 2.5 pN for a 7-μm-radius vesicle is compatible with the known value of the bending modulus κ ≃ 10 K_BT (16) and our estimated tension. We also checked that the force and thus the tension remains constant during the tube growth (Fig. 8, which is published as supporting information on the PNAS web site), which requires that sufficiently few tubes are pulled from the same vesicle; we made sure that it was indeed the case in our experiments.

For DHPE-Biot-Rhod concentrations >0.01 mol%, tubes could be formed consistently in less than a few minutes. In contrast, for concentrations <0.01 mol%, no tube could be extracted over a period of >3 h. This finding suggests the existence of a threshold for the concentration of biotinylated lipids in the membrane corresponding to a threshold for the motor density on the vesicle. Equivalently, at fixed motor density, there is a maximal tension above which no tubes can be extracted (data not shown). This finding corroborates the data published in ref. 11.

We used fluorescence videomicroscopy to follow the growth of single tubes (Fig. 1A). The fluorescence intensity and, therefore, the distribution of motors along the tube are inhomogeneous, especially at the tip, where an excess of fluorescence can be seen (Fig. 1B and Movie 1, which is published as supporting information on the PNAS web site).

The fluorescence distribution along the tube for each frame (Fig. 1B) was determined. An example of the resulting space–time plot is given in Fig. 1C; it is a three-dimensional diagram, showing fluorescence intensity (z axis, color coded) as a function of the position along the tube path (y axis) and time (x axis). We observed that, on every frame, the tip was more fluorescent than the rest of the tube. The rest of the image, where no tube could be seen, was not fluorescent. The position of the tip of the tube was determined by detecting the position of the transition between the maximum intensity and the background. The instantaneous velocity of tube growth between two consecutive images was calculated by derivation of the position of the tip as a function of time.

The average velocity, calculated over 20 different experiments where a single tube was pulled from the GUV, was 0.09 ± 0.06 μm/s for an average membrane tension of 2 × 10^–4 N/m. The growth velocity is the velocity of kinesins effectively pulling the tube. It is smaller than the velocity obtained in a bead assay, which, as discussed below, corresponds to the velocity of kinesins at vanishing load, V₀ = 0.6 ± 0.1 μm/s. Bead assays have been performed in the same experimental context as tube assays (molecular motors from the same batch, MT network obtained with the same protocol, same buffers and ATP concentration), and the measured velocity is in good agreement with data by other groups (10, 14).

Theoretical Analysis

To describe theoretically the tube extraction, we consider the three regions sketched in Fig. 2B, namely, the vesicle, the tube, and the tip. Motors located at the tip of the tube are the only motors able to exert forces on the membrane. Indeed, the forces transmitted to the tube by the other motors moving on the MT are of hydrodynamic origin and cannot exceed a few percent of the force needed to extract a tube (see Discussion). A finite force is thus applied to each motor in the tip region. As the velocity of motors decreases with applied load (10), these motors move more slowly than free motors moving along the tube. Therefore, there is an accumulation of motors at the tip. Moreover, those motors working to pull the tube detach from the MT faster than motors along the tube. The loss of working motors is compensated, under certain conditions, by the incoming flux of motors from the tube. At the same time, the tube is constantly fed by motors coming from the vesicle (Fig. 2C). In what follows, we mathematically describe the coupled dynamics of the different regions and determine self-consistently the tube motion.

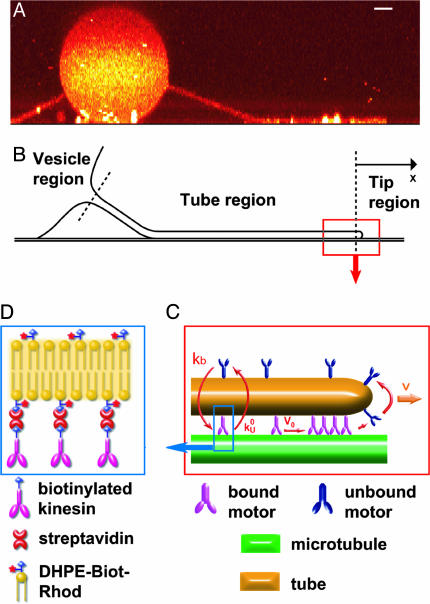
Fig. 2.

Sketch of the main features of the system. (A) Confocal side-view image of a membrane tube representing the typical geometry of the system and suggesting the natural regions dividing it. The binding sites of motors were not specifically labeled. (Bar, 2 μm.) (B) Schematic representation of the different regions (vesicle, tube, and tip). (C) Sketch of the tube-tip boundary and tip region representing the accumulation process at the tip (V < V₀). V is the velocity of the tube and of bound motors at the tip; V₀ is the zero-load velocity of bound kinesins. k⁰_u and k_b are the unbinding rate at zero load and the binding rate of kinesins onto MTs, respectively. We schematically represent the accumulation of motors at the tip. (D) Binding a biotinylated kinesin to a rhodamin-labeled biotinylated lipid (DHPE-Biot-Rhod) through a streptavidin molecule.

Tip Region. We define the tip as the front part of the tube where motors apply forces. Bound motors are those attached to the tube and to the MT, whereas unbound motors are only attached to the tube (Fig. 2C). The dynamics of motors at the tip is given by the conservation equations for the numbers of bound motors n_b and unbound motors n_u,

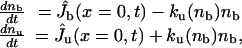[1]

where Ĵ_b and Ĵ_u are, respectively, the flux of bound and unbound motors expressed in the tube reference frame, and k_u(n_b) is the unbinding rate of bound motors. The tube is along the x axis (oriented along the direction of the tube motion); the origin x = 0 is at the position of the tip (Fig. 2B). Note that we have neglected the binding events at the tip. The time required for leaving the tip by diffusion is indeed much smaller than the binding time. With the values measured in this work, the ratio is <10^–3. The total force F₀ that the motors exert is the critical force necessary to pull a tube from a membrane, 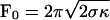(9), where σ is the membrane tension and κ is the membrane bending rigidity. The unbinding rate of the bound motors from the MT, k_u, depends on the force applied to each bound motor F_m, which is assumed, for the sake of simplicity, to be equally distributed between all motors in the tip, F_m = F₀/n_b. Kramers' rate theory (17) leads to

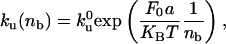[2]

where k⁰_u is the unbinding rate at vanishing force and a is a length in the nanometer range characterizing the potential barrier between bound and unbound states. As a first approximation, we assume that the velocity V of a bound motor is a linearly decreasing function of the applied force V = V₀ (1 – F_m/F_s), where F_s is the stall force of the motor. As the membrane tube is pulled by bound motors, in a mean field description, its growth velocity is the velocity V of the pulling motors.

Tube Region. We describe the dynamics along the tube by two populations of motors, namely bound and unbound motors, which are characterized by their linear densities ρ_b and ρ_u. Bound motors move essentially with the constant velocity V₀ of a motor under vanishing load, and detach stochastically from the MT at a rate 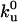. The motion of unbound motors is restricted to the tube surface and has both diffusive and convective components in the laboratory reference frame. The convective feature stems from the membrane flow resulting from the tube extension. It corresponds almost to pure convection at the velocity V, because the buffer viscosity is 2 orders of magnitude smaller than that of the membrane (Fig. 2C). Unbound motors also bind stochastically to the MT at a rate k_b. Thus, the mean-field dynamic equations for bound and unbound motors can be written as

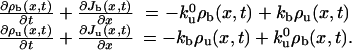[3]

In the laboratory reference frame, the flux of bound motors reads J_b(x, t) = V₀ρ_b(x, t), whereas the flux of unbound motors is J_u(x, t) = Vρ_u(x, t) – D∂_xρ_u(x, t)(D being the diffusion constant of unbound motors). We ignore here the variations of the motor velocity with the density of motors. At very high density of motors, this approximation breaks down and, for instance, the motion of one motor could be hindered by the preceding motors leading to the formation of traffic jams (18, 19). Experimental data support this low-density assumption, as explained below.

Vesicle Region. The motors on the vesicle have an initial surface density ρ_∞, which evolves to a space–time-dependent value ρ_m. The typical time scale at which the vesicle radius R varies is larger than any time scale involved in tube extraction; we thus consider the radius R as constant. Furthermore, the convection of motors on the vesicle can be shown to be negligible compared to diffusion for all practical purposes. Therefore, we write a diffusion equation for the surface density of motors ρ_m as (∂_t – D∇²)ρ_m = 0. Continuity conditions for density and flux of motors at the contact between the vesicle and the tube set the boundary conditions and couple the dynamics of these two regions.

Analytical Results. The quasistationary solutions of Eq. 3 for the motor density profiles {ρ_b,ρ_u} along the tube are exponentially decaying functions of the distance from the tip with a characteristic length scale λ. The decay length λ is much larger than the typical size of the tip region, which is in the nanometer range and cannot be resolved by our optical measurements. The value of λ is independent of the particular definition of the tip and is fixed by the dynamics of motors along the tube.

During the initial stages of tube extraction (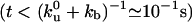), the tube length Vt is always smaller than λ, which is given in this regime by the diffusion length 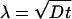, and the density profiles can be considered as linear. They can be calculated by imposing the continuity of fluxes and densities at the vesicle–tube contact and considering the velocity V to be independent of time. To extract tubes from the vesicle, there are two conditions to be fulfilled. The incoming flux of bound motors must balance the motor loss at the tip, i.e., Ĵ_b(x = 0, t) = k_u(n_b)n_b, and the velocity V must be positive. If the first condition is prevalent (flux limited regime), there is a single relevant dimensionless parameter, ν, that characterizes the various dynamical regimes at short time scales

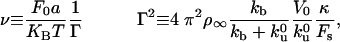[4]

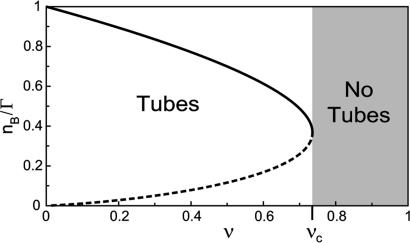
where Γ sets the scale for the number of bound motors n_b at the tip, and ν comes in the argument of the exponential in Eq. 2 as νΓ/n_b. These dimensionless numbers appear naturally by equating the flux of incoming bound motors to the rate of motor loss at the tip: Ĵ_b(x = 0, t) = k_u(n_b)n_b. In Fig. 3, we represent the analytical solutions of the latter equation, which fixes the number of bound motors at the tip as a function of ν. Actually, ν is a bifurcation parameter and the system undergoes a saddle–node bifurcation at ν_c = 2 e^–1 ≃ 0.74 (where e is the base of the natural logarithm). ν_c is a critical value below which there are stable solutions for the system, meaning that motors are able to pull tubes from the membrane. For ν > ν_c, no solutions exist and, therefore, no tubes can be extracted from the vesicle. As a consequence, there is a threshold 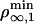for the surface density of motors on the vesicle above which tubes can be extracted

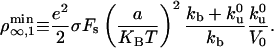[5]

At threshold, i.e., 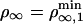, the number of bound motors at the tip is given by 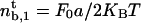, and the velocity 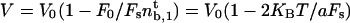is finite and independent of membrane tension and curvature. If the most restrictive condition is V ≥ 0 (stall regime), the threshold is given by V = 0. The number of bound motors at threshold is given by 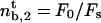which, together with flux conservation, leads to a minimal density

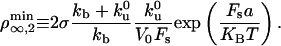[6]

If 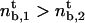, the expression for the density threshold is given by Eq. 5, and conversely if 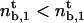by Eq. 6. Interestingly, the crossover between the two regimes depends on motor properties only: the flux-limited regime is expected if the stall force F_s is larger than 2K_BT/a, and the stall regime is expected if F_s is smaller than 2K_BT/a.

Fig. 3.

Bifurcation diagram showing the stable (continuous line) and unstable (dashed line) solutions of the system in the flux limited regime. For ν < ν_c, motors are able to extract tubes. For ν > ν_c (gray region), there are no solutions (motors are not able to extract tubes).

Therefore, above 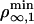or 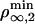depending on the regime, tubes can be extracted from the vesicle and the number of bound motors at the tip n_b ranges between max {F₀a/2K_BT, F₀/F_s} ≤ n_b ≤ Γ. On the contrary, below the threshold concentration, no tube can be extracted. Similarly, tube extraction can be monitored by changing the tension σ at constant motor density ρ_∞. It is important to understand the dynamical nature of both thresholds: a minimum flux of bound motors toward the tip is required to balance the detachment flux of bound motors which, in turn, depends strongly on the force applied per motor. Note that the bifurcation is not related to the existence of an overshoot in the static force/length relation for tube extraction (9). A threshold has also been predicted in ref. 11 by using a simplified approach that does not take into account the transport of motors along the tube. Here, we give a complete description of the transport that characterizes quantitatively both the threshold and the motor distribution.

To understand the experimental density profiles, we study the long time scale behavior (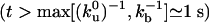). Imposing continuity conditions for densities and fluxes at the vesicle–tube boundary and assuming that the tube velocity V varies only weakly during tube extraction, we find a decay length λ for the density profiles that reads

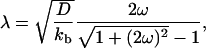[7]

where 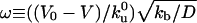is the ratio between the average distance 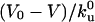, over which a bound motor travels along the tube before detaching from the MT, and the average distance 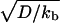that an unbound motor can travel before reattaching to the MT. The existence of a connection region between the vesicle and the part of the tube in contact with the MT (Fig. 2 A and B), together with continuity conditions, imply that no stationary state can be reached at constant tension. The value of ω distinguishes two limiting dynamical regimes at long time scales. If 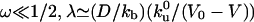and, at the scaling level, the number of bound motors grows very slowly with time n_b ∼ t^1/4. If ω » 1/2, the decay length is 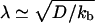and does not depend on the velocity V. In this regime, the number of bound motors grows like n_b ∼ t^1/3. This slow increase of the number of motors pulling the tube with time is consistent with our quasisteady-state approximation.

These dynamical regimes provide a good description of the tube motion as long as the density of motors just behind the tip remains small; this is true under typical experimental conditions. At very long times, the steric interactions between motors become important and lead to the formation of a traffic jam of bound motors behind the tip (18, 19). Fig. 4A supports the low-density approximation as it shows an exponential decay of the motor density. The flux of motors toward the tip is compensated to some extent by the growth of the tube itself, which keeps the densities low enough. If the tube growth is stopped by an external perturbation, self-dilution of the motors disappears and a micrometer-sized traffic jam develops at the tip (Fig. 9, which is published as supporting information on the PNAS web site).

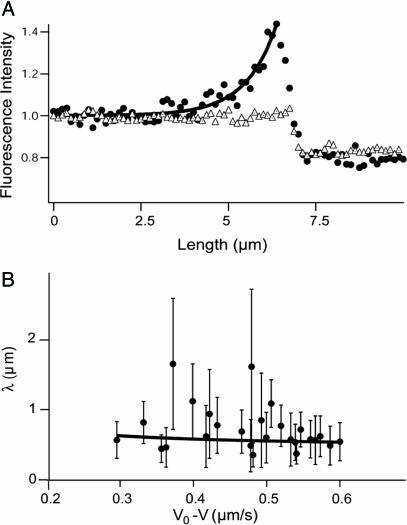
Fig. 4.

Quantitative analysis of the motor distribution. (A) Fluorescence intensities along the tube path normalized by the average intensity far from the tip. Filled circles, the binding sites of motors were labeled with DHPE-Biot-Rhod; triangles, membrane was labeled with BODIPY PC; the binding sites of motors were not specifically labeled (control experiment); solid line, exponential fit of the intensity profile represented by the circles. The best fitting value for the characteristic length λ is 1.0 μm. (B) Characteristic length λ as a function of V₀ – V for 370 measurements from 20 different tubes. Each point corresponds to the average λ (and associated standard deviation) for measurements with the same velocity. The continuous line corresponds to the one parameter weighted nonlinear fit by using Eq. 7, 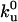= 0.42 s^–1 (20) and V₀ = 0.6 μm/s. Each weight is given by the normalized inverse of the variance associated to that point. The only fit parameter is k_b/D and its best fitting value is 4.7 ± 0.5 μm^–2. Using D = 1.0 ± 0.5 μm²/s leads to k_b = 4.7 ± 2.4 s^–1. We have further checked that reasonable variations of k⁰_u do not affect significantly this value.

Discussion

We now compare the theoretical predictions to the experimental results. The distribution of bound and unbound motors is found experimentally from the fluorescence intensity along the tube. Fig. 4A shows an example of an instantaneous fluorescence profile. The motor density decreases exponentially from the tip of the tube as expected theoretically. When the membrane was labeled by using a fluorescent lipid with no biotin function (BODIPY PC) and motors were not specifically labeled (control experiment), fluorescence was uniform along the extracted tube, and no accumulation at the tip was observed (Fig. 4A).

The decay length λ has been measured for various tubes with different velocities V (≃370 measurements) at a concentration of 0.1 mol% biotinylated lipids in the membrane. The value ranges between 0.4 μm < λ < 1.8 μm (Fig. 4B). The comparison of these values with the theoretical predictions of Eq. 7 allows the determination of the binding rate k_b of kinesin on MTs in a one parameter fit, provided that we know D, V₀, and .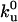

We used fluorescence recovery after photobleaching experiments (see Materials and Methods) to measure the diffusion constant D of the biotinylated lipid–streptavidin–kinesin in the membrane, D = 1.0 ± 0.5 μm²/s (data are shown in Fig. 10, which is published as supporting information on the PNAS web site). As mentioned above, V₀ is obtained from the velocity measured in bead assays in absence of external load. Indeed, the friction force exerted on the bound motors moving along the tube is given, according to Einstein's law, by F_H = K_BTV₀/D ≃ 2.4 × 10^–3 pN, which is totally negligible compared to the stall force of kinesins. We used 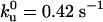(20) and V₀ = 0.6 μm/s to obtain k_b = 4.7 ± 2.4 s^–1. This analysis provides us with the measurement of the binding rate k_b in a tubular geometry similar to in vivo conditions.

As pointed in the theoretical section, the threshold regime is determined by motor properties only. The wild-type kinesin has been extensively studied (10, 21, 22) in conditions close to ours. In particular, both F_s and a have been measured: F_s ≃ 6 pN and a ≃ 1.3 nm (23, 24). The values lead to 2K_BT/a ≃ 6 pN, which shows that our system is almost at the transition between the two regimes. We can further calculate both 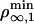and 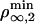. We find that 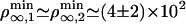μm^–2, which compares favorably well with the experimental value ρ_∞ ≃ (2 ± 1) × 10¹⁴ m^–2 (0.01 mol% of biotinylated lipids and 0.4 nm² for the surface of a lipid in the membrane). At threshold, both cases correspond to a number of pulling motors 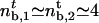. Away from threshold, for 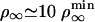(same tension), we can also calculate the number of motors at the tip without any adjustable parameter. When we use flux balance (represented in Fig. 3) and Eq. 4, we find n_b ≃ 24 motors. These numbers are rather small, which implies that fluctuations may play an interesting role in the process. The fluctuation characteristics of the tube growth require both experimental and theoretical investigation.

So far, we have considered that bound motors outside the tip do not exert any significant force on the tube. This consideration is indeed legitimate: a conservative estimate of the friction force close to the threshold is F_F ≃ 2π rρ_∞F_HL ≤ 10^–4 F₀ « F₀ (in which we have chosen the tube length L to be a few times the tube radius r). Away from threshold, F_F ≤ 10^–1 F₀ < F₀, which is again negligible and justifies our previous assumptions.

The existence of a threshold for tube extraction is important in that it shows that cells can switch transport on or off when needed. This switch could be done by two different strategies. The first mechanism involves the control of the density of motors attached to the membrane, either by regulating the number of available motors, or by regulating the number of motor binding sites on the membrane. The concentration of active motors inside specialized membrane domains would then be an important feature for the understanding of the secretory pathway regulation (5). The second strategy involves the control of membrane tension. Tension can be changed very rapidly and globally on a membrane, thus providing a very fast way to monitor tube growth.

We have provided here a fully quantitative analysis of in vitro formation of membrane nanotubes in our minimal system. Therefore, we are in a position to investigate the selective addition of proteins known to play a role in motor membrane complexes (25).