Phospholipid bilayer surface configuration probed quantitatively by ³¹P field-cycling NMR

Abstract

³¹P relaxation of the diester phosphate of phospholipids in unilamellar vesicles has been studied from 0.004 to 11.7 T. Relaxation at very low fields, below 0.1 T, shows a rate increase that reflects a residual dipolar interaction with neighboring protons, probably dominated by the glycerol C3 protons. This interaction is not fully averaged by faster motion such as rotational diffusion perpendicular to the membrane surface. The remaining dipolar interaction, modulated by overall rotational diffusion of the vesicle and lateral diffusion of the lipid molecules, is responsible for the very low-field relaxation. These measurements yield a good estimate of the time-average angle between the membrane surface and the vector connecting the phosphorus to the glycerol C3 protons, based on the classic theory by Woessner [Woessner, D. E. (1962) J. Chem. Phys. 37, 647–654]. Dynamic information is also obtained. Implications for solid-state NMR and other studies are discussed.

Much remains to be known about the details of the configuration and dynamics of the phosphodiester region of phospholipid bilayer membranes, despite a large body of work (1, 2). Yet such knowledge is likely to be very useful in understanding how proteins and assemblies interact with this interfacial region. For example, there is indirect evidence that the peripheral membrane protein phosphatidylinositol-specific phospholipase inserts a tryptophan residue into a phosphatidylcholine membrane surface, which in turn activates the enzyme toward its substrates, but how this happens in detail is unknown (3, 4).

The lack of structural information for phospholipid polar and interfacial moieties results from the difficulty in obtaining crystals and making other ordered structures that are necessary for most structural techniques. Even when available, the resemblance of such ordered structures to membranes functioning in vivo can be questioned. Modern methods of NMR spectroscopy are generally difficult to apply to this problem, mainly because of the slow rate of tumbling of molecules in reasonable analogs of biological membranes such as vesicles. Most NMR studies (¹H, ¹³C, and ²H) of membranes have focused on acyl chain dynamics (5–7). Phosphorus-31 NMR, which would appear ideally suited for obtaining information on the phosphodiester linkage conformation and dynamics, has seen limited use, because ³¹P resonances in phospholipid aggregates exhibit a large linewidth due to their chemical-shift anisotropy (CSA) [although this property had made this nucleus very useful in characterizing the phase behavior of phospholipid bilayers (5)]. ³¹P chemical shifts in phosphodiesters embedded in membranes do reflect orientation of chemical bonds relative to the membrane surface but not in a very usefully specific way. Structures deduced from other NMR data suffer from unknown dynamic averaging effects. Computer simulations show great promise to eventually give completely detailed information (8, 9) but still need to be validated with quantitative experiments.

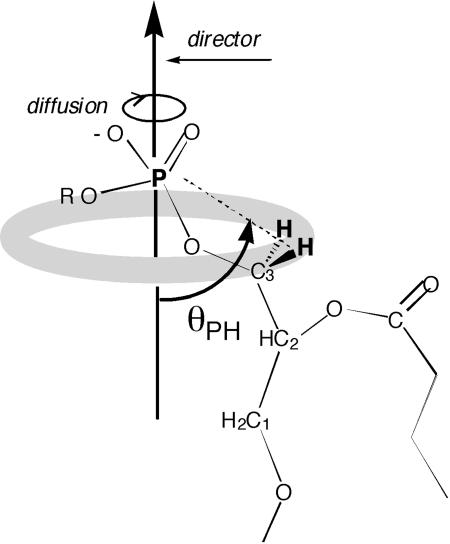
As a contribution to this problem, we have estimated the angle θ_PH between the vector connecting the phosphorus to its nearest protons and the vector perpendicular to the membrane surface (see Fig. 1), simply by performing nuclear magnetic spin-lattice relaxation measurements over a wide-field range, based on the technique of high-resolution field cycling described elsewhere (10, 11). Orientation information obtained from relaxation measurements has been a persistent theme in NMR over the years (12), but our approach is based on the symmetry inherent in the accepted model of many phospholipid membranes: (i) the membrane has a well defined time-average surface; (ii) individual phospholipid molecules, on average, are oriented perpendicular to this surface; (iii) each has internal motions occurring with a short timescale, as well as slower motions; and (iv) among the latter, the slowest are likely to include rotational diffusion of the entire molecule about an axis perpendicular to the membrane surface (this axis is known as the “membrane director” or below as the “director”), as well as much slower lateral diffusion about the surface and viscous overall rotation of the vesicle (13).

Fig. 1.

The angle θ_PH that we measure is the time average, over many nanosececonds, of the angle between the P-to-H vector and the director vector (perpendicular to the time average of the membrane surface). The rotation of the individual lipid molecule about the director makes the phosphorus see a ring of proton magnetization (indicated here by the shaded ring) at the lowest magnetic fields. It is easy to show from classical physics that the field on the axis of the ring is decreased by the factor S_L = (1/2)(3cos²θ_PH –1) when the protons are dynamically delocalized uniformly over the ring. This averaged field is the same as that which would be felt by the phosphorus spin if there were a fictitious proton spin the same distance away, on the director axis, with a magnetic moment equal to that of a proton but multiplied by S_L.

The angle determination that we describe utilizes relaxation due to the magnetic dipolar interaction between the ³¹P nuclear magnetic moment and that of a nearby proton spin, modulated by motion of the phospholipid. (In the case we are considering, there are two such protons, namely the two glycerol C3 protons, which, for now, we treat as equivalent, or nearly so.) It is well known that this interaction is averaged to zero by isotropic motion in solution that makes all orientations of the molecule relative to the external magnetic field equally probable. In the present case, however, this averaging is typically only ≈90% completed by rotational diffusion about the director and by other internal motions, because these motions by themselves do not sample equally over all possible orientations of the lipid relative to the field. The remaining averaging is completed by much slower head-to-tail reorientation of the molecule due to a combination of overall reorientation of the vesicle and the lateral diffusion of molecules from one side of the entire vesicle to the other. The timescale for these latter processes is ≈1 μs, whereas the diffusion around the director, and internal motions, have a timescale of a few nanoseconds or less. The remaining unaveraged part of the dipolar interaction, in fact, should observably split the phosphorus resonance in lamellar samples.

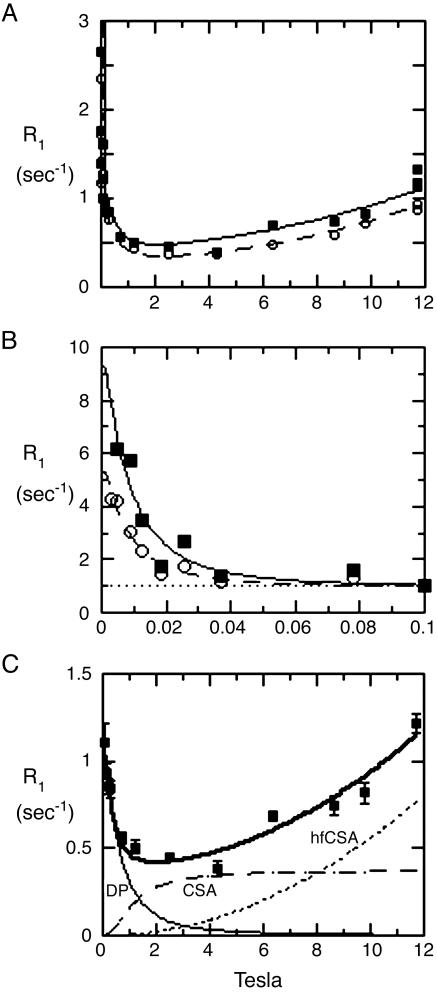
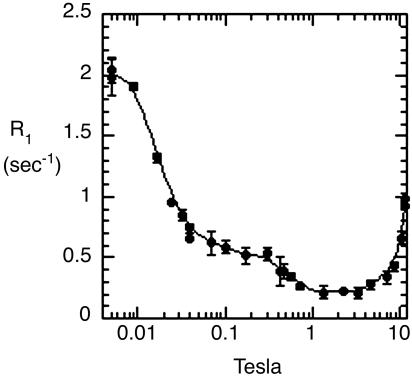
We observe the remaining unaveraged “residual dipolar coupling” indirectly in freely tumbling vesicles in solution, as manifested by an increase (or “dispersion”) of the relaxation rate that we see when the angular precession rate (2π times the resonance frequency) of the phosphorus is comparable to, or less than, the order of magnitude of the tumbling rate of the vesicle (10⁶ radians per second or less). The rise in relaxation rate is thus seen at fields of <≈0.01 T (100 G) for small (≈200- to 300-Å diameter) vesicles (Fig. 2 A and B). We have reported (13) relaxation measurements at fields between 1,000 G and 11.7 T in a variety of lipid vesicles, which give dynamic and distance information (13).

Fig. 2.

Relaxation rates of the ³¹P nuclear spins of each phospholipid in sonicated unilamellar vesicles containing a 1:1 mixture of POPC (▪) and DOPMe (○). The NMR peaks of the two species are well resolved and were identified from prior studies. (A) The entire data set is plotted at a gain too high for the lowest-field points, but that shows the high-field data most clearly. (B) Horizontally expanded plot of the lowest-field points at suitable lower gain. Note that the definite differences between the two species in rates in B are larger than the differences between them in A. Note also the well defined baseline (dotted line) in B, of ≈1 sec^–1, that is subtracted in data analysis, as described in Materials and Methods. The theoretical curves are obtained from a fit as described in Materials and Methods.(C) The data taken on POPC above 0.1 T were fitted to a standard theoretical model, as described (13). The dotted curves marked CSA, and hfCSA are approximate contributions to the relaxation of the nuclear spin due to its CSA, which is relatively unimportant for the present article except as a source of error. The thin solid line at the bottom left marked DP (for dipolar) is an estimate of the contribution to the relaxation rate from the magnetic dipolar interaction of the phosphorus spin with nearby proton spins. The upper thick solid curve is the sum of these three contributions. The DP curve has two adjustable parameters, a correlation time and an effective distance between the phosphorus and the nearby protons. The two theoretical CSA curves have two additional adjustable parameters that determine the vertical scale of each.

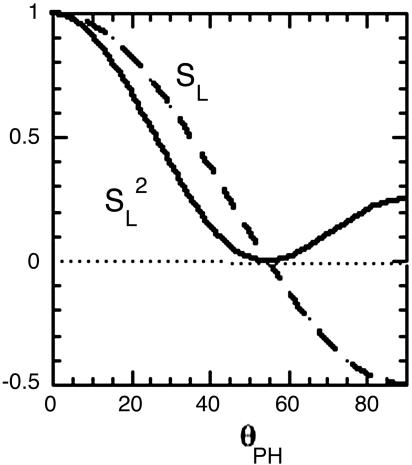
The relation between this residual decoupling and the molecular geometry is provided by the classic paper by D. E. Woessner (14). It predicts that the size of the residual phosphorus–proton dipolar interaction is equal to the normal dipole interaction for the same pair of nuclei at their actual distance, reduced by a parameter we call S_L, where S_L = (1/2)(3cos²θ_PH – 1), and θ_PH is the angle between the P-to-H internuclear vector and the director vector (see Fig. 1). This prediction means that the residual dipolar interaction goes through zero (when cos²θ_PH equals 1/3) and reverses sign as a function of θ_PH. The sign reversal is of no consequence by itself, because the relaxationrate contribution due to any interaction is proportional to the square of the interaction or in this case (1/4)(3cos²θ_PH – 1)² (see Fig. 3), which goes through a parabolic null, as a function of θ_PH, in the vicinity of the point where cos²θ_PH equals 1/3.

Fig. 3.

The relative size of the dipolar interaction (dashed line) due to a proton diffusing rapidly in a circle, as seen by a phosphorus nucleus situated on the axis perpendicular to the rotation. The interaction is averaged over a timescale that is long compared with the inverse of the rotational diffusion rate of the proton on the circle. It is plotted as a function of the angle between the rotation axis (in the present case, the director) and the P-to-H vector (see Fig. 1) and equals S_L = (1/2)(3 cos²θ_PH – 1). The director tumbles slowly on the microsecond timescale, and the resulting very low-field relaxation rate that we measure is proportional to the square of this interaction, or 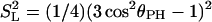(solid line).

Several spectroscopic methods have been described and used (2, 15) to obtain dynamic and structural information, including orientation information from a residual dipolar interaction, like that we describe here. An alternate way to think about the measurements we describe here is to first consider that the dipolar interaction is reduced, as is well known, to a residual interaction by motion of the lipid with respect to the membrane, whose director is considered to be at some arbitrary fixed direction with respect to the external magnetic field. The residual dipolar interaction produces splittings in spectra that have been used previously to estimate orientations. Then, in vesicles, the director changes orientation relative to the magnetic field on the microscopic scale, reducing the splitting to a relaxation phenomenon that we report here (see Supporting Text, which is published as supporting information on the PNAS web site).

The validity of either approach is adversely affected by the many internal motions the phospholipids may have, with a timescale in the range of 10 ns or less (13). Furthermore, there is ambiguity in our method about which protons are contributing to the measurement, unless some selective deuteration of the sample is used. However, we do not think this is such a serious problem, because we can easily compare a variety of samples and use relaxation data at a higher field to partly cancel the effects due to internal motions, and we get new dynamic information from the same sample, as we have discussed (13).

Details of how we apply the Woessner prediction (14) to obtain the internuclear vector orientation θ_PH will be presented later. As will be seen, the data lead not to a unique angle θ_PH but to four possible values. We may not be able to distinguish among these values from our methods, but they can be compared with molecular dynamics simulations (which can also help to correct for effects of faster internal molecular motion) to help select one of the four angles we predict.

Materials and Methods

Samples and NMR methods were as described (13). All phospholipids were obtained from Avanti Polar Lipids and used without further purification. Small phospholipid vesicles (250- to 300-Å average diameter) were prepared by sonication of lipids rehydrated in 50 mM Tris, pH 7.5/25–35% D₂O until maximum clarity; large unilamellar vesicles of 1-palmitoyl-2-oleoylphosphatidylcholine (POPC) were prepared by extrusion of the hydrated lipids through polycarbonate membranes (100-nm pore diameter) by using a Lipofast extruder from Avestin (Ottawa).

For field-cycling measurements (13, 16), a shortened conventional 8-mm NMR tube was attached to a plastic shuttle piston that was moved up and down by mild suction and pressure inside a precision 20.3-mm inside-diameter glass shuttle tube. To extend our measurements to fields below 0.1 T, we added a removable brass extender to the top of our shuttle tube, so that the sample could be moved to a point ≈12 cm above the top of the magnet where the field is ≈40 mT. We mounted a Helmholtz coil centered at this point to buck this field to zero, under simple computer control (17). Further details are found in ref. 16. An entire data set on a typical sample, such as that shown in Fig. 1, requires ≈48 h of spectrometer time, by using 5–10 mM of phospholipid in a 0.7-ml volume. Although, to our knowledge, our results and interpretation are unique, the experimental method (11, 13), while unusual, is not new (10).

Data for fields above 0.1 T were computer-fit as described in our earlier paper (13), ignoring data taken below 0.1 T (see Fig. 2C). Data for fields below 0.1 T were then treated by first subtracting a baseline R(0), which is the zero-field intercept of the computer fit to the higher-field data. For example, as shown in Fig. 2, this baseline is ≈1.1 sec^–1 for both species shown. The data thus modified were then fit to the same standard Solomon dipolar relaxation formula that we used previously to calculate the dipolar relaxation above 0.1 T [curve marked DP (for dipolar) in Fig. 2C] but with different fitting parameters: a correlation time τ_v that is in the microsecond range, and a vertical scale parameter R_v(0). The parameter τ_v is expected to be the usual standard correlation time for dipolar interaction due to head-to-tail rotational diffusion. In this case, it can be calculated from the Stokes–Einstein rotational diffusion coefficient and the lateral diffusion rate of individual molecules (see Supporting Text) of the lipid. The parameter R_v(0) is the rise in relaxation rate at very low field, above the baseline rate R(0) extrapolated from data taken above 0.1 T. Examples of this fitting procedure are shown in Fig. 2B. The parameter R_v(0) is not of interest, except that it was used to calculate the area under the low-field dispersion (such as the curves in Fig. 2B). Area ratios were then calculated from the fitted curves, and angles were calculated as discussed later.

Results and Discussion

We have used a pneumatic sample shuttling device to measure ³¹P nuclear spin-lattice relaxation over nearly four orders of magnitude below 11.7 T. Fig. 2 A shows a complete plot of the ³¹P relaxation rate R₁ for a mixed small unilamellar vesicle of POPC and dioleoylphosphatidylmethanol (DOPMe) (1:1), whose resonances are well resolved. This article focuses on the rises in rates at very low fields shown expanded in Fig. 2B, which are due to the residual dipolar interaction modulated by head-to-tail tumbling from overall vesicle tumbling and from lateral diffusion, on roughly a microsecond timescale. Visually, it is clear that the relaxation rate differs significantly between the two phospholipid species at these low fields below 0.1 T, much more so than at higher fields. We recently published extensive data and discussion about dipolar relaxation of the phosphate at these higher fields (0.1–3 T), including preliminary data on the effect of the peripheral membrane protein phosphatidylinositol-specific phospholipase C (3, 4) on the ³¹P relaxation rates (13). These observations are consistent with the previous observations on this enzyme that were mentioned in the introduction.

Main Results. The conclusions are based on the ratios of the areas under two curves, which describe the contributions of the magnetic dipolar interaction to nuclear spin relaxation: (i) the curve due to the residual dipolar interaction after averaging by all higher-frequency motions and associated with the very low-frequency head-to-tail diffusion of the lipids in the microsecond region; and (ii) the area under the entire contribution of the same dipolar interaction, from all motions and at all fields. The areas in question are, respectively, the area under curves like that in Fig. 2B, obtained in some cases with good accuracy after subtraction of the baseline R(0), as indicated in the legend to Fig. 2; and the area just mentioned plus the area under the curves for the same sample from data at higher fields, for example, the area under the curve marked DP in Fig. 2C. As already mentioned, theory (14) states that this area ratio should equal = (1/4)(3cos²θ_PH – 1)², provided that internal motions can be ignored.

We have studied a variety of samples at very low fields and have tabulated the area ratios, scaling factors R_v(0), and correlation times, τ_v, in Table 1. The values of τ_v are ≈1 μs, except for the large vesicle sample, and their significance here is that they are roughly what is expected for the overall rotational correlation time of these small vesicles. We also tabulate values of the angle (Fig. 1) of θ_PH deduced from the area ratios by setting the ratio equal to (1/4)(3cos²θ_PH – 1)² and solving for the angle.

Table 1. Correlation times, extrapolated R_v(0), dipolar area ratios, and θ_PH angles for a variety of phospholipid vesicles.

Sample*	τv, μs	Rv(0), s-1	Area ratio†	θPH(+)‡	θPH(-)‡
POPC/DOPMe
POPC	0.54 ± 0.10	8.4 ± 2.3	0.080	43.7	67.7
DOPMe	0.54 ± 0.19	4.4 ± 0.5	0.046	46.3	64.2
POPC
small	0.77 ± 0.13	20.0 ± 3.8	0.124	41.1	71.7
large	≈37§	2,800§	0.28§
diC7PC	0.31 ± 0.04	1.9 ± 0.1	0.058	45.4	65.4
POPC/POPA
POPC	0.40 ± 0.11	8.8 ± 1.4	0.122	41.2	71.5
POPA	0.48 ± 0.30	9.0 ± 1.7	0.048	46.2	64.4

diC₇PC, diheptanoylphosphatidylcholine; POPA, 1-palmitoyl-2-oleoyl phosphatidic acid.

^*All samples are 5 mM each phospholipid (1:1 for binary lipid vesicles) in 25% D₂O at 22°C.

^†The area ratio is the experimental area under the low-frequency dispersion curve, such as the curve in Fig. 2B divided by the sum of the area under the low- and high-frequency (the curve marked DP in Fig. 2C) dipolar dispersion curves.

^‡In calculating θ_PH from the area ratio, there are two possible magnitudes or roots depending on the assumed sign of the square root of (1/4)(3cos²θ_PH - 1)². The tabulated θ_PH(+) and θ_PH(-) are, respectively, these values for positive or negative signs of that root.

^§The rapid rise in relaxation rate prevented us from taking sufficient data to fit the relaxation profile as we did for the other samples. Instead, we estimated τ_v from the known size of these vesicles and fixed this parameter in the computer fit of the few points above baseline that we took. See Supporting Text for details.

Unfortunately, the determination of this angle is ambiguous, because there are two solutions to this equation, as indicated in Table 1. The ambiguity is really 4-fold, because we also do not know whether the proton or the phosphate is closest to the surface. The more polar phosphate is likely to be closer to solvent, as shown in Fig. 1, but the other possible orientations with the protons closer to the solvent cannot be ruled out from the data presented.

Before showing some more detailed data and discussing errors and corrections to these angle determinations, we point out some general features. All of the area ratios are rather small, and therefore the deduced angles θ_PH are close to the “magic angle” (as it is known to NMR workers) of 54.7° where (3cos²θ_PH – 1) = 0. If it were also true that the correct angles for all those values are in only one of the two columns of Table 1, then the range of angles would be very small, within only 5°. This possible uniformity suggests that all these phospholipids represent a sort of default conformation for the surface, a conclusion that would not be surprising but would be a useful generalization.

The determination of θ_PH is exquisitely accurate when different phospholipids are studied in the same vesicle. This point is illustrated by the nearly 2-fold variation in relaxation at very low field, shown for the two components in the mixed vesicle in Fig. 2. Our analysis implies that this is due to a difference of only 3° in θ_PH between the two species. The absolute error due to reasons discussed below may be larger than this difference, but there is reason to hope from this observation that small differences in geometry can be inferred. This reasoning, of course, is based on the assumption that the correct θ_PH values belong to the same column of Table 1.

Above, we have optimistically ignored relaxation due to the protons attached to the nearest carbons of the head group (that is, the choline -OCH₂-protons for POPC and the –OCH₃ protons for DOPMe). One reason for this optimism is that the possible angles θ_PH, as well as the distance r_eff, which is a weighted effective distance from phosphorus to surrounding protons extracted from data above 0.1 T (see refs. 11 and 13), determined for phosphatidic acid (more specifically, 1-palmitoyl-2-oleoylphosphatidic acid), which has no such head-group protons, are similar to those for the other phospholipids. We expect to clarify this point further by selectively deuterating the choline and methyl protons and to be able to draw further conclusions about dynamics.

A possible explanation for our proposed lack of much relaxation from the nearest choline linker protons in POPC is that the vicinal P—O bond is rotated so that on average these protons are more or less trans to the phosphorus, >0.5 Å further away than the glycerol C3 protons. However, this suggestion appears to be at odds with most models that have been proposed for the head-group region.

The apparent lack of relaxation of phosphate by the head-group methyl protons for DOPMe, indicated by the similarity of the ³¹P relaxation for POPC and DOPMe (this paper and ref. 13), is also a problem. A reduction in their effectiveness could arise from a large-amplitude motion of the methyl group relative to the phosphate on the picosecond timescale. Evidence that this methyl group undergoes rapid internal motion is provided by the low T₁ relaxation rate of its protons compared with the same rate for the terminal alkyl side-chain methyl protons (see figure 7A inset in ref. 13). Further speculation along these lines is unwarranted pending further measurements based on deuteron labeling.

We have already established in the cases of POPC and DOPMe that exchangeable protons such as those of bound water do not contribute to relaxation, by substituting D₂O for the mostly H₂O solvent, with no change in relaxation.

So far, and in Table 1, we have not attempted to differentiate between the two glycerol C3 protons, which we think are predominantly responsible for the dipolar relaxation that we have been discussing. It is possible that one of these protons is close to the minimum distance to the phosphates allowed by normal bond angles, and the other is further enough away to reduce its relaxation effect by a factor of order one-half or less. Within the probable errors of our measurement and interpretation, that means that the angle deduced as described above will be close to that for the nearest of the two C3 protons.

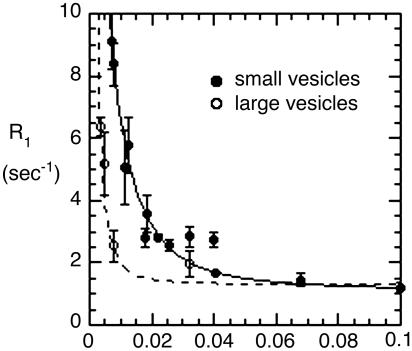
Additional Data. Now we present partial plots of data on some more samples listed in Table 1, to indicate how these support the picture outlined above. Fig. 4 compares extreme low-field data for POPC vesicles prepared in two ways: (i) by sonication, to produce ≈300-Å-diameter vesicles, and (ii) by extrusion to generate large unilamellar vesicles with an average diameter of 1,000 Å. We have compared such samples (13) at fields above 0.1 T and found that they had similar R₁ behavior in this range, as expected if the size of the vesicles does not much affect the internal motion or rotational diffusion about the director. In Fig. 4, we see, on the other hand, a very big difference below 0.1 T, presumably due to the very long head-to-tail rotational correlation time τ_v for the larger samples compared with the smaller ones. For both vesicles, we cannot follow the relaxation to zero field, but for the POPC in small vesicles, the data can be fit as described to obtain an extrapolated value for the zero-field data and a reasonable estimate for the rotational correlation function. For the larger vesicles, the corresponding curve is expected to be much narrower on the field axis and much higher at zero field, and an accurate extrapolation cannot be made. However, the behavior at low field is consistent with the much slower tumbling of the large vesicles contributing to relaxation of the phosphate group, much more at very low field (see Supporting Text).

Fig. 4.

Very low-field relaxation rates for POPC vesicles of 300- to 350-Å diameter (•) and larger vesicles (○, 1,000-Å diameter) of the same phospholipid. For the small unilamellar vesicle sample, the curve is the best fit using the limiting relaxation rate obtained from analyzing data from 0.1 to 1 T. The data for the larger vesicles are not adequate for an accurate two-parameter fit to the expression for dipolar relaxation but were fit by using an assumed value of 80 μs for τ_v (see Table 1, footnote §).

Similar relaxation curves from 0.004 to 11.74 T can also be obtained for micellar samples such as diheptanoylphosphatidylcholine (diC₇PC) (Fig. 5). This short-chain phospholipid forms moderately long rod-shaped micelles (18). Fig. 5 is plotted on a semilogarithmic scale, so that the entire range of data can be seen in one plot. This deemphasizes the features shown in Fig. 3 for the diC₇PC micelle, but in fact the same features, as in plots for vesicles, are all present. The relaxation rates above 0.1 T are similar to those for POPC small unillamellar vesicles, with the exception that most relaxation rates are smaller, as might be expected for these smaller and more loosely packed aggregates. The fitting parameters derived from the relaxation rate at very low field are smaller than for small unilamellar vesicles (Table 1), but the interesting result is that the area ratio is in the same range as for the bilayer samples, and therefore the θ_PH values are also similar. This observation is consistent with the speculation above that the data may indicate a default geometry for the phospholipid surface, and it may be reassuring for solution studies of integral membrane proteins based on micellar models.

Fig. 5.

Field dependence of the relaxation rate of the ³¹P resonance of diheptanoylphosphatidylcholine (10 mM) micelles.

Corrections to Theory and Fitting Errors. The average angles listed in Table 1 are undoubtedly in error, because the theory neglects the effect of internal motion. This is probably the largest source of error in these estimates. Less serious, most probably, are noise-induced fitting errors resulting from inability to separate the high-field components shown as curves DP, CSA, and hfCSA in Fig. 2C. These are discussed in slightly more detail in Supporting Text. Some of these errors and poorly known parameters, such as the distance between the phosphorus nucleus and the C3 protons, may cancel to some degree by use of area ratios, but others will not.

We could try to correct for these and other errors and uncertainties by decreasing all of the area ratios by some factor before setting them equal to the expression and solving for θ_PH. If we take this factor to be 0.5, which might be suggested from the discussion in Supporting Text, then the largest predicted change in θ_PH among the values tabulated (Table 1) is for POPC small vesicles and is only 4°, from 41.1 to ≈45°. Although this correction is probably in the right direction and may indicate the general degree of uncertainty in our major conclusions, we prefer not to show results corrected in such an arbitrary way, because doing so might convey an incorrect impression of their precision. In any case, the correction is relatively small and is expected to be similar for all of the examples tabulated.

Conclusion

The residual dipolar interaction that we measure with reasonable accuracy has been measured spectroscopically for other internuclear vectors in membranes (2, 15, 19, 20). These spectroscopic measurements have the advantage of less ambiguity due to the possibility of multiple interaction partners. In the case of interactions involving protons, they can clarify the question of which or how many protons are predominantly interacting with a given carbon or phosphorus, without the use of selective and possibly difficult deuteration of proton sites. With a few exceptions (2, 19, 20), these have been short-range measurements, and most have involved isotopic labeling.

However, the method we describe has not previously been used in this way, and the measurements we describe here and in ref. 13 are of interest in their own right. Field-cycling measurements provide important additional dynamic information. They do not require isotope labeling to draw conclusions about structure and thus allow us to compare a range of different lipids rapidly, as we report here, although isotope labeling will certainly be useful in this context. In particular, we can usually monitor these internuclear vectors for multiple phospholipids in the same membrane, and the interaction we describe here is long-range, important, and universally present.

The approach could be used in other ways for example, it could be applied to other nuclear spin pairs with the aid of isotope labeling. If a connecting vector between interaction partners were approximately parallel to the director (19), then the relaxation dispersion, analogous to the one we find at around 2 T for the diester phosphorus (13), would be vastly reduced, whereas the very low-field dispersion would be enhanced.

Besides the dipolar-based methods that we describe herein, the shift due to the time-averaged CSA interaction of ³¹P can be measured in a variety of lipids and used to extract structural information (21). A relaxation measurement that has yet to be exploited is T₁ relaxation at high field in vesicles, which depends strongly on the relative orientation of the director and the CSA tensor (13). The same measurement could be performed as a function of the angle between the director and the magnetic field, and the residual dipolar splitting of the ³¹P spectrum by protons could also be measured directly. Another possibility is measurement of CSA relaxation at very high fields (20 T or higher), in the hope of seeing a departure of the rate from the square-law with field dependence that we reported earlier (13). The timescale of the high-frequency internal motion that this relaxation reports might then be better estimated, and as a result, the amplitude of these motions could also be estimated.

The highly developed discipline of protein-structure determination by NMR relies heavily on imported information from simulations and from simulations themselves, as well as isotope labeling. The fewer number of atoms in a lipid compared with a protein, which might make a pure NMR determination of lipid structure possible, may encourage optimism for such attempts, but this advantage must surely be largely cancelled by the greater internal motion that occurs at every point of the lipid compared with a protein. Simulations of the motion of entire large models of phospholipid bilayers are now feasible and will become more accurate as time passes (8, 9). The best role for tools like NMR may be to provide as stringent a test of, and some guidance to, these models as far as possible.