Welcoming natural isotopic abundance in solid-state NMR: probing π-stacking and supramolecular structure of organic nanoassemblies using DNP

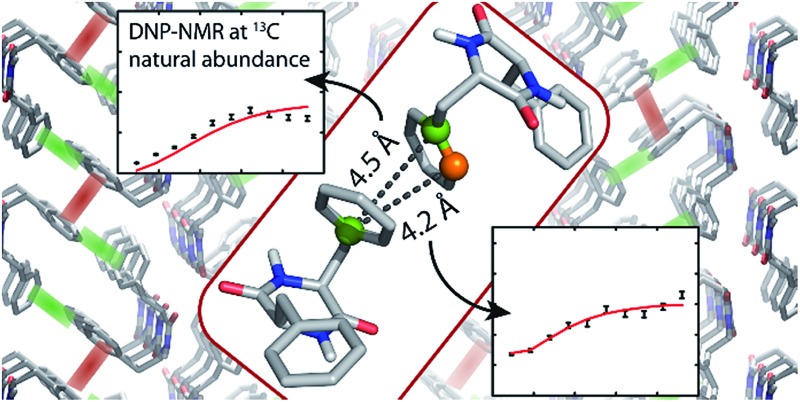
The low natural abundance of ¹³C combined with MAS-DNP enables ¹³C–¹³C polarization transfer up to ∼7 Å and observation of π-stacking.

Abstract

The self-assembly of small organic molecules is an intriguing phenomenon, which provides nanoscale structures for applications in numerous fields from medicine to molecular electronics. Detailed knowledge of their structure, in particular on the supramolecular level, is a prerequisite for the rational design of improved self-assembled systems. In this work, we prove the feasibility of a novel concept of NMR-based 3D structure determination of such assemblies in the solid state. The key point of this concept is the deliberate use of samples that contain ¹³C at its natural isotopic abundance (NA, 1.1%), while exploiting magic-angle spinning dynamic nuclear polarization (MAS-DNP) to compensate for the reduced sensitivity. Since dipolar truncation effects are suppressed to a large extent in NA samples, unique and highly informative spectra can be recorded which are impossible to obtain on an isotopically labeled system. On the self-assembled cyclic diphenylalanine peptide, we demonstrate the detection of long-range internuclear distances up to ∼7 Å, allowing us to observe π-stacking through ¹³C–¹³C correlation spectra, providing a powerful tool for the analysis of one of the most important non-covalent interactions. Furthermore, experimental polarization transfer curves are in remarkable agreement with numerical simulations based on the crystallographic structure, and can be fully rationalized as the superposition of intra- and intermolecular contributions. This new approach to NMR crystallography provides access to rich and precise structural information, opening up a new avenue to de novo crystal structure determination by NMR.

Introduction

Organic self-assembled structures find applications in fields ranging from medicine to molecular electronics.¹ Their huge popularity stems from the fact that large and complex structures can be formed from comparably small building blocks that are easy to fabricate and functionalize. Non-covalent interactions like hydrogen bonding, ionic and aromatic interactions as well as hydrophobic effects play a key role in the self-assembly process and govern the shape, and physical properties of the supramolecular structure.^2,3 Therefore, their thorough understanding is crucial for the rational design of new and improved structures. This requires precise structural knowledge, both on the molecular and the supramolecular level.

Solid-state nuclear magnetic resonance (ssNMR) spectroscopy is the method of choice for structural investigations at atomic resolution when single-crystal X-ray diffraction (XRD) cannot be successfully applied. However, NMR suffers from low sensitivity, which is aggravated by the low natural isotopic abundance (NA) of the key nuclei ¹³C and ¹⁵N (1.1% and 0.37%, respectively). Hence, the probability of encountering a particular ¹³C–¹³C spin pair, e.g. for 2D correlation experiments and/or internuclear distance measurements, is as low as ∼0.01%. Therefore, structure determination of NA samples by ssNMR has to rely heavily on complementary techniques like powder XRD and density functional theory (DFT), the combination of which is usually termed NMR crystallography.⁴

In this work, we prove the feasibility of a novel strategy for solving 3D structures of organic nanoassemblies, which we introduced recently.^5–7 Our approach crucially requires recording NMR data on the samples at their low NA, firstly for spectral assignment,^5,7–9 and secondly for extraction of structural information (using for instance dipolar recoupling experiments).^5,6,10 Dramatically reduced sensitivity resulting from the low NA is compensated for by using magic-angle spinning dynamic nuclear polarization (MAS-DNP). As clearly demonstrated in this work, experiments at the NA of ¹³C yield unprecedented spectra, which would be impossible to obtain with isotopically labeled material. For instance, long distance polarization transfers can occur thanks to significantly reduced dipolar truncation^11,12 effects, and the corresponding ¹³C peak resolution is substantially improved, owing to the absence of broadening from one-bond J _CC-couplings.

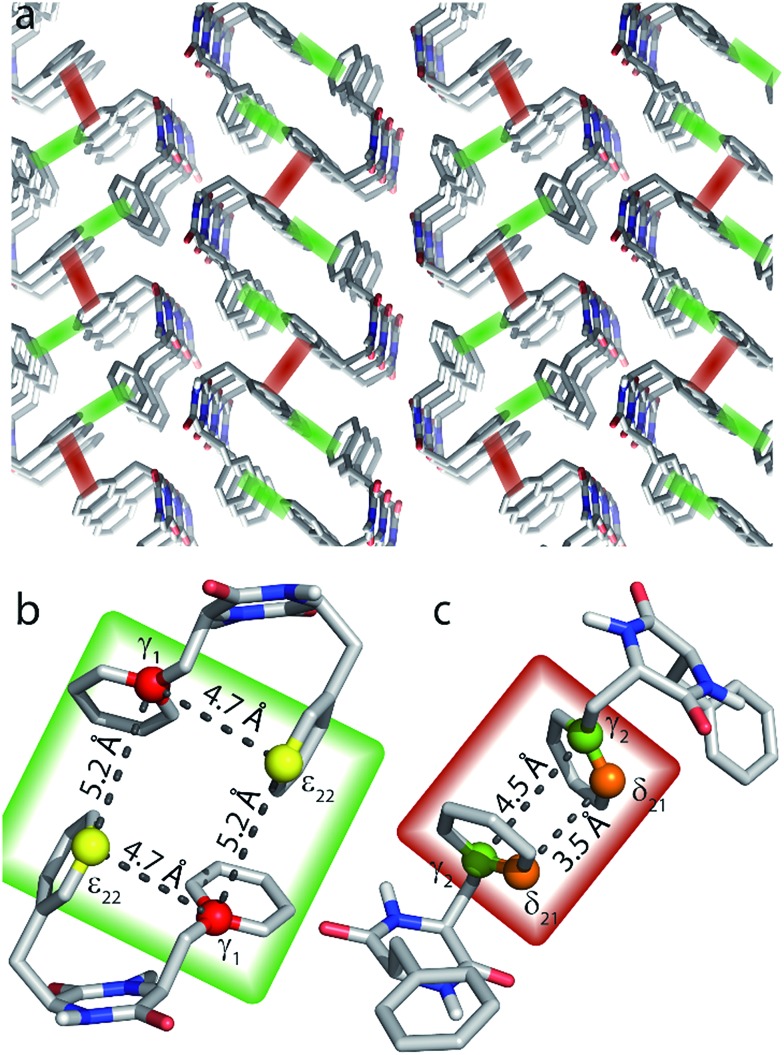
The capabilities of our approach are demonstrated on a self-assembled organic structure, with an emphasis on aromatic interactions. We focus on the cyclic diphenylalanine peptide (cyclo-FF, Fig. 1a) which self-assembles into nanotubes or nanowires.^13,14 Cyclo-FF nanowires possess semiconducting properties and strong blue fluorescence,¹⁴ and surface coating with cyclo-FF nanotubes can provide highly hydrophobic self-cleaning surfaces, ultra-capacitors for energy storage, and microfluidic chips.¹³ Apart from hydrogen bonding between the backbone amides, aromatic interactions between the phenyl rings are the main driving forces in cyclo-FF self-assembly, with both parallel and perpendicular π-stacking occurring.^14,15 In addition to this structure determining function, aromatic moieties often constitute the main functional part of molecular assemblies, owing to the possibilities of energy and charge transport through their π-systems.^16–19 Therefore, probing π-stacking interactions is of high interest. Numerous ssNMR studies have been discussed in the literature which rely on probing the aromatic proton spins.^20,21 Here we show an alternative powerful approach based on the observation of π-stacking through ¹³C–¹³C correlation spectra.

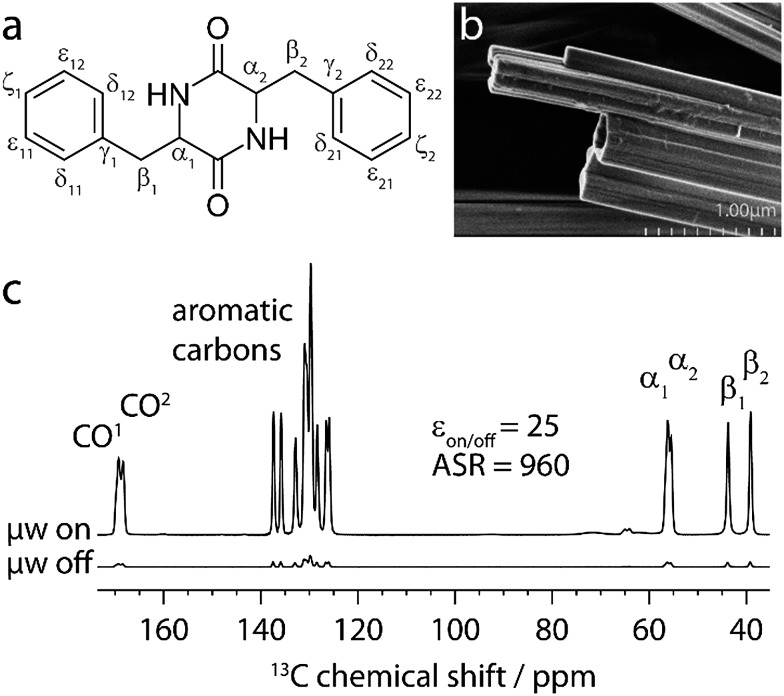
Fig. 1. (a) Chemical structure of cyclo-FF. (b) Scanning electron microscopy image of cyclo-FF nanotubes. (c) ¹³C CPMAS spectra of cyclo-FF with and without microwave (μw) irradiation. ε _on/off describes the ratio of peak heights of the two spectra. The ASR is the ratio of the signal-to-noise per unit square root of time between the spectrum recorded with μw irradiation and a CPMAS spectrum taken in a conventional ssNMR experiment.

The experiments presented here were also made possible by the use of the dipolar recoupling pulse sequences S₃ and [S₃] (“bracketed S₃”),^22,23 which facilitate the recoupling of carbons with large chemical shift anisotropy (CSA), such as carbonyl and aromatic carbons. Based on this, we achieved well-resolved ¹³C–¹³C dipolar correlation spectra of aromatic carbons, and polarization transfer dynamics that can be completely rationalized by numerical simulation. Contributions from numerous intermolecular contacts and notably several π-stacking interactions were detected. We discuss the information content of the polarization transfer curves and corresponding treatment as the superposition of intra- and/or intermolecular spin pair contributions. Furthermore, the limits for neglecting dipolar truncation for ¹³C at NA are examined. The data and the in-depth analysis provided here demonstrate the benefits of working with ¹³C at its NA. Taking all factors into account, we show that these experiments are sensitive to distances up to ∼7 Å for cyclo-FF, which is supported by the excellent agreement of experimental data with simulated polarization transfers based on the crystal structure.

Experimental

DNP sample preparation of cyclo-FF

All chemicals were purchased from Sigma-Aldrich and used without further purification, unless otherwise stated. The cyclo-FF DNP sample was prepared by adapting the existing protocol:⁶ cyclo-FF powder (20 mg, Bachem, Weil am Rhein, Germany) was dissolved under gentle heating in hexafluoroisopropanol (750 μl). The solution was added dropwise and under continuous sonication to a solution of AMUPol²⁴ (0.3 mg, SATT Sud Est, Marseille, France), trehalose dihydrate (0.5 mg) and D₈-glycerol (2 mg) in D₂O (2.5 ml) and D₄-methanol (0.5 ml), causing instant precipitation of cyclo-FF nanotubes. The mixture was transferred into a Petri dish and dried slowly under reduced pressure, while repeatedly stirring it with a spatula. After sufficient drying time (10–13 h), a wet paste was obtained and packed into a 3.2 mm thin-wall zirconia rotor. This process was repeated once more to fill up the rotor. It was observed that the slow drying process and the retaining of moisture at all times are beneficial for optimal MAS-DNP sensitivity.

DNP-enhanced ssNMR experiments

The experiments were performed on a wide-bore AVIII 400 MHz (¹H Larmor frequency) Bruker DNP-NMR spectrometer equipped with a 263 GHz gyrotron, a μw transmission line and a low temperature 3.2 mm MAS-DNP probe in double-resonance mode operating at ∼105 K. All spectra were recorded at a MAS frequency of 13.889 kHz with a recycle delay of 6.5 s. More details on the experimental conditions and data extraction can be found in the ESI.†

Simulation of polarization buildup curves

All simulations were done using the SPINEVOLUTION package.²⁵ The atomic coordinates were taken from the X-ray structure of cyclo-FF,¹⁵ and the CSA tensors (ESI Table S1†) were calculated using DFT-GIPAW, except the isotropic chemical shifts which were taken from experimental data. The simulations were done with the ZCW^26–28 scheme of powder averaging with 233 pairs (α and β angles) of crystal orientations each averaged over 48 γ-angles.

DFT-GIPAW

Quantum chemical calculations on the cyclo-FF crystal structure were run using the planewave pseudopotential approach, with the gauge including projector augmented wave (GIPAW) method²⁹ for computation of CSA tensors. The calculations were performed with the PWSCF module version 5.2.1, and GIPAW version 5.1. within the Quantum ESPRESSO package.³⁰ Norm-conserving pseudopotentials of the Troullier–Martins type³¹ were used for all atoms, employing the PBE exchange–correlation functional.^32,33 The crystal structure of cyclo-FF¹⁵ was used as an initial input, and hydrogen positions were optimized prior to GIPAW calculations. A planewave cutoff energy of 96 Ry, and a 2 × 2 × 2 Monkhorst–Pack k-point grid³⁴ were used. The results are summarized in the ESI (Table S1†) and were used as an input in SPINEVOLUTION simulations.

Optimization of the molecular structure

TINKER molecular modeling software package³⁵ version 7.1 was used for scanning the potential energy surface and ORCA³⁶ version 3.0.2 was used for geometry optimization and computation of ¹³C CSA tensors. Computational details are given in the ESI.†

Results and discussion

Experimental challenges and strategies

MAS-DNP can enhance the sensitivity of ssNMR experiments by transferring polarization from unpaired electron spins to atomic nuclei using high-power high-frequency microwave irradiation.^37–39 In recent years, it has enabled numerous experiments that were unfeasible with standard high-field NMR systems, such as the acquisition of signals from diluted species as well as nuclei with low gyromagnetic ratio and/or low NA.^40–47 In addition, advanced experiments probing ¹³C–¹³C and ¹⁵N–¹³C proximities through 2D correlation spectra recorded at NA are within reach.^5,7,8,10

In this context, important steps have been taken towards 3D (supramolecular) structure determination at NA with the help of DNP. Takahashi et al. reported for the first time the detection of NA intermolecular ¹³C–¹³C cross peaks.⁶ Later, Mollica et al. recorded double quantum (DQ) buildup curves, which were shown to be sensitive to intermolecular distances and allowed the identification of the correct crystal structure among a set of proposed structures.¹⁰ In parallel to their work, we also advanced further towards structure determination, and specifically focus in this paper on the potential of extracting internuclear distances from dipolar recoupling experiments.

The DNP process requires sample preparation that ensures a uniform distribution of the polarizing agent.⁴⁸ We have recently introduced an efficient, matrix-free (MF) protocol for the preparation of cyclo-FF for DNP.⁶ It is a solution-based method where nanotubes are formed in the presence of the biradical polarizing agent. This protocol was developed because direct impregnation of cyclo-FF powder with a radical-containing solution does not lead to an efficient DNP process. For experiments presented in this work, we followed the MF protocol, and improved the NMR sensitivity by replacing the previously employed polarizing agent with the AMUPol biradical.²⁴

The ¹H–¹³C cross-polarization (CP) MAS spectra of cyclo-FF with and without microwave irradiation are shown in Fig. 1c. The improved sample preparation results in a higher DNP enhancement (ε _on/off = 25), and more importantly an increased Absolute Sensitivity Ratio (ASR = 960)⁵ as compared to the sample used previously (8.8, and 390, respectively). The improved ASR (sensitivity ratio between 100 K DNP and conventional room temperature (RT) experiments) signifies that experiments can be run six times faster than before, which was already 5 orders of magnitude faster than when using conventional ssNMR. Note that the ASR is very high in this case because of the long ¹H T ₁ relaxation time of cyclo-FF at RT (¹H T ₁ > 600 s),⁶ but that the approach presented here would also be possible on powdered samples with a smaller ASR, combined with a shorter ¹H T ₁ at RT (e.g. ASR ∼ 10, ¹H T ₁ ∼ 3 s).

Measuring distances between ¹³C nuclei using ssNMR can be achieved through the use of specific radiofrequency (RF) pulse sequences, such as dipolar recoupling sequences.¹² Since the dipolar coupling between two spins is inversely proportional to the cube of the distance between them, distances can be extracted from plots of the buildup of transferred polarization as a function of increasing recoupling times.

In the context of dipolar recoupling, the characterization of aromatic systems is particularly challenging because of the large CSA of their ¹³C nuclei (up to 200 ppm), which is significantly larger than that of most other ¹³C moieties.⁴⁹ Since the efficiency of most recoupling pulse sequences decreases dramatically in the presence of large CSA (see ESI Fig. S3†), we chose the S₃ and [S₃] pulse sequences, which were recently developed by Edén and coworkers, and are robust to high CSA values.^22,23 These sequences were originally designed for the very fast MAS regime (ν _r ≥ 60 kHz) where they work without additional ¹H decoupling.²² They were later shown to also be efficient in the moderate spinning regime, if the spinning frequencies are considerably larger than the strength of the CSA (ν _r ≥ 1.5ν _CSA) and high power ¹H decoupling is applied.²³ Considering the CSAs of aromatic carbons (up to ∼20 kHz at 9.4 T) and the available spinning frequencies of our commercial DNP setup (max. 14 kHz), these conditions are by far not met here. Despite this, we show that efficient polarization transfer involving aromatic spins can be achieved with S₃ and [S₃] under DNP conditions. As an additional benefit, these pulse sequences have very low RF power requirements (ν _nut = ν _r/2). Therefore, they allow long recoupling times without any detrimental effects on the hardware, which is mandatory for observation of long distance contacts. This also means that the recoupling bandwidth is limited to ∼7 kHz under our experimental conditions (ν _r = 13 889 Hz), which is however sufficient for the studies reported herein at 9.4 T.

In ¹³C–¹³C dipolar recoupling experiments performed on samples at NA, only a small part of the detected signal comes from polarization transfer in ¹³C–¹³C spin pairs. The dominating but undesired part originates from uncoupled ¹³C spins and has to be suppressed, either by the use of selective pulses or by a double quantum filter (DQF). Taking this into account, two complementary experimental strategies for recording polarization buildup curves and extracting structural information are employed. The first one makes use of selective pulses, such that the buildups can be recorded from a series of 1D spectra. This offers the advantage of very short experimental times. In the second, more traditional strategy, a series of DQF 2D double quantum-single quantum (DQ-SQ) correlation spectra is recorded. This (time-consuming) approach is preferred when the involved spins have similar isotropic chemical shifts, such that selective pulses cannot be conveniently applied. This was for instance the case for recoupling experiments between aromatic carbons. In the following sections, we will present and analyze in detail both experimental approaches on cyclo-FF.

The 1D approach: results and discussion

Experimental results

The position of the aromatic rings with respect to the central diketopiperazine ring gives important information on the conformation of the cyclo-FF molecule. We therefore chose to probe distances from the two carbonyls to the aromatic carbons, employing selective pulses for the acquisition of a series of 1D spectra as described above. The isotropic chemical shifts of the carbonyls are well enough separated from the aromatics to allow the use of selective pulses, but are still within 5 kHz, which can be covered by the bandwidths of S₃ and [S₃].

The pulse sequence used in the experiment is shown in Fig. 2a. After an initial CP step from DNP-enhanced protons to carbons, the CO magnetization is selectively flipped back to the z-axis from the transverse plane. During the following recoupling period, this magnetization is transferred to aromatic carbons, using the dipolar recoupling sequence [S₃]. After a selective readout pulse on the aromatics, their magnetization is detected.

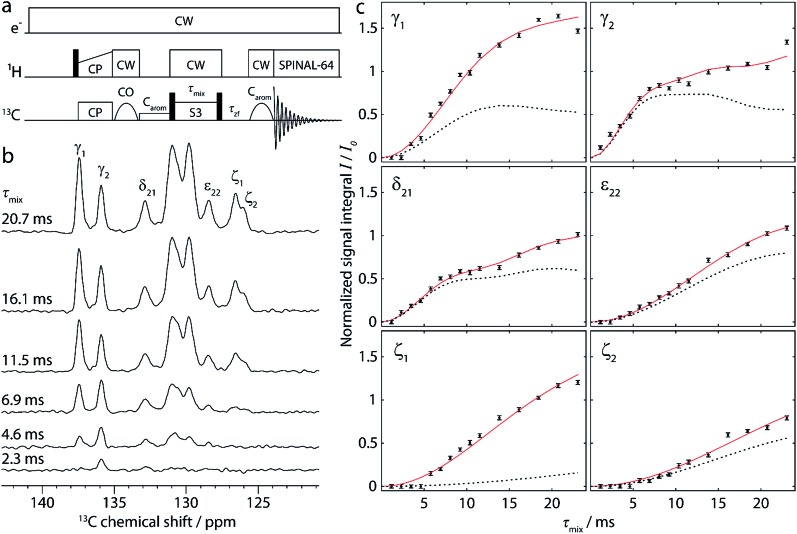
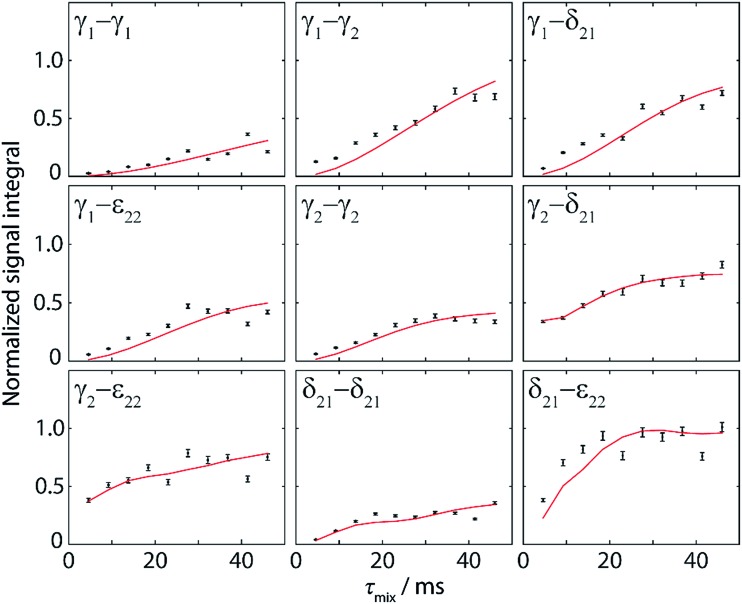
Fig. 2. (a) Pulse sequence for the 1D approach, used to obtain buildup curves for polarization transfer from carbonyl to aromatic carbons. [S₃] is employed as the dipolar recoupling sequence, with the π/2 bracketing pulses indicated as black bars on the ¹³C channel. The recoupling time (τ _mix) is incremented to record the buildup curves. More details are given in the text. (b) Aromatic region of selected 1D spectra, recorded on cyclo-FF with the pulse sequence shown in (a) using different recoupling times τ _mix, as indicated in the figure. (c) Full experimental polarization buildups (black points) for the six peaks labeled in (b). Error bars denote the average noise integral over 2 ppm. Red solid and black dotted lines show the SPINEVOLUTION simulations of the buildups based on the cyclo-FF crystal structure,¹⁵ respectively taking into account all distances up to 7 Å (red) or intramolecular distances only (black). The simulated curves are fitted to experimental points with the amplitude factor A (see Table 1). Note that the experimental signal integral (I) is normalized with respect to the initial polarization of CO spins (I ₀) in such a way that the initial available polarization in a particular ¹³CO–¹³C_arom spin pair is 1 (more details in the ESI†). This allows a direct comparison to the output of numerical simulations (the amplitude factor A is expected to be close to 1).

The pulse sequence allows a straightforward measurement of polarization buildup on the aromatic carbons by following their signal intensity as a function of the incremented recoupling period. Due to the CO-selective excitation pulse (followed in addition by a selective saturation pulse on aromatics), no magnetization is present on the aromatics at the beginning of the recoupling period. The selective pulse on the aromatics after recoupling ensures that the large magnetization of uncoupled CO spins remains along the z-axis and does not perturb the detection of the much smaller aromatic signals. This avoids the use of a DQF, which would decrease the sensitivity of the experiment by a factor of 2. It should be noted that this advantage can only be taken for pure double-quantum (e.g. [S₃]) recoupling sequences. Sequences like S₃, which contain both ZQ and DQ terms, would require the use of a DQF for the observation of polarization transfer. Overall, the 1D approach benefits from immensely decreased experimental times compared to the acquisition of DQF 2D spectra. In addition, data extraction by deconvolution and integration of 1D spectra is relatively straightforward.

A selection of 1D spectra acquired with the sequence of Fig. 2a using different recoupling times (τ _mix) is presented in Fig. 2b. The full dataset, consisting of 15 1D spectra, was recorded in ∼7 h, corresponding to only 28 min per spectrum. From each spectrum, the integrals of six peaks (Cγ₁, Cγ₂, Cδ₂₁, Cε₂₂, Cζ₁, and Cζ₂) were extracted after deconvolution. The large central peaks (128–126 ppm) could not be reliably deconvoluted due to the contributions of too many carbons (Cδ₁, Cδ₂₂, Cε₁, and Cε₂₁).

Fig. 2c shows the resulting polarization buildup curves for the six peaks (black points). They are normalized with respect to the initial polarization on the carbonyls, taking into account the number of COs per molecule and the fraction of them which is coupled to another ¹³C spin (1.1%, see ESI for more details†). As a result, the y-axes in Fig. 2c reflect the absolute transferred polarization and can thus be directly compared to numerical simulations.

All buildup curves display polarization transfer efficiencies far above the expected maximum for a single spin pair under these conditions (∼0.38 in numerical simulations). This is a clear indicator that various spin pairs contribute additively to each buildup curve. For instance, both CO¹ and CO² can provide polarization because they are excited simultaneously. Thus, two different intramolecular polarization transfer pathways are possible for each peak, and the sum of their contributions can give rise to a maximum polarization of ∼0.76. This number is still exceeded in the majority of cases, which indicates that intermolecular distances contribute as well (discussed in more detail below).

The six experimental buildup curves possess distinctly different features. For instance, while most peaks build up continuously, the Cγ₂ and Cδ₂₁ signal intensities slightly level out before rising again. Moreover, the Cγ₂ peak has a faster initial buildup, most probably indicating the presence of a very short CO-Cγ₂ distance compared to all other distance contributions here. The Cγ₁ peak, on the other hand, has a slower initial buildup, but rises to higher intensity at longer mixing times, suggesting a higher total number of distances involved in the buildup.

The reason for the additive contribution of distances to the buildup curves lies in the NA nature of the sample. Nearly all ¹³C–¹³C spin pairs are isolated (surrounded by ¹²C), such that the polarization transfer between them is not detrimentally affected by the presence of a third ¹³C spin, even over longer distances. In addition, all different kinds of spin pairs are randomly distributed in the sample. Each spin pair leads to a typical polarization buildup depending on the internuclear distance, and it is the addition of these individual contributions that yields the experimentally observed buildups. Similar observations have been reported by Brouwer et al. in the process of structure determination of zeolites, where they probed the slightly more abundant ²⁹Si spins.^50,51

Overall, the buildup curves contain a high level of information. As described above, some qualitative information is already accessible from a relative comparison between the different curves. However, the extraction of quantitative distance information requires the use of numerical simulations for comparison and fitting.

Numerical simulations

In order to relate the experimental polarization buildup curves to the crystal structure and evaluate their consistency, the expected polarization buildups were simulated numerically with SPINEVOLUTION,²⁵ taking into account the known distances from the crystal structure of cyclo-FF.¹⁵

As a first step, the behavior of S₃ and [S₃] under the experimental conditions employed here was investigated in more detail, since these conditions do not comply with the recommended regime (ν _r < ν _CSA instead of ν _r ≥ 1.5ν _CSA).²³ Numerical simulations (see ESI Fig. S4 and S5†) show that polarization can still be transferred efficiently with S₃ and [S₃] under our experimental conditions. However, the buildup curves for [S₃] exhibit a strong dependency on all CSA parameters. More precisely, the asymmetry and anisotropy affect the overall polarization transfer amplitude, without having a major influence on the shape of the curve. On the other hand, a change of the orientation of the principal axes of the CSA tensor can change this shape significantly. To run accurate simulations, the magnitudes and orientations of the ¹³C CSA tensors of cyclo-FF were computed with the gauge-including projector-augmented wave (GIPAW)²⁹ approach, using its implementation in the Quantum ESPRESSO³⁰ software package. The crystal structure of cyclo-FF¹⁵ served as the initial input for the DFT calculations, and hydrogen atom positions were optimized before the GIPAW calculations.

The expected polarization buildups were then simulated with SPINEVOLUTION, based on the CSA tensor parameters from the DFT computations, atomic positions from the crystal structure, and isotropic chemical shifts from the experiment. The polarization buildups for all relevant spin pairs were simulated separately, and the individual curves were then co-added for each peak. It is important to stress again that, although several different distances contribute to each buildup curve, we consider these contributions to be coming from isolated spin pairs. Deviations from this approximation by the presence of a third spin leading to dipolar truncation at NA will be discussed later in this paper.

Notably, our concept of data analysis differs from those employed previously in similar contexts of ¹³C–¹³C¹⁰ or ²⁹Si–²⁹Si⁵¹ recoupling experiments at NA, which rely on analytical functions to describe polarization transfers. We instead chose to use numerical simulations, since they can easily account for, among other things, isotropic and anisotropic chemical shift effects.

Intra- and intermolecular contributions

In a first approximation, the experimental data was compared to simulated buildup curves that take into account only intramolecular spin pairs. These intramolecular distances are shown as bold italic in Table 1, and the corresponding simulations are shown as dotted lines in Fig. 2c. Each simulated curve represents the sum of two contributions, as in our case polarization transfer to an aromatic carbon can originate from CO¹ or CO². The intramolecular distances are generally the shortest distance contributions to the experimental buildup curves, except for the Cζ₁ peak. Consequently, the initial polarization buildups are mainly determined by those, as evident from Fig. 2c. At the same time, however, all experimental buildups deviate from the simulations at longer mixing times, which highlights the contribution of intermolecular contacts.

Table 1. Distances from CO¹ and CO² to surrounding aromatic carbons up to a limit of 7 Å (ref. 15).

	Cγ1	Cγ2	Cδ21	Cε22	Cζ1	Cζ2
Distances from CO1/Å a	3.8	3.7	4.6	4.5	4.3	5.3
	4.9	6.0	5.9		5.1	6.9
	5.3	6.5			6.5
	5.5				6.8
					6.9
Distances from CO2/Å a	4.2	3.0	3.3	5.0	4.9	5.1
	4.2	5.3	6.5	5.5	5.4	6.3
	6.5		6.7		6.4	6.8
					6.5
					6.5
Total number of distances	7	5	5	3	10	5
A b	0.88	1.14	0.91	1.15	0.73	0.97
RMSD	0.07	0.06	0.03	0.02	0.05	0.04

^aIntramolecular distances are shown as bold italic.

^bFactor for scaling the amplitude of the simulated curves to experimental data as used in Fig. 2c, obtained by minimizing the root mean square deviation (RMSD) between experiment and simulation.

The extent of this deviation can be rationalized by the number and magnitude of intermolecular distances, which are listed up to a limit of 7 Å in Table 1. For example, the experimental data for the Cγ₁ peak starts to deviate significantly from the simulation for intramolecular distances at mixing times as short as ∼6 ms, and rises to more than three times the simulated intensity. This can be explained by the high number of comparably short intermolecular distances (four distances ≤ 5.5 Å). The Cζ₁ buildup shows an even more drastic deviation, which results from the fact that the intramolecular distances here are very long (6.4 and 6.5 Å) compared to other distances. The buildup curve of Cζ₁ is therefore almost exclusively determined by intermolecular spin pairs. Deviations between intramolecular simulations and experimental data are less pronounced for the other four peaks, since there the intramolecular spin pairs represent the two shortest distance contributions, separated from the next longer ones by at least 0.5 Å.

This comparison shows that the inclusion of intermolecular spin pairs into the simulation is essential for a thorough explanation of the polarization buildup curves. To obtain more accurate simulated curves, all distances in Table 1 were taken into account. The amplitudes of the calculated curves were adjusted to the experimental points by fitting an individual amplitude factor A for each curve (I _exp = A × I _sim). The results of the full simulations, including scaling by A, are shown as red lines in Fig. 2c. The optimized amplitude factors A with corresponding RMSD values are summarized in Table 1.

The full simulation is in excellent agreement with the experimental data. Notably, no systematic deviation at longer mixing time is observed, which would have indicated relaxation-related losses during the recoupling. Even small features like the changes in slope for Cγ₂ and Cδ₂₁ are reproduced by simulation. Furthermore, all amplitude scaling factors lie between 0.7 and 1.2, which is reasonably close to the theoretically expected value of 1 (see also next section). This indicates that it is indeed possible to directly relate experimental data to the polarization transfer efficiency. This constitutes a big advantage, as precious information on the approximate number of distances contributing to a buildup curve can be extracted. Furthermore, the fact that the experiments are clearly sensitive to intermolecular contacts is highly encouraging, as these are imperative for supramolecular structure elucidation.

Dipolar truncation effects at NA

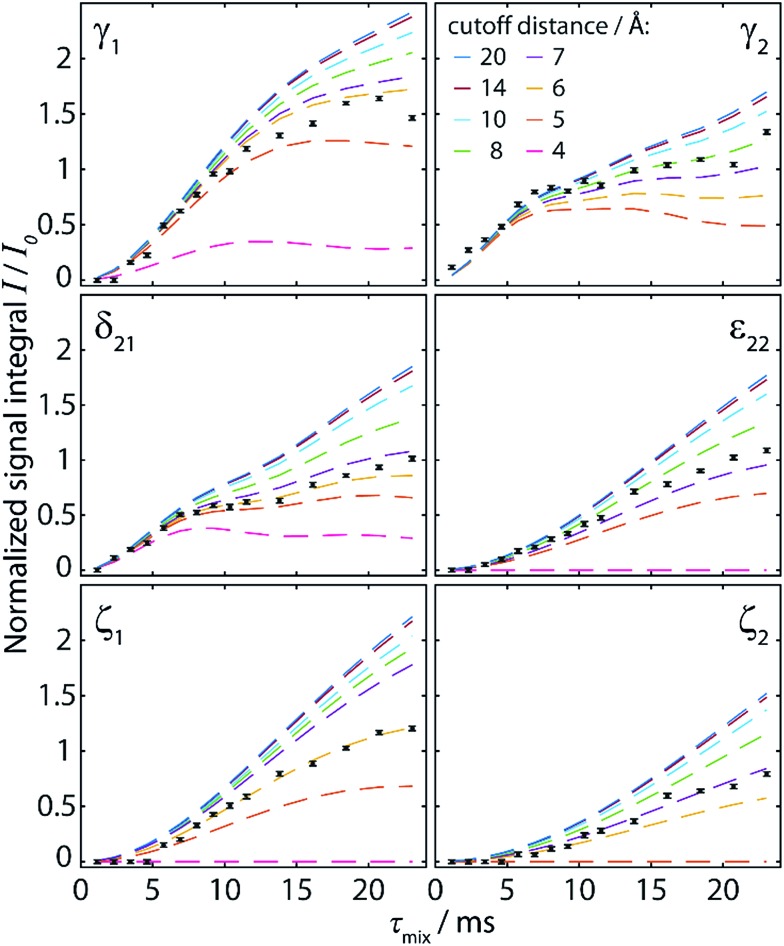
In order to investigate the origin of the small deviations of A from unity reported in Table 1, we simulated buildup curves which take into account the cumulative contribution of all ¹³C spin pairs falling below increasing cutoff distances from 4 Å to 20 Å. These simulations are shown as dashed lines in Fig. 3 without any scaling (A = 1.0) in order to allow direct comparison to experimental points. For the considered range of mixing times (up to 25 ms), the simulated buildup curves keep rising to higher intensities upon the inclusion of longer distances up to ∼14 Å. This appears surprising since the polarization transfer under [S₃] for a single 14 Å distance within 25 ms recoupling time is negligibly small. However, the number of possible spin pairs at such long internuclear distances becomes so high that their cumulative contribution gets significant (e.g. for cyclo-FF there are about 30–40 different spin pairs whose distances lie between 10 and 14 Å for a total of 60–70 distances below 14 Å).

Fig. 3. Simulated polarization buildup curves (dashed lines) for the experiment shown in Fig. 2, taking into account the cumulative contribution of all spin pairs whose internuclear distance lies below a cutoff distance increased from 4 Å to 20 Å. The y-axis corresponds to the absolute transferred polarization, and no scaling has been applied to the simulated curves. Experimental points (black points) are identical to those given in Fig. 2c, including normalization with respect to the CO polarization.

A re-evaluation of potential dipolar truncation effects at the NA of ¹³C becomes necessary when considering the possibility of observing such long distance polarization transfers. To this end, we need to estimate the probability of finding a third ¹³C spin in a defined volume around the respective ¹³C–¹³C two-spin system, which is demarcated by their internuclear distance. At the NA of ¹³C, this probability is n _C × 1.1%, with n _C being the number of carbon atoms in the considered volume. Accordingly, the polarization transfer efficiency is expected to be lowered by this percentage. The effect increases with the number of atoms in the volume, and thus with the internuclear distance for the considered polarization transfer. Hence, no polarization transfer can statistically be observed between two spins which are at such a distance that the corresponding volume around the spin pair contains 91 carbons or more, as there will always be a third ¹³C spin truncating the desired transfer. An exact definition of the “truncating” volume is beyond the scope of this paper, and this crude model also does not consider cases in which polarization transfer is only partially truncated. Nevertheless, from the crystal structure of cyclo-FF, the limit of ∼100 carbon atoms is found within a sphere of radius 8 Å. It is therefore very unlikely that polarization transfers over this distance can be observed in cyclo-FF, even with considerably longer mixing times. This illustrates the limits of the idealized two-spin system model used here to rationalize polarization transfer in NA samples.

Comparison of experimental data (black points in Fig. 3) with the simulated polarization buildup curves for different cutoff distances confirms this crude approximation. Indeed, most of the experimental points for the 6 different polarization buildups lie between the corresponding simulated buildup curves with 6 and 8 Å cutoff distance. In addition, it should be noted that for cutoff distances higher than 7 Å, the shape of the simulated buildup curves does not change significantly anymore, but only their amplitude increases. This finding supports our strategy of including only distances up to 7 Å in the simulations used to characterize the experimental buildups. With this procedure, the shape of the buildup curves can be modelled correctly, using solely an amplitude factor (A) to then fit the simulations to the experimental points. This factor, which should theoretically be unity, takes into account deviations owing to some longer distance transfers, partial dipolar truncation, and the influence of experimental errors and/or instabilities. The different number and distribution of long-distance contributions for each peak also justifies the use of different amplitude factors as opposed to other reported fitting procedures which use a global amplitude factor.^10,51 In the case of cyclo-FF, our fitting procedure exclusively returns well defined amplitude factors close to 1 (see Table 1), which confirms the validity of our approach. A more detailed discussion of the behavior of A and the RMSD with increasing cutoff distances can be found in the ESI.†

The 2D approach: results and discussion

Aromatic–aromatic 2D correlation spectra

Besides the 1D approach illustrated above, the more traditional way for recording polarization buildup curves is the acquisition of a series of DQF 2D correlation spectra, which is the second experimental strategy we present in this article. As the observation of π–π interactions is a particularly interesting challenge, this 2D approach will be demonstrated on correlation spectra between aromatic carbons. Their small isotropic chemical shift range (∼15 ppm) makes their analysis by the 1D approach difficult, and hence the acquisition of 2D spectra inevitable.

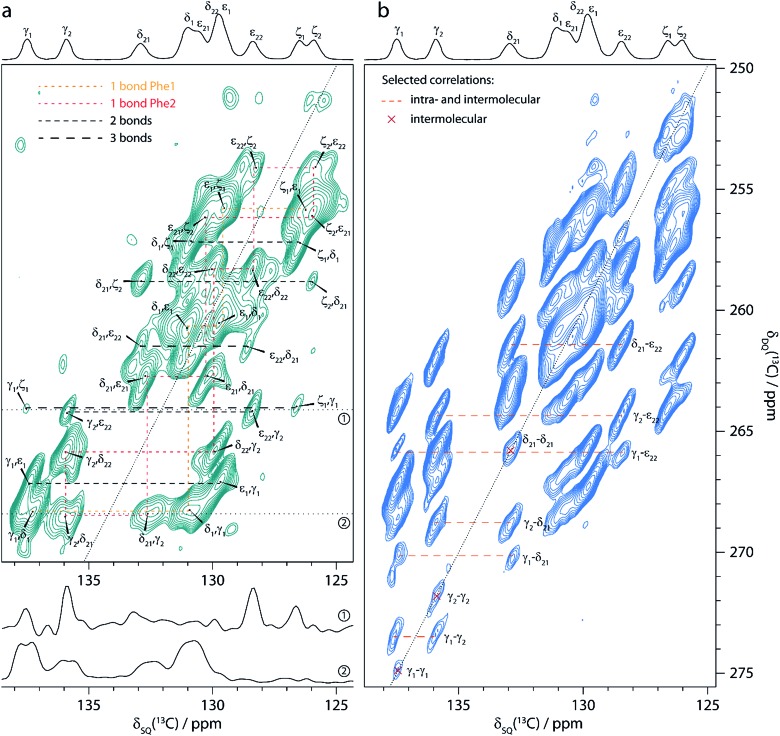
Accordingly, we recorded ¹³C–¹³C DQ-SQ correlation spectra of cyclo-FF, focusing specifically on the aromatic region. Owing to its excellent CSA compensating properties, S₃ was employed as the dipolar recoupling sequence. Fig. 4 shows two of the spectra obtained, using total recoupling times of 2.3 ms (a) and 13.8 ms (b). Nicely resolved correlations among aromatic carbons are observed, highlighting the excellent performance of S₃ for recoupling carbons with large CSA. The spectra presented here are the first ¹³C–¹³C dipolar correlation spectra showing such well-resolved correlations between aromatic carbons.

Fig. 4. Aromatic region of ¹³C–¹³C DQ-SQ correlation spectra of cyclo-FF, obtained with the dipolar recoupling sequence S₃ applied during total recoupling times (DQ excitation plus reconversion) of 2.3 ms (a) and 13.8 ms (b). The spectra were recorded in ∼18.5 h (a) and ∼7.4 h (b), respectively. ¹³C CPMAS spectra are shown above for illustrative purposes. Note the overlapping δ₁ and ε₁ resonances of one of the phenyl rings compared to the resolved resonances (δ₂₁, δ₂₂, ε₂₁ and ε₂₂) for the second ring. The up- and downfield shifts of ε₂₂ and δ₂₁, respectively, are signs of intermolecular interactions, in this case of parallel π-stacking.^6,15 Cross sections along the black dotted lines (δ _DQ = 264.1 ppm and δ _DQ = 268.5 ppm) in (a) are displayed below and show the narrowing of linewidths for long distance peaks (upper cross section, linewidths 40–50 Hz) compared to cross-peaks arising from directly bonded carbons (lower cross section, linewidths > 100 Hz). Resolved cross-peaks used for the buildup analysis (see Fig. 5) are labeled in (b). Among them, select pure intermolecular peaks are marked by a red cross, and select peaks resulting from intra- and intermolecular contributions are connected with an orange dashed line.

The spectrum in Fig. 4a was acquired with the shortest possible mixing time, using one S₃ block for DQ excitation and reconversion each (2.3 ms in total), and contains mainly one-bond correlations. It can thus be used for complete assignment of all aromatic resonances as illustrated in the figure. In addition, correlation peaks of lower intensity can be observed, which arise from polarization transfers over distances corresponding to two or three bonds within one phenyl ring.

The spectrum acquired with a longer mixing time (13.8 ms, Fig. 4b) looks remarkably different from the previous one. Numerous additional peaks can be observed, e.g. between the Cγ resonances. They arise from long distance correlations, occurring between carbons from different phenyl rings. Notably, the Cγ₁–Cγ₁ cross-peak demonstrates that polarization transfers over distances of more than 6 Å can be observed (shortest distance between two Cγ₁ atoms is 6.2 Å, see Table 2). Moreover, this peak is one of several autocorrelation cross-peaks appearing on the DQ diagonal. As a DQF was implemented in the pulse sequence, they have to originate exclusively from intermolecular correlations, which makes them particularly valuable for the investigation of the supramolecular assembly.

Table 2. Distances between selected aromatic carbons up to a limit of 7 Å (ref. 15).

	Cγ1–Cγ1 a	Cγ1–Cγ2	Cγ1–Cδ21	Cγ1–Cε22	Cγ2–Cγ2 a	Cγ2–Cδ21	Cγ2–Cε22	Cδ21–Cδ21 a	Cδ21–Cε22
Distances/Å b	6.2	4.9	4.7	4.7	4.5	1.4	2.4	3.5	2.8
	6.2	6.2	6.0	5.2	6.2	4.2	4.5	6.2	4.2
	6.6	6.6	6.4	5.4	6.2	5.0	5.5	6.2	4.7
		6.8		5.8		6.4	6.7		5.7
		6.9
Total number of distances per molecule c	1.5	5	3	4	1.5	4	4	1.5	4
A d	1.55	1.45	1.37	0.61	1.61	0.78	0.98	1.08	0.93
RMSD	0.06	0.09	0.09	0.09	0.05	0.04	0.08	0.04	0.13

^aIntermolecular autocorrelation peaks.

^bIntramolecular distances are shown as bold italic.

^cDistances in autocorrelation peaks are counted as half for each molecule because they are “shared” between two molecules.

^dFactor for scaling the amplitude of the simulated curves to experimental data as used in Fig. 5, obtained by minimizing the RMSD between experiment and simulation.

Another striking difference between the two spectra in Fig. 4 is a splitting of some cross-peaks along the direct detection dimension, which is only observed at short mixing time. This splitting occurs for correlation peaks that correspond to a one-bond contact, and is caused by the ¹ J _CC-coupling between the two directly bonded carbons. Since the size of the ¹ J _CC-coupling (55–60 Hz for monosubstituted benzenes⁵²) is similar to the peak linewidths (40–60 Hz), it is barely resolved and clearly constitutes the limiting factor for resolution. It results in considerable line broadening and reduced signal-to-noise (S/N) ratios for one-bond cross-peaks. In NA samples, correlation peaks over longer distances are sharper (see cross sections in Fig. 4a) since the detected carbons mostly do not have a directly bonded ¹³C spin and the size of two-bond and longer-range J _CC-couplings is negligible compared to the ¹³C linewidths obtained here. At the same time, peaks which are split at short mixing time appear also sharper at longer mixing times (e.g. the Cγ₁–Cδ₂₁ correlation), as contributions of spin pairs with longer internuclear distances (and therefore free of ¹ J _CC-coupling) are becoming active. They benefit from increased S/N and readily dominate the spectrum.

The spectra presented here illustrate the advantages of NA measurements for the acquisition of 2D spectra. The drastically reduced dipolar truncation allows straightforward observation of long distance correlations, including exclusively intermolecular contacts which appear as diagonal peaks in DQF experiments. Moreover, all correlations except the ones between directly bonded carbons are free from ¹ J _CC-broadening, which can lead to improved resolution, as shown here. Considering these factors, it becomes evident that a spectrum with the resolution and intermolecular information content as shown in Fig. 4b would not be possible to record on a fully isotopically labeled sample.

Observation of π-stacking

For the investigation of π-stacking interactions, buildup curves for polarization transfer between aromatic carbons are required. For this purpose, a series of ten DQ-SQ correlation spectra was recorded in the same manner as the spectrum in Fig. 4b, using ten different recoupling times. Peak volumes for nine isolated correlation pairs (labeled in Fig. 4b) were then extracted with Monte-Carlo volume extraction after shearing of the spectra (see ESI for more details about processing of the spectra and peak volume extraction†).

These experimental points (black points) along with the simulated polarization buildup curves (red solid lines) are shown in Fig. 5 for the different spin pairs. In order to normalize the experimental data, we took the Cγ₂–Cε₂₂ and Cε₂₂–Cγ₂ cross-peaks at the first point of the buildup (2D spectrum at τ _mix = 4.6 ms) as reference points. They have the advantage of being free of one-bond J-coupling, and their summed volume (V ₁ + V ₂) corresponds to a two-bond distance transfer, which can be compared to the simulated expected transfer efficiency (S). The ratio S/(V ₁ + V ₂) was then taken as the normalization factor for all integrated intensities given as experimental points in Fig. 5. Notably, this procedure can be done without knowledge of the crystal structure, because the length of a two-bond distance in a phenyl ring is well-known.

Fig. 5. Normalized experimental (black points) and simulated (red lines) polarization buildup curves for aromatic–aromatic spin pairs in DQ-SQ correlation spectra. Experimental points were obtained from Monte-Carlo integration of 9 different cross-peak pairs as shown in Fig. 4b for ten mixing times ranging from 4.6 ms to 46 ms. Error bars indicate the error in volume extraction using the Monte-Carlo method. Normalization of the experimental points is explained in the text. The simulated curves take into account all distances up to 7 Å and are fitted to experimental points with an amplitude factor A (see Table 2).

Similar observations as in the 1D approach can be made for the buildup curves obtained from 2D spectra, with notably the contribution of multiple distances resulting in higher transferred intensities than the theoretical maximum for a single spin pair (∼0.21). In contrast to the buildup curves obtained with the 1D approach, several correlations here have contributions from distances shorter than 3 Å, originating from spin pairs within one phenyl ring (Cγ₂–Cδ₂₁, Cγ₂–Cε₂₂, and Cδ₂₁–Cε₂₂). Accordingly, their buildup curves start with high intensity at the first point (reflecting a fast initial buildup), whereas the transferred polarization for all other correlations is significantly lower at such a short mixing time.

For a better evaluation of the experimental data, full simulations of the expected polarization buildup curves were run with SPINEVOLUTION, in the same manner as for the 1D buildup curves. Accordingly, distances up to 7 Å were taken into account (summarized in Table 2). As for the 1D approach, the simulated data was fitted to the experimental points with the amplitude factor A. A good agreement between experiment and simulation is again obtained. The more complex nature of 2D experiments leads however to a lower accuracy when compared to the 1D approach, as revealed by higher RMSDs and larger deviations from unity for the amplitude factor A (see Table 2). This can be explained by the possibility of a direct normalization of 1D spectral intensities as well as by the simpler signal integration of 1D peaks. Moreover, the acquisition of the complete set of 2D spectra requires several days and is hence more susceptible to spectrometer instabilities.

Nevertheless, these experiments constitute a powerful approach for the investigation of π-stacking. It is clearly possible to observe correlations that arise from structurally important π–π interactions, which are illustrated in Fig. 6. For instance, the parallel π-stacking in cyclo-FF (Fig. 6c) is well described by the Cγ₂–Cγ₂ and the Cδ₂₁–Cδ₂₁ polarization buildup curves. Indeed, the distances describing this interaction are by far the shortest contributions and therefore dominate the buildup curves. For the perpendicular π-stacking, the involved Cγ₁–Cε₂₂ distances are illustrated in Fig. 6b, with the shortest distance being intramolecular (4.7 Å) and the next longer distance (5.2 Å) arising from the π–π interaction. This second example illustrates the strength and the challenges of our experiments. They are clearly sensitive to π–π contacts and can be used to probe π-stacking. On the other hand, however, it is challenging to distinguish the “relevant” π–π contacts from other contributions like intramolecular distances. In this respect, peaks on the diagonal are particularly interesting as they do not contain intramolecular contributions.

Fig. 6. (a) Crystal structure of cyclo-FF¹⁵ with perpendicular and parallel π–π interactions highlighted in green and red, respectively. (b and c) Close-up of perpendicular (b) and parallel (c) π-stacking. The highlighted distances can be probed by the 2D experiments presented in this paper. Note that the relevant carbon atoms and distances are highlighted for illustrational purposes on the same pair of cyclo-FF molecules. However in a sample at NA, it is highly unlikely to have four ¹³C isotopes occurring in only two cyclo-FF molecules. The highlighted distances contribute individually to the polarization transfer in different molecule pairs across the sample.

Perspectives in structure determination

After the thorough analysis and rationalization of polarization buildup curves based on the cyclo-FF crystal structure, we now focus on perspectives for the extraction of structural information in the case of an unknown structure. These considerations are based on the experimental approach described in this contribution, which is DNP-enhanced solid-state NMR on samples at NA. As a first step for structure determination of supramolecular systems, determination of the molecular conformation in the supramolecular structure is essential and will be discussed below. We will then move to the perspectives for de novo fitting of polarization buildup curves.

Determination of molecular conformation

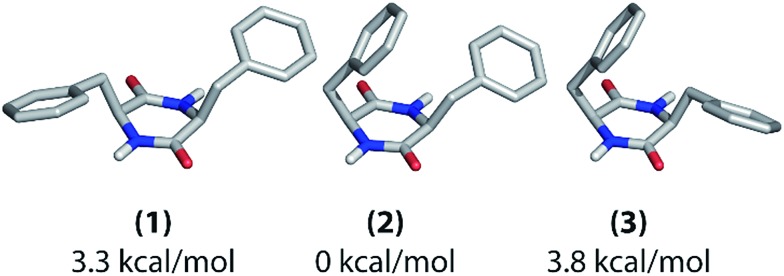
The fairly simple molecular structure of cyclo-FF allows a relatively straightforward optimization of its conformation by computational methods. This structural optimization and its evaluation in combination with NMR data are demonstrated in the following. A conformational search of the entire potential energy surface of an isolated cyclo-FF molecule was carried out using the software TINKER.³⁵ Six local minima were obtained whose geometries were then optimized with the molecular DFT software ORCA.³⁶ After optimization, the three lowest energy structures (Fig. 7) were regarded as possible molecular conformations of cyclo-FF in the nanotubes studied here. Their energies all lie within 4 kcal mol^–1, which is in the range of the energy of non-covalent interactions like hydrogen bonding or π-stacking.

Fig. 7. Possible molecular conformations of cyclo-FF as determined with computational structure optimization. Their relative energies with respect to (2) are given below the structures.

These three structures mainly differ in the positioning of the phenyl rings with respect to the central ring. In structure (1), they both point away from the central ring, whereas one of them is bent over it in the other two structures. In structure (2), the phenyl ring which points away is oriented towards the NH group of the central ring, whereas it is oriented towards the carbonyl group in structure (3). Overall, there are two asymmetric (2 and 3) and one nearly C ₂-symmetric structure (1). Structure (2) has the lowest energy in vacuum.

The different experimental chemical shifts for the two amino acids suggest that an asymmetric structure is present in the nanotubes, such as found in structures (2) and (3). The experimental 1D polarization buildup curves from carbonyl to aromatic carbons should be a suitable way for further probing the positioning of the phenyl rings. The buildups for the two Cγ and the two Cζ resonances, respectively, are clearly different from each other (Fig. 2), which again suggests the presence of structure (2) or (3) (see also ESI Fig. S7†). Discrimination between (2) and (3) should be possible based on the buildups of the Cγ peaks. As described before in this work, the shortest (and mostly intramolecular) distances determine the initial slope of the polarization buildup curves. When considering the shortest CO–Cγ₁ and CO–Cγ₂ distance, respectively, one can see that they are considerably different in structure (2) (3.9 and 3.0 Å), but of comparable length in structure (3) (3.2 and 3.1 Å). Experimentally, the initial buildups for both peaks are clearly different (Fig. 2b and c), which infers the presence of structure (2) in the solid state. This is also illustrated in Fig. S7† (top panels) where experimental data and intramolecular simulations for the three candidate structures are compared, and the best agreement at short mixing times is obtained for structure (2).

In brief, all these experimental observations and the calculated energy are consistent with a conformation very similar to structure (2) being present in the cyclo-FF self-assembled nanotubes, which is confirmed by its crystal structure. It should be kept in mind, however, that the computational structural search and optimization have been performed on a single molecule in vacuum. Intermolecular interactions were not taken into account, which could potentially change the energetic situation. Despite that, the described method leads to the globally correct structure of cyclo-FF, also signifying that the geometry of the assembly is mainly determined internally on the molecular level.

The example of cyclo-FF shows that the combination of NMR and computational methods can already give an idea of the molecular conformation and provide a valuable entry point for further structural investigations of the supramolecular assembly. The precise methodology of how to model the molecular structure will have to be adjusted to the molecule under investigation, e.g. depending on its size and rigidity/flexibility, and may require more experimental input than shown here.

De novo fitting of polarization buildup curves

For full structural studies of self-assembled systems, we expect internuclear distance measurements to play a key role. The quality of the data presented here demonstrates great potential towards this goal in NA samples. Still, a few limitations have to be kept in mind.

The strong CSA orientation dependency of the S₃ and [S₃] sequences (see ESI Fig. S4 and S5†) constitutes a restriction when investigating carbons with a large CSA. Even though the polarization buildup for most orientations does not vary much around an average curve, the occurrence of extreme cases can never be ruled out. Faster spinning would help in this regard, as it decreases the CSA dependency of the polarization transfer and also increases the bandwidth of the sequences. Although the current commercial DNP-NMR system does not allow for faster spinning, technical solutions are under development, such as faster sample spinning with cryogenic helium gas^53,54 or the use of smaller rotor diameter MAS-DNP probes.⁵⁵ On the other hand, the CSA dependency of the buildup curves does not only constitute a restriction, but also contains valuable information on the orientations of the moieties studied, which could be extracted in favorable cases.

Another factor to be considered is the number of distances contributing to one particular buildup curve. Cyclo-FF is a relatively small molecule in a densely packed structure and many distances below 7 Å occur for the same spin pair. In such a case, a de novo fitting of buildup curves becomes very complicated and ambiguous. This aspect is particularly problematic when several contributing distances are of comparable length, as for instance in the CO–Cγ₁ polarization buildup. On the other hand, when the distances differ by more than ∼0.5 Å as for CO–Cγ₂ and CO–Cδ₂₁ buildups, distinct features occur in the buildup curves and show great promise for a de novo fitting. The extraction of distance information can therefore be expected to be considerably easier for molecules larger than cyclo-FF.

The fitting procedure can also be simplified when some distances are already known, as for example the distances within one phenyl ring or other intramolecular distances in the case where molecular conformation was determined previously. By simulating the expected polarization buildup for the known distances and subtracting it from the experimental curves, the number of distances to be determined can be reduced, leading to a simplification of the fitting procedure.

It is noteworthy that some information can be extracted from experimental polarization buildups without a complete fitting of the curves. For instance, the initial rise of the buildup curve contains information on the shortest distance(s) involved. In addition, the possibility of normalizing experimental data according to the initial polarization as shown in the 1D approach is a great advantage as it directly gives an approximation of the number of distances which contribute to a buildup curve.

For a full structure determination, our experiments can of course be extended to non-aromatic carbons, e.g. probing Cα and Cβ carbons. In this case, not only S₃ and [S₃], but also other dipolar recoupling sequences can be considered. In particular for the measurement of relatively short distances (<3 Å), alternative sequences should be employed that have a slower polarization buildup and/or shorter sequence blocks. Overall, the quality of our data shows that a de novo fitting of polarization buildup curves is within reach.

Conclusions

The work presented here provides the framework for a novel strategy for structure determination of organic solids, based on DNP-enhanced ssNMR experiments at NA. In particular, we show that experiments at the low NA of ¹³C are highly worthwhile, regardless of the availability of an equivalent isotopically labeled compound. Different and often even more informative spectra can be obtained from NA samples, owing to the possibilities of long distance polarization transfers, simultaneous undisturbed observation of different distances for the same spin pair and detection of intermolecular contacts. Such NA experiments are made possible by MAS-DNP, which is employed to compensate for the drastically reduced sensitivity.

This paper focuses on dipolar recoupling experiments to probe structural information. Two complementary experimental approaches are presented. The first one allows polarization buildup curves to be obtained from a series of 1D spectra, enabled by the use of selective pulses. It has the advantages of very short experimental times (less than half a day for 15 points here) and results in very precise buildup curves. The second approach is more universally applicable and consists in the more traditional way of recording a series of 2D DQ-SQ spectra to follow the buildup of different cross-peaks.

Both approaches are demonstrated on nanotubes of cyclo-FF, investigating structurally relevant distances between carbonyl and aromatic carbons (1D approach) and among the aromatics (2D approach). The efficient recoupling of such carbons with very large CSAs is made possible by the S₃ and [S₃] pulse sequences, which additionally allow the use of sufficiently long recoupling times required to probe long distances. Using these sequences, the polarization buildup curves obtained with both approaches can be fully rationalized with numerical simulations based on the cyclo-FF crystal structure. Their detailed analysis reveals that each curve consists in the superposition of different distance contributions, reaching up to a remarkable length of ∼7 Å. A theoretical description of these contributions as isolated spin pairs is shown to be sufficient, making the analysis straightforward and simple. In addition, we demonstrate that dipolar truncation plays a role even in samples at NA when polarization transfers over longer distances are considered, and prohibits the detection of very long distances (longer than ∼7 Å in cyclo-FF). In view of the ultimate goal of supramolecular structure determination, the sensitivity of these experiments to intermolecular distances is of extreme importance. Furthermore, we demonstrate the feasibility of probing π-stacking through ¹³C–¹³C 2D correlation spectra, shining light on one of the most important non-covalent interactions in supramolecular systems. The wealth of structural information contained in polarization buildup curves measured on organic samples at NA, combined with the simplicity of their theoretical description as added isolated contributions, make up the beauty of this approach to NMR crystallography. It will certainly unfold its power not only for structure validation or refinement as reported by Mollica et al. ¹⁰ and in our contribution, but can also be expected to enable de novo crystal structure determination by NMR in the future.