Abstract
We have developed a set of graph theory-based tools, which we call Comparative Analysis of Protein Domain Organization (CADO), to survey and compare protein domain organizations of different organisms. In the language of CADO, the organization of protein domains in a given organism is shown as a domain graph in which protein domains are represented as vertices, and domain combinations, defined as instances of two domains found in one protein, are represented as edges. CADO provides a new way to analyze and compare whole proteomes, including identifying the consensus and difference of domain organization between organisms. CADO was used to analyze and compare >50 bacterial, archaeal, and eukaryotic genomes. Examples and overviews presented here include the analysis of the modularity of domain graphs and the functional study of domains based on the graph topology. We also report on the results of comparing domain graphs of two organisms, Pyrococcus horikoshii (an extremophile) and Haemophilus influenzae (a parasite with reduced genome) with other organisms. Our comparison provides new insights into the genome organization of these organisms. Finally, we report on the specific domain combinations characterizing the three kingdoms of life, and the kingdom “signature” domain organizations derived from those specific domain combinations.
With complete genomes of >100 organisms already known and hundreds of genomes in the final stages of assembly, there is less and less excitement associated with the completion of yet another genome. Genomic projects, to some extent, are victims of their own success—the pace of sequencing is outstripping our ability to analyze and comprehend all the new information. We lack the right tools, and perhaps even the right paradigm, to fully understand the wealth of information contained in even the smallest genome. Most genome analyses do not go much beyond presenting simple statistics, overview of existing pathways, and perhaps some examples of novel or conspicuously missing elements (Frishman et al. 2003). New ideas for genome description, however, are emerging, and they are often based on tools and techniques developed in other scientific fields that routinely deal with analysis of large and complex systems. These descriptions offer new insights into our understanding of organisms (Galperin and Koonin 2000; Jeong et al. 2001). In this spirit, we present here a series of analyses and comparisons between genomes based on a graph theory description of relations between domains in proteins.
Domain fusion/shuffling is one of the most important events in the evolution of modern proteins (Patthy 1999; Kriventseva et al. 2003). The majority of proteins, especially in high organisms, are built from multiple domains (modules) that can be found in various contexts in different proteins. Such domains usually form stable three-dimensional structures even if excised from a complete protein, and perform the same or similar molecular functions as parts of the protein. Databases of domains and associated tools for efficient recognition of domains in new proteins have been developed, including Pfam (Bateman et al. 2002), SMART (Schultz et al. 1998), PRODOM (Servant et al. 2002), CDD (Marchler-Bauer et al. 2003), INTERPRO (Mulder et al. 2003), DALI (Holm and Sander 1998), CATH (Orengo et al. 1997), and SCOP (Murzin et al. 1995). Supported by these databases, domain architectures in proteins (Bashton and Chothia 2002) and statistics of domain combinations (Apic et al. 2001) have been extensively analyzed.
Several applications of domain combination analysis, developed in the past few years, followed the realization that if two domains can be found in one protein their functions must somehow be related. For example, Bork et al. investigated the co-occurrence of domain families in eukaryotic proteins to predict protein cellular localization (Mott et al. 2002). The more popular approaches, however, were to explore the link between domain fusion and protein interactions (Enright et al. 1999; Marcotte et al. 1999b). Initial results were very encouraging, but the very high number of false predictions indicates that such interpretation of the co-occurrence of the two domains in the same protein might be too narrow; the relationship between two proteins can often be conceptual, such as catalyzing two different steps in the same reaction (Marcotte et al. 1999b) rather then physical. Tools have also been developed to characterize functions of large proteins by integrating the functions of domains present in these proteins (Enright et al. 1999; Marcotte et al. 1999a,b; Enright and Ouzounis 2001).
Graph theory-based methods have been developed to study the global properties of domain graphs (Wuchty 2001) and other biological networks including protein interaction networks (Snel et al. 2002), metabolic networks (Ravasz et al. 2002) and transcriptional regulation networks (Guelzim et al. 2002; Shen-Orr et al. 2002). These studies focused on the global analysis of biological networks to elucidate their general characteristics such as scale-free character (Jeong et al. 2000; Wuchty 2001) and modularity (Ravasz et al. 2002; Shen-Orr et al. 2002; Snel et al. 2002). Very few methods have been developed to compare biological networks across different organisms and to analyze them in detail. One of the exceptions was the comparison, using the network alignment, of protein interaction networks of Saccharomyces cerevisiae and Helicobacter pylori to extract the conserved pathways between the two organisms (Kelley et al. 2003).
In the work presented here, we do not insist on any single interpretation of domain fusion. We believe that whatever the reasons are for two or more domains being fused into one protein, analysis of such fusions in the global picture of a genome domain graph may provide new insights into the function of specific domains, and into comparisons between organisms. At the same time, we do not limit the analysis to the global properties of domain graphs. Instead, we focus on detailed structures of domain graphs, the modularity, connectivity, and internal structure of the domain graph, which are applied to the functional study of protein domains. It should also be noted that the term “domain graph” in this paper describes the domain organization of proteins; this term is also used in the literature to denote a different type of relationship between proteins based on the structural similarity of domains (Dokholyan et al. 2002; Hou et al. 2003; Shakhnovich et al. 2003).
The set of tools developed here, Comparative Analysis of Protein Domain Organization (CADO), has three major functions: (1) Provide a global view of domain organization in an entire genome. (2) Discover clusters of domains by domain clustering. (3) Compare domain graphs between genomes. These tools have been applied to survey and compare the domain graphs of 53 organisms. Among the questions we studied are the modularity of domain graphs and the functional homogeneity of the domains in a cluster, and the commonalities and differences of various organisms and kingdoms in terms of domain organization.
RESULTS
Domain Graphs in a Single Genome
General Properties of Organism Domain Graphs
Domain graphs as described here are similar to the domain graphs discussed in previous works (Wuchty 2001). The general observations made previously are confirmed in this study, despite some differences in methodology and the significant growth of domain libraries. Our calculations confirm that domain graphs are composed of a giant component and some small “islands” of domains (Newman et al. 2001), they are scale-free as characterized by a power-law distribution of domain connections (Jeong et al. 2000), and they show modularity as characterized by a high clustering coefficient (Wagner and Fell 2001; see Methods).
The number of domains, the number of domain combinations, and the size of the giant component (as measured by the number of domains it consists of) of each organism (Supplemental Table) increase with the complexity of the organisms, but very slowly compared with the increase in the number of predicted open reading frames (ORFs) in each genome (Fig. 1). As noticed many times before, all of the multicellular eukaryotes have many more domain combinations than prokaryotes or single-cellular eukaryotes (represented in our study by only one representative, yeast), even though the numbers of domains present in their genomes are not significantly different. This observation corresponds to a well-known characteristic of eukaryotic proteins that tend to be longer and contain more domains than archaeal or bacterial proteins. The rapid increase of the number of ORFs in these genomes may be the result of genome and gene duplications that are important for the evolution of complexity (Holland 1999). These events, however, do not significantly change the number of domains and domain combinations.
Figure 1.
A comparison of the number of ORFs, domains, domain combinations, and size of the giant component in domain graphs across genomes (see Supplemental Table A for details). The genomes are separated into archaeal, bacterial, and eukaryotic genomes by two lines; in each kingdom, the genomes are ranked according to the number of ORFs. The last six eukaryotic genomes have many more ORFs than the others, and they are not shown in the graph for clarity.
Modularity of Domain Graphs and Functional Homogeneity of Domain Clusters
Domain graphs have higher modularity (see Methods) than random scale-free graphs, with an average clustering coefficient of 0.45 for the giant components and 0.14 for the overall domain graphs. This implies that some groups of domains form almost independent networks, and they connect weakly to the rest of the domain graph. Based on this observation, domain graphs can be further dissected into clusters of domains by clustering domains according to their topological overlap (see Methods).
In biological networks, clusters in a connected graph are often used to infer the relationship between its elements. For example, it has been shown that clusters of genes based on the genomic association have a homogeneous functional composition (Snel et al. 2002). To apply the clustering of domain graphs to the functional study of domains, we need to first prove that domains clustered together in the domain graph have homogeneous functions. It is also important to explore the correlation between the size of the clusters and their functional homogeneity, testing if we can choose proper cluster size in the clustering procedure for effective functional study of the domains.
Our results (see Fig. 2 and the following discussion) confirm that (1) the domains that are clustered together in the domain graph have similar functions; and (2) the clusters have higher functional homogeneity when the domain graphs are dissected into smaller clusters. In our study, the functional distance between domains was defined according to the Gene Ontology (GO) functional category (Ashburner et al. 2000; see Methods). We defined the Functional Homogeneity Index (FHI) of the domain clusters in a domain graph as the average functional distance between any two domains (with functional annotation) in the same cluster (a smaller index means a higher functional homogeneity). Similarly, we defined the FHI of the domain combinations as the average functional distance between any two directly connected domains (see Methods) in the domain graph.
Figure 2.
The correlation of functional homogeneity of the domain clusters with the cluster size in Saccharomyces cerevisiae. The functional homogeneity index (FHI) of domain combinations within the clusters and the FHI of domain combinations between the clusters are also shown for comparison. See text for details.
To show the functional homogeneity of domain clusters, we use S. cerevisiae as an example. In its domain graph, the FHI of all domain pairs is 4.7, the FHI of connected domain pairs is 4.0, and the FHI of domain combinations is 1.7, reflecting the fact that directly connected domains have more similar functions compared with indirectly connected or disconnected domains. The entire domain graph was divided into clusters at different levels. For instance, if we chose cluster size 5, the domain graph was divided into clusters each having no more than five domains. The functional homogeneity test reveals that the functional homogeneity of the domain clusters is correlated with the cluster size: smaller clusters have higher homogeneous functions. The small domain clusters have a stronger functional homogeneity when compared with the domain combinations between clusters (i.e., domains in two different clusters; Fig. 2). For instance, when the cluster size is 5, the FHI of the domain clusters is 1.1, even smaller than the FHI of all domain combinations (1.7). Such a result can be explained by the big difference between the functional homogeneity of domain combinations within clusters (FHI 0.70) and the functional homogeneity of domain combinations between clusters (FHI 2.54). This result illustrates the advantage of using clusters over single domain combinations to study the function of domains, because some domain combinations, that is, the domain combinations between clusters, do not necessarily imply similar functions (Fig. 2).
The significance of functional homogeneity of domain clusters was calculated by a permutation test. The FHIs of domain clusters in real S. cerevisiae domain graphs at all levels (Fig. 2) are all significantly lower than those clusters in a random domain graph with the same graph topology but rearranged domains. For instance, for cluster size 20, the FHI of the domain clusters in this domain graph is 2.6 with a P-value of 1.8e – 27 (using 10,000 simulations). The same calculation was run for all the domain graphs studied here, in all cases showing significant functional homogeneity of domain clusters (see Supplemental Table B).
Application of Modularity in Functional Annotation
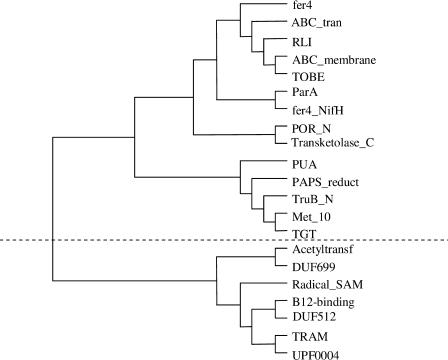
The modularity characteristic of a domain graph and the functional homogeneity of domain clusters allow us to assign function to uncharacterized domains according to the function of other domains in the same cluster. As an example, Figure 3 shows the clustering result of the giant component of the domain graph of P. horikoshii. Two almost independent clusters were detected. They were connected by a single domain combination of ABC_tran and Acetyltransf (Pfam nomenclature is used for all domains presented in this paper) as shown in Figure 4. One cluster contains domain Acetyltransf (present in proteins with N-acetyltransferase functions; Neuwald and Landsman 1997), TRAM (predicted to be an RNA-binding domain; Anantharaman et al. 2001), Radical_SAM (found in SAM proteins that cleave S-adenosylmethionine through an unusual Fe/S center and catalyze diverse reactions; Sofia et al. 2001), B12-binding domain, and three uncharacterized domains, DUF699, DUF512, and UPF0004. We predict the functions of these uncharacterized domains according to their associated domains with known functions. For example, the DUF699 may be involved with N-acetyltransferase functions, and DUF512 may take part in some enzymatic reaction involving the Fe/S center. This conclusion is partly supported by the results of fold recognition and distant homology recognition: FFAS (Rychlewski et al. 2000) predicts DUF512 to be related to NifB/MoaA Fe-S oxireductase (data not shown).
Figure 3.
The clustering of domains from the giant component of genome Pyrococcus horikoshii, based on topological overlapping. The graph was drawn by TreeView (Page 1996).
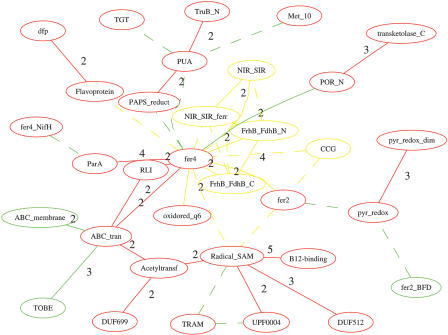
Figure 4.
The comparison between the domain graph of Methanopyrus kandleri AV19 (mka) and that of Pyrococcus horikoshii (pho). Only the largest component of their “combined” domain graph is shown with the common and specific domain and domain combinations shown in different colors: common in red, mka-specific in yellow, and pho-specific in green. The edges of weight 1 are shown in dashed lines; otherwise, the weight is shown along with the edges. See text for details.
Domain combinations that connect two domain clusters are also important, providing unique coupling between otherwise independent processes. In particular, we concentrated our attention on unique domain combinations providing the only connection between two clusters of domains, and we call these combinations bridges. For instance, the domain combination of ABC_tran and Acetyltransf in P. horikoshii described above (Figs. 3 and 4) is a bridge in this sense. We can expect that mutations or deletions in bridge domains would decouple the two networks represented by the clusters and result in significant phenotypes. We found 151 domain combinations to be bridges in several genomes that connect two clusters each having at least three domains (Supplemental Table C).
Comparing Domain Organizations of Various Organisms
Comparison of Domain Graphs
Domain graphs of individual organisms were compared with each other to identify the similarities and differences between their domain organizations. In the first of the two examples presented here, the domain graph of P. horikoshii, an extremophile, was compared with that of Methanopyrus kandleri AV19. The largest component of the combined domain graphs of these two organisms, with highlighted differences between them, is shown in Figure 4. Briefly, most differences are found in domain combinations of fer4 (George et al. 1985) with other domains, highlighting the differences in metabolism of these otherwise closely related Archaea. In P. horikoshii, a small cluster of domains, PAPS_reduct, PUA, Met_10, TruB_N, and TGT, is connected to the core of the giant component by the domain combination between fer4 and PAPS_reduct and the combination between fer4 and PUA. In contrast, in M. kandleri AV19 the domain combinations between fer4 with other domains, such as Radical_SAM, fer2, and CCG generate a more tightly connected domain graph in this organism. A possible interpretation of the connection difference is that P. horikoshii, as an extremophile, uses a much smaller range of nutrients, thus reducing the need for coupling the electron-transfer domain fer4 to a variety of enzymes.
In the second example, the domain graph of Haemophilus influenzae was compared with that of Escherichia coli K12. Both organisms belong to γ-proteobacteria, but the former has a much smaller (reduced) genome (Tatusov et al. 1996). Figure 5 shows a highly connected graph of domains that are involved with the bacterial two-component system (TCS; Hoch 2000; Studholme and Dixon 2003) and the phosphoenolpyruvate-dependent phosphotransferase system (PTS; Saier and Reizer 1994), such as domain response_reg, EAL, PAS, PTS_IIB, and PEP-utilizers. The connectivity clearly reflects the fact that multidomain bacterial proteins that comprise the constituents of the PTS and TCS have undergone extensive shuffling during their evolution (Reizer and Saier 1997). More interestingly, Figure 5 shows H. influenzae has fewer domains and domain combinations than E. coli, and the differences between these two domain graphs are concentrated on the domains that are involved with the two bacterial regulatory systems TCS and PTS. TCS has two components: the first component acts as the sensor, and the second is the response regulator. Many domains that are involved with both components are missing in H. influenzae, including sensor domains (e.g., PAS, EAL, Hpt, BLUF, and HAMP) and domains in transcriptional regulators (e.g., LytTr and Autoind_bind). H. influenzae still has some domains involved in TCS, such as response_reg (an input domain in the response regulator), Sigma54_activat (a domain in the response regulator that interacts with σ54), HAMP (a sensor domain), HisKa (a sensor domain), HTH-8 (a DNA-binding domain), and GerE (a DNA-binding domain). The domain graph of H. influenzae also has fewer domains and domain combinations involved in the PTS system compared with E. coli. In contrast, the organization of domains involved in a wide range of metabolic enzymes that are regulated by amino acid concentration is very similar between these two organisms, with domain ACT in the center of one domain cluster that has combinations with many other domains. All the above results show that H. influenzae has much simplified regulatory systems TCS and PTS but a similar regulatory system involved with amino acid concentration as compared with E. coli.
Figure 5.
The comparison between the domain graph of Haemophilus influenzae (hin) and that of Escherichia coli K12 (eco). Only the largest component of their “combined” domain graph is shown with the common and specific domain and domain combinations shown in different colors: common in red, hin-specific in yellow, and eco-specific in green. The edges ofweight 1 are shown in dashed lines, others in straight lines. See text for details.
Phylogenetic Profiling of Domains and Domain Combinations
Phylogenetic profiling is a simple yet helpful tool for the functional study of domains and their combinations. Similar to tools used by other groups (Pellegrini et al. 1999), it records the presence or absence of a given domain or domain combination in various genomes. For instance, once a bridge domain is identified, phylogenetic profiling can be used to help confirm its presence/absence in other genomes and hence its overall importance. Certain domain combinations form bridges between two clusters of domains in some genomes, whereas in others more connections are added (type 1), indicating a stronger connection between the clusters. Our previous example of the domain combination of ABC_tran with Acetyltransf belongs to this type (Table 1). Domain combinations that form bridges in some of the genomes, but are completely missing in other genomes, are grouped into the second type. A typical case is the combination of domain HD (metal-dependent phosphohydrolases; Aravind and Koonin 1998) and domain KH (present in a wide variety of quite diverse nucleic-acid-binding proteins; Musco et al. 1996). Although both domains are universally distributed in all organisms, their combination is only found in bacteria (10 out of 30; Table 1). The type 1 and type 2 bridges are reliable because they are found in several related organisms and their existence confirms the relationships between domain clusters. In contrast, the third type of bridge includes domain combinations that are found in very few unrelated genomes, indicating that they might be an artificial result or a random combination that does not necessarily imply a functional relationship between the connected clusters. An example of this type is the domain combination between response_reg (response regulator receiver domain; Pao and Saier 1995) and pyr_redox (a small NADH binding domain found in pyridine nucleotide-disulphide oxidoreductase; Table 1; Mande et al. 1996). This domain combination has only been found in Streptomyces coelicolor A3(2). Despite both domain predictions being statistically significant (response_reg with an E-value of 4.0e – 09 and pyr_redox with an E-value of 1.4e – 28 in protein gi|8347031), this combination is very doubtful because there is a lack of any functional relationship between these two domains and because of the incompatible phylogenetic profiles of both domains (Table 1).
Table 1.
Phylogenetic Profiles of Selected Domains and Domain Combinations
Comparing Domain Organizations of the Kingdoms
Domain graphs of all the genomes studied here were compared with each other to extract common and specific domains and domain combinations of each of the kingdoms (Bacteria, Archaea, and Eukaryota; see Methods). Overall, many more specific domain combinations were found in eukaryotic genomes (280 in total) than in bacterial (40) and archaeal (7) genomes. The common and specific domain combinations were further mapped onto a “combined” domain graph, composed of all domains and combinations from all the genomes, to give an overview of the distribution of specific domains and domain combinations (Fig. 6). The analysis of this domain graph shows that both common and specific combinations are clustered into components, making it possible to derive kingdom “signature” domain organizations from those components. Selected examples are shown below, and a complete list of common and specific combinations is given in Supplemental Table D.
Figure 6.
The specific domains and combinations in the domain graph. Archaeal-specific domains and combinations are shown in yellow, bacterial-specific in blue, and eukaryotic-specific in green. The common domains and combinations in all genomes are shown in red. The remaining domains and combinations are shown in gray.
Common Domain Organization in All Genomes
Only 13 domain combinations were detected in all the genomes, but this number increased to 50 when we adopted a weaker definition (i.e., combinations are found in at least 80% of the organisms). It is a surprisingly small number compared with the size of the entire domain graph (5236 combinations in total). Most of those domain combinations are found in fundamental proteins; also, some may be artifacts of domain definitions, where Pfam domain definitions do not correspond to structurally independent modules. One cluster of common combinations contains domains EFG_C, EFG_IV, GTP_EFTU, GTP_EFTU_D2, and GTP_EFTU_D3, which represent various elongation factors involved in DNA regulation. Another cluster of common combinations contains domains RNA_pol_Rpb1_1, RNA_pol_Rpb1_2, RNA_pol_Rpb1_3, RNA_pol_Rpb1_4, RNA_pol_Rpb1_5, RNA_pol_Rpb2_6, and RNA_pol_Rpb2_7, which are found in RNA polymerase Rpb1 and RNA polymerase Rpb2.
Eukaryotic “Signature” Domain Organizations
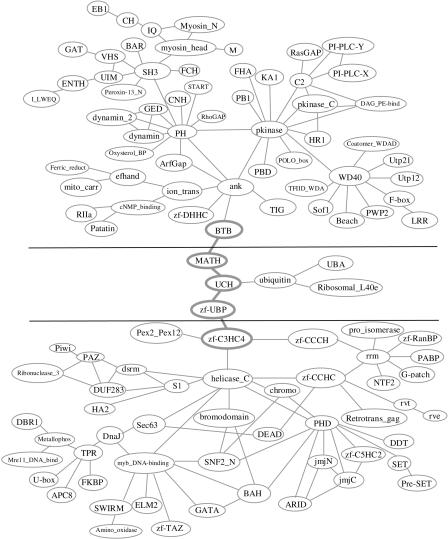
We found 280 specific combinations that were further divided into several components in eukaryotic genomes. Those components can be treated as the eukaryotic “signature” domain organizations. The largest eukaryotic signature domain organization contains 114 domains and 141 combinations (see Fig. 7). It is further divided into three clusters, based on the functional annotations of the domains in the component and the inspection of the domain graph.
Figure 7.
The largest eukaryotic “signature” domain organization. The graph was drawn manually for clarity based on a graphviz layout. See text for details.
One cluster (middle in Fig. 7) is related to ubiquitination (Hershko et al. 2000; Jones et al. 2002). It contains domain ubiquitin, UCH (found in ubiquitin C-terminal hydrolases), UBA (found in several proteins having connections to ubiquitin and the ubiquitination pathway), MATH (found in ubiquitin C-terminal hydrolases), and zf-UBP (which displays some similarities with the Zn-binding domain of the insulinase family and is found only in a small subfamily of ubiquitin C-terminal hydrolases). Although the phylogenetic profiles of these domains show they are eukaryotic-specific accompanied by a rare presence in prokaryotic genomes except for the universally distributed domain UBA, all the domain combinations in this cluster are eukaryotic-specific. It is well known that the ubiquitin-conjugation system is responsible for regulating the rates of turnover of a wide variety of regulatory proteins in eukaryotes (Hershko et al. 2000; Jones et al. 2002).
The domains in the second cluster are mostly related to DNA-binding activity and RNA-binding activity, both of which are involved in various functions including transcriptional regulation, alternative splicing, DNA-repair, and the like (bottom in Fig. 7). This cluster is a network of zinc fingers (Evans and Hollenberg 1988). Variant zinc fingers are found in this cluster, including the classical zinc-finger domain zf-C2H2, zf-C3HC4, PHD domain (found in nuclear proteins involved in chromatin-mediated transcriptional regulation; Aasland et al. 1995), zf-CCCH (found in proteins from eukaryotes involved in cell cycle or growth phase-related regulation; Carballo et al. 1998), zf-CCHC (mostly from retroviral gag proteins; Katz and Jentoft 1989), zf-RanBP (found in Ran-binding proteins and others; Yaseen and Blobel 1999), zf-C5HC2 (predicted zinc finger with eight potential zinc-ligand-binding residues), U-box (related to the zf-C3HC4 but lacks the zinc-binding residues; Aravind and Koonin 2000), zf-TAZ (TAZ zinc finger of CBP; Ponting et al. 1996), and GATA (GATA zinc finger, found in GATA transcriptor factors). The zinc fingers (e.g., PHD, zf-CCHC, and zf-C3HC4), along with other highly connected domains, such as helicase_C (helicase conserved C-terminal domain), rrm (found in a variety of RNA-binding proteins; Birney et al. 1993), SNF2-N (found in proteins involved in a variety of processes including transcription regulation, DNA repair, DNA recombinations), and myb_DNA-binding (found in Myb proteins), determine the topology of this cluster.
We grouped the remaining domains in the third cluster (top in Fig. 7). Three highly connected domains, PH, pkinase, and ank, determine the topology of this cluster. This cluster might be involved in several different functions because the ank domain occurs in many functionally diverse proteins mainly from eukaryotes, and the PH domain occurs in a wide range of proteins involved in intracellular signaling or as constituents of the cytoskeleton.
The domain zf-C3HC4, a RING-finger domain of 40 to 60 residues (Borden and Freemont 1996), and its combinations are studied here because of their important roles in connecting two clusters in the largest eukaryotic signature domain organization (Fig. 7). Until now, the exact molecular function of the RING-finger domain was unknown. Although several groups have suggested that RING-containing proteins are directly involved in specific DNA binding because of the presence of the RING finger (Lovering et al. 1993; Kanno et al. 1995), there is no convincing evidence supporting the contention that the RING finger is a nucleic-acid-binding domain. Instead, evidence has shown that the RING finger might be involved with protein–protein interactions and in some cases in multiprotein complexes (Saurin et al. 1996; Joazeiro et al. 1999). On the other hand, a growing body of evidence indicates that the ubiquitin system is involved with transcriptional regulation, although ubiquitin-mediated proteolysis and gene transcription are seemingly not related to each other (Muratani and Tansey 2003). Our domain graph analysis provides a new proof of the connection between these two systems. In the domain graph, domain zf-C3HC4 links the cluster of domains associated with ubiquitin and the cluster of domains associated with the DNA/RNA-binding function, which indicates that zf-C3HC4 may be involved with both the DNA-binding and protein–protein interaction functions.
Bacterial Signature Domain Organizations
We found 40 bacterial-specific domain combinations divided into several components, which could be treated as bacterial signature domain organizations. The first component contains four domains. Three of them (DNA_ligase_N, DNA_ligase_OB, and DNA_ligase_ZBD) are found in NAD-dependent DNA ligases, which catalyze the crucial step of joining the breaks in duplex DNA during DNA replication, repair, and recombination. The fourth domain, BRCT, is found predominantly in proteins involved in cell cycle checkpoint functions responsive to DNA damage (Bork et al. 1997). All four domains are necessary for the NAD-dependent DNA ligases, which are bacterial-specific with one exception in the eukaryotic virus Amsacta moorei entomopoxvirus (AmEPV), the first example of an NAD+ ligase from a source other than bacteria (Sriskanda et al. 2001). Another component is composed of four domains, B3_4 and B5 (found in tRNA synthetase β-subunits), FDX-ACB (anticodon binding domain, found in some phenylalanyl tRNA synthetases), and tRNA_bind. Although those domains are found in most organisms, their combinations are bacterial-specific except for the combination between domains B3_4 and B5 (Table 1), reflecting that specific domain combinations can be built from common domains (Apic et al. 2001).
DISCUSSION
In this study, we have described a set of graph theory tools that can be used for characterizing domain graphs as well as comparing them among different organisms. By studying the topology of graph domains, we can derive important clues to the functional roles of domains and their combinations. Graph analysis can identify domain organization features, such as clusters or bridges, which are not available from a standard type of analysis provided by a list of domain combinations. One example, showing the central role of the zf_C3HC4 domain was discussed here in detail; many more examples can be found at the CADO Web site. By comparing domain graphs of several genomes using CADO, we identified not only universal but also kingdom-specific combinations. These combinations provide important clues to domain functions and relations between organisms.
Certainly, the specificity study of domain organizations is not limited to the three kingdoms. We can compare any arbitrary set of organisms with others or even search for groups of organisms that share some specific domain combinations. We identified the domains and combinations specific for only two kingdoms, or, in other words, specifically missing in the other one. For example, domains PCRF and RF-1 (found in peptide chain release factors) are specific for bacterial and eukaryotic but not archaeal genomes, whereas domains eRF1_1, eRF1_2, and eRF1_3 (found in release factor eRF1) are specific for archaeal and eukaryotic but not bacterial genomes, although they are all involved with the ubiquitous process of protein biosynthesis. Such specific domains and combinations might provide additional clues to the study of the relationships between specific pathways in each of the three kingdoms. Other useful tests might be to compare the hyperthermophilic organisms with the other organisms to identify their specific domain organizations, or to compare the pathogenic organisms with nonpathogenic ones to extract domain organizations possibly related to virulence.
As discussed above, domain graphs analyze one specific type of functional coupling of domains—their fusion into one protein. We can easily imagine that other mechanisms, such as coregulation or cocompartmentalization, may play a similar functional role, but would be missed in the domain graph language. Yet the fact that some organisms chose this particular way of coupling of the two domains tells us about the functional relation between the domains and about the similarity between regulatory mechanisms for a given process in two (or more) organisms. CADO, applied here to analyze domain graphs, provides a general framework for dissecting, as well as comparing large networks. It can also be applied to biological networks other than domain graphs, or even to nonbiological networks.
The real challenge, however, of describing the functional relations between proteins in a genome comes from its multidimensional nature—one can imagine that several other types of relations between proteins can also be defined and described in a similar language. Although there are some pioneering works, such as the inference of a complete protein–protein interaction network of organisms by combining both experimental and computational results (Jeong et al. 2001), it is both a challenging and a very interesting problem to rebuild a complete picture of genome regulations from several types of partial networks or from different information sources.
METHODS
Domain Graph
A “domain graph” is defined as an undirected graph consisting of all domains (vertices) present in a given protein data set (Wuchty 2001). We link two vertices with an edge if and only if both domains are present in at least one protein (domain combination). For example, one protein containing three domains forms a triangle in the domain graph (Fig. 8A). The “degree” of a vertex is defined as the number of its “nearest neighbors” (i.e., the vertices that have direct connection to this vertex). The “weight” of an edge is defined as the number of proteins containing both domains connected by the edge. The “shortest path” between vertices is computed by the Floyd shortest path algorithm (Minieka 1978). Two domains are “disconnected” if their shortest path in the domain network is infinite; otherwise they are connected, either “directly connected” (i.e., domain combination) or “indirectly connected” (there is a path between two domains). A domain graph is partitioned into connected components (Minieka 1978). As is typical in scale free graphs, we found that a majority of domains in any given genome form a single component that is much bigger than the others in a domain graph. We call this component the “giant component” of a domain graph and the others “islands.” A domain combination (an edge in the domain graph) is called a “linker” if it connects two relatively independent domain clusters. We say that a linker forms a “bridge” when it is the only connection between clusters (single cut-edge).
Figure 8.
(A) A schematic demonstration of the construction of a domain graph. Four domains (a, b, c, and d) are present in two given proteins. As a result, a domain graph with four vertices and four edges is formed. The vertices represent the domains with the same color. (B) The process of Comparative Analysis of Protein Domain Organization (CADO). Two domain graphs are shown in blue and pink (top) and their common organization is shown in brown in the bottom.
A graph has a “scale-free” topology if its degree distribution decays as a power law, P(k) ∼ K–γ (Jeong et al. 2000). A distinguishing feature of scale-free graphs is the existence of a few highly connected vertices. A graph has “modularity” if it is organized into many small but highly connected clusters (Wagner and Fell 2001). The clustering coefficient for a vertex i is defined as Ci = 2n/ki(ki – 1), where ki is the number of vertex i nearest neighbors and n represents the number of direct links connecting the ki nearest neighbors of vertex i. Ci averaged over all domains of a domain graph is a measure of the graph's potential modularity.
Domain Graph Dissection
The domain graph can be further dissected into smaller clusters to obtain a more detailed view of the domain organizations and its internal structure. “Average-linkage clustering” (Ravasz et al. 2002) was used to dissect the domain graphs. First, the similarity of two domains is defined as their “topological overlap.” The topological overlap of two domains i and j is defined as OT(i, j) = Jn(i, j)/[(ki + kj)/2], where Jn(i, j) denotes the number of vertices to which both i and j are linked (+1 if there is an edge between i and j). Our definition is slightly different from that used in one previous paper (Ravasz et al. 2002): the Jn(i, j) is divided by the average of the nearest neighbors of vertices i and j instead of their minimal. In the case of domain organizations, it appears improper to treat two domains topologically equal if one domain has three nearest neighbors and the other domain has 100 nearest neighbors, even though these two domains share the same three nearest neighbors. With the topological overlap matrix of the domains in a genome, an average-linkage clustering is performed to divide the domains into clusters, which can be further analyzed for the functional study of domains.
Comparative Analysis of Domain Organization (CADO)
Comparisons of domain organizations across different genomes were done by comparing their corresponding domain graphs, as Figure 8B shows. Given a set of domain graphs, we defined the common domain combinations as edges that are present in all the domain graphs in the set; the specific domain combinations of a given set of domain graphs as the edges that are present in all the domain graphs from this set but absent in all other domain graphs. We allowed a certain degree of flexibility in the definition of specific combinations to take into account those occasions when domains were not predicted completely because of the defects of the prediction programs. Combinations found in most (i.e., >80%) of the domain graphs of one set but absent in most (i.e., >80%) of the remaining domain graphs were considered as specific combinations. The specific combinations were further studied in the context of their relationship with other domains in the domain graph. This process is called Comparative Analysis of Protein Domain Organization (CADO), which is implemented with C++ under Linux. The domain graphs were drawn with the graphviz package (http://www.graphviz.org).
Domain Assignment
We used Pfam version 7.8 (including 5049 domains; Bateman et al. 2002) and a domain recognition package hmmer-2.2g to predict domains. To guarantee that the predicted domains used in CADO are significant, we used the two-level score cutoff system of Pfam to evaluate the hits, that is, only hits with an E-value of <0.05 and a score better than the curated cutoffs were kept. We combined searching results of local alignment and global alignment. A post process was applied to remove the predicted domains of a protein overlapped with the domains of higher reliability.
Functional Similarity Between Domains
The functional similarity between two domains was defined according to GO, whose terms are organized in directed acyclic graphs (DAGs; Ashburner et al. 2000). The GO database and the GO annotation of Pfam domains were downloaded from the GO Web site (http://www.geneontology.org/). We used the path distances between GO terms as the similarity measurement of GO terms. As one Pfam domain can be assigned to multiple GO terms, we defined the functional distance between two Pfam domains as the minimum of the distances between the GO terms that are associated with the Pfam domains.
Genome Data
The present analysis covered 53 genomes in total, including 16 archaeal, 30 bacterial, and seven eukaryotic genomes. All of the proteomes were downloaded from the NCBI GenBank database (ftp://ftp.ncbi.nlm.gov), except the Takifugu rubripes proteome was downloaded from http://genome.jgi-psf.org/fugu6/fugu6.download.ftp.html and the Ciona intestinalis proteome was downloaded from http://genome.jgi-psf.org/ciona4/ciona4.download.ftp.html. The genomes and their codes are 16 archaeal genomes, Archaeoglobus fulgidus (afu), Halobacterium sp. NRC-1 (hal), Methanocaldococcus jannaschii (mja), Methanopyrus kandleri str. AV19 (mka), Methanosarcina acetivorans str. C2A (mac), Methanosarcina mazei (mma), Methanobacterium thermoautotrophicum (mth), Thermoplasma acidophilum (tac), Thermoplasma volcanium (tvo), Pyrococcus abyssi (pab), Pyrococcus furiosus (pfu), Pyrococcus horikoshii (pho), Pyrobaculum aerophilum (pae), Sulfolobus solfataricus (sso), Sulfolobus tokodaii (sto), Aeropyrum pernix (ape), and Agrobacterium tumefaciens str. C58 (atu); 30 bacterial genomes, Brucella melitensis (bme), Rickettsia prowazekii (rpr), Caulobacter crescentus (ccr), Ralstonia solanacearum (rso), Neisseria meningitides (mme), Escherichia coli K12 (eco), Haemophilus influenzae (hin), Pseudomonas aeruginosa (per), Vibrio cholerae (vch), Campylobacter jejuni (cje), Helicobacter pylori 26695 (hpy), Streptomyces coelicolor A3(2) (sco), Mycobacterium leprae (mle), Mycobacterium tuberculosis H37Rv (mtu), Bacillus subtilis (bsu), Clostridium acetobutylicum (cac), Lactococcus lactis subsp. Lactis (lla), Mycoplasma pulmonis (mpu), Streptococcus pyogenes (spy), Mycoplasma pneumoniae (mpn), Ureaplasma urealyticum (uur), Synechocystis sp. PCC 6803 (spc), Thermotoga maritime (tma), Deinococcus radiodurans (dra), Chlamydia trachomatis (ctr), Chlamydia muridarum (cmu), Chlamydophila pneumoniae CWL029 (cpn), Borrelia burgdorferi (bbu), and Treponema pallidum (tpa); seven eukaryotic genomes, Saccharomyces cerevisiae (sce), Drosophila melanogaster (dme), Arabidopsis thaliana (ath), Caenorhabditis elegans (cel), Fugu rubripes (fug), Ciona intestinalis (csa), and Homo sapiens (hsa).
Acknowledgments
We thank Slawek K. Grzechnik for his assistance in computations of domain assignments. We thank Bruce Worcester for help in editing. We appreciate all helpful comments from the anonymous reviewers, especially on the statistical test of the functional homogeneity of domain clusters, and the explanation of the connection between the ubiquitination system and gene expression. The research described in this manuscript was supported by NIH grant GM60049.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
E-MAIL yye@burnham.org; FAX (858) 646-3171.
E-MAIL adam@burnham.org; FAX (858) 646-3171.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1610504.
Footnotes
[Supplemental material is available online at www.genome.org and http://ffas.ljcrf.edu/DomainGraph.]
References
- Aasland, R., Gibson, T.J., and Stewart, A.F. 1995. The PHD finger: Implications for chromatin-mediated transcriptional regulation. Trends Biochem. Sci. 20: 56–59. [DOI] [PubMed] [Google Scholar]
- Anantharaman, V., Koonin, E.V., and Aravind, L. 2001. TRAM, a predicted RNA-binding domain, common to tRNA uracil methylation and adenine thiolation enzymes. FEMS Microbiol. Lett. 197: 215–221. [DOI] [PubMed] [Google Scholar]
- Apic, G., Gough, J., and Teichmann, S.A. 2001. Domain combinations in archaeal, eubacterial and eukaryotic proteomes. J. Mol. Biol. 310: 311–325. [DOI] [PubMed] [Google Scholar]
- Aravind, L. and Koonin, E.V. 1998. The HD domain defines a new superfamily of metal-dependent phosphohydrolases. Trends Biochem. Sci. 23: 469–472. [DOI] [PubMed] [Google Scholar]
- Aravind, L. and Koonin, E.V. 2000. The U box is a modified RING finger—A common domain in ubiquitination. Curr. Biol. 10: R132–R134. [DOI] [PubMed] [Google Scholar]
- Ashburner, M., Ball, C.A., Blake, J.A., Botstein, D., Butler, H., Cherry, J.M., Davis, A.P., Dolinski, K., Dwight, S.S., Eppig, J.T., et al. 2000. Gene ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bashton, M. and Chothia, C. 2002. The geometry of domain combination in proteins. J. Mol. Biol. 315: 927–939. [DOI] [PubMed] [Google Scholar]
- Bateman, A., Birney, E., Cerruti, L., Durbin, R., Etwiller, L., Eddy, S.R., Griffiths-Jones, S., Howe, K.L., Marshall, M., and Sonnhammer, E.L. 2002. The Pfam protein families database. Nucleic Acids Res. 30: 276–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birney, E., Kumar, S., and Krainer, A.R. 1993. Analysis of the RNA-recognition motif and RS and RGG domains: Conservation in metazoan pre-mRNA splicing factors. Nucleic Acids Res. 21: 5803–5816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borden, K.L. and Freemont, P.S. 1996. The RING finger domain: A recent example of a sequence-structure family. Curr. Opin. Struct. Biol. 6: 395–401. [DOI] [PubMed] [Google Scholar]
- Bork, P., Hofmann, K., Bucher, P., Neuwald, A.F., Altschul, S.F., and Koonin, E.V. 1997. A superfamily of conserved domains in DNA damage-responsive cell cycle checkpoint proteins. FASEB J. 11: 68–76. [PubMed] [Google Scholar]
- Carballo, E., Lai, W.S., and Blackshear, P.J. 1998. Feedback inhibition of macrophage tumor necrosis factor-α production by tristetraprolin. Science 281: 1001–1005. [DOI] [PubMed] [Google Scholar]
- Dokholyan, N.V., Shakhnovich, B., and Shakhnovich, E.I. 2002. Expanding protein universe and its origin from the biological Big Bang. Proc. Natl. Acad. Sci. 99: 14132–14136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enright, A.J. and Ouzounis, C.A. 2001. Functional associations of proteins in entire genomes by means of exhaustive detection of gene fusions. Genome Biol. 2: RESEARCH0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enright, A.J., Iliopoulos, I., Kyrpides, N.C., and Ouzounis, C.A. 1999. Protein interaction maps for complete genomes based on gene fusion events. Nature 402: 86–90. [DOI] [PubMed] [Google Scholar]
- Evans, R.M. and Hollenberg, S.M. 1988. Zinc fingers: Gilt by association. Cell 52: 1–3. [DOI] [PubMed] [Google Scholar]
- Frishman, D., Mokrejs, M., Kosykh, D., Kastenmuller, G., Kolesov, G., Zubrzycki, I., Gruber, C., Geier, B., Kaps, A., Albermann, K., et al. 2003. The PEDANT genome database. Nucleic Acids Res. 31: 207–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galperin, M.Y. and Koonin, E.V. 2000. Who's your neighbor? New computational approaches for functional genomics. Nat. Biotechnol. 18: 609–613. [DOI] [PubMed] [Google Scholar]
- George, D.G., Hunt, L.T., Yeh, L.S., and Barker, W.C. 1985. New perspectives on bacterial ferredoxin evolution. J. Mol. Evol. 22: 20–31. [DOI] [PubMed] [Google Scholar]
- Guelzim, N., Bottani, S., Bourgine, P., and Kepes, F. 2002. Topological and causal structure of the yeast transcriptional regulatory network. Nat. Genet. 31: 60–63. [DOI] [PubMed] [Google Scholar]
- Hershko, A., Ciechanover, A., and Varshavsky, A. 2000. The ubiquitin system. Nat. Med. 6: 1073–1081. [DOI] [PubMed] [Google Scholar]
- Hoch, J.A. 2000. Two-component and phosphorelay signal transduction. Curr. Opin. Microbiol. 3: 165–170. [DOI] [PubMed] [Google Scholar]
- Holland, P.W.H. 1999. Gene duplication: Past, present and future. Cell Dev. Biol. 10: 541–547. [DOI] [PubMed] [Google Scholar]
- Holm, L. and Sander, C. 1998. Dictionary of recurrent domains in protein structures. Proteins 33: 88–96. [DOI] [PubMed] [Google Scholar]
- Hou, J., Sims, G.E., Zhang, C., and Kim, S.H. 2003. A global representation of the protein fold space. Proc. Natl. Acad. Sci. 100: 2386–2390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong, H., Tombor, B., Albert, R., Oltvai, Z.N., and Barabasi, A.L. 2000. The large-scale organization of metabolic networks. Nature 407: 651–654. [DOI] [PubMed] [Google Scholar]
- Jeong, H., Mason, S.P., Barabasi, A.L., and Oltvai, Z.N. 2001. Lethality and centrality in protein networks. Nature 411: 41–42. [DOI] [PubMed] [Google Scholar]
- Joazeiro, C.A., Wing, S.S., Huang, H., Leverson, J.D., Hunter, T., and Liu, Y.C. 1999. The tyrosine kinase negative regulator c-Cbl as a RING-type, E2-dependent ubiquitin-protein ligase. Science 286: 309–312. [DOI] [PubMed] [Google Scholar]
- Jones, D., Crowe, E., Stevens, T.A., and Candido, E.P. 2002. Functional and phylogenetic analysis of the ubiquitylation system in Caenorhabditis elegans: Ubiquitin-conjugating enzymes, ubiquitin-activating enzymes, and ubiquitin-like proteins. Genome Biol. 3: RESEARCH0002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanno, M., Hasegawa, M., Ishida, A., Isono, K., and Taniguchi, M. 1995. mel-18, a Polycomb group-related mammalian gene, encodes a transcriptional negative regulator with tumor suppressive activity. EMBO J. 14: 5672–5678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz, R.A. and Jentoft, J.E. 1989. What is the role of the cys–his motif in retroviral nucleocapsid (NC) proteins? Bioessays 11: 176–181. [DOI] [PubMed] [Google Scholar]
- Kelley, B.P., Sharan, R., Karp, R.M., Sittler, T., Root, D.E., Stockwell, B.R., and Ideker, T. 2003. Conserved pathways within bacteria and yeast as revealed by global protein network alignment. Proc. Natl. Acad. Sci. 100: 11394–11399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriventseva, E.V., Koch, I., Apweiler, R., Vingron, M., Bork, P., Gelfand, M.S., and Sunyaev, S. 2003. Increase of functional diversity by alternative splicing. TIG 19: 124–128. [DOI] [PubMed] [Google Scholar]
- Lovering, R., Hanson, I.M., Borden, K.L., Martin, S., O'Reilly, N.J., Evan, G.I., Rahman, D., Pappin, D.J., Trowsdale, J., and Freemont, P.S. 1993. Identification and preliminary characterization of a protein motif related to the zinc finger. Proc. Natl. Acad. Sci. 90: 2112–2116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mande, S.S., Sarfaty, S., Allen, M.D., Perham, R.N., and Hol, W.G. 1996. Protein–protein interactions in the pyruvate dehydrogenase multienzyme complex: Dihydrolipoamide dehydrogenase complexed with the binding domain of dihydrolipoamide acetyltransferase. Structure 4: 277–286. [DOI] [PubMed] [Google Scholar]
- Marchler-Bauer, A., Anderson, J.B., DeWeese-Scott, C., Fedorova, N.D., Geer, L.Y., He, S., Hurwitz, D.I., Jackson, J.D., Jacobs, A.R., Lanczycki, C.J., et al. 2003. CDD: A curated Entrez database of conserved domain alignments. Nucleic Acids Res. 31: 383–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcotte, E.M., Pellegrini, M., Ng, H.L., Rice, D.W., Yeates, T.O., and Eisenberg, D. 1999a. Detecting protein function and protein–protein interactions from genome sequences. Science 285: 751–753. [DOI] [PubMed] [Google Scholar]
- Marcotte, E.M., Pellegrini, M., Thompson, M.J., Yeates, T.O., and Eisenberg, D. 1999b. Combined algorithm for genome-wide prediction of protein function. Nature 402: 83–86. [DOI] [PubMed] [Google Scholar]
- Minieka, E. 1978. Path algorithms. In Optimization algorithms for networks and graphs, pp. 41–84. Marcel Dekkar, New York.
- Mott, R., Schultz, J., Bork, P., and Ponting, C.P. 2002. Predicting protein cellular localization using a domain projection method. Genome Res. 12: 1168–1174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulder, N.J., Apweiler, R., Attwood, T.K., Bairoch, A., Barrell, D., Bateman, A., Binns, D., Biswas, M., Bradley, P., Bork, P., et al. 2003. The InterPro database, 2003 brings increased coverage and new features. Nucleic Acids Res. 31: 315–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muratani, M. and Tansey, W.P. 2003. How the ubiquitin-proteasome system controls transcription. Nat. Rev. Mol. Cell. Biol. 4: 192–201. [DOI] [PubMed] [Google Scholar]
- Murzin, A.G., Brenner, S.E., Hubbard, T., and Chothia, C. 1995. SCOP: A structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 247: 536–540. [DOI] [PubMed] [Google Scholar]
- Musco, G., Stier, G., Joseph, C., Castiglione Morelli, M.A., Nilges, M., Gibson, T.J., and Pastore, A. 1996. Three-dimensional structure and stability of the KH domain: Molecular insights into the fragile X syndrome. Cell 85: 237–245. [DOI] [PubMed] [Google Scholar]
- Neuwald, A.F. and Landsman, D. 1997. GCN5-related histone N-acetyltransferases belong to a diverse superfamily that includes the yeast SPT10 protein. Trends Biochem. Sci. 22: 154–155. [DOI] [PubMed] [Google Scholar]
- Newman, M.E.J., Strogatz, S.H., and Watts, D.J. 2001. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. 64: 026118. [DOI] [PubMed] [Google Scholar]
- Orengo, C.A., Michie, A.D., Jones, S., Jones, D.T., Swindells, M.B., and Thornton, J.M. 1997. CATH—A hierarchic classification of protein domain structures. Structure 5: 1093–1108. [DOI] [PubMed] [Google Scholar]
- Page, R.D.M. 1996. TREEVIEW: An application to display phylogenetic trees on personal computers. Computer Appl. Biosci. 12: 357–358. [DOI] [PubMed] [Google Scholar]
- Pao, G.M. and Saier, M.H.J. 1995. Response regulators of bacterial signal transduction systems: Selective domain shuffling during evolution. J. Mol. Evol. 40: 136–154. [DOI] [PubMed] [Google Scholar]
- Patthy, L. 1999. Protein evolution, pp. 142–183. Blackwell Science, Malden.
- Pellegrini, M., Marcotte, E.M., Thompson, M.J., Eisenberg, D., and Yeates, T.O. 1999. Assigning protein functions by comparative genome analysis: Protein phylogenetic profiles. Proc. Natl. Acad. Sci. 96: 4285–4288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponting, C.P., Blake, D.J., Davies, K.E., Kendrick-Jones, J., and Winder, S.J. 1996. ZZ and TAZ: New putative zinc fingers in dystrophin and other proteins. Trends Biochem. Sci. 21: 11–13. [PubMed] [Google Scholar]
- Ravasz, E., Somera, A.L., Mongru, D.A., Oltvai, Z.N., and Barabasi, A.-L. 2002. Hierarchical organization of modularity in metabolic networks. Science 297: 1551–1555. [DOI] [PubMed] [Google Scholar]
- Reizer, J. and Saier, M.H.J. 1997. Modular multidomain phosphoryl transfer proteins of bacteria. Curr. Opin. Struct. Biol. 7: 407–415. [DOI] [PubMed] [Google Scholar]
- Rychlewski, L., Jaroszewski, L., Li, W., and Godzik, A. 2000. Comparison of sequence profiles. Strategies for structural predictions using sequence information. Protein Sci. 9: 232–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saier, M.H.J. and Reizer, J. 1994. The bacterial phosphotransferase system: New frontiers 30 years later. Mol. Microbiol. 13: 755–764. [DOI] [PubMed] [Google Scholar]
- Saurin, A.J., Borden, K.L., Boddy, M.N., and Freemont, P.S. 1996. Does this have a familiar RING? Trends Biochem. Sci. 21: 208–214. [PubMed] [Google Scholar]
- Schultz, J., Milpetz, F., Bork, P., and Ponting, C.P. 1998. SMART, a simple modular architecture research tool: Identification of signaling domains. Proc. Natl. Acad. Sci. 95: 5857–5864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Servant, F., Bru, C., Carrere, S., Courcelle, E., Gouzy, J., Peyruc, D., and Kahn, D. 2002. ProDom: Automated clustering of homologous domains. Brief Bioinform. 3: 246–251. [DOI] [PubMed] [Google Scholar]
- Shakhnovich, B.E., Dokholyan, N.V., DeLisi, C., and Shakhnovich, E.I. 2003. Functional fingerprints of folds: Evidence for correlated structure–function evolution. J. Mol. Biol. 326: 1–9. [DOI] [PubMed] [Google Scholar]
- Shen-Orr, S.S., Milo, R., Mangan, S., and Alon, U. 2002. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 31: 64–68. [DOI] [PubMed] [Google Scholar]
- Snel, B., Bork, P., and Huynen, M.A. 2002. The identification of functional modules from the genomic association of genes. Proc. Natl. Acad. Sci. 99: 5890–5895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sofia, H.J., Chen, G., Hetzler, B.G., Reyes-Spindola, J.F., and Miller, N.E. 2001. Radical SAM, a novel protein superfamily linking unresolved steps in familiar biosynthetic pathways with radical mechanisms: Functional characterization using new analysis and information visualization methods. Nucleic Acids Res. 29: 1097–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sriskanda, V., Moyer, R.W., and Shuman, S. 2001. NAD+-dependent DNA ligase encoded by a eukaryotic virus. J. Biol. Chem. 276: 36100–36109. [DOI] [PubMed] [Google Scholar]
- Studholme, D.J. and Dixon, R. 2003. Domain architectures of σ54-dependent transcriptional activators. J. Bacteriol. 185: 1757–1767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatusov, R.L., Mushegian, A.R., Bork, P., Brown, N.P., Hayes, W.S., Borodovsky, M., Rudd, K.E., and Koonin, E.V. 1996. Metabolism and evolution of Haemophilus influenzae deduced from a whole-genome comparison with Escherichia coli. Curr. Biol. 6: 279–291. [DOI] [PubMed] [Google Scholar]
- Wagner, A. and Fell, D.A. 2001. The small world inside large metabolic networks. Proc. R Soc. Lond. B Biol. Sci. 268: 1803–1810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wuchty, S. 2001. Scale-free behavior in protein domain networks. Mol. Biol. Evol. 18: 1694–1702. [DOI] [PubMed] [Google Scholar]
- Yaseen, N.R. and Blobel, G. 1999. Two distinct classes of Ran-binding sites on the nucleoporin Nup-358. Proc. Natl. Acad. Sci. 96: 5516–5521. [DOI] [PMC free article] [PubMed] [Google Scholar]
WEB SITE REFERENCES
- ftp://ftp.ncbi.nih.gov/; NCBI GenBank.
- http://ffas.ljcrf.edu/DomainGraph; CADO.
- http://genome.jgi-psf.org/ciona4/ciona4.download.ftp.html; Ciona intestinalis.
- http://genome.jgi-psf.org/fugu6/fugu6.download.ftp.html; Fugu rubripes sequence.
- http://www.geneontology.org/; GO.
- http://www.graphviz.org/; graphviz.