Vibration pattern of the organ of Corti up to 50 kHz: Evidence for resonant electromechanical force

Abstract

Electromechanical force derived from the soma of the outer hair cell has long been postulated as the basis of the exquisite sensitivity of the cochlea. The problem with this postulate is that the electrical source and mechanical load for the electromechanical outer hair cell might be severely attenuated and phase-shifted by the electrical impedance of the cell and the mechanical impedance of the organ of Corti, respectively. Until now, it has not been possible to experimentally derive the high-frequency electrically induced force at the reticular lamina when the cells are embedded within the organ of Corti. In the study reported here, we succeeded in determining the frequency spectrum of the force up to 50 kHz. This was achieved by measuring both the electrically induced velocity and the mechanical impedance at different radial positions on the reticular lamina without tectorial membrane and with clamped basilar membrane. Velocity was measured with a laser interferometer and impedance, with a magnetically driven atomic force cantilever. The electromechanical force, normalized to the electric current density, exhibited a broad amplitude maximum at 7–20 kHz with a quality factor, Q_3dB, of 0.6 - 0.8. The displacement response was independent of frequency up to 10–20 kHz. The force response compensates for the viscoelastic impedance of the organ of Corti, extending the amplitude response of the organ to high frequencies. It is proposed that the electrical phase response of the cell is compensated with Zwislocki's original mechanism of a parallel resonance in the tectorial membrane–stereocilia complex.

The exquisite sensitivity, frequency selectivity, and dynamic range of hearing in mammals exist not only at the level of the primary auditory neurones but also at the level of the basilar membrane (BM) (1). It is widely believed that this nonlinear tuned BM response is due to an intracochlear source of mechanical energy (2–4). There is compelling experimental evidence that the mechanical energy derives from the electromechanical action of the soma of outer hair cells (OHCs) (5–7): a small number of electromotile OHCs amplify BM motion at low sound pressure levels, thereby enhancing mechanical and neural sensitivity in a narrow frequency-specific region of the cochlea (8). The effective stimulus for this somatic force is a change of the transmembrane potential (9); the force can follow the transmembrane potential up to at least 50 kHz (10).

The major problem with this mechanism is that, when expressed relative to stereocilia deflection, the change of transmembrane potential, the receptor potential, is severely band-limited due to the electrical time constant of the basolateral cell wall (11, 12). For OHCs isolated from the basal cochlear turn, the 3-dB frequency of the receptor potential, relative to stereocilia displacement, is ≈6 octaves (oct) below the place frequency on the BM (13); this implies an attenuation of at least 36 dB. Clearly, if the required electromechanical force really does derive from the soma and not from the stereocilia, the latter mechanism having been postulated based on the electromechanical properties of stereocilia of vestibular hair cells in lower vertebrates (14), then some yet-unknown mechanism is required to compensate for the relatively long time constant. For a debate of somatic versus stereociliary electromechanics as the source of intracochlear mechanical energy, refer to the transcript of an open discussion moderated by Allen (15).

A variety of compensatory mechanisms has been proposed (16–21). However, most suffer from their range being of limited effect or from an absence of direct experimental evidence of their existence. Presently, there are two promising compensatory mechanisms, one extracellular (22) and the other intracellular (20, 21), and both are resonance mechanisms. An extracellular mechanism, a mechanical resonance in the radial motion of the tectorial membrane (TM), has long been proposed as a mechanism for increasing cochlear sensitivity (4, 22–26). However, it was not until recently that direct evidence for this mechanism was provided: (i) by measurement of a resonance in the radial motion of the TM (27, 28), (ii) by demonstrating that BM motion is less sensitive (35 dB) in genetically modified mice with detached TM (29), and (iii) by demonstrating radial TM motion in a complex continuum model of the cochlea (30). An intracellular mechanism, a piezoelectric resonance in the OHC, has been shown theoretically to increase the bandwidth of the electrical admittance of the cell (20, 21); the resonance is located in the upper hearing range (21). Importantly, the resonant frequency coincides with the resonant frequency of the second-order overdamped resonance, which describes the electromechanical displacement response of the isolated OHC, loaded only by extracellular fluid, which was reported by Frank et al. (10). Further support of the piezoelectric resonance of OHCs was provided by the finding that electrical stimulation in vivo can induce BM motion at frequencies up to at least 100 kHz (31).

With both of these resonance mechanisms in mind, we measured the electrically induced velocity at different radial points on the reticular lamina (RL) in an in vitro preparation of the guinea-pig cochlea. We also evaluated the corresponding electromechanical force by measurement of the mechanical impedance of the organ of Corti at these radial positions. A magnetically driven atomic force cantilever was used to measure the impedance; we recently presented this new technique (32). Stimulus frequencies extended up to 67 kHz, well above the upper frequency limit of ≈45 kHz in these animals (33). To perform these experiments, we carefully dissected away the TM, thus removing a resonance source. The BM was clamped mechanically to allow investigation of the mechanics of the organ of Corti without the influence of the BM. We demonstrate multimodal vibration of the organ of Corti and resonant mechanical force.

Methods

Preparation and Measurement. Preparations were made from the first three turns of the mature guinea-pig cochlea at distances of 3–17 mm from the round window. Animals weighed 300–400 g, had a positive Preyer's reflex, and were killed by rapid cervical dislocation. Care and maintenance of the animals were in accordance with institutional and state guidelines. Immediately after removal of the bulla (≈1 min postmortem), the sample was placed in ice-cooled Hanks' balanced salt solution (Sigma; supplemented with 4.1 mM NaHCO₃ and 10 mM Hepes buffer, adjusted to 310 ± 10 milliosmolar, pH 7.38 ± 0.02). The solution warmed up to room temperature (20–22°C, controlled) within the preparation time (≈20 min). The preparation included the modiolar bone, BM, and overlying organ of Corti of a half to a full cochlear turn (Fig. 4 and Supporting Text, which are published as supporting information on the PNAS web site). The TM was removed.

The preparation was fixed with Vaseline to a custom-made support within the experimental chamber, with the BM lying flat on the support. There was a 100-μm-wide slit in the support to allow passage of electric current. Hydrodynamic and surface adhesion forces were sufficiently large to ensure that the BM was mechanically clamped; this was confirmed by measuring BM velocity to be below the noise floor (-30 dB).

Velocity in response to a multitone stimulus (81 frequencies) was measured with a laser Doppler vibrometer, as described in Supporting Text, and extensively presented in Scherer and Gummer (32).

Vibration measurements typically began 40 min postmortem. Typically, 50 min were required for a complete set of measurements in one cochlea. In control experiments, repeat measurements were made during a time span of ≈100 min; no significant changes were observed.

Electrical Stimulation of the Organ of Corti. Electrical stimulation of the organ of Corti was via platinum electrodes, one below and two above the organ of Corti (Supporting Text and Fig. 4). The extracellular electric field parallel to the principal axis of the OHC was 18–36 μV/μm per frequency point. For this range, at a given frequency, we estimate (Supporting Text) a maximum transmembrane potential change of 0.3–0.6 mV for the shortest (30 μm) and 0.8–1.6 mV for the longest (90 μm) OHCs. These values are much less than the maximum ac receptor potential of OHCs, which can be at least 7 mV (34). Displacement amplitude was expressed relative to extracellular current density, which was 1–2 mA/cm², depending on frequency. Current was measured via a 0.9-Ω resistor; the area was ≈1 cm², estimated from the electrode arrangement. Due to the small radial distance between OHCs compared with the distance between electrodes, the stimulus is assumed equal for all rows of OHCs. Velocity of a cotton fiber (40-μm diameter held 3 mm from one end) in extracellular solution was less than the background noise level; this served as a preliminary control that the electrically induced motion of the organ of Corti is not due to electrophoretic fluid drag.

Mechanical Impedance of the Organ of Corti. The mechanical driving point impedance of the organ of Corti was measured with a ferromagnetically coated atomic force cantilever (SC-MFM, Team Nanotec, Villingen-Schwenningen, Germany), with its tip placed on the RL. The RL was preloaded to a surface indentation of 1 μm. This new technique is extensively described in Scherer and Gummer (32). Briefly, a calibrated mechanical force is applied to the cantilever via an external magnetic field. Measurement of the resulting cantilever velocity by using the laser Doppler vibrometer yields the point impedance of the underlying organ of Corti. The noise floor was derived from the cantilever velocity measured with the tip in contact with the support. The noise floor decreased from 10 pm at 480 Hz to 0.1 pm at 67 kHz (effective averaging time, 25 s).

Results

Displacement. Electrically induced displacement of the RL is presented for 61 cochleae, which appeared to be in good morphological condition: (i) orderly arrangement of cells, (ii) cylindrically shaped OHCs, and (iii) RL aligned along its entire length with the focal plane of the microscope. One longitudinal location was examined in each cochlea. Measurements were made at up to nine radial positions. Examples are given in Figs. 1 and 2 and statistical data related to the shape of the spectra are in Table 1, which is published as supporting information on the PNAS web site.

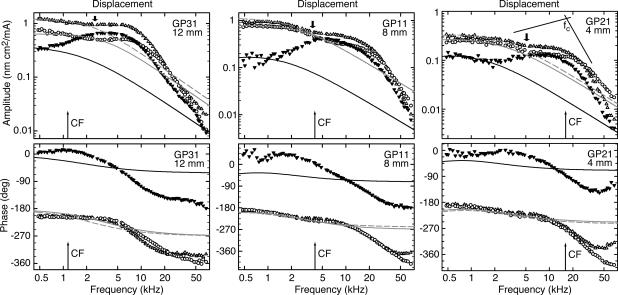
Fig. 1.

Displacement amplitudes (Upper) and phases (Lower) for three preparations, at 12 (Left), 8(Center), and 4 (Right) mm from the basal end of the BM. Thin arrows: CFs calculated from the tonotopic map in Tsuji and Liberman (55): 1.2, 4.2, and 15.2 kHz. Data (symbols) and hypothetical responses (lines) are for IHCs (▾, full black line) and OHCs of the first (○, full gray line) and second (Δ, broken gray line) rows. The lines give the displacement responses to a hypothetical, frequency-independent force acting on the (measured) impedance at the respective position. The amplitude of this test force is scaled arbitrarily to match the measured displacement amplitudes at 480 Hz. Above 4–5 kHz for OHCs and 1–2 kHz for IHCs, the measured displacement is higher than expected for a constant force. The measured frequency responses correspond to a second-order low-pass filter. The appearance of inflection points (thick arrows) in the amplitude responses implies that the filter is not a resonant one. The cutoff frequency, f_c, quantifies the onset of the high-frequency amplitude roll-off and is defined as the intersection of two regression lines (thin lines illustrating the case for an IHC): one just below and the other above f_c, in the asymptotic high-frequency amplitude region. GPX, experiment identifier.

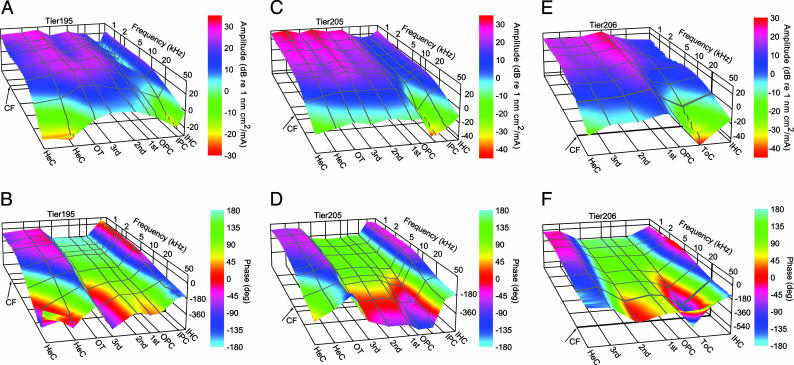
Fig. 2.

Displacement amplitudes (A, C, and E) and phases (B, D, and F) at different radial positions for three preparations. Distances are 11 (A and B), 6 (C and D), and 3 (E and F) mm from the basal end of the BM. Arrows, CFs calculated from the tonotopic map in Tsuji and Liberman (55): 1.6, 8, and 20.9 kHz. Radial positions are IHC, inner pillar cells (IPC), tunnel of Corti (ToC), outer pillar cells (OPC), first- to third-row OHCs, outer tunnel (OT), and Hensen's cells (HeC). Notice phase reversals between IPC and OPC and between second OHC and OT. Note that phase jumps randomly when amplitudes approach the noise level (typically, -30 to -40 dB). TierX, experiment identifier.

Inner Hair Cell (IHC) Motion Relative to First- and Second-Row OHCs. First, the most salient feature, found in all recordings, was that for all stimulus frequencies, the motion of the IHC RL was ≈180° out of phase with the motion of the first- and second-row OHCs (Figs. 1 Lower and 2 B, D, and F). (Henceforth, we no longer specify that RL motion is meant; for example, OHC motion means motion of the RL at the OHC.) These two OHC rows have similar amplitude and phase responses, except above ≈30 kHz, where the phase lag of the first row tends to be slightly larger than that of the second row, particularly in the basal turn. Taken together, the data (below 30 kHz) mean that these two OHC rows contract (elongate) in unison, causing the RL of the IHC to move toward scala vestibuli (tympani).

Second, for all three cell types, the high-frequency amplitude slope was approximately -12 dB/oct [-11.6 ± 1.4 dB/oct for first- and second-row OHCs (n = 167) and -14.1 ± 1.9 dB/oct for IHCs (n = 62)] and the high-frequency extreme lagged the low-frequency extreme by ≈180° (188 ± 38° for first- and second-row OHCs and 181 ± 27° for IHCs). This means that the frequency responses are those of a second-order low-pass filter. The IHCs exhibit a maximum, so that the low-pass filter might be referred to as a (under-damped) resonant filter. The maximum is evident as attenuation (10–20 dB) of the low-frequency response relative to that for the OHCs. Although the OHC response is superficially similar to an overdamped resonant filter, there usually existed an inflection point in the amplitude response (thick arrows in Fig. 1), somewhere between 2 and 5 kHz, which also coincided with a phase lag of 45° relative to low frequencies. This implies that the two-pole filter is not a resonant one, but is a combination of two first-order low-pass filters with different 3-dB frequencies, the first of which is located in the region of 2–5 kHz.

Third, the cutoff frequency of the amplitude response, defined as the intersection of two regression lines (Fig. 1) below and above the cutoff frequency (33), was situated near the characteristic frequency (CF) for the mean basal-turn location [18.7 ± 5.1 kHz for first-row OHC (n = 19), 17.7 ± 6.7 kHz for second-row OHC (n = 30), and 14.9 ± 3.1 kHz for IHC (n = 24)]. The cutoff frequency decreased exponentially with position along the cochlea, but the space constant (11.2 ± 1.0 mm/oct for first-row OHC, 9.3 ± 1.0 mm/oct for second-row OHC, and 23.3 ± 3.8 mm/oct for IHC) was so long compared with that for CF (3.6 mm/oct according to ref. 33) that in the second and third cochlear turns the cutoff frequency was located at least two oct above CF. In other words, so far as cochlear function is concerned, these filter functions for the OHCs are effectively all-pass functions. A similar conclusion was drawn for the electromechanical displacement of the isolated OHC (10).

Third-Row OHC Motion. The third-row OHCs moved with similar amplitudes as the first- and second-row OHCs (Fig. 2). They usually moved in phase with these two OHC rows in the second and third turns (29/32 and 16/17 cases, respectively), but for the first turn, about half (11/24) exhibited antiphase motion (Fig. 2F). For the case of antiphase motion relative to the first- and second-row OHCs, the third-row OHCs moved in phase with the outer tunnel and Hensen's cells.

Tunnel of Corti. The motion of the inner border of the inner pillar head was almost identical to that of the adjacent IHC (Fig. 2); amplitude and phase differences were <5 dB and 5°, respectively. A similar observation was made for the outer border of the outer pillar head and the first-row OHC (Fig. 2 B and D); the differences were <5 dB and 5°. Because the IHC moves in counterphase to the first- and second-row OHCs, there must be a pivot point somewhere near the attachment of the inner and outer pillar heads. In addition, displacement amplitude and phase at the attachment region were very sensitive to small radial changes in the measurement position and sometimes depended strongly on frequency (Fig. 2 A, C, and E). We therefore conclude that this pivot point is radially located near the attachment between inner and outer pillar heads, and that its exact position changes somewhat with frequency.

Hensen's Cells and Outer Tunnel. Hensen's cells and the RL of the outer tunnel moved in opposite phase to the first- and second-row OHCs (Fig. 2). Therefore, another pivot point, in addition to the one at the tunnel of Corti, must exist between second-row OHCs and the outer tunnel, either medial or lateral to the third-row OHCs. In the first cochlear turn, the pivot point was lateral to the third-row OHCs in about half of the cases (54%), and for the second and third cochlear turns, the pivot point was usually (91–94%) lateral to the third-row OHCs.

Effect of Drugs on Displacement. In these experiments, all agents that affected the electrically induced displacement did so by attenuating the amplitude response independent of frequency but without affecting the phase response. An example is given in Fig. 5, which is published as supporting information on the PNAS web site, together with details of the perfusion system.

Blockers of Electromechanical Transduction. Nonspecific electrically induced motion of the organ of Corti was tested by application of blockers of electromechanical transduction. First, sodium salicylate is known to reduce electromotility (35, 36), axial cell stiffness (35), and nonlinear capacitance (36). Within 5–10 min after perfusion with 0.2–10 mM, salicylate reversibly reduced displacement amplitudes, equally at IHCs and OHCs, by factors of 0.54 ± 0.22 for 0.2 mM salicylate (n = 13), 0.39 ± 0.11 for 1 mM salicylate (n = 6), and 0.34 ± 0.08 for 10 mM salicylate (n = 11). The mean attenuation for all concentrations was 0.44 ± 0.20 (n = 30). Second, because electromotility depends on intracellular Cl^- (19, 37), and because niflumic acid, a nonspecific anion channel inhibitor, reduces non-linear capacitance (19), we tested the chloride channel blocker anthracene-9-carboxylic acid [9-AC (38)]. Within 3–5 min of perfusion, 9-AC of concentration 0.2–1 mM reversibly reduced displacement amplitudes by a factor of 0.24 ± 0.05 (n = 8). Taken together, the experiments with these two blockers unequivocally demonstrate that the electrically induced displacement of the organ of Corti derives from the electromechanical action of the OHCs and not from electrophoretic fluid drag or from surface charges.

Blockers of Channels at the Apical Surface. To examine the possibility of current flow-through channels at the OHC apical surface, stereocilia, and cuticular plate, we perfused with a mixture containing 600 μM dihydrostreptomycin for mechano-sensitive transducer channels (39), 600 μM suramin for P_2X-receptors (40), and 10 μM carboxyeosin for Ca²⁺-ATPase (41). Moreover, KCl was replaced with CsCl to block potassium currents. This mixture had no significant effect on displacement (n = 3), as examined over a period of 20 min after perfusion. These results suggest that current through channels at the apical surface is negligible under our experimental conditions.

Blockers of Channels at the Basal Surface. To examine the possibility of current flow-through channels at the OHC basal surface, we perfused with a mixture containing the apical-surface blockers and blockers of cation channels in the basal wall: 100 nM tetrodotoxin for the Na⁺ channels (42), 200 μM linopirdine for the KCNQ4-channels (43), 10 μM paxilline for the BK channels (44), and 30 μM tubocurarine for the α-9 receptors (45). This mixture reversibly reduced the displacement amplitudes by a factor of 0.55 ± 0.06 (n = 3), within 3–5 min after perfusion. As a test of the significance of this block, in a further set of experiments, we augmented this mixture with a combination of 200 μM anthracene-9-carboxylic acid, which we have shown to block electromechanics, and another Cl^- channel blocker, 50–100 μM tamoxifen (46). This mixture reversibly reduced the displacement amplitudes by a factor of 0.14 ± 0.02 (n = 3), within 3–5 min after perfusion. This suggests a multiplicative effect of the blockers of electromechanics and cation channels in the basal wall. [Tamoxifen alone had no significant effect (n = 5).] Taken together, these results suggest that, in this experimental configuration, current enters the OHC through the basal cell membrane.

Force. In 30 of the preparations for which the electrically induced velocity was measured, the mechanical driving-point impedance at the different radial positions on the RL was also measured. This allowed the electrically induced force at the different radial locations to be derived from the product of the impedance and the electrically induced velocity (Supporting Text). Examples are given in Fig. 3, and statistical data related to the shape of the spectra are in Table 2, which is published as supporting information on the PNAS web site.

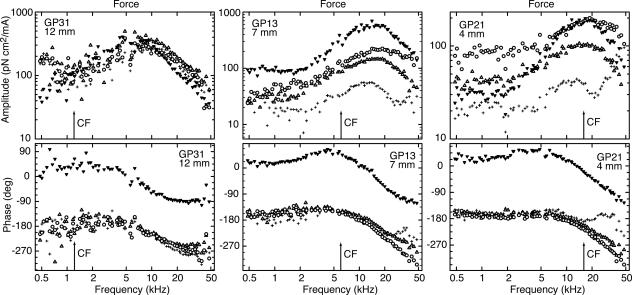
Fig. 3.

Force amplitudes (Upper) and phases (Lower) for three preparations at 12 (Left), 7 (Center), and 4 (Right) mm. Arrows, CFs calculated from the tonotopic map in Tsuji and Liberman (55): 1.2, 5.8, and 15.2 kHz. Data symbols are for IHCs (▾) and OHCs of the first (○), second (Δ), and third (+) rows. The maximum is most pronounced for the IHC. Above the frequency of the maximum, amplitudes and phases correspond to a low-pass filter of order between one and two. GPX, experiment identifier.

Force at IHC Relative to Forces at First- and Second-Row OHCs. The most salient and consistent finding was that force, both at the IHC and the OHCs of the first and second rows, always exhibited a resonance. The resonance was broad, it was quantified by the quality factor, Q_3dB, defined as the reciprocal of the relative 3-dB bandwidth. On average, Q_3dB was 0.6–0.8; there was no statistical difference between values of the different cochlear turns. The peak frequency was similar to CF in the basal turn, but in the more apical turns, it was several oct above CF. Amplitudes were roughly constant between 0.48–2 kHz with values of 30–100 pN cm²/mA for the OHCs and 10–70 pN cm²/mA for IHCs. The peak amplitude relative to these low-frequency values was 8 ± 2 dB for the OHCs (n = 68) and 17 ± 3 dB for the IHCs (n = 38).

As with the displacement phases, all preparations exhibited a phase difference of ≈180° between the IHC and the OHCs of the first and second rows. However, in contrast to the displacement data, the phase lag between the low- and high-frequency extremes was not consistently near 180° but ranged between 90° and 200°, with no obvious dependence on radial or longitudinal recording locations. Some of this variation is obviously related to the fact that the resonance is broad and that the highest measurement frequency of 50 kHz was insufficient to distinguish a high-frequency asymptote. However, data from the third cochlear turn clearly indicate that the frequency range was sufficient at this longitudinal location, and the phase lag was nevertheless close to 90°. A corresponding observation was made for the high-frequency amplitude slopes, which ranged from -4 dB/oct to -10 dB/oct. In other words, the resonance is not a simple second-order resonance as found for lumped systems but, according to the phase data, is indicative of a system with order between about one and two (or between 2/3 and 5/3 based on the high-frequency amplitude slopes).

Force at Third-Row OHCs. Force spectra at third-row OHCs were different from those at the first- and second-row OHCs: (i) in most cases, amplitudes were 5–10 dB smaller; (ii) in the first and second cochlear turns, the phase lag between low and high frequencies was never >90°, whereas in the third turn, there were three subpopulations grouped around 90°, 270°, and 450°; and (iii) two amplitude peaks, separated by a dip, often occurred (70% data). In most cases (23/25), low-frequency force at all three rows of OHCs was in phase. The exceptions were two preparations in the first cochlear turn, where the force at the third row was in counter phase to that of the other two rows.

Discussion

For sensory and motoric cells embedded in the organ of Corti, these experiments have shown that neither the displacement nor the force responses at the RL, induced by the electromechanical action of the OHCs, suffers from significant attenuation or phase lag over the frequency region for which the cells are required to process low-amplitude sound. Most importantly, the force exhibited a broad resonance.

We have also shown that the RL does not move as a rigid plate in response to the electromechanical action of the OHCs but moves as a frequency-independent double lever with two pivot points. We have also found these two pivot points in the presence of the TM (unpublished observations). Presumably, under in vivo conditions, this active (electrically induced) deformation of the organ adds vectorially to the passive “rotating wedge” motion observed in the in vitro preparations in which the BM is stimulated by fluid motion (47–49).

Wide-Band Displacement Response. The relatively flat displacement responses (up to at least CF) might have been expected from our experimental configuration, provided the organ of Corti were purely elastic. Thus, by means of channel blockers, we showed that the excitation current entered the cells not through (known) channels at the apical surface but through the OHC soma. Theoretically, for isotropic electrical conditions, the change of transmembrane potential due to an external electrical field must be independent of frequency for our experimental condition, because with the current entering the soma, this potential will be determined by the ratio of the electrical impedances of the entry and exit pathways, which in turn is equal only to the inverse of the ratio of these path lengths. In other words, theoretically, we have a frequency-independent voltage divider, akin to the one for electrical stimulation of an isolated OHC held in a glass capillary (9). However, contrary to displacement responses in the latter recording configuration (10), the displacement response of the RL in situ could not be described by that of a second-order overdamped resonant system. Instead, the response was that of a second-order nonresonant low-pass filter. The nonresonant characteristic can be readily understood from the mechanical impedance and force, as described in the next section.

Here it should be emphasized that, although the wide-band displacement response can be explained by this general voltage-divider argument, the exact current pathway is unknown. The results suggest that the current enters through the basal wall, but it could enter through yet-unidentified channels at the apical surface. This uncertainty means that the results do not allow definite conclusions to be drawn about generation mechanisms of the high-frequency transmembrane potential in vivo, for example, whether derived from the extracellular potential gradient between scalae media and tympani as proposed in ref. 16. It also means that we cannot exclude purely electrical mechanisms for solving the time-constant problem, such as those proposed in refs. 16, 18, and 19.

Resonant Force Response. The most surprising feature was the shape of the force response, which exhibited a broad resonance at 7–20 kHz, depending on the position along the cochlea (Fig. 3). This is in agreement with theoretical results by Spector et al. (20) and Weitzel et al. (21), who predict an electromechanical resonance of the OHC at high frequencies caused by the piezoelectric properties of the cell's lateral wall. The broad maximum significantly extends the frequency response of the organ's displacement response. This is important, because the organ of Corti is not purely elastic; it is viscoelastic at functionally relevant frequencies (32). Whereas for a constant force, displacement amplitudes would drop above ≈4 kHz due to the viscoelastic impedance of the organ (lines in Fig. 1), a force increasing with frequency above 4 kHz compensates the viscoelastic impedance and leads to the observed wide-band displacement response (symbols in Fig. 1). [This compensation is largest for the basal turn (Fig. 1), where it can be as much as 20–30 dB.] Indeed, the first low-pass filter apparent in the displacement response (amplitude inflection and 45° phase lag at 2–5 kHz, thick arrows in Fig. 1) is probably due to this viscoelastic impedance. Then, the second low-pass filter in the displacement response derives from the force relative to the extracellular potential. Its cutoff frequency, obtained from the cutoff frequency, f_c, of the displacement response, ranges from 9.5 to 18.7 kHz, depending on position along the cochlea (Table 1). The two most likely origins of this filter are: either the motor molecule acts as a lossy capacitor at these high frequencies and the transmembrane potential is frequency-independent, or conversely, the transmembrane potential is low-pass filtered at these high frequencies and the motor molecule is frequency-independent, at least up to 40 kHz. Measurement of the transmembrane potential should resolve this issue.

Importantly, the IHC exhibited a larger force gain, relative to low frequencies, than the OHCs: on average, 17 dB compared with 8 dB. This is evident because of attenuation of the low-frequency response of the IHC. Remembering that the organ of Corti is a fluid-filled viscoelastic tube, the most parsimonious explanation for the larger IHC gain is that at lower frequencies, the force developed by the OHCs is increasingly coupled longitudinally through the fluid rather than radially to the IHC.

If the change of transmembrane potential is estimated from the voltage drop along the cell (see Methods), and a voltage-divider ratio of unity is assumed, then the low-frequency OHC forces are on the order of 50–300 pN/mV. However, because the change of transmembrane potential is only an approximate upper bound, these normalized forces could be larger. Nevertheless, they agree with more recent published estimates of 50–100 pN/mV (10, 50–53). Because in our preparation OHCs are mechanically coupled, these force estimates provide an upper bound for isolated OHCs. Importantly, the forces are produced for changes of transmembrane potential that are much less than the saturating ac receptor potential of OHCs (see Methods).

Implications for Cochlear Amplification. Due to the frequency response of the purely viscoelastic impedance of the organ (32) and the broad maximum in force amplitude, no displacement resonances of the organ of Corti appeared below 50 kHz. Acknowledging the caveat that the preparation is not an in vivo one, this leads to the conclusion that the localized amplification of the BM traveling wave cannot be accounted for by a place-specific resonance of the organ of Corti. Therefore, an important assertion based on our data is that a putative second resonance providing local amplification to the BM traveling wave can occur, if at all, only at the TM level. Furthermore, the phase opposition in auditory nerve fiber responses of IHCs and OHCs suggested by Zwislocki (54) concurs nicely with the counter-phasic motion of these cells at the RL level.

Although the broad resonant amplitude response of the force might compensate the amplitude attenuation caused by the relatively long time constant of the basolateral cell membrane, it is unlikely to compensate the phase roll-off. This is because the phase response of the force for frequencies up to CF was almost independent of frequency (the largest phase delay at CF was ≈45° in the basal turn; Fig. 3). Consequently, the 90° phase delay introduced by the membrane time constant cannot be compensated by this mechanism; if not compensated, the OHC in vivo will act as an active attenuator (27). However, it could be compensated by the TM resonance suggested by Zwislocki (26), in which TM inertia and stereocilia bending compliance form a parallel resonance tuned below CF. The resulting 180° phase rotation near CF will ensure that the electromechanical OHC force is in the correct phase to cause active amplification rather than active attenuation (27).

Conclusion

We propose that the time-constant problem is solved by the synergistic action of two resonant systems: (i) the piezoelectric resonance in the OHC proposed by Spector et al. (20) and Weitzel et al. (21) is mainly responsible for amplitude compensation, and (ii) the parallel resonance of the TM–stereocilia complex proposed by Zwislocki (26) is mainly responsible for phase compensation.