Abstract
In this paper, we demonstrate velocity-level closed-loop control of a tethered magnetic capsule endoscope that is actuated via serial manipulator with a permanent magnet at its end-effector. Closed-loop control (2 degrees-of-freedom in position, and 2 in orientation) is made possible with the use of a real-time magnetic localization algorithm that utilizes the actuating magnetic field and thus does not require additional hardware. Velocity control is implemented to create smooth motion that is clinically necessary for colorectal cancer diagnostics. Our control algorithm generates a spline that passes through a set of input points that roughly defines the shape of the desired trajectory. The velocity controller acts in the tangential direction to the path, while a secondary position controller enforces a nonholonomic constraint on capsule motion. A soft nonholonomic constraint is naturally imposed by the lumen while we enforce a strict constraint for both more accurate estimation of tether disturbance and hypothesized intuitiveness for a clinician's teleoperation. An integrating disturbance force estimation control term is introduced to predict the disturbance of the tether. This paper presents the theoretical formulations and experimental validation of our methodology. Results show the system's ability to achieve a repeatable velocity step response with low steady-state error as well as ability of the tethered capsule to maneuver around a bend.
I. Introduction
Magnetic actuation is the favored method of active locomotion of robotic capsule endoscopes throughout the gastrointestinal tract [1]. Owing to the ability to produce clinically relevant forces given a relatively small form factor, permanent magnets have been the preferred source of magnetic field gradient resulting in a standard configuration of an external permanent magnet (EPM) that drives an internal magnet-embedded capsule. As a result of magnetic force having an inverse-quartic relationship with distance, fine motions of the EPM are necessary to impart precise movements of the controlled capsule; commonly achieved by mounting the EPM on the end-effector of a serial manipulator [2]. Although this methodology has been shown feasible in locomotion through the colon, open-loop driving has been shown to last over twice as long as a procedure with a standard endoscope [3]. Reduction in procedure time is critical for clinical acceptance of magnetic colonoscopy.
Previous studies relied on the operator commanding the motion of a robot's end-effector, or EPM. The resulting capsule motion is neither intuitive nor smooth as the capsule is driven indirectly and movements do not necessarily coincide with that of the robot's end-effector (i.e. the capsule is stuck behind a haustral fold). Considering the large force gradient in permanent magnet actuation, irregular (segmented and jerky) motion, as well as loss of magnetic coupling, is commonplace. Real-time feedback of capsule position and orientation allows for closed loop control of the device that may aid in diminishing the aforementioned adverse behaviors. Localization schemes have been introduced that conveniently utilize the actuator's magnetic field as well as proprioceptive sensing without the need for additional hardware [4], [5]. Closed loop control has previously been shown on a constrained 2D platform [6] as well as in a tank of water for application in gastric screening [7]. Mahoney et al. developed a mathematical relationship between robot joint velocities and capsule position and heading to achieve 5 degree-of-freedom (DoF) control where 3 DoFs in position control utilized feedback while 2 DoFs in orientation were controlled in open-loop. Assumptions of low capsule velocity and acceleration as well as that of the capsule's magnetic moment vector aligning with the EPM's field were made. This was the first demonstration of closed loop control for digestive screening; however, the experimental setup was constrained in that localization of the capsule was achieved by external cameras, and thus required additional implementation of clinically relevant localization.
In this paper, we present closed-loop velocity control of a tethered magnetic endoscope for colonoscopy. While building on the theoretical control scheme of Mahoney et al., we introduce feedback orientation control to achieve 5 DoF closed-loop control and keep all aspects of the platform clinically relevant as shown in Fig. 1. The localization utilized in this platform [5] relies only on its internal sensors and the actuating magnet. The soft-tethered magnetic capsule maintains all functionality of a traditional endoscope and hence a tether is necessary for introduction of standard endoscopic tools. Our control scheme accounts for disturbances that result from the tether, as well as external forces from the environment. Mahoney et al. implemented position-level control on the capsule by commanding it to pass through a desired trajectory that was a set of points arranged in a specified manner. In a position control scheme, the error is computed according to a fixed approaching waypoint, that results in a decrease in error and, in turn, a decrease in velocity until the next waypoint is set. In velocity control, on the other hand, smoother motion is possible because this deceleration does not occur. We wish to minimize effects of such jerky motion as, eventually, this capsule's camera view must be utilized not only for directing locomotion, but also for careful diagnostics of colonic tissue. We have thus implemented a velocity controller that commands a constant velocity from the capsule as a trajectory is traversed. A set of points is used to set a preliminary desired path shape, and furthermore, a cubic spline is then fit onto these points to provide a smooth trajectory. The tethered capsule is then commanded to follow this trajectory while maintaining its heading always aligned with this path, and thus nonholonomic. We have validated our methodology in both a dynamic simulation environment as well as on our experimental platform.
Fig. 1.
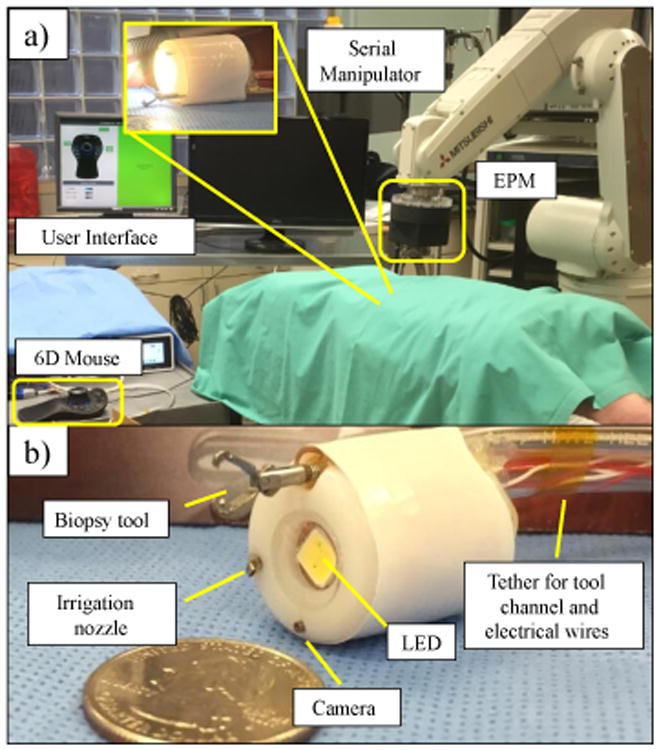
(a) Experimental platform (b) Soft-tethered endoscopic capsule
II. Platform and Software Environment
The soft-tethered capsule endoscopy system is inspired by the magnetic-air-capsule [8] with a design that preserves the capabilities of traditional endoscopes: vision, illumination, passage of endoscopic tools, irrigation and insufflation. The soft-tether encloses a tool channel that allows the passage of traditional endoscopic tools that are used for biopsy and administration of therapy. Additional channels in the soft-tether allow for irrigation, insufflation, and the routing of electrical wires. The capsule (20 mm diameter, 22 mm length) that is attached to the end of the soft-tether contains six Hall-effect sensors and an inertial measurement unit that are used for real-time localization. A cylindrical permanent magnet (D77-N52, 7/16″ diameter and length, axial magnetization with residual flux density of 1.48 T, K&J Magnetics Inc, USA) is used for magnetic manipulation. A 6-DoF serial manipulator (RV-6SDL, Mitsubishi Corp, Japan) is used to hold the external cylindrical permanent magnet (N52, 4″ diameter and length, axial magnetization with residual flux density of 1.48 T, ND_N-10195, Magnet World Inc., USA) at its end-effector.
A. Magnetic Localization
The configuration of permanent magnets in our system allows for 3-DoF control in position and 2-DoF control in orientation. Thus, a localization system capable of detecting the pose of the capsule in at least 5-DoF is necessary for feedback control. In this paper, we use a localization scheme that provides 6-DoF pose of the capsule as described in [5]. The scheme exploits the magnetic field of the external permanent magnet that is already present in the system for maneuvering the capsule. The six Hall-effect sensors in the capsule are arranged such that they provide an estimate of the 3D magnetic field vector at the center of the capsule. These sensors are placed strategically around the internal magnet of the capsule to minimize the influence of its own field. The inertial measurement unit is used to compute the orientation of the capsule, which, in conjunction with the orientation of the EPM obtained from the manipulator forward kinematics, is used to express the magnetic field vector at the capsule in EPM frame. The capsule's position is then computed by searching through an a priori generated magnetic field map. The magnetic field map is generated offline using finite element analysis software such as COMSOL (COMSOL Multiphysics, Sweden) by numerically solving for the magnetic field of the EPM on a uniform grid of points according to the magnetic current model [5] of an axially magnetized cylindrical magnet:
| (1) |
where p is a point on the uniform grid, p″ is a point on the surface of the permanent magnet and jm is the equivalent surface current density. The symmetry of the magnetic field about the magnet's longitudinal axis is exploited to dramatically improve the efficiency of the search algorithm where instead of searching the entire 3D map, only one quadrant of a plane is searched, thereby allowing real-time localization.
B. Dynamic Simulation Environment
Software for our platform was written using the open-source Robotic Operating System (ROS) [9]. We developed a simulation of our experimental setup using Gazebo, an open-source simulation environment with a built-in physics engine. In this environment, we are able to simulate factors such as component weights, tether dynamics, and friction. Since Gazebo does not yet have the capability to simulate continuum objects, the tether was modelled with a large number of short links joined by 2-DoF universal joints. Additionally, we have built a custom plugin to simulate magnetic interaction [10]. Support between Gazebo and ROS allows for Gazebo to emulate a node, and thus all code, excluding the magnetic localization algorithm, is executed identically whether running a simulation or on the physical platform.
III. Control
The theoretical formulation presented here builds upon the work of Mahoney et al. [7] with certain expressions repeated for completeness of formulation and with nomenclature maintained whenever possible. Throughout this text we designate vectors with a lowercase bold letter (v), matrices with an uppercase (M), the rate of change of a parameter with respect to time with a dot (v̇), and a hat over a vector to indicate a magnitude of unity (v̂). The actuator's (EPM) and capsule's position vectors are denoted by pa and pc, respectively, with the relative position vector between the two denoted by p = pc − pa. The actuator's and capsule's respective magnetic moment vectors are denoted by ma and mc.
A. Theoretical Modeling
The EPM and capsule's magnet are each treated as a point-dipole resulting in the following expressions for the respective magnetic force and torque imparted on the capsule by the EPM:
| (2) |
| (3) |
where D = 3p̂p̂⊤ − I and Z = I − 5p̂p̂⊤
The serial manipulator's geometric Jacobian relates joint velocities to velocities in task space (ẋ = JR(q)q̇). The axial symmetry of the EPM results in a loss of degree of freedom about the axis aligned with m̂a and thus results in a rank-deficient Jacobian. As specified in [7], the following expression denotes the imparted rate of change in position and heading of the actuator magnet resulting from the manipulator's joint speeds:
| (4) |
Where S(a) ∈
 (3) denotes the skew-symmetric form of the cross-product operation.
(3) denotes the skew-symmetric form of the cross-product operation.
We developed the Jacobian matrix JF(p, m̂a, m̂c) ∈ ℝ6×9 to linearize the aforementioned force and torque expressions with respect to the system's state variables as follows:
| (5) |
We rearrange terms to utilize JR:
| (6) |
which can be written as:
| (7) |
where Jacobian JFA denotes the actuating-force-torque Jacobian:
| (8) |
The expression above is then used to compute desired actuator joint velocities that are then integrated and sent to the robot's low-level controller. The above expression is solved for q̇ and results in the following:
| (9) |
Here, is the weighted least-squares inverse of the actuating-force-torque Jacobian where JW = WxJFAWq with Wx and Wq respectively denoting task and joint space diagonal weight matrices that are selected to punish motion in specified DoFs.
B. Trajectory Generation
The colon has a diameter of approximately 7 cm that contains multiple bends and is deformable owing to mesentery fixation in only certain segments of the lumen [11]. Although the capsule is intended to be teleoperated when in clinical use, we now focus our attention on control and thus set a fixed trajectory that is commanded and followed autonomously. The input to the controller algorithm is a set of pre-defined trajectory points that roughly describe the trajectory. A spline is then generated once the control algorithm begins that fits a curve that is smooth up to second degree between the path points. A continuum in curvature allows for smooth nonholonomic motion. A sample fitting between a few points is shown in Fig. 3.
Fig. 3.
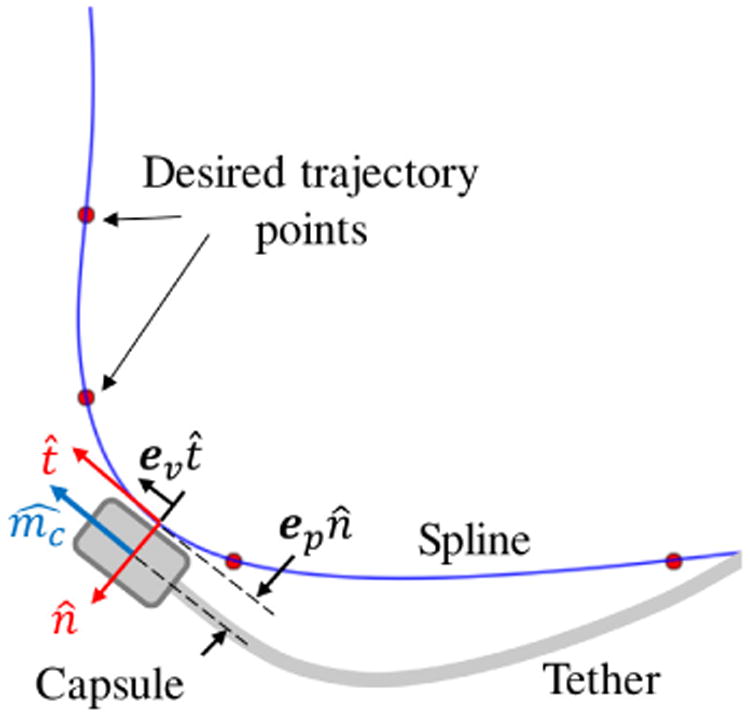
Spline fitted to a small number of desired trajectory points.
The use of cubic spline interpolation allows us to create a smooth curve that passes through any number of desired points, allowing us to specify trajectories by a variable number of waypoints. This curve is a stitching of cubic polynomials that join at knots (the waypoints) and, unlike Bezier curves, the order of polynomial functions does not increase with an increased number of waypoints and thus does not become computationally overbearing [12]. An additional benefit is that the path, by definition, passes through all waypoints giving more controllability in path generation. This is especially important in ensuring that curve is not generated in an area outside of our desired path (i.e. experimental pseudo-colon acrylic tube). Conditions such as the curve passing through the ith and i + 1th waypoints with defined second and third order polynomial coefficients and minimized bending throughout the path allow for computing a single solution. We utilize the python SciPy Interpolation package [13] based on algorithms developed by de Boor [14], Cox [15], and Dierckx [16].
C. Velocity Control
In developing a closed-loop control scheme, our main aim was to establish a smooth and controllable motion of the capsule. In our previous work [10], we have observed jagged motion resulting from the capsule approaching waypoints one-by-one, and thus have implemented velocity control to smooth out motion. The implemented control scheme is shown in figure Fig. 2. At each time increment, we estimate the net force applied on the capsule and calculate desired forces and torques that will drive the capsule to minimize error from the commanded velocity input. We use the dipole-dipole model to estimate the magnetic forces and torques applied to the capsule and use a feed-forward resistance term to estimate the forces applied to the capsule from the tether. These resistance forces are assumed to always act in the negative tangent direction with respect to the nearest spline point. This feed-forward term is denoted as follows:
Fig. 2.
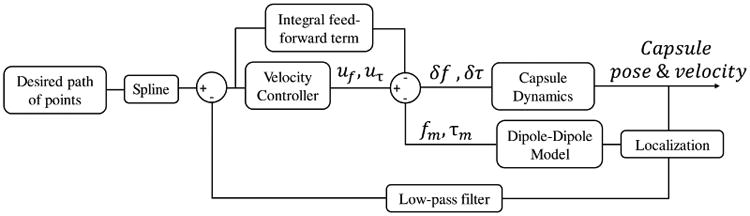
Control loop of tethered magnetic capsule system.
| (10) |
where eν = ṗcdes − ṗc denotes the velocity error vector. This can be thought of as the accumulation of the shortcoming in force to impart motion on the capsule. If there were no resistance forces, any applied force would result in motion. A velocity error therefore indicates the presence of resistance force and it is accumulated by the feed-forward term. Measurement of acceleration directly would serve as a more direct indication of resistance, however, this would consist of highly noisy measurements and is therefore avoided. In the following expressions, we denote position error as ep = pcdes − pc, and the directions of the tangent and normal vectors at the point on the spline that is closest to the center of the capsule by t̂ and n̂, respectively, as seen in figure Fig. 3. The desired position is not the desired next position as would be used in a position control scheme, rather the nearest point on the spline. The orientation error is denoted as eo = ĥc × ĥdes where ĥc and ĥdes are the current and desired capsule headings, respectively. A desired velocity of constant magnitude is commanded in the direction of t̂, onto which the velocity error is projected. A proportional position control acts on the error projected onto n̂ and enforces nonholonomic motion. The expression for desired force is as follows:
| (11) |
The summation of forces on the capsule results in the final commanded increments in force and torque:
| (12) |
IV. Experimental Validation
The velocity control algorithm was first validated in our simulation environment where parameters such as capsule trajectory and position could be monitored in real-time. Conducting virtual experiments enabled us to tune control parameters before implementing our algorithms on the physical platform. Although these parameters had to be fine-tuned on the physical platform owing to an imperfect simulation, this initial guess significantly reduced both algorithm development time and aided in avoiding faulty situations where high robot joint velocities were observed.
Two types of trajectories, each with five trials, were then implemented. A straight line trajectory was used to asses the step response of the controller while a trajectory with a single bend was used to assess how well the controller followed a given trajectory.
A. Validation on Experimental Platform
The experimental setup shown in Fig. 4 consists of the 6 DoF serial manipulator, the soft-tethered capsule and an acrylic tube that provided nonholonomic constraints akin to the colon. In order to create an environment with realistic friction and resistance forces as would be found in a real colon, the tube was lubricated before the trials. Waypoints were created to follow the shape of the tube and, as previously described, the controller generates a smooth spline trajectory that passes through each of the input waypoints.
Fig. 4.
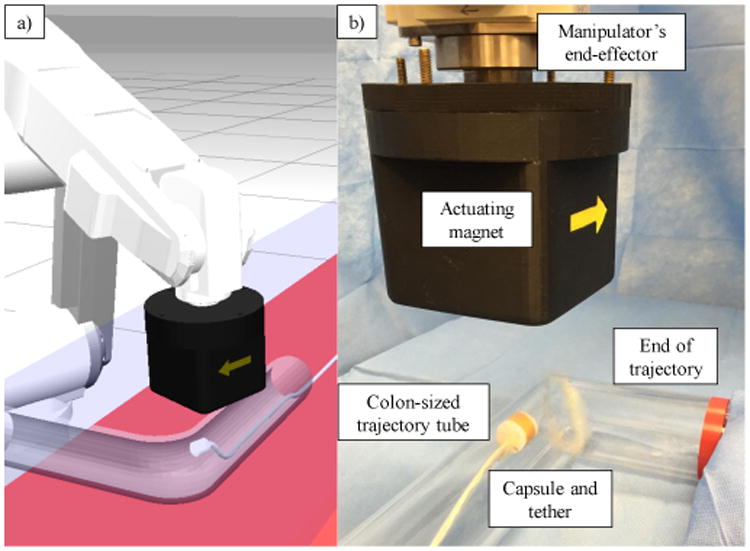
(a) Gazebo simulation environment with physics engine and a custom built magnetic interaction plugin. (b) Experimental setup with tethered capsule, robot manipulator and physical tube providing nonholonomic constraints.
The step response (conducted on the straight segment of the of the acrylic tube) of the velocity controller to a step input of 0.01 m/s is shown in Fig. 5. The velocity shown is computed by low pass filtering the discrete time derivative of the position output of the magnetic localization algorithm. The average rise time (time to 90% of reference input) was 2.51 s, however, because this value is dependent on the cutoff frequency of the low pass filter, it is not a true representation of the rise time. The average maximum velocity error during the ten seconds after the rise time is 0.005 m/s while the average root mean square error during the same period is 0.002 m/s. The fluctuations seen in velocity result from random environmental variables such as friction that varies with the height of the external magnet and alignment of the tether. Although this fluctuation is acceptable considering that it is in velocity, the colon is highly lubricated and we hypothesize that this fluctuation will be reduced.
Fig. 5.
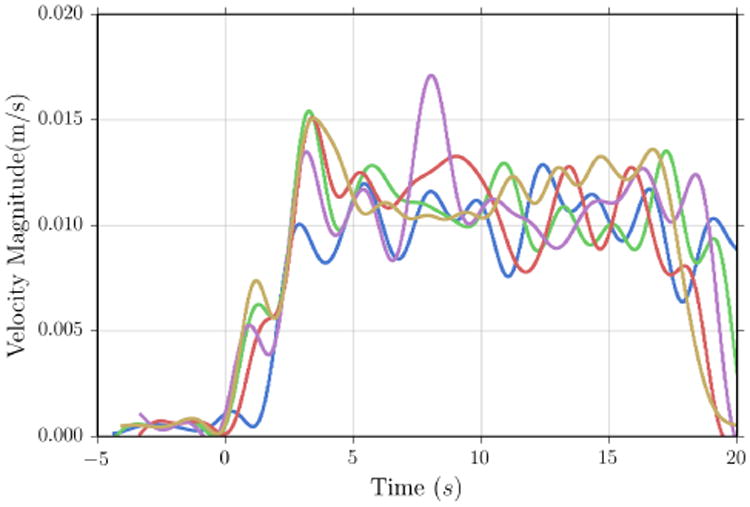
Step response of velocity controller to a reference velocity of 0.01 m/s in a straight line trajectory.
The results from five trials of the velocity controller following a curved trajectory are shown in Fig. 6. This trajectory was chosen as it exemplifies the challenges faced when attempting to maneuver the capsule around a corner in the lumen while maintaining a specified heading and pitch/tilt angle. The speed of the capsule during each trial remained reasonably close to the commanded speed except when making the turn. The deviation can be attributed to the sharp corner in the tube, which causes the capsule to get stuck until its heading is tangent to the lumen of the vertical segment of the tube. The corner also becomes a pivot about which a moment is developed by the tether. The capsule's drift to the left side of the spline in Fig. 6 can be attributed to this disturbance in moment. A feed-forward torque compensation term is necessary to eliminate this error but requires further study of tether mechanics. The trajectory shown in red is an outlier with a loop in the corner of the trajectory. This odd shape resulted from the tether becoming stuck at the entrance of the tube, resulting in the EPM exerting a large force on the capsule, and once the tether's static friction was overcome, the capsule shot forward.
Fig. 6.
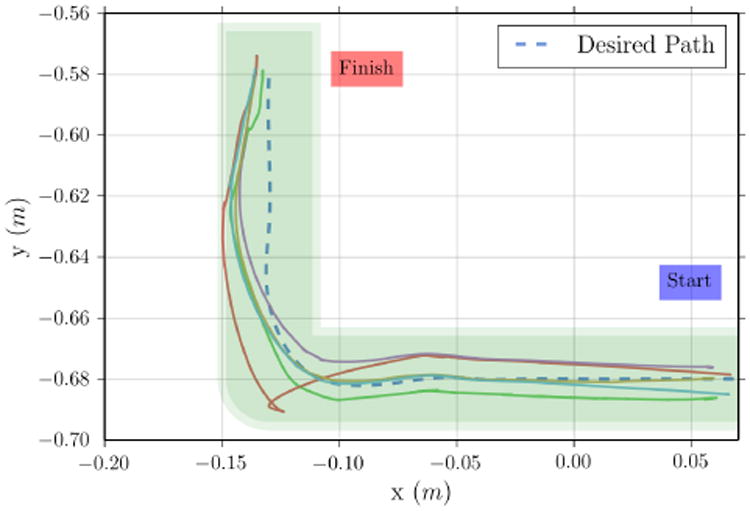
Trajectory with a single curve demonstrating trajectory following. The shaded region indicates the physical tube (5 cm internal diameter).
Considering the average length of the colon being approximately 185 cm (187.7 cm ± 19.0 in men, 182.2 ± 18.1 cm in women) [17], our mock-trajectory (32 cm long) is about 17% of the length of a colon. An average path traversing time of 33.38 seconds thus results in a predicted total colon traversing time of 193 seconds, which is significantly less than open-loop driving of a tethered capsule in a phantom colon (556 ± 188 seconds) and matched the time to completion in the same phantom using a standard endoscope (194 ± 158 seconds) [3]. The experimental setup is significantly different and these figures are presented for conceptual comparison only. An additional study is necessary for true comparison.
V. Conclusion
We have demonstrated closed-loop velocity control of a tethered colon traversing capsule. Real-time magnetic localization is used along with a nonholonomic motion control to drive the capsule through a trajectory at a desired velocity. A smooth trajectory is developed via spline interpolation of a set of desired waypoints. The Robotic Operating System was used along with a dynamic simulation environment for algorithm development. Experimental results demonstrate successful velocity regulation as well as trajectory following through a curve that is indicative of a common colon bend. This control implementation in the presence of a variable disturbances from tether weight and friction reinforces the effectiveness of magnetic capsule locomotion in a clinically relevant evaluation platform.
In this study, a predefined trajectory was followed autonomously by the capsule; however, the aim of our research is in expanding the control methodology for eventual tele-operation. This can perhaps be implemented by real-time generation of short splines based on joystick input. We wish to implement a control strategy that consists of a clinical user commanding directional velocities of the capsule in real-time while the serial robot undergoes necessary, and safe, motions to impart the desired capsule motion. We hypothesize that implementation of an intuitive teleoperation strategy is feasible and necessary for translating this technology to clinical use.
Acknowledgments
This research was supported in part by the National Institute of Biomedical Imaging and Bioengineering, USA of the National Institutes of Health under award no. R01EB018992, in part by the National Science Foundation, USA under grant no. CNS-1239355 and no. IIS-1453129, and in part by the National Science Foundation Graduate Research Fellowship Program under grant no. 1445197. Any opinions, findings, conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Institutes of Health or the National Science Foundation.
References
- 1.Sliker LJ, Ciuti G. Flexible and capsule endoscopy for screening, diagnosis and treatment. Expert Review of Medical Devices. 2014;11(6):649–666. doi: 10.1586/17434440.2014.941809. [DOI] [PubMed] [Google Scholar]
- 2.Slawinski PR, Obstein KL, Valdastri P. Emerging issues and future developments in capsule endoscopy. Techniques in Gastrointestinal Endoscopy. 2015;17(1):40–46. doi: 10.1016/j.tgie.2015.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Arezzo A, Menciassi A, Valdastri P, Ciuti G, Lucarini G, Salerno M, Di Natali C, Verra M, Dario P, Morino M. Experimental assessment of a novel robotically-driven endoscopic capsule compared to traditional colonoscopy. Digestive and Liver Disease. 2013;45(8):657–662. doi: 10.1016/j.dld.2013.01.025. [DOI] [PubMed] [Google Scholar]
- 4.Popek K, Abbott J. 6-d localization of a magnetic capsule endoscope using a stationary rotating magnetic dipole field. Hamlyn Symp Med Robotics. 2015:47–48. [Google Scholar]
- 5.Di Natali C, Beccani M, Valdastri P. Real-time pose detection for magnetic medical devices. IEEE Trans Magn. 2013;49(7):3524–3527. [Google Scholar]
- 6.Salerno M, Rizzo R, Sinibaldi E, Menciassi A. Force calculation for localized magnetic driven capsule endoscopes. Proc 2013 Robotics and Automation Conf, IEEE. 2013:5354–5359. [Google Scholar]
- 7.Mahoney AW, Abbott JJ. Five-degree-of-freedom manipulation of an untethered magnetic device in fluid using a single permanent magnet with application in stomach capsule endoscopy. Int J Rob Res. 2015 Feb;35(1-3):129–147. [Google Scholar]
- 8.Valdastri P, Ciuti G, Verbeni A, Menciassi A, Dario P, Arezzo A, Morino M. Magnetic air capsule robotic system: Proof of concept of a novel approach for painless colonoscopy. Surgical Endoscopy. 2012;26(5):1238–1246. doi: 10.1007/s00464-011-2054-x. [DOI] [PubMed] [Google Scholar]
- 9.Quigley M, Conley K, Gerkey BP, Faust J, Foote T, Leibs J, Wheeler R, Ng AY. Ros: An open-source robot operating system. ICRA Workshop on Open Source Software. 2009 [Google Scholar]
- 10.Taddese AZ, Slawinski PR, Obstein KL, Valdastri P. Proc 2016 Robotics: Sci and Syst. AnnArbor, Michigan: Jun, 2016. Closed loop control of a tethered magnetic capsule endoscope. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Valdastri P, Simi M, Webster RJ., III Advanced technologies for gastrointestinal endoscopy. Annu Review of Biomedical Eng. 2012;14:397–429. doi: 10.1146/annurev-bioeng-071811-150006. [DOI] [PubMed] [Google Scholar]
- 12.Chen Y. High-order polynomial interpolation based on the interpolation center's neighborhood the amendment to the runge phenomenon. Software Eng, 2009 WCSE'09 WRI World Congress on, IEEE. 2009;2:345–348. [Google Scholar]
- 13.Jones E, Oliphant T, Peterson P, et al. Scipy: Open source scientific tools for Python – interpolation package. [accessed 2016-03-01];2001 Online. [Online] Available: http://www.scipy.org/doc/scipy/reference/interpolate.html.
- 14.De Boor C. On calculating with b-splines. J of Approximation Theory. 1972;6(1):50–62. [Google Scholar]
- 15.Cox MG. The numerical evaluation of b-splines. IMA J of Applied Math. 1972;10(2):134–149. [Google Scholar]
- 16.Dierckx P. An improved algorithm for curve fitting with spline functions. Department of Computer Science, KU Leuven; Leuven, Belgium: 1981. [Google Scholar]
- 17.Alazmani A, Hood A, Jayne D, Neville A, Culmer P. Quantitative assessment of colorectal morphology: implications for robotic colonoscopy. Med Eng Phys. 2016 Feb;38(2):148–154. doi: 10.1016/j.medengphy.2015.11.018. [DOI] [PubMed] [Google Scholar]


