Abstract
Nearly all protein functions require structural change, such as enzymes clamping onto substrates, and ion channels opening and closing. These motions are a target for possible new therapies; however, the control mechanisms are under debate. Calculations have indicated protein vibrations enable structural change. However, previous measurements found these vibrations only weakly depend on the functional state. By using the novel technique of anisotropic terahertz microscopy, we find that there is a dramatic change to the vibrational directionality with inhibitor binding to lysozyme, whereas the vibrational energy distribution, as measured by neutron inelastic scattering, is only slightly altered. The anisotropic terahertz measurements provide unique access to the directionality of the intramolecular vibrations, and immediately resolve the inconsistency between calculations and previous measurements, which were only sensitive to the energy distribution. The biological importance of the vibrational directions versus the energy distribution is revealed by our calculations comparing wild-type lysozyme with a higher catalytic rate double deletion mutant. The vibrational energy distribution is identical, but the more efficient mutant shows an obvious reorientation of motions. These results show that it is essential to characterize the directionality of motion to understand and control protein dynamics to optimize or inhibit function.
Introduction
Many proteins must undergo a series of conformational changes to perform their biological function. Enzymes, for example, have distinct structures as the free enzyme moves to substrate bound and product release states. The efficiency of these large-scale structural changes is remarkable. Calculations have indicated that long-range collective vibrations within the protein enable these structural changes. This implies that perturbing these motions by mutations and small molecule strategic binding can optimize or diminish protein biological function. This notion is controversial and only recently have experiments verified that such long-range vibrations even exist in proteins (1, 2, 3, 4, 5, 6). There is evidence that nature uses such dynamical control for survival. Antibiotic resistance mutations have been found to develop at regions distant from protein active sites (7, 8, 9). These mutations could not provide resistance by changing the chemical bonding with the antibiotic, but could affect the long-range motions that enable the structure to accommodate the drug. While these mutations naturally occur when the microbe is challenged, laboratory design of mutations and allosteric inhibitors continues to be limited by the inability to detect a dependence of protein long-range vibrations on inhibitor binding or mutation.
Here we directly measure the directionality of the vibrations with the recently introduced anisotropic terahertz microscopy (ATM) optical technique, and the vibrational energy distribution with inelastic neutron scattering (INS) of the enzyme chicken egg white lysozyme (CEWL). Lysozyme provides a natural defense against Gram-positive bacteria by catalyzing the hydrolysis of 1,4-β-linkages between N-acetyl-D-glucosamine (NAG) and N-acetylmuramic acid (NAM) in the peptidoglycans of the bacterial cell wall. The CEWL structure can be viewed as two domains with a cleft in between, and has two major motions—the hinge-bending motion and the torsional motion—about the cleft. The hinge-bending motion is associated with the binding of the NAG-NAM chain into the cleft. This binding distorts the chain and provides access to the CEWL residues Glu35 and Asp52, which enable the hydrolysis of the chain bonds and the cleavage of the chain (10).
The dynamics are characterized for the free enzyme and the enzyme bound with an inhibitor (tri-N-acetyl-D-glucosamine, 3NAG) in the substrate cleft. We find the directionality of the motions changes dramatically, while the energy distribution, i.e., the vibrational density of states (VDOS), is only weakly sensitive to inhibitor binding. Our results reveal that previous measurements found very little change in the intramolecular protein dynamics for different functional states because they primarily measure the VDOS and not directions of motion (5, 11, 12, 13, 14, 15). The new ATM method is sensitive to these important dynamical changes, and exposes that standard protein characterization techniques can be blind to the critical processes contributing to biology.
How the directionality of vibrations contributes to function is revealed by simulations of wild-type (WT) CEWL and mutated CEWL with a higher activity rate over WT, despite the mutation being far from the active site (16, 17). While the calculated energy distribution and isotropic absorbance show no change in the internal dynamics, the calculated anisotropic absorbance shows an obvious reorientation of the motions with mutation, consistent with the catalytic rate changing due to the mutant’s dynamics (18). Thus, if one focuses solely on measurements of the energy distribution, it is likely that key dynamical shifts with mutation and ligand binding will be missed. Further, the result demonstrates the fundamental importance of the directionality of motions to catalytic efficiency.
Materials and Methods
Protein crystallization
The CEWL tetragonal lysozyme crystals, space group (P43212), are grown as described in Acbas et al. (4). Tri-N-acetyl-D-glucosamine (3NAG) inhibitor bound crystals are similarly grown with the adding of an equal molar amount of 3NAG inhibitor as the protein to the well solution. Protein crystals are grown to a sufficiently large size, >200 μm on the (110) face.
Anisotropy terahertz microscopy
The ATM system (4) is used to perform room temperature near field tetrahertz (THz) transmission measurements on CEWL and CEWL-3NAG tetragonal crystals, mounted over a 200 μm diameter aperture on a 200 μm thick stainless steel plate with a plastic wrap backing on the underside. A drop of paraffin oil covers the crystal and aperture. The sample plate is placed directly on the electrooptic detection crystal and a lid is added to enclose the sample area in a hydration cell. Sample hydration is regulated by a Dew Point Generator (LI-COR Biosciences, Bad Homburg, Germany) throughout the measurement. The THz is incident on the (110) crystal face and the initial 0° sample orientation is aligned using the crystal facets such that the [001] crystal axis is parallel to the THz polarization direction. The sample is rotated 15° between measurements, for a full 360° rotation. By taking the difference between the absorbance at one orientation relative to the reference orientation (0°, [001] axis), ATM isolates the protein intramolecular vibrations from the strong isotropic absorbance of the water in the crystal (typically 50% of crystal volume (19)) as well as other isotropic contributions. For incoherent neutron scattering measurements, CEWL and CEWL-3NAG powders are hydrated to a water content of 0.32 g D2O/g protein. The incoherent scattering signal is dominated by the nonexchangeable protons of the protein and polysaccharide, and the D2O hydration layer signal can be safely neglected. The native structure was monitored before and after measurements by circular dichroism measurements.
Neutron scattering
INS experiments were performed at the time-of-flight spectrometer IN4 at the Institut Laue-Langevin (Grenoble, France) (20). Due to the isotropic nature of the samples, the dynamical structure factor S(Q,E) depends on the wave-vector transfer modulus Q = |Q|. The incident wavelength of 2.2 Å, results in a Q range from 0.9 to 4.8 Å−1.
The generalized VDOS function G(E) is related to the dynamical structure factor by
| (1) |
where and W(Q) are the incoherent cross section and the Debye-Waller factor of hydrogen atoms, respectively, and n(E) is the Bose-Einstein factor. The experimental Gexp(E) has been calculated by integrating Eq. 1 over the accessible angular range (21). The VDOS G(E) has been calculated in absolute units from Gexp(E) by using a procedure already exploited by Balog et al. (12). In more detail:
| (2) |
where values are the hydrogen mean squared displacements (MSDs) derived within the Gaussian approximation to fit the elastic intensity measured on IN4 in the Q-region up to 2 Å−1, while
| (3) |
where M is the protein mass.
The vibrational entropy change per mole protein upon binding has been calculated under the harmonic approximation from (22)
| (4) |
where kB is the Boltzmann constant, and GCEWL(E) and GCEWL-3NAG(E) are the VDOS of CEWL and CEWL-3NAG.
For the conformational entropy determination, temperature-dependent incoherent elastic neutron scattering measurements were performed at the backscattering spectrometer IN13 (Institut Laue-Langevin, Grenoble, France), using the incident neutron wavelength λ = 2.23 Å, corresponding to an energy resolution of ΔE = 8 μeV (full width at half-maximum). Again, the hydrogen MSDs have been derived using the Gaussian approximation to fit the measured elastic intensity in the Q region up to 2 Å−1.
The conformational entropy change per side chain upon binding is estimated from (23)
| (5) |
where R is the gas constant and VCEWL-3NAG and VCEWL are the accessible volumes of the conformational space occupied by the average protein side chain of the complex and the free protein, respectively. In the Gaussian approximation is directly proportional to V2/3, thus
| (6) |
where and are the conformational MSD of the complex and the unbound protein, respectively. We decomposed the into the sum of the vibrational and the conformational components. The can be directly estimated in the low-temperature range below 100 K, where the measured , has a purely vibrational character, as conformational changes are frozen out. This trend for can be then extrapolated up to room temperature in the harmonic approximation (24). This allows for the assessment of the conformational component over the entire temperature range.
Molecular dynamics calculations
CHARMM (25) is used for molecular dynamics simulations and normal mode analysis (NMA). Protein structures PDB: 1BWH (26) and PDB: 1HEW (27) from the Protein Data Bank are used for the free and 3NAG bound lysozyme structures, respectively. The mutated protein structures are made by deleting residues Arg14 and His15 from the PDBs: 1BWH and 1HEW structure files, ligating the backbone at residues Leu13 and Gly16, and performing an energy minimization of these two residues to fix the bond lengths of the backbone. The 3NAG is bound at the ABC binding site only, for both WT and mutant CEWL molecule simulations (27).
CHARMM-GUI (28) is used to initialize the PDB structures into the CHARMM format. All-atom parameter and topology sets 36 for proteins (29) and carbohydrates (30) are utilized for the lysozyme protein and 3NAG inhibitor, respectively. The crystal waters are removed and replaced with a 6 Å water layer, modeled using TIP3 explicit solvent, from 2.5 to 8.5 Å from the protein surface. The system is minimized by 100 steps of steepest descent to settle the waters toward the protein surface. The protein charge is neutralized by adding eight randomly placed chlorine atoms such that they are within 5.5 Å from the protein surface or another ion. Overlapping waters are deleted. The system is minimized again with 200 steps steepest descent and 10,000 steps of adopted basis Newton-Raphson or until a tolerance of an average energy gradient of 0.01 kcal/Å is reached. The system is heated using the DYNAmics command by 5 K every 2500 steps with a 1 fs time step from 110 to 300 K, then kept at a 300 K bath. The atomic coordinates are saved every 100 time steps to the trajectory file. The equilibration is done at 300 K for 3 ns. Translation and rotation is removed every 200 steps during both the heating and equilibration. The root MSD relative to the starting structure is plotted per frame and is found to strongly vary for the first 1 ns of the simulation. After this, the root MSD is found to remain fairly constant. To ensure equilibrium dynamics for the calculations, the first 1.2 ns are removed. Each remaining frame of the structure is fit/merged to the initial structure from before the heating process to remove any additional changes in rotation or translation. All evaporated waters are removed by deleting waters farther than 8.5 Å from the protein surface. Forty random frames are chosen from the remaining 1.8 ns trajectory. For each frame, waters >7 Å from the protein surface are removed and the system is again minimized fully through two iterations of 100 steps steepest descent and an adopted basis Newton-Raphson minimization until a tolerance of an average energy gradient of 10−7 kcal/Å is reached. NMA is performed on each minimized structure to obtain the vibrational mode frequencies, eigenvectors, and dipole derivatives (transition dipole).
The VDOS spectra are determined using the frequencies from the NMA, which are sorted into a histogram with a 5 cm−1 bin width followed by averaging of VDOS from each of the 40 structures. The isotropic absorbance, , is determined by
| (7) |
where ν and γ are the frequency and the linewidth, respectively. The values νi and are the normal mode frequency and the dipole derivative of the ith mode, respectively. A constant linewidth of γ = 4 cm−1 is assumed. The normal mode ensemble analysis (NMEA) isotropic absorbance is determined by averaging the results of the 40 spectra.
The expected anisotropic THz microscopy spectrum is determined for each minimized structure as described in Acbas et al. (4). The crystal absorbance, , is
| (8) |
where ν, γ, , and are the frequency, the linewidth, the eight rotation matrices for the protein arrangements in the unit cell for the space group P43212, and the THz polarization unit vector, respectively. The values νi and are the normal mode frequency and the dipole derivative of the ith mode, respectively. All of the anisotropic results are calculated for the same measurement configuration as the ATM measurements of WT CEWL, with the THz light incident on and perpendicular to the (110) crystal face and 0° orientation of the polarization along the [001] crystal axis. The absorbance relative to the 0° reference orientation is determined by Δabscalc = absxtal − absxtal,ref. The 40 calculated ATM spectra are then averaged to obtain the NMEA ATM spectra for the free and bound, WT, and mutated lysozyme.
Results and Discussion
Anisotropic THz spectroscopy
We use the new technique of ATM to examine how the directionality of motions change with inhibitor binding. The method has been shown to directly measure the optically active protein intramolecular vibrations (4). In this technique, the THz light absorbance of an aligned molecular sample (protein crystals in this case) is measured as a function of the light’s polarization direction relative to the sample’s orientation.
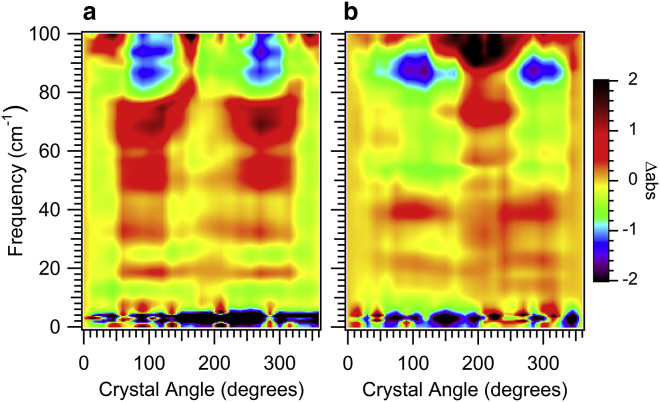
ATM spectra obtained for both free and 3NAG inhibitor bound CEWL tetragonal lysozyme crystals are shown in Fig. 1, a and b, respectively. The change in absorbance relative to the reference polarization direction, the [001] crystal axis, is shown as a function of crystal rotation and frequency (4). The crystal is rotated in the (110) plane. Distinct resonances are observed for both the free and 3NAG bound lysozyme. For free CEWL, resonances are observed at 20, 32, 54, 70, 86, and 94 cm−1 at 90° sample rotation. The 3NAG bound CEWL anisotropic spectrum is considerably different with resonances at 22, 40, and 88 cm−1, and with the large resonances at 54 and 70 cm−1 conspicuously absent. The measurements have 180° periodicity and 90° symmetry, which is expected for the tetragonal crystal symmetry (31).
Figure 1.
ATM measurements of the change in protein vibration directionality with inhibitor binding. Measured Δabs of (a) a free CEWL crystal and (b) a bound CEWL-3NAG inhibitor crystal. The THz light is incident perpendicular to the (110) tetragonal crystal face, with alignment of the THz polarization along the [001] axis at 0°. To see this figure in color, go online.
Neutron scattering
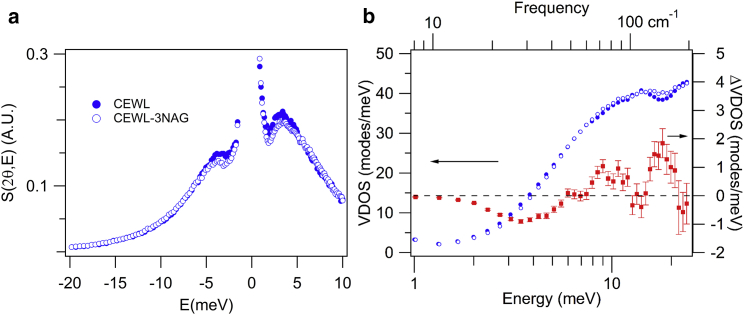
In Fig. 2 a, we show the incoherent dynamical structure factor, S(2θ,E) (average wavevector Q = 2.85 Å−1), of CEWL and CEWL-3NAG. Both samples show an inelastic broad feature centered at ∼3 meV (24.2 cm−1), which has been previously observed for several proteins (32, 33). A small difference between the CEWL and the CEWL-3NAG dynamical structure factor can be observed, with the signal from the free protein being larger than that of the inhibitor bound protein. This trend is the signature of a vibrational stiffening in the complex, consistent with the first calculations of the hinge-bending vibration stiffening (34).
Figure 2.
Measured dynamical structure factor and change in vibrational density of states of free and 3NAG inhibitor bound CEWL. (a) Dynamical structure factor measured with INS at Q = 2.85 Å−1 and at a temperature of 100 K for free (solid circles) and 3NAG bound (open circles) CEWL. The spectra have been normalized with respect to the elastic peak at the lowest Q value. (b) (Left axis) Vibrational density of states from INS measurements of free (blue solid circles) and 3NAG bound (blue open circles) CEWL. (Right axis) The difference in density of states between bound and free CEWL (red circles). To see this figure in color, go online.
The VDOS derived from S(2θ,E) are shown in Fig. 2 b, and nearly overlay. The difference in the VDOS with inhibitor binding is also shown in the figure. The difference shows that the VDOS of free lysozyme is larger than that of the complex in the energy range between 1 and 6 meV (48.4 cm−1), consistent with the trend for the S(2θ,E). Above this energy, the opposite behavior is observed, with the complex having a larger VDOS.
A recent optical Kerr effect study also found small spectral changes with 3NAG binding that highly resemble the VDOS measurements (5). The two peaks centered at ∼10 meV (81 cm−1) and 18 meV (145 cm−1) in the measured VDOS appear as a single broad peak at 12 meV (97 cm−1) in the optical Kerr effect measurements.
We note that below 1 meV (8 cm−1), there is a slight increase (<6%) in the VDOS with binding, consistent with previous calculations (35, 36) and measured VDOS change for dihydrofolate reductase (12). This low-frequency increase reflects the increase in number of vibrations of the complex with the loss of the translational and rotational degrees of freedom of the free ligand.
Vibration directionality versus energy distribution
The large change in the anisotropic absorbance (Δabs) with inhibitor binding appears to be at odds with the subtler changes measured in the VDOS. The differences in the spectra must be due to changes in the intramolecular vibrations. The CEWL and CEWL-3NAG samples have the same protein alignment in the same (P43212) crystal symmetry group, and the same (110) crystal face is measured, eliminating these possible differences in the spectra. Vibrations of the crystal lattice, phonons, are expected at somewhat lower frequencies, and the expected change in lattice phonons with inhibitor binding is slight (37, 38). However, the changes we see are more than the expected slight shifts from phonon modes. For example, the 50 cm−1 band nearly disappears with binding, with a new 40 cm−1 band emerging. The crystal structures for free and inhibitor bound CEWL (26, 27) are nearly identical, with a <3% surface area exposure increase with binding (39, 40), resulting in only a slight change the intermolecular forces for the crystal phonons. The apparent inconsistency with the VDOS measurements is resolved by noting that the VDOS is the energy distribution of the vibrations averaged over all directions, whereas the anisotropic absorbance of the aligned molecules measures the directionality of the vibrations.
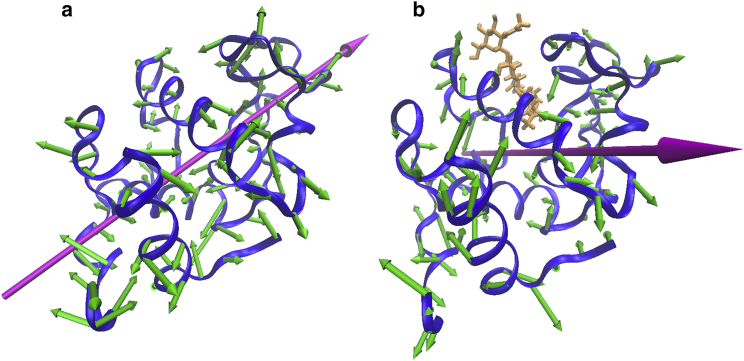
Fig. 3 illustrates how a change in the direction of motion can give rise to a difference in the anisotropic spectra. The vector diagrams for the atomic displacements (only C-α molecule displacements drawn) for two vibrations are shown. The vibration shown in Fig. 3 a corresponds to the mainly hinging motion of free CEWL at 55 cm−1. Also shown is the direction of the net change of the molecule’s electric dipole for this vibration, the transition dipole direction. The THz light polarization lies in the plane of the page and, as the sample is rotated in this plane, the transition dipole will align with the light polarization, leading to resonant absorption. With inhibitor binding, the directions of the vibrations shift. A vibration for CEWL-3NAG at 56 cm−1 is shown in Fig. 3 b. This vibration has torsional motion with mainly out-of-plane displacements. The transition dipole points roughly perpendicular to the plane in which the THz polarization lies, so that the absorption is independent of the rotation of molecule in the plane. A large anisotropic absorbance in the free-state can then diminish or disappear in the bound state due to a reorientation of the transition dipole, such as seen at 54 cm−1 in the measurements shown in Fig. 1. The ATM spectra indicate a strong shift in the direction of motions with inhibitor binding. We examine whether calculations of the VDOS, isotropic absorbance, and anisotropic absorbance using NMA are consistent with this result.
Figure 3.
Changes in vibrational direction with binding. Protein vibrations indicating (a) a clamping motion around the binding site at 55 cm−1 from NMA of free CEWL and (b) a twisting around the binding site at 56 cm−1 for 3NAG bound CEWL. (Orange) 3NAG inhibitor; (fuchsia) transition dipole direction. To see this figure in color, go online.
Normal mode ensemble analysis calculations
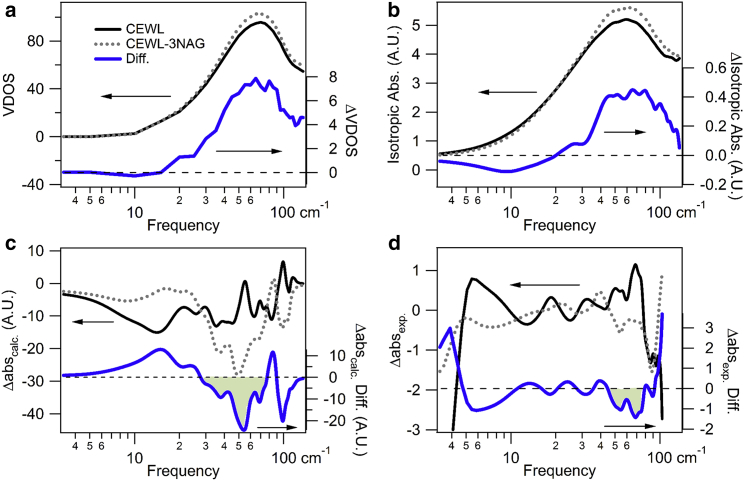
At nonzero temperatures, a protein thermally occupies a number of structural configurations. To account for this in the calculations, we average the NMA results for multiple minimized structures, and refer to these calculations as NMEA. In Fig. 4 a, we show the calculated VDOS for free and 3NAG bound CEWL, as well as the difference. The broad smooth peak of the calculated VDOS agrees with the neutron measurements shown in Fig. 2 b. The NMEA-calculated VDOS change with inhibitor binding has a peak decrease at 10 cm−1 and a peak increase at 60 cm−1, which are red shifted from the measured VDOS decrease at 30 cm−1 and increase at 75 cm−1.
Figure 4.
Increasing spectral definition with anisotropic optical absorption for CEWL and CEWL-3NAG. Calculated (a) VDOS and (b) isotropic absorbance show small changes with inhibitor binding, whereas the (c) calculated anisotropic absorbance show a large sensitivity to the binding. (d) ATM measurements indeed show narrow band resonant changes with binding. The free CEWL (black solid lines) and CEWL-3NAG bound (gray dashed lines) spectra are shown on the left axes, and the difference between bound and free spectra (blue solid lines) are shown on the right axes. The symmetry for the anisotropic calculations reflects the experimental configuration. To see this figure in color, go online.
In Fig. 4 b we show the calculated isotropic absorbance for free and 3NAG bound CEWL, corresponding to optical absorption for random molecular alignment, as for a solution phase measurement. The isotropic absorbance is very similar to the VDOS; however, the decrease in absorbance with inhibitor binding at 10 cm−1 is more prominent and extends to 20 cm−1. The isotropic optical absorbance fluctuates with frequency more than the VDOS, due to the dependence of the optical absorbance on how well the vibration couples to light.
In Fig. 4 c we show the calculated anisotropic absorbance for the same sample configuration as the measurements in Fig. 1 at 90°. For comparison, we plot the measurement results in Fig. 4 d. The calculated anisotropic absorbance has a considerably stronger frequency variation than the VDOS and isotropic absorbance, consistent with the ATM measurements. The frequency variation arises from the dependence of the absorption on the relative alignment of the light polarization and the vibration’s transition dipole: the directionality of motion. Also shown in Fig. 4 c is the calculated difference in the anisotropic absorbance between the free and inhibitor bound CEWL. The calculated anisotropic spectra are different than those measured, but the calculated change of Δabs with binding does show the same strong decrease in absorbance at 70 cm−1 as in the measurement.
The calculated ATM spectra are complex, showing a majority of strong negative Δabs peaks, which are listed in Table S1. There are large changes with inhibitor binding, and Δabs peaks either shift in frequency, invert in sign, or both. While the analysis of the overall spectra is beyond the scope of this report, we note the 35 cm−1 negative peak in the free WT CEWL shifts slightly to 37 cm−1 for the WT CEWL-3NAG and nearly doubles in magnitude with binding, suggesting that the 35 cm−1 resonance reorients further into the plane of the THz polarization with inhibitor binding.
Impact of protein motion directionality on function
The overall agreement of the calculations with the measurements provides confidence in the NMEA approach to test the functional consequences of intramolecular vibrations. We compare NMEA calculations of WT CEWL to a mutant where Arg14 and His15 are deleted. This double deletion mutant (DD CEWL) is of particular interest, with respect to structural dynamics. While the two deletions are far from the catalytic site, the mutant has a 1.4 increase in the catalytic rate but no change to the binding rate. Because the mutations cannot directly affect the biochemistry, it is possible that the mutations change the internal dynamics, which contribute to the catalysis (40, 41).
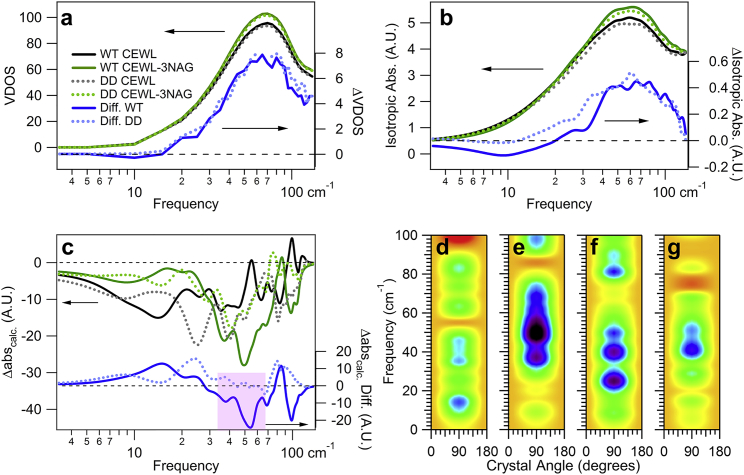
Fig. 5 shows the comparison of the NMEA calculations for WT CEWL and DD CEWL. In Fig. 5 a, we compare the VDOS for the free and inhibitor bound systems, and find the VDOS are essentially identical. The VDOS does not reveal dynamical differences. While the absolute isotropic absorbance shown in Fig. 5 b shows a slight decrease in the absorbance for the mutant in both the free and bound states, the change in the isotropic absorption with inhibitor binding for WT and DD CEWL is again identical!
Figure 5.
Sensitivity of intramolecular vibrations to mutations. Calculated (a) VDOS and (b) isotropic absorbance for free and inhibitor bound WT and DD CEWL. The units for the difference (right axis) are the same as the left axis. These calculations reveal little difference in the dynamics for the two proteins, whereas (c) the relative anisotropic absorbance at 90°, shows the directionality of vibrations clearly changes. The spectra (a–c) are calculated for free WT CEWL (black solid line), 3NAG bound WT CEWL (green solid line), for free DD CEWL (gray dashed line), 3NAG bound DD CEWL (green dashed line), and the difference spectra with binding for WT CEWL (blue solid line) and DD CEWL (blue dashed line). Calculated Δabs spectra of (d) a free WT CEWL, (e) a bound WT CEWL-3NAG inhibitor, (f) a free CEWL mutant, and (g) a bound CEWL-3NAG inhibitor mutant. The color scale follows that in Fig. 1; however, the range here is [−30, +15]. The symmetry for the anisotropic calculations reflects the experimental configuration. To see this figure in color, go online.
In contrast, a change in the internal dynamics between WT and DD CEWL is evident in the calculated anisotropic absorbance, as seen in Fig. 5, c–g. Fig. 5 c shows the anisotropic absorbance for the 90° rotation direction. While there are obvious differences in the free WT and free DD spectra, what is of note is how the directions of motions change with substrate binding for the two. The solid lines for the free and bound WT show large changes with binding over the entire frequency range, whereas the dotted lines for DD CEWL nearly overlay for in the 33–66 cm−1 range, as emphasized by the highlighted difference in Fig. 5 c. When we compare the spectra of all four, in Fig. 5, d–g, we see that there are prominent resonances in the WT bound, DD free, and DD bound (Fig. 5, e–g) at ∼40 and ∼50 cm−1 that are absent for WT free CEWL (Fig. 5 d). That is, the motions that are present in the bound WT already exist in the free mutant. The displacements associated with the 40 and 50 cm−1 resonances may enhance the proximity of catalytically important amino acids to the ligand region, with resultant increased reaction rate, as previous computational results have suggested (41, 42). The differences between the WT bound and DD bound anisotropic spectra emphasize the changes in dynamics with mutation. For example, the decreased anisotropic absorbance at 60 cm−1 of the bound DD CEWL compared to the bound WT may be arising from a decrease in vibrations that act to hinder the catalysis in the WT. The vibrational directionality measurements and calculations give new insight into the influence of dynamics on function, which is not detected in VDOS alone.
The critical biological importance of the vector displacements compared to the scalar energy distribution was previously suggested by computational studies of HIV 1 reverse transcriptase (HIV 1 RT) and α-lytic protease (43, 44). For HIV 1 RT, elastic network analysis found inhibitors nevirapine and efavirenz primarily reorient the vibrations (43). The α-lytic protease calculations found the binding pocket vibrations of the M190A mutant shift from symmetrical to asymmetrical, allowing the pocket to accommodate the additional binding partners, explaining the observed increase in promiscuity (44). The CEWL ATM measurements provide experimental support that vibrational directionality has functional significance.
Conformational entropy
Collective vibrations potentially contribute to protein biological function through the configurational entropy. Configurational entropy consists of contributions from vibrational motions and conformational changes. Analyses up to this point have determined either the vibrational or conformational entropy contributions. Here, we combine elastic and inelastic neutron scattering to estimate both contributions, providing a more complete picture for the role of configurational entropy in complexation. We estimate a vibrational entropy contribution to the free energy −TΔS = −8 ± 2 kJ/mol, from our VDOS measurements at T = 300 K. A favorable contribution of vibrational entropy has been found also for dihydrofolate reductase with the drug methotrexate binding from INS (12). On the other hand, we find the conformational entropy contribution for 3NAG binding to CEWL as −TΔS = 20 ± 10 kJ/mol determined by our elastic neutron scattering measurements. The results indicate that the CEWL-3NAG binding is not entropically favorable, consistent with previous NMR results of the conformational entropy alone (45).
Determination of vibrational motions
In addition to their entropic contribution, collective vibrations can influence biochemistry by steering protein structure toward intermediate state configurations (46, 47, 48). To test this idea, a measurement needs to be sensitive to the specific vibrational displacements. VDOS cannot be used for such characterization. To have such sensitivity, distinct frequency ranges in the VDOS would need to be dominated by specific directions of motion. Neither our measurements nor our calculations find such spectral distinctions in the VDOS. The anisotropic absorbance measurements, on the other hand, by their very nature, are direction-sensitive measurements.
The strong features in the measured anisotropic spectra ideally could be identified with specific motions that steer the structure toward functional conformational changes. Typically, vibration identification can be done by comparison with calculations. For simple molecules, individual vibrations are separated in frequency, and calculations are sufficiently accurate that identification with the measurements is straightforward (49, 50). However, spectral assignment for complex macromolecules, such as proteins, is challenged by the close frequency spacing of individual vibrations and computational accuracy. The NMEA-calculated VDOS has the same qualitative frequency dependence and change with inhibitor binding; however, the red-shifted peak frequencies of the calculated VDOS and calculated change in the VDOS peaks highlight net deficiencies in the calculations. These include nonoptimized water modeling, lack of polarizability in the force field, imprecise inhibitor binding location (10, 27), and percent occupancy (27). The computational inaccuracies that lead to the small differences between the calculated and measured VDOS spectra are amplified in the anisotropic absorbance calculations, significantly hampering identification of the motions measured.
The challenge of structural motion identification is more fundamental than the accuracy of the force field. Independent of the precise agreement with the measurements, potentially the calculations can be analyzed themselves to determine whether functionally important protein regions are impacted by the directionality of vibrations. This was done previously by projecting calculated vibrational displacement vectors onto a localized functional displacement (43, 44, 51). However, those calculations used a single minimized starting structure and studied individual vibrational frequencies, each with a unique displacement vector, allowing for a net analysis of the motion. In fact, the energy landscape is rugged, with many local minima corresponding to slightly different configurations and a protein will sample these minima in time. We find while the calculated VDOS and isotropic absorbance show high overlap for different minimized structures, the vibrational displacements have large variations. Therefore, using the projections of the vibrational displacements of a single minimized structure is not reliable for capturing the overall protein dynamics. As the VDOS is typically used to evaluate the NMA output, previous investigators may have only tested for variation with the VDOS alone, and thus were not aware that the orientation of motions varies with starting structure. We account for the occupation of different configurations through the NMEA approach and remarkably, specific bands emerge from the averaging of the anisotropic spectra with a convergence attained with averaging at ∼40 starting structures. However, by correctly accounting for the occupation of multiple configurations, the method to identify specific motions is made more complex. A resonant band not only corresponds to a number of vibrations for a single minimized structure due to the density of vibrations for the complex molecule, it also reflects different vibrations from the different minimized structures, each with their own displacement eigenvectors. It is essential to use a method such as NMEA to accurately predict the anisotropic response. However, the approach necessitates the development of methods to distill the averaged spectra to determine specific motional changes that give rise to the calculated differences with mutation and binding. Such methodology is beyond the scope of this work.
Conclusions
Protein vibrations potentially steer structural changes necessary for function. We report that the experimental determination of the interconnected motional networks cannot be achieved using techniques that primarily measure the vibrational energy distribution. We find only broad subtle changes in the measured VDOS with inhibitor binding for CEWL, and a net entropy decrease in the bound state (52). However, by using ATM, a new anisotropic optical technique, we measure sharp distinct changes in the directions of vibrational displacements. Our computational comparison of WT CEWL and a double deletion mutant with a higher catalytic rate shows that only the orientation of motions changes with the mutation, possibly leading to the enhanced catalysis. The VDOS is not sensitive to changes in the structural dynamics with the mutation. It is therefore essential to use directionally sensitive techniques such as ATM to characterize the intramolecular protein dynamics and determine their biological impact such as mutational outcomes, inhibitor design, and predictive docking modeling (46, 51, 53, 54, 55, 56, 57, 58, 59, 60).
Author Contributions
K.A.N. performed anisotropic terahertz microscopy measurements, calculations, analyzed data, and wrote the article; M.X. performed anisotropic terahertz microscopy measurements and data analysis in support of this work; E.H.S. grew and characterized crystals; A.P. and A.O. performed the neutron scattering measurements, data analysis, and wrote the article; A.G.M. designed and conceived measurements, analyzed data, and wrote the article; and all authors discussed the results and contributed significantly to the writing of the article.
Acknowledgments
All molecular dynamics calculations were performed using facilities provided by The Center for Computational Research, SUNY, Buffalo.
We are thankful for the support of National Science Foundation MRI2 grant No. DBI2959989, IDBR grant No. DBI 1556359, MCB grant No. MCB1616529, and the Department of Energy BES grant No. DE-SC0016317.
Editor: Jane Dyson.
Footnotes
One table is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30074-7.
Contributor Information
Katherine A. Niessen, Email: kniessen@buffalo.edu.
Andrea G. Markelz, Email: amarkelz@buffalo.edu.
Supporting Material
References
- 1.Xie A., van der Meer A.F., Austin R.H. Excited-state lifetimes of far-infrared collective modes in proteins. Phys. Rev. Lett. 2002;88:018102. doi: 10.1103/PhysRevLett.88.018102. [DOI] [PubMed] [Google Scholar]
- 2.Liu D., Chu X.Q., Chen S.-H. Studies of phononlike low-energy excitations of protein molecules by inelastic x-ray scattering. Phys. Rev. Lett. 2008;101:135501. doi: 10.1103/PhysRevLett.101.135501. [DOI] [PubMed] [Google Scholar]
- 3.Paciaroni A., Orecchini A., Sacchetti F. Vibrational collective dynamics of dry proteins in the terahertz region. J. Phys. Chem. B. 2012;116:3861–3865. doi: 10.1021/jp211190q. [DOI] [PubMed] [Google Scholar]
- 4.Acbas G., Niessen K.A., Markelz A.G. Optical measurements of long-range protein vibrations. Nat. Commun. 2014;5:3076. doi: 10.1038/ncomms4076. [DOI] [PubMed] [Google Scholar]
- 5.Turton D.A., Senn H.M., Wynne K. Terahertz underdamped vibrational motion governs protein-ligand binding in solution. Nat. Commun. 2014;5:3999. doi: 10.1038/ncomms4999. [DOI] [PubMed] [Google Scholar]
- 6.Levantino M., Schirò G., Cammarata M. Ultrafast myoglobin structural dynamics observed with an x-ray free-electron laser. Nat. Commun. 2015;6:6772. doi: 10.1038/ncomms7772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Toprak E., Veres A., Kishony R. Evolutionary paths to antibiotic resistance under dynamically sustained drug selection. Nat. Genet. 2011;44:101–105. doi: 10.1038/ng.1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wu T.D., Schiffer C.A., Shafer R.W. Mutation patterns and structural correlates in human immunodeficiency virus type 1 protease following different protease inhibitor treatments. J. Virol. 2003;77:4836–4847. doi: 10.1128/JVI.77.8.4836-4847.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Goldfarb N.E., Ohanessian M., Dunn B.M. Defective hydrophobic sliding mechanism and active site expansion in HIV-1 protease drug resistant variant Gly48Thr/Leu89Met: mechanisms for the loss of saquinavir binding potency. Biochemistry. 2015;54:422–433. doi: 10.1021/bi501088e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.von Dreele R.B. Binding of N-acetylglucosamine to chicken egg lysozyme: a powder diffraction study. Acta Crystallogr. D Biol. Crystallogr. 2001;57:1836–1842. doi: 10.1107/s0907444901015748. [DOI] [PubMed] [Google Scholar]
- 11.Gabel F., Weik M., Zaccai G. Effects of soman inhibition and of structural differences on cholinesterase molecular dynamics: a neutron scattering study. Biophys. J. 2005;89:3303–3311. doi: 10.1529/biophysj.105.061028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Balog E., Becker T., Smith J.C. Direct determination of vibrational density of states change on ligand binding to a protein. Phys. Rev. Lett. 2004;93:028103. doi: 10.1103/PhysRevLett.93.028103. [DOI] [PubMed] [Google Scholar]
- 13.Tzeng S.R., Kalodimos C.G. Dynamic activation of an allosteric regulatory protein. Nature. 2009;462:368–372. doi: 10.1038/nature08560. [DOI] [PubMed] [Google Scholar]
- 14.Whitmire S.E., Wolpert D., Birge R.R. Protein flexibility and conformational state: a comparison of collective vibrational modes of wild-type and D96N bacteriorhodopsin. Biophys. J. 2003;85:1269–1277. doi: 10.1016/S0006-3495(03)74562-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen J.Y., Knab J.R., Markelz A.G. Terahertz dielectric assay of solution phase protein binding. Appl. Phys. Lett. 2007;90:243901. [Google Scholar]
- 16.Mine S., Tate S., Imoto T. Analysis of the relationship between enzyme activity and its internal motion using nuclear magnetic resonance: 15N relaxation studies of wild-type and mutant lysozyme. J. Mol. Biol. 1999;286:1547–1565. doi: 10.1006/jmbi.1999.2572. [DOI] [PubMed] [Google Scholar]
- 17.Imoto T., Ueda T., Yamada H. Lysozyme requires fluctuation of the active site for the manifestation of activity. Protein Eng. 1994;7:743–748. doi: 10.1093/protein/7.6.743. [DOI] [PubMed] [Google Scholar]
- 18.Antoniou D., Basner J., Schwartz S.D. Computational and theoretical methods to explore the relation between enzyme dynamics and catalysis. Chem. Rev. 2006;106:3170–3187. doi: 10.1021/cr0503052. [DOI] [PubMed] [Google Scholar]
- 19.Matthews B.W. Solvent content of protein crystals. J. Mol. Biol. 1968;33:491–497. doi: 10.1016/0022-2836(68)90205-2. [DOI] [PubMed] [Google Scholar]
- 20.Bée M. Localized and long-range diffusion in condensed matter: state of the art of QENS studies and future prospects. Chem. Phys. 2003;292:121–141. [Google Scholar]
- 21.Taraskin S.N., Elliott S.R. Connection between the true vibrational density of states and that derived from inelastic neutron scattering. Phys. Rev. B. 1997;55:117–123. [Google Scholar]
- 22.Maradudin A.A., Weiss G.H., Montroll E.W. Academic Press; New York: 1963. Theory of Lattice Dynamics in the Harmonic Approximation. [Google Scholar]
- 23.Fitter J. A measure of conformational entropy change during thermal protein unfolding using neutron spectroscopy. Biophys. J. 2003;84:3924–3930. doi: 10.1016/S0006-3495(03)75120-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Paciaroni A., Cinelli S., Onori G. Effect of the environment on the protein dynamical transition: a neutron scattering study. Biophys. J. 2002;83:1157–1164. doi: 10.1016/S0006-3495(02)75239-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Brooks B.R., Bruccoleri R.E., Karplus M. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 26.Dong J., Boggon T.J., Helliwell J.R. Bound-solvent structures for microgravity-, ground control-, gel- and microbatch-grown hen egg-white lysozyme crystals at 1.8 Å resolution. Acta Crystallogr. D Biol. Crystallogr. 1999;55:745–752. doi: 10.1107/s0907444998016047. [DOI] [PubMed] [Google Scholar]
- 27.Cheetham J.C., Artymiuk P.J., Phillips D.C. Refinement of an enzyme complex with inhibitor bound at partial occupancy. Hen egg-white lysozyme and tri-N-acetylchitotriose at 1.75 Å resolution. J. Mol. Biol. 1992;224:613–628. doi: 10.1016/0022-2836(92)90548-x. [DOI] [PubMed] [Google Scholar]
- 28.Jo S., Kim T., Im W. CHARMM-GUI: a web-based graphical user interface for CHARMM. J. Comput. Chem. 2008;29:1859–1865. doi: 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- 29.Miao Y., Yi Z., Smith J.C. Temperature-dependent dynamical transitions of different classes of amino acid residue in a globular protein. J. Am. Chem. Soc. 2012;134:19576–19579. doi: 10.1021/ja3097898. [DOI] [PubMed] [Google Scholar]
- 30.Guvench O., Mallajosyula S.S., MacKerell A.D., Jr. CHARMM additive all-atom force field for carbohydrate derivatives and its utility in polysaccharide and carbohydrate-protein modeling. J. Chem. Theory Comput. 2011;7:3162–3180. doi: 10.1021/ct200328p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Niessen K., Xu M., Markelz A.G. Terahertz optical measurements of correlated motions with possible allosteric function. Biophys. Rev. 2015;7:201–216. doi: 10.1007/s12551-015-0168-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Doster W., Cusack S., Petry W. Dynamic instability of liquidlike motions in a globular protein observed by inelastic neutron scattering. Phys. Rev. Lett. 1990;65:1080–1083. doi: 10.1103/PhysRevLett.65.1080. [DOI] [PubMed] [Google Scholar]
- 33.Orecchini A., Paciaroni A., Cannistraro S. Low-frequency vibrational anomalies in β-lactoglobulin: contribution of different hydrogen classes revealed by inelastic neutron scattering. J. Phys. Chem. B. 2001;105:12150–12156. [Google Scholar]
- 34.Bruccoleri R.E., Karplus M., McCammon J.A. The hinge-bending mode of a lysozyme-inhibitor complex. Biopolymers. 1986;25:1767–1802. doi: 10.1002/bip.360250916. [DOI] [PubMed] [Google Scholar]
- 35.Tidor B., Karplus M. The contribution of vibrational entropy to molecular association. The dimerization of insulin. J. Mol. Biol. 1994;238:405–414. doi: 10.1006/jmbi.1994.1300. [DOI] [PubMed] [Google Scholar]
- 36.Moritsugu K., Njunda B.M., Smith J.C. Theory and normal-mode analysis of change in protein vibrational dynamics on ligand binding. J. Phys. Chem. B. 2010;114:1479–1485. doi: 10.1021/jp909677p. [DOI] [PubMed] [Google Scholar]
- 37.Achterhold K., Keppler C., Parak F.G. Vibrational dynamics of myoglobin determined by the phonon-assisted Mössbauer effect. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:051916. doi: 10.1103/PhysRevE.65.051916. [DOI] [PubMed] [Google Scholar]
- 38.Meinhold L., Merzel F., Smith J.C. Lattice dynamics of a protein crystal. Phys. Rev. Lett. 2007;99:138101. doi: 10.1103/PhysRevLett.99.138101. [DOI] [PubMed] [Google Scholar]
- 39.Son I., Shek Y.L., Chalikian T.V. Volumetric characterization of tri-N-acetylglucosamine binding to lysozyme. Biochemistry. 2012;51:5784–5790. doi: 10.1021/bi3006994. [DOI] [PubMed] [Google Scholar]
- 40.Cameron D.L., Jakus J., Cooper A. Pressure perturbation calorimetry and the thermodynamics of noncovalent interactions in water: comparison of protein-protein, protein-ligand, and cyclodextrin-adamantane complexes. J. Phys. Chem. B. 2010;114:16228–16235. doi: 10.1021/jp107110t. [DOI] [PubMed] [Google Scholar]
- 41.Núñez S., Antoniou D., Schwartz S.D. Promoting vibrations in human purine nucleoside phosphorylase. A molecular dynamics and hybrid quantum mechanical/molecular mechanical study. J. Am. Chem. Soc. 2004;126:15720–15729. doi: 10.1021/ja0457563. [DOI] [PubMed] [Google Scholar]
- 42.Antoniou D., Schwartz S.D. Protein dynamics and enzymatic chemical barrier passage. J. Phys. Chem. B. 2011;115:15147–15158. doi: 10.1021/jp207876k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Temiz N.A., Bahar I. Inhibitor binding alters the directions of domain motions in HIV-1 reverse transcriptase. Proteins. 2002;49:61–70. doi: 10.1002/prot.10183. [DOI] [PubMed] [Google Scholar]
- 44.Miller D.W., Agard D.A. Enzyme specificity under dynamic control: a normal mode analysis of α-lytic protease. J. Mol. Biol. 1999;286:267–278. doi: 10.1006/jmbi.1998.2445. [DOI] [PubMed] [Google Scholar]
- 45.Moorman V.R., Valentine K.G., Wand A.J. The dynamical response of hen egg white lysozyme to the binding of a carbohydrate ligand. Protein Sci. 2012;21:1066–1073. doi: 10.1002/pro.2092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Meireles L., Gur M., Bahar I. Pre-existing soft modes of motion uniquely defined by native contact topology facilitate ligand binding to proteins. Protein Sci. 2011;20:1645–1658. doi: 10.1002/pro.711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tama F., Brooks C.L., Brooks L. Symmetry, form, and shape: guiding principles for robustness in macromolecular machines. Annu. Rev. Biophys. Biomol. Struct. 2006;35:115–133. doi: 10.1146/annurev.biophys.35.040405.102010. [DOI] [PubMed] [Google Scholar]
- 48.Henzler-Wildman K.A., Thai V., Kern D. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 49.Williams M.R.C., Aschaffenburg D.J., Schmuttenmaer C.A. Intermolecular vibrations in hydrophobic amino acid crystals: experiments and calculations. J. Phys. Chem. B. 2013;117:10444–10461. doi: 10.1021/jp406730a. [DOI] [PubMed] [Google Scholar]
- 50.Jepsen P.U., Clark S.J. Precise ab-initio prediction of terahertz vibrational modes in crystalline systems. Chem. Phys. Lett. 2007;442:275–280. [Google Scholar]
- 51.Yu X., Leitner D.M. Chromophore vibrations during isomerization of photoactive yellow protein: analysis of normal modes and energy transfer. Chem. Phys. Lett. 2004;391:181–186. [Google Scholar]
- 52.Grossman M., Born B., Havenith M. Correlated structural kinetics and retarded solvent dynamics at the metalloprotease active site. Nat. Struct. Mol. Biol. 2011;18:1102–1108. doi: 10.1038/nsmb.2120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Williams G.S.B., Hossain A.M., Bagdassarian C.K. Evolution of rate-promoting oscillations in a model enzyme. J. Phys. Chem. B. 2003;107:12527–12533. [Google Scholar]
- 54.Gabba M., Poblete S., Fitter J. Conformational state distributions and catalytically relevant dynamics of a hinge-bending enzyme studied by single-molecule FRET and a coarse-grained simulation. Biophys. J. 2014;107:1913–1923. doi: 10.1016/j.bpj.2014.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mehboob S., Guo L., Johnson M.E. Glutamate racemase dimerization inhibits dynamic conformational flexibility and reduces catalytic rates. Biochemistry. 2009;48:7045–7055. doi: 10.1021/bi9005072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Onuchic J.N., Kobayashi C., Baldridge K.K. Exploring biomolecular machines: energy landscape control of biological reactions. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2006;361:1439–1443. doi: 10.1098/rstb.2006.1876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Karunakaran V., Benabbas A., Champion P.M. Investigations of low-frequency vibrational dynamics and ligand binding kinetics of cystathionine β-synthase. J. Phys. Chem. B. 2010;114:3294–3306. doi: 10.1021/jp909700r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Doshi U., McGowan L.C., Hamelberg D. Resolving the complex role of enzyme conformational dynamics in catalytic function. Proc. Natl. Acad. Sci. USA. 2012;109:5699–5704. doi: 10.1073/pnas.1117060109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ming D., Wall M.E. Quantifying allosteric effects in proteins. Proteins. 2005;59:697–707. doi: 10.1002/prot.20440. [DOI] [PubMed] [Google Scholar]
- 60.Straub J.E., Thirumalai D. Exploring the energy landscape in proteins. Proc. Natl. Acad. Sci. USA. 1993;90:809–813. doi: 10.1073/pnas.90.3.809. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.