Effects of Polymer Length and Salt Concentration on the Transport of ssDNA in Nanofluidic Channels

Abstract

Electrokinetic phenomena in micro/nanofluidic channels have attracted considerable attention because precise control of molecular transport in liquids is required to optically and electrically capture the behavior of single molecules. However, the detailed mechanisms of polymer transport influenced by electroosmotic flows and electric fields in micro/nanofluidic channels have not yet been elucidated. In this study, a Langevin dynamics simulation was used to investigate the electrokinetic transport of single-stranded DNA (ssDNA) in a cylindrical nanochannel, employing a coarse-grained bead-spring model that quantitatively reproduced the radius of gyration, diffusion coefficient, and electrophoretic mobility of the polymer. Using this practical scale model, transport regimes of ssDNA with respect to the ζ-potential of the channel wall, the ion concentration, and the polymer length were successfully characterized. It was found that the relationship between the radius of gyration of ssDNA and the channel radius is critical to the formation of deformation regimes in a narrow channel. We conclude that a combination of electroosmotic flow velocity gradients and electric fields due to electrically polarized channel surfaces affects the alignment of molecular conformations, such that the ssDNA is stretched/compressed at negative/positive ζ-potentials in comparatively low-concentration solutions. Furthermore, this work suggests the possibility of controlling the center-of-mass position by tuning the salt concentration. These results should be applicable to the design of molecular manipulation techniques based on liquid flows in micro/nanofluidic devices.

Introduction

An increased demand for analytical capability in the biological sciences has prompted the development of micro/nanofluidic devices that enable the manipulation and analysis of biological molecules with higher speed and accuracy than conventional technologies. These new devices have significant potential in the fields of molecular biology and biophysics. Among the various technologies being researched, the stability and size-controllability of solid-state nanochannels show promise with regard to the fabrication of ideal, robust platforms for biomolecular separation, detection, and analysis (1, 2, 3, 4, 5, 6, 7, 8).

One of the most well-studied topics concerning nanofluidic devices is the controllability of transport velocity and conformational change of biopolymers. Various strategies have been proposed to control the translocation velocity of electrically charged polymers, such as tuning of wall surface charges (9), ion concentrations (10, 11), temperature gradients (12), solution viscosity (13), and pore dimensions (14). However, these efforts have not yet been shown to improve the controllability. Thus, the development of biopolymer analysis platforms will require a detailed understanding of biopolymer transport dynamics on the nanoscale, to overcome these remaining challenges.

Recent experimental works have partially addressed the polymer-length dependent mobility that is evident in nanochannels, as a means of allowing the velocity control of biopolymers. Although a constant mobility independent of polymer length was demonstrated in a capillary with a 60 nm diameter (4, 15, 16, 17), this control was lost when employing nanoslits with a height of 20 nm (4, 18). Cross et al. (4) reported that the effect of polymer length, N, on the mobility of DNA can be described by a scaling law as N^−1/2 in a 19-nm-deep nanoslit. Cao and Yobas (19) found a significant length dependence of the electrophoretic mobility of DNA in a nanocapillary and nanowire array. Rahong et al. (8) proposed two different separation mechanisms associated with the dsDNA length and the density of the nanowire array. These experiments (4, 8, 19) were carried out using long-chain double-stranded DNA (dsDNA > 10³ bp) molecules and small slit heights to evaluate the separation. The results demonstrated that electrophoretic mobility was primarily affected by both the polymer length and the channel size.

The separation and velocity control of short-chain single-stranded DNA (ssDNA) is currently an important issue in DNA sequencing, and our own group has developed coarse-grained models of DNA to assist in investigating transport properties (14, 20, 21, 22). In this prior work, the time spans and folded structures of dsDNA passing through nanogaps (14) or nanowire arrays (6) were determined, using practical spatial and temporal dimensions. More recently, a technique for manipulating microparticles mimicking charged polymer chains was successfully demonstrated by applying AC electric fields across a micropore, such that the motions of microparticles could be aligned in the radial direction depending on the field frequency (23). However, the placement and conformation of polymer chains can be controlled even more precisely in nanochannels exposed to electroosmotic flow (EOF) fields. Furthermore, when the channel radius approaches the thickness of the electric double layer (EDL), the effect of the electrically polarized channel surfaces has been shown to play an important role in polymer transport (24, 25). Clarification of the DNA deformation process in nanochannels in response to wall surface charges and ion concentrations is also of great importance to the further development of nanofluidic devices such as nanopore-based sequencers (26).

Polymer transport regimes (27, 28) are frequently employed to illustrate the static conformations of confined macromolecules. These include the radius of gyration (R_g), $R_g\ll a$ (bulk regime), R_g ≈ a (de Gennes regime (27)), and l_p ≈ a (Odijk regime (28)), where R_g is the radius of gyration of the polymer, a is the channel radius, and l_p is the persistence length. These regimes represent distinct confinement effects on the polymer conformations and transport dynamics in nanochannels.

Computational studies of polymer transport phenomena in nanochannels have also been found to provide significant insight regarding the dynamics of biopolymers (14, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41). In previous works, Luo et al. (34) and Luo and Metzler (35) numerically investigated the movement of polymers through nanochannels and nanopores, while Slater et al. (36, 37) performed pioneering work in the field of the electrokinetic transport of DNA by developing coarse-grained models. Jendrejack et al. (39, 40, 41) theoretically and computationally clarified the shear-induced migration and confinement effects on long-chain DNA dynamics in microfluidic devices. Based on these previous studies, this project assessed the transport of short-chain ssDNA through nanochannels using computational simulations. In particular, this study focused on the dependence of polymer mobility, deformation characteristics, and spatial distribution on the salt concentration in a narrow channel with dimensions comparable to the EDL thickness.

Specifically, the transport properties of ssDNA in a nanochannel were simulated using Langevin dynamics (LD) in conjunction with a bead-spring model to determine the relationships among the polymer length, salt concentration, and deformation process in EOF fields. As a result of these LD simulations, detailed characteristics of ssDNA, such as off-centered alignment in the nanochannel stretching or compressing the polymer chain, were elucidated on a realistic spatiotemporal scale. These results are expected to be applicable to the development of techniques for the manipulation and velocity control of ssDNA during transport.

Materials and Methods

Electroosmotic flow in a cylindrical nanochannel

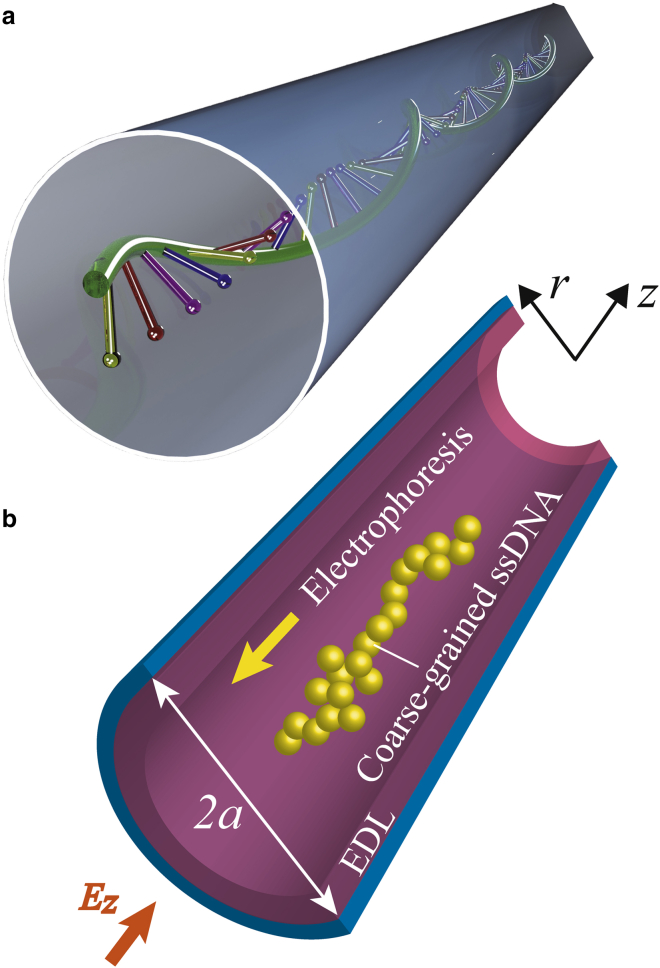
Fig. 1 presents a schematic illustration of ssDNA undergoing electrophoretic transport through a cylindrical nanochannel. Here, the liquid flows induced by interactions between the electrically charged channel surfaces and the polar solvent also affect the polymer translocation. Focusing on this velocity field, we investigated the electrokinetic transport of ssDNA in nanochannels. Under the influence of an axial electric field, E_z, applied along the nanochannel, charged molecules and liquids are forced to migrate along the z axis. Additionally, the ζ-potential of the channel surfaces forms an EDL and a nonuniform electric field, E_r, along the r axis, such that E_r(r) = −dϕ/dr. Based on previous theoretical studies (14, 42), an electric field can be separated into two components, such as E_z and E_r. Here, we assume that E_z is axially constant over an infinitely long narrow channel. When a nanochannel is situated within a wider flow channel, the electric fields resulting from the streaming potential are highly concentrated and almost uniform along the channel (14, 42). Furthermore, the pressure gradient along the z axis is assumed to be negligibly small in this study, based on conventional EOF models (43). The EOF velocity, u_z(r), will vary along the radial direction and can be written in the cylindrical coordinate system as follows:

$$u_z\left(r\right)=\frac{{\epsilon }_0\epsilon E_z\zeta }{\eta }\left[\frac{I_0\left(\kappa r\right)}{I_0\left(\kappa a\right)}-1\right],$$ (1)

where ε₀ is the dielectric constant of a vacuum, ε is the relative dielectric constant of the solution, and η is the viscosity of the solution. I₀ is the zeroth-order modified Bessel function and κ is the reciprocal of the Debye length, λ_D:

$$\kappa =\frac{1}{{\lambda }_D}=\sqrt{\frac{e^2\sum _i{n}_i{z}_i^2}{{\epsilon }_0\epsilon k_{\text{B}}T}},$$ (2)

where k_B is the Boltzmann constant, n_i is the bulk concentration of the ith electrolyte species, and z_i is the valence of the electrolyte. The relationship between λ_D and salt concentration, C (M), for monovalent ions based on Eq. 2 is summarized in Table 1, where C is determined from n_i divided by Avogadro’s number. The electric potential, ϕ(r), in the nanochannel is calculated as follows:

$$\varphi \left(r\right)=\zeta \frac{I_0\left(\kappa r\right)}{I_0\left(\kappa a\right)}.$$ (3)

In these simulations, the channel surface was either positively or negatively polarized, and the applied ζ-potential was controlled between −25 and 25 mV. The bulk viscosity of water, η, was set to 0.893 × 10⁻³ Pa s and a uniform electric field of E_z = 1.0 × 10⁵ V/m was applied along the z direction. The EOF was found to become stronger with increases in the ζ-potential because the highly concentrated electrolyte ions in the EDL dragged the solvent molecules.

Figure 1.

Schematic illustrations of (a) ssDNA passing through a cylindrical nanochannel and (b) a coarse-grained bead-spring model of the polymer chain. The longitudinal electric field, E_z, results in electrophoresis of the negatively charged DNA and an EOF due to the wall surface charges. The surface of the nanochannel is either negatively or positively charged associated with the ζ-potential. A nonconstant viscosity layer is known to exist very near the surface, and EDLs affect the EOF flow pattern. To see this figure in color, go online.

Table 1.

Relationship between EDL Thickness, λ_D, and Ion Concentration, C

C (M)	λD (nm)
1	0.3
2 × 10−2	2
4 × 10−3	5
9 × 10−4	10
4 × 10−4	15

The electrokinetic transport phenomena introduced above involve both electrophoresis and electroosmosis (44). Theoretical approaches to electroosmosis typically require several assumptions to simplify the original problem and so reduce the physical and mathematical complexities. A lack of knowledge regarding the viscosity gradients near the channel surfaces often leads to overestimation of the EOF flow rate (45). These factors should be taken into consideration in future work to obtain a better understanding of viscous flows very near the channel surfaces. In this work, we also examined a numerical approach to determine the EOF velocity profile in the presence of viscosity gradients near the channel walls as shown in the Supporting Material. As a result, it was found that these viscosity gradients did not seriously affect the translocation properties of the ssDNA model. Thus, hereafter, we apply a constant viscosity for the solution in a cylindrical nanochannel.

Langevin dynamics simulation using a coarse-grained ssDNA model

Using the EOF velocity fields described above, an LD simulation was performed to investigate the behavior of ssDNA translocating through a cylindrical nanochannel. The presence of solvent molecules that cause thermal fluctuations was treated as a random force acting on the ssDNA (14, 20, 38). In this project, we applied an in-house coarse-grained bead-spring model based on prior theoretical studies (14, 20, 38) that have already provided some fruitful computational results in conjunction with experimental data (21, 22, 46). In the coarse-grained model, nucleotides consisting of base, sugar, and phosphate groups are treated as a single particle, and 12 nt are replaced by a coarse-grained bead to represent the physical properties of ssDNA, such as the R_g, diffusion coefficient, and electrophoretic mobility. A brief description of the simulation methodology and its validation is also provided in Supporting Material.

The polymer length was varied by using different values for N, the number of coarse-grained beads, such as N = 1, 5, 10, 20, 30, and 50, corresponding to ssDNA lengths of 12, 60, 120, 240, 360, and 600 nt, respectively. The R_g of ssDNA ranges from 5 to 25 nm, reproducing the theoretical value represented by the persistent length, σ = 5 nm for ssDNA, and the contour length, L = Nσ, such that R_g = $\sqrt{\sigma L/3}$ (15), and these values are equivalent to a 30 nm channel diameter (Fig. S1 in the Supporting Material). Therefore, our system corresponds to a de Gennes regime, a ≈ R_g (27), or a bulk regime, a > R_g. In these transport regimes, we assume that hydrodynamic interactions resulting from the anisotropic behavior of solvent molecules have a negligible impact on the transport of ssDNA from an overdamped point of view (47, 48, 49, 50). Although the importance of interactions between the target molecules and the surrounding liquid in narrow spaces has been recognized, there is not yet a suitable solution for this problem. Thus, we did not employ any specific model for hydrodynamic effects in this study. Our millisecond-range simulation focused on averaged ssDNA transport properties, and so hydrodynamic effects were screened in the case of the coarse-grained model.

The electrically charged molecules moved in a mean field generated by the presence of electrolyte ions, assuming that the distribution of the surrounding ions was not disturbed. Although a number of solvent molecules and ions varies near each polymer molecule, as shown in a previous study (51), these coarse-grained beads represented a sufficiently screened mass and so did not directly interact with their surroundings. There is a limitation associated with treating electrical charges in terms of electrokinetics and coarse-grained models; it must be assumed that electrical charges are strongly attracted to the coarse-grained bead or wall surfaces but do not interact with one another (52). Therefore, E_r and E_z can also be separated as in conventional models. The motions of the free charges represented by electrolyte ions were obtained from molecular dynamics simulations, although such calculations may not be helpful in terms of simulating practically observable spatiotemporal scales (51). The quantities of electrical charges on the ssDNA and in the nanochannel are compared in Supporting Material. The electrical charge densities were found to differ by more than one order of magnitude, except in the case of λ_D = 2 nm (C = 2 × 10⁻² M), and so the separation was considered to be acceptable. These assumptions were verified by determining specific values of ξ and q to reproduce the physical properties of ssDNA provided in Table 2.

Table 2.

Electrical Charge, q, and Friction Coefficient, ξ, for Various Polymer Lengths, N

N	q (−e)	ξ (10−12 kg/s)	q/ξ (10−8 m2/Vs)
1	4.01	21.42	3.00
5	1.88	10.02	3.00
10	1.36	7.28	2.99
20	0.97	5.18	3.00
30	0.82	4.40	3.00
50	0.65	3.47	3.00

In the time evolution process, the Langevin equation was numerically integrated with time steps of 1.0 ps over a 2.0 ms period for a single run. An electric field in the z-direction was applied to obtain an electric force, with E_z = 1.0 × 10⁵ V/m. Initially, equilibrated ssDNA was placed in the cylindrical nanochannel and was forced to move along E_z in the EOF. A time span of at least 1.0 ms was required for the preparatory computations to achieve a steady motion and after that, data sampling was carried out in the steady state for 1.0 ms. For each condition, a minimum of 20 runs was performed to obtain simulation data. Verification of these computational conditions is also described in Supporting Material.

Results and Discussion

Dependence of ssDNA mobility on ion concentrations

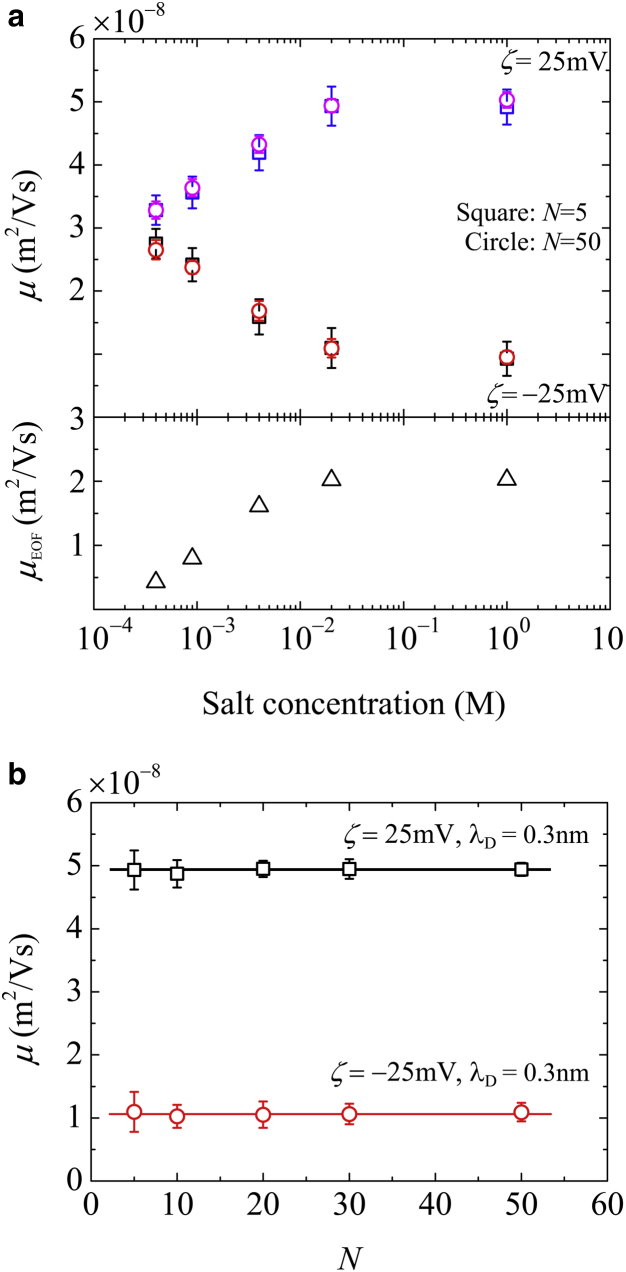
Fig. 2 a shows the electrophoretic mobility of coarse-grained ssDNA, μ (= v_c/E_z, where v_c is the velocity of the center of mass along the z axis), as a function of ion concentration for both positive and negative ζ-potentials. The EOF mobility, μ_EOF (= u_z/E_z), was also evaluated at r = 0. This graph demonstrates the significant effect of the ion concentration on the transport of the long polymer chains. Increases in C evidently caused a pronounced shift in the mobility. In the case of N = 50, the mobility was reduced from 2.7 × 10⁻⁸ to 1.1 × 10⁻⁸ m²/Vs for ζ = −25 mV and increased from 3.3 × 10⁻⁸ to 5.0 × 10⁻⁸ m²/Vs for ζ = 25 mV. Due to the negative ζ-potential, the direction of the EOF was opposite to the ssDNA transport direction and the electrophoretic mobility decreased with increasing C for both N = 5 and 50, as shown in Fig. 2 a. In contrast, for the positive ζ-potential, the mobility increased with C due to the EOF being in the same direction as the ssDNA transport. This result suggests the possibility of controlling the translocation velocity of the polymer chains by effectively inducing EOFs as a function of C. However, as shown in Fig. 2 b, the electrophoretic mobility was not affected by N, even though it was modulated in the nanochannel compared to that in a free solution. The electrophoretic mobility can be approximated by the superposition of μ_EOF and the mobility in a free solution, μ_free, such that μ ≈ μ_EOF + μ_free. Similar observations concerning the length-independent mobility of DNA even in nanochannels as the result of saturated confinement effects have been reported for long-chain dsDNA (4, 8). Either increasing the nanoslit height (4) or decreasing the DNA length (8) leads to a loss in separation resolution. This constant mobility of long-chain dsDNA is believed to break down in nanoslits narrower than 20 nm (4, 18), in which the DNA molecules interact strongly with the wall surfaces and inelastically dissipate their energy due to friction on the nanoscale (16). This issue has attracted much attention and is still being debated. Our simulation results demonstrate that the electrophoretic mobility of short-chain ssDNA is length-independent in a straight nanochannel with a 30 nm diameter. In practical applications, the velocity control of short-chain ssDNA in nanopores or separation in nanochannels involves a greater degree of confinement, such as occurs in gel media (27) and artificial nanochannels with nanoscale obstacles (8, 19).

Figure 2.

Electrophoretic mobility, μ, of ssDNA in the presence of an EOF with negative and positive ζ-potentials as functions of (a) ion concentration, and (b) polymer length, N. In (a), μ is presented for the cases of N = 5 (squares) and 50 (circles), and the EOF mobility, μ_EOF, values are also shown (triangles). To see this figure in color, go online.

Molecular conformations of coarse-grained ssDNA in a nanochannel

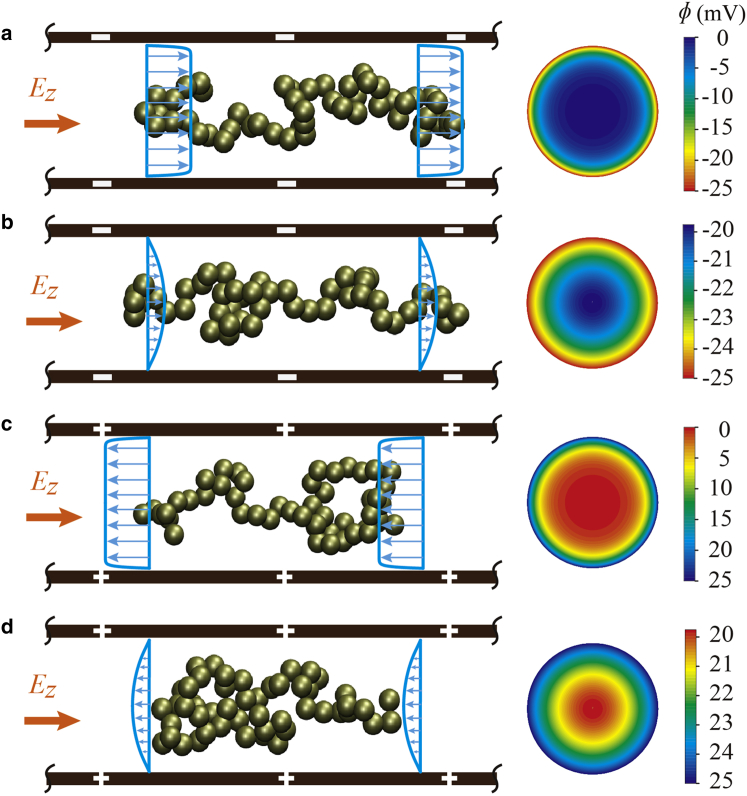
Fig. 3 presents the typical conformations of ssDNA in a nanochannel as obtained from the LD simulations, in which ion distributions in the nanochannel are affected by the radial electric field E_r. In the case of a negative (positive) ζ-potential, E_r repels (attracts) negatively charged molecules. The right panel in Fig. 3 presents color maps for the electrostatic potential across the nanochannel cross section. At λ_D = 0.3 nm (C = 1 M), as shown in Fig. 3 a, the steep gradient in the ϕ-values resulted in a strong E_r, ranging from 0 at the center to 8.2 × 10⁷ V/m at the channel surface. A broader distribution is evident at λ_D = 15 nm (C = 4 × 10⁻⁴ M), varying from E_r = 0 V/m at the center to 7.4 × 10⁵ V/m at the channel surface. These data indicate that altering C caused λ_D to vary and this, in turn, produced a flow profile transition from plug flow to Poiseuille-like flow, as shown in Fig. 3, a and b, respectively. At positive ζ-potentials, the direction of the EOF was opposite to the direction obtained with a negative potential, as shown in Fig. 3, c and d. The molecular conformations resulting from the LD simulations demonstrate a typical deformation trend inside the nanochannel, affected by both the EOF and E_r. The velocity gradient of the EOF-induced shear force between two coarse-grained molecules in different stream lines tends to stretch the bonds between neighboring molecules. These trends are discussed in more detail below.

Figure 3.

Images showing the results of LD simulations for both (a and b) −25 mV and (c and d) 25 mV ζ-potentials (left panel) and the electrostatic potential, ϕ, in the channel cross section (right panel). Various combinations of ζ and EOF cause specific deformation patterns in the polymer chain, including a pluglike EOF with λ_D = 0.3 nm (a and c) and a Poiseuille-like EOF with λ_D = 15 nm (b and d). To see this figure in color, go online.

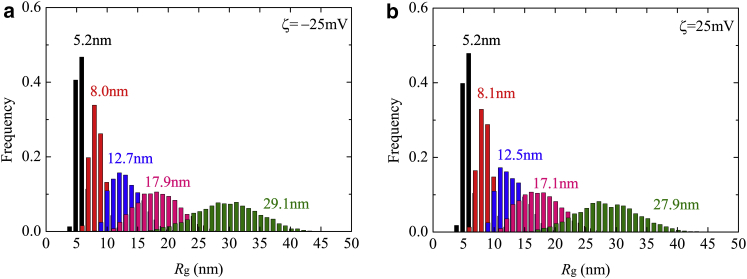
Fig. 4 presents the temporal and ensemble averages of R_g for N values from 5 to 50. The definition of R_g is also provided in Supporting Material. R_g and the deviation of the distribution both increased with increasing N at both negative and positive ζ-potentials. Based on the R_g of ssDNA in a free solution, this value will exceed the channel radius when N is above 20 (see also Fig. S1). This explains why the deviation of R_g increased so dramatically above N = 20. In addition, an unexpected nonmonotonic change in R_g is observed here. At N = 5, the short chain length limited the deformation of the ssDNA and so there was almost no variation in R_g. For N = 10, the average R_g value decreased from 8.1 to 8.0 nm upon switching the ζ-potential from positive to negative. In contrast, the average R_g increased by 1.6, 4.7, and 4.3% for N = 20, 30, and 50, respectively, upon applying a negative ζ-potential instead of a positive potential. This result demonstrates that switching the ζ-potential affects the polymer conformation in the nanochannel.

Figure 4.

Distributions of R_g in the nanochannel for a variety of N resulting from (a) ζ = −25 mV and (b) ζ = 25 mV. Mean values of R_g in the case of N = 50 are 29.1 and 27.9 nm for ζ = −25 and 25 mV, respectively. (Black, N = 5; red, N = 10; blue, N = 20; pink, N =30; green, N = 50.) To see this figure in color, go online.

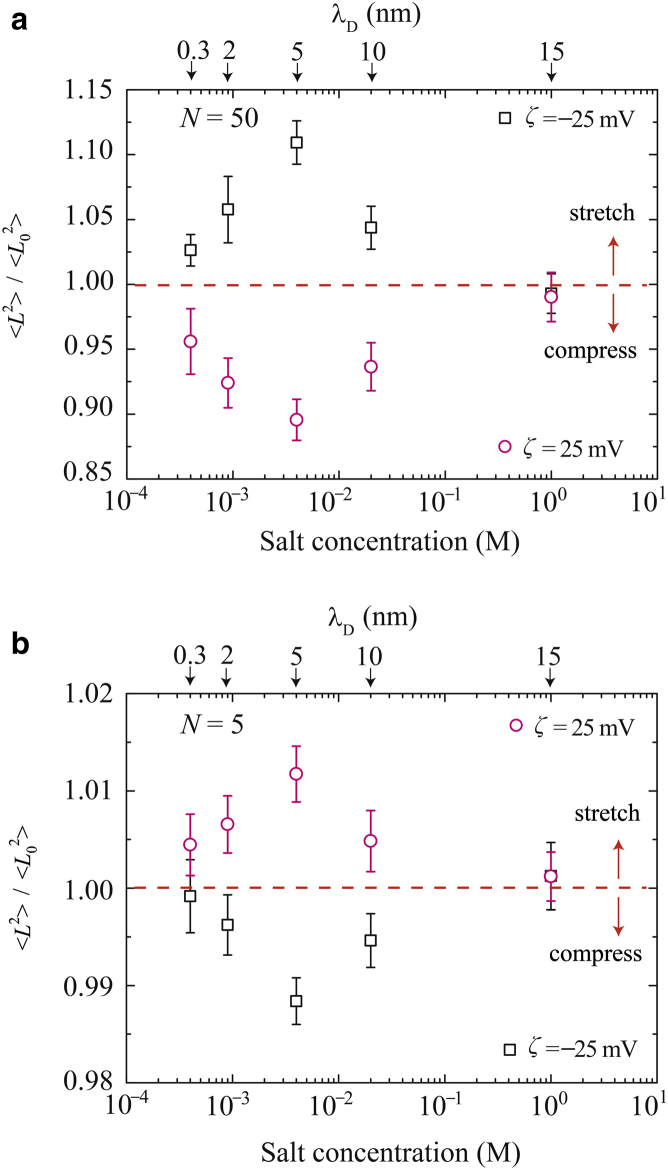
To characterize the deformation of the ssDNA in the nanochannel, we evaluated the mean-square end-to-end distances, $\langle L^2\rangle$, of polymer chains exposed to the E_r and EOF, and compared these values to those predicted for equilibrium in the nanochannel, $\langle L_0^2\rangle$. The ratio of these values, $\langle L^2/L_0^2\rangle$, indicates the degree of polymer deformation, whether by stretching (>1) or compression (<1). Fig. 5, a and b, presents the histograms of these ratios for N = 50 and 5, respectively, as functions of the ζ-potential and λ_D. As can be seen, the ratio varied nonmonotonically as a function of C. The compression and stretching of the ssDNA were greatest at C = 4 × 10⁻³ M (λ_D = 5 nm). At ζ = 25 mV, the plot shows a deviation between 0.89 and 0.99, implying a maximum 11% compressive deformation of the long-chain ssDNA (N = 50). In contrast, a maximum stretch of 10% was obtained from a negative ζ-potential. These trends were reversed in the case of N = 5, as shown in Fig. 5 b. In this scenario, the distribution concentrates near $\langle L^2/L_0^2\rangle =1.00$, and the deformation is <2%.

Figure 5.

Mean-square end-to-end distances, $\langle L^2\rangle$, of ssDNA exposed to E_r in a nanochannel at various values of z potential and λ_D. Here $\langle L^2\rangle$ is normalized by the mean-square end-to-end distance, $\langle L_0^2\rangle$, in an equilibrated solution in the channel. Data are shown for the polymer lengths (a) N = 50 and (b) 5. To see this figure in color, go online.

Radial positioning of a polymer chain in a nanochannel

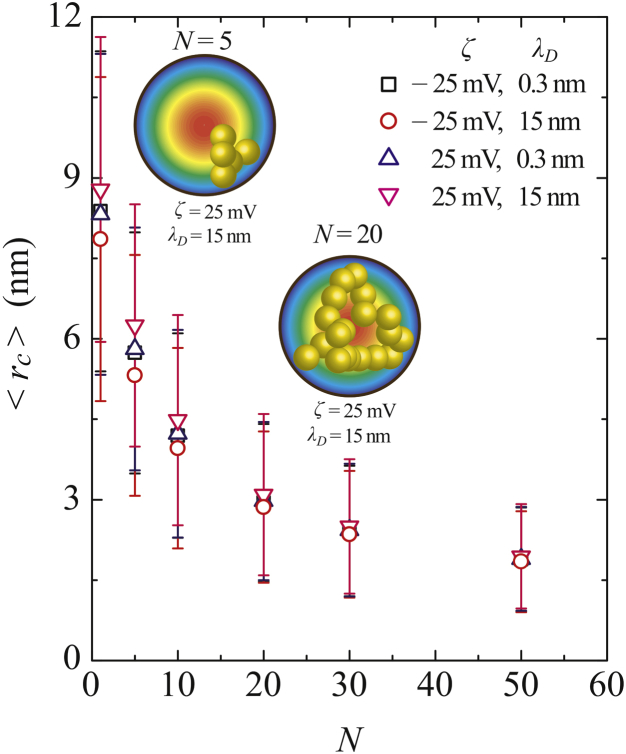
The ensemble average of the mass-center radial position $\langle r_c\rangle$ of the ssDNA was subsequently evaluated as a function of N. Fig. 6 demonstrates that the center of mass tended to concentrate near the center of the nanochannel with increasing N, regardless of the sign of the ζ-potential or the λ_D. Above N = 20, in the range of R_g > a, the long polymers were tightly packed in the nanochannel and thus, the center of mass was located in the center of the channel as a result of the distribution of the connected beads. However, in the case of short polymers (such as N = 1, 5, and 10), $\langle r_c\rangle$ appeared to become more sensitive to the ζ-potentials of −25 and +25 mV at λ_D = 15 nm (C = 4 × 10⁻⁴ M), as shown in Fig. 6. The different polymer structures at N = 5 and 20 are also provided in this figure. At N < 20, the numerical data show large deviations because the effect of thermal fluctuations dominated the motion, in addition to electric forces resulting from the wall potential. Although the short-chain ssDNA appeared to be more readily controlled by applying electric fields, the Brownian motion of these molecules disturbed the alignment of the molecules. As a consequence of the specific polymer conformations, $\langle r_c\rangle$ tended to monotonically approach the channel center with increasing N as the molecules were exposed to the EOF fields. As N increased, the long polymer chains behaved as though they are coiled within the inner wall of the cylinder. This explains why the center of mass of long-chain ssDNA always appeared near the channel center and there was no difference between positive and negative ζ-potentials.

Figure 6.

Ensemble averages of the center-of-mass radial position, $\langle r_c\rangle$, as a function of the polymer length, N, at ζ = −25 mV, λ_D = 0.3 nm (black squares); ζ = −25 mV, λ_D = 15 nm (red circles); ζ = 25 mV, λ_D = 0.3 nm (blue triangles); and ζ = 25 mV, λ_D = 15 nm (pink inverted triangles). The error bars that represent the standard deviations reflect the Brownian motion of ssDNA inside the nanochannel. To see this figure in color, go online.

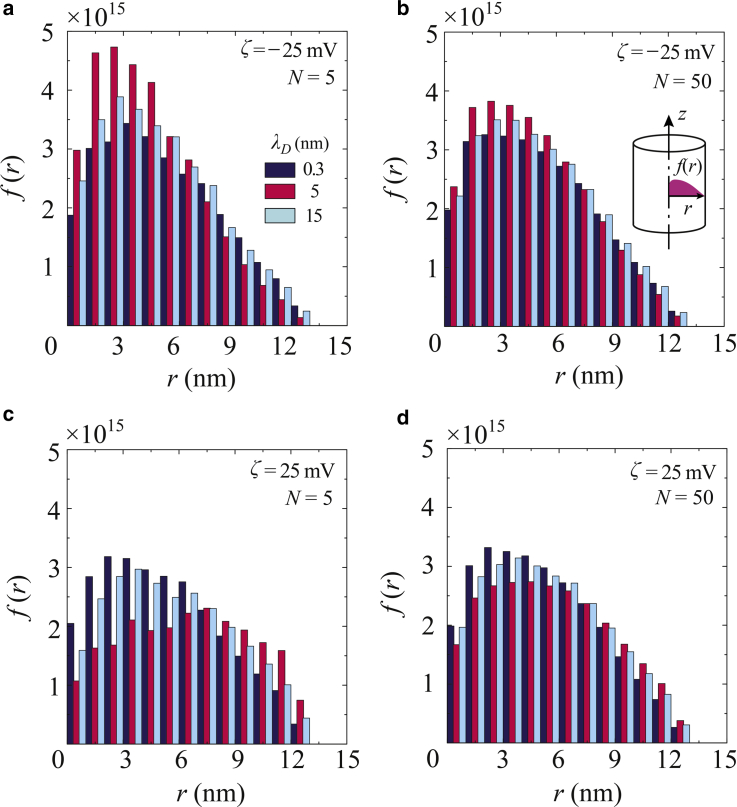
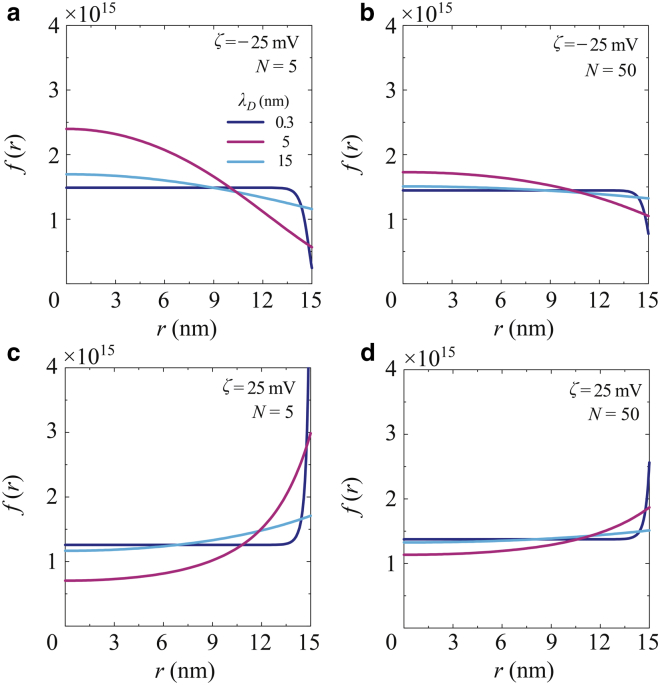
Fig. 7 presents the distribution functions, f(r), of the radial positions of coarse-grained beads in the channel for a variety of λ_D, where f(r) is discretized and normalized, such that $2\pi {\sum }_{i=1}^n{r}_{i}f\left(r_i\right)\Delta r=1$. Here, we set Δr = a/n, where n = 15 for a = 15 nm, such that Δr = 1 nm. During the LD simulation run, the radial position of each individual bead was calculated at 10 μs intervals during the last 1.0 ms of simulation time. The results showed the detailed behavior of each bead as well as that of the center of mass, as presented in Fig. 6. For the negative ζ-potential, as shown in Fig. 7, a and b, the coarse-grained beads appear to have been repelled by the surface potentials and thus migrate toward the channel center. At N = 5, as in Fig. 7 a, E_r clearly pushed the distribution in the radial direction and, at λ_D = 5 nm (C = 4 × 10⁻³ M), the peak position at approximately r = 2.5 nm was the nearest to the center. Because of the spring force between the connected beads, the peak positions were not coincident with the center, which is obviously different from the random walk of a single particle. For λ_D = 15 nm, E_r was also broadly expanded along the channel cross section and so the charged beads were exposed to the electric field. In contrast, the electric force was weakened in the case of a thick EDL and the peak position was further from the center than in the case of λ_D = 5 nm (C = 4 × 10⁻³ M). At N = 50, as shown in Fig. 7 b, there was not such a clear difference in the distributions as a function of λ_D. It is evident that, especially in the case of short polymer chains, the negative ζ-potential and EDL thickness can potentially affect the positioning of the ssDNA in the channel. At a positive surface potential, as shown in Fig. 7, c and d, although the electrically charged molecules were attracted to the wall surface, they were also repelled due to the elastic wall potential. As a result, peak positions appeared apart from the attractive wall surface. It is especially evident in Fig. 7 c that the histograms exhibit different peaks depending on λ_D. At λ_D = 5 nm (C = 4 × 10⁻³ M), the ssDNA was more strongly attracted to the surface. Some hot spots through which there was greater bead movement were obvious as the result of the coexistence of radial electric fields, the EOF, and the elastic wall potential. Conversely, the distributions were not so clearly distinguished based on variations in λ_D. The short-chain ssDNA appears to have been particularly affected by these factors and these variables may therefore play a significant role in defining the radial positions of molecules in conjunction with negatively polarized channel surfaces. Fig. 7 shows an off-center distribution of the connected beads in the channel in the presence of E_r and the EOF. Butler et al. (53) has reported that the maximum distribution of polymer molecules modeled by a dumbbell structure similarly appears at an off-center position in response to an applied external force and imposed flow field, based on the kinetic theory. This study confirmed these previous results in terms of the coarse-grained LD model simulating ssDNA on practical spatial and temporal scales.

Figure 7.

Discretized distribution functions, f(r), of the radial positions of individual coarse-grained beads in a channel at λ_D = 0.3, 5, and 15 nm, for (a and b) a negative ζ-potential of −25 mV and polymer lengths of (a) N = 5 and (b) 50, and for (c and d) a positive ζ-potential of 25 mV and (c) N = 5 and (d) 50. The radial position of each molecule was sampled at 10 μs intervals over the last 1.0 ms of simulation time. To see this figure in color, go online.

Theoretical approach to the molecular distribution in a nanochannel

For comparison purposes, we also carried out a numerical analysis by solving Nernst-Planck and Poisson equations, as described below. In these analyses, electrically charged single particles with diffusion coefficients and electrophoretic mobilities equal to those of coarse-grained ssDNA responded to E_r and EOF more obviously, and the radial distributions reflected the attractive and repulsive interactions in the nanochannel. In this case, ionic currents and the EOF due to the transport of electrolyte ions were assumed to be at a steady state. Thus, the electrostatic potential, ϕ, and the velocity field, u, of the EOF are solved analytically. Additionally, it was assumed that the electric fields could be represented as separate transversal and longitudinal components:

$$\mathbf{E}=E_r{\mathbf{e}}_r+E_z{\mathbf{e}}_z=-\frac{\text{d}\varphi }{\text{d}r}{\mathbf{e}}_r+E_z{\mathbf{e}}_z.$$ (4)

In such a field, the behavior of negatively charged beads can be evaluated. When the number density, n, of beads, the charge, q, the friction coefficient, ξ, and the diffusion coefficient, D, are fixed, the flux, f = (f_r, f_z), can be expressed as follows:

$$f_r\left(r\right)=-\frac{q}{\xi }\frac{\text{d}\varphi }{\text{d}r}n-D\frac{\text{d}n}{\text{d}r}=0$$ (5)

and

$$f_z\left(r\right)=\frac{q{E}_z}{\xi }n+u_{z}n.$$ (6)

Assuming a uniform electric field, E_z, the ion distribution gradient along the z axis is negligibly small. Solving Eq. 5 with the fluctuation-dissipation theorem, such that ξD = k_BT, we obtain

$$n\left(r\right)=n_0\text{exp}\left[-\frac{q\varphi }{k_{\text{B}}T}\right],$$ (7)

where n₀ is a constant. At this point, f_z is normalized to the channel cross-section to allow a qualitative discussion of the results. According to Eqs. 6 and 7, we obtain

$$f_z\left(r\right)=\frac{\left[\frac{q{E}_z}{\xi }+u_z\right]\text{exp}\left[-\frac{q\varphi }{k_{\text{B}}T}\right]}{2\pi {\int }_0^a\left[\frac{q{E}_z}{\xi }+u_z\right]\text{exp}\left[-\frac{q\varphi }{k_{\text{B}}T}\right]r\text{d}r}.$$ (8)

The EOF velocity, u_z, and ϕ were determined from Eqs. 1 and 3, respectively, and the other properties were set to those of the water, as noted above.

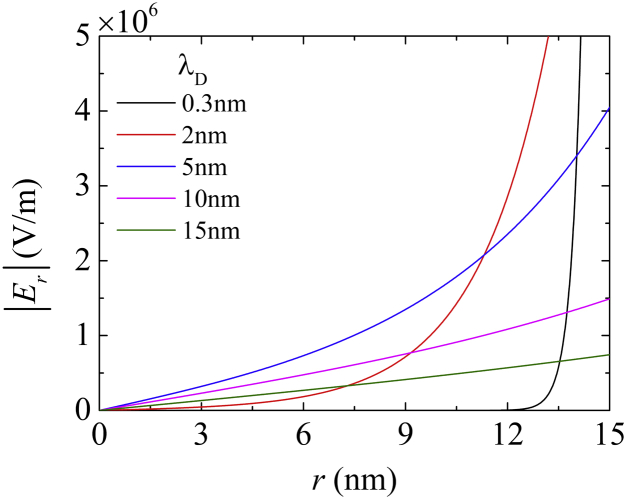
Fig. 8 presents the electric field strengths in terms of the channel radial position calculated from Eq. 3, such that E_r = −dϕ/dr. Varying the salt concentration affected E_r in two respects: the magnitude and the effective area. The highest salt concentration, C = 1 M and λ_D = 0.3 nm, resulted in an extremely short-range but strong E_r on the order of 10⁷ V/m, within a span of 2 nm from the wall surface. It is evident that there was a critical point near λ_D = 5 nm (C = 4 × 10⁻³ M) at which the E_r plot transitioned from an exponential curve to a linear relationship. Further decreases in C reduced the magnitude of the E_r that broadly affected the channel. This critical condition clearly modified the distribution of electrically charged particles, as described below.

Figure 8.

Radial electric field strengths, E_r, as a function of the radial position, r, in a nanochannel at different salt concentrations. (Black line, λ_D = 0.3 nm; red line, λ_D = 2 nm; blue line, λ_D = 5 nm; pink line, λ_D = 10 nm; green line, λ_D = 15 nm.) The radial electric field was calculated using Eq. 2. To see this figure in color, go online.

Fig. 9 shows the distribution function, f_z, using q and ξ as the parameters that determine the properties of the ssDNA, as summarized in Table 2. Fig. 9 a presents the results for ζ = −25 mV, q = −1.88e, and ξ = 10.02 × 10⁻¹² kg/s in the case of N = 5. As λ_D was increased, the charged particles tended to locate near the center and exhibited a minimum peak position when λ_D = 5 nm (C = 4 × 10⁻³ M). Equation 5 demonstrates that the repulsive force from the channel surface was significantly stronger than the diffusive force at λ_D < 5 nm (C > 4 × 10⁻³ M). Further increases in λ_D (>5 nm) moved the distribution away from the center. In addition, Eqs. 1 and 8 demonstrate that the EOF velocity field that varied with r enhanced the off-center behavior. In the case of q = −0.649e and ξ = 3.47 × 10⁻¹² kg/s for N = 50, as shown in Fig. 9 b, the difference between the peaks in each distribution was reduced at ζ = −25 mV, compared with the values in Fig. 9 a. Conversely, at ζ = 25 mV, the negatively charged particles were attracted to the positively charged surface, as in Fig. 9 c, such that the charged particles shielded the wall surface in conjunction with an extremely thin EDL of λ_D = 0.3 nm. The greatest variation in radial distribution occurred at λ_D = 5 nm (C = 4 × 10⁻³ M). At λ_D > 5 nm (C < 4 × 10⁻³ M), the particles were weakly attracted to the center. At ζ = 25 mV for N = 50, as shown in Fig. 9 d, the particles dissociated from the surface, although the attractive force from the channel surface remained in effect.

Figure 9.

Radial distribution functions, f(r), of electrically charged particles in a nanochannel at λ_D = 0.3, 5, and 15 nm, obtained by solving the Nernst-Planck and Poisson equations (Eqs. 14 and 15), for (a and b) a negative ζ-potential of −25 mV and (a) N = 5 and (b) 50, and for (c and d) a positive ζ-potential of 25 mV and (c) N = 5 and (d) 50. Here f(r) is normalized by ${\int }_0^{a}2\pi f\left(r\right)r\text{d}r=1$. To see this figure in color, go online.

These theoretical results indicate that the deformation evident in Fig. 5 and the distribution shown in Fig. 7 actually result from the electric force due to the presence of E_r as shown in Fig. 8, because the ssDNA experiences either repulsive or attractive electric force in the radial direction. More importantly, the deformation and distribution of the polymer both exhibit nonmonotonic behavior because of the combined effects of the magnitude and effective range of E_r. In the case of 30 nm diameter channel, preparing λ_D = 5 nm (C = 4 × 10⁻³ M), the broadly distributed E_r effectively works on the conformation change and deformation of the ssDNA. On the other hand, excessively high and low concentrations both do not contribute to generate the meaningful electric nor EOF fields for the polymer chain. The important thing is to create the most effective E_r against the channel size. Nanochannels are available to realize the optimized fields with moderate concentrations comparatively easily preparing in experiments. Consequently, the distribution shown in Fig. 7 demonstrates that polymers tend to be transported through the off-center regions of a nanochannel having a 30 nm diameter. This explains the experimental observation of a reptationlike motion of DNA in a 30 nm nanoslit, which is clearly different from the behavior seen in less confined nanoslits (wider than 40 nm) (24). Our study confirms that surface charges (in addition to confinement effects) influence the transport mechanism of biopolymers when the channel dimension is reduced to <30 nm (that is, a value comparable to λ_D).

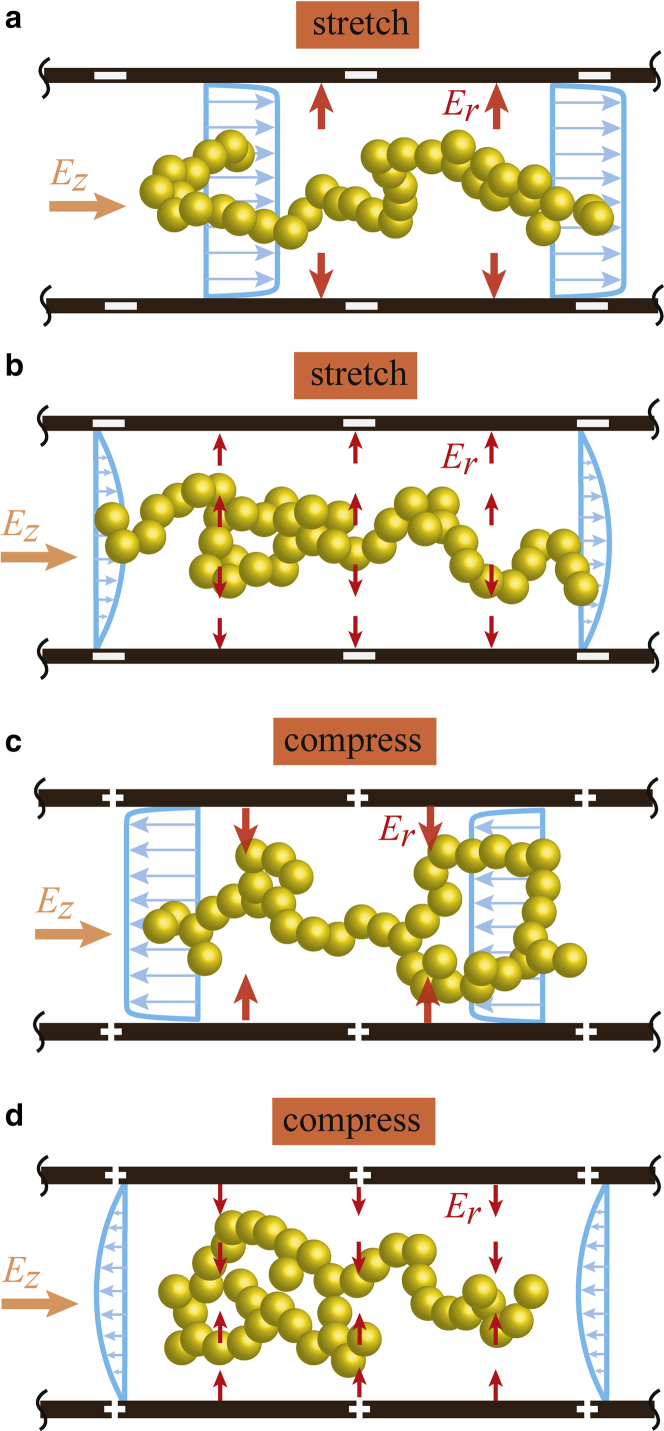
The results described above for long-chain ssDNA (N ≥ 20) are summarized schematically in Fig. 10. In the case of negatively polarized wall surfaces, the EOF and the electrophoretic transport of the ssDNA are in opposite directions, as in Fig. 10, a and b. In this scenario, a thin EDL at high concentrations results in a pluglike EOF that is almost constant regardless of r, as presented in Fig. 10 a. As the molarity decreases, the flow field clearly generates a velocity gradient that causes a relative velocity difference between molecules in different stream lines. Additionally, due to the radial electric force, the effective volume of the nanochannel decreases and the polymer chain is stretched, as in Fig. 10 b. In contrast, positively polarized wall surfaces provide electrokinetic transport of the ssDNA in the same direction as the EOF, as in Fig. 10, c and d. The radial electric force, which becomes stronger at medium ion concentrations, induces intramolecular interactions and compressive deformations along the axial direction, as in Fig. 10 d.

Figure 10.

Schematic representations of the ssDNA transport mechanism in a nanofluidic channel resulting from the LD simulations. The DNA chain experiences a repulsive (a and b) or attractive (c and d) forces in the radial direction caused by negative or positive ζ-potentials, respectively. Depending on the ion concentration, a strong electric force acts on the molecule in the EDL. (a and b) Due to the negative ζ-potential, the channel surface repels the negatively charged DNA toward the center, the EOF field causes intramolecular interactions in the polymer chain, and the velocity gradient at lower ion concentrations results in stretching of the polymer structure as shown in (b). (c and d) The positive ζ-potential attracts the DNA to the channel surface and the EOF velocity gradient deforms the molecule in a dilute solution. As a result, the polymer structure is compressed as shown in (d). To see this figure in color, go online.

These results suppose an interesting idea that negatively charged polymer chains can be stretched by using negatively charged surface channels with the optimized salt concentrations, where EOF fields driven by counter cations effectively work to reduce the translocation velocity of the polymers. This is a desirable technology in single molecule analysis using nanopore devices, in which capture and reading of base sequences must be carried out simultaneously (24, 25, 26).

Conclusions

Simulating the EOF velocity fields in a cylindrical nanochannel with a 15 nm radius allowed the characterization of the electrokinetic transport regimes of ssDNA via LD simulations in conjunction with a coarse-grained model. The validity of this model was verified by evaluating the diffusion coefficient, electrophoretic mobility, and radius of gyration in a free solution. The charged polymer transport properties in EOF fields were evaluated and some useful results were obtained. Focusing on the case in which R_g is similar to or greater than the radius of the channel cross section, the relationship between the flow field and the deformation of the polymer conformation was evaluated. The electric force in the channel primarily results from the ζ-potential, and this force repels (attracts) negatively charged ssDNA molecules at negative (positive) surface potentials. In the transport regime, short-chain ssDNA tends to be strongly affected by the radial electric field, the EOF, and the wall potential. Furthermore, as the ion concentration is decreased, the EOF exhibits apparent velocity gradients that lead to intramolecular interactions between the coarse-grained ssDNA molecules. Especially in dilute electrolyte solutions, setting the direction of the EOF forward or backward to the direction of the ssDNA electrophoresis leads to a deformation regime in which polymer chains are compressed or stretched, respectively. Consequently, the possibility of controlling the velocity of polymer transport by modifying the EOF profile and ζ-potential is evident.

This study is relevant to the fields of polymer physics and applied biophysics. These findings may also lead to the development of novel single-molecule manipulation techniques in liquid flows. Examples of possible applications include recently reported experiments aimed at slowing ssDNA translocation through a nanochannel by adjusting the electric potential (54), and stretching ssDNA exposed to external liquid flows near substrate surfaces (55, 56).

Author Contributions

W.Q. mainly developed the computational models and performed the LD simulations; and W.Q., K.D., and S.K. contributed equally in writing the main text.

Editor: Andrew Spakowitz.