Modeling the Actin.myosin ATPase Cross-Bridge Cycle for Skeletal and Cardiac Muscle Myosin Isoforms

Abstract

Modeling the complete actin.myosin ATPase cycle has always been limited by the lack of experimental data concerning key steps of the cycle, because these steps can only be defined at very low ionic strength. Here, using human β-cardiac myosin-S1, we combine published data from transient and steady-state kinetics to model a minimal eight-state ATPase cycle. The model illustrates the occupancy of each intermediate around the cycle and how the occupancy is altered by changes in actin concentration for [actin] = 1–20$K_{\text{m}}$. The cycle can be used to predict the maximal velocity of contraction (by motility assay or sarcomeric shortening) at different actin concentrations (which is consistent with experimental velocity data) and predict the effect of a 5 pN load on a single motor. The same exercise was repeated for human α-cardiac myosin S1 and rabbit fast skeletal muscle S1. The data illustrates how the motor domain properties can alter the ATPase cycle and hence the occupancy of the key states in the cycle. These in turn alter the predicted mechanical response of the myosin independent of other factors present in a sarcomere, such as filament stiffness and regulatory proteins. We also explore the potential of this modeling approach for the study of mutations in human β-cardiac myosin using the hypertrophic myopathy mutation R453C. Our modeling, using the transient kinetic data, predicts mechanical properties of the motor that are compatible with the single-molecule study. The modeling approach may therefore be of wide use for predicting the properties of myosin mutations.

Introduction

The actomyosin ATPase cycle has been studied since myosin was first isolated and recognized as an ATPase (1, 2, 3). The biochemical kinetics of the cycle have been defined using steady-state and transient kinetics methods for different myosin isoforms (both muscle and non-muscle) and under a range of different experimental conditions (4, 5). The major events around the cycle remain the same for all myosins studied to date (see Fig. 1), but with alterations in the overall cycle speed and the fraction of the cycle time spent in the different intermediate states around the cycle, i.e., the duty ratio (6, 7, 8). These alterations in the cycle tune the myosin to a specific function, which for the sarcomeric myosin IIs include shortening velocity, steady-state force, and efficiency, defined as force per ATP, etc. (9). Although these results have led to a good understanding of the molecular and structural changes in the cycle, understanding how these operate in the cell is often more difficult. Two missing elements in any model of the cycle in solution are how load on the motor alters the cycle and the effective actin concentration the myosin is exposed to. Any model of the cross-bridge cycle has to build in these two elements to create a description of the working system. We present here a cross-bridge model that examines these two elements in relation to the differences between the major muscle myosin II isoforms, fast skeletal myosin (rabbit myosin 2a) and the two human cardiac isoforms, α and β. The β-cardiac isoform is identical to the slow muscle isoform.

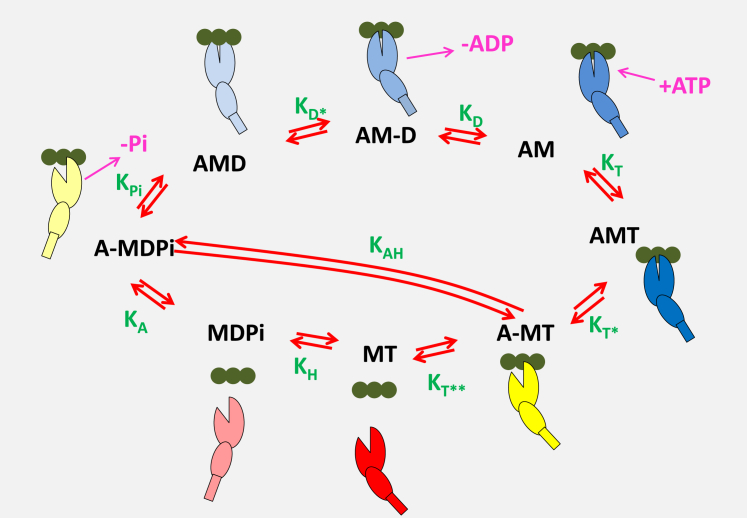
Figure 1.

A minimal ATPase actin-myosin cycle is defined by eight states and nine equilibrium constants. The actin monomers, A, along an actin filament are shown as three green solid circles, and the motor domain of myosin, M, is represented as two ellipses, the larger representing the upper and lower 50 k domain, with a cleft separating the two domains, and the smaller representing the converter domain, with a rectangular lever arm. The relative movements of these domains represent the structural conformations of myosin in each state. The actin-myosin cycle includes ATP binding to rigor-like complex, AM, forming the AMT state (equilibrium constant for the transition, $K_{\text{T}}$ = [AMT]/[AM][T]), followed by a rapid change in myosin conformation leading to the cleft opening in the A-MT state $\left(K_{{\text{T}}^{\ast }}\right)$ and subsequent rapid detachment of actin $\left(K_{{\text{T}}^{\ast \ast }}\right)$. A conformational change in the head following the opening of the 50 kDa cleft leads to the recovery stroke and hydrolysis of ATP transitioning into the MDPi state $\left(K_{\text{H}}\right)$. Then, the myosin can reattach to actin, forming the A-MDPi state $\left(K_{\text{A}}\right)$ and after the cleft closure, the power stroke and Pi release, transitioning into an AMD state $\left(K_{\text{Pi}}\right)$ in which ADP remains firmly attached to myosin. This state allows a conformational change into the AM-D state $\left(K_{{\text{D}}^{\ast }}\right)$, from which ADP is released $\left(K_{\text{D}}\right)$ and the cycle is completed. The step labeled $K_{\text{AH}}$ allows for possible hydrolysis of ATP while myosin remains attached to actin. For simplicity, ATP and ADP in state labeling are denoted as T and D, respectively, and inorganic phosphate as Pi. A hyphen indicates a relatively weak association between the species. The equilibrium constants between the states are denoted in green letters and represent a ratio between forward (clockwise) and reverse state-transition rate constants. Note that the nomenclature for rate and equilibrium constants uses the subscripts A, D, Pi, and T to indicate the species binding to or released from myosin in each second-order step. An asterisk (^∗) indicates that an isomerization event is linked with the second-order binding or dissociation event. The only exceptions are $K_{\text{H}}$ and $K_{\text{AH}}$, which are the ATP hydrolysis steps with or without actin attached.

We recently completed a kinetic analysis of the slow skeletal/β-cardiac muscle isoform of both bovine (10) and human myosin II (11). The step size and load dependence of the ADP release step has recently been defined for the human and porcine β-cardiac isoform (12, 13). It is therefore a good time to attempt to model the complete ATPase cycle for this well-defined slow muscle isoform (MyHC7) and compare it with the closely related faster isoforms, i.e., the isoform found in the human atrium, α-cardiac (MyHC6), which we have also studied (11) and the well characterized fast skeletal 2a isoform from rabbit (MyHC2).

The work presented here is part of a broader effort to develop a suite of programs (MUSICO) that can model different aspects of muscle contraction from the molecular interaction of individual proteins through to the contracting muscle fiber. Here, the ATPase cycle is modeled as a first step in this process. For a quantitative understanding of the ATPase in solution, the data analysis should be performed on an actomyosin-ATPase cycle model with a sufficient number of states, as, for example, the minimal cycle set out in Fig. 1. In this ATPase cycle, there are eight intermediates defined by nine equilibrium and 18 rate constants. Since the rate and equilibrium constants are not independent, only 18 constants are required for a complete description of the cycle. From the published transient kinetic studies, it is possible to define many of the constants. As set out in the methods for the β-myosin and listed in Table S1, three forward rate constants ($k_{{\text{D}}^{\ast }}$, $k_{{\text{T}}^{\ast }}$, and $k_{\text{H}}$) and two equilibrium constants ($K_{\text{T}}$ and $K_{\text{D}}{K}_{{\text{D}}^{\ast }}$) can be measured with a precision of at least 20%. Three steps are defined as diffusion limited, with a minimum value of 10⁷ M⁻¹ s⁻¹ ($k_{\text{A}}$, $k_{\text{T}}$, and $k_{-\text{D}}$), and two other events are estimated to be too fast to measure and therefore have little influence on the modeling ($k_{{\text{T}}^{\text{∗∗}}}$, and $k_{-\text{A}}$), which together allows one equilibrium constant and three rate constants to be defined by a detailed balance ($K_{\text{T}}$, $k_{\text{D}}$, $k_{-{\text{D}}^{\ast }}$, and $k_{-T}$). The remaining five constants ($K_{\text{A}}$, $K_{\text{H}}$, $K_{\text{AH}}$, and the rate constants $k_{-\text{Pi}}$ and $k_{-\text{T}}$) can be defined by fitting the model to the actin dependence of the steady-state ATPase data, and that analysis is presented here.

The experimental data used show clear differences between the three myosin isoforms. Our modeling illustrates how the properties of the isolated motor define the overall properties of the cycle, and how the myosin isoform can define the velocity at which the myosins can move actin, the load dependence of the cycle, and the force-generating capacity. In broad-brush terms, the predictions based on simple-solution kinetic measurements are compatible with the known properties of muscle fibers expressing these isoforms. Exact matching of the model to the data is not to be expected, since additional parameters come in to play in the contracting muscle fiber, such as the relative geometry of the actin myosin filaments, the stiffness of the structural elements, and the ancillary proteins such as troponin, titin, and myosin-binding protein C. Thus, our aim here is not to match the fiber properties precisely, but to explore the extent to which the myosin isoform properties themselves define the contraction properties of the sarcomere.

Materials and Methods

The rate kinetic process for the ATP cycle shown in Fig. 1 can be described as a system of linear equations that define the rate of change in state concentration as a function of the instantaneous fluxes between the states:

$$d\mathbf{C}\text{/}dt=\mathbf{K}\mathbf{C},$$ (1)

where $\mathbf{C}$ is a vector of the eight state concentrations that form the ATP-ase cycle (Fig. 1), i.e., $\mathbf{C}={\left\{\left[\text{MDPi}\right],\left[\text{A}\text{-}\text{MDPi}\right],\left[\text{AMD}\right],\left[\text{AM}\text{-}\text{D}\right],\left[\text{AM}\right],\left[\text{AMT}\right],\left[\text{A}\text{-}\text{MT}\right],\left[\text{MT}\right]\right\}}^{\text{T}}$, and $\mathbf{K}$ is a matrix defining the state transition rates from and into each state. The general solution of this system of equations provides the transient response of each state from an initial state to the steady-state solution. However, the matrix $\mathbf{K}$ is singular, because the sum of all the rows is a row of zeroes, and therefore, the determinant of $\left|\mathbf{K}\right|=0$. Thus, for a unique solution of Eq. 1, it is necessary to replace one row in $\mathbf{K}$ by the constraint equation coefficients derived from preservation of myosin species, i.e., the sum of concentrations of all states containing myosin should be equal to the total myosin concentration, $\left[{\text{M}}_{\text{tot}}\right],$ at any instant $t$ (14, 15, 16):

$$K=\begin{array}{c}\begin{array}{cccccccc}\text{MDPi}& \text{A}\text{-}\text{MDPi}& \text{AMD}& \text{AM}\text{-}\text{D}& \text{AM}& \text{AMT}& \text{A}\text{-}\text{MT}& \text{MT}\end{array}\\ \left[\begin{array}{cccccccc}-k_{\text{A}}\left[\text{A}\right]-k_{-\text{H}}& k_{-\text{A}}& 0& 0& 0& 0& 0& k_{\text{H}}\\ k_{\text{A}}\left[\text{A}\right]& -k_{-\text{A}}-k_{\text{Pi}}-k_{\text{AH}}& k_{-\text{Pi}}\left[\text{Pi}\right]& 0& 0& 0& k_{-\text{AH}}\left[\text{A}\right]& 0\\ 0& k_{\text{Pi}}& -k_{-\text{Pi}}\left[\text{Pi}\right]-k_{{\text{D}}^{\ast }}& k_{-{\text{D}}^{\ast }}& 0& 0& 0& 0\\ 0& 0& k_{{\text{D}}^{\ast }}& -k_{-{\text{D}}^{\ast }}-k_{\text{D}}& k_{-\text{D}}\left[\text{ADP}\right]& 0& 0& 0\\ 0& 0& 0& k_{\text{D}}& -k_{-\text{D}}\left[\text{DP}\right]-k_{\text{T}}\left[\text{TP}\right]& k_{-\text{T}}& 0& 0\\ 0& 0& 0& 0& k_{\text{T}}\left[\text{TP}\right]& -k_{{\text{T}}^{\ast }}-k_{-T}& k_{-{\text{T}}^{\ast }}& 0\\ 0& k_{\text{AH}}& 0& 0& 0& k_{{\text{T}}^{\ast }}& -k_{{\text{T}}^{\text{∗∗}}}-k_{-{\text{T}}^{\ast }}-k_{-\text{AH}}\left[\text{A}\right]& k_{-{\text{T}}^{\text{∗∗}}}\left[\text{A}\right]\\ 1& 1& 1& 1& 1& 1& 1& 1\end{array}\right]\end{array}$$

In the steady state, the increment in state concentration is equal to zero, i.e., $d\mathbf{C}\text{/}dt=0$, and after inclusion of the conservation of myosin species constraint, the steady-state concentrations can be calculated from

$$\mathbf{C}={\mathbf{K}}^{-1}\mathbf{B},$$ (2)

where vector $\mathbf{B}={\left(\mathrm{0,0,0},0,\mathrm{0,0,0},\left[{\text{M}}_{\text{tot}}\right]\right)}^{\text{T}}$ includes the total concentration of myosin that is typically an input parameter. The system of equations (Eq. 2) is nonlinear, because the state transition rates $k_{\text{A}}$, $k_{-{\text{T}}^{\text{∗∗}}},$ and $k_{-\text{AH}}$ depend on the concentration of available actin sites, $\left[\text{A}\right]$, that is a priori unknown, but for a known number of myosins bound to actin (in six actin-myosin states), the concentration of available actin sites can be calculated from

$$\left[\text{A}\right]=\left[{\text{A}}_{\text{tot}}\right]-\left(\left[\text{A}\text{-}\text{MDPi}\right]+\left[\text{AMD}\right]+\left[\text{AM}\text{-}\text{D}\right]+\left[\text{AM}\right]+\left[\text{AMT}\right]+\left[\text{A}\text{-}\text{MT}\right]\right)$$

Thus, the concentration [A] can only be obtained iteratively. The first-order differential Eq. 2 is solved numerically by a forward iterative procedure. Setting the initial value as [A] = [A_tot] in each time step, after updating [A] in each iteration, the solution of Eq. 2 is typically obtained in <20 iterations.

Parameter estimation methods

There are many different methods for estimating parameters by fitting experimental data, for example, the widely used global fitting KinTek Explorer (17, 18, 19). This global fitting software is successfully used for estimating rate and equilibrium constants for ATPase by globally fitting transient kinetic data of the Dbp5 ATPase cycle (20). However, the global fitting methods may not be appropriate for fitting experiments with simulations requiring a long time for each iteration and very large number of iterations, so we have developed several methods for estimating the model parameters for fitting kinetics data (21). The effective method for parameter estimation is the damped least-square (DLS) method, i.e., the Levenberg-Marquardt inversion, because of two important features: a quantitative evaluation of the uniqueness of the estimated parameters and the degree of parameter interdependence via a parameter resolution matrix (21, 22). The DLS method is based on the iterative minimization of the mean-square error of the model predictions with respect to experimental observations. In this study, we estimate the rate transition constants of the ATPase cycle shown in Fig. 1 by minimizing the variance between the predicted steady-state ATPase rates over a range of actin concentrations. The observations covered a range of independent variables, wide enough to uniquely resolve the set of model parameters for each myosin isoform. These observations, ${\mathit{d}}_{\text{obs}}\left(\left[\text{A}\right]\right)$, are represented by a set of N values of the ATPase rate sampled at discrete actin concentrations. The deviation of the model predictions from the experimental observations is represented by the mean-square error, which is an integral measure of the “goodness” of the model-prediction fit to the observations. Minimization of the mean-square function provides the set of (free) parameters that best fit the experimental data using the iterative procedure described in (21).

The sensitivity of the model responses to each of the estimated parameters is examined by the resolution matrix, $R$ (an $m\times m$ matrix), at convergence: when $R\sim I$, the estimated model parameters are uniquely determined, whereas when the matrix $R$ has appreciable non-zero off-diagonal elements, variations of a particular parameter can be compensated by adjustments of other parameters that fit the experimental data equally well, suggesting that the parameters are interdependent and cannot be uniquely resolved. Furthermore, if all the elements in a row of the resolution matrix are small then the corresponding parameter cannot be estimated for the given data set, because the error is affected very little, even by large changes in this parameter.

In DLS, the iterative process is stopped when the error and the norm of the increment of the estimated parameters are less than the prescribed respective tolerances. Also, the maximal number of iterations is usually limited (here, the limit was 100) and the convergence is typically reached in 30–50 steps).

Estimation of rate constants

Choosing a set of rate constants for this study depends upon having a good estimate of the steady-state ATPase data and a complete set of the rate constants for the cycle depicted in Fig. 1. The problem is that the conditions used for such measurement rarely match. The key ATPase measurements are obtained in solution by estimating the ATPase turnover rate, $v$, as a function of varying actin concentration. These define $V_{\text{max}}$ and $K_{\text{m}}$ via the classical Michaelis-Menten equation, $v=V_{\text{max}}\left[\text{A}\right]/\left(\left[\text{A}\right]+K_{\text{m}}\right)$. Actin-activated ATPase assays require very low ionic strengths for the value of $K_{\text{m}}$ to be in an accessible range of actin concentrations. ATPase assays cannot normally be performed at actin concentrations >100 μM (5 mg/mL) because of the high viscosity of the solution and the excessive amounts of actin required. Thus, ATPase assays are restricted to ionic strengths <0.03 M. In contrast, most assays of the cycle transient kinetics have used a much higher ionic strength to be close to those under physiological conditions. Here, we use complete fast kinetic data sets collected at 25 and 100 mM KCl for both the rabbit fast-skeletal muscle S1 (predominantly the 2a isoform) and human β-cardiac/slow skeletal isoform. ATPase data have been published for both proteins (rabbit (23) and β-cardiac (24)) at 25 mM KCl. The transient data for rabbit fast-skeletal and human β-cardiac S1 at 100 mM KCl are from (11). The data for the β-cardiac S1 at 25 mM KCl were published in (25), and the rabbit data were collected specifically for this work using approaches identical to the ones in that study. The values used are listed in Table 1. The assignment of each rate and equilibrium constant is set out below for β-cardiac at 25 mM KCl, and the same approach was taken to assign the values for other proteins (see Table S1 in the Supporting Material for detailed information).

Table 1.

Rate and Equilibrium Constants Used for Modeling the ATPase Cycle

Equilibrium Rate Constants	Units	Fast Skeletal	HC WT β-S1	HC WT α-S1	HC R453C-S1
Km		101.0	39.55	67.8	28.0
Vmax		29.3	5.94	18.0	5.0
$K_{\text{A}}$	μM−1	0.008∗	0.0107∗	0.011∗	0.012∗
$K_{\text{Pi}}$	mM	100.0	100.0	100.0	100.0
$K_{{\text{D}}^{\ast }}$	−	50.0	0.167	50.0	0.050
$K_{\text{D}}$	μM	100.0	36.00	197.0	33.3
$K_{\text{T}}$	μM−1	0.005	0.003	0.004	0.003
$K_{{\text{T}}^{\ast }}$	−	1507	154.0	150.0	150.0
${\mathit{K}}_{{\text{T}}^{\text{∗∗}}}$	μM	1000	1000	1000	1000
$K_{\text{H}}$	−	10.22∗	8.9136∗	4.061∗	7.419∗
$K_{\text{AH}}$	−	75.15∗	63.145∗	52.76∗	150.3∗
Forward Rate Constants
$k_{\text{A}}$	μM−1 s−1	3.819∗∗	10.75∗∗	10.68∗∗	11.87∗∗
$k_{\text{Pi}}$	s−1	45.25∗∗	15.95∗∗	32.14∗∗	17.58∗∗
$k_{{\text{D}}^{\ast }}$	s−1	300.0	59.0	100.0	39.70
$k_{\text{D}}$	s−1	1000	1000	1970	1000
$k_{\text{T}}$	μM−1 s−1	7.785∗∗	10.05∗∗	27.57∗∗	10.72∗∗
$k_{{\text{T}}^{\ast }}$	s−1	1507	1543	1800	1500
$k_{{\text{T}}^{\text{∗∗}}}$	s−1	1000	1000	1000	1000
$k_{\text{H}}$	s−1	143.1∗∗	12.47∗∗	77.17∗∗	10.39∗∗
${\mathit{k}}_{\text{AH}}$	s−1	150.3∗∗	12.63∗∗	79.14∗∗	10.52∗∗
Backward Rate Constants
$k_{-\text{A}}$	s−1	500	1000	1000	1000
$k_{-\text{Pi}}$	mM−1 s−1	0.452∗	0.159∗	0.321∗	0.176∗
$k_{-{\text{D}}^{\ast }}$	s−1	6.0	354.0	2.0	794.0
$k_{-\text{D}}$	μM−1 s−1	10.0	27.80	10.0	30.3
$k_{-\text{T}}$	s−1	1557∗	3349∗	6597∗	3350∗
$k_{-{\text{T}}^{\ast }}$	s−1	1.0	10.0	12.0	10.0
${\mathit{k}}_{-{\text{T}}^{\text{∗∗}}}$	μM−1 s−1	1.0	1.0	1.0	1.0
$k_{-\text{H}}$	s−1	14.0	1.4	19.0	1.4
$k_{-\text{AH}}$	s−1	2.0	0.2	1.50	0.07

[ATP] = 5 mM and [ADP] = [Pi] = 0 mM are the standard initial rate ATPase conditions. Values marked with a single asterisk (^∗) are fits to the ATPase data shown in Figs. 2A and 3A, and those marked with a double asterisk (^∗∗) are calculated from these fitted values. The rest of the values were assigned as described in Materials and Methods.

For each step i in the cycle of Fig. 1 we can define $K_i=k_i\text{/}{k}_{-i}$ where $K_i$ is the equilibrium constant of the ith step and $k_i$ and $k_{-i}$ are the forward and reverse rate constants (defined in a clockwise direction in Fig. 1), respectively. Note that the nomenclature for rate and equilibrium constants uses the subscript (A, D, Pi, or T) to indicate the species binding or released from myosin in each second-order step. An asterisk (^∗) indicates that it is an isomerization event linked with the second-order binding or dissociation event. The only exceptions are $K_{\text{H}}$ and $K_{\text{AH}}$, which are the ATP hydrolysis steps with or without actin attached. Defining any two of the three parameters experimentally is sufficient; the third can be calculated from the first two. ATP binding occurs in two steps, of which a rapid equilibrium step, $K_{\text{T}}$, is defined experimentally in transient studies. The forward rate constant, $k_{\text{T}}$, is assumed to be diffusion limited (a nominal value of 10⁷ M⁻¹ s⁻¹ is assigned to all diffusion-limited steps), and the reverse rate constant, $k_{-\text{T}}$, is obtained by the calculation $k_{-\text{T}}$ = 10⁷/3.06 × 10³ = 3270 s⁻¹ (illustrated for the β-cardiac myosin; see Table 1 for the estimated value from the data fit). On ATP binding, the actomyosin complex undergoes a rapid isomerization controlled by $k_{{\text{T}}^{\ast }}$, which is measured as the limiting rate of ATP binding as 1540 s⁻¹. This is a largely irreversible step, so the reverse rate constant, $k_{-{\text{T}}^{\ast }}$, is set at a nominal 10 s⁻¹, giving $K_{{\text{T}}^{\ast }}$ as 154. Actin then rapidly detaches with a rate constant, $k_{{\text{T}}^{\text{∗∗}}}$, that is at least as fast as $k_{{\text{T}}^{\ast }}$ and is set at a nominal 1000 s⁻¹, and the reverse rate is set at 1 μM⁻¹ s⁻¹, to give an affinity of actin for MT of ∼1 mM, ∼10-fold weaker than that expected for MDPi. The rate constant for the ATP hydrolysis step is set either by quenched-flow studies or as the maximum rate of the tryptophan fluorescence change on ATP binding to S1, having a typical rate of $k_{\text{H}}+k_{-\text{H}}\sim$ 15 s⁻¹. The equilibrium constant is not well defined but is thought to be between 1 and 10, and we have (initially) assigned $k_{\text{H}}$ = 14 s⁻¹ and $k_{-\text{H}}$ = 1.4 s⁻¹ (see Table 1 for the estimated value from the data fit). Actin rebinding occurs from the MDP states, and actin induces the release of Pi and the transition to the force-developing, strongly attached AMD state. Neither of these steps can be easily distinguished from the preceding or following steps in a direct assay. The values were therefore defined from the fit to the actin dependence of the steady-state ATPase data.

A load-dependent isomerization of AMD follows Pi release, and the forward rate constant is directly measured for β S1 by displacing ADP by a large excess of ATP. This defines $k_{{\text{D}}^{\ast }}$ as 59 s⁻¹ and the amplitude analysis defines $K_{{\text{D}}^{\ast }}$ as 0.167 and hence $k_{-{\text{D}}^{\ast }}$ as 354 s⁻¹. This step is thought to define the maximal shortening velocity of muscle fiber contraction. It cannot be measured for rabbit muscle S1, as $K_{{\text{D}}^{\ast }}$ is ≫1. Estimates of the value of this equilibrium constant from Pi binding studies suggest a value of ∼50 (26). The overall affinity of ADP for A.M, $K_{\text{dissn}}$, was measured by competition with ATP binding, $K_{\text{dissn}}=K_{\text{D}}{K}_{{\text{D}}^{\ast }}\text{/}\left(1+K_{{\text{D}}^{\ast }}\right)$, to give the value of $K_{\text{D}}$ listed. The ADP binding rate constant is assumed to be fast and diffusion limited, whereas the ADP release is set at a nominal 1000 s⁻¹. All parameters used and calculated here are listed in Table 1 for each of the isoforms.

There is evidence that at high actin concentrations, ATP hydrolysis and reversal of the recovery stroke can take place while myosin remains bound to actin, since if this were zero, the ATPase rate would decline at very high actin concentrations (27). To allow for this, we have included the step with equilibrium constant $K_{\text{AH}}$. We made no assumption about this step, but allowed a value to be fitted within the limits of the overall detailed balance of the two half cycles shown in Fig. 1.

Fitting data procedure

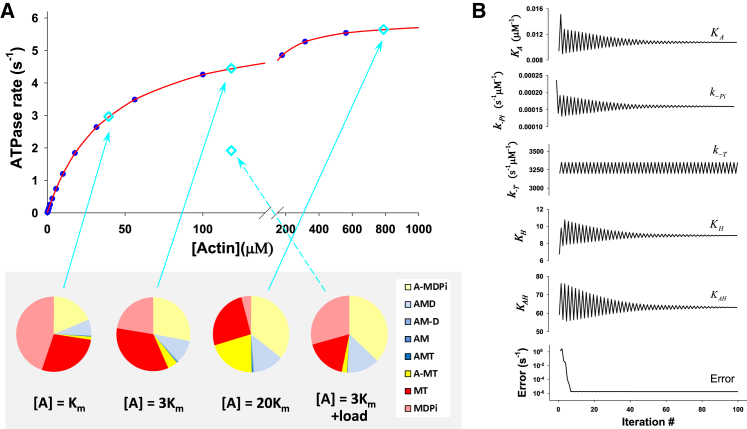
To quantitatively understand the ATPase process with the eight-state model shown in Fig. 1, it is necessary to know 18 rate or equilibrium constants. From multiple measurements and the analysis shown above, it is possible to define 13 rate constants; thus, the remaining five can be obtained by fitting the ATPase data by predictions of steady-state ATPase from the solution of Eq. 2. Note that when fitting to steady-state ATPase data in which initial rates are measured, the concentrations of ADP and Pi are assumed to be zero, such that Pi and ADP release are irreversible. However, we include estimates of the two equilibrium constants $K_{\text{Pi}}$ and $K_{{\text{D}}^{\ast }}$ to allow a detailed balance calculation. Using known values of the rate constants in the cycle, we estimated unknown values of the equilibrium constants $K_{\text{A}}$, $K_{\text{H}}$, and $K_{\text{AH}}$ and the rate constants $k_{-\text{Pi}}$ and $k_{-\text{T}}$ by the DLS algorithm (21). The rapid convergence of parameters and the diagonal terms in the resolution matrix having values >0.8 indicate well resolved and independent parameters.

Results

Table 1 lists the rate and equilibrium constants for each of the steps in the cycle outlined in Fig. 1 for the human β-cardiac motor domain (or S1). Where measured, each of these kinetic constants was defined at ∼25 mM KCl and 20°C, with a precision of at least 20%, and others were assumed from known limits, i.e., the diffusion-limited rapid equilibrium step, or by detailed balance as set out in the Materials and Methods section. The values undefined in the ATPase cycle are the affinity of actin for the M.ADP.Pi complex ($K_{\text{A}}$ in Fig. 1), the rate and equilibrium constants of Pi release, $K_{\text{Pi}}$, and, for human myosins, the equilibrium constant of the ATP hydrolysis step. One other step not well defined is the affinity of the MT state for actin $\left(K_{\text{T∗∗}}\right)$, which is normally assumed to be very weak but, since very high actin concentrations were modeled, this affinity was set to 1 mM, ∼10-fold weaker than the actin affinity for MDPi $\left(K_{\text{A}}\right)$. We then also need to include values for the rate and equilibrium constants of the on-actin hydrolysis step $\left(K_{\text{AH}}\right)$, as might be found in sarcomere. We used published values for the steady-state ATPase $V_{\text{max}}$ and $K_{\text{m}}$ for the same isoform (24) and fitted the model to the data (Fig. 2). The resulting fitted values are listed in bold in Table 1; the convergence of fitted parameters for human β-cardiac-S1 is shown in Fig. 2 B, and those for rabbit fast skeletal, human cardiac α-S1, and human cardiac β-R453C-S1 are shown in Fig. S1.

Figure 2.

Modeling the ATPase cycle for β-cardiac myosin. (A) The best fit of ATPase rate versus actin concentration, [A], for HC WT β-S1. Data in blue are the predicted ATPase rates based on the published $V_{\text{max}}$ and $K_{\text{m}}$ values, and data in red indicate the best fit of the model in Fig. 1 to the data. The constants used and derived in the fitting are listed in Table 1. The state occupancies for each of the intermediates in the cycle are given in a pie chart, color coded to match the intermediates in Fig. 1. These are shown for three actin concentrations (blue diamonds), [A] = $K_{\text{m}}$, 3$K_{\text{m}}$, and 20$K_{\text{m}}$, and at 3$K_{\text{m}}$ under load (see text). (B) The convergence of the equilibrium constants, $K_{\text{A}}$, $K_{\text{H}}$, and $K_{\text{AH}}$, and reverse rate constants, $k_{-\text{Pi}}$, and, $k_{-\text{T}}$, by DLS for the damping parameter ε = 0.25 (21). All free parameters converge at 30–50 iterations except $k_{-\text{T}}$, where value varies between 3200 and 3350 s⁻¹, but this variation does not affect the error, suggesting that the value of this parameter cannot be resolved for this experiment (see Table 1). The mean-square error (21) converges quickly to a normalized value, Error = $\sqrt{{\Vert e\Vert }_2^2/N}$ <2 × 10⁻⁶ s⁻¹, and the fit of data is excellent. The resolution matrix for this fitting procedure is listed in Table 2.

In Fig. 2 A, the predicted ATPase rates as a function of actin concentration for human β-cardiac-S1 (based on the published $V_{\text{max}}$ and $K_{\text{m}}$ values) are shown as blue circles, and the red line is the best fit to the model. The convergence of the fitted parameters during the simulation is illustrated in Fig. 2 B, and the resolution matrix for each fitted parameter is listed in Table 2. These show that the values rapidly converge and are all well defined, with the exception of $k_{-\text{T}}$, the rate constant for ATP dissociation from the rigor A.M complex, which is fast at ∼3000 s⁻¹, and whose precise value has little influence on the fitting process.

Table 2.

Resolution Matrix for the β-Cardiac Isoform

HC WT β−S1			$K_{\text{A}}$	$k_{-\text{Pi}}$	$k_{-\text{T}}$	$K_{\text{H}}$	$K_{\text{AH}}$
$K_{\text{A}}$	0.0107∗	μM−1	0.9092∗∗	0.3125	−0.0001	−0.2264	−0.2320
$k_{-\text{Pi}}$	0.159∗	s−1 mM−1	0.3125	0.9586∗∗	0.0001	0.2510	0.2524
$k_{-\text{T}}$	3349∗	s−1	−0.0001	0.0001	1.4 × 10−6∗∗	0.0002	0.0002
$K_{\text{H}}$	8.91∗	−	−0.2264	0.2510	0.0002	0.8109∗∗	−0.1840
$K_{\text{AH}}$	63.14∗	−	−0.2320	0.2524	0.0002	−0.1840	0.8117∗∗

Values marked with a single asterisk (^∗) are included to emphasize fitted parameters and with a double asterisk (^∗∗) resolution matrix diagonal values.

It is important to notice that the excellent fits do not guarantee that the parameters are uniquely defined. Having diagonal terms of order 0.9 provides large confidence that the separation between parameters is very good but not perfect (having a value of 1). Off-diagonal terms <0.25 show only weak interdependence, typical for fits of real data. However, the diagonal value of $k_{-\text{T}}$ is very small, implying that from these data, $k_{-\text{T}}$ cannot be estimated and that the small values from off-diagonal terms are irrelevant. This also suggests that using different values for $k_{-\text{T}}$ may not affect the other estimated parameters because of the small values of diagonal terms, i.e., extremely weak interdependence.

Before considering the implication of the results, we examined the robustness of the values used. For each of the fixed values (the non-bold values in Table 1, based on measurements or estimates), we changed the value by either +20% or −20% and refitted the ATPase data. In almost all cases, the fitted parameters changed by <2%; only in the case of a change in $K_{\text{D}}$ or $K_{{\text{D}}^{\ast }}$ were larger changes seen, with $k_{\text{Pi}}$ and $K_{\text{A}}$ changing by up to 7% (see Table S4). This indicates that the fitting is relatively independent of the fixed parameter values in the range ±20%. The same test was run for the fitted parameter values; i.e., we altered one of the fitted parameters (e.g., $k_{\text{H}}$) by ±20% and refitted the data. As can be seen from the fitted values in Table 1, both $k_{\text{Pi}}$ and $k_{\text{H}}$ have similar values, ∼3 × $V_{\text{max}},$ and contribute significantly to the overall ATPase $V_{\text{max}}$. Consequently, an increase in $k_{\text{H}}$ requires a decrease in $k_{\text{Pi}}$ and vice versa (see Table S5). A similar change in the actin affinity, $K_{\text{A}}$, was also required to fit the data. A change in $K_{\text{H}}$ also requires a similar change in $K_{\text{AH}}$ for thermodynamic balance. The quality of the fit judged by the error term (see Fig. 2 B) remains very good. The errors reach the major minimum after ∼10 iterations, with small damped fluctuations in error afterward concurrently displaying gradual convergence of the fitted values toward the best-fit solution. Thus, although the values are well defined by the fit, the values show some, typically minor, degree of dependence on each other.

Because these values may not be fully independent of each other, we examined the influence of the 20% change in $k_{\text{H}}$ and fitted values of $k_{\text{Pi}}$ and $K_{\text{A}}$ for the occupancy of the other states in the cycle. Since the overall ATPase rate (or the flux) does not change, there is little change in any of the strongly attached states in the cycle (<1%). The effect is just a redistribution between [MT], [MDPi], and [A-MDPi] to maintain the same flux through this part of the cycle (see Table S6).

Fig. 2 A illustrates, in a pie chart, the predicted occupancy of each of the states in the cross-bridge cycle model (each state is color-coded to match Fig. 1) for three actin concentrations, [A] = $K_{\text{m}}$, 3$K_{\text{m}}$, and 20$K_{\text{m}}$, where the corresponding ATPase rates are 50%, 75%, and 95%, respectively, of $V_{\text{max}}$. These three conditions were used to demonstrate how the cycle changes with increasing actin concentration. This also indicates how the situation my appear in an unloaded motility assay or rapidly contracting muscle fiber where the value and the meaning of actin concentration remains undefined because of the geometric constraints of the system. The pie charts give a visual indication of how the occupancy of each of the cycle intermediates changes, and it allows an easy comparison between actin concentrations and different myosin isoforms (see below). Table S2 gives the calculated values for the state occupancy in each case, and Table 4 summarizes the changes in the sum of detached (Fig. 1, red), weakly bound (yellow), and strongly bound (blue) states. As expected, an increase in actin concentration results in a gradual shift from detached (MT and MDPi) to actin-attached states, with the detached MDPi falling from 0.45 to 0.042 as the actin concentration increases from $K_{\text{m}}$ to 20 $K_{\text{m}}$. The weakly attached A-MDPi state (light yellow) predominates (0.36) at saturating actin concentrations, and the sum of MT (dark red) and A-MT (dark yellow) gives a further 0.46. The only other highly occupied species is the strongly bound AMD complex (light blue), which increases from 0.068 at [A] = $K_{\text{m}}$ to 0.13 at [A] = 20 $K_{\text{m}}$.

Table 4.

Effect of Actin Concentration on the Fractional Occupancy of ATPase Cycle Intermediates

	ATPase (s−1)	Detached	Weakly Attached	Strongly Attached	Duty Ratio	Velocity (μm s−1)
Fast Skeletal
[A] = $K_{\text{m}}$ = 101 μM	14.7353	0.5775	0.3478	0.0747	0.0747	0.9862
[A] = 3 $K_{\text{m}}$	22.0896	0.3498	0.5382	0.1120	0.1120	0.9860
[A] = 20 $K_{\text{m}}$	28.0331	0.1049	0.7529	0.1422	0.1422	0.9857
HC WT β-S1
[A] = $K_{\text{m}}$ = 39.55 μM	2.9744	0.7263	0.2002	0.0734	0.0734	0.2023
[A] = 3 $K_{\text{m}}$	4.4614	0.5655	0.3241	0.1103	0.1103	0.2021
[A] = 20 $K_{\text{m}}$	5.6619	0.2984	0.5606	0.1410	0.1410	0.2008
HC WT α-S1
[A] = $K_{\text{m}}$ = 67.8 μM	9.0033	0.5985	0.3013	0.1001	0.1001	0.4497
[A] = 3 $K_{\text{m}}$	13.5034	0.3820	0.4676	0.1504	0.1504	0.4489
[A] = 20 $K_{\text{m}}$	17.1395	0.1355	0.6732	0.1914	0.1914	0.4477
HC R453C β-S1
[A] = $K_{\text{m}}$ = 28 μM	2.5013	0.7298	0.1528	0.1174	0.1174	0.1065
[A] = 3 $K_{\text{m}}$	3.7525	0.5769	0.2468	0.1763	0.1763	0.1064
[A] = 20 $K_{\text{m}}$	4.7601	0.3365	0.4389	0.2246	0.2246	0.1060

The detached states are MT and MDPi; weakly attached states are A-MT + A-MDPi; and strongly attached states = DR = AMD + AM-D + AM + AMT. Velocity = $d\times \text{ATPase/DR}$, where $d$ = 5 nm.

Notably, the fraction of states that are strongly attached almost doubles, increasing from 0.073 to 0.141 as the actin concentration increases from $K_{\text{m}}$ to 20 $K_{\text{m}}$. This fraction of strongly attached states is equal to the duty ratio, $\text{DR}$, i.e., the fraction of the ATPase cycle during which a cross-bridge is strongly attached. This number then allows an estimate of the maximal velocity (in a motility assay or muscle shortening), $V_{\text{o}}$, from the equation $V_{\text{o}}=d\text{/}\tau$, where $d$ is the myosin throw, i.e., the distance over which myosin can produce force, and $\tau$ is the lifetime of the attached state. The lifetime of the attached state is equal to $DR$/ATPase rate (the ATPase rates are also listed in Table 4 for each actin concentration); hence, $V_{\text{o}}=d\times ATPase\text{/}DR$. The calculated values of $V_{\text{o}}$ are listed in Table 4 and show that for a working stroke of 5 nm the velocity is ∼0.20 μm·s⁻¹. The estimate of velocity is independent of the actin concentration above $K_{\text{m}}$, which is compatible with observations from the in vitro motility assays.

It is also possible to estimate the effect of a load on the ATPase cycle of a single myosin motor, and this will be considered in the Discussion. The model generates overall properties of the β-myosin isoform that are similar to those expected from contracting muscle fibers containing the isoform. In the next section, the same approach is developed for a set of well-defined myosin isoforms.

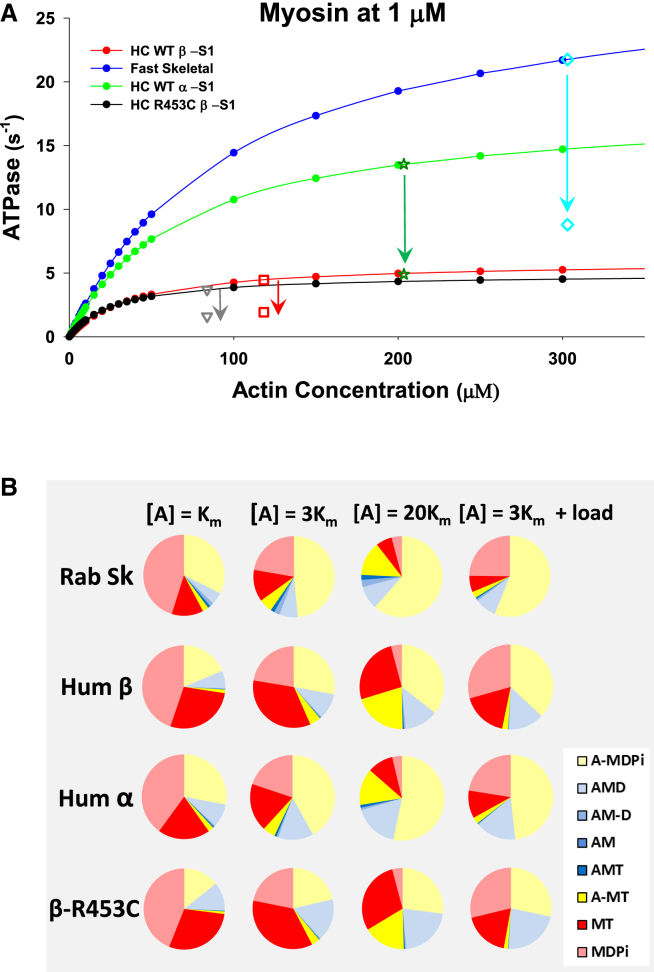
Fast skeletal myosin S1 from rabbit is the best biochemically defined fast muscle myosin, and as illustrated in Fig. 3 A, the fit of the model to the ATPase data was well defined. The resolution matrix indicated a similar quality of the fit (Table 3; and see Fig. S1 and Table S3). The state occupancies are shown in Fig. 3 B and Tables 4 and S2.

Figure 3.

Details of the fit to the ATPase data and the state occupancy of intermediates in the ATPase cycle for four muscle myosin isoforms. (A) The dependence of the ATPase cycle on actin concentration and (B) the occupancy of each of the intermediates in the ATPase cycle at three different actin concentrations, [A] = $K_{\text{m}}$, 3$K_{\text{m}}$, and 20 $K_{\text{m}}$, corresponding to 0.5, 0.75, and 0.95 of $V_{\text{max}}$. The presentation also includes predictions for how the state occupancy would change for the [A] = 3$K_{\text{m}}$ conditions if the actomyosin system were loaded such that the isomerization steps controlling both Pi and ADP release were reduced by a factor of 3 (see text for details). The values generated for the pie charts are given in Table S2. Note that low-actin-concentration-state occupancies were dominated by MDPi (range 0.40–0.45) and to a lesser extent by A-MDPi (0.19–0.32). The MT form was more variable (0.13–0.29), reflecting the wide variation in the rate constant of the ATP hydrolysis step $\left(k_{\text{H}}\right)$. As actin increased, there was a shift in occupancy from MDPi to A-MDPi, as expected with MDPi almost negligible at [A] =20$K_{\text{m}}$. A-MDPi dominates (0.35–0.62) at [A] = 20$K_{\text{m}}$, but with significant contributions from both MT (0.06–0.26) and A-MT (0.14–0.21). The presence of a large amount of A-MT is due to the value of the weak affinity of MT for actin, here assigned to 1 mM at 25 mM KCl and expected to be three times weaker at 100 mM KCl. Thus, the A-MT would only be significant in a sarcomere if the local actin concentration exceeded 1 mM at physiological salt concentrations. The occupancy of MT is much larger in β- than in α- and skeletal isforms, reflecting the slower hydrolysis rate constant for β. The major form tightly bound to actin was AMD, and this had a higher occupancy in β and α than in skeletal myosin at all actin concentrations, reflecting the slower ADP release rate constants $\left(k_{\text{D}}\right)$ in the β- and α-isoforms.

Table 3.

Resolution Matrix Diagonal Values, ${\mathit{R}}_{\text{d}}$, for Each Isoform

	Units	Fast Skeletal	HC WT β-S1	HC WT α-S1	HC R453C-S1
${\mathit{R}}_{\text{d}}\left({\mathit{K}}_{\text{A}}\right)$	−	0.981	0.909	0.993	0.966
${\mathit{R}}_{\text{d}}\left({\mathit{k}}_{-\text{Pi}}\right)$	−	0.953	0.959	0.997	0.910
${\mathit{R}}_{\text{d}}\left({\mathit{k}}_{-\text{T}}\right)$	−	2.5 × 10−6	1.4 × 10−6	2.3 × 10−6	0.15 × 10−6
${\mathit{R}}_{\text{d}}\left({\mathit{K}}_{\text{H}}\right)$	−	0.849	0.811	0.960	0.856
${\mathit{R}}_{\text{d}}\left({\mathit{K}}_{\text{AH}}\right)$	−	0.813	0.812	0.981	0.858
Error	s−1	7.050 × 10−6	1.430 × 10−6	7.060 × 10−6	2.310 × 10−6

Complete tables are available in the Supporting Material.

A further isoform that we have characterized is the human α-cardiac myosin (11), but this isoform has only been well defined at 100 mM KCl, i.e., at conditions where the actin dependence of the steady-state ATPase cannot be measured with any precision. The effect of salt on each of the steps of the ATPase cycle is well defined for the rabbit fast muscle myosin and human β-cardiac data, as listed in Table S1. The differences between 25 and 100 mM KCl for the measured parameters are very similar for both proteins. The major effect of KCl concentration, apart from the expected change in actin affinity, is on the equilibrium constants of ATP binding $\left(K_{\text{T}}\right)$ which is ∼3-fold weaker at 100 mM KCl for both rabbit skeletal and human cardiac S1. The effect on all other steps is modest in comparison. The exception is the ADP affinity, which is quite distinct for the two myosins; ADP binding is weak (120 μM) and relatively independent of KCl for rabbit fast muscle S1, whereas it is much tighter and salt dependent for human β-myosin (∼20 μM at 100 mM KCl and ∼6 μM at 25 mM KCl). On the assumption that α-cardiac myosin is like rabbit fast muscle in its weak affinity for ADP, the 100 mM KCl values of rate and equilibrium constants can be corrected to 25 mM KCl, as shown in Table S1, and the 25 mM KCl data are listed in Table 1. The reliability of the assumptions made here will be considered in the Discussion. The actin dependence of the ATPase data has been defined for several α-myosin isoforms, and in general, the $V_{\text{max}}$ of the ATPase and the velocity of shortening is ∼2–3 times those of the β-isoform from the same species under the same experimental conditions (28). Since separation of pure α and β isoforms is not simple, we have assumed a threefold difference in the $V_{\text{max}}$ of the ATPase. We therefore repeated the modeling for the α-cardiac data with values of constants listed in Table 1. Once again, the ATPase data can be well defined for all fitted constants (Figs. 3 A and S1; Tables 4 and S2).

The R453C mutation in β-cardiac myosin is a classic severe hypertrophic myopathy mutation that, without intervention, results in a 50% mortality rate in heterozygotic carriers of the mutation by the age of 40 (29). We defined the properties of this mutation in the human β-cardiac myosin motor domain by transient kinetics (10), and steady-state kinetics, as well as from single-molecule and ensemble mechanical data collected by collaborators (25). The transient kinetic data were collected at 100 mM KCl and have been corrected to the 25 mM KCl data, as was done for the α-cardiac data (see Table S1), and the fits to the ATPase data were once again very good (Figs. 3 A and S1; Tables 4 and S2).

With the model well-defined by the experimental data for the three myosin isoforms, we can consider the details of the model and how each isoform differs in the state occupancy of each intermediate in the ATPase cycle, the predicted velocities, and the duty ratios, as well as how these parameters depend on actin concentration. As there are many different comparisons to be drawn between the different data sets, only the major issues will be highlighted here; further consideration will be given to the isoform differences in the Discussion. Note that for these ATPase cycles, the concept of a simple rate-limiting step does not apply, as has been recognized in enzymology for a number of years. Multiple states contribute to the overall balance of the cycle, and small changes in any step can and will alter the balance of events in the cycle. This is why understanding the role of individual point mutations in a myosin requires a detailed study of the cycle.

As seen for the β-cardiac myosin, in all cases the state occupancies shifted from detached (MT and MDPi) to attached states as the actin concentration increased. Even though the actin concentrations used in the simulation result in the same degree of saturation of the ATPase velocity, each myosin isoform has a distinct distribution of states. At [A] = $K_{\text{m}}$ $\left(v=0.5V_{\text{max}}\right)$, rabbit skeletal myosin has fractional occupation of 0.58 for the detached states, 0.35 for weakly attached states, and 0.075 for strongly attached states (note that the values are rounded to two significant digits here, resulting in the total being <1). Distributions within these categories are given in Table 4 and listed in more detail in Fig. 3 B and Table S2. β-cardiac myosin has identical state occupancy of the strongly attached state and hence the same duty ratio as the skeletal isoform, 0.073, but there is a lower occupancy of the weakly attached states, 0.20. This alteration in the balance of the cycle is caused by a reduction in the rate constants controlling both ADP release and ATP hydrolysis. Together, the two result in a slower cycling speed and a retained duty ratio. However, the slower hydrolysis step results in greater occupancy of the MT complex and lower A-MDPi. In contrast, the α-isoform has a higher duty ratio, 0.10, than either β or skeletal muscle 2A and a distribution between detached and weakly attached states similar to that of the skeletal isoform. As actin concentration increases the strongly attached states increase but the duty ratio remains the same for the skeletal and β-isoforms, saturating at ∼0.14, whereas the α-isoform is higher at 0.19. Note that the β-cardiac isoform at 20$K_{\text{m}}$ actin has more than twice the fraction of detached states compared to the skeletal isoform due to the slower rate constant of the hydrolysis step, whereas the α-isoform is more similar to the skeletal isoform.

As for the β-isoform, the ATPase rates and the duty ratio can be used to estimate the unloaded shortening velocity. From the data in Table 4, in each case, the predicted velocity is independent of the actin concentration and the α-isoform has a predicted velocity of 0.45 μm/s for a 5 nm step, more than twice that of the β-isoform (0.20 μm/s). The skeletal isoform velocity, 0.99 μm/s, is twice that of the α-isoform. The relative values here are similar to those measured for the same myosin isoforms in motility assays, but it is difficult to find measurements for all three isoforms under identical conditions. Absolute values do vary from laboratory to laboratory. Most recent values are collected at higher temperatures of ∼30–35°C, and velocity has a very marked temperature dependence (30, 31). Values from the rat muscle isoforms give 0.62 μm/s for the slow β-isoform and 2.6 μm/s for the fast 2a isoform at 20°C, and these values are ∼5 times faster at 30°C (31). The rat isoforms are expected to be twofold faster than the human isoforms, with rabbit isoforms between those of rat and human (32).

The R453C mutation in human β-cardiac myosin results in severe hypertrophic cardiomyopathy. Our published analysis of this mutation (10) indicated that the major changes were a reduction in the rate constants of the ATP hydrolysis step $\left(k_{\text{H}}\right)$ and the isomerization controlling ADP release $\left(k_{{\text{D}}^{\ast }}\right)$. Putting these numbers into the model along with the ATPase data of Sommese et al. (25) gave the following predictions. Compared to the data for wild-type β, the duty ratio was increased by ∼59% at each actin concentration, whereas the predicted velocity of shortening was reduced by almost 50%. The increased duty ratio and slower velocity are both the result of the longer lifetime of the AMD state. The longer-lived AMD state results in a higher occupancy of the force-holding (AMD) state and therefore predicts a higher force capacity for this mutation than for the wild-type. This is compatible with the measured single-molecule force (increased by 50%), increased ensemble force, and reduced motility assay velocity (reduced by 36%) reported for this mutation by Sommese et al. (25).

Discussion

Defining a precise ATPase cycle for muscle myosins is a first step toward developing an accurate multiscale model that can be used for interpreting single-molecule mechanical measurements, motility assays, data from Ca²⁺-regulated ATPase models, and contracting sarcomeres. The advantage of having a well-defined ATPase cycle is that the subsequent models are more highly constrained, allowing focus to be on the key additional processes, including the geometry of the available myosin binding sites on actin (see Mijailovich et al. (33)), the effect of load on individual motors or on an ensemble, and the modulation of the cycle events by regulatory systems. Such a model is under construction (MUSICO (33, 34, 35, 36, 37, 38, 39, 40, 41)), but it needs good experimental data for each different muscle system, collected as nearly as possible under identical experimental conditions (ionic strength, temperature, etc.). This is a challenge, as ATPase assays, motility assays, and muscle fiber mechanics all have their own preferred conditions. Transient kinetics can be collected under most solution conditions provided the proteins are stable over the time course of the measurement and at temperatures from 0° to 40°C (42).

The experimental data used here for both human β-cardiac and rabbit fast muscle myosin were collected under very similar conditions and, as seen, the predictions for duty ratio for these two isoforms are very similar. The R453C transient kinetic data were collected at a higher ionic strength than the ATPase data and then corrected to the lower ionic strength. The similar effects of salt on the parameters for wild-type β-cardiac and rabbit fast muscle suggest that the corrections applied will be reasonably accurate. This is particularly so as the R453 residue is not a surface-exposed residue and therefore is unlikely to be influenced directly by the solution ionic strength. However, it would be essential to confirm the R453C data at the lower ionic strength for modeling of this mutant to be developed further. Here, the intention is to demonstrate the potential of this modeling approach.

The data for the α-cardiac isoform has both the ionic strength corrections for the transient kinetic data and the ATPase data and were extrapolated from closely related studies. These data are therefore less reliabe. Our primary reason for including them here is to emphasize the potential of the approach. There are very few studies of atrial myosin from any source, and the Deacon et al. work (11) is the only transient kinetic study of the atrial isoform from human or any other myosin source. There are myofibril studies from atrial and ventricle tissue that predominantly express α- or β-myosin isoforms, respectively, and several studies of atrial and ventricular myosin ATPases and motilities have been reported (43, 44, 45). In any future detailed study of the atrial isoforms, it would be helpful to match the experimental conditions to those used here to facilitate comparisons using this modeling approach.

We use, as far as possible, strict criteria for including experimental data in our analysis, i.e., that single pure myosin isoforms were used in all experiments and the data were collected under the same experimental conditions of temperature and ionic strength. Other comparative data exist that do not match the exact details. Of significance is the work of White and a series of colleagues, who made a direct measurement of the rate constant for Pi release at saturating actin concentrations using the phosphate-binding protein (46, 47). Under a slightly different ionic strength condition, they estimated Pi release to be 75–77 s⁻¹ for rabbit S1, which is about twice our estimate of 45 s⁻¹. Similar measurements on porcine β-cardiac S1, a close analog of human β-S1, estimates Pi release to be 17 s⁻¹ (48), which compares well with our estimate of 16 s⁻¹. Note, however, that our fitting approach does show a co-dependence of $k_{\text{Pi}}$ on the rate of the ATP hydrolysis step, $k_{\text{H}}$. In our current assays, the measurement of Pi release requires larger quantities of protein than are currently accessible for the human proteins. In general, our analysis is in broad agreement with the studies of White and colleagues and indicates that both $k_{\text{Pi}}$ and $k_{\text{H}}$ have a major influence on the $V_{\text{max}}$ of the ATPase cycle, although the relative importance of each may vary with ionic strength and temperature.

Comparisons of isoforms

To a first approximation, muscle fibers expressing a single myosin isoform differ markedly in the maximal velocity of contraction and much less so in the isometric force (when correction is made for the density of myofilaments in the muscle fibers (9, 49)). Alongside this, single-molecule studies of myosin II isoforms suggest that there is little variation in the step size, duty ratio, or force per cross-bridge between muscle myosin II isoforms (44), implying little change in cross-bridge stiffness between myosin isoforms. Changes in contraction parameters between isoforms are therefore thought to be largely due to the velocity of the ATP driven cycle (the steady-state ATPase cycle for an unloaded system) and how much load affects the cycle. The data presented here illustrate how the unloaded systems change for the three isoforms considered in terms of cycle speed and duty ratio, and they can be used to predict the unloaded velocity (from a motility assay or muscle fiber contraction). We have also explored how a load might affect each cycle differently for a single myosin motor assuming no change in the cross-bridge stiffness between isoforms. The load dependence of an ensemble of myosin motors could be subject to a variety of additional sources of compliance, such as filament compliance.

The data indicate, as expected, that all three myosin isoforms are low-duty-ratio motors. Rabbit skeletal and human β-cardiac myosin are almost identical in this respect, with a duty ratio of 0.11 at an actin concentration equivalent to 3$K_{\text{m}}$. The α-isoform is slightly higher at 0.15, but the difference is moderate and could be due to differences in the experimental conditions used and the corrections applied. From the duty ratios and ATPase rates and a 5 nm step size, velocities were predicted that are compatible with those expected from experimental studies: 1–2 μm/s for the fast muscle (for a 5- to 10-nm cross-bridge throw), reduced by 50% for the α-isoform and by 80% for the β-isoform (5, 44).

There have been two reports of the effect of load on the ADP release step from the β-isoform, and in both studies (12, 13), the data were fitted to a model where the load dependence of the rate constant for ADP release, $k\left(F\right)$, is defined by

$$k\left(F\right)=k_{\text{o}}{e}^{\left(-F\times {\delta }_{\text{det}}/k_{\text{B}}\ast T\right)}$$

where $k_{\text{o}}$ is the rate constant for ADP release in the absence of load, $F$ is the force on the cross-bridge, ${\delta }_{\text{det}}$ is the distance to the transition state, $k_{\text{B}}$ is Boltzmann’s constant, and T is the temperature.

We took the simplest approach to examine how the cycle would be influenced by such a load on a single molecule (i.e., no cooperative effects that would apply in an ensemble system). We assumed, based on the single-molecule measurements, which give ${\delta }_{\text{det}}$ as ∼0.9 nm, that a 5 pN load would reduce ADP release by a factor of 3. For simplicity, we applied the same threefold reduction in the rate constant for the force generating transition coupled to Pi release $\left(k_{\text{Pi}}\right)$. We assumed the same value of ${\delta }_{\text{det}}$ for all three isoforms to evaluate how the cycle itself influences the load dependence of the isoforms. The effects of any change in ${\delta }_{\text{det}}$ or in the stiffness of the cross-bridge would be additive to those illustrated here.

The result for [A] = 3$K_{\text{m}}$ (see Table 5) shows that the load would have a very similar effect on the velocity for both cardiac isoforms, falling by ∼65%, whereas for the fast muscle isoform the reduction is lower at 57%. This is as expected from well-defined force velocity curves from individual muscle fibers, where the contraction velocity for slow β-myosin muscle fibers has a greater sensitivity to load. Interestingly, our data predict that the α-isoform has a very similar sensitivity of velocity to load but maintains an ∼2-fold higher ATPase cycling rate compared to the β-isoform. The effects on the ATPase cycling rates were different: the α-cardiac and fast muscle isoforms are inhibited to the same extent (−61.4%), whereas the β-isoform is only slightly less inhibited, by 56%. This difference in the effect of load on the ATPase and velocity emphasizes the decoupling of ATPase and velocity cycles, as first pointed out by White and collaborators (50).

Table 5.

Predicted Effect of Load on the ATPase Cycle when Actin Concentration is 3 $K_{\text{m}}$

	ATPase (s−1)	Detacheda	Weakly Attacheda	Strongly Attacheda	Duty Ratiob	Velocity (μm s−1)	Δ% AMDc	Δ% Velocityc	Δ% ATPasec
Fast Skeletal
[A] = 3 $K_{\text{m}}$	22.0896	0.3498	0.5382	0.1120	0.1120	0.9860
[A] = 3 $K_{\text{m}}$, loaded	8.5232	0.3130	0.5866	0.1004	0.1004	0.4245	15.75	−56.9	−61.4
HC WT β-S1
[A] = 3 $K_{\text{m}}$	4.4614	0.5655	0.3241	0.1103	0.1103	0.2021
[A] = 3 $K_{\text{m}}$, loaded	1.9720	0.4677	0.3930	0.1393	0.1393	0.0708	32.52	−64.9	−55.7
HC WT α-S1
[A] = 3 $K_{\text{m}}$	13.5034	0.3820	0.4676	0.1504	0.1504	0.4489
[A] = 3 $K_{\text{m}}$, loaded	5.1737	0.3305	0.5082	0.1612	0.1612	0.1605	14.94	−64.2	−61.4
HC R453C β-S1
[A] = 3 $K_{\text{m}}$	3.7525	0.5769	0.2468	0.1763	0.1763	0.1064
[A] = 3 $K_{\text{m}}$, loaded	1.6619	0.4714	0.3003	0.2283	0.2283	0.0364	32.84	−65.7	−55.7

^aFractional occupancy for the detached, weakly attached, and strongly attached states.

^bRatio of strongly attached myosins to total myosin heads.

^cPercent change in the parameter upon applying a load.

If the tightly bound ADP state, AMD, is considered to be the primary force-holding state, then the effect of load on the occupancy of this state is of interest. For both the fast muscle and the α-cardiac myosin isoforms, the load increases the fractional occupancy of this state by ∼15% (from 0.074 and 0.135, respectively, in unloaded conditions; see Tables 5 and S2), whereas the β-isoform occupancy increases by 32.5% (from 0.10), emphasizing again the greater sensitivity of the β-isoform to load.

One of the clear results from the modeling is that the predicted velocity is independent of actin concentration. This is a result of ATPase and the duty ratio having the same dependency on actin concentration; thus, $V_{\text{o}}=d\times ATPase\text{/}DR$ is independent of actin concentration. The actin dependence of the duty ratio results from the actin dependence of the cycling time (=1/ATPase), whereas the strongly attached state lifetime, $\tau$, is primarily controlled by the ADP-release rate constant and is independent of actin concentration. Thus, the velocity only depends upon the strongly attached lifetime and is independent of the actin-dependent ATPase rate.

In our modeling, we used three different actin concentrations to explore how the balance of the cycle changes for different levels of actin activation. This raises the question of the appropriate actin concentration for comparison with a myosin in the sarcomere. Most models use an estimate for the fraction of myosin heads attached to actin (strongly bound or the sum of weak and strongly bound) in the contraction sarcomere. These vary from 1–5% strongly attached cross-bridges in a rapidly shortening muscle to ∼20% under isometric conditions. At the lowest concentrations modeled ([A] = $K_{\text{m}}$), the estimate of strongly attached bridges is 7–10% without load for all three wild-type isoforms, and the weakly attached bridges vary from 20 to 35% for different isoforms. Thus, the average actin concentration “seen” by a myosin head in the sarcomere would be of the order of the $K_{\text{m}}$ value for actin while rapidly shortening. Of course, individual myosin heads would be exposed to a wide range of apparent actin concentrations in an isometric fiber, which is why we used the higher actin concentration of 3$K_{\text{m}}$ to model the effect of load. The load-bearing strongly attached heads are those that are most likely to bind actin at the specific filament overlap considered. These issues will be considered further in the sarcomeric version of this model (MUSICO (33)).

R453C

We include the data for one β-cardiac myosin mutation here to illustrate the potential power of the approach for dissecting the effect of point mutations on myosin activity. R453C is a severe hypertrophic cardiomyopathy mutation, and our published analysis (10) of this mutation indicated a significant reduction in the rates of the ATP hydrolysis step $\left(k_{\text{H}}\right)$ and ADP release $\left(k_{{\text{D}}^{\ast }}\right)$. Including these values in the model gave the following predictions. The velocity was reduced by 47% compared to the wild-type, whereas the duty ratio increased by 60% and the occupancy of the AMD state increased from 0.102 to 0.169, a 66% increase (Tables 4 and S2). Thus, a muscle expressing only this isoform would be expected to contract more slowly and develop higher forces due to the greater fraction of strongly attached force-holding states. The influence of load, with the same assumptions as for the wild-type protein, show a 65.7% reduction in velocity, similar to the 65% reduction for the wild-type, and a slightly smaller reduction in the ATPase rate of 55.7% (61% for the wild-type), whereas the occupancy of the AMD state increased markedly, by 32.8%, from 0.117 fraction occupancy, compared to 32.5% for the wild-type, as shown in Table 5. These numbers can be compared to the motility and single-molecule data for this mutant from Sommese et al. (25). They found that the single-molecule force generation increased by 50%, from 1.4 pN for the wild-type to 2.1 pN for the mutant. This compares with our predicted 66% increase in the strongly attached AMD state or the 60% increase in duty ratio. In the motility assay, Sommese et al. (25) reported that the velocity was reduced by 24%, from 0.8 μm/s for the wild-type to 0.61 μm/s for the mutant, and that the velocity was more readily inhibited by a load using an actin cross-linker. Our data suggest a larger reduction in velocity of 47% compared to the wild-type, and a reduction in velocity by a similar percentage (65%) caused by a load of 5 pN for wild-type and R453C.

The data used here are all referenced to 25 mM KCl—lower than that found in a muscle fiber. The transient kinetic data in Table S1 indicate how some of these steps are affected by salt, but estimating salt effects on the actin affinity and Pi release steps remains inaccessible to solution measurements at physiological ionic strengths. Even some motility assays and single-molecule assays are best performed at low salt because of the low probability of a cross-bridge being bound to actin at the higher ionic strengths. Muscle fiber or myofibril studies provide information concerning these events, but the assays report on ensemble behavior and are affected by the three-dimensional geometry of the filaments. These require a different modeling approach (33), which is under development, but having the majority of the ATPase cycle well defined puts limits on the remaining variables in such models.

What we have demonstrated here is that studies of the unloaded solution ATPase cycle can define the properties of myosin isoforms and of mutations in the motor domain. Studies allow predictions and set limits on the mechanical behavior of each isoform. Each of the isoforms studied here has a specific relationship between the cycle and the predicted mechanical events, which can define some of the properties of the contracting muscle fiber, such as maximum velocity and load sensitivity. In the next stage of developing our multilevel modeling package (MUSICO), we will examine how the properties of the individual myosin isoforms defined here modulate the calcium regulation of the thin filament and the mechanical properties of a contracting sarcomere. For example, the differences in the number and lifetimes of the strongly attached AMD cross-bridge for each isoform might be expected to influence the switching between on and off states of the thin filament.

Author Contributions

S.M.M. designed research, performed research, contributed to development of analytic tools, analyzed data, and wrote the article. D.N. developed the computational tools. M.S. contributed to the development of the computational tools and performed data fitting and data analysis. B.S. supervised and coordinated development of computational tools, fitting data, and data analysis. J.W. contributed to data preparation and data analysis. Z.U. contributed to data preparation and data analysis. M.A.G. contributed to research design, data analysis, and writing the article.

Editor: Enrique De La Cruz.