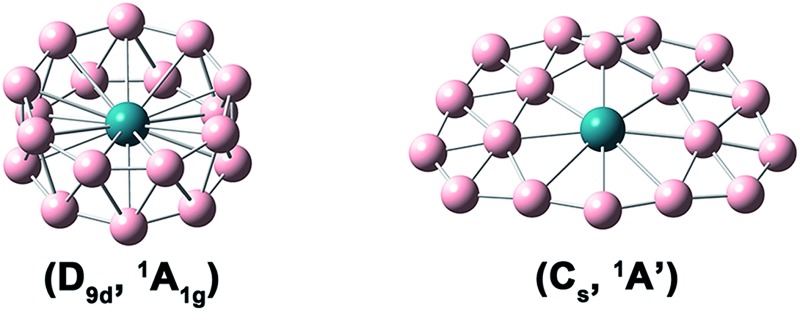
 Two nearly degenerate isomers, one a drum and the other quasi-planar, are discovered for the gaseous RhB18
– cluster, revealing a competition between the metallo-boronanotube and metallo-borophene structures.
Two nearly degenerate isomers, one a drum and the other quasi-planar, are discovered for the gaseous RhB18
– cluster, revealing a competition between the metallo-boronanotube and metallo-borophene structures.
Abstract
Metal-doped boron clusters provide new opportunities to design nanoclusters with interesting structures and bonding. A cobalt-doped boron cluster, CoB18 –, has been observed recently to be planar and can be viewed as a motif for metallo-borophenes, whereas the D 9d drum isomer as a motif for metallo-boronanotubes is found to be much higher in energy. Hence, whether larger doped boron drums are possible is still an open question. Here we report that for RhB18 – the drum and quasi-planar structures become much closer in energy and co-exist experimentally, revealing a competition between the metallo-boronanotube and metallo-borophene structures. Photoelectron spectroscopy of RhB18 – shows a complicated spectral pattern, suggesting the presence of two isomers. Quantum chemistry studies indicate that the D 9d drum isomer and a quasi-planar isomer (C s) compete for the global minimum. The enhanced stability of the drum isomer in RhB18 – is due to the less contracted Rh 4d orbitals, which can have favorable interactions with the B18 drum motif. Chemical bonding analyses show that the quasi-planar isomer of RhB18 – is aromatic with 10 π electrons, whereas the observed RhB18 – drum cluster sets a new record for coordination number of eighteen among metal complexes. The current finding shows that the size of the boron drum can be tuned by appropriate metal dopants, suggesting that even larger boron drums with 5d, 6d transition metal, lanthanide or actinide metal atoms are possible.
1. Introduction
The electron deficiency of boron has given rise to interesting structures and bonding in both elemental boron and boron compounds.1,2 Combined photoelectron spectroscopy (PES) and quantum chemistry theoretical studies over the past decade have also uncovered an interesting landscape for size-selected boron clusters (Bn –) from planar structures to borospherene cages.3–6 The cationic boron clusters (Bn +) have been found, by ion mobility experiment and theoretical calculations, to be planar up to n = 15 and tubular (or double-ring) for n > 15.7 Even though the B20 neutral boron cluster was first suggested to be tubular,8 an UV-IR double-resonance experiment failed to detect such structures.9 The discovery of the planar B36 – cluster with a hexagonal hole has provided indirect evidence for the viability of monolayer 2D borons, which we dubbed borophene.10 The recent experimental syntheses of borophenes on silver substrates,11,12 as proposed by theoretical calculations,13–15 have stimulated significant interests in the properties and structures of this new 2D boron material.
Heteroatom-doping can be used to modify and expand significantly the structures and properties of boron clusters. Inspired by the double aromaticity in the D 8h B9 – molecular wheel,16 a design principle has been proposed to produce transition metal centered borometallic molecular wheels.17 Combined PES and theoretical studies have characterized a series of these metal centered boron mono-wheels (M©Bn –) with n ranging from 8 to 10.18 However, the metal-doped CoB12 – and RhB12 – clusters were found to have half-sandwich-like structures, with the metal atom bonded to the quasi-planar B12 motif.19 Computational studies have suggested that 3d-transition-metal-doped boron clusters MB2n can form tubular (drum) structures with n from 6 to 8, but become cage-like structures with n from 9 to 10.20,21 Recently, joint PES and theoretical studies have shown that CoB16 – and MnB16 – indeed have drum structures with the metal atom sandwiched by two B8 rings and a record coordination number of sixteen.22,23 An interesting question is if larger metal-centered drum structures are still possible with even higher coordination numbers?
Very recently, a joint PES and theoretical investigation has shown that CoB18 – is a planar cluster with the Co atom being an integral part of the boron network, suggesting the possibility of metallo-borophenes,24 in which metal atoms are doped into the plane of borophenes.25 The putative CoB18 – drum isomer turns out to be much higher in energy, because the B18 tubular motif is too large to allow effective interactions between the Co 3d and the B 2p orbitals. Is it possible to design larger boron drums if transition metals with suitable sizes are used? A more important question is what governs the formation of drum structures or planar structures, which are motifs of metallo-boronanotubes and metallo-borophenes, respectively.
In the current work, we report a PES and theoretical investigation on RhB18 – to explore the possibility of a D 9d drum with an 18-coordinated Rh atom. PES of RhB18 – suggests the existence of isomers with a complicated spectral pattern. Global minimum searches along with calculations at different levels of density functional theory (DFT) and wavefunction theory (WFT) show that a perfect D 9d drum and a quasi-planar (C s) structure are nearly degenerate and are competing for the global minimum. The quasi-planar isomer is observed to be responsible for the main PES features, whereas the drum isomer corresponds to the weak PES features. Chemical bonding analyses show that the quasi-planar structure is aromatic with 10 delocalized π electrons. Significant covalent interactions are found between the Rh 4d and the B 2p orbitals, stabilizing the drum structure and pushing the limit of coordination number to eighteen. The current results show that there is a competition between quasi-planar structures and drum structures, depending on the size of the metal atoms and the bonding strength between them and the B atoms. Our results show that it is plausible to design metallo-boronanotubes and metallo-borophenes using different metal dopants with different sizes and bonding strengths.
2. Experimental method
The experiment was carried out using a magnetic-bottle PES apparatus equipped with a laser vaporization supersonic cluster source, details of which has been published elsewhere.26 The RhB18 – cluster was generated by laser vaporization of a Bi/10B/Rh composite target. The Bi component acted as a binder for the target preparation and also provided the Bi– atomic anion for PES calibration. A helium carrier gas seeded with 5% argon was used to quench the plasma, initiating nucleation and cluster formation. Clusters formed in the nozzle were entrained in the carrier gas and went through a supersonic expansion to form a collimated cluster beam after a skimmer. Anion clusters were extracted from the molecular beam and analyzed by a time-of-flight mass spectrometer. The RhB18 – anion of interest was mass-selected, decelerated, and photodetached by the 193 nm (6.424 eV) radiation from an ArF excimer laser or the fourth harmonic radiation (266 nm, 4.661 eV) from a Nd:YAG laser. Photoelectrons were collected at nearly 100% efficiency by a magnetic bottle and analyzed in a 3.5 meter long electron flight tube. The spectra were calibrated using the known spectrum of Bi– and the energy resolution of the apparatus was ΔE k/E k ≈ 2.5%, that is, ∼25 meV for 1 eV electrons.
3. Theoretical methods
The global minimum structure of RhB18 – was searched using the TGMin code10 developed based on the constrained basin-hopping algorithm,27 which was done initially using the PBE exchange–correlation functional28 with the basis sets of double-ζ plus one polarization function (DZP)29 in the ADF 2013.01 program.30 Low-lying isomers were then re-optimized at both the PBE and hybrid PBE0 levels31 using the triple-ζ plus one polarization function (TZP) Slater-type basis sets29 to obtain refined relative energies. The small frozen core approximation was applied to the [1s2–3d10] core of Rh and the [1s2] core of B. Vibrational frequencies were computed for each isomer to verify the minimum on the potential energy surface. For the four lowest-lying isomers, we performed single-point WFT calculations at the level of coupled-cluster theory with single, double and perturbative triple excitations [CCSD(T)]32,33 using the MOLPRO 2012 software package.34 The geometries used in the CCSD(T) calculations were based on those obtained from the PBE0/TZP method. We used the all-electron triple-ζ basis set (cc-pVTZ) for B35 and the Stuttgart energy-consistent relativistic pseudo-potentials (ECP10MDF) with the corresponding ECP10MDF_VTZ basis set for Rh.36
The first ADEs and VDEs of the two lowest-lying isomers were calculated at the DFT level. Electron detachment energies from the ground state were calculated using the ΔSCF-TDDFT approach with the statistically averaged orbital potential (SAOP)37 via the ADF 2013.01 code, as outlined previously.38 The chemical bonding of the two most stable isomers was investigated using the adapted natural density partitioning (AdNDP) method39 at the PBE0 level of theory using cc-pVTZ and ECP10MDF_VTZ basis sets for B and Rh, respectively. The structural and chemical bonding pictures were visualized by GaussView.40
4. Experimental results
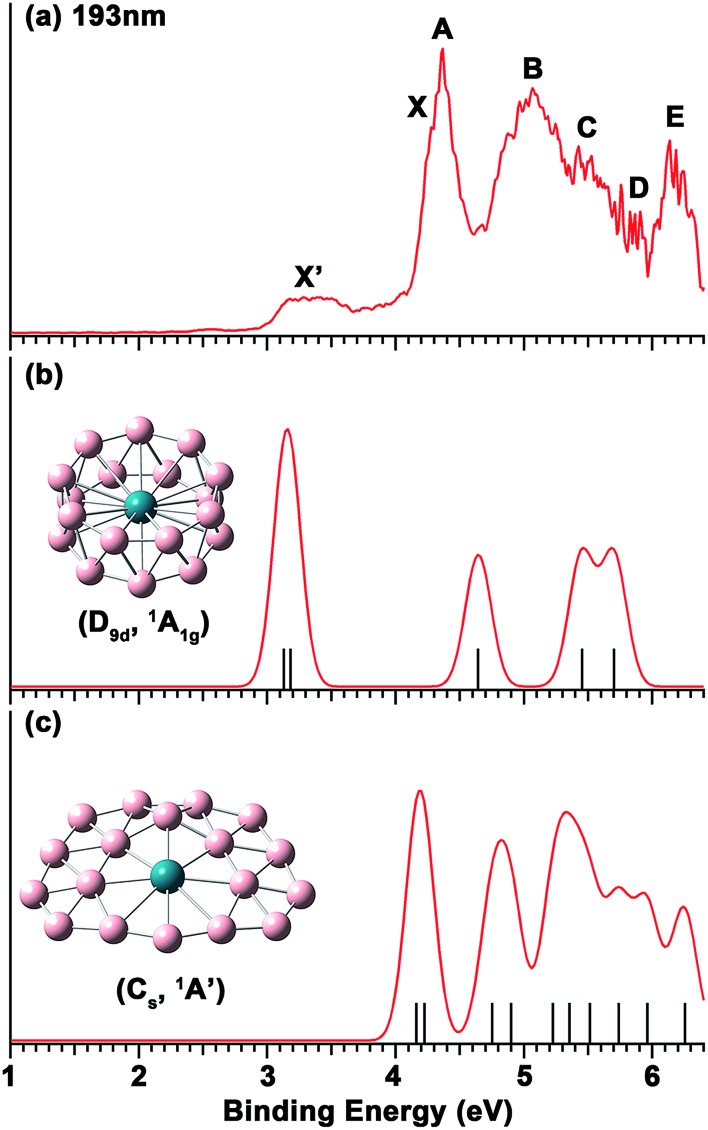
The photoelectron spectrum of RhB18 – at 193 nm shown in Fig. 1a displays a complicated spectral pattern with numerous broad detachment features. The relatively sharp and intense bands X and A are not resolved in the 193 nm spectrum, but can be seen more clearly in the 266 nm spectrum in Fig. S1.† Following an energy gap after band A, broad and continuous spectral features appear between 4.6 and 5.9 eV, suggesting a high density of final electronic states and possibly large geometry changes upon electron detachment. The B, C and D labels are given in this spectral range simply for the sake of discussion. At the high binding energy side, a well-separated and broad band E is observed at a vertical detachment energy (VDE) of 6.13 eV. The onset of band X yields an adiabatic detachment energy (ADE) of 4.10 eV. The measured VDEs for all the PES bands are summarized in Table 1, where they are compared with the theoretical data.
Fig. 1. (a) The photoelectron spectrum of RhB18 – at 193 nm (6.424 eV). (b) Simulated spectrum for the D 9d isomer of RhB18 –. (c) Simulated spectrum for the C s quasi-planar isomer of RhB18 –. The vertical bars in (b) and (c) represent the calculated VDEs given in Table 1. The simulated spectra were obtained by fitting the calculated VDEs with unit-area Gaussian functions of 0.1 eV half-width.
Table 1. Experimental VDEs (in eV) of RhB18 – compared with those calculated at the TD-DFT (SAOP)/TZP level of theory.
| Feature | VDE (exp.) | Electron configuration e | VDE (calc.) |
| D 9d isomer | |||
| X′ a | ∼3.2 | …5eu 45eg 46eu 46a1g 26eg 4 4a2u1 | 3.13 c |
| …5eu 45eg 46eu 46a1g 2 6eg34a2u 2 | 3.18 | ||
| …5eu 45eg 46eu 4 6a1g16eg 44a2u 2 | 4.64 | ||
| …5eu 45eg 4 6eu36a1g 26eg 44a2u 2 | 5.45 | ||
| …5eu 4 5eg36eu 46a1g 26eg 44a2u 2 | 5.70 | ||
| C s isomer | |||
| X b | 4.25(5) | …16a′211a′′217a′212a′′218a′213a′′219a′214a′′215a′′220a′2 21a′ 1 | 4.16 d |
| A | 4.38(5) | …16a′211a′′217a′212a′′218a′213a′′219a′214a′′215a′′2 20a′ 121a′2 | 4.22 |
| B | ∼5.0 | …16a′211a′′217a′212a′′218a′213a′′219a′214a′′2 15a′′ 120a′221a′2 | 4.75 |
| …16a′211a′′217a′212a′′218a′213a′′219a′2 14a′′ 115a′′220a′221a′2 | 4.90 | ||
| C | ∼5.5 | …16a′211a′′217a′212a′′218a′213a′′2 19a′ 114a′′215a′′220a′221a′2 | 5.22 |
| …16a′211a′′217a′212a′′218a′2 13a′′ 119a′214a′′215a′′220a′221a′2 | 5.36 | ||
| …16a′211a′′217a′212a′′2 18a′ 113a′′219a′214a′′215a′′220a′221a′2 | 5.51 | ||
| D | ∼5.9 | …16a′211a′′217a′2 12a′′ 118a′213a′′219a′214a′′215a′′220a′221a′2 | 5.74 |
| …16a′211a′′2 17a′ 112a′′218a′213a′′219a′214a′′215a′′220a′221a′2 | 5.96 | ||
| E | 6.13(6) | …16a′2 11a′′ 117a′212a′′218a′213a′′219a′214a′′215a′′220a′221a′2 | 6.25 |
aThe first experimental ADE of band X′ is 2.98 ± 0.08 eV.
bThe first experimental ADE of band X is 4.10 ± 0.06 eV.
cThe first ADE was calculated to be 2.93 eV from PBE0/TZP calculations for the drum isomer.
dThe first ADE was calculated to be 4.10 eV from PBE0/TZP calculations for the quasi-planar isomer.
eThe orbitals for the electron-detachment are marked in bold face.
The weak and broad signals (X′) at the low binding energy side suggest that they come from a different isomer of RhB18 –. At 266 nm, this part of the spectrum is not much better resolved, but almost continuous signals are observed (Fig. S1†). The higher binding energy detachment transitions of the isomer are likely buried in the signals of the main isomer. The first VDE and ADE are, respectively, estimated as ∼3.2 and 2.98 eV for the X′ band.
5. Theoretical results
To search for the global minimum structure of RhB18 –, we generated more than 10 000 possible structures using the TGMin program at the PBE/DZP level of theory. Low-lying isomers were re-optimized at the PBE0/TZP and PBE/TZP levels of theory. Forty-two structures were found within 45 kcal mol–1 of the global minimum, as shown in Fig. S2.† Single-point energies at the CCSD(T)/B/cc-pVTZ/Rh/ECP10MDF_VTZ level of theory were also calculated for the four lowest-lying isomers to better establish the order of the relative energies.
At the PBE0/TZP level of theory, a perfect D 9d drum isomer I (D 9d, 1A1g) was found to be most stable, with a quasi-planar isomer II (C s, 1A′) lying 4.90 kcal mol–1 higher. At the PBE/TZP level of theory, the C s quasi-planar isomer II was found to be the global minimum, with the drum isomer I being 3.52 kcal mol–1 higher in energy. Using the optimized RhB18-clusters, the estimated binding energies of isomers I and II relative to Rh and unrelaxed B18- are 201.19 and 189.94 kcal mol–1, respectively, at the PBE level of theory. At the more accurate CCSD(T) level, isomer I was instead found to be the global minimum with isomer II lying 5.29 kcal mol–1 higher, which is similar to the PBE0 results. Thus, both isomers I and II were found to be rather close in energy, competing for the global minimum at different levels of theory. Since the two isomers have very different structures, entropy could play an important role in determining their energetic stability at finite temperatures. Thus, we also calculated the Gibbs free energies of these two isomers at the PBE0 level of theory from 100 to 1000 K, as shown in Fig. S3.† Apparently, the quasi-planar isomer II is favored entropically and becomes more stable than the drum isomer I above 650 K at the PBE0 level of theory. However, the relative energies of the two isomers are very close to each other in the whole temperature range and they could coexist in a wide range of temperatures. Therefore, these isomers are nearly degenerate and their relative energy is rather small, making it difficult to resolve the relative stability of the two isomers using approximate theoretical methods and truncated basis sets.
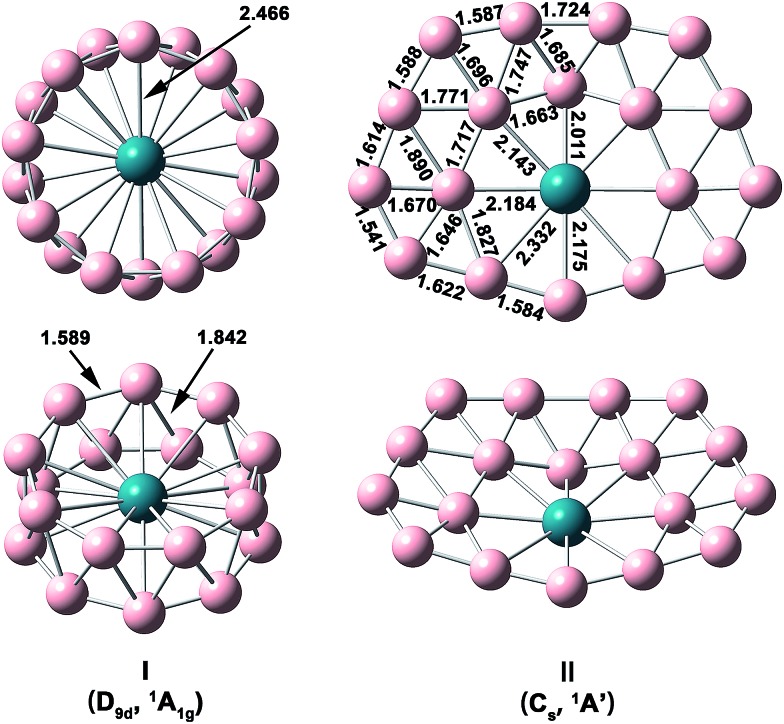
The optimized structures and bond lengths of isomers I and II at the PBE0/TZP level are presented in Fig. 2. The B–B bond lengths in each B9 ring of the RhB18 – drum isomer is 1.59 Å, very close to the corresponding values in the Rh©B9 molecular wheel (1.54 Å)41 and the drum clusters CoB16 – (1.55–1.63 Å)22 and MnB16 – (1.58–1.62 Å).23 The structure of the quasi-planar isomer II is convex with the inner boron atoms buckled out. One of the inner B atoms is forced to be penta-coordinated and it exhibits the most significant buckling. The Cartesian coordinates of isomers I and II are given in Table S1.†
Fig. 2. Structural details of the two lowest-lying isomers of RhB18 – at PBE0/TZP with their point-group symmetries and spectroscopic states. All distance are in Å.
6. Comparison between experiment and theory
The calculated VDEs for the drum and quasi-planar isomers at the TD-DFT(SAOP)/TZP level are compared with the experimental data in Table 1, while the simulated spectra obtained by fitting a unit-area Gaussian function of 0.1 eV to each VDE are compared with the experimental spectrum in Fig. 1. Both isomers have closed-shell electron configurations and their valance molecular orbitals (MOs) are shown in Fig. S4 and S5.† With the single-particle approximation, one-electron detachment from each occupied valence orbital yields a single detachment channel, giving rise to relatively simple simulated spectra. The first and second computed VDEs of the quasi-planar RhB18 – are 4.16 and 4.22 eV, which are very close to each other and are in excellent agreement with the observed major detachment features X and A. There are eight more detachment channels below 6.3 eV for the quasi-planar isomer, consistent with the highly congested experimental spectrum.
The calculated first and second VDEs of the drum isomer of RhB18 – are also very close to each other and are in excellent agreement with the weak broad X′ feature at ∼3.2 eV. The HOMO–1 of the RhB18 – drum isomer (6eg, Fig. S4†) is degenerate; electron detachment from this MO would induce a strong Jahn–Teller effect, consistent with the broad width of the X′ band. There are three more detachment channels for the drum isomer within the experimental spectral range, but they are expected to be buried in the congested spectral features of the main quasi-planar isomer. Overall, the combined theoretical data for the two isomers are in good agreement with the experimental spectrum, lending considerable credence for the quasi-planar and drum structures identified theoretically as the two lowest lying isomers for RhB18 –.
While the drum isomer is the global minimum at the CCSD(T) and PBE0 levels of theory it appears to be the minor isomer observed experimentally. This could be due to the entropical effect, i.e., the quasi-planar isomer is more favored at finite temperatures. The experimental temperature of the RhB18 – cluster was not known, but should be below room temperature,42 at which the drum isomer is still more stable according to the PBE0 result (Fig. S3†). It is very likely that the relative energies of the two isomers are much closer than PBE0 or the approximate single-point CCSD(T) calculations suggested, i.e. the two isomers are essentially nearly degenerate on the basis of the current experimental results. As noted earlier, at the PBE level of theory, the quasi-planar isomer is indeed more stable than the drum isomer, consistent with the latter being the minor isomer.
7. Discussion
7.1. Chemical bonding in the drum structure of RhB18 –
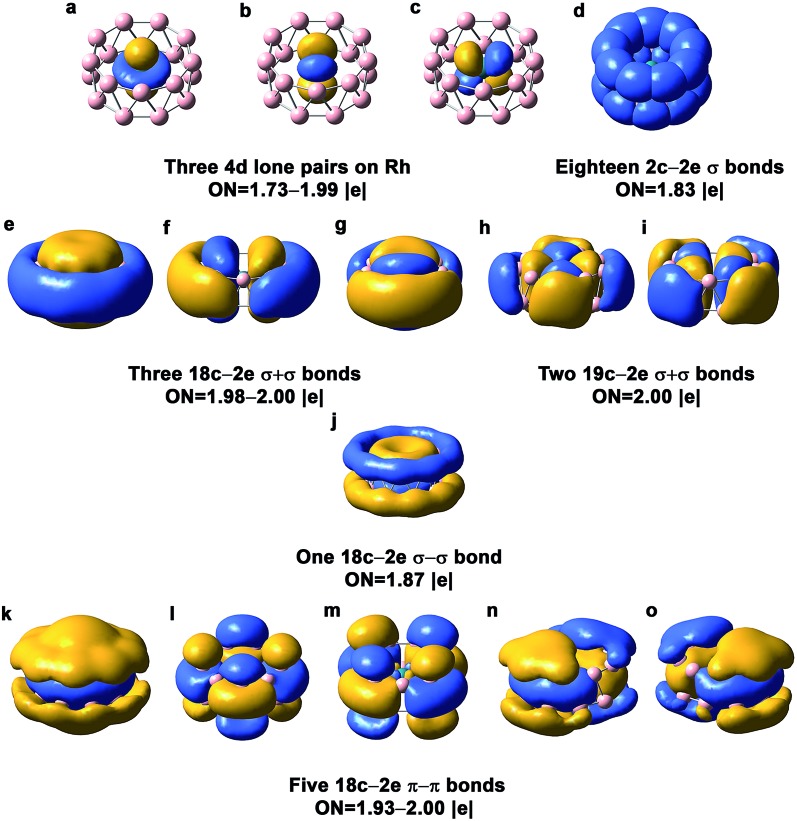
The chemical bonding in the drum and quasi-planar isomers of RhB18 – has been analyzed using the AdNDP method,39 which yields both localized and delocalized bonds simultaneously and provides chemically intuitive bonding pictures for complicated molecular systems. The chemical bonding in the RhB18 – drum isomer (Fig. 3) is reminiscent of the bonding pattern in the CoB16 – and MnB16 – drums.22,23 There are basically four different types of bonds in the drum isomer, corresponding to the four rows in Fig. 3. The first row displays essentially localized bonds, including the three out-of-plane Rh 4d electron pairs and eighteen localized 2c–2e B–B bonds on the two B9 rings. The occupation number (ON) of the Rh 4dz2 electron pair is 1.99|e|, suggesting little interaction with the B18 drum motif. The ON of the Rh 4dxz and 4dyz electron pairs is 1.73|e|, indicating that 0.27 electron from each Rh 4d orbital participates in weak π bonding with the B18 drum. The next three rows in Fig. 3 describe delocalized bonding between the two B9 rings or between the central Rh atom and the B18 drum motif. The “+” sign means that the delocalized bonds between the two B9 rings overlap positively, and vice versa. The second row shows three 18c–2e σ + σ bonds and two 19c–2e σ + σ bonds. The three 18c–2e bonds represent strong bonding interactions between the three delocalized σ bonds in each B9 ring, while the two 19c–2e bonds represent strong covalent bonding between the two in-plane Rh 4d orbitals (4dxy and 4dx2–y2) and the B 2p orbitals on the B18 drum motif. These Rh and B18 bonding interactions can also be seen from the 4eg MOs in Fig. S4,† where the 7eg LUMO represents the antibonding interactions between the Rh 4d orbitals and the B18 drum motif. There is only one 18c–2e σ–σ bond shown in the third row of Fig. 3. The last row consists of five 18c–2e π–π bonds, representing bonding interactions between the delocalized π bonds on each B9 ring. There is significant charge transfer from Rh to the drum framework of B18, which was calculated to be 0.83 e based on the Mulliken population analysis at the PBE0 level.
Fig. 3. AdNDP chemical bonding analyses for the D 9d drum isomer of RhB18 – at the PBE0 level. ON stands for occupation number.
It is interesting to compare the stabilities of the RhB18 – and CoB18 – drum isomers. While the B18 motif is similar in the two clusters, the less contracted 4d orbitals of Rh allow better overlap with the B 2p orbitals on the B18 motif than the Co 3d orbitals do, as revealed by the valence shell orbital radii of Co 3d (0.358 Å) and Rh 4d (0.604 Å).43 Although the bond length between Rh and B (2.47 Å) in the drum isomer is still longer than the single Rh–B bond (2.10 Å) according to the covalent radii for Rh and B proposed by Pyykkö,44,45 the high coordination number is sufficient to yield strong interactions between Rh and the B18 drum motif. On the other hand, the 2.47 Å Co–B bond length in the CoB18 – drum isomer is much longer than the single Co–B bond (1.96 Å), making it much less stable relative to the planar global minimum of CoB18 –.
7.2. Chemical bonding in the quasi-planar structure of RhB18 –
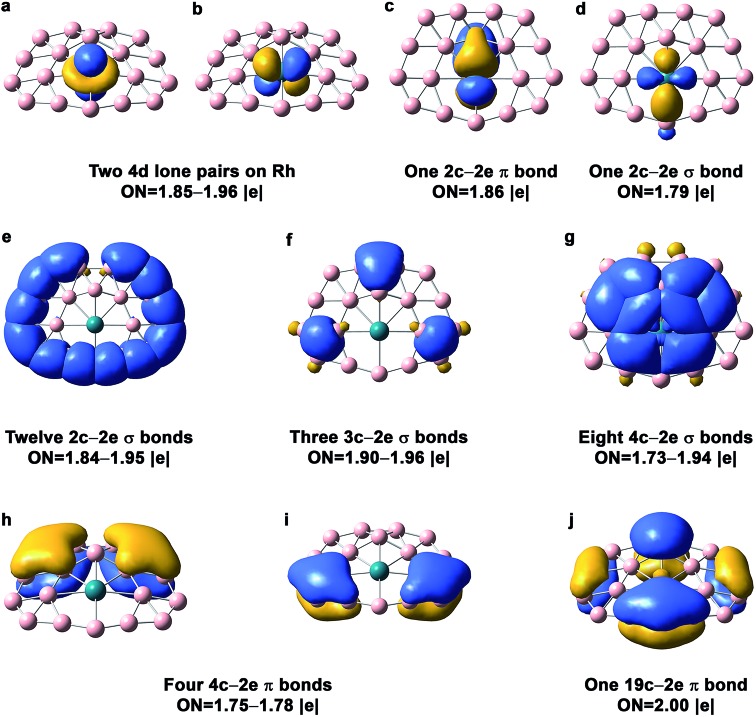
The AdNDP bonding analysis for the quasi-planar RhB18 – is shown in Fig. 4. The first row in Fig. 4 includes two 4d lone pairs on Rh (4dz2, 4dxz) and localized π and σ bonding between Rh and two of its neighboring B atoms. It is interesting to see that there are only twelve 2c–2e peripheral B–B σ bonds (Fig. 4e). The long peripheral B–B bond (1.724 Å, Fig. 2) corresponds to a 3c–2e σ bond, as shown in Fig. 4f, which also contains two additional 3c–2e σ bonds. Fig. 4g shows eight 4c–2e σ bonds, four of which describe delocalized σ bonding between Rh and its neighboring B atoms and the other four describe delocalized σ bonding between the first and second B layers around the Rh atom. The Rh atom is coordinated with eight boron atoms via the four 4c–2e delocalized σ bonds and the two localized bonds in Fig. 4c and d. In addition to the four 4c–2e σ bonds, the bonding between the inner and outer B shells is described by the three 3c–2e σ bonds in Fig. 4f. The third row in Fig. 4 consists of five delocalized π bonds on the boron motif, rendering aromaticity to the quasi-planar isomer of RhB18 –. We also find that there is even more charge transfer from Rh to the planar boron framework than to the drum framework, calculated to be 1.06 e at the PBE0 level.
Fig. 4. AdNDP chemical bonding analyses for the C s quasi-planar isomer of RhB18 – at the PBE0 level. ON stands for occupation number.
While the delocalized π bonding in the quasi-planar RhB18 – is similar to that in the planar CoB18 – cluster,24 the coordination environment for Rh is different from that for Co. In the planar CoB18 – cluster, Co is coordinated by seven B atoms, whereas Rh is coordinated by eight B atoms in the quasi-planar RhB18 –. Because of the smaller size of Co, the inner B7 ring has the right size to fit Co to give rise to a perfectly planar structure for CoB18 –. However, the larger Rh requires a B8 ring for its first coordination shell in the quasi-planar RhB18 –.
7.3. Competition between the drum and quasi-planar structures in metal-doped boron clusters
Small boron clusters have been found to be planar and electron delocalization in both the σ and π frameworks have been shown to be the major driving force.3,4,6 The tubular or drum structure was first shown to be viable for the neutral B20 cluster and was suggested to be the embryo for boron nanotubes.8 Ion mobility and DFT calculations suggested that cationic boron clusters (Bn +) were all tubular for n > 15.7 However, for anionic Bn – clusters no tubular clusters have been observed up to n = 40.5,6 The curvature in tubular boron clusters may make the 2D electron delocalization unfavorable, so planar structures are favored. Clearly, the metal–boron interactions in CoB16 – and MnB16 – are critical in stabilizing the tubular structures. In CoB18 –, because of the small size of Co atom the B18 drum motif is too large to allow effective Co–B interactions, resulting in the planar global minimum instead. Thus, there is a fine balance between M–B interactions in the drum isomers and 2D electron delocalization. In RhB18 –, the slightly larger size of Rh makes the drum isomer competitive with the quasi-planar isomer and both are observed experimentally. Thus, it is conceivable that larger drums are possible with 5d, 6d or even lanthanide and actinide elements.
8. Conclusions
In summary, we have observed that in the RhB18 – cluster a perfect D 9d drum and a quasi-planar (C s) isomer are competing for the global minimum and both are observed experimentally. In the drum structure, the Rh atom features a record high coordination number of eighteen (CN = 18). The C s quasi-planar isomer consists of a Rh atom coordinated with eight boron atoms in its first shell and an incomplete second shell of ten boron atoms. The quasi-planar isomer of RhB18 – is aromatic with 10 π electrons. The interactions between the Rh 4d orbitals and the B18 drum motif are favorable to make the D 9d drum isomer competitive with the quasi-planar isomer. The current work pushes the limit in coordination number in chemistry, suggesting that the size and bonding strength of the metal atom determines if a planar or tubular structure is more stable in the mid-sized metal-doped boron clusters. These insights can help design metallo-boronanotubes and metallo-borophenes by tuning the interaction between the metal and the boron atoms.
Acknowledgments
The experimental work done at Brown University was supported by the National Science Foundation (CHE-1632813). The theoretical work done at Tsinghua University was supported by NKBRSF (2013CB834603) and NSFC (21433005, 91426302 and 21590792) of China. The calculations were performed using supercomputers at the Computer Network Information Center, Chinese Academy of Sciences, Tsinghua National Laboratory for Information Science and Technology, and Lüliang Tianhe-2 Supercomputing Center.
Footnotes
References
- Albert B., Hillebrecht H. Angew. Chem., Int. Ed. 2009;48:8640–8668. doi: 10.1002/anie.200903246. [DOI] [PubMed] [Google Scholar]
- Lipscomb W. N. Science. 1977;196:1047–1055. doi: 10.1126/science.196.4294.1047. [DOI] [PubMed] [Google Scholar]
- Alexandrova A. N., Boldyrev A. I., Zhai H. J., Wang L. S. Coord. Chem. Rev. 2006;250:2811–2866. [Google Scholar]
- Sergeeva A. P., Popov I. A., Piazza Z. A., Li W. L., Romanescu C., Wang L. S., Boldyrev A. I. Acc. Chem. Res. 2014;47:1349–1358. doi: 10.1021/ar400310g. [DOI] [PubMed] [Google Scholar]
- Zhai H. J., Zhao Y. F., Li W. L., Chen Q., Bai H., Hu H. S., Piazza Z. A., Tian W. J., Lu H. G., Wu Y. B., Mu Y. W., Wei G. F., Liu Z. P., Li J., Li S. D., Wang L. S. Nat. Chem. 2014;6:727–731. doi: 10.1038/nchem.1999. [DOI] [PubMed] [Google Scholar]
- Wang L. S. Int. Rev. Phys. Chem. 2016;35:69–142. [Google Scholar]
- Oger E., Crawford N. R. M., Kelting R., Weis P., Kappes M. M., Ahlrichs R. Angew. Chem., Int. Ed. 2007;46:8503–8506. doi: 10.1002/anie.200701915. [DOI] [PubMed] [Google Scholar]
- Kiran B., Bulusu S., Zhai H. J., Yoo S., Zeng X. C., Wang L. S. Proc. Natl. Acad. Sci. U. S. A. 2005;102:961–964. doi: 10.1073/pnas.0408132102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romanescu C., Harding D. J., Fielicke A., Wang L. S. J. Chem. Phys. 2012;137:014317. doi: 10.1063/1.4732308. [DOI] [PubMed] [Google Scholar]
- Piazza Z. A., Hu H. S., Li W. L., Zhao Y. F., Li J., Wang L. S. Nat. Commun. 2014;5:3113. doi: 10.1038/ncomms4113. [DOI] [PubMed] [Google Scholar]
- Mannix A. J., Zhou X. F., Kiraly B., Wood J. D., Alducin D., Myers B. D., Liu X., Fisher B. L., Santiago U., Guest J. R., Yacaman M. J., Ponce A., Oganov A. R., Hersam M. C., Guisinger N. P. Science. 2015;350:1513–1516. doi: 10.1126/science.aad1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (a) Feng B., Zhang J., Zhong Q., Li W., Li S., Li H., Cheng P., Meng S., Chen L., Wu K. Nat. Chem. 2016;8:563–568. doi: 10.1038/nchem.2491. [DOI] [PubMed] [Google Scholar]; (b) Xu S., Zhao Y., Liao J., Yang X., Xu H. Nano Res. 2016 doi: 10.1007/s12274-016-1148-0. [DOI] [Google Scholar]
- Liu Y., Penev E. S., Yakobson B. I. Angew. Chem., Int. Ed. 2013;52:3156–3159. doi: 10.1002/anie.201207972. [DOI] [PubMed] [Google Scholar]
- Liu H., Gao J., Zhao J. Sci. Rep. 2013;3:3238. doi: 10.1038/srep03238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z., Yang Y., Gao G., Yakobson B. I. Angew. Chem. 2015;127:13214–13218. [Google Scholar]
- Zhai H. J., Alexandrova A. N., Birch K. A., Boldyrev A. I., Wang L. S. Angew. Chem., Int. Ed. 2003;42:6004–6008. doi: 10.1002/anie.200351874. [DOI] [PubMed] [Google Scholar]
- (a) Romanescu C., Galeev T. R., Li W. L., Boldyrev A. I., Wang L. S. Angew. Chem., Int. Ed. 2011;50:9334–9337. doi: 10.1002/anie.201104166. [DOI] [PubMed] [Google Scholar]; (b) Ito K., Pu Z., Li Q. S., Schleyer P. v. R. Inorg. Chem. 2008;47:10906. doi: 10.1021/ic800993b. [DOI] [PubMed] [Google Scholar]
- Romanescu C., Galeev T. R., Li W. L., Boldyrev A. I., Wang L. S. Acc. Chem. Res. 2013;46:350–358. doi: 10.1021/ar300149a. [DOI] [PubMed] [Google Scholar]
- Popov I. A., Li W. L., Piazza Z. A., Boldyrev A. I., Wang L. S. J. Phys. Chem. A. 2014;118:8098–8105. doi: 10.1021/jp411867q. [DOI] [PubMed] [Google Scholar]
- Xu C., Cheng L. J., Yang J. L. J. Chem. Phys. 2014;141:124301. doi: 10.1063/1.4895727. [DOI] [PubMed] [Google Scholar]
- Tam N. M., Pham H. T., Duong L. V., Pham-Ho M. P., Nguyen M. T. Phys. Chem. Chem. Phys. 2015;17:3000–3003. doi: 10.1039/c4cp04279d. [DOI] [PubMed] [Google Scholar]
- Popov I. A., Jian T., Lopez G. V., Boldyrev A. I., Wang L. S. Nat. Commun. 2015;6:8654. doi: 10.1038/ncomms9654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jian T., Li W. L., Popov I. A., Lopez G. V., Chen X., Boldyrev A. I., Li J., Wang L. S. J. Chem. Phys. 2016;144:154310. doi: 10.1063/1.4946796. [DOI] [PubMed] [Google Scholar]
- (a) Li W. L., Jian T., Chen X., Chen T. T., Lopez G. V., Li J., Wang L. S. Angew. Chem., Int. Ed. 2016;55:7358–7363. doi: 10.1002/anie.201601548. [DOI] [PubMed] [Google Scholar]; (b) Li Y. Nano Res. 2016;9:1877–1878. [Google Scholar]
- Zhang H., Li Y., Hou J., Tu K., Chen Z. J. Am. Chem. Soc. 2016;138:5644–5651. doi: 10.1021/jacs.6b01769. [DOI] [PubMed] [Google Scholar]
- Wang L. S., Cheng H. S., Fan J. J. Chem. Phys. 1995;102:9480. [Google Scholar]
- Goedecker S. J. Chem. Phys. 2004;120:9911. doi: 10.1063/1.1724816. [DOI] [PubMed] [Google Scholar]
- Perdew J. P., Burke K., Ernzerhof M. Phys. Rev. Lett. 1996;77:3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- van Lenthe E., Baerends E. J. J. Comput. Chem. 2003;24:1142–1156. doi: 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
- ADF and SCM, Theoretical Chemistry, Vrijie Universiteit, Amsterdam, The Netherlands, 2013, http://www.scm.com. [Google Scholar]
- Adamo C., Barone V. J. Chem. Phys. 1999;110:6158. [Google Scholar]
- Purvis III G. D., Bartlett R. J. J. Chem. Phys. 1982;76:1910. [Google Scholar]
- Scuseria G. E., Janssen C. L., Schaefer H. F. J. Chem. Phys. 1988;89:7382. [Google Scholar]
- Werner H. J., et al., MOLPRO 2008, http://www.molpro.net.
- Dunning Jr T. H. J. Chem. Phys. 1989;90:1007. [Google Scholar]
- Peterson K. A., Figgen D., Dolg M., Stoll H. J. Chem. Phys. 2007;126:124101. doi: 10.1063/1.2647019. [DOI] [PubMed] [Google Scholar]
- Schipper P. R. T., Gritsenko O. V., van Gisbergen S. J. A., Baerends E. J. J. Chem. Phys. 2000;112:1344–1352. [Google Scholar]
- Li J., Li X., Zhai H. J., Wang L. S. Science. 2003;299:864–867. doi: 10.1126/science.1079879. [DOI] [PubMed] [Google Scholar]
- Zubarev D. Y., Boldyrev A. I. Phys. Chem. Chem. Phys. 2008;10:5207–5217. doi: 10.1039/b804083d. [DOI] [PubMed] [Google Scholar]
- Dennington R., Keith T. and Millam J., GaussView, version 4.1, Semichem, Inc, Shawnee Mission, KS, 2007.
- Li W. L., Romanescu C., Galeev T. R., Piazza Z. A., Boldyrev A. I., Wang L. S. J. Am. Chem. Soc. 2012;134:165–168. doi: 10.1021/ja209808k. [DOI] [PubMed] [Google Scholar]
- Akola J., Manninen M., Häkkinen H., Landman U., Li X., Wang L. S. Phys. Rev. B: Condens. Matter. 1999;60:R11297. [Google Scholar]
- Mann J. B., Atomic Structure Calculations II. Hartree–Fock wave functions and radial expectation values: hydrogen to lawrencium, LA-3691, Los Alamos Scientific Laboratory, USA, 1968. [Google Scholar]
- Pyykkö P., Atsumi M. Chem.–Eur. J. 2009;15:12770–12779. doi: 10.1002/chem.200901472. [DOI] [PubMed] [Google Scholar]
- Pyykkö P. J. Phys. Chem. A. 2015;119:2326–2337. doi: 10.1021/jp5065819. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.