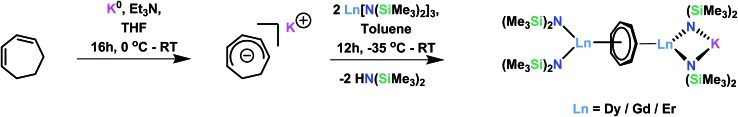 Lanthanide inverse sandwich compounds of the cycloheptatrienyl trianion give rise to ferromagnetic exchange and slow relaxation of the magnetisation.
Lanthanide inverse sandwich compounds of the cycloheptatrienyl trianion give rise to ferromagnetic exchange and slow relaxation of the magnetisation.
Abstract
The preparation of η-cyclopentadienyl (η5-C5R5), η-arene (η6-C6R6), and η-cyclooctatetraenyl (η8-C8R8) bridging motifs are common in organometallic chemistry; however, the synthetic preparation of η-cycloheptatrienyl (η7-C7R7) bridging motifs has remained a synthetic challenge in 4f chemistry. To this end, we have developed a synthetic route towards a series of rare dinuclear organolanthanide inverse sandwich complexes containing the elusive η7-C7H7 bridge. Herein, we present the structures and magnetic properties of the lanthanide inverse sandwich complexes [KLn2(C7H7)(N(SiMe3)2)4] (Ln = GdIII (1), DyIII (2), ErIII (3)) and [K(THF)2Er2(C7H7)(N(SiMe3)2)4] (4). These compounds are the first single-molecule magnets (SMMs) to feature this type of bridging motif. Furthermore, η7-C7H7 was found to efficiently promote ferromagnetic exchange interactions between metal ions. Variable temperature dc magnetic susceptibility measurements and subsequent simulations give significant exchange constants of J = +1.384, +1.798, and +3.149 cm–1 and dipolar constants of J = –0.603, –0.601, and –0.475 cm–1 for compounds 2–4, respectively. Frequency dependent ac susceptibility measurements under an applied static field resulted in the observation of dual relaxation processes, and brought forth a greater understanding of the intermolecularly driven process at high frequency. In particular, this type of analysis of compound 3 under 800 Oe elicited an energy barrier of U eff = 58 K. Ab initio calculations were performed in order to understand the nature of magnetic coupling and the origin of slow relaxation of magnetisation. Through these studies, the effect of the amido ancillary ligands on the magnetic axiality of the lanthanide ions was found to be competitive with the crystal field of the η7-C7H7 π-electron cloud. Our findings suggest that the tunability of the dipolar and exchange components of the magnetic interactions lie within the dihedral angle imposed by the amido ligands, thus offering potential for the development of new exchange coupled lanthanide systems.
Introduction
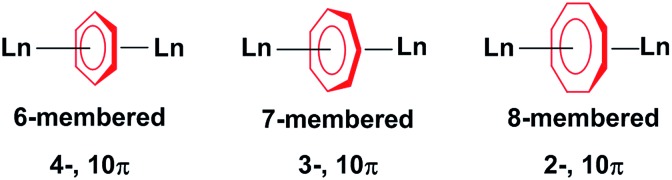
The use of η-cyclopentadienyl (η5-C5R5), η-arene (η6-C6R6) and η-cyclooctatetraenyl (η8-C8R8) ligands in the synthesis of organolanthanide complexes is widespread. These complexes have been extensively studied for their unique physical properties arising from their core 4f orbitals. While the cycloheptatrienyl trianion was first spectroscopically characterised by Bates et al. in 1977;1 only a single example of a η7-C7R7 lanthanide complex is known.2 There are only four reported examples of the isolation of f-element compounds with η-cycloheptatrienyl,2–4 and only two of those reports describe their use in dinuclear systems.2,4 The limited exploration of such species resides in the difficulty of the synthetic preparation and isolation of the elusive 10π-electron 7-membered ring with f-elements (Chart 1).
Chart 1. LnIII ions bridged by 6-, 7- and 8-membered rings.
The amplified interest in the isolation of dinuclear lanthanide complexes with different bridging motifs arises from the ability to probe magnetic communication between metal ions, as they represent the most fundamental unit with which to study magnetic exchange interactions. Some of these reported molecules exhibit slow relaxation of magnetisation below their blocking temperature; these molecules are termed Single-Molecule Magnets (SMMs).5–11 Since the discovery of the first organometallic SMMs in 2010,12 several complexes have been reported to exhibit this nanomagnetic behavior.13–17 Most of the examples described are mononuclear compounds, however, the study of dinuclear systems is of the utmost importance when we consider the technological requirements of the future. In regard to SMMs, these include increasing the total spin of molecular magnets through expanding the number of paramagnetic centres. While many different bridging systems exist,14,18,19 few examples have demonstrated the importance of planar aromatic organometallic ligands towards garnering favourable magnetic interactions.20–22 These systems are an appealing design strategy as they may be employed as building blocks to generate higher nuclearity compounds, while they are more notably effective in harnessing the inherent magnetic anisotropy of 4f and 5f ions.13,15–17,23,24 Our recent reports with cyclooctatetraenyl20,21 and arene-bridged22 systems shows that a weak, yet non-negligible, interaction can be observed with coupling constants between GdIII ions of –0.644 cm–1 and –0.488 cm–1 respectively, utilizing the isotropic spin Hamiltonian (H = –2JS a S b, S a = S b = 7/2) for each system respectively. Herein, the role of the 7-membered cycloheptatrienyl ring in the magnetic exchange between lanthanide ions will be examined and compared with its counterparts, the 6- and 8-membered rings (Chart 1). We investigate how subtle structural differences in a family of rare inverse sandwich compounds influence the overall magnetic properties and clearly demonstrate the significance of the 7-membered ring on the bridging interactions and magnetic axiality. We report for the first time GdIII, DyIII, and ErIII compounds with the cycloheptatrienyl bridge. The synthesis, structure, and magnetic characterization of three isostructural dinuclear complexes, [KLn2(C7H7)(N(SiMe3)2)4] (Ln = GdIII (1), DyIII (2), ErIII (3)) and one structurally analogous complex, [K(THF)2Er2(C7H7)(N(SiMe3)2)4] (4) is presented.
Results and discussion
Syntheses and structures
Since the first report of the synthesis of a uranium cycloheptatrienyl sandwich complex in 1995,3 there has been limited exploration into the isolation of other f-element complexes containing cycloheptatrienyl. However, other areas of chemistry, such as organic chemistry, have made use of the 6π-electron cycloheptatrienyl cation (the tropylium ion),25 and there have been reports of the 10π-electron derivative in transition metal chemistry.26 Thus, the preparation of the above mentioned complexes, 1–4, was carefully designed to result in the facile formation of the trianion through employing chemistry that is previously known for lanthanide ions. In particular, this chemistry involves the polarisation of C–H bonds,27 and is further complemented by highly basic and sterically demanding ancillary ligands.
Inspired by the work of Arliguie et al.,4 who had utilized borohydride chemistry towards the isolation of an f-element η7-C7H7 complex, we attempted to utilize lanthanide borohydrides to support the inverse sandwich architecture. However, due to the highly reactive/reducing nature of the borohydrides and the non-innocent character of the cycloheptadienide ligand, the isolation of such systems proved to be difficult. In order to combat the aforementioned issue, we employed bis(trimethylsilyl) amido ancillary ligands and have since prepared a series of dinuclear complexes of Ln = DyIII, GdIII, ErIII (Scheme 1). The synthesis of LnIII[N(SiMe3)2]3 was first reported by Bradley et al.,28,29 and has since been revisited in order to investigate the SMM properties of the complexes, which arise from their distinctive crystal field.30 Conversely, the seven-membered bridging motif may be prepared from the commercially available 1,4-cycloheptadiene, where upon a one-electron reduction with potassium metal in the presence of Et3N, cycloheptadienide (C7H9 –) (Scheme 1) is afforded. The salt, KC7H9, remains stable for several days under inert conditions at –35 °C.
Scheme 1. Synthesis of [KLn2(C7H7)(N(SiMe3)2)4]” (Ln = DyIII, GdIII, ErIII).
Solutions of lanthanide tris(bis(trimethylsilyl) amido) and potassium cycloheptadienide are combined at –35 °C in toluene and warmed to room temperature gradually. Further reduction of the cycloheptadienide to the aromatic trianion, cycloheptatrienyl, is supported by a mechanism previously reported by Miller and Dekock.27 Initial coordination of the LnIII ion results in polarisation of the methylene C–H bond and subsequent proton abstraction by a strong base. Interestingly, it was first postulated that the highly basic nature of the C7H9 – may be responsible for this abstraction, resulting in the formation of 1,4- and 1,3-isomers of cycloheptadiene. However, in this case, the loss of an amido ligand from each of the bridging LnIII ions may suggest that abstraction occurs via the amido, thus inducing the generation of soluble HN(SiMe3)2 species. The presence of such species was observed in the crude 1H NMR of compound 3 as a singlet at 0.1 ppm in toluene-d8 at 298 K, further supporting this hypothesis.
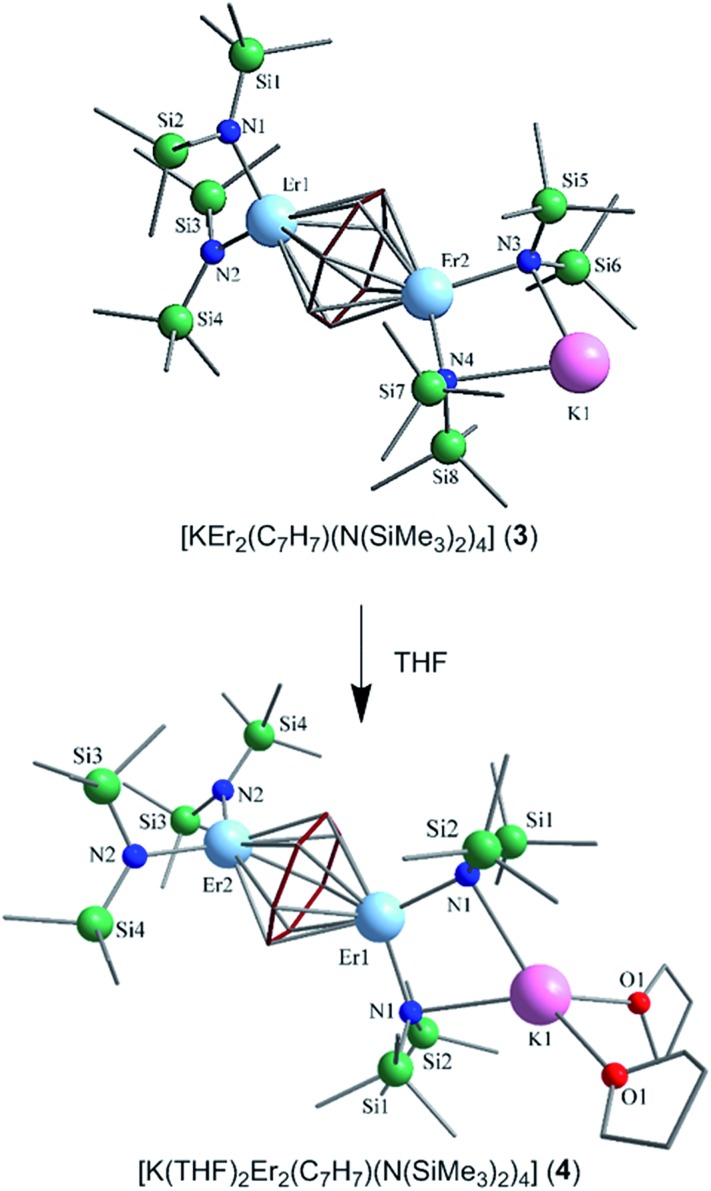
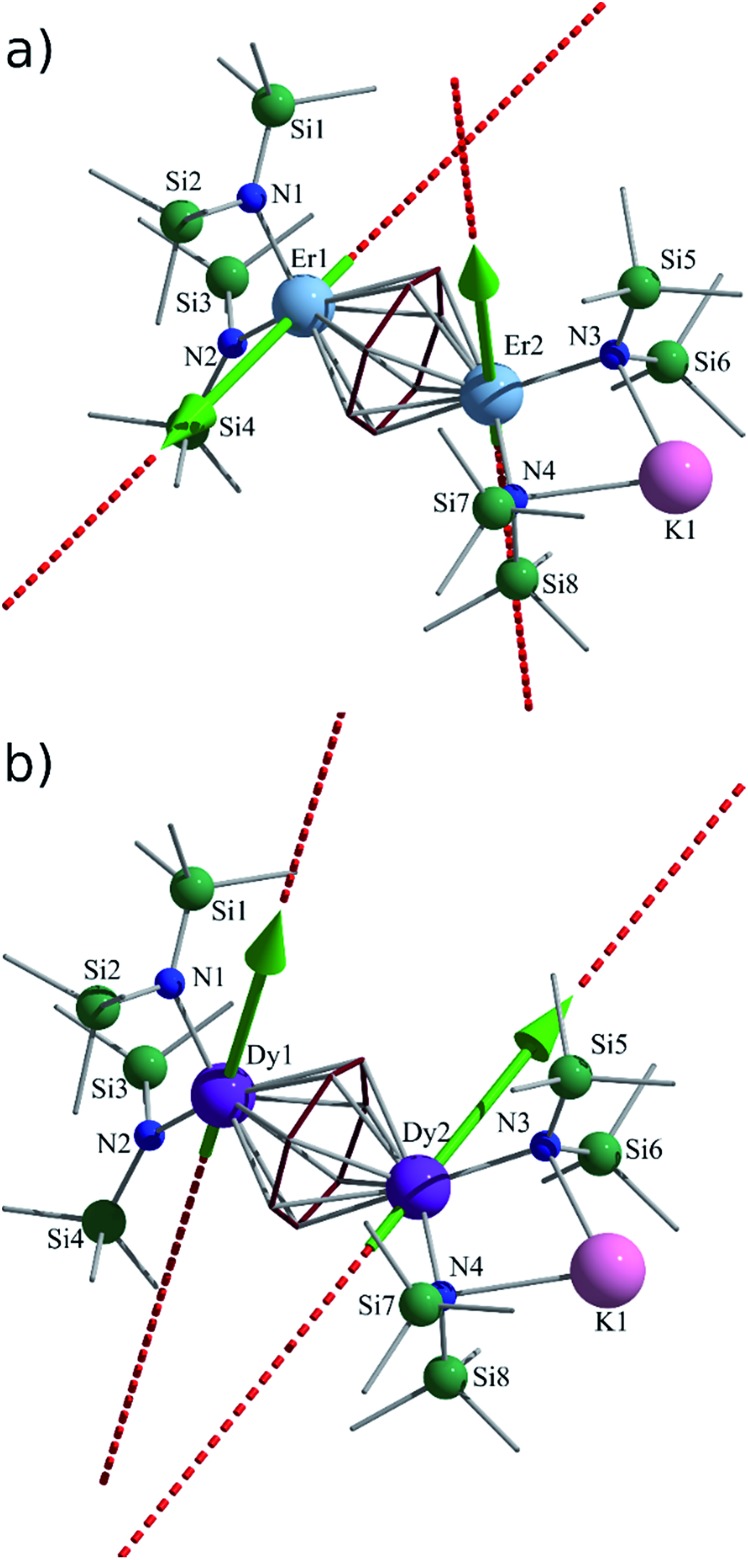
Nevertheless, collection of the filtrate followed by treatment with toluene and hexanes yields compounds 1–3. Conversely, the solvated derivative, compound 4, can be obtained from 3 via extraction into THF (Fig. 1), resulting in the coordination of two molecules of THF to the bound potassium ion, and thereby limiting intermolecular interactions. X-ray quality crystals of 4 were isolated from the subsequent treatment with a toluene/hexanes mixture, confirming the nature of the solvated species.
Fig. 1. SCXRD structures for compounds 3 (top) and 4 (bottom). The cycloheptatrienyl ligand is displayed in dark red. Colour code: light blue (ErIII), pink (K), green (Si), blue (N), red (O), grey (C). H atoms have been omitted for clarity.
Single-crystal X-ray diffraction (SCXRD) studies reveal that compounds 1–3 are isostructural and crystallize in the monoclinic space group P21/n. On the other hand, the analogous compound 4 crystallizes in the monoclinic space group C2/c. The structure of the ErIII analogue, 3, will be the representative structure described herein (Fig. 1, top). The molecular structure of 3 reveals an inverse cycloheptatrienyl sandwich complex. The dinuclear compound is composed of two ErIII ions bridged by the 10π-electron cycloheptatrienyl C7H7 3– trianion in a η7-bound fashion, with an Er–C bond distance range of 2.484(8)–2.629(9) Å. The remaining coordination environment is occupied by two [N(SiMe3)2]– ligands. Interestingly, one K ion is bound to one side of the molecule via N atoms (N3, N4) from the [N(SiMe3)2]– ligands, thus making this dinuclear unit unsymmetrical. Due to this binding configuration, the N3···Er2···N4 angle of 98.6(2)° is much smaller than the N1···Er1···N2 angle of 105.7(2)°. It is noteworthy that in the case of 4, due to crystal packing effects the symmetry of the molecule is slightly higher than in 3.
Close inspection of the packing arrangement of 3 reveals a close contact between the K ion and a carbon atom (C14) from the [N(SiMe3)2]–, which subsequently promotes a linear chain-like arrangement of the molecules (Fig. S4†). Interestingly, in the case of compound 4 we still observe a head-to-tail packing arrangement generating a chain-like array, however, there are no close contacts that exist beyond H–H interactions (Fig. S5†).31 In regard to compound 3, the intramolecular Er–Er distance of 3.9580(7) Å is slightly shorter than the distance observed in a COT″ (1,4-bis(trimethylsilyl)cyclooctatetraenyl dianion) bridged Er2 dimer (4.1109(5) Å) or an arene bridged Er2 compound (4.067(1) Å).21,22 A similar Sm2 inverse sandwich analogue was reported with a bridging COT and terminal [N(SiMe3)2]– ligands with a Sm–Sm distance of 4.308(1) Å.32 However, the larger distance in the case of the Sm example is primarily due to the larger ionic radii of the SmIII ion. Finally, it is noteworthy that the NdIII analogue of the reported example exhibits a Nd–Nd distance of 4.213(3) Å, this is presumably a result of the electron rich borohydride ancillary ligands, which allow for increased electron donation to the electropositive NdIII ions.2
The central cycloheptatrienyl ligand adopts a planar geometry, owing to its 10π-electron aromatic configuration, with the largest atom deviation being 0.06 Å out of the plane formed by the seven C atoms. The high charge (–3) and planarity of the bridging ligand, along with the close proximity of ErIII ions, is expected to lead to non-negligible magnetic interactions via the delocalised π-orbitals of the cycloheptatrienyl ligand. Therefore, this molecule represents an ideal candidate to probe the exchange interactions between metal ions, while also studying the ligand field effects of the bridging unit in comparison with its COT and arene counterparts.
Static magnetic properties
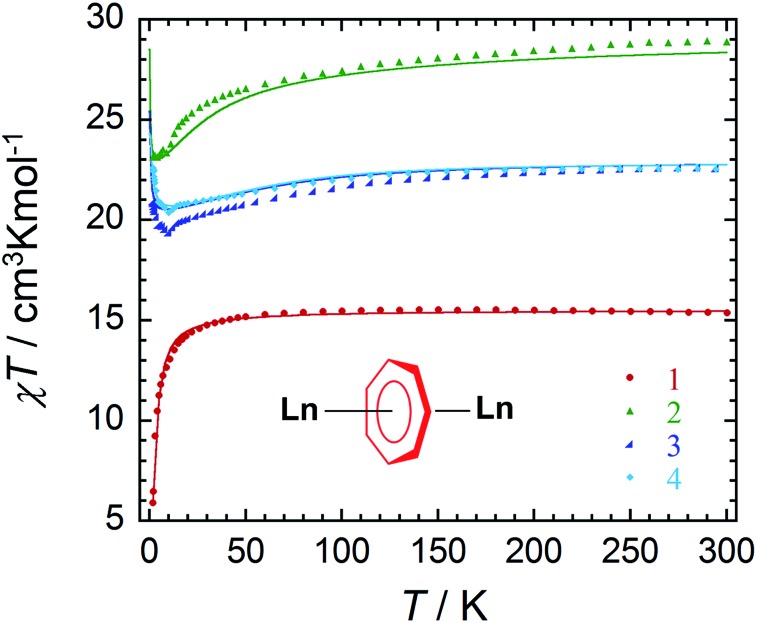
Direct current (dc) and alternating current (ac) magnetic susceptibility measurements were performed using a SQUID magnetometer on crushed crystalline samples of complexes 1–4, prepared under an inert atmosphere. Variable temperature magnetic susceptibility measurements under a 0.1 T applied field in the temperature range of 1.9–300 K are shown in Fig. 2. At room temperature, the χT values of complexes 1–4 are 15.37, 28.34, 22.54 and 22.49 cm3 K mol–1, respectively. These values are in good agreement with the expected theoretical values of 15.76 (GdIII: 8S7/2, S = 7/2, L = 0, g J = 2), 28.34 (DyIII: 6H15/2, S = 5/2, L = 5, g J = 4/3) and 22.49 cm3 K mol–1 (ErIII: 4I15/2, S = 3/2, L = 6, g J = 6/5) for two non-interacting lanthanide ions. For 1, the χT product remains constant down to 50 K, followed by a gradual decrease with temperature to reach a minimum value of 5.84 cm3 K mol–1 at 1.9 K. This downturn of the χT product can be attributed to the intramolecular antiferromagnetic interactions between the spin carriers (4.0869(7) Å). Owing to the isotropic nature of GdIII ions, the strength of interactions between the two lanthanide ions can be quantified. Application of the Van Vleck equation to the Kambe's vector coupling method was completed by using the isotropic spin Hamiltonian H = –2JS a S b, with S a = S b = 7/2, which was used to fit the variation of χT vs. T. The best-fit yielded a J value of –0.134 cm–1 for compound 1. The obtained J value is rather weak as a consequence of the shielded f-orbitals of GdIII having minimal orbital overlap with the bridging ligand.
Fig. 2. Temperature dependence of the χT product at 0.1 T for compound 1 (), 2 (▲), 3 (), and 4 (♦), with χ being the molar magnetic susceptibility per molecule defined as M/H. The solid line for 1 represents the fit as determined from the application of the 2J formalism. The solid lines for 2–4 correspond to ab initio calculated magnetic susceptibilities, using the method described in the text. The calculated susceptibility for 2 has been scaled by +2.5%.
In comparison with the 6- and 8-membered rings, the obtained coupling constant for GdIII is slightly smaller, and unfortunately did not lead to a direct trend related to ring size and charge density. When considering both the dipolar and exchange contributions to the coupling, as determined by ab initio methods (vide infra), both components for the 7-membered ring remain the smallest of any of the computed parameters. Perhaps an explanation for this lies within the ligand field contributions from the ancillary ligands. This may be considered from a formal charge perspective, such that the cycloheptatrienyl bridge adopts a formal charge of –3, which, when distributed over seven atoms, is diluted to approximately –0.43 per C atom. Conversely, the charge distribution over the amido N atom remains highly concentrated. Thus the interaction with the amido ligands remains dominant (vide infra) compared to the donating ability of the bridging C7-moiety. This was further proven through our computational studies of the main magnetic axis and LoProp charges (vide infra). Lastly, the presence of the potassium ion prevents the LnIII ions from receiving equal electronic donation from the amido ancillary ligands, where the electron density of N3 and N4 would be split between Er2 and K1, thereby making Er2 less electron rich in comparison to Er1.
In the case of the anisotropic compounds 2–4, the χT profile differs significantly from the GdIII analogue. For example, the χT product of compound 2 decreases very slowly from 300 K with temperature, followed by a more rapid decrease below 20 K to reach a minimum value of 23.15 cm3 K mol–1 at 1.9 K. On the other hand, the χT product of compounds 3 and 4 exhibit a slightly different trend upon decreasing temperature. The χT products for compounds 3 and 4 decrease gradually from 300 K to minimum values below 15 K of 19.64 cm3 K mol–1 and 20.53 cm3 K mol–1, respectively. This decrease in the χT product is followed by a rapid increase below 10 K to reach maximum values of 20.92 cm3 K mol–1 and 22.58 cm3 K mol–1, respectively. The final increase in the value of the χT product is attributed to intramolecular ferromagnetic interactions between the ErIII ions. This will be further confirmed through ab initio calculations (vide infra).
As seen in Fig. S6–S9,† the field dependence of the magnetisation measurements performed at low temperatures exhibit non-saturation, even at 7 T and 1.8 K, for all compounds. This can be attributed to weak intramolecular antiferromagnetic interactions between the LnIII ions, thereby making the low lying excited states accessible by applying a magnetic field, even at the lowest measurable temperature of 1.8 K. This finding is further exemplified through our computational study, where the energies of the first and second excited states are minimally separated from the ground state (vide infra). In the case of compounds 2–4 the presence of magnetic anisotropy is also likely to contribute to this lack of saturation in the magnetisation. Contrary to the COT″ bridged counterparts, no hysteretic behaviour was observed down to 1.8 K and therefore alternating current (ac) magnetic susceptibility measurements were performed to investigate the potential SMM behaviour of the anisotropic compounds 2–4.
Dynamic magnetic properties
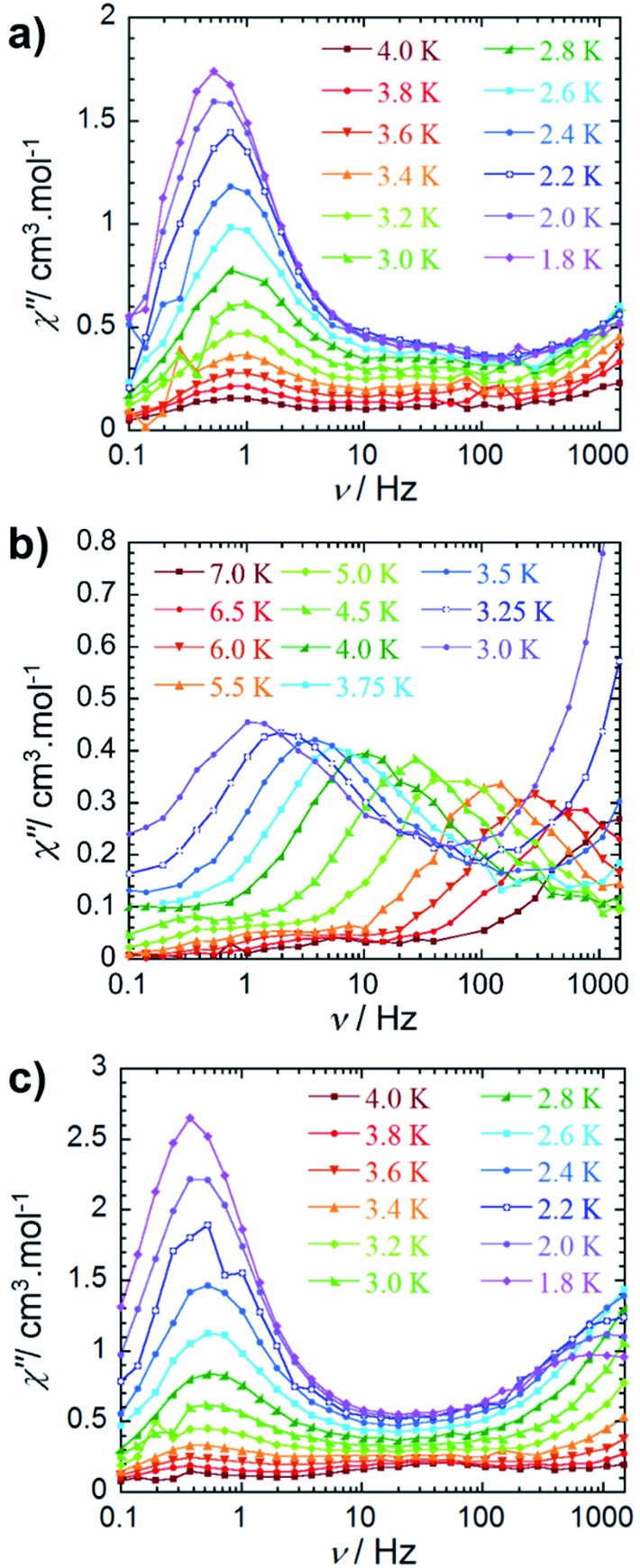
An ac field of 3.78 Oe was utilized to probe the slow relaxation dynamics of compounds 2–4, however, no ac signal was observed at zero applied dc field for all compounds. This is common for lanthanide systems with significant quantum tunnelling of magnetisation (QTM). However this QTM can be minimised upon application of a static dc field. As such, a frequency dependent signal was observed for all three compounds (Fig. 3 and S10–S12†) with the application of an optimised dc field. With respect to compound 2, the application of an optimal dc field of 2000 Oe allowed for the observation of a low frequency process below 4 K. The out-of-phase susceptibility of this processes exhibited minimal shifting in peak maxima with regards to frequency upon decreasing temperature. This type of behaviour may be indicative of a dominant QTM regime. This is not surprising due to the potential for low lying exchange coupled states, thereby enabling a shortcut in the energy barrier such that the first excited exchange state lies only minimally above the ground state with a calculated energy of 1.9 × 10–5 cm–1 (vide infra Table 2). However, we cannot rule out the possibility of intermolecular interactions, as application of large static fields has been shown to propagate spin–spin interactions.33,34 These types of interactions may lead to the formation of magnetic domains, consequently precluding the analysis from a molecular perspective. Due to these phenomena, an effective energy barrier for this process could not be extracted from this data set. Alternatively, a frequency-dependent χ″ signal was observed under a static dc field for 3 (Fig. 3b). The lack of overlapping peak maxima at low temperatures suggests that QTM is minimized with the application of an optimal static field of 800 Oe.
Fig. 3. Frequency dependence of the out-of-phase (χ″) ac susceptibility (a) for 2 under H dc = 2000 Oe, (b) for 3 under H dc = 800 Oe and (c) for 4 under H dc = 2000 Oe between 0.1 and 1000 Hz, at indicated temperatures. See the ESI† for data collected under H dc = 1000 Oe for compound 4.
Table 2. Exchange coupled states and their magnetic anisotropy in compounds 2–4, employing the reported coupling parameters. Exchange and dipolar coupling parameters are given with respect to eqn (1).
| 2 | 3 | 4 |
| J dip = –0.603 | J dip = –0.601 | J dip = –0.475 |
| J exch = +1.384 | J exch = +1.798 | J exch = +3.149 |
| Low-lying exchange coupled states (cm –1 ) | ||
| 0.000000 | 0.000000 | 0.000000 |
| 0.000019 | 0.000032 | 0.000077 |
| 0.391064 | 0.598359 | 1.337034 |
| 0.391092 | 0.598405 | 1.337149 |
| 69.220130 | 74.152765 | 68.455939 |
| 69.220149 | 74.152981 | 68.461815 |
| 69.503274 | 74.260012 | 68.544184 |
| 69.503276 | 74.260236 | 68.550104 |
| g Z values a in the ground and first excited exchange doublet states | ||
| 29.8 | 28.5 | 27.9 |
| 22.3 | 21.6 | 22.4 |
a g X = g Y = 0 for Ising doublets, according to the Griffith's theorem;62 (i.e. for systems with even number of electrons).
Observation of the shifting of peak maxima to lower frequencies below 7 K demonstrates the presence of slow relaxation of magnetisation in 3, indicating field-induced slow relaxation. From the χ″ data measured between 7 and 3 K, the Arrhenius law (τ = τ 0 exp(U eff/kT)) was employed in order to extract an effective energy barrier of 58 K, and a pre-exponential factor of 2.9 × 10–8 s (Fig. S13†). More notably, the frequency dependent behaviour is mostly likely attributed to single-ion properties, as the observation of a second relaxation process at high frequencies becomes evident below 3.75 K. Full analysis of this process could not be completed due to the frequency limitations (0.1–1500 Hz) of the magnetometer. From a structural perspective, the observed single-ion behaviour of 3 is not surprising given the non-centrosymmetric nature of the molecule. Inequivalent metal ion sites have elicited dual relaxation processes at low temperatures in previous studies.35–41 However, with respect to compound 3, this is easily visualized via the lack of an inversion centre within the molecule as a consequence of the coordinated potassium ion.
The observed magnetic behaviour of 3 greatly contrasts with the results obtained for the DyIII analogue, 2, suggesting that the cycloheptatrienyl trianion, along with the [N(SiMe3)2]– ancillary ligands, provide a more suitable ligand field for ErIII ions. These findings strongly correlate with our previous studies on COT″ bridging ligands, where the zero field energy barrier was improved upon from 25 K for the DyIII analogue to 306 K for ErIII.20,21 Additionally, we further exemplified that the ligand field provided by the delocalised π-cloud promoted greater magnetic axiality in ErIII ions over DyIII ions in single-ion sandwich complexes of COT.42 While this remains true of the delocalised π-cloud and ErIII ions in the present study, the effects of the amido ligands prove dominant over the cycloheptatrienyl, effectively generating greater magnetic axiality in 2 (vide infra). This is in accordance with previous studies, such that the axial orientation of highly charged negative donor atoms favour the oblate electron density of DyIII ions.43–48
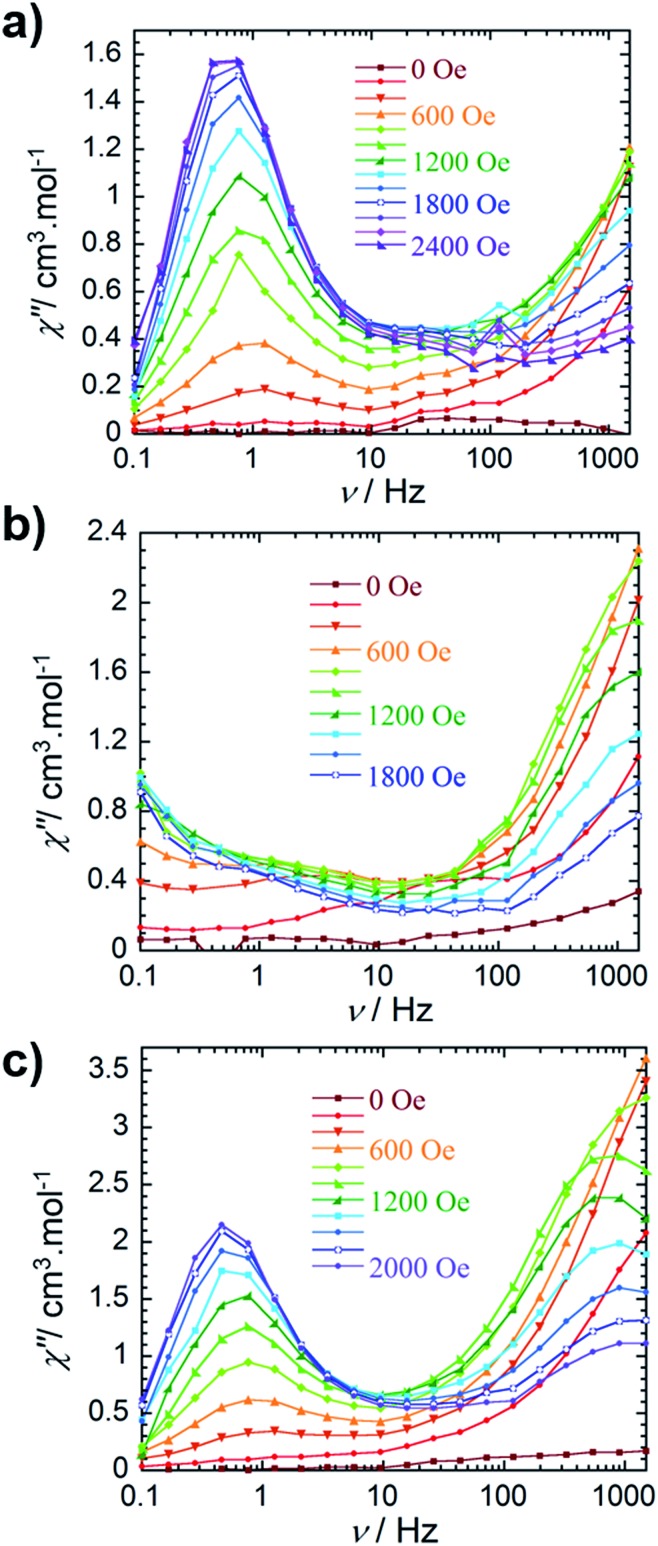
The out-of-phase magnetic susceptibility of 4 reveals two independent relaxation processes below 4 K, similar to compound 3 (Fig. 3c and S11†). Once again this is not surprising given the unsymmetrical nature of the complex.35–40 In order to probe each of these processes, an optimal dc field of 1000 Oe was used to elucidate the nature of the high frequency process, whereas an optimal field of 2000 Oe was employed in the study of the low frequency process. Unfortunately, the nature of the collected data precluded the extraction of an energy barrier to spin reversal, however, it did prove fruitful in gaining a further understanding of the interactions occurring within this system. Interestingly, the low frequency processes exhibit similar characteristics to 2, where upon decreasing temperature, the resulting out-of-phase signal increases in intensity, but demonstrates little-to-no frequency dependent behaviour. Again, this is most likely a result of the low-lying excited exchange states, which promote QTM. Our computational studies (vide infra) elucidated a first excited state energy of 7.7 × 10–5 cm–1 for compound 4 further supporting the nature of this process. Once more, it is worth noting that at large magnetic fields it becomes difficult to infer whether the observed properties are solely molecular in nature, due to the potential of induced spin–spin intermolecular interactions.33,34 Nonetheless, the presence of the secondary relaxation process at higher frequencies exhibits a shifting peak maxima towards lower frequency upon decreasing temperature (Fig. 3c). Interestingly, this plot is characterised by decreasing susceptibility intensity for an iso-temperature curve with decreasing temperature. This type of behaviour has been similarly noted in Single-Chain Magnets (SCMs), where inter-chain spin–spin interactions give rise to decreasing susceptibility values.49,50 Even under the optimal field of 1000 Oe, there is a decrease in intensity of the peaks for the out-of-phase component (Fig. S11†). While it is difficult to fully conclude the nature of the high frequency process, the preliminary data would suggest that the fundamental component relies on an intermolecularly driven process/relaxation. This finding may also explain the tails observed in the high frequency region of the out-of-phase susceptibility for compounds 2 and 3. In fact, it is not uncommon in lanthanide-based systems to observe a secondary process as a result of intermolecular interactions.34,51–53 Further investigation into the frequency dependent ac susceptibility measurements as a function of dc field for 2–4 (Fig. 4), reveal an unusual field dependence in the second relaxation, such that the high frequency process appears to be augmented by weak static fields, this is likely a result of a direct relaxation process which is promoted by neighbouring spins40,54 thus supporting the proposed intermolecularly driven relaxation process.
Fig. 4. Frequency dependence of the out-of-phase (χ″) ac susceptibility collected at 2 K (a) for compound 2, (b) for compound 3 and (c) for compound 4 at indicated dc fields.
Ab initio studies
Ab initio calculations for 2–4 were performed in order to gain additional insight into the electronic and magnetic structures of these compounds. All calculations performed were CASSCF/RASSI/SINGE_ANISO,55 and employed SCXRD structural data. Electronic and magnetic properties of the individual LnIII sites were obtained through fragment ab initio calculations. The calculated structures have identical structures to those obtained for complexes 2–4, where the neighbouring lanthanide sites are computationally replaced by the diamagnetic LuIII. The CASSCF wavefunction includes all possible electron distributions within the 4f9 (for DyIII) and 4f11 (for ErIII) shells only, while the remaining orbitals were kept doubly occupied. The orbitals and coefficients of the individual configurations were optimized self consistently for all electronic states arising from this definition of the active space. The spin–orbit interaction (described within the AMFI approximation) includes all optimized spin states for Er (3 and 4), while for 2 we could only mix a limited amount of states, namely 21 spin sextet, 128 spin quartet and 130 spin doublet states, which resulted in 898 spin–orbit levels. The obtained low-lying states, arising from the ground J = 15/2 multiplet on individual LnIII sites, are provided in Table 1.
Table 1. Electronic and magnetic properties of the individual metal sites in compounds 2–4, obtained from ab initio calculations (in cm–1).
|
2
|
3
|
4
|
|||
| Dy1 | Dy2 | Er1 | Er2 | Er1 | Er2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 116 | 69 | 122 | 74 | 68 | 88 |
| 328 | 270 | 148 | 138 | 136 | 149 |
| 530 | 441 | 211 | 188 | 182 | 199 |
| 720 | 614 | 262 | 231 | 228 | 249 |
| 851 | 754 | 334 | 285 | 289 | 332 |
| 1010 | 854 | 525 | 476 | 476 | 523 |
| 1214 | 1021 | 573 | 501 | 508 | 589 |
| Main values of the g tensor in the ground Kramers doublet | |||||
| 0.008 | 0.027 | 0.016 | 0.013 | 0.007 | 0.019 |
| 0.020 | 0.089 | 0.039 | 0.057 | 0.049 | 0.064 |
| 18.825 | 18.370 | 17.763 | 17.978 | 17.883 | 17.782 |
| Angle with the N–Ln–N plane (degrees) | |||||
| 1.3 | 1.3 | 87.0 | 88.6 | 89.3 | 90.0 |
Structural features determining the orientation of local magnetic axes on LnIII sites
As can be observed in Table 1, the g tensors in the ground Kramers doublet states of the individual sites in compounds 2–4 are relatively axial in nature (g X,Y ≪ g Z). The axiality of the ground doublet states are also related to the axiality of the crystal field acting on the LnIII sites. For the DyIII sites, the main anisotropy axis is oriented in the plane of the N–Dy–N atoms (Table 1) almost parallel to the N–N direction (Fig. 5b). This orientation is related to the much stronger crystal field effect arising from the N atoms. In particular, the calculated LoProp charges56 on N atoms (–1.28) are the largest among all neighbouring atoms of the LnIII sites. The covalent ligand field effect arising from the N atoms is also dominant among all neighbouring atoms. This is revealed by the Dy–N bonds, which are the shortest formed by the lanthanide sites in this environment. In this respect, the role of the central ring in the local axiality of the DyIII sites is diminished, and is in fact rather destructive as compared to the ligand field imposed by amido groups. In the case where the central ring and the neighbouring LnIII site were absent, the magnetic axiality on one DyIII site would be significantly stronger. These findings were not surprising given that recent reports have demonstrated the significant impact of highly anionic donor ligands in linear-like coordination geometries, with which such compounds should theoretically yield staggering energy barrier values.44–47
Fig. 5. Ab initio calculated main anisotropy axes (dashed lines) on Ln sites in the ground state for (a) 3 and (b) 2. The green arrows show the orientation of local magnetic moments on Ln sites in the ground exchange coupled state.
In stark contrast to the findings for DyIII, significantly different orientations for the ground state magnetic anisotropies were observed for the ErIII sites in compounds 3 and 4 (Table 1, Fig. 5a). For these compounds, the main magnetic axes are oriented almost perpendicular to the N–Er–N planes. This drastic change in the orientations of the main magnetic axes between DyIII and ErIII atoms in a very similar axial ligand field is due to the opposite signs of the Stevens parameters, α and β, which are related to the second and fourth rank operators of the ground ionic J = 15/2 multiplet for DyIII and ErIII.57 This is seen from the fact that the anisotropy of the highest (8th) Kramers doublet of the DyIII sites (which are greatly destabilized due to the crystal field) is in fact almost parallel to the anisotropy of the ground doublet for the ErIII ion in the same crystal field, thus demonstrating the complementary nature of DyIII and ErIII ions. This effect was previously observed in the case of [Er(COT)2]– and [Dy(COT)2]– anions.42 Similar arrangements of the local magnetic axes were revealed with the previously studied Er2C6 (η6-C6R6) compounds.22 Parameters of the ab initio calculated crystal field for the investigated Ln sites in 2–4 are given in Table S2.†
Exchange interaction in 2–4
The above reported ab initio results for separate LnIII sites in 2–4 were further employed in the computation of the exchange spectrum and magnetic properties of the dinuclear complexes using the POLY_ANISO program.58,59 In this approach, the exchange interaction between magnetic sites is considered within the Lines model,60 describing the exchange interaction between the localized spins in the absence of the spin–orbit interaction on sites by one parameter for the interacting metal pair. By explicitly considering the spin–orbit interaction on metal sites, the Lines model leads to an exchange matrix, which effectively describes the anisotropic exchange interaction between sites. In particular, the contribution of the intramolecular dipole–dipole magnetic coupling is accounted for exactly, because all of the necessary data are made available through the ab initio calculations. On the basis of the resulting exchange spectrum of the entire system, all macroscopic magnetic properties were computed. The total magnetic interaction (exchange + dipolar) between the lowest Kramers doublets on lanthanide sites can be cast in a good approximation by the non-collinear Ising Hamiltonian:
| Ĥexch = –(Jexch + Jdip)Ŝ1zŜ2z | 1 |
where J exch and J dip are parameters of the exchange and dipolar couplings respectively, while Ŝ 1z = 1/2 is the pseudospin of the ground states of the metal sites. Best-fit exchange parameters, J exch, and the calculated parameters of the dipolar magnetic coupling, J dip, for the investigated compounds, alongside the resulting exchange spectra are given in Table 2.
An alternative approach for the estimation of the exchange coupling parameters in di- and poly-nuclear compounds is given by the broken-symmetry density functional theory approach (BS-DFT).61 Unfortunately, the BS-DFT approach is not directly applicable for most of the lanthanides given the multiconfigurational nature of their ground states and their near-degenerate status as a result of weak crystal field effects. However, an estimation of the exchange in lanthanide-containing compounds is still achievable from the BS-DFT calculations. To this end, the “isotropic” closest metals computationally replace the “anisotropic” metal sites of the investigated compounds, while the ligand framework is kept intact. BS-DFT calculations are performed straightforwardly for the “isotropic” equivalent of the investigated compound. The extracted J iso parameter has to be later rescaled to reflect the exchange Hamiltonian between the true spins of the original “anisotropic” metal sites. This method was employed with reasonable success in several previous studies.63 For the present compounds, the estimated exchange parameters from the BS-DFT studies are ferromagnetic 1.14 cm–1 for 2, 2.45 cm–1 for 3 and 3.16 cm–1 for 4, correlating reasonably with the ferromagnetic exchange values obtained within the Lines model (Table 2). A comparison between the calculated and measured magnetic susceptibilities is depicted in Fig. 2. We notice a clear reduction in the dipolar magnetic coupling values for 2–4 with respect to our previously investigated dinuclear compounds containing a 6-membered bridging moiety.22 The reduction of J dip is attributed to the different relative orientations of the local magnetic axes of the two LnIII sites, imposed by the different dihedral angles between the N–Ln–N planes. Thus, by controlling this angle through synthetic means we could, in principle, modify the magnetic dipolar interaction (and possibly the exchange) in such compounds. Through this study, we attempted to computationally assess the role of the dihedral angle between N–Ln–N planes in the dinuclear model systems 2–4, as well as the role of the bridging ligand, in the magnetic behaviour as compared to those with 6- and 8-membered bridging rings. The results show that the dihedral angle in all three cases is very similar, while the Ln–Ln distance decreases with increasing bridging ring size. We conclude, therefore, that the bulky ancillary ligands (i.e. [N(SiMe3)2]– ligands), and the resulting crystalline packing, are the factors responsible for defining the relative orientations of the local anisotropy axes and dipolar magnetic interaction in this series of compounds.
Conclusions
Compounds 1–4 represent the first examples of SMMs based on the cycloheptatrienyl trianion ligand. The synthetic route to achieve the aforementioned compounds has been carefully designed to yield the facile formation of the trianion, taking advantage of sterically demanding and highly basic ancillary ligands. When combined with lanthanide ions, this type of bridging motif generates a weak, yet non-negligible, magnetic coupling constant of J = –0.134 cm–1 for the isotropic analogue. Through computational modelling of the anisotropic compounds, we elucidated that exchange coupling is more significant than dipolar coupling, with the largest J exch being +3.149 cm–1 for compound 4, thereby demonstrating the desirable effects of the 7-membered bridging moiety in generating exchange coupled dinuclear lanthanide systems. This is an area of significant modern interest in quantum physics, where mediating the interaction of two metal centres via tuning the redox properties of the bridging motif is a method to induce significant quantum communication.64,65 Moreover, the incorporation and measurement of these materials in molecular spintronics devices are often limited to the millikelvin regime,66 where the surface effects of such materials is only beginning to be better understood.62 Hence, increasing the energy barrier to spin reversal of SMMs will relax the rigorous experimental requirements for studying these systems. Thus, the current high-energy barriers associated with 4f ions, attributed to single-ion behaviour, will not be sufficient. It is vital that we look for more creative ways to induce significant interactions between lanthanide ions.
Acknowledgments
The work was financially supported by the University of Ottawa, the Canadian Foundation for Innovation (CFI), and the Natural Sciences and Engineering Research Council Canada (NSERC) for Discovery and RTI grants. L. U. is a postdoctoral fellow of the Fonds Wetenschappelijk Onderzoek-Vlaanderen and also gratefully acknowledges the INPAC and Methusalem grants of KU Leuven.
Footnotes
References
- Bahl J. J., Bates R. B., Beavers W. A., Launer C. R. J. Am. Chem. Soc. 1977;99:6126–6127. [Google Scholar]
- Arliguie T., Lance M., Nierlich M., Ephritikhine M. J. Chem. Soc., Dalton Trans. 1997:2501–2504. [Google Scholar]
- Arliguie T., Lance M., Nierlich M., Vigner J., Ephritikhine M. J. Chem. Soc., Chem. Commun. 1995:183–184. [Google Scholar]
- Arliguie T., Lance M., Nierlich M., Vigner J., Ephritikhine M. J. Chem. Soc., Chem. Commun. 1994:847–848. [Google Scholar]
- Sessoli R., Gatteschi D., Caneschi A., Novak M. A. Nature. 1993;365:141–143. [Google Scholar]
- Blagg R. J., Muryn C. A., McInnes E. J. L., Tuna F., Winpenny R. E. P. Angew. Chem., Int. Ed. 2011;50:6530–6533. doi: 10.1002/anie.201101932. [DOI] [PubMed] [Google Scholar]
- Ako A. M., Hewitt I. J., Mereacre V., Clérac R., Wernsdorfer W., Anson C. E., Powell A. K. Angew. Chem., Int. Ed. 2006;45:4926–4929. doi: 10.1002/anie.200601467. [DOI] [PubMed] [Google Scholar]
- Williams U. J., Mahoney B. D., DeGregorio P. T., Carroll P. J., Nakamaru-Ogiso E., Kikkawa J. M., Schelter E. J. Chem. Commun. 2012;48:5593–5595. doi: 10.1039/c2cc31227a. [DOI] [PubMed] [Google Scholar]
- Brown A. J., Pinkowicz D., Saber M. R., Dunbar K. R. Angew. Chem., Int. Ed. 2015;54:5864–5868. doi: 10.1002/anie.201411190. [DOI] [PubMed] [Google Scholar]
- Li Q. W., Liu J. L., Jia J. H., Chen Y. C., Liu J., Wang L. F., Tong M. L. Chem. Commun. 2015;51:10291–10294. doi: 10.1039/c5cc03389f. [DOI] [PubMed] [Google Scholar]
- Craig G. A., Marbey J. J., Hill S., Roubeau O., Parsons S., Murrie M. Inorg. Chem. 2015;54:13–15. doi: 10.1021/ic5024136. [DOI] [PubMed] [Google Scholar]
- Layfield R. A., McDouall J. J. W., Sulway S. A., Tuna F., Collison D., Winpenny R. E. P. Chem.–Eur. J. 2010;16:4442–4446. doi: 10.1002/chem.201000158. [DOI] [PubMed] [Google Scholar]
- Layfield R. A. Organometallics. 2014;33:1084–1099. [Google Scholar]
- Pugh T., Tuna F., Ungur L., Collison D., McInnes E. J. L., Chibotaru L. F., Layfield R. A. Nat. Commun. 2015;6:7492. doi: 10.1038/ncomms8492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang S.-D., Wang B.-W., Sun H.-L., Wang Z.-M., Gao S. J. Am. Chem. Soc. 2011;133:4730–4733. doi: 10.1021/ja200198v. [DOI] [PubMed] [Google Scholar]
- Trifonov A. A., Shestakov B., Long J., Lyssenko K., Guari Y., Larionova J. Inorg. Chem. 2015;54:7667–7669. doi: 10.1021/acs.inorgchem.5b01318. [DOI] [PubMed] [Google Scholar]
- Meihaus K. R., Long J. R. J. Am. Chem. Soc. 2013;135:17952–17957. doi: 10.1021/ja4094814. [DOI] [PubMed] [Google Scholar]
- Pugh T., Vieru V., Chibotaru L. F., Layfield R. A. Chem. Sci. 2016;7:2128–2137. doi: 10.1039/c5sc03755g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habib F., Murugesu M. Chem. Soc. Rev. 2013;42:3278–3288. doi: 10.1039/c2cs35361j. [DOI] [PubMed] [Google Scholar]
- Le Roy J. J., Jeletic M., Gorelsky S. I., Korobkov I., Ungur L., Chibotaru L. F., Murugesu M. J. Am. Chem. Soc. 2013;135:3502–3510. doi: 10.1021/ja310642h. [DOI] [PubMed] [Google Scholar]
- Le Roy J. J., Ungur L., Korobkov I., Chibotaru L. F., Murugesu M. J. Am. Chem. Soc. 2014;136:8003–8010. doi: 10.1021/ja5022552. [DOI] [PubMed] [Google Scholar]
- Huang W., Le Roy J. J., Khan S. I., Ungur L., Murugesu M., Diaconescu P. L. Inorg. Chem. 2015;54:2374–2382. doi: 10.1021/ic5029788. [DOI] [PubMed] [Google Scholar]
- Magnani N., Apostolidis C., Morgenstern A., Colineau E., Griveau J.-C., Bolvin H., Walter O., Caciuffo R. Angew. Chem., Int. Ed. 2011;50:1696–1698. doi: 10.1002/anie.201006619. [DOI] [PubMed] [Google Scholar]
- Liu S.-S., Ziller J. W., Zhang Y.-Q., Wang B.-W., Evans W. J., Gao S. Chem. Commun. 2014;50:11418–11420. doi: 10.1039/c4cc04262j. [DOI] [PubMed] [Google Scholar]
- Huang W., Diaconescu P. L. Dalton Trans. 2015;44:15360–15371. doi: 10.1039/c5dt02198g. [DOI] [PubMed] [Google Scholar]
- Green M. L. H., Ng D. K. P. Chem. Rev. 1995;95:439–473. [Google Scholar]
- Miller J. T., Dekock C. W. J. Organomet. Chem. 1981;216:39–48. [Google Scholar]
- Bradley D. C., Ghotra J. S., Hart F. A. J. Chem. Soc., Chem. Commun. 1972:349–350. [Google Scholar]
- Bradley D. C., Ghotra J. S., Hart F. A. J. Chem. Soc., Dalton Trans. 1973:1021–1027. [Google Scholar]
- Zhang P., Zhang L., Wang C., Xue S. F., Lin S. Y., Tang J. K. J. Am. Chem. Soc. 2014;136:4484–4487. doi: 10.1021/ja500793x. [DOI] [PubMed] [Google Scholar]
- Wolstenholme D. J., Cameron T. S. J. Phys. Chem. A. 2006;110:8970–8978. doi: 10.1021/jp061205i. [DOI] [PubMed] [Google Scholar]
- Schumann H., Winterfeld J., Esser L., Kociok-Köhn G. Angew. Chem., Int. Ed. 1993;32:1208–1210. [Google Scholar]
- Habib F., Korobkov I., Murugesu M. Dalton Trans. 2015;44:6368–6373. doi: 10.1039/c5dt00258c. [DOI] [PubMed] [Google Scholar]
- Meihaus K. R., Rinehart J. D., Long J. R. Inorg. Chem. 2011;50:8484–8489. doi: 10.1021/ic201078r. [DOI] [PubMed] [Google Scholar]
- Liu C.-M., Zhang D.-Q., Zhu D.-B. Inorg. Chem. 2013;52:8933–8940. doi: 10.1021/ic4011218. [DOI] [PubMed] [Google Scholar]
- Guo Y.-N., Xu G.-F., Gamez P., Zhao L., Lin S.-Y., Deng R., Tang J., Zhang H.-J. J. Am. Chem. Soc. 2010;132:8538–8539. doi: 10.1021/ja103018m. [DOI] [PubMed] [Google Scholar]
- Fatila E. M., Rouzieres M., Jennings M. C., Lough A. J., Clérac R., Preuss K. E. J. Am. Chem. Soc. 2013;135:9596–9599. doi: 10.1021/ja403794d. [DOI] [PubMed] [Google Scholar]
- Das S., Dey A., Biswas S., Colacio E., Chandrasekhar V. Inorg. Chem. 2014;53:3417–3426. doi: 10.1021/ic402827b. [DOI] [PubMed] [Google Scholar]
- Feng M., Pointillart F., Lefeuvre B., Dorcet V., Golhen S., Cador O., Ouahab L. Inorg. Chem. 2015;54:4021–4028. doi: 10.1021/acs.inorgchem.5b00272. [DOI] [PubMed] [Google Scholar]
- Ren M., Xu Z.-L., Wang T.-T., Bao S.-S., Zheng Z.-H., Zhang Z.-C., Zheng L.-M. Dalton Trans. 2016;45:690–695. doi: 10.1039/c5dt03800f. [DOI] [PubMed] [Google Scholar]
- Venugopal A., Tuna F., Spaniol T. P., Ungur L., Chibotaru L. F., Okuda J., Layfield R. A. Chem. Commun. 2013;49:901–903. doi: 10.1039/c2cc38036f. [DOI] [PubMed] [Google Scholar]
- Ungur L., Le Roy J. J., Korobkov I., Murugesu M., Chibotaru L. F. Angew. Chem., Int. Ed. 2014;53:4413–4417. doi: 10.1002/anie.201310451. [DOI] [PubMed] [Google Scholar]
- Rinehart J. D., Long J. R. Chem. Sci. 2011;2:2078–2085. [Google Scholar]
- Gregson M., Chilton N. F., Ariciu A.-M., Tuna F., Crowe I. F., Lewis W., Blake A. J., Collison D., McInnes E. J. L., Winpenny R. E. P., Liddle S. T. Chem. Sci. 2016;7:155–165. doi: 10.1039/c5sc03111g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chilton N. F. Inorg. Chem. 2015;54:2097–2099. doi: 10.1021/acs.inorgchem.5b00089. [DOI] [PubMed] [Google Scholar]
- Chilton N. F., Goodwin C. A. P., Mills D. P., Winpenny R. E. P. Chem. Commun. 2015;51:101–103. doi: 10.1039/c4cc08312a. [DOI] [PubMed] [Google Scholar]
- Ungur L., Chibotaru L. F. Phys. Chem. Chem. Phys. 2011;13:20086–20090. doi: 10.1039/c1cp22689d. [DOI] [PubMed] [Google Scholar]
- Chen Y.-C., Liu J.-L., Ungur L., Liu J., Li Q.-W., Wang L.-F., Ni Z.-P., Chibotaru L. F., Chen X.-M., Tong M.-L. J. Am. Chem. Soc. 2016;138:2829–2837. doi: 10.1021/jacs.5b13584. [DOI] [PubMed] [Google Scholar]
- Allão Cassaro R. A., Reis S. G., Araujo T. S., Lahti P. M., Novak M. A., Vaz M. G. F. Inorg. Chem. 2015;54:9381–9383. doi: 10.1021/acs.inorgchem.5b01431. [DOI] [PubMed] [Google Scholar]
- Tangoulis V., Lalia-Kantouri M., Gdaniec M., Papadopoulos C., Miletic V., Czapik A. Inorg. Chem. 2013;52:6559–6569. doi: 10.1021/ic400557f. [DOI] [PubMed] [Google Scholar]
- Rinehart J. D., Meihaus K. R., Long J. R. J. Am. Chem. Soc. 2010;132:7572–7573. doi: 10.1021/ja1009019. [DOI] [PubMed] [Google Scholar]
- Cosquer G., Pointillart F., Golhen S., Cador O., Ouahab L. Chem.–Eur. J. 2013;19:7895–7903. doi: 10.1002/chem.201300397. [DOI] [PubMed] [Google Scholar]
- Ren M., Bao S.-S., Ferreira R. A. S., Zheng L.-M., Carlos L. D. Chem. Commun. 2014;50:7621–7624. doi: 10.1039/c4cc02085e. [DOI] [PubMed] [Google Scholar]
- Car P.-E., Perfetti M., Mannini M., Favre A., Caneschi A., Sessoli R. Chem. Commun. 2011;47:3751–3753. doi: 10.1039/c0cc05850e. [DOI] [PubMed] [Google Scholar]
- Aquilante F., De Vico L., Ferré N., Ghigo G., Malmqvist P.-A., Neogrády P., Pedersen T. B., Pitoňák M., Reiher M., Roos B. O., Serrano-Andrés L., Urban M., Veryazov V., Lindh R. J. Comput. Chem. 2010;31:224–247. doi: 10.1002/jcc.21318. [DOI] [PubMed] [Google Scholar]
- Gagliardi L., Lindh R., Karlstrom G. J. Chem. Phys. 2004;121:4494–4500. doi: 10.1063/1.1778131. [DOI] [PubMed] [Google Scholar]
- Abragam A. and Bleaney B., Electron Paramagnetic Resonance of Transition Ions, Clanderon, Oxford, 1970. [Google Scholar]
- Chibotaru L. F., Ungur L. J. Chem. Phys. 2012;137:064112. doi: 10.1063/1.4739763. [DOI] [PubMed] [Google Scholar]
- Ungur L., Thewissen M., Costes J.-P., Wernsdorfer W., Chibotaru L. F. Inorg. Chem. 2013;52:6328–6337. doi: 10.1021/ic302568x. [DOI] [PubMed] [Google Scholar]
- Lines M. E. J. Chem. Phys. 1971;55:2977–2984. [Google Scholar]
- Ruiz E., Cano J., Alvarez S., Alemany P. J. Comput. Chem. 1999;20:1391–1400. [Google Scholar]
- Griffith J. S. Phys. Rev. 1963;132:316–319. [Google Scholar]
- Langley S. K., Wielechowski D. P., Vieru V., Chilton N. F., Moubaraki B., Abrahams B. F., Chibotaru L. F., Murray K. S. Angew. Chem., Int. Ed. 2013;52:12014–12019. doi: 10.1002/anie.201306329. [DOI] [PubMed] [Google Scholar]
- Lehmann J., Gaita-Arino A., Coronado E., Loss D. Nat. Nanotechnol. 2007;2:312–317. doi: 10.1038/nnano.2007.110. [DOI] [PubMed] [Google Scholar]
- Wagner S., Kisslinger F., Ballmann S., Schramm F., Chandrasekar R., Bodenstein T., Fuhr O., Secker D., Fink K., Ruben M., Weber H. B. Nat. Nanotechnol. 2013;8:575–579. doi: 10.1038/nnano.2013.133. [DOI] [PubMed] [Google Scholar]
- Vincent R., Klyatskaya S., Ruben M., Wernsdorfer W., Balestro F. Nature. 2012;488:357–360. doi: 10.1038/nature11341. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.