A multi-enzyme model for pyrosequencing

Abstract

Pyrosequencing is a DNA sequencing technique based on sequencing-by-synthesis enabling rapid real-time sequence determination. This technique employs four enzymatic reactions in a single tube to monitor DNA synthesis. Nucleotides are added iteratively to the reaction and in case of incorporation, pyrophosphate (PPi) is released. PPi triggers a series of reactions resulting in production of light, which is proportional to the amount of DNA and number of incorporated nucleotides. Generated light is detected and recorded by a detector system in the form of a peak signal, which reflects the activity of all four enzymes in the reaction. We have developed simulations to model the kinetics of the enzymes. These simulations provide a full model for the Pyrosequencing four-enzyme system, based on which the peak height and shape can be predicted depending on the concentrations of enzymes and substrates. Simulation results are shown to be compatible with experimental data. Based on these simulations, the rate-limiting steps in the chain can be determined, and K_M and k_cat of all four enzymes in Pyrosequencing can be calculated.

INTRODUCTION

Most of the DNA sequencing work performed thus far has employed the Sanger DNA sequencing technique originally developed 27 years ago. Although, this technique has gone through major technical developments to reduce the cost and increase the speed by three orders of magnitude, it faces limitations for future applications. Both cost and speed of DNA sequencing need to be reduced at least by another three to four orders of magnitude, which is unlikely to be performed with Sanger DNA sequencing due to difficulty of miniaturizing the steps involved in this technique. Therefore, several new techniques have been proposed. These include sequencing-by-hybridization (1–3), massively parallel bead arrays (4), single molecule detection techniques [such as GeneEngine Technology (www.usgenomics.com) molecular resonance sequencing (www.mobius.com), enzyme-dependent FRET for single-molecule DNA sequencing (www.visigenbio.com)], single-molecule nanopore sequencing (5), and sequencing-by-synthesis such as polony sequencing (6), Single Molecule Arrays (www.solexa.com) and Pyrosequencing (7,8). Among all the mentioned techniques, only Pyrosequencing and Sanger sequencing have been used for de novo sequencing. Pyrosequencing is more amenable to miniaturization and integration with upstream procedures into a single chip where hundreds of thousands of sequencing reactions could be performed in parallel.

Pyrosequencing is a real-time method catalyzed by four kinetically well-balanced enzymes: DNA polymerase, ATP sulfurylase, firefly luciferase and apyrase. Each nucleotide is provided and tested individually for its incorporation into the DNA template. Each nucleotide incorporation event is accompanied by release of inorganic pyrophosphate (PPi) in a quantity equimolar to the number of incorporated nucleotides. Release of PPi triggers the ATP sulfurylase reaction resulting in a quantitative conversion of PPi to ATP. ATP is readily sensed by firefly luciferase producing light, which is proportional to the amount of DNA and number of incorporated nucleotides. Nucleotides, including unreacted dNTP and the generated ATP are degraded by apyrase allowing iterative addition of dNTP to the solution. The overall reactions involved are depicted graphically in Figure 1. The detailed enzymatic reactions from incorporation of dNTP into DNA to light production can be presented by the equation set shown in Scheme 1.

Figure 1.

The general principle of the Pyrosequencing reaction system.

Scheme 1. Pyrosequencing enzymatic reactions.

The activity of all four enzymes can be directly studied in real-time, providing a detailed picture of the kinetics of the enzymes involved in generating a Pyrosequencing peak. The light generated from the reactions is directly proportional to the number of incorporated nucleotides, so the raw data can represent a very accurate and quantitative signal. This feature has enabled quantitative DNA sequencing, which is now being used for different applications including CpG island sequencing (9), sequencing of multiple co-infected viruses in a sample (10), sequencing of heteroplasmic DNA (11), etc. Pyrosequencing has gone through major technical developments (7,12–15) to become a versatile technique for different applications, most notably, analysis for single nucleotide polymorphisms (16), tag sequencing (17), microbial typing (18), sequencing of difficult secondary DNA structures (19) and gene re-sequencing (20).

The first step towards miniaturization of Pyrosequencing is to understand the detailed reaction–diffusion kinetics of the enzymes involved in this system. Such a reaction–diffusion model could be used to optimize the geometry and timescales of a miniaturized DNA sequencing system. In this paper, simulation results are presented based on reaction kinetics for the four enzymes involved in Pyrosequencing. These simulations combine kinetic models for each of the enzymes and can predict the rate of photon generation for different enzyme combinations. We have applied the simulations to do a detailed analysis of the Pyrosequencing chemistry. These simulations provide a better understanding of the limiting factors in the system, which is useful for optimizing the concentrations of enzymes and substrates for longer read lengths and for verifying the completion of nucleotide incorporation, both of which are essential for extending the usefulness of the Pyrosequencing technique (21). Furthermore, addition of diffusion models to the kinetic equations would allow the simulation of chip-based formats for Pyrosequencing to investigate effects of DNA immobilization on light generation and to compare various architectures in terms of nucleotide delivery and light-spreading effects. Although, we are only discussing models based on the Pyrosequencing enzyme system, similar analytical techniques might be applied to any multi-enzyme system.

In this paper, a brief overview of the Pyrosequencing chemistry is given, which provides a description and model for the activity of each of the enzymes. In order to demonstrate the validity and accuracy of computer simulations based on these models, experiments are performed with various combinations of enzymes. For each of these experiments, the peak shapes of the output light intensity are compared to the ones given by simulations. We also discuss the shape of the Pyrosequencing signal and the effects of various enzymatic parameters on it. Furthermore, calculations are presented for the extraction of values of K_M and k_cat for each of the four enzymes from the simulations to facilitate a comparison with previous literature results.

MATERIALS AND METHODS

Pyrosequencing

Pyrosequencing is performed in a volume of 50 μl on an automated PSQ96MA system (www.pyrosequencing.com). The needed ingredients such as the substrates and enzymes are loaded into a few wells in a standard 96-well plate, and reactions are set off by dispensation of an initiating material from the cartridge. For experiments involving polymerase and DNA, dNTP is dispensed, for luciferase reactions ATP is dispensed, and for luciferase/sulfurylase mixtures, either ATP or PPi are used to initiate the reactions. The Pyrosequencing software records the light signal corresponding to each of the wells in the 96-well format, and saves the data graphically.

Synthesis and purification of oligonucleotides

Romo-loop DNA 5′-TTTTTTTTTTTTTTTTTTTTGCTGGAATTCGTCAGACTGGCCGTCGTT-TTACAACGGAACGTTGTAAAACGACGG was synthesized and HPLC purified by Operon (www.operon.com). The downstream sequence of the underlined base (A) hybridizes with the region between the bold and the underlined base, forming a loop with a single-ended tail. The 3′ end of the downstream sequence has a free OH group allowing extension by DNA polymerase. The bold sequence acts as the template and is sequenced in Pyrosequencing.

Dispensed material: ATP, dNTP and PPi

A 50 μM solution of pyrophosphate was prepared and 100 μl was added to the cartridge for dispensation. ATP (100 mM) was diluted to 10 μM, and 100 μl was added to the cartridge for dispensation into the luciferase and luciferase/sulfurylase enzyme combinations. These values are chosen to be relatively high since only 0.2 μl of the substance in the cartridge is dispensed into the 50 μl solution. Therefore, the actual concentrations in the solution are a factor of 250 less. The final concentrations of ATP and PPi in the solution become 0.04 and 0.2 mM, respectively.

Enzyme and substrate concentrations

To test the efficiency and linearity of pyrophosphate to ATP conversion, different concentrations of luciferase were used. A 14.7 μg/μl solution of luciferase is diluted to concentrations of 100 ng, 500 ng, 1 μg, 5 μg, 20 μg and 100 μg for the experiments: 25 mU of apyrase and 65 mU of sulfurylase were added to each sample for corresponding experiments.

Computer simulations

Simulations are performed using MATLAB Version 6 (from Mathworks) and Virtual Cell (www.nrcam.uchc.edu) (22). These programs can solve differential equations for reaction kinetics. These equations provide reaction rates in terms of the forward and reverse reaction constants as well as concentrations of the chemical species involved. For instance, for a simple reaction shown in Scheme 2, the reaction rate differential equation is

Scheme 2. Simple reaction with forward and reverse constants.

where [A], [B] and [AB] represents concentration of A, B and AB respectively, k_f and k_r are forward and reverse reaction constants, and d[AB]/dt is the rate of product release.

In a similar fashion, the reaction rate can be written for the case of a typical enzymatic reaction shown in Scheme 3. In this scheme, S represents the substrate, E is the enzyme, ES is the enzyme–substrate complex and P is the product. For this reaction, the rates are

Scheme 3. Simple enzymatic reaction.

and rate of product release is

By solving the coupled equations consisting of these four differential equations in time, one can find the concentration of all species involved in the reactions up to any given point in time. These coupled differential equations can be solved by various techniques. In the simplest method (called Euler method), a specific time step (Δt) is chosen. Then the four continuous-time equations are converted to their discrete-time equivalents, as shown for the first reaction for example:

where the (n+1) indices indicate concentration values at time (n+1)Δt, and n indices indicate concentrations at time nΔt. Using a set of these equations, and given values at nΔt, it is possible to calculate the concentration values at (n+1)Δt. If Δt is taken sufficiently small, the solution to discrete-time equations is similar to continuous-time solutions. More complex numerical methods can dramatically improve the efficiency of the solution, compared to using Euler's method (23).

For each enzyme in Pyrosequencing, either an appropriate model taken from the literature has been adopted, or a simple model based on a general enzymatic reaction is picked when no relevant model was found in the literature. Based on these models, the kinetic differential equations can be written for each enzyme as shown above. These differential equations are then solved by solvers like MATLAB or Virtual Cell to determine the change in concentrations over time.

Enzyme models

As discussed in previous sections, the Pyrosequencing signal represents the activity of four coupled enzymatic reactions, which produce a light signal when a nucleotide is incorporated into the DNA strand. The activity of each enzyme needs to be modeled separately, and then combined to give a model for the entire Pyrosequencing system. Simulation of a multiple enzyme system is a challenging task because (i) detailed kinetic data for most of the enzymes are not available in the literature, (ii) the cooperation, competition or any other enzyme interactions need to be considered and (iii) kinetics of different enzymes very sensitive to reaction conditions. Detailed kinetics of Klenow fragment of DNA polymerase I (24) and firefly luciferase (25) are found in the literature. Different kinetic models were tried for sulfurylase and apyrase, which are both based on the simple single-substrate model. The enzyme models are based on physical models and are not merely based on mathematical fits. The models are composed of a sequence of steps representing meaningful physical or chemical transformations in the enzyme activity. We have assumed throughout this study that these models are fixed since they represent the actual physical or chemical changes. Only the parameters in these models are tweakedwhere necessary to match simulations with experimental data and to get an acceptable prediction of the details of these reactions. These parameters are assumed to be variable due to temperature or solution characteristics. Having detailed kinetics for polymerase and luciferase and partial data for sulfurylase (26) and apyrase (27), we simulated the full Pyrosequencing reaction system. In the rest of this section, the model for each of the enzymes is presented in detail.

Kinetic model for Klenow fragment DNA polymerase

For Klenow fragment (KF) DNA polymerase, a detailed kinetic model has been proposed (24). The model is shown in Scheme 4, and reaction coefficients are given in Table 1. The first step in the reaction is binding of KF polymerase to DNA, which is followed by trapping of dNTP by the complex. Subsequent to formation of the complex, polymerase goes through a conformation change, specified as conversion of polymerase to polymerase′ in the reactions. This step is not actually a chemical reaction, but is included to model the time delay associated with the physical transformation of the polymerase molecule. Nucleotide is then incorporated into the DNA and PPi is produced but is still contained in the complex. In the next steps, PPi is released after another conformational change in polymerase, and finally polymerase–DNA binding is broken, so that polymerase can go through a similar cycle with another DNA molecule.

Scheme 4. Detailed kinetic model of Klenow DNA polymerase.

Table 1. Rates for kinetic mechanism of Klenow fragment polymerase.

Reaction	Forward and reverse constants
polymerase + DNAn ⇄ polymerase·DNAn	k1DNA = 1.2 × 107 M−1 s−1
	k−1DNA = 0.06 s−1
polymerase·DNAn + dNTP ⇄ polymerase·DNAn·dNTP	k1dNTP = 1 × 107 M−1 s−1
	k−1dNTP = 50 s−1
polymerase·DNAn·dNTP ⇄ polymerase′·DNAn·dNTP	k3 = 50 s−1
	k−3 = 3 s−1
polymerase′·DNAn·dNTP ⇄ polymerase′·DNAn+1.PPi	k4 = 150 s−1
	k−4 = 37.5 s−1
polymerase′·DNAn+1·PPi ⇄ polymerase·DNAn+1.PPi	k5 = 15 s−1
	k−5 = 15 s−1
polymerase·DNAn+1·PPi ⇄ polymerase·DNAn+1 + PPi	k1PPi = 1150 s−1
	k−1PPi = 5 × 106 M−1 s−1
polymerase·DNAn+1 ⇄ polymerase + DNAn+1	k1DNA = 1.2 × 107 M−1 s−1
	k−1DNA = 0.06 s−1

For such enzymatic reactions, the rates of consumption of the substrates, production of the intermediate complexes and release of products are described mathematically as

In these equations DNA_n is the DNA molecule with the length n, and DNA_n+1 is the same DNA, which has been extended by one nucleotide. Note that these equations are only for a single step of incorporation, i.e. extending DNA once. In order to simulate two or more nucleotide incorporations, the system of differential equations shown above needs to be solved sequentially, which start with DNA_n+1 and go through similar complex structures (but with DNA_n+1 replaced by DNA_n). In this case, the output product would be DNA_n+2.

These equations can be converted to discrete-time models and solved in time to find the rate of PPi release given the initial concentrations of DNA, polymerase and dNTP.

Furthermore, these equations can predict how much of DNA is not extended in a given time. This feature is specifically useful for Pyrosequencing, since complete extension is needed in each step of nucleotide addition because non-synchronized extension causes erroneous Pyrosequencing signals, and limits read length.

Kinetic model for ATP sulfurylase

No detailed kinetic model was found for ATP sulfurylase from yeast. Therefore, we used a simple enzyme–substrate model with one intermediate step. The model is given in Scheme 5, and constants are given in Table 2. According to this model, PPi first binds to ATP sulfurylase forming the sulfurylase·PPi complex, followed by conversion of PPi to ATP, and release of ATP and ATP sulfurylase. Forward reaction constants are chosen based on the values of K_M and k_cat for the enzyme taken from (26). The reverse reaction constants are chosen to provide a better matching between the simulated results and experiments. It was found that a considerable reverse reaction rate is necessary to obtain a decent match to experiments with the luciferase/sulfurylase enzyme combination while dispensing ATP. It was observed that by adding ATP to the mixture, ATP (and hence the light signal) decayed faster than predicted merely by luciferase activity, indicating that the sulfurylase reverse path is consuming ATP as well as producing PPi. This has also been shown in the earlier literature (28).

Scheme 5. Proposed kinetic model for sulfurylase.

Table 2. Rates for kinetic mechanism of ATP-sulfurylase.

Reaction	Forward and reverse constants
sulfurylase + PPi ⇄ sulfurylase·PPi	k1sulfurylase = 5.5 × 106 M−1 s−1
	k−1sulfurylase = 11.94 s−1
sulfurylase·PPi ⇄ sulfurylase + ATP	k2sulfurylase = 30.76 s−1
	k−2sulfurylase = 2.5 × 107 M−1 s−1

The set of differential equations for ATP–sulfurylase reaction model are given as

Kinetic model for firefly luciferase

Luciferase activity has been modeled in detail in (25). The chain reactions are presented in Scheme 6, which depicts different steps of the reaction. According to this model, luciferase can go through two paths depending on which substrate binds to it first. As will be further clarified in the discussion section, the luciferase–luciferin binding path is dominant because the concentration of luciferin is much higher than that of ATP. Also, the forward reaction constant is higher for binding of luciferase and luciferin than for luciferase and ATP. Furthermore, in Pyrosequencing reactions, ATP is released after dNTP is dispensed, while luciferin is already in the mixture and can bind to luciferase first. In the next step, the two possible complexes (luciferase·ATP and luciferase·luciferin) bind to the other substrate to form the luciferase·ATP·luciferin complex, where the two parallel paths converge. This complex is then decomposed to release PPi and luciferyladenylate. This reaction only proceeds in the forward direction according to (25). Subsequently, AMP, light photons (hν) and luciferase·hydroxyluciferin complex are generated. This complex then dissociates to luciferase and hydroxyluciferin. Furthermore, a degradation mechanism is included in Brovko et al. model (25) to account for degradation of the luciferase complexes. The degradation rates are considered to be similar for luciferase, luciferase·ATP, luciferase·luciferin and luciferase·ATP·luciferin, while it is considered different for the luciferase·hydroxyluciferin complex.

Scheme 6. Detailed kinetic model of firefly luciferase.

Reaction constants for luciferase activity are given in Table 3. The forward and reverse constants for each of these steps are taken from (25), but have been slightly modified to provide a better match with Pyrosequencing experimental data. These modifications are justified based on the difference between the Pyrosequencing conditions and the experimental conditions under which these models were developed. The most significant changes were in values of k₁^luc, k₂^luc and k₃^luc. The specified ranges for these variables in (25) were 2 ± 1 × 10⁴ M⁻¹ s⁻¹, 30 ± 10 s⁻¹ and 10 ± 3 s⁻¹, respectively, whereas the best fit in this work was found to be with values of 4.32 × 10⁴ M⁻¹ s⁻¹, 19.2 s⁻¹ and 0.96 s⁻¹. Discrepancies may be due to variations in the luciferase source age of use or variations in the solution such as pH.

Table 3. Rates for kinetic mechanism of firefly luciferase.

Reaction	Forward and reverse constants
luciferase + ATP ⇄ luciferase·ATP	k1luc = 4.32 × 104 M−1 s−1
	k−1luc = 3.5 s−1
luciferase·luciferin + ATP ⇄ luciferase·ATP·luciferin
luciferase + luciferin ⇄ luciferase·luciferin	k1′luc = 1 × 106 M−1 s−1
	k′luc−1 = 10 s−1
luciferase.ATP + luciferin ⇄ luciferase·ATP·luciferin
luciferase·ATP·luciferin ⇄ luciferyladenylate + PPi	k2luc = 19.2 s−1
	k−2luc = 0 M−1 s−1
luciferyladenylate ⇄ luciferase·hydroxyluciferin + AMP + hν	k3luc = 0.96 s−1
	k−3luc = 0 M−2 s−1
luciferase·hydroxyluciferin ⇄ luciferase + hydroxyluciferin	k4luc = 0.1 s−1
	k−4luc = 1 × 106 M−1 s−1
luciferase ⇄ luciferaseinact	k5luc = 2.6 × 10−5 s−1
luciferase·ATP ⇄ luciferase·ATPinact	k−5luc = 0 s−1
luciferase·luciferin ⇄ luciferase·luciferininact
luciferase·ATP·luciferin ⇄ luciferase·ATP·luciferininact
luciferase·hydroxyluciferin ⇄ luciferase·hydroxyluciferininact	k6luc = 3.0 × 10−4 s−1
	k−6luc = 0 s−1

Differential equations based on this model can be described as

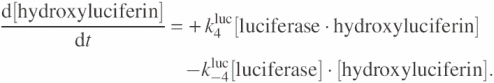
These differential equations demonstrate how ATP is converted to a light signal. The light signal is treated in the equations like a chemical species, i.e. in the form of a concentration. In order to get the actual count of generated photons, we multiply the rate of change by the time step (Δt), by the reaction volume (50 μl), and by Avogadro's number (6 × 10²³).

Kinetic model for apyrase

To our knowledge, no detailed kinetic data is available for apyrase from potato. This enzyme degrades most naturally occurring nucleotides including dNTP and ATP (however, with different efficiencies) (29). In the Pyrosequencing reaction system, the efficiency of degradation is monitored by following the decrease in light intensity as a result of ATP degradation. This enzyme has dramatically simplified the use of commercial Pyrosequencing technology since it degrades excess nucleotide enabling iterative addition of nucleotides without adding new enzymes and substrates to the system. For apyrase, a model based on the simple enzyme–substrate interaction model is used. ATP degradation reactions include formation of apyrase·ATP complex, enzymatic reaction of apyrase on captured ATP, release of byproducts such as AMP and Pi molecules, and release of apyrase back into the solution. Reaction of apyrase with dNTP is modeled with two simple steps: capture of dNTP by apyrase followed by formation of apyrase·dNTP complex, and dissociation of the complex to apyrase and dNDP. Simulations demonstrated that these simple models provide sufficient accuracy for modeling the enzymatic activity of apyrase.

Reaction models are summarized in Scheme 7, and the corresponding constants are given in Table 4. Note that reaction rates are chosen based on the values of K_M and k_cat from the literature (27). This is clarified in more detail in the upcoming sections.

Scheme 7. Proposed kinetic model for apyrase for (a) ATP (b) dNTP.

Table 4. Rates for kinetic mechanism of apyrase.

Reaction	Forward and reverse constants
apyrase + ATP ⇄ apyrase·ATP	k1apyrase_ATP = 8.75 × 106 M−1 s−1
	k−1apyrase_ATP = 3600 s−1
apyrase·ATP ⇄ apyrase·AMP·2Pi	k2apyrase_ATP = 4800 s−1
	k−2apyrase_ATP = 50 s−1
apyrase·AMP·2Pi ⇄ apyrase + AMP + 2Pi	k3apyrase_ATP = 600 s−1
	k−3apyrase_ATP = 0 M−3 s−1
apyrase + dNTP ⇄ apyrase·dNTP	k1apyrase_dNTP = 3.33 × 106 M−1 s−1
	k−1apyrase_dNTP = 0 s−1
apyrase·dNTP ⇄ apyrase + dNDP	k2apyrase_dNTP = 400 s−1
	k−2apyrase_dNTP = 0 M−1 s−1

The model for apyrase activity on ATP is formulated by the following equations:

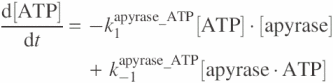
and for apyrase–dNTP reaction models are as

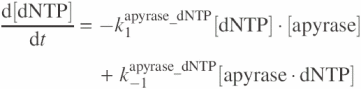
Combining Pyrosequencing enzyme models

The differential equations presented above model the four enzymes involved in standard Pyrosequencing. These models are now combined to represent a general model for Pyrosequencing. In combining the differential equations, if a chemical species is involved in more than one independent reaction, the right side of the differential equations determining the rate for that species are added together. For instance, since ATP is a substrate for both luciferase and apyrase and a product of ATP sulfurylase, the differential equations for the rate of change of ATP concentration due to activity of these three enzymes are combined by adding the corresponding equations for ATP as follows:

Modeling of the detection system

The other feature included in the simulations is a model for the detection system. The CCD camera used in the PSQ96MA system has a constant integration time of 1 s. This is taken into account in the simulations by adding up the photons generated in the reactions during each one second period. Furthermore, the start of the integration is not synchronized with the dispensation of the reaction initiator from the cartridge. This causes a time shift in the curve depending on when the dispensation (start of the reaction) actually takes place with respect to the start of the one second integration period of the CCD camera. This affects the light signal at the first integration point. This effect is modeled in the simulations by a variable offset indicating the time of the first integration with respect to the starting point of the reactions. This number, which has a value between zero and one, is synchronized with the corresponding experiment to provide a more meaningful comparison to the experimental time-to-peak value.

Calculation of enzyme K_M and k_cat in the Pyrosequencing system

As mentioned earlier, forward and reverse reaction constants for ATP sulfurylase and apyrase were chosen based on the literature values for K_M and k_cat. In order to check validity of the kinetics used for these enzymes as well as polymerase and luciferase, we extracted K_M and k_cat from the simulations. For a simple enzyme model as in Scheme 3, with k₋₂ = 0, K_M and k_cat can be directly calculated as

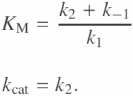
But for a complicated system as for some of the models presented in this paper, K_M and k_cat cannot be easily calculated, and have to be extracted from simulations. The procedure for extraction of K_M and k_cat from simulations is based on the definitions of these entities. Another relevant constant for each enzyme is v_max, which is defined as the saturated initial velocity of the reaction. As substrate concentration is increased, the initial velocity of the reaction saturates at a rate, which is v_max. In order to get to this saturation point, the amount of substrate needs to be increased substantially compared to the enzyme concentration. k_cat is obtained directly from v_max as follows:

where [E] is the concentration of the enzyme, and k_cat is in units of 1/s. K_M is also defined in terms of v_max. It is the substrate concentration which gives a reaction rate equal to half of v_max.

An important note here is that in order to measure v_max, K_M and k_cat in steady state. The reaction initially does not have a single rate since the rate of consumption of substrate is larger than the rate of release of the product. Initially, the intermediate substrate–enzyme complexes are at zero concentration so the reverse reactions are not taking place and all reactions are proceeding in the forward direction. It takes a while for all the intermediate complexes to reach steady state, where the rates of all reaction steps become equal. The maximum reaction rate (v_max) needs to be taken in this steady-state condition.

Effect of mixing on Pyrosequencing

One of the features of the PSQ96MA machine is that it allows choosing the shaking frequency of the plate. This frequency can be set to 0, or varied from 20 to 35 r.p.m.. Experiments were done with the same reaction mixture at various mixing speeds to look into the effect of mixing on the Pyrosequencing signal.

RESULTS

To validate the models presented for the enzymes, experiments were performed with various combinations of enzymes in the PSQ96MA machine. The light signals produced in experiments were then compared to the corresponding signals from simulations.

These enzyme combinations and the comparison of simulation and experimental data for each subset of the Pyrosequencing enzymes are presented in this section. Since the detection system senses the light signal, and luciferase is the enzyme producing photons, all enzyme combinations must obviously contain luciferase.

Luciferase

To investigate luciferase reactions in the Pyrosequencing buffer system, only luciferase was added to the substrate mixture (obtained from Pyrosequencing) in a well, and reaction was initiated by dispensing ATP. The simulated curve is shown compared to the experimental signal from the PSQ96MA machine in Figure 2(a). These curves are obtained for the case of 20 μg of luciferase and with an initial ATP concentration of 4 × 10⁻⁸ M. The symbols on the simulation curve are the integration points, which are spaced 1 s apart. These points have been connected by straight lines. Although, the experimental trace is similarly piecewise linear, this is not obvious from the curve due to resolution limitations of the digitization process.

Figure 2.

Simulation versus experimental peak curves for (a) luciferase initiated by ATP dispensation, (b) luciferase/apyrase enzyme combination initiated by ATP dispensation, (c) luciferase/sulfurylase enzyme combination activity initiated by ATP dispensation, (d) luciferase/sulfurylase/apyrase enzyme combination initiated by ATP dispensation, (e) luciferase/sulfurylase/apyrase enzyme combination initiated by PPi dispensation. All cases are with 20 μg of luciferase. The variations in experimental peak heights are within ±5%.

As seen in Figure 2(a), simulation and experimental results match quite well in terms of time-to-peak and decay, after fine-tuning some of the reaction constants. The peak heights in simulations are scaled to match the experimental data. The need for scaling arises from the fact that experimental peak heights in the PSQ software are specified in terms of an arbitrary unit, while the simulation peaks are in actual photons/s. In order to be able to do a direct comparison, the simulation results need to be scaled by a constant factor. This factor specifies the arbitrary unit of the PSQ96MA system in terms of real number of photons/s produced in the reactions. By matching the simulation peak to the experimental peak in the luciferase experiments, a value of 1.2 × 10⁸ is obtained, which is used for scaling all the other combinations of enzymes as well.

Peak heights versus luciferase concentration for both simulation and experiment are shown in Figure 3(a). The peak is an almost linear function of the luciferase concentration. However, the peak heights are predicted to saturate after a threshold luciferase concentration. As can be seen in Figure 3(a), peak intensities for various luciferase concentrations match very well with values from simulations. Up to 20 μg of luciferase is in the valid range of the model used for luciferase. At higher concentrations, some non-linear kinetics might govern the chemistry.

Figure 3.

Simulation and experimental results for peak height versus amount of luciferase in (ng) for (a) luciferase, (b) luciferase/apyrase, (c) luciferase/sulfurylase, (d) luciferase/sulfurylase/apyrase (ATP and PPi dispensation).

Luciferase + apyrase

Apyrase is the degrading enzyme for ATP and dNTP. In presence of apyrase, the light signal fades away faster compared to the previous case since both enzymes compete for ATP, which causes its faster depletion. This also results in the peak height being smaller compared to the similar case without apyrase. The simulated curve and the actual curve from dispensation of ATP into the solution are given in Figure 2(b). Clearly, addition of apyrase to the mixture decreases the peak height considerably, i.e. from ∼1400 to ∼800 units for 20 μg of luciferase. In Figure 3(b), peak height versus luciferase concentration for both simulation and experiment are shown.

Luciferase + sulfurylase

A combination of luciferase and sulfurylase can use two substrates (ATP or PPi) to produce light. The reactions are also coupled in the sense that luciferase converts ATP to PPi, and sulfurylase converts PPi back to ATP forming a loop, which results in production of a constant light signal (30). Very small degradation of the light signal is observed in the absence of apyrase. The simulation versus experimental results are depicted in Figure 2(c). For this case, ATP was dispensed. However, PPi could be dispensed producing similar results. A constant light signal is obtained in the simulations, while in experiments the light decays slowly over time. We speculate that this is due to consumption of APS, which has not been captured by the models for the kinetic activity of luciferase in the simulations. Simulations successfully capture the initial light peak before reaching the constant plateau. This initial peak is caused by dispensing a large amount of ATP, so that not only luciferase but also sulfurylase consumes ATP and converts it to PPi. This continues until ATP is depleted and the light intensity starts to decrease. At some point, after ATP has been depleted enough, sulfurylase starts to convert PPi to ATP and the coupled loop reactions begin. Peak heights are given in Figure 3(c) versus luciferase concentrations for both simulation and experiment.

Luciferase + sulfurylase + apyrase

For this mixture, reactions are triggered by dispensation of PPi or ATP. The light signal is expected to fade away over time due to the degrading functionality of apyrase. Figure 2 (d and e) shows the simulation and experimental peaks for dispensing ATP and PPi, respectively. For these cases, 20 μg of luciferase, and 65 and 25 mU of sulfurylase and apyrase have been used, respectively. As can be seen in Figure 2 (d and e), matching is relatively good for ATP dispensation case in terms of peak height, time-to-peak and the decay, whereas the decay is not as good for the case of PPi dispensation. This might be due to the fact that luciferase and sulfurylase models do well are accurate for the dispensed concentration of ATP, whereas the simple model used for sulfurylase is not sufficiently accurate when large amounts of PPi is present in the solution. Peak heights versus luciferase concentration for simulation and experiment are given in Figure 3(d), and demonstrate good matching.

In other experiments, the linearity of the peak intensity to ATP concentration has been investigated. It is expected that the product release changes linearly with the concentration of the input species. This was demonstrated to be true for simulation and experiment (data not shown).

Luciferase + sulfurylase + polymerase + apyrase

The entire Pyrosequencing enzyme system can be modeled by combining the models for all four enzymes. For this case, dNTP is dispensed into the mixture, leading to production of light by going through the entire enzymatic chain. Simulation and experimental results are shown in Figure 4(a) for the Pyrosequencing peak. As can be seen, peak height, time-to-peak and decay of the light signal match very well between simulations and experiments. It is interesting that although matching of the simulation and experimental data is not as good for the luciferase/sulfurylase/apyrase case when dispensing PPi, simulations become more accurate when polymerase models are added to the system. This is due to the fact that in the latter case, PPi is being generated by polymerase activity, and its rate of production is far slower compared to the case when a large concentration of PPi is directly dispensed into the well. This implies that for the Pyrosequencing regime of operation (in terms of PPi release) the sulfurylase models are sufficiently accurate. The linearity of the light signal to the amount to DNA is shown in Figure 4(b) for both simulation and experiment. This linearity is valid for up to 5 pmol of DNA. For higher amounts of DNA, the peak heights start deviating from a linear correlation (data not shown.) The linearity at higher amounts of DNA might be affected by a saturating effect, which can be captured in the models by the effect of insufficient dNTP to react with DNA.

Figure 4.

(a) Simulation versus experimental peak curve for polymerase/luciferase/sulfurylase/apyrase enzyme combination activity initiated by dNTP dispensation. (b) Peak height in arbitrary units versus DNA concentration in (pmol) for Pyrosequencing enzyme combination; simulation versus experimental data. The variations in experimental peak heights are within ±5%.

One interesting measurement is calculation of time-to-peak of the photon intensity for various enzyme combinations. This data is provided in Table 5. More time is needed in cases where more enzymatic steps are taken for conversion of the dispensed material to photons. Time-to-peak of the luciferase/apyrase combination is the least, whereas when dNTP is dispensed and all four enzymes in Pyrosequencing are involved, the time-to-peak is maximum.

Table 5. Time-to-peak of the photon intensity for various enzyme combinations.

Enzyme combination	Time-to-peak (s)
luciferase, apyrase	1.0
sulfurylase, luciferase, apyrase	3.3
polymerase, sulfurylase, luciferase, apyrase	4.1

Extraction of K_M and k_cat from simulations

Table 6 summarizes the calculated values of K_M, and k_cat from simulations for polymerase, sulfurylase, luciferase and apyrase, along with the literature values. For sulfurylase and apyrase, the forward and reverse constants are chosen based on the known values of K_M and k_cat from equations given in the Materials and Methods section. The literature values of K_M and k_cat for exonuclease-deficient Klenow fragment Polymerase are taken from (31). For luciferase, the constants needed some modifications to match the experimental results, as explained. Therefore, the values of K_M and k_cat are somewhat different from the literature values. We attribute this to dependence of enzyme activity to age of use, source of the enzymes and solution characteristics such as pH.

Table 6. Literature and calculated values of K_M and k_cat for Pyrosequencing enzymes.

Enzyme	Literature KM (μM)	Literature kcat (s−1)	Calculated KM (μM)	Calculated kcat (s−1)
Klenow-DNA polymerase	3.3–6.5	0.006–0.3	3.35	0.1
ATP-sulfurylase	7	38	7.7 (PPi)	30.76
Firefly luciferase	20	0.015	3	0.06
Apyrase	120	500	110 (ATP)	515

Mixing effect

Experiments with various shaking speeds indicated that, in order for the reactions to go to completion, allowing iterative nucleotide additions, the well contents need to be shaken to provide effective mixing of the ingredients. Experiments indicate that without efficient mixing, Pyrosequencing reactions do not proceed effectively, and complete extension of all DNA molecules, which is essential for Pyrosequencing, does not take place. This causes multiple light peaks for repeated dispensation of the same nucleotide. This clearly indicates a non-synchronized extension for each of the dispensation steps. Varying the shaking frequency between 20 and 50 r.p.m. did not seem to have a significant effect on peak heights implying that all these speeds provide effective mixing of ingredients.

DISCUSSION

Pyrosequencing represents a complex enzyme system due to presence of chain reactions and competing reactions in the system. In order to have a better understanding of the kinetics of the Pyrosequencing reaction system, a few more analytical simulations with all enzyme models are performed. Based on these simulations, the bottlenecks in the entire process with the four enzymatic reactions are found. Also, the effects of various enzymes on the shape of the Pyrosequencing signal were investigated. In addition, the effect of mixing is further discussed.

Bottlenecks in the enzyme chain reactions

A feature of the calibrated simulations is the ability to analyze the reactions in more detail and to find which of the enzymes are most important in determining characteristics such as peak height, time-to-peak or the decay rate. Furthermore, we can find out the dominant paths and bottlenecks for each of the enzymes as well as for the entire enzymatic chain involved in Pyrosequencing. This means that some of the reaction steps play a more important role in determining the overall speed of the Pyrosequencing reactions in general. In order to find these rate-limiting steps, we changed the forward reaction constants by ±20%. Then, we observed how this change translated to a change in the product release rate.

Based on these simulations, we could determine the bottleneck steps determining the conversion rate for each of the four enzymes. The bottleneck in polymerase activity is the first step, i.e. binding of DNA and polymerase. The ±20% changes in the forward reaction constants for this step produces the most significant change in the rate of PPi release. For sulfurylase, the first reaction in the chain, i.e. binding of sulfurylase and ATP dominates. For luciferase, there are two steps which are the slowest steps determining the overall reaction rate. These two steps are binding of luciferase to ATP and conversion of luciferyladenylate into luciferase·hydroxyluciferin, AMP and light. It is also observed that of the two paths involving binding of luciferase to either ATP or luciferin, the former is the dominant path, i.e. changing the rates of the luciferase–luciferin binding path would not affect the output considerably. For apyrase, the change in AMP release is affected the most by binding of apyrase to ATP and transformation of apyrase·ATP to apyrase·AMP·2Pi complex.

We then varied the most important rates for each of the four enzymes, which were found from the previous set of simulations and examined the corresponding changes in the shape of the Pyrosequencing peak. This enables us to conclude, which enzymes are most important in determining the shape of the peak, as shown in Table 7. The major changes, which represent limiting steps, are shown in bold characters in the table. The most important factors determining the rate of production of photons (d[Photon]/dt) are the bottleneck steps involving luciferase and sulfurylase. A change in the ATP/luciferase binding by ±20%, causes almost a similar change in the photon production rate. The effect of binding of sulfurylase to PPi is somewhat less. The peak height is mostly affected by the same two steps as well. The Apyrase–ATP binding step is also found to be of importance. Time-to-peak is affected by the first steps of sulfurylase and apyrase activity, as well as the photon production step of the luciferase reactions. Further, it can be concluded that polymerization is not the bottleneck in the Pyrosequencing reaction.

Table 7. Change in rate of photon production, peak height and time-to-peak of the photon intensity by changing effective rates for each of the four enzymes by ±20%.

Enzyme	Change	Change in d[photon]/dt (%)	Change in peak height (%)	Change in time-to-peak (%)
	Normal	0.00	0.00	0.00
Polymerase	k5 * 1.2	0.17	0.02	−0.36
Polymerase	k5 * 0.8	−0.32	−0.03	0.55
Polymerase	k1DNA * 1.2	3.61	0.49	−2.40
Polymerase	k1DNA * 0.8	−5.13	−0.90	3.65
Polymerase	k1dNTP * 1.2	0.56	0.08	−0.62
Polymerase	k1dNTP * 0.8	−0.96	−0.15	0.96
Sulfurylase	k1sulfurylase * 1.2	15.39	11.51	−4.01
Sulfurylase	k1sulfurylase * 0.8	−16.65	−13.31	5.06
Sulfurylase	k2sulfurylase * 1.2	7.75	7.63	−1.01
Sulfurylase	k2sulfurylase * 0.8	−9.74	−9.58	1.46
Luciferase	k1luc * 1.2	19.87	19.83	−0.01
Luciferase	k1luc * 0.8	−19.91	−19.89	0.01
Luciferase	k2luc * 1.2	2.72	2.69	−0.15
Luciferase	k2luc * 0.8	−3.83	−3.78	0.22
Luciferase	k3luc * 1.2	8.60	2.30	−5.36
Luciferase	k3luc * 0.8	−10.55	−3.40	7.57
Apyrase	k1apyrase_ATP * 1.2	−4.83	−8.30	−4.09
Apyrase	k1apyrase_ATP * 0.8	5.37	10.03	5.22
Apyrase	k2apyrase_ATP * 1.2	−2.01	−3.53	−1.76
Apyrase	k2apyrase_ATP * 0.8	2.63	4.80	2.46

Significant changes are specified in bold characters.

In order to find out the effect of enzyme concentration on characteristics of the peak signal, we changed the concentrations of the enzymes by ±20% and investigated the change in photon production rate, peak height and time-to-peak. As seen in Table 8, luciferase concentration affects the photon production rate and peak height almost proportionally, while having no considerable effect on the time-to-peak. Time-to-peak is mostly determined by the apyrase and sulfurylase concentrations. High concentrations of apyrase in the solution decreased the light signal, which is expected due to the degrading activity of apyrase. Significant changes are specified in bold.

Table 8. Change in rate of photon production, peak height and time-to-peak of the photon intensity by changing each of the four enzyme concentrations by ±20%.

Experiment description	Change in d[photon]/dt *(%)	Change in peak height *(%)	Change in time-to-peak *(%)
Normal	0.00	0.00	0.00
[Polymerase] * 1.2	3.83	0.53	−2.52
[Polymerase] * 0.8	−5.54	−1.00	3.92
[Sulfurylase] * 1.2	9.41	4.74	−4.02
[Sulfurylase] * 0.8	−11.49	−6.54	5.46
[Luciferase] * 1.2	19.87	19.84	−0.01
[Luciferase] * 0.8	−19.91	−19.89	0.00
[Apyrase] * 1.2	−5.19	−8.43	−3.91
[Apyrase] * 0.8	5.71	10.15	5.05

Significant changes are specified in bold characters.

Mixing effect

We believe that incomplete extension with low shaking speed is caused by insufficient mixing, which limits the instant reaction of the chemicals resulting in inefficient Pyrosequencing reactions. This is explained by comparing diffusion length of molecules to dimensions of a 50 μl liquid content in the well. Assuming the diffusion constant of a large molecule to be 10⁻⁷ cm²/s, the total distance these molecules travel on average in 60 s is on the order of 0.05 mm, which is much less than dimensions of a 50 μl liquid volume (∼3.5 mm). Thus, these molecules do not have enough time to diffuse to every point inside the well without continuous mixing. By adding proper equations (including hydrostatic and diffusion equations) to the reaction equations described here, the effects of geometry of the reaction volume can be quantitatively modeled. Such a model becomes an important tool for optimizing microwell dimensions and timescales of reactions in a miniaturized Pyrosequencing system.

CONCLUSION

Models for the activity of the enzymes were combined to simulate the Pyrosequencing enzyme system to predict the photon generation and extent of reaction completion based on the concentration of substrates and enzymes involved. Accuracy of the simulations was verified through experiments with different combinations of enzymes. Values of K_M and k_cat for the enzymes were extracted from the models and were shown to be in reasonable agreement with literature values. These simulations provide insight into the bottlenecks of the entire enzymatic chain, and can thus enable optimization of the chemistry, and improvement of the read length. Adding diffusion equations to the model will provide a valuable engineering design aid for scaling down the DNA sequencing system.