Abstract
The study considers the problem of estimating incidence of a non remissible infection (or disease) with possibly differential mortality using data from a(several) cross-sectional prevalence survey(s). Fitting segmented polynomial models is proposed to estimate the incidence as a function of age, using the maximum likelihood method. The approach allows automatic search for optimal position of knots and model selection is performed using the Akaike Information Criterion. The method is applied to simulated data and to estimate HIV incidence among men in Zimbabwe using data from both the NIMH Project Accept (HPTN 043) and Zimbabwe Demographic Health Surveys (2005–2006).
Keywords: Incidence rate, mortality, prevalence, segmented polynomials, maximum likelihood estimation, model selection
1. Introduction
Accurate incidence estimates of chronic infections such as HIV are essential to monitor the epidemic, determine public health priorities and assess impact of interventions. In the case when infections are silent events, estimation of incidence is difficult. The most direct approach is through observational studies, in which subjects are periodically monitored for infection. Another approach consists of converting available prevalence data, i.e. the estimated proportion of infected individuals, into incidence using statistical or mathematical techniques.
The second approach is more popular because, in general, prevalence data are easier to obtain. Several authors have investigated the relationship between prevalence and incidence and derived methods for incidence estimation. Carone et al. [1] discussed incidence estimation from prevalence cohort, Podgor and Leske [2] and Elandt-Johnson and Johnson [3] presented deterministic methods; Gregson et al. [4] proposed to model incidence rate as a continuous function of age, assumed that age specific incidence and infection related mortality remain constant over time and fitted the prevalence predicted by his model to the observed prevalence using the maximum likelihood method. Similar approach was proposed by Ades and Nokes [5] in which the incidence rate was modelled as a function of both time and age. These parametric approaches may suffer from misspecification.
Another approach to estimating the incidence of an infection from prevalence data was presented by Keiding [6]. He used a compartmental model composed of three states: healthy, ill and dead and three corresponding transition rates; the incidence corresponding to the transition rate from healthy to ill. He described these transitions with dependence on age, time and disease duration in the special case of time independence, in which information about the onset of the disease is not given. He thus proposed to estimate the incidence using maximum likelihood estimation and kernel smoothing. However, in some cases, individual data can be hardly obtained and, furthermore, the choice of the optimal bandwidth is commonly encountered.
Brunet and Struchiner [7] have similarly developed a compartment model to derive a general formula expressing the incidence as a function of excess mortality rates and prevalence using data from repeated prevalence surveys. Transition intensities were modeled based on dependence on age and time. They suggested to fit the observed prevalence surface using local polynomial fitting and approximate the incidence using the mean value theorem. Building in similar idea, Mahiane et al. [8] proposed instead to locally approximate the derivative of the prevalence and insert these derivatives into the formula for incidence. However, both approaches assumed that the excess mortality was known. Furthermore, the first procedure faced the common problem of choosing the position of knots which may be of importance since the procedure does not account for the sample size used to estimate the prevalence. The latter procedure, however, required to determine the including window whose optimal choice is yet to be investigated.
It appears, from previous attempts to estimate incidence from prevalence data that either parametric model must be postulated or the derivative(s) of the prevalence must be estimated. The first appoach necessitates strong a priori estimates and may suffer from misspecification. The second approach appears more appealing since, in principle, it should require less or weaker assumptions. The problem then reduces to estimating derivative(s) from noisy data. The natural approach is thus to use local polynomial fitting that has an abundant literature (see for example [9, 10] and references therein). But because the instantaneous excess mortality as a function of age and time depends on the past incidence in the considered population, that approach requires external studies to obtain that excess mortality estimates every time incidence estimates are needed. To alleviate this problem, in this paper, we consider an approach that uses intrinsic excess mortality that depends on age and time since infection and can be obtained once.
This paper presents a method to estimating the incidence of irreversible infections using data from a(several) cross sectional prevalence survey(s). Using a(several) cross sectional study(ies) requires the assumption that the incidence does not vary over time (or is time-constant by interval) but eventually varies as a function of age. The remainder of this paper is organized as follows. Section 2 discusses the relationship between the true proportion of infected (i.e. the true prevalence), the incidence and the excess mortality. Section 3 presents a summary of the class of functions we assume the incidence belongs to, and Section 4 discusses the estimation procedure. Section 5 illustrates numerical results from both a simulation study and HIV incidence estimation among men in Zimbabwe, using data from the NIMH Project Accept (HPTN 043) project and HIV data from the Zimbabwe Demographic Health Surveys (DHS) 2005–2006 [11]. Finally, Section 6 is devoted to concluding remarks.
2. Derivation of the incidence from prevalence
Let us consider a non remissible infection with differential mortality, i.e. an infection such that individuals infected with the agent transmitting that infection have a higher mortality rate and remain infected until they die. The probability that a randomly selected individual aged a at time t is infected with that agent can be viewed as the prevalence, p(a, t). Let λ(a) and h(a, w) be the hazard of becoming infected at age a and the hazard of dying due to causes related to the infection at age a given that the infection occured at age w. Without loss of generality, we can assume that the time originates when the infection is introduced in the population of interest. Then, for simplicity in the presentation, assume that two surveys were conducted at times t1 and t2 (0 ≤ t1 < t2). Our aim here is to find an estimator of the incidence in the interval (t1, t2). Of course, we assume that t1 and t2 are close enough so that we can assume that the incidence is not time dependant in that interval.
It is reasonable to assume that the background mortality, i.e. mortality not related to the infection is independent of the excess mortality. Let us further assume that either there is no migration or the differences between both the prevalence and incidence of the migrant and non-migrant populations are negligible. Thus, if we only consider the individuals who were alive at time t1, the probability that an individual aged a is infected (and alive) at time t2 is:
where ã = min(a − t2 + t1, a0), a0 ≥ 0 is the minimum age considered and s*(a, ã) is the probability that an individual who was infected at age ã is still alive at age a, and M(a, ã) is the probability to survive from ã to a for uninfected individuals. On the other hand, the probability that an individual aged a is uninfected (and alive) at time t2 is
Therefore, the prevalence of the infection among individuals aged a at time t2, , can be expressed as a function of the prevalence at time t1, the incidence in the interval (t1, t2) and the intrinsic excess mortality:
| (1) |
In general, the function s*(a, ã) depends on the incidence prior the first survey. Though studies can be designed to estimate that function, we propose to use the prevalence data at time t1 and take advantage of the fact that the intrinsic excess mortality is known. In effect, since it can be assumed that p(a0, t) = 0 for all t, we can choose t0 such that the oldest person in the data set was not infected before t0, i.e. t0 ≤ t1 − amax + a0, where amax is the age of that oldest person at time t1. Then, we can apply the procedure that will be presented later to find λ0, a representation of the incidence in the interval (t0, t1), and estimate s* thanks to Equation (2):
| (2) |
The draw back of this approach is that t1 − t0 may be too large for the incidence to be assumed to be constant in the interval (t0, t1). However, this limitation is not inherent to the methodology but rather to the availability of the data.
In the case where the infection does not induce excess mortality, we have H(a, ã) = 1, ∀a and s*(a, ã) = 1, ∀a ≥ ã, and Equation (1) reduces to:
Equation (1) shows that the prevalence is a non linear function of the incidence and involves arduous calculations. Numerical integrations may be required, depending of the intrinsic excess mortality and the family to which the incidence belongs to. One can reduce both the numerical cost and the risk of misspecification by carefully choosing the class of functions where the incidence is searched for.
3. Model for the incidence
Generally, for established infections, reasonnable guess of a familly to model incidence shape can be made by experts. For example, Williams et al. [12], based on the information available on sexual beharviours, assumed that the incidence of HIV as a function of age had the shape of a log-normal distribution curve. Gregson et al. [4] instead assumed that the incidence curve of the same infection had the shape of a Gaussian distribution. One may imagine that, in a setting where the main route of infection is not the sexual one, different famillies must me investigated. We propose here to search for the incidence in a larger class of functions that not only reduce the numerical cost but also allows handling the constraint λ ≥ 0 easily. Furthermore, the approach can easily be applied to different settings and to other infections, provided the intrinsic excess mortality is known. Concreatly, we can only assume that the incidence is two time differentiable and search for it in the family of piecewise polynomials of degree two. More precisely, let l, u ∈ ℝ, l < u, and let X = (l, u). Let us assume that ∃m ∈ ℕ* and a sequence x0 = l < x1 < … < xm = u such that:
| (3) |
with
| (4) |
where (αk, βk, γk)k=1,…m ∈ ℝ3m satisfy the constraints:
| (5) |
and
| (6) |
Given the sequence x0, …, xm, the family of functions λ described by equations (3)–(6) can be represented by (α1, β1, γ1) if m = 1, and by (α1, β1, γ1, (δk, γk)k=2,…,m) if m ≥ 2, where δk = xk−1 − xk−2 for k = 2, …, m. In fact, the case m = 1 is an obvious consequence of (3)–(4). Now, let m ∈ ℕ\ {0, 1} and (αk, βk, γk)k=1,…m ∈ ℝ3m such that the constraints (5) are satisfied. Thus, for k = 2, …, m, we have
| (7) |
where we adopted the convention that a sum over an empty set is zero, i.e. Σi<j<k,i≥1 γi (xi − xi−1) (xj − xj−1) = 0 if the set {(i, j) ∈ ℕ × ℕ such that 1 ≤ i < j < k} is empty.
The proof of System (7) is straightforward and shows that our family of functions λ defined by (3)–(6) can be identified as a subset of
where, for simplicity of notation, we set δ1 = β1.
The set ℳm is itself a subset of the well known space of second order splines with knots at x1, …, xm. Equation (4) ensures that λ is continuous while equation (5) ensures its differentiability. That class of functions is included in a class of function studied by Gallant and Fuller [10] who proposed an algorithm for estimating the parameters, including the position of the knots in the context of least square method. In the case when the number and position of knots need to be estimated, the set of canditate functions can be identified by a subset of ∪m∈ℕ* ℳm.
The choices of the number and of the position of knots may be of importance since we are trying to estimate a function that is the closest possible to the true incidence curve. This problem is often encountered when using splines to smooth data. In the context of B-splines, Craven and Wahba [13] considered a Sobolev’s space and proposed to use the generalized cross validation criterion in order to select the model, assuming that the position of knots was known. Recently, several approaches have been proposed for optimal number and position of knots in the context of B-splines (see [14] and [15]).
Here, in a context similar to that of Gallant and Fuller [10], the position of knots, that are given by δk, k ≥ 2, can be easily estimated because our objective function will be differentiable with respect to these parameters. In order to determine the optimal number of knots, we will follow Molinari et al. [14] and Jacobson and Murphy [15] and explore model selection procedures such as the Akaike Information Criterion (AIC). And, since we are using the maximum likelihood method, for large samples, if the true parameter is in the interior of the space of parameters, the asymptotic theory for regular models is valid and the delta method can be used for confidence interval estimation.
4. Estimation procedures
4.1. Case of a single survey conducted at time t2
4.1.1. Incidence estimation using individual data
Let us assume that our data set consist of N individuals aged ai (i = 1, …, N) whose infection statuses yi are observed at time t2, where yi = 1 if the individual is infected, and 0 otherwise. Assume that the individuals in our sample are independent and that the ages ai are well spread across X = (l, u), where l is the lowest age at which an individual may become infected and u is the maximum age considered. For each individual i, yi is the realization of the random variable Yt2 (ai) that gives the infection status of an individual i randomly selected in the general population at time t2. Thus Yt2 (ai) follows a Bernoulli distribution with parameter p(ai, t2), where p(a, t2) represents the true prevalence for individuals aged a at time t2.
Let us further assume that ∃t1 < t2 such that the prevalence at time t1, p(·, t1), and the probability that individuals aged ã and infected at time t1 survives until t2, s*(a, ã), are known. Thus, as indicated by Equation (1), the prevalence at time t2 is a response to the incidence, λ(·), in the inveral (t1, t2); i.e. p(ai, t2) ≡ p(ai, t2; λ), ∀i. Under these assumptions, we can use the maximum likelihood method to estimate the incidence. In effect, the likelihood of our observations is:
| (8) |
where g(ai) is a density function for the sampling process. If there is no reason to believe that g depends on λ, we can easily estimate λ by maximizing (8). This is equivalent to finding
| (9) |
Now, we can apply the AIC to select the best estimate of λ in the class ∪m∈ℕ* ℳm:
| (10) |
where . In the applications, because of practical considerations, we estimated the parameters for m = 1, 2, 3 and 4 and m providing the lowest AIC was then selected. This appeared to work well in the examples consired in this paper and the AIC was either strictly increasing or convex and the maximum value of selected m was 3. One may consider increasing the maximum m, depending on the sample size and/or the infection studied.
4.1.2. Incidence estimation using grouped data
The procedure outlined above can be adapted in the case where grouped data rather than individual data are provided. This is the case when the investigator only has time-dependent prevalence data. In effect, in practice, data are often available as summaries of surveys and, moreover, grouped data can be easy to handle and allows avoiding numerical cost that can result when using individual data. However, since incidence estimation is a local problem, data should be grouped such that |ai+1 − ai| is as small as possible. In the case of sexually transmitted infections, a one-year interval grouping should be enough. Otherwise, if the prevalence data are not collected at regular age interval the shape of the incidence curve may be altered. In this paragraph, ai, i = 1 …, N denotes the ages when the prevalence was measured. Thus, if ni is the number of individuals surveyed at aged ai, Equation (9) can be re-written as:
| (11) |
where p̃(ai, t2; λ) is the estimated prevalence at time t2, for individuals aged ai. Then, Equation (10) can also be used for model selection.
4.2. Case of multiple surveys
In the case of multiple surveys conducted at times t1 < t2 … < tJ, J ∈ ℕ*, one may consider adding a time component, including interactions between time and age, to the incidence and estimate the whole surface representing incidence as a function of time and age. This necessitates that many surveys have been conducted at regular time intervals. Furthermore, parameters estimation can be time consuming because of the high complexity involved in conducting constrained optimisation over a large dimensional parameter. To overcome this problem, we propose to apply a multi-step procedure. The algorithm consists of estimating on subsequent intervals λj, j = 0, …, J, assuming λ is not time dependant in each interval and use both the fitted prevalence and the s* obtained at step j − 1 in lieu of the missing true functions. For the step 0, t0 can be chosen as indicated in Section 2.
4.3. Confidence Intervals
We propose to use the bootstrap methods for estimating confidence intervals of the incidence. This bootstrap consists of sampling individuals with replacement and apply the estimation porcedure to the bootstrapped samples. Then the percentile method can be used to derive confidence interval for each age.
In the case of grouped data, the boostrap procedure can consist of sampling the prevalence at each time and for each age and applying the estimation to the bootstrapped prevalence. If the distributions of the observed sample are known, one can sample directly from these distributions. Otherwise the sample sizes used to obtain the observed prevalence should be available. One can then generate bootstrapped prevalence by sampling the number of cases from binomial distributions and divide these numbers by the number of trials; i.e. for each age a and time t, the bootstrapped prevalence is p*(a, t) = n*(a, t)/N(a, t), were N(a, t) is the number of individuals used to obtain the observed prevalence p(a, t) and n*(a, t) follows a binomial distribution ℬ(N(a, t), p(a, t)).
The bootstrap approach allows accounting for variability due to sampling in all the surveys.
4.4. Software
The method was implemented and Simulations were performed using the R programming language [16]. Software in the form of R code is freely available online at INSERT/THE/LINK/HERE.
5. Numerical experiments
5.1. Simulation of an HIV epidemic
One can show that (see Online Supporting Information of [8]), if an infection with intrinsic differential mortality h is introduced in a population at time t = 0, then the true prevalence at time t ≥ 0 for individuals aged a is given by:
| (12) |
where λ, the true incidence, is allowed to depend on age and time and, as in Section 2, h is the hazard of death related to the infection and ϕ satisfies: ϕ(a, t) = 0 if t ≥ a and ϕ(a, t) = a − t if a > t.
Equation (12) was used to obtain the true prevalence in our simulated epidemic where we allowed the incidence to vary as function of both time and age. More precisely, the true incidence was varying as a function of age and time as described by Equation (13):
| (13) |
where the function imax(t) allows changing the maximum incidence as a function of time in the population and is defined by
and, for any set A, 𝟙A(x) = 1 if x ∈ A, and 𝟙A(x) = 0 if x ∉ A.
The hazard of dying as a function of age at infection for causes related to the infection, h, was modelled as a Weibull distribution as indicated Todd et al. [17]:
| (14) |
where
This allows simulating an HIV epidemic with four phases: the age specific incidence was constant in time (measured in years) in the first phase (from 0 to 12), increasing in the second (12 to 18), constant in the third (18 to 24) and decreasing in the last phase (24 to 30). Two cross-sectional surveys were simulated at times (4, 10), (12, 18), (25, 30) and we applied the methodology presented above to obtain a representation of the incidence in each of these intervals. We used the generated age and time specific prevalence to simulate the infection status of individuals in these surveys. Data from each survey consisted of age and HIV status of 5, 000 individuals: 200 for each age from 15 to 29 years and 100 for each age from 30 to 49 years. The accuracy and precision of the estimated incidence were investigated by comparing the results of 1, 000 simulated data sets per scenario, to the input values.
Model selection was performed by using the AIC as indicated in Section 4. The optimal number of subdivision was determined once, when using the “observed” sample. This number was kept constant throughout the boostrap procedure. The number of subdivisions (m − 1) appeared to be equal to 2 though the position of the knots varied from 20.36 to 25.69.
Simulated and estimated incidence and prevalence are displayed in Figure 1. They show that, in the case where the true incidence does not vary as a function of time, the approach can give relatively good estimates. In this simulated example (see Figure 1 (a)) even with small incidence and prevalence and a sample size of 5, 000 individuals, the 95% confidence surface contained the true incidence curve. In the case where the incidence varied as a function of time, with the time trend very pronounced (see Figure 1 (b)), the estimated curve was close to the incidence at the mid-point of the time-interval. When the time-trend was not very pronounced (see Figure 1 (c)), the intersection between the confidence interval obtained for each age and the range in which the true incidence varied was only empty for the youngest age observed. This indicates that our method provides a good representation of the underlying incidence.
Figure 1.
Observed and fitted prevalence (left) and true and estimated incidence (right) in the simulated population. Confidence limits were obtained using the bootstrap re-sampling method with 1000 replications. The shaded area represents the 95% confidence region
5.2. Real data example
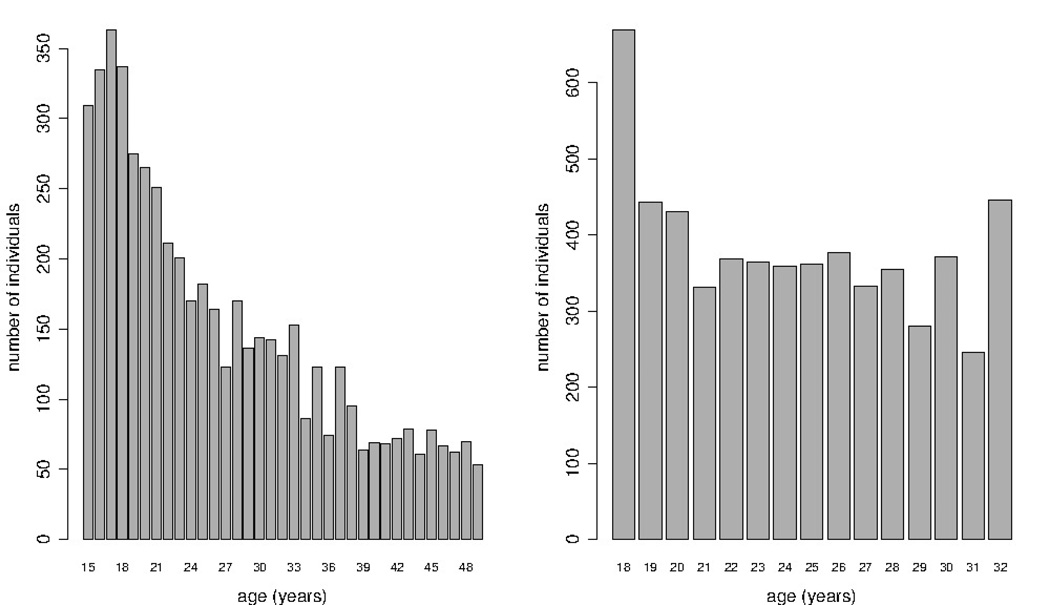
The method was illustrated to estimate HIV incidence among men in Zimbabwe, in the time interval 2006–2010, using data from the NIMH Project Accept (HPTN 043) project which was conducted in 2010 and HIV data from the Zimbabwe DHS (2005–2006). The Accept project was described elsewhere [18, 19]. We used data from the cross-sectional survey of 18–32 years old men. We were interested in age and HIV statuses of the 5, 736 men participants included in this analysis. The age distribution of the sampled individuals is presented in Figure 2. It suggests that the sampling procedure was such that the mode is the youngest age group and the age distribution of older individuals was almost uniform. The overall HIV prevalence among these individuals was about 8%.
Figure 2.
Age distributions of the men aged 15–49 in the Zimbabwe DHS 2006 (left) and of the men aged 18–32 recruited in the NIMH Project Accept in Zimbabwe (right)
The HIV data from the Zimbabwe DHS 2005–2006 were used to estimate the age-specific prevalence among men in Zimbabwe in 2006. The Zimbabwe DHS 2005–2006, a population-based cross-sectional survey conducted by the Central Staistical Office and the Measure DHS Program, has been described elsewere [11]. Here, we used the available age and HIV statuses of 5306 men aged 15–49 years. The age distribution of the sampled individuals aged 15–49 is available in Figure 2, though only data from the individuals younger than 32 is important for our incidence estimation in the age group 18–32. The age distribution in the DHS appears to be different from the one of the HPTN 043. The overall prevalence was about 14% while the prevalence in the age group 18–32 was about 11%. This suggests that there was a decrease in prevalence, in the age group 18–32, from 2006 to 2010.
Individuals were grouped per age in years rounded to the closest integer and the sample weights used derive the observed age-specific prevalence. This study assumed that intrinsic HIV mortality was given by Formula (14) and, to account for the availability of Anti-Retroviral Therapy (ART), we used the survival function as estimated among HIV infected individuals who initiated ART in Southern Africa [20]. Thus, because ART was not widely available in Zimbabwe before 2006 (see [21]), we used H(a, w) as given by Formula (14) to account for the survival of HIV in the first step of our procedure consisting of smoothing the 2006 prevalence. However, because UNAIDS estimated that about 39.7% of adult HIV infected individuals in Zimbabwe were on ART in 2009 (see [21]), we accounted for HIV related death among people who initiate ART in the time interval 2006–2010. When modelling the 2010 prevalence, we replaced H(a, w) in Formulas (1) and (2) with:
where is the survival function of the double Weibull distribution that characterizes the survival among HIV infected individuals who initiated ART in Southern Africa [20].
We assumed that HIV was introduced in Zimbabwe in 1980, which implies that, borrowing notations of Section 4, 2006 and 2010 correspond to t1 = 26 and t2 = 30, respectively. We further assumed that individuals in our cohorts could become exposed to HIV at the age of 10. The estimation procedure presented in Section 4 was applied to the data set. The AIC was minimum for m = 3 and 1 for t1 and t2, respectively. Figure 3 presents the fitted and observed prevalence from the two surveys as well as the estimated incidence as a function of age. It shows that the incidence was relatively small for the ages 18-to-24 and increased slowly thereafter. The cummulative incidence until the age of 24 was as small as 0.040 (95% CI: 0.026–0.065), corresponding to an annual incidence rate of about 0.0029 (95% CI: 0.0018–0.0046). The cummulative incidence until 32 years was 0.19 (95% CI: 0.14–0.23), corresponding to an annual incidence of about 0.0085 (95% CI: 0.0064–0.010 while the mean incidence, which was calculated by using the number of individuals in each age group as weight, was 0.011 (95% CI: 0.0085–0.015).
Figure 3.
Observed and fitted prevalence (left) and estimated incidence (right) among men in Zimbabwe. Confidence intervals were obtained using the bootstrap re-sampling method with 1000 replications. The shaded area represents the 95% confidence region
Sensitivity analysis was performed to assess the effect of ART coverage on our estimates. In the first set of analyses, we assumed that none of the individuals surveyed had ever started ART. Under that assumption, the cummulative and mean incidence were 0.19 (95% CI: 0.15–0.24) and 0.012 (95% CI: 0.0091–0.015), respectively. In the second set of analyses, we assumed a 100% ART coverage and estimated the cummulative and mean incidence to be 0.18 (95% CI: 0.13–0.22) and 0.011 (95% CI: 0.0075–0.014), respectively.
6. Concluding Remarks
This paper presents an approach to estimate incidence of a chronic infection in a population. The approach consists of using data from a cross sectional prevalence survey and assumes that the incidence is constant over time intervals but not age. The method is general in the sense that the incidence curve is searched for in the broad class of segmented polynomials with unspecified number and position(s) of knots. Segmented polynomials of degree 2 are minimal to ensure the differentiability of the incidence curve and provide a numerical advantage. They allow hadling the constraint on the positivity of the incidence easily. Bootstrap method was proposed for confidence interval estimation.
In the case when the infection induces a differential mortality, the method requires the knowledge of the hazard of dying from causes related to the infection as a function of time since infection. For HIV, that function has been obtained before the era of ART and for people who initiated ART. We were therefore able to account for the introduction of ART in our real data example. This did not seem to have a considerable effect on our estimates most likely because our cohort only contained relatively young individuals. One may, however, need to be more careful in considering the availability of the ART when trying to estimate HIV incidence among older people using prevalence data.
Our method appears to work reasonably well in reconstructing incidence over the course of a simulated epidemic with various phases. It allows analysing grouped data since these are easily available, easy to handle and can be analysed at low computational cost. A concurrent approach is to use tests for recent infection in a single prevalence survey. When the required parameters are well known, that approach can give good estimates of the (mean) incidence and can be used to evaluate effects of interventions at population level, using data from a single survey (see [22] and [23]). However, that approach can only be used when individual data are available and requires that additional data be collected for infected individuals. Morever, in the case of HIV incidence estimation, though a combination of available assays appeared to have better performance (see for example [18]), the derivation of the incidence itself necessitates estimation of parameters such as false recent rates, sensitivity and/or mean window. These parameter are obtained under several assumptions on the epidemic including the predominant sub-type of the HIV in the region where the incidence is to be estimated. Further more, that approach would require considerably large sample size to obtain precise age-specific incidence.
We applied our method to estimate incidence using data from two cross-sectional surveys in Zimbabwe. This study used self-reported age and, as any study using self-reported data, is subject to bias due to misreporting. In general, this potential bias can only be assessed or corrected if information on how individuals misreport their age is available. Our overall incidence estimates (for the age-group 18–32) was in the range of the 0.0078 (95% CI: 0.0024-0.0013) obtained when using the multi-assay algorithm (see [18] for description of the multi-assay algorithm). Similarly, our incidence estimates (for the age-group 18–24) was in agreement with the 0.0044 (95% CI: 0.0015–0.0073) corresponding to the annual incidence for the age group 18–24, using the same algorithm. This suggests that we can obtain reliable age specific incidence of HIV using prevalence data and mortality estimates from various sources.
The model presented in this paper can easily be generalized or adapted to examine the incidence as a function of non time-dependent demographics such as gender. One may, for instance, consider proportional incidence model or even estimate incidence rate ratios. The model can also be adapted to estimating the effects of dynamical interventions such as male circumcision, provided the rate at which individuals receive that intervention is correctly modelled.
Finally, one should note that, because the problem of estimating incidence is local rather than global, for the method presented here to be more accurate, the grouping of data should be such that the grid points where the proportions (or prevalence) are estimated are relatively close to each other and prevalence surveys should be conducted on a regular basis in order to keep track of the incidence trend.
Acknowledgments
This work was sponsored by the Johns Hopkins University Center for AIDS Research (Grant Number 1P30AI094189 from the National Institute of Allergy And Infectious Diseases), the U.S. National Institute of Mental Health as a cooperative agreement, through contracts U01MH066687 (Johns Hopkins University - David Celentano, PI); U01MH066688 (Medical University of South Carolina - Michael Sweat, PI); U01MH066701 (University of California, Los Angeles - Thomas J. Coates, PI); and U01MH066702 (University of California, San Francisco - Stephen F. Morin, PI).
In addition, this work was supported as HPTN Protocol 043 through contracts U01AI068613/UM1A068613 (HPTN Network Laboratory-Susan Eshleman, PI); U01AI068617/UM1AI068617 (SCHARP - Deborah Donnell, PI); and U01AI068619/UM1AI068619 (HIV Prevention Trials Network - Sten Vermund/Wafaa El-Sadr, PIs) of the Division of AIDS of the U.S. National Institute of Allergy and Infectious Diseases; and by the Office of AIDS Research of the U.S. National Institutes of Health. Additional support was provided by the Division of Intramural Research, National Institute of Allergy and Infectious Diseases, National Institutes of Health. Views expressed are those of the authors, and not necessarily those of sponsoring agencies.
We thank the communities that partnered with us in conducting this research, and all study participants for their contributions. We also thank study staff and volunteers at all participating institutions for their work and dedication.
Many thanks to Professor Lawrence H. Moulton for his interest in this work.
References
- 1.Carone M, Asgharian M, Wang MC. Nonparametric incidence estimation from prevalent cohort survival data. Biometrika. 2012;99(3):599–613. doi: 10.1093/biomet/ass017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Podgor MJ, Leske MC. Estimating incidence from age-specific prevalence for irreversible diseases with differential mortality. Stat Med. 1986;5(6):573–578. doi: 10.1002/sim.4780050604. [DOI] [PubMed] [Google Scholar]
- 3.Elandt-Johnson R, Johnson N. Survival models and data analysis. New York: Wiley; 1980. [Google Scholar]
- 4.Gregson S, Donnelly CA, Parker CG, Anderson RM. Demographic approaches to the estimation of incidence of HIV-1 infection among adults from age-specific prevalence data in stable endemic conditions. AIDS. 1996 Dec;10(14):1689–1697. doi: 10.1097/00002030-199612000-00014. [DOI] [PubMed] [Google Scholar]
- 5.Ades AE, Nokes DJ. Modeling age- and time-specific incidence from seroprevalence:toxoplasmosis. Am. J. Epidemiol. 1993 May;137(9):1022–1034. doi: 10.1093/oxfordjournals.aje.a116758. [DOI] [PubMed] [Google Scholar]
- 6.Keiding N. Age-specific incidence and prevalence: A statistical perspective. Journal of the Royal Statistical Society. Series A (Statistics in Society) 1991;154(3):371–412. [Google Scholar]
- 7.Brunet RC, Struchiner CJ. A non-parametric method for the reconstruction of age- and time-dependent incidence from the prevalence data of irreversible diseases with differential mortality. Theor Popul Biol. 1999 Aug;56(1):76–90. doi: 10.1006/tpbi.1999.1415. [DOI] [PubMed] [Google Scholar]
- 8.Mahiane GS, Ouifki R, Brand H, Delva W, Welte A. A general HIV incidence inference scheme based on likelihood of individual level data and a population renewal equation. PLoS ONE. 2012;7(9):e44–e377. doi: 10.1371/journal.pone.0044377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wegman EJ, Wright IW. Splines in statistics. Journal of the American Statistical Association. 1983;78(382):351–365. doi: 10.1080/01621459.1983.10477955. [DOI] [PubMed] [Google Scholar]
- 10.Gallant AR, Fuller WA. Fitting segmented polynomial regression models whose join points have to be estimated. Journal of the American Statistical Association. 1973;68(341):144–147. [Google Scholar]
- 11.Central Statistics Office MII. Final country report: Zimbabwe demographic health survey. Harare: Macro International Inc.; 2007. [Google Scholar]
- 12.Williams B, Gouws E, Wilkinson D, Karim SA. Estimating HIV incidence rates from age prevalence data in epidemic situations. Stat Med. 2001 Jul;20(13):2003–2016. doi: 10.1002/sim.840. [DOI] [PubMed] [Google Scholar]
- 13.Craven P, Wahba G. Smoothing noisy data with spline functions. Numerische Mathematik. 1978;31(4):377–403. [Google Scholar]
- 14.Molinari N, Durand JF, Sabatier R. Bounded optimal knots for regression splines. Computational Statistics & Data Analysis. 2004;45(2):159–178. doi: http://dx.doi.org/10.1016/S0167-9473(02)00343-2. [Google Scholar]
- 15.Jacobson TJ, Murphy MJ. Optimized knot placement for B-splines in deformable image registration. Med Phys. 2011 Aug;38(8):4579–4582. doi: 10.1118/1.3609416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2015. URL http://www.R-project.org/, ISBN 3-900051-07-0. [Google Scholar]
- 17.Todd J, Glynn JR, Marston M, Lutalo T, et al. Time from HIV seroconversion to death: a collaborative analysis of eight studies in six low and middle-income countries before highly active antiretroviral therapy. AIDS. 2007 Nov;21(Suppl 6):55–63. doi: 10.1097/01.aids.0000299411.75269.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Laeyendecker O, Piwowar-Manning E, Fiamma A, et al. Estimation of HIV incidence in a large, community-based, randomized clinical trial: NIMH project accept (HIV Prevention Trials Network 043) PLoS ONE. 2013;8(7):e68–e349. doi: 10.1371/journal.pone.0068349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Coates TJ, Kulich M, Celentano DD, Zelaya, et al. Effect of community-based voluntary counselling and testing on HIV incidence and social and behavioural outcomes (NIMH Project Accept; HPTN 043): a cluster-randomised trial. Lancet Glob Health. 2014 May;2(5):e267–e277. doi: 10.1016/S2214-109X(14)70032-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Estill J, Aubrière C, Egger M, Johnson L, Wood R, Garone D, Gsponer T, Wandeler G, Boulle A, Davies MA, et al. Viral load monitoring of antiretroviral therapy, cohort viral load and hiv transmission in southern africa: a mathematical modelling analysis. AIDS. 2012 Jul;26(11):1403–1413. doi: 10.1097/QAD.0b013e3283536988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.UNAIDS. Unaids report on the global aids epidemic. publication. unaids, 2010. Technical Report Web. 2015 Feb 23;
- 22.Auvert B, Mahiane GS, Lissouba P, Moreau T. Statistical power and estimation of incidence rate ratios obtained from BED incidence testing for evaluating HIV interventions among young people. PLoS ONE. 2011;6(8):e21–e149. doi: 10.1371/journal.pone.0021149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brookmeyer R, Laeyendecker O, Donnell D, Eshleman SH. Cross-sectional HIV incidence estimation in HIV prevention research. J. Acquir. Immune Defic. Syndr. 2013 Jul;63(Suppl 2):S233–S239. doi: 10.1097/QAI.0b013e3182986fdf. [DOI] [PMC free article] [PubMed] [Google Scholar]