Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Mar 20;7:44629. doi: 10.1038/srep44629

Optical determination of Shockley-Read-Hall and interface recombination currents in hybrid perovskites

Valerio Sarritzu 1, Nicola Sestu 1, Daniela Marongiu 1, Xueqing Chang 1, Sofia Masi 2, Aurora Rizzo 2, Silvia Colella 2,3, Francesco Quochi 1, Michele Saba 1,a, Andrea Mura 1, Giovanni Bongiovanni 1,b
PMCID: PMC5357960  PMID: 28317883

Abstract

Metal-halide perovskite solar cells rival the best inorganic solar cells in power conversion efficiency, providing the outlook for efficient, cheap devices. In order for the technology to mature and approach the ideal Shockley-Queissier efficiency, experimental tools are needed to diagnose what processes limit performances, beyond simply measuring electrical characteristics often affected by parasitic effects and difficult to interpret. Here we study the microscopic origin of recombination currents causing photoconversion losses with an all-optical technique, measuring the electron-hole free energy as a function of the exciting light intensity. Our method allows assessing the ideality factor and breaks down the electron-hole recombination current into bulk defect and interface contributions, providing an estimate of the limit photoconversion efficiency, without any real charge current flowing through the device. We identify Shockley-Read-Hall recombination as the main decay process in insulated perovskite layers and quantify the additional performance degradation due to interface recombination in heterojunctions.

Six decades after the demonstration of the first silicon photovoltaic cell1, only a limited number of semiconductors enable single junction photovoltaic devices with power conversion efficiencies (PCEs) exceeding 20%2. Among these, hybrid organic-inorganic perovskites (HPs) represent an emerging class of solution-processed semiconductors3,4,5,6,7,8,9,10 with the potential to approach the Shockley-Queisser limit of the PCE11 and the prospect to be integrated with established commercial technologies to fabricate cheap, multi-junction solar cells12,13, with even higher efficiencies.

The rapid increase in photovoltaic performance has been accompanied by intense research on the photophysics of these materials14,15,16,17,18,19,20,21,22. A key aspect of photoconversion in HPs is the recombination current, a ubiquitous mechanism of energy loss in solar cells. Photovoltaic devices operate as non-ideal current generators in which a fraction of photogenerated electrons and holes recombines inside the cell, feeding the internal diode current instead of being injected into the external load23. Minimal recombination energy losses are achieved in the ideal case in which electron-hole pairs decay only radiatively; in this regime, the recombination resistance is maximized, and so is the cell voltage. The external electroluminescence quantum yield (EQYEL) quantifies the amount of radiative recombination with respect to non-radiative losses; the best solar cells show the highest EQYEL (10−3–10−1) and therefore operate at a voltage as close as possible to the semiconductor band gap—up to 0.78 Eg in GaAs24 and very recently 0.76 Eg in HP8,20,25,26,27.

The simplest architecture of heterojunction solar cells consists of a light absorber sandwiched between two charge-selective semiconductor layers, one of which allows the flow of photoexcited electrons (ETL) but blocks the transmission of holes, while the other conveys only photoexcited holes (HTL) to the opposite electrode (Fig. 1). Nonradiative decay channels are typically associated with two possible mechanisms: one is related to the presence of intragap recombination centres in the absorber; the other one is due to the recombination at the two heterojunctions between the absorber and the transport layers (HTL or ETL), such as back-recombination of electrons (holes) collected by the ETL (HTL) with holes (electrons) accumulating at the interface with the absorber. Information on which annihilation process dominates can be inferred from the ideality factor m of the diode current28,29, typically extracted by fitting the charge current-voltage (I-V) characteristics. However, given the logarithmic dependence of the cell voltage on the recombination rate, the determination of the ideality factor is not very reliable, especially for HP solar cells, where hysteresis and degradation effects may lead to distortion of the I-V characteristics. So far, the values reported for HPs mainly lie in the range 1.7–230,31,32,33,34, but extend as far down as 1.2 and up to 535,36. As a consequence, it is difficult to identify from the electrical characterization what recombination processes limit the photoconversion efficiency, and therefore to elaborate an informed strategy to improve the devices.

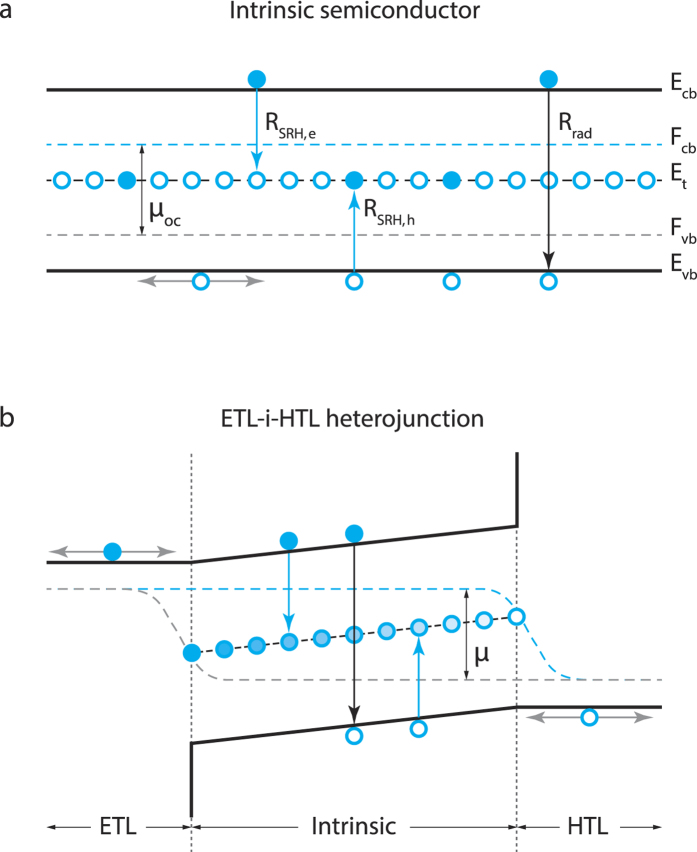
Figure 1. Electron and hole energetics and recombinations in perovskites and perovskite-based solar cells.

Figure 1

Open in a new tab

(a) Stand-alone intrinsic layer. The free energy μoc of photogenerated electron-hole pairs is equal to the energy splitting of the quasi-Fermi levels of electrons in the conduction (Fcb) and valence (Fvb) bands. No electric voltage is present between the two sides due to the absence of electron- and hole-selective contacts. An empty trap level Et in the mid-gap is assumed. RSRH,e(h) is the Shockley-Read-Hall recombination rate of electrons (holes) per unit of volume. Correspondingly, Rrad refers to radiative recombinations. (b) HTL-i-ETL double heterojunction. The difference between Fcb in the ETL and Fvb in the HTL is given by μ = eV, where V is the circuit voltage of the solar cell in absence of electrical losses. As shown in Supplementary Fig. 2, equilibrium conditions of the solar cell in the dark impose that the concentration of trapped electrons varies across the intrinsic layer: trap levels at the centre of the i-semiconductor traps are half-filled so that the recombination rate RSRH,e(h) of the excess carriers is quite large. Conversely, trap levels close to the ETL (HTL) are filled (empty), no trapping of electrons (holes) by mid-gap states is thereby possible, leading to negligible RSRH,e(h) values.

Here we propose an optical experimental method to estimate the voltage drop caused by each type of nonradiative channel. Instead of the I-V curves, we studied the free energy of the electron-hole pairs (μ) as a function of the intensity of the exciting light (Iex), namely the μ-Iex characteristics. We then show how to get information on the ideality factor and recombination channels. Since no charge current flows, the optical approach can be used to study the double heterojunctions composing the solar cells, as well as the two single heterojunctions and the absorbing layer alone, thereby providing a comparative method to discriminate between interface and bulk recombination.

Results

All-optical determination of the electron-hole free energy

According to the theory of non-equilibrium semiconductors, the free energy (or chemical energy) of photogenerated electron-hole pairs, μ, is equal to the energy splitting of the quasi-Fermi levels of electrons in the conduction (Fcb) and valence (Fvb) bands, respectively. To provide an expression for μ in terms of measurable optical quantities, we consider Kirchhoff’s law of radiation, which represents the detailed balance between emission and absorption, generalized by Würfel to account for non-equilibrium electron and hole populations37:

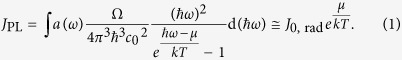graphic file with name srep44629-m1.jpg

JPL is the emitted photon current density, proportional to the external photoluminescence intensity, while a(ω) denotes the absorptivity, which depends both on the absorption coefficient and film thickness. Ω is the effective external emission angle. The right-hand side of equation (1) is valid for excitation levels typical of solar illumination, for which the Bose function can be substituted by the Boltzmann distribution. Equation (1) provides the analytical relation between JPL, μ, and the photon current density J0,rad emitted by the semiconductor in thermal equilibrium with the environment (μ = 0)38. To our purposes, JPL can be opportunely expressed in terms of the external photoluminescence quantum yield (EQYPL), defined as the ratio between JPL and the absorbed excitation photon flux, that is 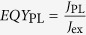Inline graphic. With this substitution, equation (1) can be reformulated to explicitly link μ to EQYPL:

graphic file with name srep44629-m3.jpg

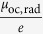in which Inline graphic represents the upper limit for the free energy when only radiative decays occur (EQYPL = 1) and in the open circuit condition. If all incident photons with energy higher than the optical gap are absorbed, Inline graphic represents the Shockley-Queisser limit to the open circuit voltage Voc7. The second term of the right-hand side of equation (2) states a simple but very useful rule: nonradiative decay channels affect the free energy only through the EQYPL, leading to a free-energy loss of In(10−1) kT = 60 meV for a factor of 10 drop of EQYPL at 300 K. Furthermore, equation (2) provides a reformulation of Kirchhoff’s law that allows us to highlight similarities between the optical and the optoelectronic reciprocity relations39. The latter ones, proposed ten years ago by Rau, connect the electroluminescent emission and photovoltaic voltage through the equations eVoc = eVoc,rad + kT ln(EQYEL) and 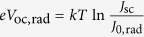Inline graphic, where eJ0,rad represents the radiative charge current in the dark, and eJsc the short-circuit charge current (note that here the symbol J is used for particle currents, not charge currents, hence the need to multiply currents by the electron charge e). Figure 1 visualizes μ for a stand-alone intrinsic semiconductor layer and for a double heterojunction (HTL-i-ETL; ‘i’ stands for the intrinsic absorber semiconductor), providing the link between μ and the circuit voltage in solar cells. In the stand-alone layer (Fig. 1a), μ = μoc is constant throughout the film but no external electric voltage is produced due to the absence of electron- and hole-selective contacts. In the HTL-i-ETL solar cell (Fig. 1b), the free energy is provided by the difference between the energies of the quasi-Fermi levels of electrons in the ETL and in the HTL at the opposite side of the device. Inline graphic in the intrinsic layer equates the circuit voltage V of the solar cell if Fcb and Fvb do not vary from the transport materials up to the external contacts.

All-optical determination of the ideality factor

The optical reciprocity relation in eq. (2) allows measuring μ without having any information on the specific microscopic mechanisms of electron-hole recombination. Nonetheless, as we are interested in uncovering the decay channels, we need to find out how these processes influence the μ-Jex characteristics. We therefore need to specify a microscopic model for recombinations. Let us consider the simplest case, in which decays of electrons and holes are driven by elementary processes such as monomolecular, bimolecular, or higher order multi-particle interactions. If the corresponding recombination rates for electrons and holes follow a power law 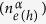Inline graphic, the relation 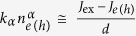Inline graphic holds under steady-state excitation (neglecting thermal excitation/recombination processes)40, where 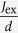Inline graphic represents the mean carrier generation rate per unit of volume, 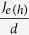Inline graphic the electron (hole) extraction rate per unit of volume, and α denotes the number of carriers involved in the recombination process (α = 1,2,3 for monomolecular, bimolecular, and trimolecular recombinations respectively). To connect μ to the free electron (ne) and hole (nh) concentrations, we use the mass action law, generalized to account for non-equilibrium carriers:

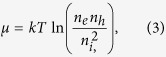graphic file with name srep44629-m12.jpg

where ni is the free-carrier concentration of the intrinsic semiconductor in the dark. Defining 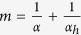Inline graphic, eq. (3) can be rewritten as:

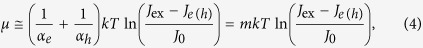graphic file with name srep44629-m14.jpg

in which J0 is a constant. For optoelectronic measurements (Je(h) ≠ 0), eq. (4) is often written by replacing μ = eV in the form 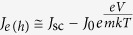Inline graphic, where m is the ideality factor of the μ-Jex curves, with J0 being the reverse bias saturation current (note again that charge currents are usually considered instead of particle currents as we are doing here). When Je(h) = 0 (μ = μoc), eq. (4) provides an all-optical route to determine the ideality factor m and consequently to identify the recombination mechanisms. Elementary electron-hole annihilation processes (α = 1,2,3,…) are associated with rational values of m. Band-to-band electron-hole recombinations (ne~nh,αe = αh = 2,) yield m = 1; nonradiative monomolecular decays of minority carriers in doped semiconductors 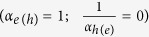Inline graphic also lead to m = 1. Auger recombinations are trimolecular processes, so 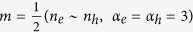Inline graphic28. Shockley-Read-Hall (SRH) nonradiative decays in the space-charge region of a p-n junction or in the intrinsic layer of a p-i-n (HTL-i-ETL) device, for which αe = αh ≅ 1, is instead characterized by m = 2 (see Supplementary Note 1)29.

Free energy and ideality factor in perovskite films

The experimental data from single HP layers allow to understand the bulk carrier recombination processes and to determine the maximum attainable free energy μoc. Figure 2a reports μoc as a function of ln(Iex), where Iex is the excitation light intensity delivered by a green CW laser (λ = 532 nm). μoc was determined from the EQYPL of MAPbI3 as a function of Iex. We analysed perovskite layers grown with several deposition methods, namely single-step and double-step techniques. According to eq. (2), it is sufficient to assess μoc,rad at just one excitation intensity, which we chose so that the absorbed photon current density of the green light and solar light at AM1.5G (Jsun, ħω > EOG) were equal (Iex = 50 mW/cm2). In the Supplementary Note 2, we show that μoc,rad can be usefully written as:

Figure 2. μ -Iex characteristics of intrinsic MAPbI3 films.

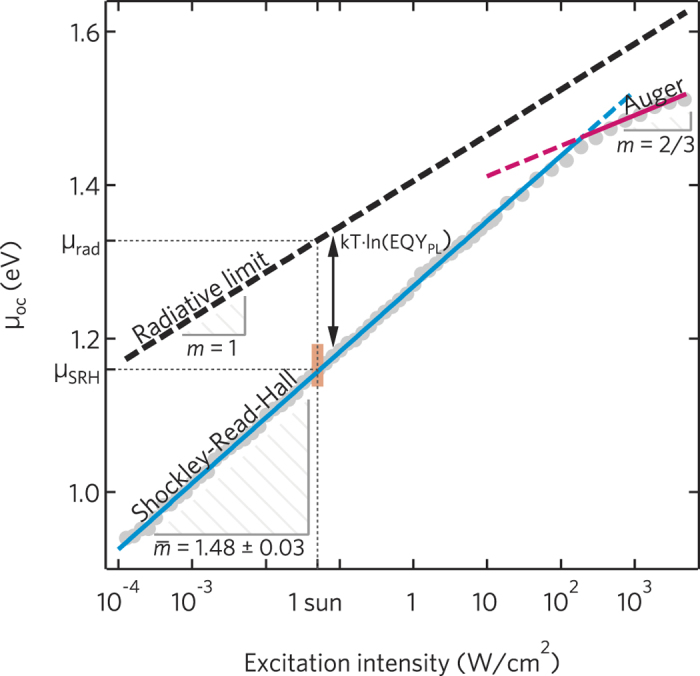
Figure 2

Open in a new tab

Grey markers represent the measured free energy μoc as a function of the excitation intensity (Iex) delivered by a CW laser at 532 nm. The orange box encloses the dispersion of μoc for samples fabricated with a variety of different techniques. For 1 mW/cm2 < Iex < 100 W/cm2, μoc depends linearly on ln(Iex) with a slope m of approximately 3/2 regardless of the fabrication method, yielding an average ideality factor 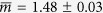Inline graphic (within one standard deviation). Shockley-Read-Hall recombinations are expected to lead to a rational ideality factor m = 3/2 at low illumination levels. The experimental slope decreases to approximately 2/3 for Iex > 100 W/cm2, as foreseen for Auger recombination. At Iex = 50 mW/cm2, the rate of photons absorbed by the film matches that one obtained at an illumination level of one sun (AM 1.5G). 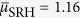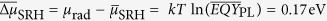At this excitation intensity, μrad = 1.33 eV while Inline graphic eV, with a free energy loss due to Shockley-Read-Hall recombinations Inline graphic.

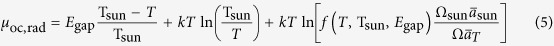graphic file with name srep44629-m18.jpg

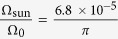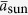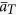In this equation, Egap = 1.602 eV is the photon energy of the optical gap (see Supplementary Note 2); Inline graphic takes into account the fact that the sun illuminates only a portion of the effective solid angle seen by the semiconductor37; Inline graphic and Inline graphic represent the spectrally averaged film absorptivity, weighted by the black-body radiation spectra at Tsun = 5541 K and T = 300 ± 20 K, respectively. The temperature T of the electron-hole gas was determined by fitting a Boltzmann distribution to the high-energy tail of the photoluminescence spectrum. f(T, Tsun, Egap) is an analytical function, whose value can be readily calculated as equal to 1.718. In the Shockley-Queisser limit, 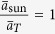Inline graphic, hence the radiative free energy only depends on Tsun and properties of the material, namely Egap and the effective working temperature T. We then obtained μoc,rad(Jsun) = 1.33 ± 0.02 eV, where the experimental error was mainly due to the uncertainty in the measurement of T. The effect of the dependence of the absorptivity on the layer thickness is within 10 meV (see Supplementary Note). Our all-optical value is in agreement with estimations of the radiative electrical voltage in HP solar cells, Voc,rad = (1.32–1.34) ± 0.02 V, as independently assessed from electrical characteristics20.

The free energy μoc was estimated through eq. (2) by simply adding to the radiative limit μoc,rad the term kTln(EQYPL) due to nonradiative recombinations. Experimental data show that μ is proportional to ln(Iex), with the slope coefficient giving the ideality factor. For 1 mW/cm2 < Iex < 100 W/cm2, the slope was close to 3/2, independently of the method used to fabricate the MAPbI3 films, with an average ideality factor 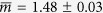Inline graphic.

In the light of the previous discussion on the m-rational values, experimental findings indicate that electrons and holes follow different power laws, and more specifically one carrier decays obeying a first order process (α = 1) while the other follows a second order process (α = 2). This asymmetry between electrons and holes is consistent with the presence of traps preferentially capturing a single carrier type. Figure 1 shows the recombination processes expected in a stand-alone, undoped HP layer, assuming empty traps40,41; fully occupied trap states would lead to similar conclusions, just swapping the roles of electrons and holes. The capture rate of electrons by intragap levels can be described as a bimolecular process, RSRH,e ∝ nh,tne, where nh,t is the density of trapped holes. However, in the intrinsic semiconductor all traps are nearly empty, so nh,t is almost equal to the density Nt of recombination centres. Consequently, the recombination process is monomolecular (αe = 1). Similarly to the case of electrons, the hole capture rate is RSRH,h ∝ nhne,t, but in this case the densities of both trapped electrons ne,t and free holes nh increase with the excitation intensity and, additionally, ne,t~nh. Hole recombination is therefore an effective bimolecular process with αh = 2; far from trap saturation, we obtain 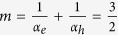Inline graphic. We thus conclude that nonradiative recombinations in HPs can be described in the framework of the SRH model. 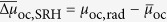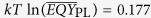In our samples, SRH recombination limits the available free energy to Inline graphic eV, with a loss at one sun excitation Inline graphic = Inline graphic eV; lower losses could be achieved by reducing the trap density.

For Iex > 100 W/cm2, m decreased to ~2/3, as expected for trimolecular annihilations via Auger decay channels. Over a wide range of excitation intensities, as in the μoc-Jex characteristics presented in this work, two (or more) elementary decay channels contribute to the recombination dynamics. Competition between them is such that the lowest-order electron-hole decays, identified by the lowest power index α and thus the highest m (nonradiative recombinations with m = 3/2 in perovskite films), dominates at low excitation intensities, while the highest order decay (nonradiative Auger recombinations with m = 2/3 in perovskite films) becomes the most important one at high excitation14,27,42,43. Similar behaviour is also observed in the I-V characteristics of a Si solar cell, where m decreases from 2 (SRH recombinations) to 1 for increasing voltage28. We rule out trap saturation because it would cause hole recombination to become monomolecular, as the population of trapped electrons becomes constant, and consequently m should increase from 3/2 to 2 (αe = αh = 1).

Free energy and ideality factor in perovskite heterojunctions

According to the optical reciprocity relation in eq. (2), the larger EQYPL, the larger the resulting free energy. Therefore, a purely optical analysis of the EQYPL ought to establish if additional interface recombination is setting stricter limits to μoc in single and double HP heterojunctions with respect to the bulk.

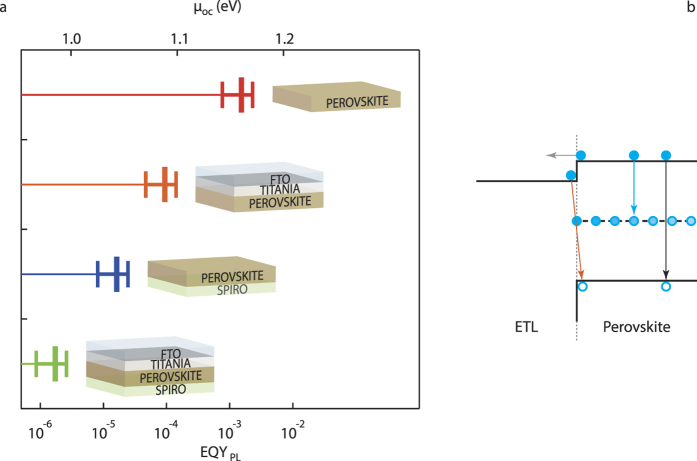
Figure 3 shows the EQYPL and corresponding μoc in these structures at an absorbed monochromatic photon density current corresponding to one sun. The standalone layer has the largest EQYPL, while significantly lower values are measured in the presence of interfaces, both in the i-ETL (perovskite-TiO2) and HTL-i (spiro-MeOTAD-perovskite) heterojunctions. Our interpretation of the evidence is that additional non-radiative recombination channels appear at both interfaces, providing faster non-radiative recombination than in the standalone layer. The full HTL-i-ETL structure, representing a contactless solar cell, shows an even lower EQYPL.

Figure 3. Comparison of the free electron-hole energy and external photoluminescence quantum yield in standalone perovskite layers and perovskite-based heterojunctions.

Figure 3

Open in a new tab

(a) Top axis: experimental free energy μoc under 50 mW/cm2 CW laser excitation at 532 nm. Bottom axis: external photoluminescence quantum yield (EQYPL) under the same conditions. The rate of photons absorbed by the film matches that of an illumination level of one sun (AM 1.5G). Two types of single heterojunctions are reported: i-ETL (where the ETL is compact TiO2) and HTL-i (where the HTL is spiro-MeOTAD). Heterojunctions introduce non-radiative recombination channels, resulting in a lower free energy with respect to the single perovskite layer. (b) Schematic representation of electron-hole recombination processes in a heterojunction: bulk Shockley-Read-Hall decays (cyan arrow), radiative decays (black arrow) and interface decays (orange arrow); the sketch refers to the ETL side interface, a similar one would describe the HTL side.

The ideality factor in the heterojunctions was investigated by studying the μ-Iex characteristics (Fig. 4), in the same way as for single HP layers (Fig. 2). Its value deviates from the 3/2 value measured in the intrinsic materials for Iex between 0.01 and 100 suns. Furthermore, the μoc-Iex characteristics show that m increases with the excitation density, contrary to what expected from the competition between elementary recombination processes. m varies from ≈ 3/2 to ≈ 2 in single heterojunctions, and from ≈ 1 to ≈ 2 in double heterojunctions.

Figure 4. μoc-Iex characteristics and ideality factor of perovskite-based single and double heterojunctions.

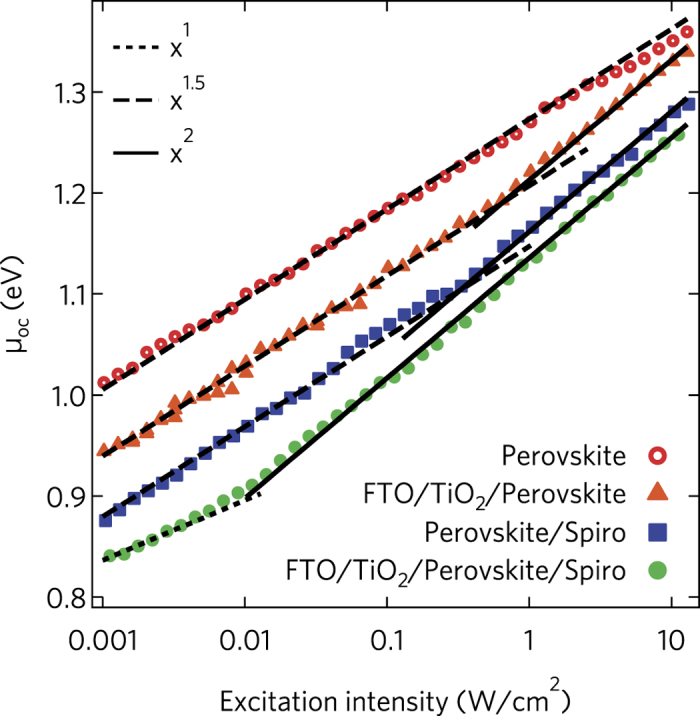
Figure 4

Open in a new tab

Markers represent the measured free energy μoc of electron-hole pairs in perovskite and perovskite-based heterojunctions as a function of the excitation intensity (Iex) delivered by a CW laser at 532 nm. Lines are provided as a guide to the eye to identify the slope of the data. The ideality factor deviates from the 1.5 value of the single hybrid perovskite layer, increasing to 2 when Iex exceeds a threshold that is peculiar to each type of heterojunction.

Possible interface recombination processes at the heterojunction interfaces are sketched in Fig. 3. In a steady-state experiment, electron (hole) transfer from the i-layer to the ETL (HTL) is compensated by electron (hole) back-transfer, preventing charge build-up at both sides of the interface. We attribute the lower EQYPL observed in our perovskite heterojunctions with respect to the HP single layers to the activation of such interface decay channels44,45. Quenching of optical excitations at interfaces has even been exploited to measure the diffusion length in HPs46,47. Interface decay processes are not elementary decays and, as in the case of SRH decays, the ideality factor is expected to increase with the excitation intensity. Excitation-dependent band bending and modification of the energy level alignment close to the junctions, e.g. due to built-in electric fields, could drive non-linear phenomena for the carrier dynamics at the two interfaces. Anyway, the fact that at one sun m ≈ 2 suggests monomolecular recombinations for both electrons and holes (αe ≈ αh ≈ 1).

Discussion

Experimental results provide a detailed assessment of the conversion efficiency of the chemical energy μ into the electrical energy eV, under the assumption of no transport and carrier collection losses, but including all the effective recombination losses. To obtain an explicit estimate of the photoconversion efficiency, let us express the extracted electron (hole) current density from the continuity equation 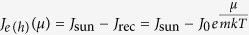Inline graphic, and the external electrical power as Je(h)μ. J0 can be experimentally estimated from the open circuit condition 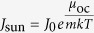Inline graphic. Figure 5 shows eJe(h)(μ) and the condition for maximum chemical energy conversion, with efficiency 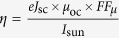Inline graphic (FFμ being the filling factor of the μ-Je(h) characteristics, and eJsc = eJsun). The points in Fig. 5 are the experimental data eJex = eJrec(μoc) from Figs 2 and 4 with the substitution 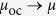Inline graphic29. In the Shockley-Queissier limit, when the solar spectrum is perfectly absorbed down to the bandgap energy, with μrad = 1.33 eV and m = 1, the ultimate limit ηSQ = 30.5% is obtained (eJsc = 25.4 mA/cm2, FFμ = 0.91). In the single HP layer, SRH limits the chemical energy to μoc = 1.16 eV and m = 1.5; furthermore, considering the actual absorption of a 250-nm thick HP film (as typical for solar cells reported in literature), the limiting photoconversion efficiency due to SRH recombination reduces to ηSRH = 23.4% (eJsc = 23.6 mA/cm2, FFμ = 0.86). The strictest limit in the investigated double heterojunctions is set by interface recombinations to μ = 0.97 eV (m ≈ 2), resulting in η = 18.2% (eJsc = 23.6 mA/cm2, FFμ = 0.80). Recently, solar cells have been reported based on HP materials with composite cations, including both organic molecules and the inorganic elements Rb and Cs, with very high external photoluminescence efficiency, up 3.6%8. Assuming no electrical losses, our analysis predicts for such cells a limit efficiency η = 26.2% (d = 400 nm, eJsc = 24.9 mA/cm2, μoc = 1.26, FFμ = 0.83).

Figure 5. Electron (hole) charge current density as a function of the free energy.

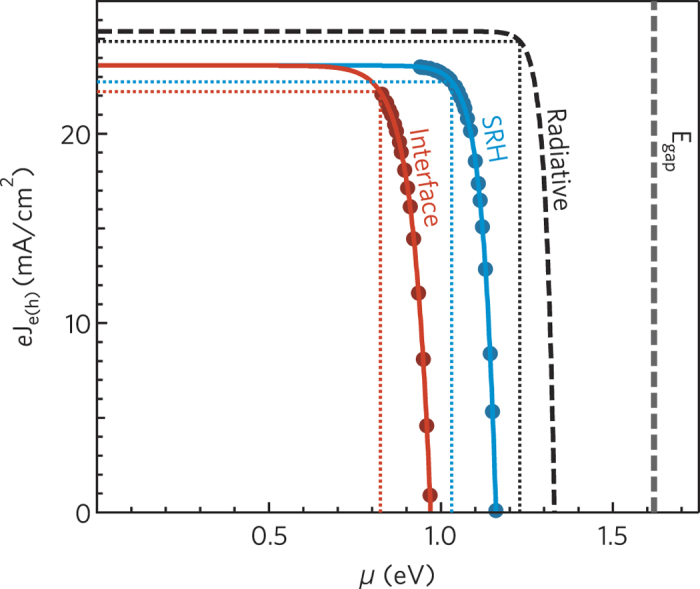
Figure 5

Open in a new tab

Solid lines represent the electron (hole) current Je(h)(μ) = Jsun − Jrec, where Jsun is the excitation current at one sun (film thickness d = 250 nm), 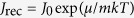Inline graphic is the diode recombination current in which m and J0 are the experimental values of the ideality factor and saturation inverse current assessed from the μ-Iex characteristics (Figs 2 and 4). Full circles stand for Je(h)(μ) estimated from the measured diode current Jrec(μoc) with the substitution μoc → μ. The dotted lines mark the point of maximum extraction of electrical power. Red curves and circles: electron (hole) current density in the double heterojunction; recombination is dominated by interface electron and hole annihilations. Cyan curves and circles: electron (hole) current density in the single hybrid perovskite layer; recombination is due to electron and hole Shockley-Read-Hall annihilations alone. Dashed line: Je(h)(μ) in the Shockley-Queissier limit.

Conclusions

The Shockley-Queissier model provides the reference, ultimate limit performance of single junction photovoltaic devices, assuming only radiative recombinations and neglecting all losses due to charge transport and extraction. We have developed an all-optical experimental method to assess the deterioration of photoconversion performances with respect to the Shockley-Queissier limit due to nonradiative recombinations. To this aim, the proposed approach allows measuring the upper limit to the open-circuit voltage of a solar cell set by nonradiative electron-hole decays in the intrinsic materials and assessing to what extent each interface in the device introduces additional recombination currents. We are able to identify the nature of decay processes, showing that recombinations in single perovskite layers can be described by the Shockley-Read-Hall model in the presence of defects that preferentially trap either electrons or holes. We estimate the ideality factor and the limit of the solar cell efficiency, without any current flowing through the device, therefore avoiding hysteresis, non-ideal contacts and charge transport losses.

Methods

Materials

All materials were purchased from Sigma-Aldrich or Alpha Aesar and used as received. Spiro-MeOTAD was purchased from Lumtec. CH3NH3I was synthesized according to a reported procedure48. CH3NH3 (27.86 ml, 40% in methanol, TCI) and hydroiodic acid (30 ml, 57 wt% in water, Aldrich) were mixed at 0 °C and stirred for 2 h. The precipitate was recovered byevaporation at 50 °C for 1 h. The product was washed with diethyl ether three times and finally dried at 60 °C in a vacuum oven for 24 h.

Sample preparation

Glass substrates (Visiontech) and FTO-coated glass substrates (Solaronix) were cleaned by ultrasonication in a deionized water, 2-propanol and acetone. Substrates were treated to the TL1-washing procedure (washed in double distilled water (Milli-Q water), hydrogen-peroxide (H2O2) and ammonia (NH3) 5:1:1 v/v at 80 °C for 10 minutes), then rinsed in double distilled water prior next depositions. A 80 nm-thick TiO2 dense hole-blocking layer (ETL) was deposited on glass/FTO by spin coating a commercial titaniumdiisopropoxidebis(acetylacetonate) solution (75% in 2-propanol, Sigma-Aldrich) diluted in butanol (0,15 M) twice at 3,000 rpm for 60 sec and annealed at 125 °C. As last step a 0.3 M solution is spin-coated, and annealed at 520 °C. The prepared CH3NH3I and commercial PbI2 (99.99% ultradry, Alfa Aesar) were stirred in a mixture of γ-butyrolactone (GBL) and DMSO (2:1vol/vol; GBL, >99%; DMSO, 99.8%; Sigma-Aldrich) at 60 °C for 12 h, to prepare a solution 1 M. The perovskite precursor solution was coated onto either glass or TiO2/FTO substrate by a consecutive two-step spin-coating process at 1,000 and 4,000 r.p.m for 10 and 60 s, respectively with a dripping of dichloromethane at 10 s to the end. After spin-coating, the films were annealed on a hotplate at 100 °C for 10 min. After cooling to room temperature, either a PMMA solution (80 mg/1 mL chloroform) or the spiro-MeOTAD solution was spin-coated on the perovskite layer at 2,500 r.p.m. for 45 s. A spiro-MeOTAD solution was prepared by dissolving 90 mg of spiro-MeOTAD in 1 ml chlorobenzene (99.8%, Sigma Aldrich), to which were added 28.8 μl of 4-tert-butylpyridine (96%, Sigma-Aldrich), 17.5 μl lithium bis (trifluoromethanesulfonyl)imide (LiTFSI) solution (520 mg LI-TSFI in 1 ml acetonitrile, 99.8%, Sigma-Aldrich). This fabrication process was carried out under controlled atmospheric conditions with a humidity of <1% and a temperature between 20 and 25 °C. From AFM measurements, we determined a perovksite film thickness of 160 nm.

FTO/TiO2/perovskite/spiro-MeOTAD device fabrication

FTO-coated glass substrates (Solaronix) were cleaned by ultrasonication in deionized water, 2-propanol and acetone. A 80 nm-thick TiO2 dense hole-blocking layer (bl-TiO2) was then deposited on the substrates by spin coating at 3,000 rpm for 60 sec and annealed at 520 °C using a commercial titanium diisopropoxide bis(acetylacetonate) solution (75% in 2-propanol, Sigma-Aldrich) diluted in butanol (0,3 M). The prepared CH3NH3I and commercial PbI2 (99%, Alpha Aesar) for the 1 M CH3NH3PbI3 solution were stirred in a mixture of γ-butyrolactone (GBL) and DMSO (2:1 vol/vol; GBL, ≥99%; DMSO, 99.8%; Sigma-Aldrich) at 60 °C for 12 h. Before use, these precursor solutions were filtrated using a hydrophilic PTFE syringe filter (pore size of 22 μm). The filtrated perovskite precursor solution was coated onto bl-TiO2/FTO substrate by a consecutive two-step spin-coating process at 1,000 and 4,000 r.p.m for 10 and 60 s, respectively with a dipping of dicloromethan at 10 sec to the end. After spin coating, the films were annealed on a hotplate at 100 °C for 10 min. After cooling to room temperature, the spiro-MeOTAD solution was spin-coated on the perovskite layer at 2,500 r.p.m. for 45 s. A spiro-MeOTAD solution was prepared by dissolving 90 mg of spiro-MeOTAD in 1 ml chlorobenzene (99.8%, Sigma Aldrich), to which were added 28.8 μl of 4-tert-butylpyridine (96%, Sigma-Aldrich), 17.5 μl lithium bis (trifluoromethanesulfonyl)imide (LiTFSI) solution (520 mg LI-TSFI in 1 ml acetonitrile, 99.8%, Sigma-Aldrich). This fabrication process was carried out under controlled atmospheric conditions with a humidity of <1% and a temperature between 20 and 25 °C. Finally, 80 nm gold was thermally evaporated on top of the device at a pressure of 5 × 10−6 mbar for 30 min to form the back contact. The active area of the complete device was 0.09 cm−2.

Absolute photoluminescence quantum yield

EQYPL was measured according to the method described by de Mello et al.49 using the beam from a diode-pumped Nd:YVO4 CW laser (Millennia V) at 532 nm as excitation. The irradiance of the beam was calculated as Eexc = P/A, where P is the optical power of the beam, measured by a bolometer, and A is beam area, measured using the knife-edge method. The samples were placed into an integrating sphere (Newport 819C-IS-5.3) and both the scattered laser light and the photoluminescence light were collected through a fibre-optic cable (Avantes FC-V200-1-SR) coupled to a grating spectrometer (Princeton Instruments Acton SpectraPro 2500i equipped with a 150 gr/mm, 600 nm blaze grating) and detected by a LN-cooled CCD camera. The laser beam was angled so that its reflection and/or the PL emission did not strike the output port directly. The spectral response of the detection system has been calibrated so that the number of counts is proportional to the number of photons collected. EQYPL was calculated as:

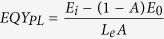graphic file with name srep44629-m32.jpg

where A = (L0 − Li)/L0 and:

(a) Le is the spectrally integrated intensity of the laser striking the inside of the empty integrating sphere;

(b) L0 is the spectrally integrated intensity of the laser striking the inside of the integrating sphere, with the sample inside the sphere but not under direct excitation;

(c) E0 is the spectrally integrated intensity of the photoluminescence from the sample under indirect excitation;

(d) Li is the spectrally integrated intensity of the laser directly illuminating the sample;

(e) Ei is the spectrally integrated intensity of the photoluminescence as a result of direct excitation.

As required by the theoretical framework, the measurements were not corrected for self-absorption.

Time-integrated photoluminescence (TIPL)

Samples were placed in a vacuum chamber and excited with a diode-pumped Nd:YVO4 CW laser (Millennia V) at 532 nm. The photoluminescence was dispersed with a grating spectrometer (Princeton Instruments Acton SpectraPro 2500i equipped with a 150 gr/mm, 600 nm blaze grating) and detected by a LN-cooled CCD camera.

Additional Information

How to cite this article: Sarritzu, V. et al. Optical determination of Shockley-Read-Hall and interface recombination currents in hybrid perovskites. Sci. Rep. 7, 44629; doi: 10.1038/srep44629 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information
srep44629-s1.pdf (4.3MB, pdf)

Acknowledgments

We thank M. Aresti, C. Cannas, A. Geddo Lehmann, C. Figus, A. Filippetti, M. Mainas, A. Mattoni, G. Mula and A. Musinu for useful discussions. We are indebted to Dr A. Cardini and the INFN (National Institute for Nuclear Physics) for lending us the integrating sphere for the quantum yield measurements. This work has been funded by Regione Autonoma della Sardegna through PO-FSE Sardegna 2007–2013, L.R. 7/2007, ‘Progetti di ricerca di base e orientata’, Projects n. CRP3-114, CRP-17571, CRP-18353, CRP-18013 and CRP- 24978, and by MIUR (Italian Ministry of University and Research) through Progetto di ricerca PON R&C 2007–2013 (Avviso n. 713/Ric. del 29 ottobre 2010) MAAT-Molecular NAnotechnology for HeAlth and EnvironmenT (Project Number: PON02_00563_3316357) and PRIN PERrovskite-based Solar cells: towards high Efficiency and lOng-term stability (PERSEO), project id 20155LECAJ. D.M. gratefully acknowledges financial support by Regione Autonoma della Sardegna, Project n° 15 ‘New materials for photovoltaics solar energy conversion’, P.O.R. Sardegna F.S.E. Operational Programme of the Autonomous Region of Sardinia, European Social Fund 2007–2013 - Axis IV Human Resources, Objective l.3 and Line of Activity l.3.1 ‘Avviso di chiamata per ilfinanziamento di Assegni di Ricerca.’ We acknowledge Progetto di ricerca PON R&C 2007–2013 (Avviso n. 713/Ric. del 29 ottobre 2010) MAAT-Molecular NAnotechnology for HeAlth and EnvironmenT (Project Number: PON02_00563_3316357). S.C. acknowledges Regione Puglia and ARTI for funding FIR - future in research projects “PeroFlex” project no. LSBC6N4 and” HyLight” project no. GOWMB21.

Footnotes

The authors declare no competing financial interests.

Author Contributions V.S. and N.S. carried out the optical experiments; D.M., X.C., S.C., S.M., A.R. prepared and characterized the materials; V.S. and G.B. analysed the data; V.S., N.S. A.M., F.Q., M.S., G.B., S.C., S.M., A.R. discussed the results; V.S., M.S. and G.B. wrote the manuscript.

References

  1. Chapin D. M., Fuller C. S. & Pearson G. L. A New Silicon p-n Junction Photocell for Converting Solar Radiation into Electrical Power. J. Appl. Phys. 25, 676 (1954). [Google Scholar]
  2. Best Research-Cell Efficiencies. NREL. nrel.gov Available at: http://www.nrel.gov/pv/assets/images/efficiency_chart.jpg (Accessed: 27 October 2016) (2016).
  3. Tsai H. et al. High-efficiency two-dimensional Ruddlesden– Popper perovskite solar cells. Nature 536, 312–316 (2016). [DOI] [PubMed] [Google Scholar]
  4. Green M. A., Ho-Baillie A. & Snaith H. J. The emergence of perovskite solar cells. Nature Photon 8, 506–514 (2014). [Google Scholar]
  5. Yang W. S. et al. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 348, 1234–1237 (2015). [DOI] [PubMed] [Google Scholar]
  6. Jung H. S. & Park N.-G. Perovskite Solar Cells: From Materials to Devices. Small 11, 10–25 (2015). [DOI] [PubMed] [Google Scholar]
  7. Sum T. C. & Mathews N. Advancements in perovskite solar cells: photophysics behind the photovoltaics. Energy Environ. Sci. 7, 2518–2534 (2014). [Google Scholar]
  8. Saliba M. et al. Incorporation of rubidium cations into perovskite solar cells improves photovoltaic performance. Science 354, 206–209 (2016). [DOI] [PubMed] [Google Scholar]
  9. Bella F. et al. Improving efficiency and stability of perovskite solar cells with photocurable fluoropolymers. Science 354, 203–206 (2016). [DOI] [PubMed] [Google Scholar]
  10. Swarnkar A. et al. Quantum dot–induced phase stabilization of α-CsPbI3 perovskite for high-efficiency photovoltaics. Science 354, 92–95 (2016). [DOI] [PubMed] [Google Scholar]
  11. Shockley W. & Queisser H. Detailed Balance Limit of Efficiency of p‐n Junction Solar Cells. J. Appl. Phys. 32, 510–519 (1961). [Google Scholar]
  12. McMeekin D. P. et al. A mixed-cation lead mixed-halide perovskite absorber for tandem solar cells. Science 351, 151–155 (2016). [DOI] [PubMed] [Google Scholar]
  13. Eperon G. E. et al. Perovskite-perovskite tandem photovoltaics with optimized band gaps. Science 354, 861–865 (2016). [DOI] [PubMed] [Google Scholar]
  14. Manser J. S. & Kamat P. V. Band filling with free charge carriers in organometal halide perovskites. Nature Photon 8, 737–743 (2014). [Google Scholar]
  15. Filippetti A. & Mattoni A. Hybrid perovskites for photovoltaics: Insights from first principles. Phys. Rev. B 89, 125203 (2014). [Google Scholar]
  16. Yang Y. et al. Observation of a hot-phonon bottleneck in lead-iodide perovskites. Nat Photon 10, 53–59 (2015). [Google Scholar]
  17. Grancini G. et al. Role of microstructure in the electron–hole interaction of hybrid lead halide perovskites. Nat Photon 9, 695–701 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Marchioro A., Teuscher J., Friedrich D. & Kunst M. Unravelling the mechanism of photoinduced charge transfer processes in lead iodide perovskite solar cells. Nature Photon 8, 250–255 (2014). [Google Scholar]
  19. Saba M., Quochi F., Mura A. & Bongiovanni G. Excited State Properties of Hybrid Perovskites. Acc. Chem. Res 49, 166–173 (2015). [DOI] [PubMed] [Google Scholar]
  20. Polman A., Knight M., Garnett E. C., Ehrler B. & Sinke W. C. Photovoltaic materials: Present efficiencies and future challenges. Science 352, 307 (2016). [DOI] [PubMed] [Google Scholar]
  21. Park N.-G., Grätzel M., Miyasaka T., Zhu K. & Emery K. Towards stable and commercially available perovskite solar cells. Nature Energy 1, 16152 (2016). [Google Scholar]
  22. Ball J. M. & Petrozza A. Defects in perovskite-halides and their effects in solar cells. Nature Energy 1, 16149 (2016). [Google Scholar]
  23. Shockley W. The Theory of p-n Junctions in Semiconductors and p-n Junction Transistors. Bell Labs Technical Journal 28, 435–489 (1949). [Google Scholar]
  24. Green M. A. Radiative efficiency of state-of-the-art photovoltaic cells. Prog. Photovolt: Res. Appl. 20, 472–476 (2012). [Google Scholar]
  25. Tvingstedt K. et al. Radiative efficiency of lead iodide based perovskite solar cells. Sci. Rep. 4, 6071 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Tress W. et al. Predicting the open-circuit voltage of CH3NH3PbI3 perovskite solar cells using electroluminescence and photovoltaic quantum efficiency spectra: The role of radiative and non-radiative recombination. Adv. Energy Mater. 5, 1400812 (2015). [Google Scholar]
  27. Colella S., Mazzeo M., Rizzo A., Gigli G. & Listorti A. The Bright Side of Perovskites. J Phys Chem Lett 7, 4322–4334 (2016). [DOI] [PubMed] [Google Scholar]
  28. Nelson J. The physics of solar cells. (Imperial College Press, 2003). [Google Scholar]
  29. Würfel P. & Würfel U. Physics of solar cells: from basic principles to advanced concepts. (Wiley-VCH Verlag GmbH & Co. KGaA, 2009). [Google Scholar]
  30. Agarwal S. et al. On the Uniqueness of Ideality Factor and Voltage Exponent of Perovskite-Based Solar Cells. J Phys Chem Lett 5, 4115–4121 (2014). [DOI] [PubMed] [Google Scholar]
  31. Shi J. et al. Hole-conductor-free perovskite organic lead iodide heterojunction thin-film solar cells: High efficiency and junction property. Appl. Phys. Lett. 104, 063901 (2014). [Google Scholar]
  32. Shockley W. & Read W. T. Jr. Statistics of the Recombinations of Holes and Electrons. Phys. Rev 87, 835–842 (1952). [Google Scholar]
  33. Wetzelaer G. J. A. H. et al. Trap‐Assisted Non‐Radiative Recombination in Organic–Inorganic Perovskite Solar Cells. Adv. Mater. 27, 1837–1841 (2015). [DOI] [PubMed] [Google Scholar]
  34. Bi D. et al. Efficient luminescent solar cells based on tailored mixed-cation perovskites. Sci Adv 2, e1501170 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Tvingstedt K. & Deibel C. Temperature Dependence of Ideality Factors in Organic Solar Cells and the Relation to Radiative Efficiency. Adv. Energy Mater. 6, 1502230 (2016). [Google Scholar]
  36. Pockett A. et al. Characterization of Planar Lead Halide Perovskite Solar Cells by Impedance Spectroscopy, Open-Circuit Photovoltage Decay, and Intensity-Modulated Photovoltage/Photocurrent Spectroscopy. J. Phys. Chem. C 119, 3456–3465 (2015). [Google Scholar]
  37. Würfel P. The chemical potential of radiation. J. Phys. C: Solid State Phys. 15, 3967–3985 (1982). [Google Scholar]
  38. El-Hajje G. et al. Quantification of spatial inhomogeneity in perovskite solar cells by hyperspectral luminescence imaging. Energy Environ. Sci. 9, 2286–2294 (2016). [Google Scholar]
  39. Rau U. Reciprocity relation between photovoltaic quantum efficiency and electroluminescent emission of solar cells. Phys. Rev. B 76, 085303 (2007). [Google Scholar]
  40. Saba M. et al. Correlated electron–hole plasma in organometal perovskites. Nat Comms 5, 5049 (2014). [DOI] [PubMed] [Google Scholar]
  41. Delugas P., Filippetti A. & Mattoni A. Methylammonium fragmentation in amines as source of localized trap levels and the healing role of Cl in hybrid lead-iodide perovskites. Phys. Rev. B 92, 045301 (2015). [Google Scholar]
  42. Cadelano M. et al. Can Trihalide Lead Perovskites Support Continuous Wave Lasing? Advanced Optical Materials 3, 1557–1564 (2015). [Google Scholar]
  43. Wehrenfennig C., Eperon G. E., Johnston M. B., Snaith H. J. & Herz L. M. High Charge Carrier Mobilities and Lifetimes in Organolead Trihalide Perovskites. Adv. Mater. 26, 1584–1589 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zhou H. et al. Interface engineering of highly efficient perovskite solar cells. Science 345, 542–546 (2014). [DOI] [PubMed] [Google Scholar]
  45. Correa-Baena J.-P. et al. Highly efficient planar perovskite solar cells through band alignment engineering. Energy Environ. Sci. 8, 2928–2934 (2015). [Google Scholar]
  46. Xing G. et al. Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic Ch3NH3PbI3. Science 342, 344–347 (2013). [DOI] [PubMed] [Google Scholar]
  47. Stranks S. D. et al. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 342, 341–344 (2013). [DOI] [PubMed] [Google Scholar]
  48. Lee M. M., Teuscher J., Miyasaka T., Murakami T. N. & Snaith H. J. Efficient Hybrid Solar Cells Based on Meso-Superstructured Organometal Halide Perovskites. Science 338, 643–647 (2012). [DOI] [PubMed] [Google Scholar]
  49. De Mello J. C., Wittmann H. F. & Friend R. H. An Improved Experimental Determination of External Photoluminescence Quantum Efficiency, Adv. Mater. 9, 230 (1997). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep44629-s1.pdf (4.3MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES