Understanding band gaps of solids in generalized Kohn–Sham theory

Significance

Semiconductors and insulators have a fundamental energy gap and absorb light at a continuum of photon energies above this gap. They also have a band structure of one-electron energies, and a band gap separating unoccupied from occupied one-electron states. When should these gaps be equal? It is known that they are not equal in the exact Kohn–Sham density-functional theory but are equal in commonly used density-functional approximations, such as the generalized gradient approximation (GGA). We show here that they are also equal (and improved) in higher level approximations, such as the meta-GGA or the hybrid of GGA with exact exchange, when the effective one-electron potential is not constrained to be a multiplication operator.

Abstract

The fundamental energy gap of a periodic solid distinguishes insulators from metals and characterizes low-energy single-electron excitations. However, the gap in the band structure of the exact multiplicative Kohn–Sham (KS) potential substantially underestimates the fundamental gap, a major limitation of KS density-functional theory. Here, we give a simple proof of a theorem: In generalized KS theory (GKS), the band gap of an extended system equals the fundamental gap for the approximate functional if the GKS potential operator is continuous and the density change is delocalized when an electron or hole is added. Our theorem explains how GKS band gaps from metageneralized gradient approximations (meta-GGAs) and hybrid functionals can be more realistic than those from GGAs or even from the exact KS potential. The theorem also follows from earlier work. The band edges in the GKS one-electron spectrum are also related to measurable energies. A linear chain of hydrogen molecules, solid aluminum arsenide, and solid argon provide numerical illustrations.

The most basic property of a periodic solid is its fundamental energy gap G, which vanishes for a metal but is positive for semiconductors and other insulators. G dominates many properties. As the unbound limit of an exciton series, G is an excitation energy of the neutral solid, but it is defined here as a difference of ground-state energies: If $E\left(M\right)$ is the ground-state energy for a solid with a fixed number of nuclei and M electrons, and if $M=N$ for electrical neutrality, then

$$G=I\left(N\right)-A\left(N\right)=[E(N-1)-E\left(N\right)]-[E\left(N\right)-E(N+1)]$$ [1]

is the difference between the first ionization energy $I\left(N\right)$ and the first electron affinity $A\left(N\right)$ of the neutral solid. Whereas I and A can be measured for a macroscopic solid, they can be computed directly (as ground-state energy differences) either by starting from finite clusters and extrapolating to infinite cluster size or (for I-A) by starting from a finite number of primitive unit cells, with periodic boundary condition on the surface of this finite collection, and extrapolating to an infinite number. Here we shall follow both approaches, which have been discussed in a recent study (1). (The energy to remove an electron to infinite separation cannot depend upon the crystal face through which it is removed, although the energy to remove an electron to a macroscopic separation, but much smaller than the dimensions of that face, may so depend. The gap is of course a bulk property.)

Band-Gap Problem in Kohn–Sham Density-Functional Theory

Kohn–Sham density-functional theory (2, 3) is a formally exact way to compute the ground-state energy and electron density of M interacting electrons in a multiplicative external potential. This theory sets up a fictitious system of noninteracting electrons with the same ground-state density as the real interacting system, found by solving self-consistent one-electron Schrödinger equations. These electrons move in a multiplicative effective Kohn–Sham (KS) potential, the sum of the external and Hartree potentials and the derivative of the density functional for the exchange–correlation (xc) energy, $E_{xc}[n_{\uparrow },n_{\downarrow }]$, which must be approximated. The simplest local spin-density approximation (LSDA) (2) is already usefully accurate for many solids. Better still are generalized gradient approximations (GGAs) (e.g., ref. 4), meta-GGAs (e.g., refs. 5 and 6), and hybrids of GGA with exact exchange (e.g., refs. 7 and 8). The additional ingredients in higher-level functionals can in principle satisfy more exact constraints, or fit data better, achieving higher accuracy. KS theory has become the most widely used (3) method to calculate the ground-state energies, energy differences, electron densities, and equilibrium structures of molecules and solids, and, with less justification, the electronic band structures of solids. For a solid, KS theory produces a band structure, one-electron energies as functions of Bloch wavevector and band index, in which there can be a nonzero band gap,

$$g={\epsilon }^{LU}-{\epsilon }^{HO},$$ [2]

the difference between the lowest-unoccupied (LU) and highest-occupied (HO) one-electron energies. We show here that under common computational conditions for solids, g equals G for a given approximate functional. How close g is to the experimental gap depends on how accurate the functional is for the ground-state energy difference G (strongly and comparably underestimated by LSDA and GGAs, but better estimated by meta-GGAs and especially hybrids).

In principle, should the band gap g equal the fundamental energy gap G? In the early 1980s, band-structure calculations were accurate enough to show that LSDA band gaps for semiconductors were often about half the measured fundamental energy gaps. Was this a failure of the LSDA effective potential to mimic the exact KS potential, or an inability of the exact KS potential (for the neutral solid) to predict the fundamental gaps, or both?

Regarding the fundamental gap G as an excitation energy, we do not expect it to equal the band gap g of the exact KS potential. But, thinking of it as a ground-state energy difference, we might hope that it is. Williams and von Barth (9) gave a clear argument to support this hope, based on three assumptions: (i) Janak’s theorem (10, 11): The one-electron energies of KS theory are derivatives of the total energy with respect to occupation number, between integer occupations, in both finite and extended systems. This is unquestionably true. (ii) When an electron is added to or removed from a solid, the density change is infinitesimal and periodic. This assumption, only possible for an extended system, is often true, although there may be exceptions in which added electrons or holes get stuck in localized states; see refs. 12 and 13 for possible examples. (iii) When an electron is added or removed, the KS potential changes only infinitesimally. This assumption seemed to follow so naturally from (ii) that it was only implicit in the argument, yet assumption (iii) is incorrect for the exact KS potential.

Other work (14–17) of the early 1980s showed that the exact KS potential jumps up by an additive-constant discontinuity when an electron is added to a neutral solid, making

$$G^{exact}=g^{exact}+xc\_discontinuity.$$ [3]

The discontinuity spoils the interpretation of g, shifting the one-electron energies without changing the density. The KS potential is a mathematical fiction, acting on noninteracting electrons to yield the true ground-state density of the neutral solid and making the one-electron energy for the highest partly occupied one-electron state equal to the true chemical potential $\mu =\partial E/\partial M$, which is itself discontinuous at zero temperature for an insulator when M crosses N. The xc discontinuity is absent in the LSDA and GGA approximations to the multiplicative xc potential, for which (17)

$$G^{approx}=g^{approx}.$$ [4]

In Eq. 4, G of Eq. 1 and g of Eq. 2 are evaluated with the same approximate functional. Whereas GGA improves ground-state energies and electron densities over LSDA, both approximations yield nearly the same band gaps g and hence fundamental gaps G, excepting some special GGAs (18). It has long been known (17) that Eq. 4 is true in LSDA and GGA, and it has been suspected (e.g., refs. 15 and 17) that LSDA and GGA band gaps are close to exact KS band gaps (but not to true fundamental gaps).

Band-Gap Problem in Generalized KS Theory

A simple, self-contained proof of our theorem will be given here. Refs. 19–22 by themselves also imply this result, as discussed in a later section.

Based mostly upon empiricism, realistic fundamental gaps for semiconductors (e.g., refs. 23 and 24) have been estimated from band gaps of hybrid functionals in generalized KS (GKS) theory, which is also an excellent starting point for simple quasi-particle corrections (25). A global hybrid replaces a fraction [e.g., 25% (7, 26, 27)] of GGA exchange with that of Hartree–Fock, and replaces the same fraction of the GGA exchange potential with that of Hartree–Fock (an integral operator, not a multiplication operator). Screened hybrids (e.g., ref. 8) additionally screen the interelectronic Coulomb potential in the exchange term, and typically improve results for semiconductors (23).

We argue that Eq. 4 is also valid within typical approximations in GKS theory, as typically implemented, extending the argument of Williams and von Barth (9) from KS to GKS theory. Thus, the improvement in the band gap that comes from using a hybrid functional reflects a corresponding improvement in the value for G of Eq. 1. Our detailed argument, presented in Appendix B: Theoretical Methods, generalizes assumption (i) of the Williams–von Barth argument (9) from KS to GKS theory, and notes that the GKS potentials, like the LSDA and GGA and unlike the exact one, have no discontinuity under change of particle number, consistent with refs. 19–22.

Although there is a formally exact GKS theory (28), here we view GKS as a small step out of KS theory, in which one can use nonempirical approximations to $E_{xc}$ that are constructed to satisfy the known exact constraints of KS theory. In rigorous KS density-functional theory, the occupied KS one-electron states are demonstrably implicit functionals of the electron density that can be used to construct a density-functional approximation, such as an explicit functional of the KS one-electron density matrix. For example, use the noninteracting kinetic energy density to construct a meta-GGA (e.g., ref. 5), or use the full KS density matrix to construct the Hartree–Fock exchange energy for a global hybrid as in ref. 7. Because the one-electron states are only implicit functionals of the density, the KS potential can be constructed only by the optimized effective potential (OEP) method (29). It is computationally easier to find the variationally optimized potential that minimizes the energy with respect to the noninteracting density matrix. The resulting GKS potential is not a multiplication operator but is in practice continuous (does not change when one delocalized electron is added to or subtracted from a solid) and self-adjoint for differentiable functionals of the noninteracting density matrix. It is an integral (Fock) operator (11) for hybrids but a differential operator (30, 31) for meta-GGAs, the same operator for occupied and unoccupied one-electron states.

The step outside KS to GKS barely affects the occupied one-electron states, the electron density, and the total energy, but not so the one-electron energies. This was first shown by comparing exchange-only OEP (KS) and Hartree–Fock (GKS) results for atoms (29, 32), and more recently by comparing the corresponding KS and GKS implementations of meta-GGAs (exchange and correlation together) for atoms (33) and solids (31). They produce closely similar results for total energies, but the KS meta-GGA band gap is close to that of LSDA and GGA, whereas the GKS meta-GGA band gap is significantly larger and more realistic.

Within xc approximations using the noninteracting density matrix, relaxing the KS demand for a multiplicative effective potential is a “practical” approximation with an unexpected benefit: It yields the interpretation of Eq. 4 for the GKS band gap of a solid, explaining how meta-GGAs and especially hybrids can improve the estimation of the fundamental energy gap of a solid: For a typical approximate functional, the GKS band gap g is the ground-state energy difference G. Improvements in G correlate at least roughly with other improvements in ground-state energy differences for integer electron numbers, relevant to atomization energies and lattice constants.

Numerical Demonstration

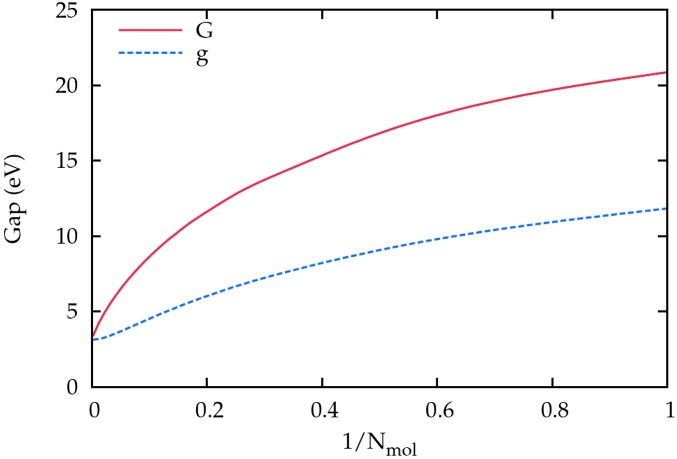
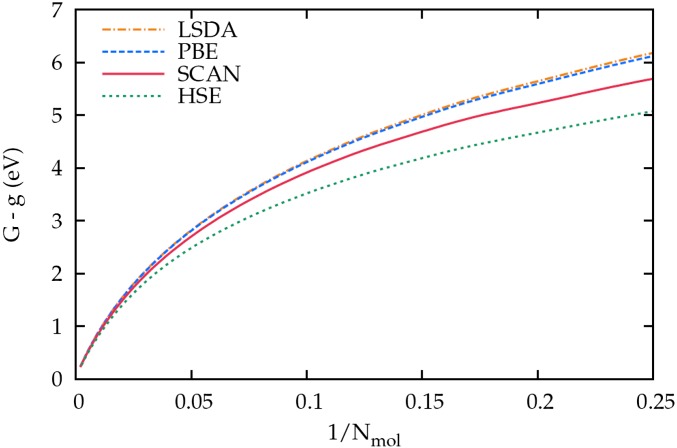
Because computational effort typically scales like the cube of the number of atoms, finite 3- and even 2D clusters are much harder to converge to the mesoscopic length scale, so we consider as a first model a finite 1D linear chain of realistic H₂ molecules. The separation between the nuclei of neighboring molecules is taken to be 1.25× the separation between nuclei within a molecule (0.74 Å), to produce a gap of order 3 or 4 eV. To demonstrate our conclusions, the model does not need to be realistic, and its exact gap does not need to be known. With an even number (two) of electrons per unit cell, this system is a band insulator. We consider chains with 1–500 molecules. At large numbers $N_{mol}$ of molecules, the correction to the limit $N_{mol}\to \infty$ is (13, 34) of order $1/N_{mol}$, simplifying the extrapolation. Figs. 1 and 2 show that for all tested approximate functionals, $G-g$ tends to zero as $N_{mol}\to \infty$. Table 1 shows limiting values. Within numerical accuracy, as $N_{mol}\to \infty$, $I\to -{\epsilon }^{HO}$, $A\to -{\epsilon }^{LU}$, and $G\to g$.

Fig. 1.

PBE GGA fundamental gap G and band gap g for a linear chain of N_mol H₂ molecules. Note that G converges to the limit $N_{mol}\to \infty$ much more slowly than g does.

Fig. 2.

Difference between the fundamental gap $G=I-A$ and the GKS band gap $g={\epsilon }^{LU}-{\epsilon }^{HO}$ for a linear chain of $N_{mol}$ hydrogen molecule.

Table 1.

Ionization energy I, electron affinity A, and fundamental gap $G=I-A$ of an infinite linear chain of H₂ molecules, evaluated by extrapolation from finite chains, and the band edges ${\epsilon }^{HO}$, ${\epsilon }^{LU}$ and band gap $g={\epsilon }^{LU}-{\epsilon }^{HO}$, in the LSDA (2), PBE GGA (4), SCAN meta-GGA (5), and HSE06 range-separated hybrid (8) functionals

eV	(I+A)/2	I	-εHO	A	-εLU	G	g
LSDA	1.65	3.14	3.13	0.16	0.17	2.98	2.96
PBE	1.67	3.24	3.23	0.09	0.10	3.15	3.13
SCAN	1.68	3.33	3.31	0.01	0.02	3.32	3.29
HSE06	1.82	3.92	3.91	−0.29	−0.28	4.21	4.18

The extrapolated band energies agree closely with those from a periodic-boundary-condition calculation (shown). $(I+A)/2$, the energy difference from the gap center to the vacuum level (15), depends only weakly on the approximation.

The positive ions show delocalization of the extra positive charge over the finite chain, even without periodic boundary conditions, as expected from the approximate functionals studied here. The negative ions are resonances, with negative electron affinity of the chain, captured by the finite basis set. But, the resonance can evolve smoothly (35) to a bound state with positive electron affinity as the chain length grows. In contrast to the situation for atoms and molecules, the resonant one-electron states of bulk solids can be converged with respect to basis set.

Ref. 36 states without an explicit proof a major result proved here: For a hybrid functional implemented in a generalized KS scheme, the band gap equals the fundamental gap within the same approximation. Refs. 36 and 37 show how to calculate the fundamental gaps of real extended solids from a given functional without extrapolating from clusters of finite size (and ref. 37 thereby finds realistic band gaps for many solids from the random phase approximation, by a method different from that of ref. 38). This makes it possible to demonstrate our conclusions for real 3D solids using a computer code with periodic boundary conditions.

To that end, we report calculations for the semiconductor aluminum arsenide and the large-gap insulator solid argon with the Perdew–Burke–Ernzerhof (PBE) GGA (4) and the PBE0 hybrid (7, 26, 27) functionals as representatives for KS and GKS methods, via the approach of refs. 36 and 37. Regular grids of n × n × n k points containing the Γ-point are used, corresponding to a collection of n × n × n primitive unit cells in periodic boundary conditions. For n → ∞ an infinite periodic solid would be obtained, forbidding symmetry-breaking localization of the added electron or hole, which we do not expect for the solids and functionals considered here. Symmetry breaking (forming polarons) can be captured by a related supercell approach (39). A self-consistent calculation for the neutral system yields a band gap g and an energy E(N). Removal of one electron from the HO orbital or one-electron state (the k point at the top of the valence band), while keeping the other occupations and orbitals unchanged, yields the non–self-consistent E_non-SCF(N − 1), whereas allowing orbital relaxation yields the self-consistent E_SCF(N − 1). Contributions to the Hartree energy and Hartree potential from the zero reciprocal lattice vector are not taken into account in the charged systems, or (as usual) in the neutral ones. This long-known approach for charged systems (40) is better justified for bulk periodic solids than for other cases (41). Thus, without any code modification, a finite energy E(N − 1) is obtained. An ionization potential I(N) is just the difference E(N − 1) − E(N), where neither energy is divided by the number of primitive unit cells. An energy E(N + 1) is obtained analogously by adding one electron to the k point representing the bottom of the conduction band. From Eq. 1 the fundamental energy gaps G_non-SCF and G_SCF, for the cases without and with orbital relaxation, respectively, are calculated. Convergence with mesh size is rapid for PBE. For PBE0, convergence is accelerated by the method of ref. 42. No physical (measurable) interpretation is intended for the gaps in Tables 2 and 3, except in the limit of large n.

Table 2.

KS (PBE) and OEP/KS and GKS (PBE0) band gap g and fundamental energy gaps G of solid AlAs, calculated according to Eq. 1 with orbitals of the neutral N-electron system G_non-SCF, or with orbitals of separate self-consistent calculations of N-, (N −1)-, and (N + 1)- electron systems G_SCF, in electron volts, as described in the text

	PBE			PBE0
Grid size	g	Gnon-SCF	GSCF	gOEP	g	Gnon-SCF	GSCF
2 × 2 × 2	1.162	1.164	1.131	1.276	2.669	2.681	2.645
4 × 4 × 4	1.321	1.324	1.321	1.490	2.635	2.639	2.638
6 × 6 × 6	1.345	1.346	1.344	1.526	2.598	2.599	2.599
8 × 8 × 8	1.349	1.349	1.348	1.534	2.583	2.584	2.584
10 × 10 × 10	1.349	1.349	1.349	1.537	2.577	2.577	2.577
12 × 12 × 12	1.349	1.349	1.349	1.536	2.575	2.575	2.575

The experimental band gap (52) of AlAs is 2.23 eV.

Table 3.

KS(PBE) and OEP/KS and GKS(PBE0) band gap g and fundamental energy gaps G of solid Ar, calculated according to Eq. 1 with orbitals of the neutral N-electron system G_non-SCF, or with orbitals of separate self-consistent calculations of N-, (N − 1), and (N + 1)-electron systems G_SCF, in electron volts, as discussed in the text

	PBE			PBE0
Grid size	g	Gnon-SCF	GSCF	gOEP	g	Gnon-SCF	GSCF
1 × 1 × 1	7.621	9.130	8.482	7.901	12.079	11.944	11.311
2 × 2 × 2	8.640	8.793	8.658	8.831	10.947	11.065	10.948
3 × 3 × 3	8.688	8.735	8.694	8.923	11.091	11.108	11.073
4 × 4 × 4	8.691	8.711	8.699	8.938	11.120	11.123	11.108
5 × 5 × 5	8.692	8.702	8.693	8.942	11.121	11.126	11.119
6 × 6 × 6	8.692	8.697	8.693	8.944	11.122	11.126	11.122
7 × 7 × 7	8.692	8.695	8.692	8.945	11.123	11.126	11.123
8 × 8 × 8	8.692	8.694	8.692	8.945	11.123	11.125	11.124

The experimental band gap (53) of Ar is 14.20 eV. For a recent comparison of GKS band gaps for many solids from GGA hybrid functionals, including PBE0 and HSE, see ref. 54.

Tables 2 and 3 show that all three gaps, g, G_non-SCF, and G_SCF, rapidly converge toward each other. The convergence of G_non-SCF and G_SCF toward each other demonstrates that orbital relaxation upon removal or addition of an electron does not play a role in infinite periodic solids, whereas the convergence of g and G_SCF toward each other represents a numerical demonstration of the theorem of this work. Comparison with the experimental gaps in the table legends shows that, as expected, the 25% exact exchange in PBE0 can be too much for small-gap solids like AlAs, and too little for large-gap solids like Ar. As expected (15, 17), the OEP or KS band gap g for PBE0 is closer to the PBE KS value than to the PBE0 GKS value.

Relation to Other Previous Work

The relation between GKS frontier orbitals and electron addition/removal energies was first shown in refs. 19–22 for both extended and finite systems and was demonstrated numerically for molecules in ref. 19. Refs. 19–22 by themselves imply our main result. Ref. 19 derives the generalized Janak theorem for a differentiable functional of the one-particle density matrix (in its equation 10), namely, the GKS LU/HO orbital energies are the chemical potentials for electron addition/removal for both finite and extended systems, in a way that differs from the derivation in our theoretical methods section. Refs. 19 and 20 show that the GKS one-electron energy gap matches the GKS derivative gap––the discontinuity in chemical potentials for electron addition and removal (equation 5 of ref. 20), which is equal to G for the exact functional and for functionals with linear behavior in M on either side of N, but generally differs from G for finite systems with approximate functionals (equation 6 of ref. 20). Ref. 20 further shows that the $E\left(M\right)$ curves are linear over M on either side of N for approximate functionals in periodic solids, and also for nonperiodic systems as $N\to \infty$ when the approximate functionals have delocalization error. But, the GKS derivative gap is not equal to G for nonperiodic systems as $N\to \infty$ for functionals with localization error, such as hybrid functionals with high fractions of exact exchange that localize an added electron or hole (20). Combined, these statements yield our main conclusion.

For KS methods using the OEP method (29) to construct the xc potential corresponding to orbital-dependent energy functionals, e.g., the exact exchange energy, the KS band gap g, and the fundamental energy gap G are different, as mentioned above. Indeed, OEP potentials do not determine an additive constant because the electron number is kept fixed. If the KS band structures are adjusted by an appropriate shift of the gap, as in ref. 36, they can be transformed into approximate quasi-particle band structures.

Conclusions

The fundamental energy gap is the most basic property of a periodic solid. It cannot be found from a single KS band-structure calculation, even with the unattainable exact density functional. Surprisingly, high-level approximations, implemented in an efficient generalized KS scheme, yield band gaps equal to the fundamental gap for a given approximate functional. Future all-purpose nonempirical approximate functionals could predict usefully correct gaps for most solids. The band edges (43) in the GKS one-electron spectrum, relevant to interface formation and redox catalysis, can also be interpreted as measurable energy differences, as shown by Eq. 6 and illustrated in Table 1. They can be found in principle by extrapolating the GKS one-electron energies of a slab or cluster.

Typical approximate functionals, as typically implemented, obey Eq. 4, as previously known (17) only for LSDA and GGA. For 3D solids (31), there is little or no improvement in G^approx from LSDA to GGAs, but substantially more from GGAs to fully nonlocal functionals, where the nonlocality of the density dependence and the usefulness of the band gap g^approx increase further from meta-GGAs to hybrids. This suggests that, in solids, the xc effects can be more long-ranged (e.g., ref. 23) than in atoms and small molecules.

The PBE0 and Heyd–Scuseria–Ernzerhof 2006 (HSE06) hybrids contain 25% of exact exchange, globally or at intermediate range, chosen to yield accurate atomization energies for molecules and related moderate-gap systems at integer electron number. The nonlinear variation of approximate total energy with electron number between adjacent integers is a problem in finite systems, but vanishes in typical solids (1, 20). PBE0 and especially HSE06 yield realistic GKS gaps for typical semiconductors. But, they can over- or underestimate gaps of other solids. For example, molecular crystals seem to need 1/ε of long-range exact exchange (44), where ε is the dielectric constant (45).

Appendix A: Computational Methods

The self-consistent all-electron results for the chain of hydrogen molecules reported here were found using the Gaussian code (46) with a small cc-pvDZ basis set, to speed up the hybrid calculations for the longer chains. Many results were checked with the ADF (47) (TZP basis) and FHI-aims (48) (NAO-VCC-2Z basis) codes. The effect of increasing the basis from cc-pvDZ to TZP is to increase the $N_{mol}\to \infty$ limits of I and A in PBE by 0.14 and 0.10 eV, respectively, and to stabilize the negative-ion resonances for some of the larger finite chains. All codes show $G-g\to \sim 0.02$ eV, which we attribute to the slow convergence of $G$ with increasing system size (Fig. 1). All extrapolations display the increase of I and decrease of A from LSDA to HSE06.

The AlAs and Ar calculations were carried out with the plane-wave program MCEXX (49) using norm-conserving PBE pseudopotentials generated by the code of ref. 50, which is based on the Troullier–Martins scheme (51). The cutoffs used for the construction of the pseudopotentials are the same as those used in ref. 37. In principle, the pseudopotential for PBE0 should be different from that for PBE, but the difference is irrelevant to our demonstration. For AlAs a lattice parameter of 5.66 Å and a plane-wave cutoff of 15 a.u. were used. The corresponding values for Ar were 5.26 Å and 30 a.u.

Appendix B: Theoretical Methods

Here, we derive the generalized Janak theorem and prove that the band gap and band edges of generalized KS theory are the appropriate ground-state energy differences, for a given approximate functional. In any constrained minimization, the Lagrange multiplier is the derivative of the minimized quantity with respect to the value of the constraint. Consider minimizing the orbital functional $E_v[\left\{f_j\right\},\left\{{\psi }_j\right\}]$, where $n\left(\overrightarrow{r}\right)={\displaystyle \sum _i{f}_i}{\left|{\psi }_i\left(\overrightarrow{r}\right)\right|}^2$ and the occupation numbers are restricted to the range $0\le f_i\le 1$ with ${\displaystyle \sum _i{f}_i}=N$, subject to constraints $f_j{\displaystyle \int d^3}r{\left|{\psi }_j\left(\overrightarrow{r}\right)\right|}^2=f_j$ guaranteeing normalization of the occupied or partly occupied orbitals. The Euler–Lagrange equation for this problem is $\delta \{E_v[\left\{f_j\right\},\left\{{\psi }_j\right\}]-{\displaystyle \sum _i{\epsilon }_i}{f}_i{\displaystyle \int d^3}r{\left|{\psi }_i\left(\overrightarrow{r}\right)\right|}^2\}=0$, where the ${\epsilon }_i$ are Lagrange multipliers. The interpretation is

$${\epsilon }_i=\partial E/\partial f_i.$$ [5]

This is a generalized Janak theorem. The same statement and derivation (11) apply to the ungeneralized KS theory. The minimizing one-electron wavefunctions are solutions of a one-electron Schrödinger equation with an optimal variational potential operator.

Consider a GKS calculation for an extended solid with an approximate xc functional, in which the ground state delocalizes the density of the added electron or hole over the infinite solid. The variation of the approximated $E$ is linear in $f_i$ because the relaxation effect on the optimal variational potential associated with the removal or addition of one electron is negligible. Then, by Eq. 5,

$$\begin{array}{l}E\left(N\right)-E(N-1)={\epsilon }^{HO}(N-\delta )\\ E(N+1)-E\left(N\right)={\epsilon }^{LU}(N+\delta ),\end{array}$$ [6]

where $\delta =0^{+}$, and

$$I\left(N\right)-A\left(N\right)={\epsilon }^{LU}(N+\delta )-{\epsilon }^{HO}(N-\delta ).$$ [7]

Here, HO and LU label the one-electron states of the (N-$\delta )$-electron system, which change only infinitesimally when M increases through integer N. If the approximate xc potential in GKS theory has no discontinuity as the electron number crosses integer N, then

$$I\left(N\right)-A\left(N\right)={\epsilon }^{LU}\left(N\right)-{\epsilon }^{HO}\left(N\right).$$ [8]

For a meta-GGA or hybrid functional, the optimum variational potential operator has been found explicitly (e.g., equation 7 of ref. 30; equation 1.7 of ref. 11) and is continuous. Thus, within LSDA, GGA, meta-GGA, or hybrid approximations, when implemented in GKS, the band gap equals the ground-state total energy difference.

In contrast, within an ungeneralized KS scheme, this statement remains true in LSDA and GGA, but not in meta-GGA or hybrid approximations. For meta-GGA and hybrid approximations, treated in OEP, as for (15) exact KS theory,

$$I\left(N\right)-A\left(N\right)={\epsilon }_{OEP}^{LU}(N+\delta )-{\epsilon }_{OEP}^{HO}(N-\delta )=\{{\epsilon }_{OEP}^{LU}(N-\delta )-{\epsilon }_{OEP}^{HO}(N-\delta )\}+\{{\epsilon }_{OEP}^{LU}(N+\delta )-{\epsilon }_{OEP}^{LU}(N-\delta )\},$$ [9]

where the first set of curly brackets is the OEP or KS band gap and the second set is the contribution from the discontinuity (15, 16) of the OEP or KS potential.