Ligand binding to telomeric G-quadruplex DNA investigated by funnel-metadynamics simulations

Significance

A thorough characterization of the binding interaction between a drug and its molecular target is fundamental to successfully lead drug design. We demonstrate that this characterization is also possible using the recently developed method of funnel-metadynamics (FM), here applied to investigate the binding of berberine to DNA G-quadruplex. We computed a quantitatively well-characterized free-energy landscape that allows identifying two low-energy ligand binding modes and the presence of higher energy prebinding states. We validated the accuracy of our calculations by steady-state fluorescence experiments. The good agreement between the theoretical and experimental binding free-energy value demonstrates that FM is a most reliable method to study ligand/DNA interaction.

Abstract

G-quadruplexes (G4s) are higher-order DNA structures typically present at promoter regions of genes and telomeres. Here, the G4 formation decreases the replicative DNA at each cell cycle, finally leading to apoptosis. The ability to control this mitotic clock, particularly in cancer cells, is fascinating and passes through a rational understanding of the ligand/G4 interaction. We demonstrate that an accurate description of the ligand/G4 binding mechanism is possible using an innovative free-energy method called funnel-metadynamics (FM), which we have recently developed to investigate ligand/protein interaction. Using FM simulations, we have elucidated the binding mechanism of the anticancer alkaloid berberine to the human telomeric G4 (d[AG₃(T₂AG₃)₃]), computing also the binding free-energy landscape. Two ligand binding modes have been identified as the lowest energy states. Furthermore, we have found prebinding sites, which are preparatory to reach the final binding mode. In our simulations, the ions and the water molecules have been explicitly represented and the energetic contribution of the solvent during ligand binding evaluated. Our theoretical results provide an accurate estimate of the absolute ligand/DNA binding free energy ($\mathrm{\Delta }{G}_{\mathrm{b}}^0$ = −10.3 ± 0.5 kcal/mol) that we validated through steady-state fluorescence binding assays. The good agreement between the theoretical and experimental value demonstrates that FM is a most powerful method to investigate ligand/DNA interaction and can be a useful tool for the rational design also of G4 ligands.

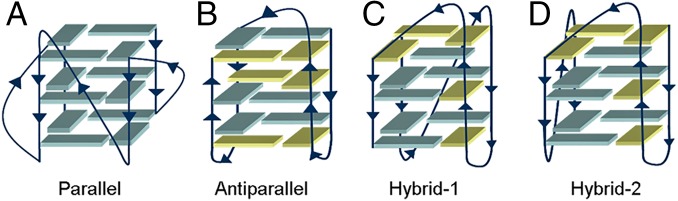
Guanine-rich sequences in human genome can organize DNA in G-quadruplex structures (hereafter named G4-DNA) formed by stack of guanines planes called G-tetrads (1). This higher-order conformation is stabilized by Hoogsteen-type hydrogen bonds and monovalent cations, like K⁺ and Na⁺, which coordinate the guanines O₆ atoms of two different G-tetrad planes. G4s are located in key regions of genome, regulating several relevant cellular functions, such as gene transcription and telomere lengthening. They are present in ribosomal DNA, RNA, and gene promoter regions as c-myc, bcl-2, or c-kit. G-rich repeats can be found also at telomeres, nucleoprotein complexes essential to preserve the genomic integrity by adopting a t-loop fold that protects chromosomes termini from end-to-end fusion (2). Telomeric DNA acts also as mitotic clock being gradually reduced at each cell division cycle until reaching the Hayflick limit, which leads the cell to senescence and apoptosis (replicative senescence) (3). The G-rich sequences at telomeres can adopt G4-DNA configurations, which stabilize the telomere organization hampering the DNA replication operated by the telomerase enzyme. This effect has been confirmed by in vitro experiments (2), and in cancer cells, where telomerase is overexpressed, the cells proliferate ad infinitum. Telomerase is indeed a specialized reverse transcriptase, which adds 5′-TTAGGG-3′ repeats to the 3′ end of telomere, thus preserving telomere length. In some kind of tumors, there exists an alternative process known as alternative lengthening of telomeres (ALT) that conserves DNA length in the absence of telomerase through telomeres recombination events. In 1991, Zahler et al. (4) found that folding of telomeric DNA in G4-DNA structures inhibits in vitro TERT activity and, more recently, even the ALT cells have been found particularly sensitive to G4-DNA formation. This information raised the interest toward molecules able to bind and stabilize G4 structures, thus altering the telomere-maintaining mechanism with potential anticancer effect (5, 6). Unfortunately, drug design of G4-DNA ligands is limited by the structural complexity and variability of G4, which can assume diverse conformations based on the syn/anti glycosidic bond orientation of guanines, different strands orientation (parallel, antiparallel, hybrid 1 and 2 types), loop size, groove width, and ionic conditions (Fig. 1) (7–10).

Fig. 1.

Schematic representation of the human telomeric G4-DNA folding topologies. (A) Parallel or propeller type, as identified by X-ray in presence of K⁺; (B) antiparallel or basket-like, as detected in Na⁺ solution; (C) hybrid type 1 and (D) hybrid type 2, both found in K⁺ solution. Syn and anti guanines glycosidic bond orientation are colored in yellow and cyan, respectively.

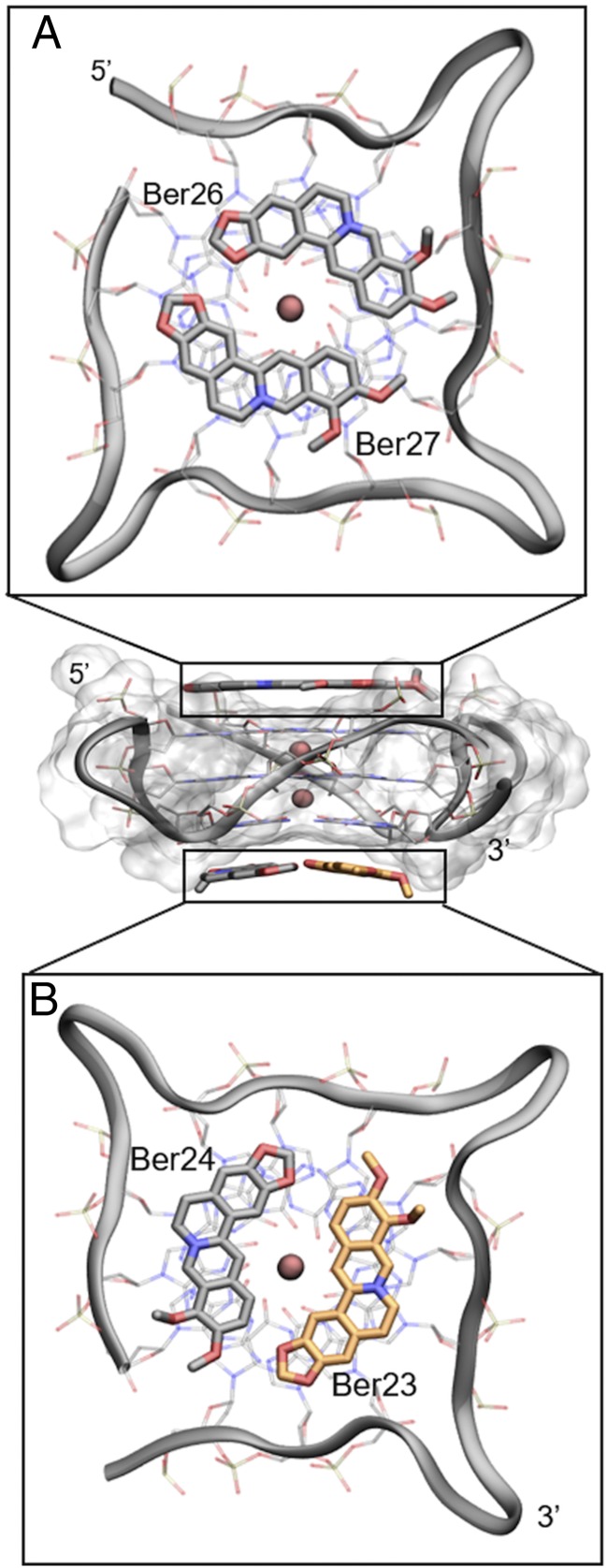
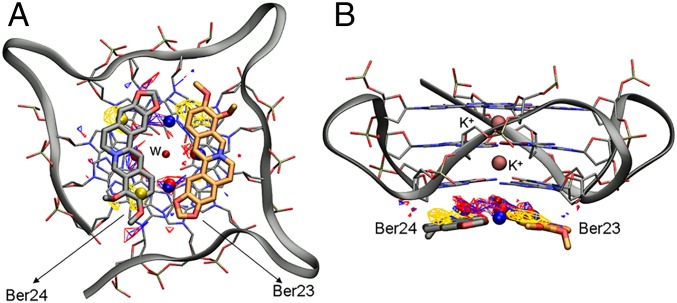
Despite such difficulties, many synthetic and natural compounds have been proposed as G4-DNA binders, and a number of these complexes have also been characterized through crystallographic and NMR studies (11–14). Looking at those structures, one might note that most of the G4-DNA ligands share some structural features. For instance, the presence of a polycyclic and planar aromatic chromophore, able to engage π–π stacking interactions with the terminal G-tetrads, and a positive charge is necessary to interact with the DNA backbone phosphate groups. The largest class of G4 ligands, which includes synthetic derivatives, such as BRACO-19, the pentacyclic acridine RHPS4 and the quinacridine MMQ₃, is known as “end-stacker” and shows a selective binding behavior toward G4 with respect to duplex DNA in the reported binding assays. These compounds show a strong binding affinity to G4-DNA and a high inhibitory activity toward telomerase (15). In addition to synthetic compounds, even natural products have emerged in the last years as an invaluable source of drug candidates with over 100 natural compounds in clinical trials (16). As a result of millions of years of evolution and selection, “nature” represents an immeasurable source of chemical entities with extraordinary chemodiversity investigated by an ever-growing number of theoretical and experimental studies (17–21). In drug discovery, they are typically used as lead compounds to achieve more potent derivatives through structural optimization (22, 23). Among natural derivatives, the most active G4-DNA ligand is Telomestatin, a macrocyclic compound isolated from Streptomyces anulatus in 2001 (24, 25). Distamycin A is another example of natural antibiotic which was found through NMR to recognize the parallel [d(TGGGGT)]₄ G4-DNA (26, 27). Also, natural alkaloids with an isoquinoline moiety are known to bind G4-DNA through stacking interactions with the G-quartets favored by the presence of π-electrons delocalized systems (28). An example of this class is berberine (Fig. 2), which exerts anticancer activities both in vitro and in vivo through multiple mechanisms (29, 30), including the inhibition of the telomerase enzyme [telomeric repeat amplification protocol (TRAP): IC₅₀ ∼ 35 µM] (31). In 2006, Franceschin et al. (32) proved that berberine is able to bind various G4-DNA structures with higher selectivity with respect to duplex DNA, and further molecular modeling studies on the parallel-stranded topology showed that it stacks over the terminal G-tetrads. Recently, experimental evidences have asserted that berberine binds also G4-DNAs located in oncogene promoters such as c-myc (28), RET (33), and c-kit (34). The binding of berberine to human telomeric G4-DNA was also investigated by NMR using different DNA topologies, such as the Tel-22 antiparallel, wtTel26, and Tel26 hybrid (parallel/antiparallel) type. These studies reveal a high ligand binding stoichiometry (>1:1) with different binding modes. The interaction of berberine with G4 depends particularly on the specific conformation assumed by DNA. In the case of antiparallel folding, berberine seems to preferentially bind to G4-DNA loops and grooves, whereas in the hybrid-type conformations the binding probably occurs at the terminal G-tetrads (35). A binding stoichiometry higher than 1:1 was also detected by the X-ray crystallography [Protein Data Bank (PDB) ID code 3r6r] (36) in a biologically relevant parallel G4-DNA. In this structure, four molecules of berberine bind to DNA with two ligands stacked at the 5′ end and other two at the 3′-end without interacting with loops and grooves. Notably, the two couples of berberine stacked at the 5′- and 3′-end differ for their binding orientation. In particular, whereas at the 5′-end the ligands (hereafter named Ber25 and Ber26) assume a parallel orientation (head-to-tail, head-to-tail), at the 3′-end they (hereafter named Ber23 and Ber24) adopt an antiparallel orientation (head-to-tail, tail-to-head) (Fig. 3).

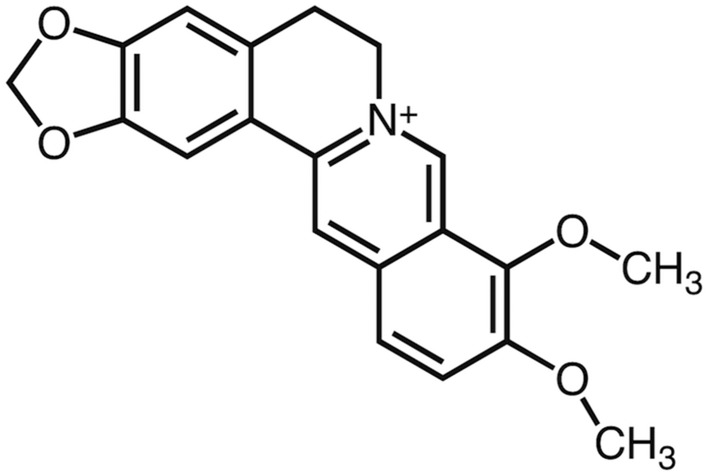
Fig. 2.

Two-dimensional chemical structure of berberine.

Fig. 3.

Lateral view of the berberine G4-DNA complex (PDB ID code 3r6r) and the different binding mode of berberines. (A) Ber25 and Ber26 at the 5′-end assume a parallel orientation. (B) Ber23 and Ber24 at the 3′-end binds instead in an antiparallel orientation. Berberine ligands are represented as sticks (orange for Ber23 and gray for Ber24, 25, and 26). G4-DNA is represented as transparent gray surface, whereas guanine tetrads in A and B are shown as transparent sticks colored by atom name. G4-DNA loops are shown instead as gray ribbon. K⁺ cations are depicted as pink spheres. Ber23 (orange stick) was subjected to FM simulation.

Taking advantage of a very recent methodological advance in ligand/protein binding simulations by Limongelli et al. (37), we investigated the binding mechanism of berberine to G4-DNA through atomistic simulations. We used the recently developed funnel-metadynamics (FM) (37), which enhances the sampling of the ligand binding process to its molecular target reducing the exploration of the unbound state. During the calculation, the full flexibility of both the ligand and DNA is considered as well as the solvent and ions effect. The whole sampling took ∼0.8 µs, and at the end of the simulation we could compute the free-energy surface (FES) of the whole binding event and provide an accurate estimate of the absolute ligand/DNA binding free energy. Our computations allowed identifying the most stable ligand binding modes and the free-energy cost to convert one binding conformation into the other. Using as a starting state the X-ray complex of G4-DNA (36) with four molecules of berberine, we investigated the binding of the ligand that showed the highest instability during preliminary molecular-dynamics (MD) simulations (Fig. S1). Our results illustrate that at the 3′-end berberine is able to bind DNA in two different ways. The lowest free-energy binding mode is similar to the X-ray pose; however, an alternative and stable binding pose exists. The role of water molecules during ligand binding was also investigated and assessed through dedicated simulations. We calculated an absolute berberine/G4-DNA binding free energy ($\mathrm{\Delta }{G}_{\mathrm{b}\hspace{0.17em}\mathrm{calc}}^0$) of −10.3 ± 0.5 kcal/mol. To validate our theoretical results and assess the reliability of the method, we measured experimentally at different salt concentration the binding free energy of berberine to the telomeric G4-DNA in the parallel conformation through fluorescence spectroscopy titration experiments ($\mathrm{\Delta }{G}_{\mathrm{b}\hspace{0.17em}\exp }^0$ = −9.3/−9.8 kcal/mol). The good agreement between calculations and experiments and the detailed structural and energetics insights provided in our study represent an important advance in ligand binding investigations to DNA and demonstrate that FM can be a useful tool for the rational design of G4-DNA ligands.

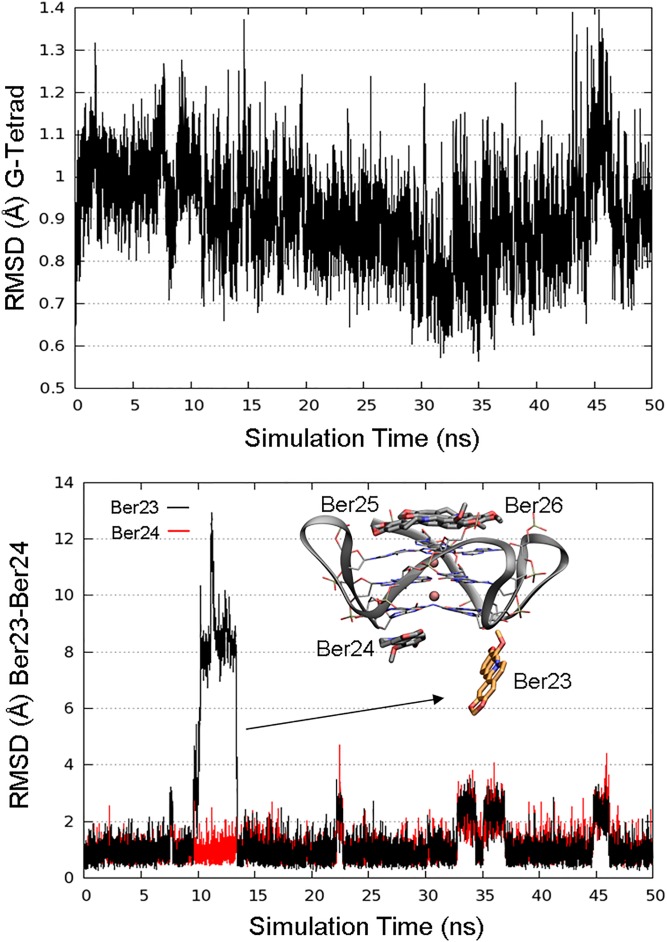
Fig. S1.

(Upper) RMSD plot of the G-tetrads along 50 ns of MD simulation. (Lower) RMSD plot of Ber23 (orange sticks). After ∼10 ns of MD simulation, Ber23 assumes a conformation almost perpendicular to the G-tetrad, recovering the original position after 3–4 ns. Residues Ber24, Ber25, and Ber26 are shown as gray sticks. K⁺ cations are depicted as pink spheres.

Results

FM Simulation.

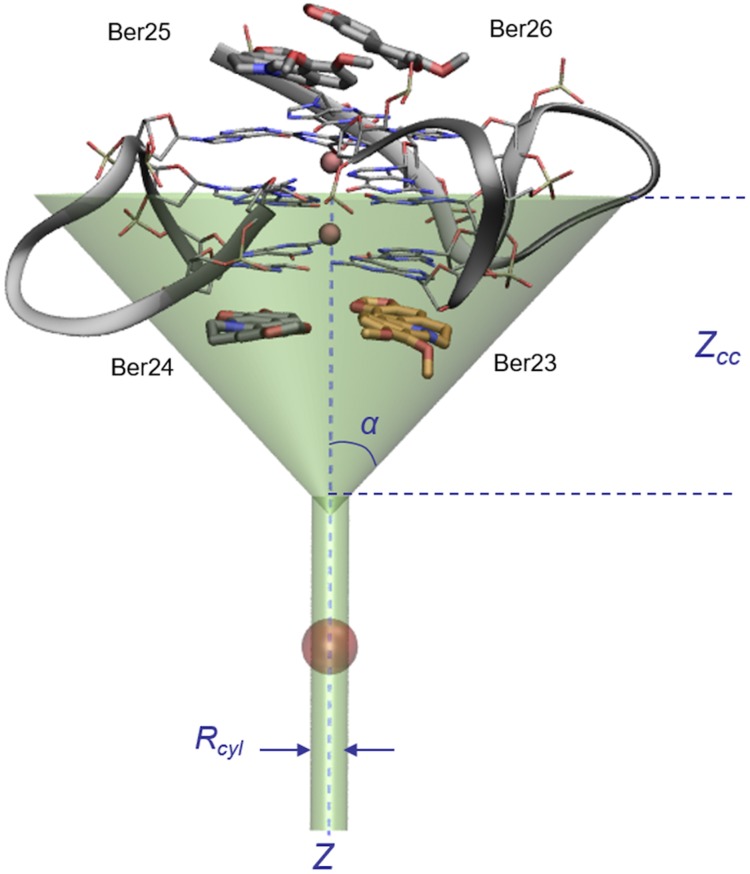
To study the binding mechanism of berberine to human telomeric G4-DNA, we used well-tempered metadynamics simulations (38). Metadynamics (39) is an enhanced sampling technique that allows sampling long-timescale events in a reasonable computational time, computing also the free-energy landscape of the process under study. The acceleration of the sampling is made possible by introducing during the simulation a history-dependent bias potential on few degrees of freedom of the system of interest, called collective variables (CVs). This technique has been already successfully used in several fields, like DNA folding (40), ligand/protein binding (41, 42), large-scale protein motion (43, 44), and chemical reactions (45), and it has been proven to be rigorously justified (46). Here, to study the berberine/G4-DNA binding process and compute the ligand/DNA absolute binding free energy, we have used a recent variant of the original method, called funnel-metadynamics (37). Using this approach, one has the advantage to reduce the phase space exploration in the unbound state, applying to the system a funnel-shaped restraint potential. This potential is a combination of a cone, which includes the binding site, and a cylindric restraint placed in the bulk water region (Fig. 4). When the ligand visits states inside the funnel volume, the potential felt by the system is null. As the ligand reaches the edge of the funnel, a repulsive bias is applied to the system. That prevents the ligand from visiting regions outside the funnel without affecting the sampling inside. As shown in Fig. 4, the funnel size should be properly chosen to include the binding site in the null potential region and maximally reduce the space to explore in the unbound state through the repulsive cylindric potential. As a result, the ligand binding, which is typically a long-timescale event, is accelerated under FM and several forth–back events between the bound and unbound states are observed. These recrossing events lead to an accurate exploration of the phase space in the ligand bound regions and a quantitatively well-characterized FES of the binding process. Furthermore, convergence of the results and accurate estimation of the ligand binding free energy is achieved in a reasonable simulation time. FM represents a useful tool in drug discovery, especially when obtaining an accurate estimation of the ligand binding free energy is needed (47). For the berberine/G4-DNA complex, the funnel restraint potential was applied to the system from the last frame of the preliminary 50-ns-long MD simulation, so as to include the ligand binding site at 3′-end in the funnel region as shown in Fig. 4. At the 5′-end site, two molecules of berberine were kept bound to DNA as in the position reported by X-ray (36). We stress that the sampling of the configurational space inside the funnel is not affected by the presence of the external restraint potential and here the simulation proceeds as regular metadynamics (Fig. S2A). Following the original paper (37), the parameters of the FM simulation, specifically angle α and distance z_cc, were chosen such that the funnel-shaped potential could not influence the ligand binding exploration at the DNA binding sites, z < z_cc. When the ligand is in the unbound state, z > z_cc, a cylindrical restraint potential is instead applied to the system. At the end of the FM simulation, the free energy can be computed considering the external potential applied to the system. A key step in metadynamics, as in other pathway free-energy methods, is the a priori identification of CVs able to describe the slowest degrees of freedom of the system and distinguish the different visited states. In the present study, with the purpose of describing the bound and unbound states of berberine, we have used a distance CV (d) defined by the center of mass of residue Ber23 and that of the middle G-tetrad of G4-DNA and a torsion CV (π), which allows the ligand to explore all its different orientations relative to DNA (Table S1). Similar CV settings have been already used with success in many other ligand binding studies (42, 48).

Fig. 4.

The funnel shape potential restraint applied at the 3′-end binding site of berberine/G4-DNA complex (PDB ID code 3r6r). The angle α is 0.75 rad, whereas z_cc is 16 Å. The cylinder radius R_cyl was set to 1 Å. The CVs (distance and torsion) were chosen to describe the binding process of Ber23, here shown as orange sticks. Residues Ber25 and Ber26, bound at the 5′-end, and Ber24, at the 3′-end, are displayed as gray sticks.

Fig. S2.

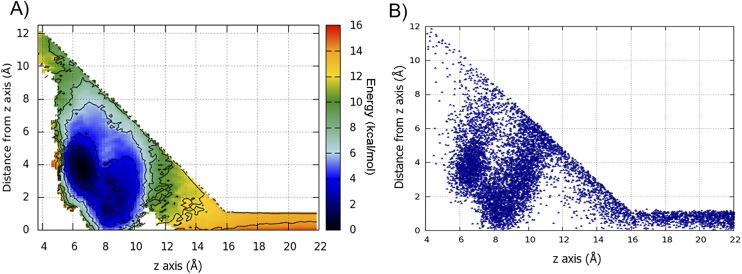
(A) The FES computed using the reweighting algorithm as a function of z axis and the distance from z axis. Isosurfaces are shown every 2 kcal/mol. The two main basins, A and B, here are merged in one deep basin, located in the middle of the conic region, where the ligand exploration is not affected by the funnel potential restraint. (B) Scatter plot of the projection of the z axis as a function of the distance from z axis of the Ber23 center of mass. The conical restraint does not influence the Ber23 exploration of the conformational space within the binding site region.

Table S1.

List of atoms that define the CVs and list of parameters used in the FM simulations

CV type	Parameters	Atoms	DNA (R), ligand (L)	σ value
Funnel potential restraint*	zcc = 16.0 Å			No σ
	α = 0.75 rad
	Rcyl = 1.0 Å
Distance		†Center of mass between C1′ of residues G3:G21:G9:G15	R	0.15
Distance		Center of mass between N1:C7 C10:C4:C2:C1 of residue Ber23	L
Torsion		†C1′ of G3	R	0.08
Torsion		†C1′ of G9	R
Torsion		Atom C18 of residue Ber23	L
Torsion		Atom C17 of residue Ber23	L
H-bond		Atoms C14:C5:N1:C16:C15 of Ber24	L	No σ
H-bond		Atoms C8:O6:N2 of G16 and atoms C8:C2 of G22	R	NN = 6, MM = 14, R0 = 4.5
				TYPE = 4
				LIMIT = 3.5
				KAPPA = 100.0
				EPS = 0.1

^*The z axis of the funnel is defined in the space x, y, z by two points: one refers to the center of mass calculated from O₆ of residues G3:G21:G9:G15 (middle tetrad), and the other was calculated from O₆ of residues G16:G10:G4:G22 (bottom tetrad). The first one also represents the origin of the z axis.

^†C1′ represents the sugar carbon.

Ligand/DNA Binding Simulations.

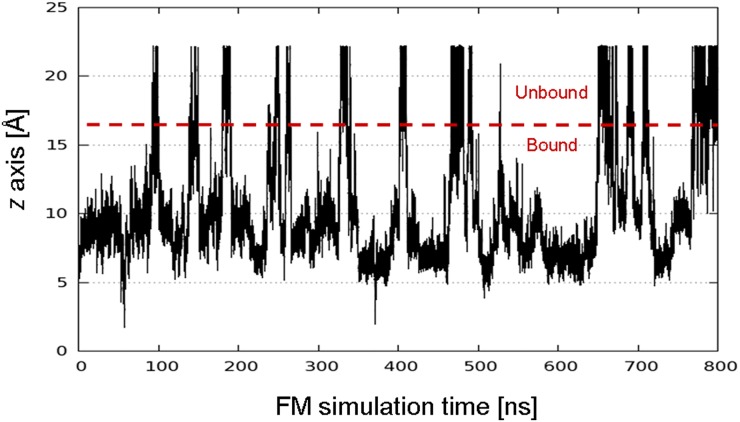
The whole sampling took ∼0.8 µs of FM simulations. The starting pose of the ligand Ber23 corresponds to the X-ray state (PDB ID code 3r6r), and then it leaves the binding site to explore the unbound region (states at z values higher than z_cc), where it is fully solvated by water molecules. The presence of the funnel restraint potential favors the observation of several forth-and-back events between the bound and unbound states of Ber23 (Fig. S3). This leads to a quantitatively well-characterized FES and an accurate ligand/DNA binding free-energy estimate (Fig. S4). We computed the binding FES as a function of d and π and calculated the absolute ligand/DNA binding free energy using Eq. 1 (Materials and Methods for details).

Fig. S3.

Plot of the projection of the center of mass of Ber23 on the funnel z axis (z-axis CV) along 800 ns of FM simulations. As shown in the plot, several recrossing events between the ligand bound and unbound states are sampled. This leads to the convergence in the estimation of the ligand/DNA G4 binding free energy.

Fig. S4.

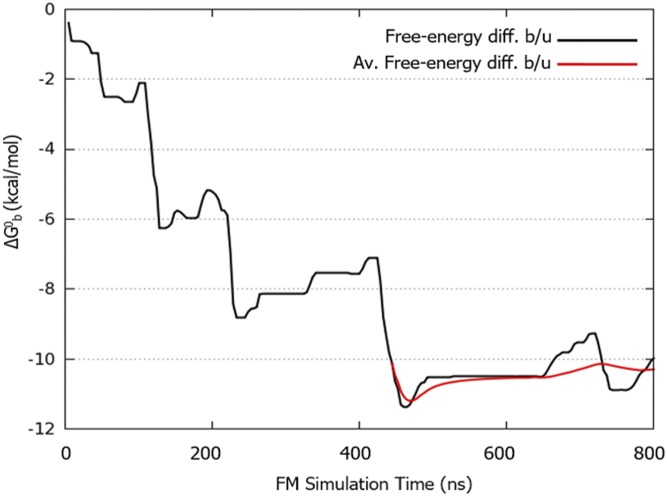
Plot of the free-energy difference between the bound and unbound state as a function of the simulation time. As bound state, we considered the lowest energy binding mode (basin A) in the FES shown in Fig. 5, which is represented by all of the poses within the distance interval 8–10 Å and the torsion interval −3.14/−2 rad. As unbound state, we considered all of the poses at distance CV equals to 20 Å. Considering R_cyl = 1.0 Å and applying the analytical correction, the weighted average estimation of the absolute berberine/G4-DNA binding free energy ($\mathrm{\Delta }{G}_{\mathrm{b}}^0$) is −10.3 ± 0.5 kcal/mol, in good agreement with the experimental value. The error is calculated as the SD from the weighted average value of $\mathrm{\Delta }{G}_{\mathrm{b}}^0$ obtained in the last part of the simulation where the binding free-energy calculation is converged.

The Berberine Binding Mode.

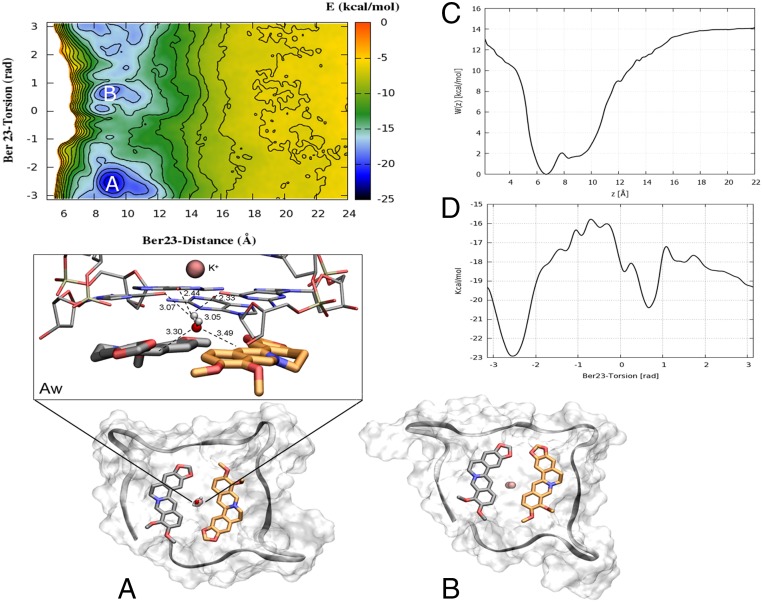
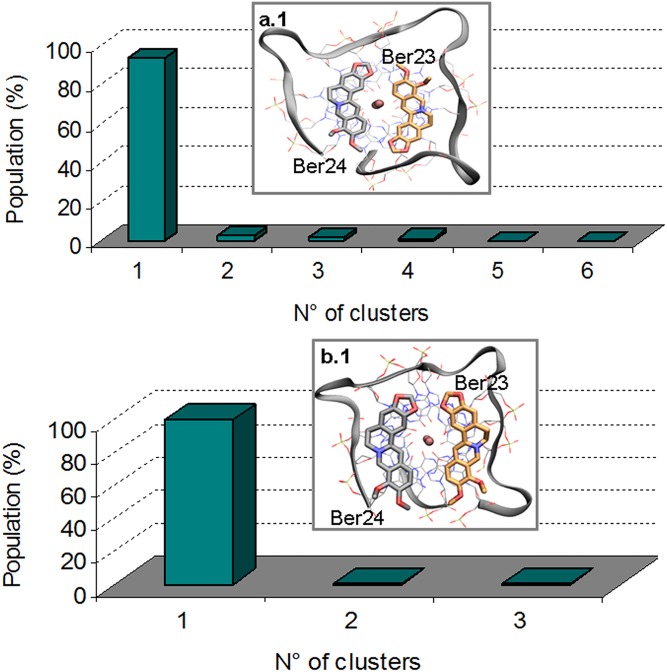
Looking at the FES shown in Fig. 5, two free-energy minima, A and B, are found. Basin A represents the lowest energy pose, and a cluster analysis (Materials and Methods for details) performed with the GROMOS algorithm (49) using a RMSD cutoff value of 0.15 nm revealed that the most representative state of this basin (92.3%) is similar to the X-ray complex (Fig. S5, upper graph). Here, the ligand Ber23 assumes an antiparallel orientation with respect to the other ligand molecule bound to 3′-end, Ber24. This pose is stabilized by a number of favorable interactions, such as the π–π stacking between the Ber23’s aromatic moiety and the nucleotides G10:G4 and the salt bridge formed by the positively charged N⁺ of Ber23 and one of the phosphate groups of DNA backbone (Fig. 5A). We note that ∼15.4% of the conformations found in cluster 1 show a water molecule engaging hydrogen bonds with the O₆ atoms of the G-tetrad G22:G16:G10:G4 residues at the 3′-end, and via C-H···O with the C3 carbons of Ber23 and Ber24 residues (Fig. 5Aw). The latter interaction is possible given the negative partial charge of the aromatic C3 carbon atom of berberine, and it is rather stable during the FM simulation with a distance between that water oxygen and the C3 carbon of 3.3 and 3.4 Å for Ber24 and Ber23, respectively. A similar water-mediated interaction has also been found by X-ray (PDB ID code 3r6r) (36), and further examples have been reported in literature in different systems (50, 51). This agreement underlines the relevance of using explicit solvent models to deal with ligand/DNA interaction and prompted us to further investigate the water role during the ligand binding (The Solvent Role in Ligand Binding).

Fig. 5.

The FES of berberine/G4-DNA computed as a function of d (in angstroms) and π (in radians) CVs. Isosurfaces are shown every 2 kcal/mol. (A) The deepest energy basin A represents a binding mode very similar to the crystallographic one, in which Ber23 (orange sticks) assumes an antiparallel orientation with respect to Ber24 (gray sticks). (Aw) Most of the conformations found in basin A are characterized by the presence of one water molecule located between the residues Ber24, Ber23, and the G-tetrad plane making C-H···O hydrogen bonds with the aromatic C3 carbons of Ber24 and Ber23 in a very similar position as found by X-ray. The distance between atoms is measured in the most populated conformation representative of the lowest energy basin A. Additional H-O-H···O hydrogen bonds are engaged with the O₆ atoms of the G-tetrad plane. (B) The second deepest energy minimum represents an alternative binding mode where Ber23 orientation is parallel with respect to Ber24. G4-DNA is displayed as gray surface, and the backbone in gray ribbon. K⁺ ions are depicted as pink spheres. Ber25 and Ber26 are omitted for clarity. (C) Potential of mean force (PMF) W(z) computed along the axis of the funnel z using the reweighting algorithm (52). The region with the ligand bound is defined as 5 ≤ z ≤ 11 Å, whereas the ligand fully solvated state is at z = 20 Å. (D) Monodimensional free energy as a function of Ber23 π (in radians).

Fig. S5.

(A.1) Clusterization of the conformations found in basin A. The 92.27% of these poses (cluster 1) correspond to the crystallographic structure. (B.1) Clusterization of the conformations found in basin B. In 86.83% (cluster 1) of these poses, Ber23 assumes a parallel orientation with respect to Ber24 (alternative pose).

The Alternative Binding Mode.

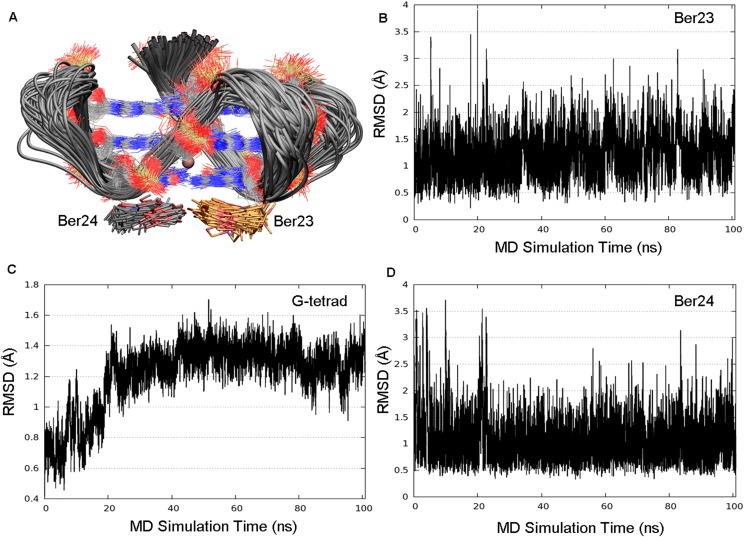
In the FES shown in Fig. 5, a second free-energy minimum B, ∼2.9 kcal/mol higher than A, is identified. A cluster analysis of the conformations present in this energy basin revealed as the most populated family (86.83%) a ligand binding mode different from the X-ray one (Fig. S5, lower graph). With respect to basin A, in basin B Ber23 is tilted of 180°. In particular, in this pose, Ber23 adopts at the 3′-end a parallel orientation relative to Ber24 with the methoxy groups of the two berberine ligands pointing in the same direction (Fig. 5B). A similar parallel orientation of the ligands is found by X-ray at the 5′-end. However, in the crystal structure, ligands at the 5′-end are sandwiched by two G4-DNA molecules that form an artificial and desolvated binding site (36). This raises doubts on the relevance of the crystallographic binding mode of berberine at the 5′-end in the solvent environment. Our finding confirms instead such pose and reveals that two molecules of berberine can bind in parallel orientation also to the 3′-end, although its interaction with G4-DNA is slightly less favorable energetically than the antiparallel binding mode A. In pose B, Ber23 engages several interactions with DNA, such as π–π stacking interactions with the aromatic rings of G10:G4 nucleotides and a salt bridge through its positively charged nitrogen atom with a phosphate group of G4-DNA backbone (Fig. 5B). We assessed the stability of this pose throughout over 100 ns of standard MD simulation, during which this binding mode and all of the ligand/DNA interactions were conserved. As shown in Fig. S6, low average RMSD values of 1.2 and 1.1 Å are computed for Ber23 and Ber24 heavy atoms, respectively (Fig. S6 B and D). Also, the G-tetrads are rather stable during this simulation with an average RMSD value of 1.2 Å (Fig. S6C). As well as for pose A, we investigated the role of waters also in state B. At variance with basin A, in B no water molecule was found between ligands and the 3′-end G-tetrad. However, further calculations and analysis were performed in this regard and are discussed in The Solvent Role in Ligand Binding.

Fig. S6.

Plots obtained after 100 ns of MD simulation on the basin B conformation at 300 K. (A) Representation of the conformational space sampled by G-tetrads (silver ribbons), Ber24 (gray sticks), and Ber23 (orange sticks) in its alternative binding pose as found in basin B. Residues Ber25 and Ber26 are not shown for clarity. (B–D) The thermodynamic stability of the basin B is further demonstrated by the very low average RMSD for Ber23, G-tetrads, and Ber24, respectively.

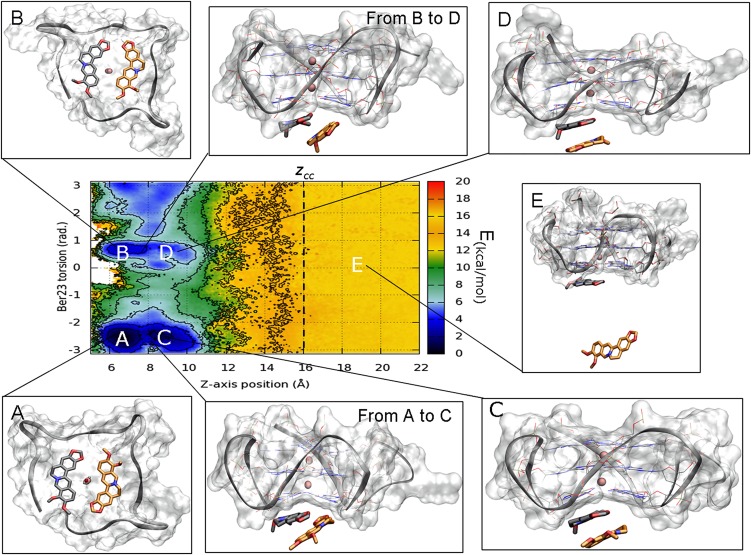
The Prebinding States.

To investigate the path followed by berberine to bind G4-DNA, we computed the FES as a function of CVs different from those biased in metadynamics. This is possible using the reweighting algorithm of Bonomi et al. (52) (Materials and Methods for details) that recomputes the Boltzmann distribution of a CV at time t of the simulation. In particular, in Fig. 6, the FES is represented as a function of Ber23 torsion CV and the funnel z-axis position CV. Using this representation, two additional energy minima C and D appear in the FES albeit at slightly higher energy values with respect to basins A and B, respectively. These two basins are very close in the CVs space to A and B and can provide mechanistic details of binding of Ber23 to G4-DNA. In particular, in basins C and D, Ber23 stacks over Ber24, however showing the antiparallel and parallel orientation between ligands as found in A and B, respectively. The poses extracted between the free-energy minima A and C, and between B and D, show the Ber23 ligand in a tilted position, assuming a halfway pose between the ligands-stacked poses, C and D, and the final binding modes, A and B. This analysis suggests that Ber23 might first interact with Ber24, and then slide toward the final binding mode to G4-DNA.

Fig. 6.

The binding FES calculated using the reweighting algorithm as a function of Ber23 π (in radians) CV and the funnel z-axis position. Isosurfaces are shown every 2 kcal/mol. Beyond the minima (A) and (B), in which the simil X-Ray and the alternative conformations are respectively found, in this FES representation two further energy basins (C) and (D) appear, elucidating the binding mechanism of Ber23 to DNA. (E) Representation of one of the isoenergetic conformations found in the unbound state when z_cc >16 Å. Here, the ligand has no contacts with the target and can assume a wide number of isoenergetic conformations. Ber25 and Ber26 are omitted for clarity.

The Unbound State.

When Ber23 explores states at z values higher than z_cc, the ligand is in the unbound state and outside the interaction range of G4-DNA (Fig. 6E). Here, the FES is flat, that is, the free energy is position and orientation independent, and the ligand is completely solvated assuming a large number of equivalent conformations. Although this behavior is to be expected, the flatness of the FES gives a measure of the convergence of our calculations.

The Absolute Berberine Binding Free Energy.

As shown in Fig. S3 (upper graph), the system visits several times the bound (z < 16 Å) and the unbound states (z > 16 Å) during the simulation. These back-and-forth events between bound and unbound states are necessary to have a quantitatively well-characterized free-energy landscape and an accurate ligand binding free-energy estimate. At the end of the simulation, using the free-energy difference between the bound and unbound state in Eq. 2, we computed a binding constant K_b of 4.5 (±2.9) × 10⁷. We note that this estimate takes into account the entropic cost of using a cylindrical restraint potential in the unbound state is calculated as $\pi R_{\mathrm{cyl}}^2$ in Eq. 2 (53). This K_b value leads to the berberine/G4-DNA absolute binding free-energy estimate ($\mathrm{\Delta }{G}_{\mathrm{b}\hspace{0.17em}\mathrm{calc}}^0$) of −10.3 ± 0.5 kcal/mol through Eq. 1 (Table 1). We provide a picture of the convergence of the binding free-energy estimation, reporting in Fig. S4 the free-energy difference between bound and unbound state as a function of the simulation time. This figure clearly shows that, although the system continues going forth and back from the bound to the unbound state, after ∼450 ns the estimation of the free-energy difference between these two states does not change significantly. Furthermore, one might note that the exploration of the lowest energy basins is not affected by the presence of the funnel restraint (Fig. S2 A and B). It is worth noting that to date the only experimental ΔG measure available is that one of berberine with the hybrid topology of the G4-DNA 22-mer (ΔG_b = −8.2 ± 0.8 kcal/mol) (54), whereas our calculations have been performed on the parallel form. To assess the reliability of the used computational method and provide a thorough comparison between theoretical and experimental berberine binding free-energy value, we reproduced experimentally the parallel form of the human telomeric G4-DNA and carried out ligand binding assays. The details are provided in the following paragraph.

Table 1.

Comparison of theoretical (FM) and experimental (EXP) absolute binding free energy (ΔG_b⁰) of berberine to the parallel conformation of the human telomeric G4-DNA

Method	ΔGb0, kcal/mol
FM*	−10.3 ± 0.5
EXP at 20 mM KCl	−9.8 ± 0.2
EXP at 50 mM KCl	−9.6 ± 0.2
EXP at 100 mM KCl	−9.3 ± 0.2

^*Mean value over the last 360 ns out of 800-ns FM.

Experimental Binding Free Energy by Steady-State Fluorescence Experiments.

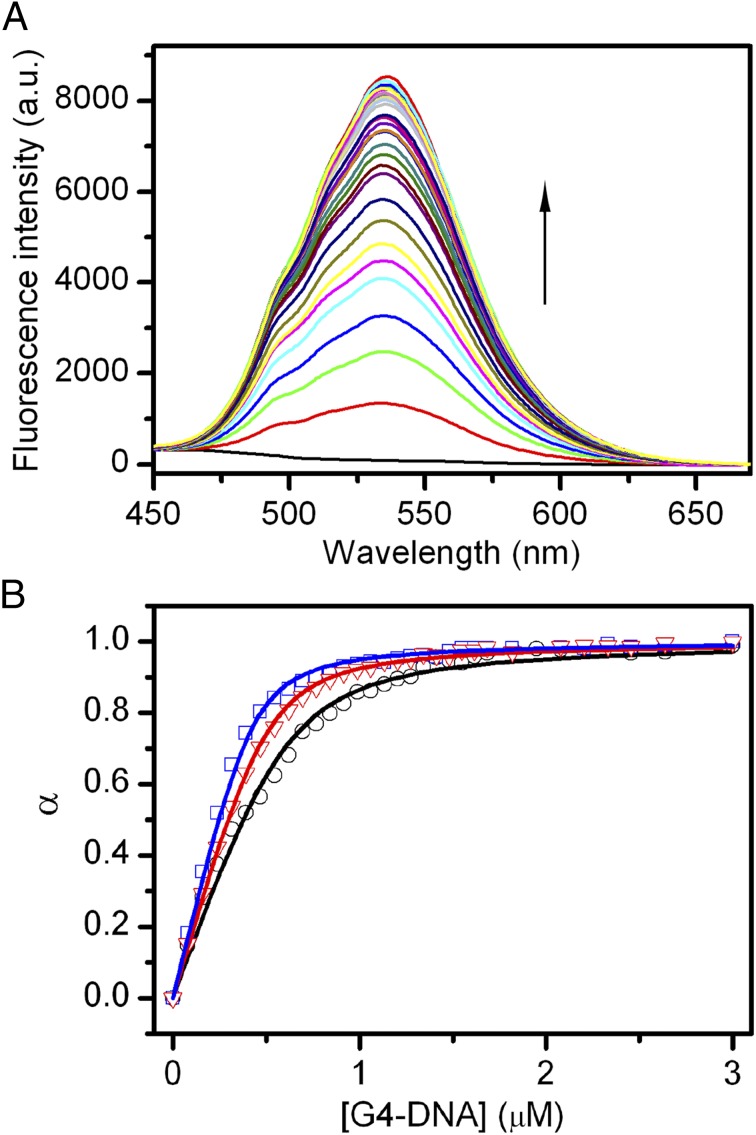
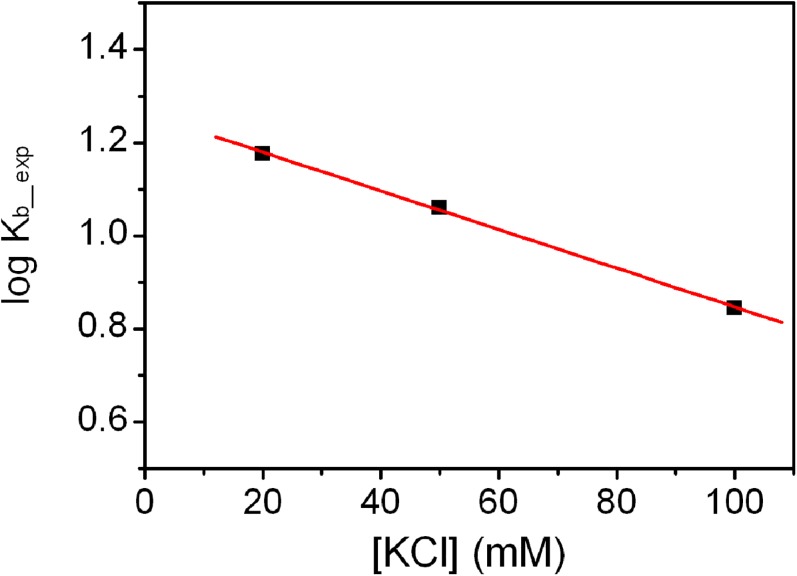
The binding of berberine to the telomeric G4-DNA in the parallel conformation was experimentally investigated by means of fluorescence titration experiments (55). Fluorescence emission spectra of the ligand in the absence and presence of increasing amounts of G4-DNA were recorded. Fig. 7A shows the effect of stepwise addition of DNA on the berberine fluorescence spectra. As clearly shown, increasing the concentration of G4 results in a gradual increase in the fluorescence intensity of berberine, until saturation is reached. The fraction of bound ligand (α) at each point of the titration was calculated following fluorescence changes at the maximum of intensity and was plotted as a function of the G4 concentration to obtain an isotherm binding curve (Fig. 7B). The curve was fitted using an independent and equivalent binding sites model (Eq. 4), by means of nonlinear regression algorithm, to give the binding constant (K_{b_exp}). The salt dependence of the binding constant was examined by performing the titrations at three KCl concentrations, 20, 50, and 100 mM. The binding constants obtained from fitting show that increasing the ionic strength slightly decreases the affinity for the binding process. Indeed, K_{b_exp} of 0.7 (±0.1) × 10⁷, 1.15 (±0.1) × 10⁷, and 1.5 (±0.1) × 10⁷ were obtained at KCl concentrations of 100, 50, and 20 mM, respectively. The observed salt dependence is expected for this type of interaction, and it is probably due to the counterion release that accompanies the binding of charged ligand. Interestingly, the linear dependence of K_{b_exp} on salt concentration (Fig. S7) allowed to extrapolate the value of binding constant to infinite KCl dilution, obtaining a theoretical value of 1.8 × 10⁷. Using the formula $\mathrm{\Delta }{G}_{\mathrm{b}}^0$ = −RT ln K_b the free-energy change at 25 °C calculated for the berberine-G4 binding ($\mathrm{\Delta }{G}_{\mathrm{b}\hspace{0.17em}\exp }^0$) ranges between −9.3 (± 0.2) kcal/mol at 100 mM KCl and −9.8 (± 0.2) kcal/mol at 20 mM KCl (Table 1), whereas at infinite KCl dilution it results to be −9.9 kcal/mol. These experimental values are in good agreement with the theoretical ligand binding free energy computed by FM ($\mathrm{\Delta }{G}_{\mathrm{b}\hspace{0.17em}\mathrm{calc}}^0$ = −10.3 ± 0.5 kcal/mol; Table 1), especially taking into account the approximations in the experimental model and the conservative error in the force field potential used in the simulations, which in the case of nucleic acids can be estimated at the least of 1.5/2 kcal/mol.

Fig. 7.

(A) Representative fluorescence emission spectra of berberine in the absence and presence of stepwise additions of G4-DNA at 25 °C (10 mM Li₃PO₄ buffer with 100 mM KCl, pH 7.0). (B) Fluorescence titration curves obtained by plotting the fraction of berberine bound (α) versus the G4 concentration for titrations carried out at 100 (black), 50 (red), and 20 (blue) mM KCl. The squares, triangles, and circles represent the experimental data; the lines are the best fit obtained with an independent and equivalent-sites model.

Fig. S7.

Salt dependence of binding constant (K_{b_exp}) for the binding of berberine to the telomeric G4-DNA. The experimental data (black squares) were used to obtain the best linear least-squares fit (red line).

The Solvent Role in Ligand Binding.

Many examples are reported in literature where the solvent molecules play a key role during ligand binding (48). In the case of berberine, our simulations and the X-ray crystallographic model (36), have shown the presence of a water molecule between the ligands and the G-tetrad at the 3′-end. This evidence suggests to further investigate the contribution of the solvent during ligand binding. Using the previously introduced reweighting algorithm (52), we performed an energetic evaluation of the presence of water molecules in the binding site. We also assessed the solvent effect on ligand binding developing an unbiased GRID-based pharmacophore model (GBPM) approach (56).

The Reweighted FES.

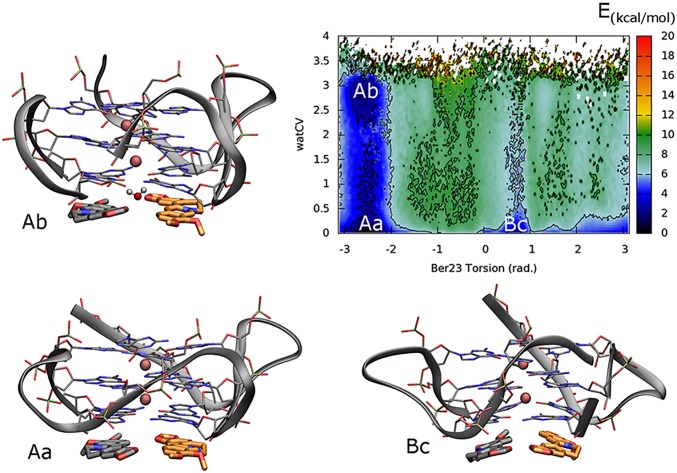
In order to assess the energetic contribution of the water solvent, we have reconstructed the FES, using the reweighting algorithm (52), as a function of two CVs: (i) the torsion CV (π) biased during the FM simulations and (ii) an interfacial water CV (watCV) (SI Materials and Methods). Specifically, whereas the former distinguishes the two binding modes, the latter indicates the presence of water molecules between the O₆ atoms of G4:G10 and those of G16:G22 nucleotides at the 3′-ends (SI Materials and Methods). Looking at the FES reported in Fig. 8, three main free-energy minima can be found. Basins Aa and Ab correspond to minima A in the original FES representation (Fig. 5), where the ligands assume the antiparallel X-ray–like orientation (π range of −3:−2 rad) in the binding site. In particular, in basin Aa, the watCV value equal to 0 indicates that no water molecule is present at the interface between the ligands and the 3′-end G-tetrad. However, an additional minimum Ab was found at slightly higher free-energy value with respect to Aa (∼1.9 kcal/mol). In this state, notable is the presence of a water molecule forming H-bond interactions with the O₆ atoms of the G4:G10 and G16:G22 nucleotides (watCV 2.5–3). The very small difference in free energy between the minima Aa and Ab indicates that the presence of waters at the interface between the ligands and the 3′-end G-tetrad is possible, but not necessary for ligand binding. On the other hand, when Ber23 binds to DNA in the alternative pose B, the presence of waters at the interface is energetically disfavored, as highlighted in the basin Bc. This different behavior is probably a consequence of the diverse morphology of the berberine pair in the two binding modes. However, additional experiments and computations are necessary to further investigate this aspect.

Fig. 8.

Representation of the reweighted FES as a function of the Ber23 π (in radians) and the interfacial water CVs. The presence of two minima (Aa and Ab) corresponding to the binding mode A indicates that water-mediated H-bonds between the ligands and DNA are possible in this pose. At variance with the binding mode A, no energetic contribution from water–bridge interactions is found in the B pose (Bc).

The GBPM.

With the aim to rationalize the solvent role, a second evaluation has been performed generating an unbiased GBPM (56) on Ber23 and Ber24 at the 3′-end binding site in the X-ray binding mode (PDB ID code 3r6r) (36). The GBPM analysis has been performed in presence of the bridging water molecule forming H-bond bridge interactions between the nucleobases at the 3′-end. This water was considered as part of the target. The utility of this method consists in proposing a possible role of the water-mediated H-bond network on the Ber23 binding affinity and also to rationally guide the structure-based design of more potent derivatives. The GBPM method, already applied to duplex and DNA recognition (57), has been performed in six steps. The first step is the GRID calculation to compute the molecular interaction fields (MIFs) based on the position of atomistic probes. Probes are parameterized to represent the chemical properties of a specific atom type. In this study, we used the DRY probe, which mimics the aromatic and aliphatic carbon atoms, to detect on the target regions with potential hydrophobic interaction, whereas the O and the N1 probes were used to mimic respectively the sp² carbonyl oxygen (hydrogen bond acceptor) and the amide NH group (hydrogen bond donor). The GBPM analysis reveals the important role of the water to mediate favorable H-bond interactions with the four O₆ atoms of the guanine residues G10:G16:G4:G22 (blue and red contour maps), whereas the hydrophobic interactions (yellow contour maps) involve the isoquinoline core of berberine (Fig. 9 A and B).

Fig. 9.

(A) Top view and (B) side view of the 3′-end Ber23 and Ber24 X-ray pose in presence of the bridging-water molecule (w) and the contour maps calculated using GBPM. Regions with favorable interactions explored by the DRY, N1, and O probes are shown as yellow, blue, and red contour maps, respectively, whereas their most relevant interaction points, identified with the Minim utility, are depicted as yellow, blue, and red spheres, respectively. K⁺ ions are represented as pink spheres. G4-DNA backbone is shown as gray ribbon, whereas the G-tetrad is shown as sticks colored by atom name. Ber23 and Ber24 residues are represented as orange and gray sticks, respectively. Ber25 and Ber26 residues are omitted for clarity.

Discussion

Elucidating the structural and energetics requisites underlying the recognition process between a ligand and its molecular target is of paramount relevance to lead successful drug design strategies. This task is even more difficult in the case of DNA that is endowed with conformational flexibility and presents solvent-exposed binding sites. Over the years, the efforts of both experimentalists and theoreticians have revealed the necessity of an important breakthrough in this field. In the present study, we have shown the potentiality of FM, an innovative free-energy method recently developed by our group (37). FM is a pathway free-energy method in which the ligand is gradually separated from the target structure. Other examples of pathway free-energy techniques are steered MD (58) and umbrella sampling (59), and other methods in which the ligand/target interactions are gradually switched off. Among these techniques are thermodynamic integration (60), free-energy perturbation (FEP) (61–63), double decoupling method (64), and double annihilation method (65, 66). At variance with the latter techniques, in FM information about the ligand binding mode is not required in advance, although the approximate location of the binding site in the target structure should be known. Using FM simulations, one can identify the lowest energy binding mode, also obtaining information about the presence of alternative higher energy binding poses and the lowest energy binding pathway. Furthermore, slow motion of the target and solvent effect in the ligand binding can be taken into account using explicit CVs (37, 41, 48). On the other hand, the choice of the CVs and the intensive computational cost of the calculation represent the main limitation for using FM on large dataset of molecules. In that case, techniques like FEP can be used to calculate the relative binding free energies for congeneric ligands (67). Based on these considerations, one might combine FM with FEP, so as to use the former in finding the correct ligand binding mode with an accurate estimation of the absolute binding free energy, and the latter to evaluate how changes in the ligand structure affect the binding affinity. Such a combined protocol might result very useful in drug design and in particular in lead optimization studies.

FM calculations have been successfully used to study ligand/protein binding interactions (47, 53, 68) and it is here applied to investigate ligand binding to DNA. Our simulations provide detailed atomistic and energetics information on the binding mechanism of an important antitumoral natural compound, berberine, to human telomeric G4-DNA. At the end of the simulations, a quantitatively well-characterized binding FES was computed that allowed identifying the most stable ligand binding poses as the lowest energy states. We found two possible binding modes of berberine in line with the available experimental data (36). In particular, in the X-ray structure (PDB ID code 3r6r), two berberine molecules are stacked at the 5′-end assuming an antiparallel orientation, whereas the other two are bound to the 3′-end in a parallel orientation. However, the presence of two DNA molecules in the single crystal cell and crystal packing effects, such as stacking interactions between nucleobases of different crystal mates, might affect the ligand binding mode. We overcome these limitations in our simulations where one single DNA molecule is present. Our results confirm and complement the experimental data revealing two ligand binding modes similar to those found by X-ray and providing further structural and energetics information on ligand binding mechanism, such as the presence of prebinding states and a quantitatively well-characterized free-energy landscape. We have validated the accuracy of our calculations performing berberine/G-quadruplex binding assays through fluorescence spectroscopy titration experiments. The calculated and experimental values of the absolute ligand/DNA binding free energy are in good agreement, especially considering the approximation of both the theoretical and experimental model. The application of FM allows overcoming limitations of the previous simulations (42, 69, 70) such as exhaustive exploration of the phase space and convergence of calculation, however conserving the full flexibility of DNA. Taking into account the conformational freedom of DNA is crucial because ligand binding might be affected by specific G4-DNA conformations (70). It has to be pointed out that, in this kind of calculations, the number and type of ligand rotatable bonds might also play a role and should be taken into account. The timescale of the conformational change of the ligand can depend on both its chemical structure and the chemical environment when the ligand is bound to the target. However, this is not the case for berberine, which is de facto a relatively rigid molecule.

Our study also provides hints for drug design. An example is the elucidation of the waters’ role in ligand binding that might suggest the design of derivatives able to replace the solvent-mediated interactions between berberine and DNA to achieve more potent and selective activity. Lead optimization studies on berberine are even favored by its chemical accessibility as demonstrated in the literature (71, 72). The present study demonstrates that FM is a most valuable method to characterize the structural and thermodynamic requisites of ligand/DNA binding, paving the way in the near future to investigations on ligand/DNA binding kinetics through free-energy calculations. These calculations can be performed using a recently developed protocol that has been successfully applied in case of ligand/protein interaction (73).

As previously stated, the fact that FM simulations are computationally intensive prevents their use on a large dataset of molecules. To date, the method has been successfully used in predicting the ligand binding mode and estimating the ligand binding free energy in single ligand/protein case studies (37, 47) or for a couple of congeneric ligands (53). However, considering the increasing computing power, we plan to use such a technique in the near future to study series of ligands, and that would represent an important advance in drug design.

Materials and Methods

MD.

The starting coordinates of the G4-DNA complexed with berberine were obtained from the Protein Data Bank (PDB ID code 3r6r) (36). All crystallographic water entries were removed. The standard parm99 Amber force field modified using the recently developed parmbsc0 parameters (74) was used for the G4-DNA, whereas for berberine the electrostatic potential (ESP) was calculated at the HF/6-31G* level using Gaussian 09 (75), and then the restrained electrostatic potential (RESP) (76) was computed using Antechamber (77). Additional counterions (K⁺) were added to the system until charge neutralization. The berberine/G4-DNA complex was first equilibrated through 5 ns of MD in NVT, NPT, and NVE conditions at 1 atm and 300 K, whereas the MD production run (50 ns) was performed in the isothermal isobaric ensemble (NPT). All of the simulations were carried out in a cubic box in explicit solvent with TIP3P water model (78) and periodic boundary conditions (SI Materials and Methods). To investigate the thermodynamic stability of the conformations of the lowest energy basins, a further MD simulation of 100 ns, in NPT ensemble at 1 atm and 300 K, was carried out.

FM.

The PLUMED plugin, version 1.3 (79), implemented in NAMD code, version 2.8 (80), was used to carry out about 800 ns of metadynamics simulations in the NVT ensemble. The bias was added on the distance (d) and torsion (π) CVs of residue Ber23 by setting Gaussian width of 0.15 Å and 0.08 rad, respectively, while the Gaussian height was at 0.1 kcal/mol. Gaussians were collected every 2 ps, so that the deposition rate was equal to 0.05 kcal/mol⋅ps. The bias factor was fixed to 12; as a consequence, the ΔT was 3600 K (SI Materials and Methods). The cone region of the funnel was built over the last MD snapshot including the whole 3′-end binding site of the G4-DNA (Fig. 4 and Table S1). The clusters analysis (Fig. S5) of the Ber23 binding conformations found in basins A and B was performed using the GROMOS algorithm (49) of the g-cluster tool implemented in the GROMACS, version 4.5, package (81). The absolute berberine/G4-DNA binding free energy was calculated using the following equation (37):

$$\mathrm{\Delta }{G}_{\mathrm{b}}^0=-\frac{1}{\beta }In\left(K_{\mathrm{b}}\right),$$ [1]

where K_b represents the equilibrium binding constant and can be computed as follows:

$$K_b=C^0\pi R_{\mathit{cyl}}^2{{\displaystyle \int }}_{\mathit{site}}dz\hspace{0.17em}{e}^{-\beta \left[W\left(z\right)-W_{\mathit{ref}}\right]},$$ [2]

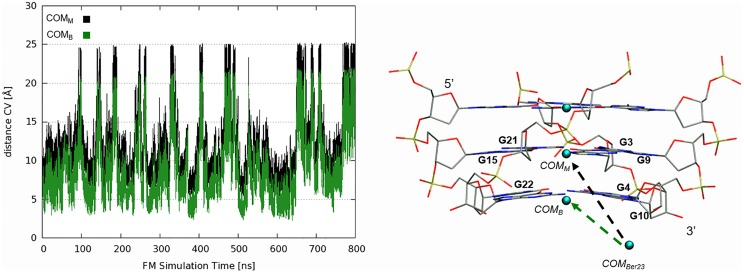
where C⁰ is the standard concentration of 1 M and is equal to 1/1.660 Å⁻³, $\pi R_{\mathrm{cyl}}^2$ is the surface of the cylinder used as restraint potential, whereas the potential W(z) and its value in the unbound state, W_ref, can be derived from potential of mean force (PMF) (Fig. 5C). β is constant and equal to 1/k_BT, where k_B is the Boltzmann constant and T the temperature of the system. Considering as cylinder radius R = 1 Å, the absolute berberine/G4 binding free energy is equal to −10.3 ± 0.5 kcal/mol. We calculated also the distance between the center of mass of berberine and that of the G-tetrad plane to which berberine is bound (COM_B) during the FM simulation. For the sake of comparison, we report this plot and that of the distance CV biased in the FM calculation (distance between the center of mass of berberine and that of the central G-tetrad plane, COM_M) in SI Materials and Methods (Fig. S8). As can be seen in Fig. S8, both the CVs (COM_B and COM_M) well represent the motion of the ligand relative to DNA. The unbiased distribution of the interfacial water CV is calculated using the reweighting algorithm introduced by Bonomi et al. (52).

Fig. S8.

(Left) Plot of the distance CV progression along the FM simulation calculated considering the center of mass of Ber23 (COM_Ber23) and the center of mass of the bottom G-tetrad (COM_B) and the middle G-tetrad (COM_M). (Right) Schematic representation of the center of mass. The COM_Ber23 has been calculated considering the atoms N1:C7 C10:C4:C2:C1 of Ber23. COM_B, and COM_M were instead calculated considering the C1′ sugar carbon of G22:G4:G10:G16, G3:G9:G21:G15 guanine residues, respectively.

Sample Preparation and Steady-State Fluorescence Experiments.

The d[TAG₃(T₂AG₃)₃] oligonucleotide from the human telomere was chemically synthesized and purified as already described (82). The oligonucleotide was dissolved in 10 mM Li₃PO₄ buffer (pH 7.0) containing 100 mM KCl. The concentration of oligonucleotide solutions was determined by UV adsorption measurements at 90 °C using the appropriate molar extinction coefficient value ε (λ = 260 nm) calculated by the nearest-neighbor model (83). Parallel G4 arrangement of telomeric DNA sequence was prepared and checked as previously described (84). Berberine chloride was purchased from Sigma-Aldrich and used without any further purification. The concentration of the berberine was determined by absorbance measurements using a molar extinction coefficient value ε (λ = 344 nm) of 22.500 M⁻¹⋅cm⁻¹. Steady-state fluorescence measurements were performed on a FP-8300 spectrofluorometer (Jasco) equipped with a Peltier temperature controller accessory (Jasco PCT-818). A sealed quartz cuvette with a path length of 1 cm was used. Both excitation and emission slits were set at 5 nm. Titration experiments were carried out at 25 °C and at three different supporting electrolyte concentrations of 100, 50, and 20 mM KCl (with 10, 5, and 2 mM phosphate buffer, respectively), by stepwise addition (3 or 4 µL) of DNA solutions (20–50 µM) to a cell containing a fixed concentration (0.9–1.2 µM) of berberine solution. Berberine was excited at 352 nm, and emission spectra were recorded between 450 and 670 nm. After each addition of DNA, the solution was stirred and allowed to equilibrate for 5 min. The observed fluorescence intensity was considered as the sum of the weighted contributions from free berberine and berberine bound to G4-DNA. The fraction of bound ligand (α) at each point of the titration was calculated following fluorescence changes at the maximum of intensity, using the following relationship:

$$\alpha =\frac{I_{\lambda }-I_{\lambda }^{\mathrm{free}}}{I_{\lambda }^{\mathrm{bound}}-I_{\lambda }^{\mathrm{free}}},$$ [3]

where I_λ represents the fluorescence intensity at each titrant concentration; I_λ^free and I_λ^bound represent the fluorescence intensity signals of the free and fully bound ligand, respectively. Titration curves were obtained by plotting α versus the DNA concentration. The association constant K_a, expressed by the inverse of the molar concentration, was estimated from this plot by fitting the resulting curve to an independent and equivalent binding site model, using the following equation (85):

$$\alpha =\left(1/2P_0\right)\left[\left(P_0+nL+1/K_{\mathrm{b}}\right)-\sqrt{{\left(P_0+nL+1/K_{\mathrm{b}}\right)}^2-4P_{0}nL}\right],$$ [4]

where L₀ is the total ligand concentration, Q is the added G4-DNA concentration, n is the stoichiometry, and K_b is the association binding constant. The binding free-energy change was calculated using the relationship ΔG_b = −RT ln K_b (R = 1.987 cal⋅mol⁻¹⋅K⁻¹, T = 298 K). The experiments were repeated three times, and the obtained results are presented as the mean ± SD.

SI Materials and Methods

System Setup and MD Protocol.

The MD starting structure of G4-DNA in complex with berberine was taken from the Protein Data Bank (PDB) with the ID code 3r6r (36). All of the crystallographic waters were removed. The electrostatic potential (ESP) of berberine was computed at the HF/6-31G* level using Gaussian 09 (75), followed by RESP charges distribution (76) calculated by mean of the Antechamber module (77). The Amber parm99 + parmbsc0 force field (74) was used for the G4-DNA. The water solvent effects were taken into account by means of the TIP3P explicit solvent model (78). K⁺ counterions were added to the system for global net charge neutralization. The final system was energy minimized and equilibrated by means of 5-ns MD run. The MD production run (50 ns) was performed with NAMD 2.8 code (80) in an isothermal–isobaric ensemble (NPT). Constant pressure (1 atm) and constant temperature (300 K) were achieved with the Piston Langevin barostat and the Langevin thermostat, respectively. A time step of 2 fs was used. All covalent bond lengths were constrained using the SHAKE algorithm, whereas long-range electrostatics effects were treated with the particle mesh Ewald method, using a grid spacing equal to 1 Å. As shown by RMSD values reported in the Fig. S1 (down plot), after ∼10 ns of MD simulation, the X-ray pose of Ber23 modified its starting configuration, assuming a nonstacking position. In particular, Ber23 moved toward the solvent and achieved an almost perpendicular orientation with respect to G4:G10. However, this motion occurs on a short timescale, because after ∼3 ns Ber23 recovered its original conformation. This behavior of Ber23 did not affect the stability of the second X-ray ligand, Ber24, and G-tetrads planes, as confirmed by the low RMSD average (upper plot); however, the higher flexibility of Ber23 led us to choose this residue for the ligand binding metadynamics simulations.

Funnel-Metadynamics Setup.

Funnel-metadynamics (FM) (37) simulations were performed using well-tempered metadynamics (38). The funnel potential was constructed considering the DNA conformation of the last MD snapshot. The funnel parameters were properly defined to include in the cone region the whole 3′-end binding site of the G4-DNA. In Table S1, the distance (d) and torsion (π) CVs, and the funnel parameters are reported. The FM simulation (800 ns) was carried out in the canonical ensemble (NVT) using the PLUMED plugin, version 1.3 (79), as implemented in version 2.8 of the NAMD code. The computational protocol was built by setting the initial Gaussians height at 0.1 kcal/mol and Gaussians width at 0.15 Å and 0.08 rad for the distance (d) and torsion (π) CVs, respectively. Gaussians were added every 1,000 steps (2 ps), so that the deposition rate was equal to 0.05 kcal/mol·ps. The bias factor was set to 12; thus, ΔT was 3600 K. During the binding/unbinding simulation of Ber23, the binding mode of the other ligand, Ber24, was constrained using an additional unbiased H-bond CV (Table S1). The clusters analysis of the conformations found in the basin A was performed using the GROMOS algorithm (49) of the g-cluster tool implemented in the GROMACS, version 4.5.5, package (81).

The Interfacial Water CV (watCV).

To estimate the energy contribution of water mediated interactions to the ligand binding, we reweighted the FES as a function of the Ber23 torsion (π) and the interfacial water CVs (watCV). The latter CV is defined as follows:

$$S_{watCV}={\sum }_i^{n_0}\left(\frac{1-{\left(\frac{\left|r_i-r_1\right|}{r_0}\right)}^n}{1-{\left(\frac{\left|r_i-r_1\right|}{r_0}\right)}^m}\right)\left(\frac{1-{\left(\frac{\left|r_i-r_2\right|}{r_0}\right)}^n}{1-{\left(\frac{\left|r_i-r_2\right|}{r_0}\right)}^m}\right),$$ [S1]

where $\left|r_i-r_1\right|$ and $\left|r_i-r_2\right|$ are the distance between the n₀ water oxygens and the O₆ atoms of G22:G16 and G10:G4 residues, respectively. The switching function parameters were defined by setting NN = 6, MM = 12, and R_0 = 4.0.

The GRID-Based Pharmacophore Model.

The GRID-based pharmacophore model (GBPM) consists in six steps (56). In the first step, three different model structures were produced: the Ber23/G4-DNA complex, the receptor, and the ligands (Ber23 and Ber24). The second step computes the GRID molecular interaction fields (MIFs) with a given probe onto the three subunit models (86). To obtain a suitable model in this study, the DRY (hydrophobic), the N1 (hydrogen bond donor), and the O (hydrogen bond acceptor) probes were used. The third step energetically compares the MIFs using the GRID GRAB tool (56), generating maps around the interaction areas. Subsequently, in the fourth step, the most relevant interaction points are identified using the MINIM utility as implemented in GRID. Such a program collects all points within a certain energy threshold, allowing the interpolation of the closest ones. This step is performed for each probe. In the fifth step, the information obtained from the different probes is unified into a preliminary pharmacophore model. Finally, the sixth step is instead dedicated to the validation of the preliminary information and the quality of the model. In this work, we carried out the GBPM analysis up to the fifth step, and we compared our predicted model with the reweighted FES obtained as a function of the ligand torsion and the interfacial water CV (Fig. 8 of the main text). The energy thresholds used were of −5.5 kcal/mol for both N1 and O probes, while −1.0 kcal/mol for the DRY probe.