Dynamics and the Regiochemistry of Nitration of Toluene

Abstract

The regiochemistry of the nitration of toluene by NO₂⁺BF₄⁻ in dichloromethane is accurately predicted from trajectories in explicit solvent. Simpler models and approaches based on transition state theory fail to account for the selectivity. Potential of mean force calculations find no free-energy barrier for reaction of the toluene/NO₂⁺BF₄⁻ encounter complex, yet the trajectories require an extraordinary 3 ps to descend an exergonic slope. The selectivity is decided late in long trajectories because their completion requires solvent and counterion reorganization. The normal descriptive understanding of the regiochemistry based on transition-state energies is unsupported.

Graphical abstract

INTRODUCTION

Philosophers of chemistry distinguish between “thick” reaction mechanisms and “thin” reaction mechanisms.¹ Thick mechanisms are complete descriptions of the atomic motions that transform reactants to products, “something like motion pictures”. More precisely, one might define a thick mechanism as the complete ensemble of trajectories accomplishing a reaction. A thin mechanism in contrast is the sequence of critical structures, the transition states and intermediates, along the path from reactants to products. Thin mechanisms are then simplifications of thick mechanisms, tractable models that are justified by the argument that no further information is needed to understand experimental observations.

The sufficiency of the thin mechanism has long been assumed in some areas of chemistry, particularly in the mechanistic study of organic reactions in solution. In the words of Gould from 1959, “If the configuration and energy of each of the intermediates and transition states through which a reacting system passes are known, it is not too much to say that the mechanism of the reaction is understood.”² In recent years, there has been a growing recognition that thin mechanisms are often unable to account for observations.^3–8 Instead, one must allow for the motions and momenta of atoms, that is, their dynamics. Classical mechanistic organic chemistry, however, could only interpret observations in terms of intermediates and transition states. This was the paradigm.

On a general level, data is inescapably initially interpreted within the available paradigms.⁹ When an observation does not fit with standard interpretive ideas, conflict can arise over its explanation. Complications are often suggested that allow the anomaly to be shoehorned into existing theory, and remaining inconsistencies may then be ignored. A consistent explanation for the observation may then only arise with the advent of new physical ideas. We describe here how this pattern applies to the understanding of the regiochemistry of nitration of toluene, and we present evidence supporting a new mechanistic understanding of these reactions based on dynamics.

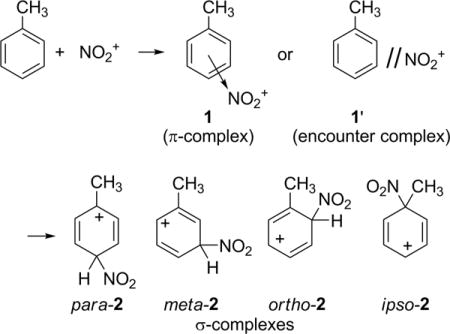
Over 50 years ago, Olah and co-workers reported unusual results in the nitration of toluene with highly reactive nitronium salts.^10,11 The essential observation was that the intermolecular selectivity between toluene and benzene is low, less than a factor of 2, while the intramolecular (positional) selectivity with toluene is high, affording only 3% of the meta-substituted product. The combination of these observations had the paradoxical effect of making the meta positions on toluene appear less reactive than individual benzene positions. The attack of NO₂⁺ on toluene is highly exothermic and its transition state was expected to be very early, yet it exhibited high positional selectivity. This was surprising. The selectivity was also unchanging regardless of the reactivity of the nitrating agent. As the barrier for nitration approaches zero, why should the selectivity be unchanged? To explain his observations, Olah proposed that the inter- and intramolecular selectivities were determined in different steps, with intermolecular selectivity determined in a rate-limiting formation of a π-complex 1 followed by positional selectivity determined in the conversion of the π-complex into the σ-complexes 2.

Olah’s proposal was very controversial. Ridd questioned the nature of the step determining the intermolecular selectivity, favoring either macroscopic mixing or microscopic diffusional encounter.¹² This criticism was contested, as it lacked the explanatory value of the π-complex in accounting for high selectivity, but considerable evidence supported encounter-controlled reactions in some nitrations.¹³ Later discussions from Olah conflated the π-complex 1 and encounter complex 1′.¹⁴ From a different perspective, it was argued that inter-/intramolecular selectivity anomalies are rare and of insufficient magnitude to require separate rate-determining and product-determining transition states (TSs).¹⁵ No agreement was reached on this issue.¹⁶

The general nature of the mechanism was itself contested. The idea that electron transfer is involved in nitration has a long history in the literature.¹⁷ In reactions of highly electron-rich aromatics, Kochi and others were able to strongly support the viability of such mechanisms.^18,19 With less electron-rich arenes such as toluene, however, Eberson argued that the uphill electron transfer would be far too slow to account for the observed rates of reactions.²⁰ Notably, the reactivity of aromatics correlates well with the stability of σ-complexes on a broad scale that includes both electron-rich and electron-poor aromatics.²¹ As with Olah before him, Kochi found the selectivity observed in toluene nitrations to be a sticking point. Kochi argued that the nearly constant regioselectivity observed for the nitration of toluene under diversely reactive conditions required the involvement of some intermediate, which he maintained as supporting electron transfer.²²

A recent paper by Koleva et al. has claimed the observation of a benzene/NO₂⁺ π-complex by direct UV–visible spectroscopy on the reaction under classical HNO₃/H₂SO₄ conditions.²³ This would be a substantial advance; Kochi had observed many electron donor–acceptor complexes of arenes with molecular NO₂–X (X = OH, OAc, NO₃, Cl, pyr, C(NO₃)₃) species,^18,22 along with NO₂⁺ σ-complexes,²⁴ but Olah’s putative NO₂⁺ π-complexes had never been observed. However, there is reason to doubt that the observed absorption is due to a benzene/NO₂⁺ π-complex. In any thermal reaction in which a mechanistic intermediate X is irreversibly converted to the product with a rate constant k (eq 1), the rate of product formation will be defined by eq 2, and the concentration of X will follow eq 3 (as a maximum, assuming a single mechanistic pathway).

$$\mathbf{A}+\mathbf{B}+\dots \rightleftharpoons \mathbf{C}\rightleftharpoons \dots \rightleftharpoons \mathbf{X}\stackrel{k}{\to }\text{product}$$ (1)

$$\text{rate}=k[\mathbf{X}]$$ (2)

$$[\mathbf{X}]=\text{rate}/k$$ (3)

Koleva et al.’s calculated barrier for product formation from the π-complex was 3–4 kcal/mol, making the rate constant ~10¹⁰ s⁻¹, and the observed rate was ~3 × 10⁻⁵ M s⁻¹. This places the expected concentration for the π-complex from eq 3 at 3 × 10⁻¹⁵ M, a concentration that is at least 9 orders of magnitude too low for the observed absorbance of ~0.5. If we assume that the extinction coefficient of the π-complex is on the order of 100 000, the observed absorbance could only be obtained if the rate constant for reaction of the π-complex were 6 s⁻¹. This requires a barrier of 16.4 kcal/mol, over 12 kcal/mol higher than the low calculated barrier. Even ignoring the large computational discrepancy, a barrier of 16 kcal/mol for a highly exothermic simple bond formation in an ion–molecule complex would be unprecedented. Importantly, this analysis does not speak to the validity of calculated π-complexes, only their observation. We will return to this issue.

Within the thin-mechanism paradigm, one is forced to associate the positional selectivity in the nitration of toluene with differing TSs leading from an initial intermediate to the regioisomeric σ-complexes. All of the mechanistic proposals agreed on this point. Until recently, chemistry had not developed the concepts needed for any alternative understanding of selectivity. We describe here how the selectivity can arise without involving either intermediates or transition states. We also show that even when transition states are present, their energies cannot be used to understand the selectivity. The selectivity is ultimately more interesting than the classical thin mechanism can depict, and its understanding requires the consideration of dynamics.

RESULTS AND DISCUSSION

Experimental Selectivity

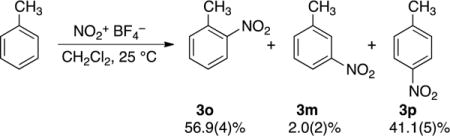
The selectivity for the nitration of toluene has been reported for over 100 different reaction conditions.¹⁴ We chose to study nitrations using the stable nitronium tetrafluoroborate (NO₂⁺BF₄⁻) salt in dichloromethane, in part due to the experimental cleanliness of the reaction and in part due to its relative computational simplicity. Almost all nitration conditions provide more ortho-nitrotoluene (3o) than para-nitrotoluene (3p), with 2–5% meta-nitrotoluene (3m), but the choice of solvent and nitrating reagent has a definite pattern of effects. Nitrations using preformed nitronium salts in polar solvents such as nitromethane or tetramethylenesulfone tend to give high 3o:3p ratios (>1.75) while nitrations in chlorinated solvents or in neat aromatic give lower 3o:3p ratios of 1.2–1.6. The 3o:3m:3p selectivity that we observe is typical for these conditions with diverse nitronium ion sources, and is nearly identical to that for a previously reported nitration in dichloromethane using tetrabutylammonium nitrate/trifluoroacetic anhydride.²⁵ The selectivity changes negligibly over a concentration range varied by 3 orders of magnitude.

Computational Method Selection

Before exploring the solution reaction, we sought to identify a DFT method that would be both practical for a broad study and energetically accurate on the gas-phase energy surface. Of a wide range of DFT methods explored (see the Supporting Information (SI)), none was completely satisfactory. Two distinct problems were encountered with DFT methods, and we ultimately were able to adequately address each problem.

The first problem was that DFT methods tend to overestimate the electrophile affinity of aromatics. The simple proton affinity of benzene was overestimated by most methods, with the exception of the M06-2X and M11 functionals, and the overestimation is worse for the affinity of NO₂⁺ to toluene (see the SI). We chose to use the M06-2X functional with a 6-311G* basis set because this combination had three attractive features: (1) It minimized the overestimation of the electrophile affinity (as gauged by G3B3 and CCSD(T) energies) versus all other methods explored with the exception of M11/6-311G*. (2) It exhibited the lowest mean absolute deviation in the relative energies of NO₂⁺/toluene σ-complexes 2, at 0.3 kcal/mol versus G3B3 energies. (3) The M06-2X/6-311G* energy profile for approach of NO₂⁺ to toluene very closely matched CCSD(T)/aug-cc-pvdz energies for N–C interatomic distances between 2 and 3.2 Å (see the SI). Because the reaction selectivity is decided in this range of the energy surface, it was judged that the M06-2X/6-311G* surface would be adequate for the purpose at hand here. The accuracy of the M06-2X/6-311G* energies was gauged again by comparison to CCSD(T)/aug-cc-pvdz energies for a series of five toluene/NO₂⁺ TSs (see below), and the relative energies agreed within 0.1 kcal/mol.

The second problem was that all DFT methods explored greatly underestimated the stability of the BF₄⁻ toward fluoride transfer to NO₂⁺, in comparison with CCSD(T)/jun-cc-pvtz calculations. The resulting unreal decomposition of NO₂⁺ BF₄⁻ in extended trajectories or any gas-phase calculation is likely a manifestation of the well-known tendency for DFT to err in the energy of dative bonds.²⁶ We addressed this problem in two ways. Because solvent-stabilization of charge leads to a barrier to the decomposition, it proved possible to locate stationary points on an M06-2X/6-311G*/PCM(CH₂Cl₂) surface, and to carry out short trajectories on this surface. Alternatively, a full range of stationary point, trajectory, and potential of mean force (PMF) calculations in explicit solvent were carried out on an ONIOM²⁷ surface, using M06-2X/6-311G* for the toluene/NO₂⁺ and PM3 for the BF₄⁻ (and CH₂Cl₂ molecules when explicit solvent was employed). On the ONIOM surface, the interaction of BF₄⁻ with NO₂⁺ occurs purely in the PM3 layer, and the PM3 surface correctly disfavors fluoride transfer from BF₄⁻ to NO₂⁺. This has the effect of avoiding the unphysical NO₂⁺ BF₄⁻ decomposition while accurately retaining the electrostatic effect of the counterion.

The Multilevel Failure of Conventional Computational Studies in Implicit Solvent

A semi-automated search algorithm was used to locate both TSs and π-complex-like minima for the reaction of toluene with either NO₂⁺ or NO₂⁺BF₄⁻. In this algorithm, classical trajectories were carried out at 25 °C on a M06-2X/6-311G*/PCM (CH₂Cl₂) (for NO₂⁺) or the ONIOM (for NO₂⁺BF₄⁻) surface, with the distance between the nitrogen atom and the nearest aromatic carbon constrained by a loose harmonic potential (set at 2.4 or 2.7 Å in the search for TSs and 3.0 Å in the search for π-complexes). In each case, over 150 points from a series of independent trajectories were extracted and used as the starting points for optimizations. Optimized structures were then systematically varied with respect to the positional orientation of the methyl group versus the NO₂⁺. Additional starting structures for optimization were chosen using researcher intuition, but in no case did this lead to a new low-energy structure.

A total of five TSs and 12 π-complex structures were located for the addition of NO₂⁺ to toluene in the M06-2X/6-311G*/PCM calculations. The addition of NO₂⁺ to toluene is highly exothermic (18–25 kcal/mol), and the calculated TSs for the addition are all quite “early.” Three of the TSs, 4a^⧧, 4b^⧧, and 4c^⧧, are shown in Figure 1a. The lowest-energy structure is surprisingly one that leads to the ipso σ-complex by intrinsic reaction coordinate (IRC) analysis, and no TS leads by IRC to the meta σ-complex. If the product ratio were predicted solely from the TS energies and IRCs in the usual fashion, the mixture of σ-complexes 2 would be 26% ipso, 20% ortho, 0% meta, and 54% para. However, the IRC analysis is misleading, because trajectories passing through each of the located TSs can in fact afford multiple products. For example, the NO₂⁺ in 4a^⧧ can ultimately attack three ring positions, i.e., the ipso and either of the two ortho positions. That is, there is a bifurcation or multifurcation of the energy surface after each TS.^{5a,c,e,g,h,j,8} Under special circumstances a statistical prediction of the selectivity is sometimes still possible using variational transition state theory and the Lluch procedure,^28,5c but attempts to locate the necessary separate variational TSs were unsuccessful here, as is often the case.^5e This precludes a statistical prediction or understanding of the selectivity, and necessitates the employment of the trajectory methods for a quantitative prediction.

Figure 1.

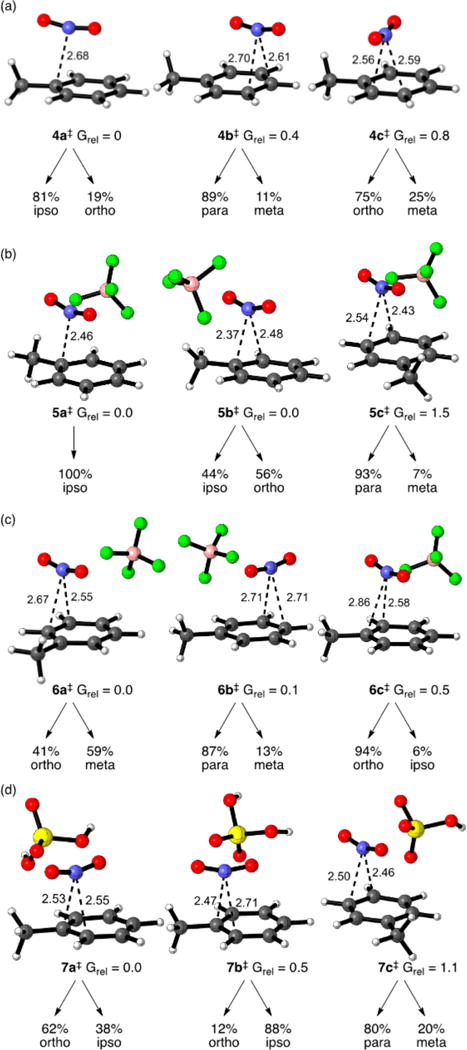
Example TSs for the nitration of toluene, along with the ratio of products obtained from quasiclassical trajectories passing through the structures. (a) NO₂⁺ without a counterion, M06-2X/PCM(CH₂Cl₂). (b) NO₂⁺BF₄⁻, M06-2X/PCM(CH₂Cl₂). (c) NO₂⁺BF₄⁻, ONIOM/PCM(CH₂Cl₂). (d) NO₂⁺/H₂SO₄, M06-2X/PCM(CH₂Cl₂).

Each of the five TSs was used as the starting point for quasiclassical direct-dynamics trajectories on the M06-2X/6-311G*/PCM surface. Each normal mode in each structure was given its zero-point energy (ZPE) plus a randomized excitation energy based on a Boltzmann distribution, along with a randomized displacement of the modes. The trajectories were then propagated forward and backward in time until σ-complexes were formed or the reactants separated to the >3 Å distance associated with the π-complex structures. After allowing for a Boltzmann weighting of the five TSs, including entropies of mixing versus the achiral 4a^⧧, and allowing for the mixtures of isomeric products obtained from each TS (see Figure 1a and the SI), the predicted mixture of σ-complexes 2 would be 21% ipso, 20% ortho, 11% meta, and 48% para.

This is a poor prediction in multiple ways. The para σ-complex is incorrectly predicted to exceed the ortho σ-complex. The predicted amount of meta complex is too high by a factor of 5. Judging by literature results, the ipso attack is also far too high; only 3.1% ipso adduct is formed under conditions that capture the intermediate σ-complex.²⁹ Overall, even after allowing for trajectory outcomes on a multifurcating surface, the toluene/NO₂⁺/implicit solvent physical model is simply inadequate for predicting or understanding the selectivity.

After including the BF₄⁻, a total of 38 TSs and 36 π-complex structures were located on the M06-2X/6-311G*/PCM (CH₂Cl₂) surface. The large number of structures with the ion pair reactant arise from a multiplicity of positions for the BF₄⁻ ion. Figure 1b shows three of the TSs, 5a^⧧, 5b^⧧, and 5c^⧧. The six lowest-energy structures are all oriented for attack at the ipso carbon, as in 5a^⧧ or the ortho carbon, as in 5b^⧧. Each of the nine lowest-energy TSs were used as the starting point for quasiclassical trajectories, following all of the procedures employed above for the cationic system. As above, the IRCs are misleading, and trajectories derived from six of the nine TSs afford a mixture of products. After allowing for a Boltzmann weighting of the nine TSs and the mixture of σ-complexes obtained from each, the predicted mixture of σ-complexes 2 would be 78% ipso, 19% ortho, 0.1% meta, and 3% para. This exceptionally poor prediction is plausibly the result of a too-tight interaction of the NO₂⁺ and BF₄⁻ ions, associated with the unreal fluoride-transfer decomposition process on DFT surfaces. The ONIOM surface described above avoids this problem.

A total of 42 TSs and 102 π-complex structures were located for the toluene/NO₂⁺BF₄⁻ reaction on the ONIOM(M06-2X:PM3)/PCM surface. The π-complex structures (see the SI) have closest C–N interatomic distances of 2.7–2.9 Å and are located in extremely shallow minima, never more than 0.7 kcal/mol below the lowest-energy TSs. The sets of located TSs and π-complexes are misleading; there are no low-energy TSs for attack at the ortho or ipso carbons because the attack has no potential-energy barrier with favorable positions of the BF₄⁻ counterion. As a result, the seemingly exhaustive search process is biased for TSs associated with barriers, with attack para or meta (e.g., 6a^⧧ and 6b^⧧) over those that face no barrier. To mitigate this problem, we located canonical variational transition states (CVTSs), e.g., 6c^⧧, for attack at the ortho and ipso positions using the no-saddle procedure of Truhlar.³⁰ Each of the low-energy TSs and CVTSs were then used as the starting point for quasiclassical trajectories as above. Twelve of the 13 sets of trajectories afford mixtures of σ-complexes. Based on a Boltzmann weighting of trajectory outcomes from comparable TSs/CVTSs (see the SI), the predicted mixture of σ-complexes 2 would be 12% ipso, 20% ortho, 27% meta, and 29% para. The predicted selectivity is notably low. This might be expected for these very early TSs, but it is clearly inconsistent with experiment.

It might be argued that calculations should be more successful in a polar sulfuric acid medium where counterion effects should be minimized. As will be discussed later, there are also reasons to consider whether TSs are more relevant to the selectivity in sulfuric acid nitrations than in the NO₂⁺BF₄⁻/CH₂Cl₂ system. For this reason, we explored the nitration of toluene with NO₂⁺ including an additional sulfuric acid molecule in M06-2X/6-311G* calculations including a PCM model for sulfuric acid (following the general process of Koleva et al.²³). A total of 28 TSs were located for the formation of the σ-complex, but none of the TSs would afford meta-2 by IRC. If TS energies by themselves were used to predict the selectivity, it would be 11% ipso, 76% ortho, 0% meta, and 13% para. As in the previous cases, however, the IRCs are misleading because most (22 out of 26 cases explored) of the TSs lead to multiple products in quasiclassical trajectories. Based on a Boltzmann weighting of outcomes from sets of trajectories based on the 26 lowest-energy TSs, the predicted selectivity would be 24% ipso, 63% ortho, 1% meta, and 12% para. This is again a poor prediction.

Overall, the attempts above to understand the selectivity of toluene nitration based on transition states failed on multiple levels. Predictions of the product ratios from the energies of TSs fail entirely to account for the selectivity. On a higher level, the pervasive implicit assumption in such a calculation, that transition states lead to a single product, fails. Finally, even when the TS studies are augmented by trajectory studies to allow for the mixture of products obtained from the various TSs, the calculations are still unable to provide a reasonable prediction of experimental observations.

When ordinary calculations employing implicit solvent models fail to account for experimental observations, it is tempting to attribute the error to inaccuracies in the potential energy surface. However, the limitations of the physical model must also be considered. One issue is that even a perfectly accurate potential energy surface may be quite misleading in comparison to the decisive free-energy surface, and the accurate allowance for entropic effects in implicit solvent is a challenging problem.³¹ A significant advantage of physical models including explicit solvent is that satisfactory methods exist to explore the solution free-energy surface directly. A second issue is that implicit solvent models do not account for the dynamics of solvent motion and reorganization. It will be seen below that the same energy surface as employed above, in combination with explicit solvent and a complete physical model including dynamics, accurately accounts for the experimental selectivity.

Although the various TSs do not account for the selectivity, there is a common structural feature worth brief consideration. That is, in 105 of the 115 TSs located, the nitronium is approaching the aromatic ring on a path that is approximately splitting two carbons. This can be seen in all of the structures in Figure 1 except 4a^⧧ and 5a^⧧. This strong tendency to approach between two carbons promotes the formation of multiple products from trajectories through the various TSs.

Potential of Mean Force Calculations in Explicit Solvent

For exploring the free-energy surface and for dynamics including solvent motion, the computational model employed consisted of toluene and NO₂⁺BF₄⁻ in a sphere of 101 CH₂Cl₂ molecules with a diameter of 25.8 Å and density 1.3. This model was explored on the QM/QM ONIOM surface, using M06-2X/6-311G* for the toluene/NO₂⁺ and PM3 for the BF₄⁻ and CH₂Cl₂. The choice of the PM3 method for the CH₂Cl₂ was based on the priority of modeling correctly the dipole moment and most of the polarizability of the real solvent, though PM3 performs poorly in modeling the intermolecular attraction of the solvent molecules (see the SI for details). We first set out to determine the general shape of the free-energy surface as the NO₂⁺BF₄⁻ approaches the toluene by determining the PMF versus nitrogen–arene carbon distance using umbrella sampling. A complication in this process is that simple biasing potentials based on individual C– N distances do not preclude attack of the NO₂⁺ on alternative arene carbons. To avoid this problem, the biasing potential was based on the distance of the nitrogen atom from six interlocking spheres centered on the arene ring carbons. The PMF obtained from this potential then represents a composite of the PMF for approach to the individual carbons, weighted by the equilibrium between the differing approaches. (See the SI for details and a comprehensive discussion.)

The PMF profile was determined in both molecular dynamics (MD) and Monte Carlo calculations. A total of 1 ns of MD was obtained on the QM/QM surface, while the Monte Carlo surface is based on 400 000 successful steps (~30%) using an efficient ad hoc stepping algorithm. The PMF was calculated by the weighted histogram analysis method.³² The results are summarized in Figure 2.

Figure 2.

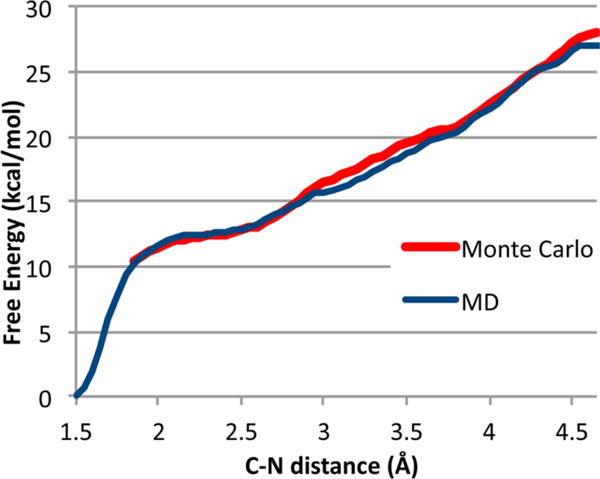
Potential of mean force curves for approach of NO₂⁺BF₄⁻ to toluene in a sphere of 101 CH₂Cl₂ molecules. The zero of energy is the para isomer of 2, and the level of the limited Monte Carlo curve is set arbitrarily.

The striking observation is that there is no free-energy barrier along the C–N distance coordinate. At any distance within 4.5 Å, approach of the NO₂⁺BF₄⁻ to the arene is favored and the system is destined to form some isomer of 2. At equilibrium, 2 is >95% para. The preference for reaction of encounter complexes over their diffusional separation is not surprising, as this is expected in the modern view of the mechanism. However, the apparent absence of transition states (more on this later) after formation of the encounter complex has never previously been suggested. This absence is in fact counter to basic ideas in all previous explanations of the selectivity.

We note in passing that the various TSs and π complexes obtained with an implicit solvent model have no physical counterpart whatsoever in explicit solvent. In the C–N distance range of 2.5–2.9 Å, where the many TSs and π-complex structures were located in implicit solvent, the free-energy profile is notably steep. Implicit solvent calculations show similar overall energetics to those obtained from the PMF, but they exhibit barriers or flattening of the potential energy curve in an area where there is no such feature on the free-energy surface.

Trajectories in Explicit Solvent

The selectivity on this exergonic slope was explored in trajectories using the identical toluene/NO₂⁺BF₄⁻/101 CH₂Cl₂ system. The starting points for trajectories were obtained from a series of independent simulations that were equilibrated at 25 °C with the distance between the NO₂⁺ nitrogen and the closest aromatic carbon constrained to ~3.4–4.0 Å using a loose biasing potential. In this distance range, the nearest carbon to the NO₂⁺ was found to vary statistically. At 250 fs intervals, structures and velocities were extracted from the equilibrating systems and integrated forward and backward in time with no constraint. In no case did the NO₂⁺ dissociate from the toluene, in keeping with the PMF curve. Instead, each trajectory resulted in the formation of one of the regioisomers of 2 (defined by a C–N distance of <1.6 Å). Most of the trajectories were stopped at the formation of 2, but a series of trajectories were continued to explore the behavior of the σ-complexes. For trajectories affording para-2, meta-2, and ortho-2, the highly acidic σ-complexes transfer a proton from the nitrated center to either the BF₄⁻ (69%) or a solvent molecule (31%) to afford the final nitration products. The median time for the proton transfer, 550 fs, reflects the lifetime of the σ-complex. No reversibility or rearrangement was observed, in keeping with the idea that the selectivity is determined kinetically in the formation of the σ-complexes. The ipso-2 complex was stable up to a time limit of 1500 fs.

The regiochemistry of σ-complex formation was independent of the starting geometry of the trajectories. This is shown by the absence of a correlation between the outcomes of the trajectories integrated forward versus backward in time (46% of the pairs afforded the same product, compared with 45% expected from a purely random distribution). A total of 672 trajectories were completed, and the results are summarized in Table 1.

Table 1.

Experimental and Trajectory-Predicted Regioselectivity in the Nitration of Toluene

	para	meta	ortho	ipso
experimental	41%	2.0 ± 0.2%	57%	a 3.1% ± 0.7%b
trajectories with toluene/NO2+BF4−/CH2Cl2	304 (45% ± 2%)	15 (2.2% ± 0.6%)	330 (53% for ortho + ipso ± 2%)	23 (3.4% ± 0.7%)
median time (fs)	2754	3815	3332	4737
equilibrium σ-complex mixturec	98%	0.01%	2%	0.002%

^aIpso attack is not measurable under our reaction conditions; the ipso-2 is expected to rearrange to ortho-2 and afford the ortho product. See ref 33.

^bFor nitration in acetic anhydride. See ref 29.

^cFrom M06-2X/6-311G*/PCM free energies. The same trend is seen in G3B3 and CCSD(T) gas-phase energies (see the SI).

A series of remarkable features were noted in the trajectories. The most striking is that they take an extraordinarily long time to afford the σ-complexes. The median trajectory time overall was 3100 fs. This should be compared with the median of 75 fs taken in nitration trajectories started from transition structures 4^⧧–7^⧧ and 50–300 fs typically required to traverse the downhill slope in a cycloaddition. The median time required to afford para-2 (Table 1) was interestingly shorter than that for other σ-complexes, with formation of ipso-2 requiring a median of 4700 fs. Notably, there are no interposing solvent molecules that could block the NO₂⁺ attack. The NO₂⁺ is often directly over a reactive aromatic carbon (Figure 3), appearing well-positioned for bond formation. Even so, product formation is over an order of magnitude slower than normally expected.

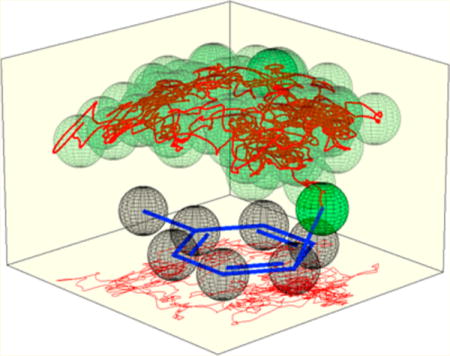
Figure 3.

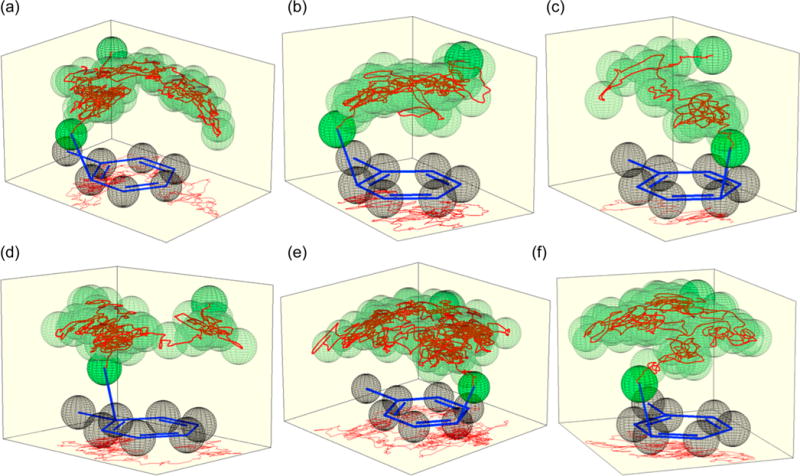
Motion of the nitrogen atom of NO₂⁺BF₄⁻ relative to the average position of the toluene carbons in trajectories in 101 CH₂Cl₂ molecules. The paths are depicted in red and the transparent green spheres are added to clarify the 3-dimensional motion. A 2-dimensional trace of the path is shown on the floor of the figures.

A second observation is that the product is not “decided”, that is, predictable from the position of the NO₂⁺ relative to the toluene, until very late in the trajectory. As can be seen in the trajectory depictions in Figure 3, the NO₂⁺ roams the area above the plane of the aromatic carbons, surprisingly avoiding the middle of the ring, moving from carbon to carbon. (See the SI for additional trajectory drawings.) The closest carbon (based on the shortest C–N distance) changes a median of 27 times over the course of each trajectory. The last switch between closest carbons happens a median of 260 fs before σ-complex formation, at a median C–N distance of 2.42 Å. Before this, the NO₂⁺ may approach multiple aromatic carbons without consummating bond formation. Prior to the final approach of the NO₂⁺ to the reacting position, 85% of the trajectories have the NO₂⁺ pass within 2.3 Å of a different carbon atom, and 25% of the trajectories have the NO₂⁺ pass less than 2.0 Å from an ultimately non-reacting carbon. The NO₂⁺ may also closely approach the reacting carbon then move away; 50% of the time that an NO₂⁺ gets within 2.0 Å of a carbon, it later retreats to >2.3 Å.

Most importantly, the trajectory outcomes accurately reproduce the experimental regioselectivity (Table 1). The comparison with experiment requires proper allowance the formation of ipso-2. Ipso attack in nitrations of alkylbenzenes is well known. In acetic anhydride the ipso σ-complex can be trapped, and the nitration of toluene in acetic anhydride affords 3.1% ± 0.7% trapped ipso adduct.²⁹ This fits perfectly with the 3.4% ipso-2 obtained from trajectories. Under our reaction conditions, the ipso-2 is not trapped, and it would be expected to undergo an exclusively intramolecular 1,2-shift of the nitro group to afford the ortho product.^33,34 M06-2X/6-311G*/PCM calculations predict that the direct intramolecular 1,2-shift can occur with a barrier of 7.7 kcal/mol. Together, the ortho and ipso trajectories afford 53% of the adducts, in comparison with 57% ortho product experimentally.

Overall, the quantitative accuracy of the selectivity prediction at each of the ring positions supports the adequacy of the computational model and the accuracy of its mechanism. In this way the results weigh strongly against the importance of electron transfer in the mechanism. This accurate prediction of the selectivity by a complete physical model should be contrasted with the failures of conventional qualitative explanations of the selectivity. A standard textbook-level explanation of the selectivity emphasizes the relative stability of the σ-complexes, but in the case of nitration this is a particularly poor predictor (Table 1). An alternative textbook approach is based on frontier orbitals. Such approaches correctly predict that the ortho and para products should be favored, but provide no guidance on the amount of meta or ipso attack to be obtained or the ratio of ortho and para products. Alternative reactions such as Friedel–Crafts acylation or bromination afford product ratios very different from that seen in nitration,¹¹ even though the frontier-orbital considerations are the same in the three reactions. In a more quantitative approach to predicting the selectivity, Galabov described a correlation of observed selectivities with the calculated relative stability of σ-complexes.³⁵ For the nitration of toluene, this correlation fails disastrously for the ortho or ipso products. That is, for the B3LYP/6-311+G(2d,2p) calculations employed by Galabov, ortho-2 is 4.0 kcal/mol less stable than para-2, and ipso-2 is 3.1 kcal/mol less stable than meta-2, but the less stable σ-complex is formed to a greater extent in each case. It should not be surprising when correlations and qualitative models fail, as in differing ways such models are quite incomplete physically. Our complete physical model here provides the first quantitatively accurate prediction of the selectivity.

The Nature of the Selectivity

Some insight into the nature of the selectivity comes from trajectories with key features of the computational model simplified. Three such models were explored: (A) trajectories in which the explicit CH₂Cl₂ is switched out for a PCM implicit solvent model; (B) trajectories in explicit CH₂Cl₂ but lacking the BF₄⁻ counterion; and (C) trajectories lacking the counterion in implicit solvent. As in the process used above for the complete model in explicit solvent, trajectories with the NO₂⁺ nitrogen loosely constrained at a distance from the aromatic carbons (see the SI for complete details) were equilibrated then periodically extracted and integrated forward and backward in time with no constraint until a σ-complex was formed.

In each case, the normal ortho–para selectivity is crippled. In simplified models A, B, and C, the meta product rises to 16%, 18%, and 23%, respectively, and the ipso product rises to 12%, 4%, and 25%, respectively. The low selectivity accompanies trajectories that afford the σ-complexes much faster than the full model, with median completion times of 1150, 800, and 1025 fs, respectively. Figure 4 depicts two example trajectories; additional examples are given in the SI. In each simplified model, the product is decided at a far earlier stage (median C– N distances of 2.9–3.2 Å) than for the complete model, and it is rare for the NO₂⁺ to approach arene carbons without reacting.

Figure 4.

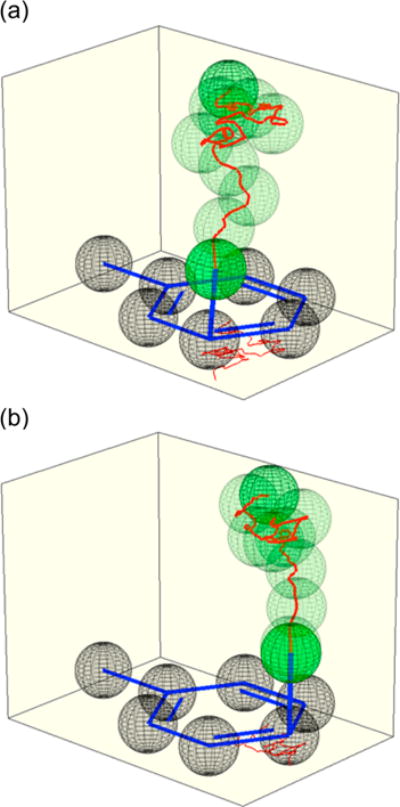
Motion of the nitrogen atom in typical trajectories using simplified models, relative to the average position of the toluene carbons. (a) NO₂⁺BF₄⁻ in a PCM implicit solvent model. (b) NO₂⁺ (no counterion) in explicit CH₂Cl₂. See the SI for additional examples.

These observations suggest that solvent dynamics are of critical importance to the selectivity. For the NO₂⁺ to attack the toluene, the process must be enthalpically downhill. It is not so initially, because the solvent and the counterion are disposed in such a way to best stabilize the positive charge of the NO₂⁺, as opposed to the quite different charge distribution in the ultimate σ-complex cation. When selected trajectory points are subjected to steepest-descent optimization with the solvent and counterion frozen, C–N bond formation does not occur unless the initial C–N distance is less than ~2.0 Å. This is quite different from the situation with an implicit solvent model, where it was found in an earlier section that the attack can be barrierless or involve transition states with a C–N distance >2.5 Å (Figure 1c). At any instant prior to <2.0 Å approach of the nitronium to the arene, the explicit solvent may be viewed as exerting a force field on the reactants that prevents consummation of the reaction.

Although the polarization of the solvent adjusts quickly to a redistribution of charge, full solvation requires reorientation of the solvent molecular dipoles. This takes time. The longitudinal and Debye dipolar relaxation times for CH₂Cl₂ are 900 and 2170 fs, respectively,³⁶ notably of similar magnitude to the length of the trajectories. Charge redistribution is too facile with the implicit solvent model because the solvation is assumed to be at equilibrium at all times, and the computationally unhindered trajectories are unselective. In addition, the BF₄⁻ counterion must reposition to minimize charge separation versus the incipient σ-complex. In the trajectories, the distance of the boron atom to the closest arene carbon shrinks from 5.4 Å at the beginning to 3.7 Å at the end of the trajectory. The counterion repositioning also takes time, and trajectories without this impediment are unphysically unselective.

What is the origin of the normal ortho–para selectivity? The NO₂⁺ awaits an enthalpically downhill path to choose one of the regioisomeric σ-complexes. The energy surface confronting the NO₂⁺ may be viewed as the superposition of the energy effects of the solvent dipoles and counterion placement on the intrinsic energetics for NO₂⁺ attack. Since the latter is energetically steeper when the attack is ortho or para, a downhill path is more quickly available for formation of ortho and para complexes than for meta or ipso complexes. In this way, the selectivity reflects the differing intrinsic energetics of the pathways, without involving transition states.

Are There Ever Transition States after Encounter? Do They Ever Control the Selectivity?

In HNO₃/H₂SO₄/water mixtures, the reaction of nitronium ions with toluene is not fully encounter-controlled. This is clear from the kinetic work of Schofield and co-workers.³⁷ Their key observation was that the bimolecular rate constant for nitration reached a maximum in this medium when the benzene ring is activated by two alkyl groups, with further activation providing no further acceleration. Schofield concluded that the reaction of highly activated aromatics with NO₂⁺ is encounter-controlled based on this leveling of the reactivity. Toluene, however, reacts at ~50% of the maximum rate, indicating that only 50% of the NO₂⁺/toluene encounters are productive. This can only be the case if there is a small but real dynamical bottleneck after encounter. In other words, in this medium there must be a TS or TSs after an intermediate.

Benzene is of course less reactive than toluene and it reacts about 40 times slower than the encounter-controlled rate. Assuming a diffusion rate in H₂SO₄/water of ~10⁹ M⁻¹ s⁻¹, the barrier for reaction of the intermediate would have a lower bound of about 7 kcal/mol (more if diffusional separation is slowed by an energetic barrier). The indisputable involvement of some form of intermediate would be consistent with the complexes calculated by Koleva et al.,²³ though the barrier for its forward reaction would have to be somewhat higher than that calculated.

This trait of reactions in HNO₃/H₂SO₄/water mixtures is different from the reactions of NO₂⁺ salts in less-coordinating organic solvents, where all observations are consistent with fully encounter-controlled rates. Encounter-controlled reactions certainly may involve TSs after encounter, but their kinetics do not require this. Counter to the ubiquitous assumption in the literature, we have seen above that the observation of positional selectivity after encounter in no way requires the involvement of TSs. The calculations here only speak to an absence of TSs in the NO₂⁺BF₄⁻/CH₂Cl₂ reaction, and it might be hypothesized that TSs are more likely to be present as the solvent becomes more coordinating of the NO₂⁺. The presence versus absence of TSs after encounter in more polar organic solvents thus remains an open question.

Even for the NO₂⁺BF₄⁻/CH₂Cl₂ reaction, transition states after encounter might be present if the reaction coordinate is defined differently. The barrierless slope of Figure 2 is based on a reaction coordinate defined by the nitrogen–arene carbon distance by itself. This coordinate is dominant in the energy of the system. However, transition state theory is if anything flexible, and in principle it may be possible to define TSs for formation of 2 from the encounter complex by employing solvent coordinates and nonequilibrium solvation/solvent friction.³⁸ Such approaches appear intractable here. It should be recognized that transition states are a useful chemical model, not a scientific requirement, and it makes little difference that a system might be shoehorned into a complex version of a model if the model cannot be used to make predictions. In contrast, the consideration of trajectories here provides both a quantitative prediction and a qualitative understanding.

This ignores the most momentous issue regarding the importance of transition states in nitration. That is, the bifurcation or multifurcation of pathways after TSs makes it unlikely that any definable TSs would account for the selectivity. None of the studies here support the validity of understanding the selectivity from transition states. Our complete model accounts for the observed selectivity without transition states. Even when well-defined transition states can be located, as with the 4^⧧, 5^⧧, 6^⧧, and 7^⧧ series of TSs, 45 out of 53 sets of trajectories started from the varies TSs afford mixtures of products. In this way, the normal description of the selectivity as resulting from TS energies is unphysical even when defined TSs are available. We cannot exclude the possibility that there are reaction conditions for which TSs determine the selectivity, but in the absence of supportive evidence this textbook idea should be abandoned for nitration.

CONCLUSIONS

The implicit assumption that a thin mechanism, one only considering transition states and intermediates, was sufficient to understand experimental observations in nitrations forced a particular description of the mechanism. Because the intermolecular and intramolecular selectivities did not fit together, it was surmised that there had to be an intermediate followed by a series of separate transition states affording each of the products. The nature of the intermediate was debated, and no proposal comfortably fit all observations, but the view that there had to be an intermediate followed by product-determining transition states was unquestioned.

This view fails. An extensive effort to account for the regioselectivity of the nitration of toluene based on TS energies in implicit solvent failed to provide reasonable predictions. The calculations do not even support the idea that the selectivity can be associated with TS energies, since most TSs lead to two products. Mechanistic details are important to the degree that they allow the prediction of experimental observations. From this, even if definable TSs are present in some nitrations, they may simply be unimportant.

In contrast, the regioselectivity with NO₂⁺BF₄⁻ in CH₂Cl₂ can be accurately predicted within a mechanism that involves no intermediates prior to the σ-complex and no transition states beyond encounter. This prediction is based on a complete physical model that includes explicit solvent and the BF₄⁻ counterion, allowing fully for their dynamics, and it provides the first quantitatively accurate prediction of the selectivity. The quantitative success of this model supports the accuracy of its mechanism. At the least, any alternative mechanism must be viewed skeptically until it can be shown to also account quantitatively for experimental observations.

When a reaction passes through a simple single transition state, the solvation at the TS will be approximately at equilibrium. This old idea allows the consideration of solvent effects on transition state energies in a way that parallels the ordinary equilibrium-solvation effects on ground-state energies, and the effect of solvent dynamics is minimal. However, this simplification does not apply when the reaction coordinate is more complicated^5b and it does not apply when there is no transition state. Solvent dynamics then play an extraordinary role in the nitration of toluene. Despite facing a uniformly exergonic slope, that is, downhill in free energy at equilibrium, the approach of the nitronium ion to the toluene is held back by solvation and counterion positioning that is not at equilibrium. The reorganization of the solvent and the counterion takes time, and the resulting slow, meandering, and often reversing approach allows the nitration to achieve selectivity. Without transition states, the choice of product is made late in the approach when the energetic attraction of the reactants finally overcomes the chaperoning by the solvent and counterion. These ideas are clearly qualitative at this this point, and chemistry in the future will need to develop a greater understanding of the nature of selectivity on downhill slopes, particularly in polar solution reactions.

Our results suggest novel methods for the control of selectivity in these reactions, which we are pursuing.