A predictive framework for evaluating models of semantic organization in free recall

Abstract

Research in free recall has demonstrated that semantic associations reliably influence the organization of search through episodic memory. However, the specific structure of these associations and the mechanisms by which they influence memory search remain unclear. We introduce a likelihood-based model-comparison technique, which embeds a model of semantic structure within the context maintenance and retrieval (CMR) model of human memory search. Within this framework, model variants are evaluated in terms of their ability to predict the specific sequence in which items are recalled. We compare three models of semantic structure, latent semantic analysis (LSA), global vectors (GloVe), and word association spaces (WAS), and find that models using WAS have the greatest predictive power. Furthermore, we find evidence that semantic and temporal organization is driven by distinct item and context cues, rather than a single context cue. This finding provides important constraint for theories of memory search.

Introduction

Findings from list-learning paradigms such as free recall demonstrate that the temporal structure of a learning experience has an important influence on how studied materials are remembered. The effects of this temporal structure are evident in the primacy and recency effects of free recall (Murdock, 1962). Furthermore, temporal structure influences the order in which memories are retrieved; participants tend to successively recall items that were presented adjacent to one another in the study list (Kahana, 1996). Although much theoretical work has focused on understanding the effects of temporal structure on memory (e.g. Raaijmakers and Shiffrin 1980; Brown et al. 2007; Howard and Kahana 2002a), research has also demonstrated that the prior experience of a participant also strongly influences search of episodic memory, in the form of semantic organization, the tendency for participants to successively recall items that are semantically related to one another (Bousfield, 1953; Glanzer, 1969; Romney et al., 1993; Howard and Kahana, 2002b). Semantic organization (also known as semantic clustering) is observed both when a list contains obvious taxonomic category structure (Bousfield, 1953; Puff, 1966), as well as when there is no systematic semantic structure to the list (Schwartz and Humphreys, 1973; Romney et al., 1993; Howard and Kahana, 2002b). Although empirical work has established the importance of semantic knowledge for shaping new episodic memories, there is little consensus about the structure of semantic knowlege or the specific mechanisms that mediate its influence on memory search (Cohen, 1963; Sirotin et al., 2005; Polyn et al., 2009; Kimball et al., 2007). Furthermore, efforts to characterize semantic organization are complicated by the simultaneous influence of temporal organization on recall sequences (Howard and Kahana, 2002b; Howard et al., 2007; Polyn et al., 2011). Here, we developed set of computational models to test different ways that temporal and semantic information might influence memory search during free recall.

Measurement of semantic organization

In order to measure semantic organization, it is necessary to specify the semantic relatedness of the studied items. Early examinations of semantic organization focused on the effect of coarse semantic structure based on taxonomic category membership (e.g. Bousfield 1953; Cohen 1963; Roenker et al. 1971). More recently, theoretical and computational advances in characterizing semantic knowledge have made it possible to calculate more sophisticated measures of semantic similarity, leading to development of a variety of models of semantic structure which allow one to assign a relatedness/similarity score to any pair of words in a corpus or word pool (Romney et al., 1993; Lund and Burgess, 1996; Landauer and Dumais, 1997; Steyvers et al., 2004; Griffiths et al., 2007; Jones and Mewhort, 2007). Despite this profusion of semantic models, it is unclear which best corresponds to the structure of semantic memory in humans.

In the domain of list-learning, the structure of a person’s semantic memory is thought to give rise to semantic organization in their recall sequences. If all pairs of items in a study list have been assigned semantic relatedness scores, semantic organization can be quantified by examining the similarity scores of neighboring pairs of items in the recall sequence. These scores are then compared to a baseline measure, representing the expected distribution of similarity scores in the absence of semantic influence. In many cases, this baseline measure has been modeled in terms of the expectation of the organizational statistic given a random ordering of the recalled words (Bousfield, 1953; Roenker et al., 1971; Stricker et al., 2002). This assumption of random sampling is problematic, as it fails to take temporal influences on recall into account. Romney et al. (1993) developed a method that accounted for differences in memorability of items from different serial positions (thus accounting for the influence of the primacy and recency effects on semantic organization), but this measure did not account for sequential dependencies due to temporal organization.

Temporal organization is a near-ubiquitous phenomenon in free-recall tasks (Kahana, 1996; Kahana et al., 2008; Sederberg et al., 2010) that can influence measures of semantic organization (Puff, 1966; Morton et al., 2013). Because of temporal organization, traditional measures of semantic organization which do not take the ordering of the input list into account, such as ratio of repetition (Bousfield, 1953), adjusted ratio of clustering (Roenker et al., 1971), and list-based clustering (Stricker et al., 2002), will be inflated whenever semantically related items are presented in proximity. This is a particularly critical issue when examining how semantic organization is influenced by manipulations of presentation order (e.g. Glanzer 1969; Borges and Mandler 1972; for a review, see Puff 1974). Morton et al. (2013) demonstrated a permutation-based technique that can be used to estimate the baseline level of semantic organization expected in the presence of temporal organization. They measured free-recall behavior on both mixed lists composed of items from different categories, and pure lists with items from a single category. They randomly relabeled the set of pure list items with the category labels from a mixed list, and calculated a semantic organization score for each of these relabeled lists, to measure the tendency for same-category items to be grouped together during recall. This randomization was repeated many times to obtain a baseline distribution of semantic organization scores. Semantic organization scores calculated for the mixed lists could then be compared to this distribution. Although this technique provides a useful estimate of the influence of temporal organization on measures of semantic organization, it relies on the assumption that semantic and temporal information do not interact with one another, an assumption that is unlikely to be valid (Glanzer, 1969; Howard and Kahana, 2002b; Polyn et al., 2011).

Simulating influences on recall organization

It is unclear whether it is possible to develop a simple measure of semantic or temporal organization that is process pure, given that these forms of information interact with one another in the cognitive system. In order to understand the nature of these interactions, researchers have developed computational models designed to characterize the joint influence of semantic and temporal structure on behavior in memory tasks (e.g., Anderson 1972; Batchelder and Riefer 1980; Romney et al. 1993; Sirotin et al. 2005; Kimball et al. 2007; Socher et al. 2009; Polyn et al. 2009). In order to properly account for the influence of semantic information on behavior, each of these models must specify the semantic relatedness of any pair of items that might be studied. These semantic relatedness values have been drawn from existing models of semantic knowledge, such as latent semantic analysis (LSA; Landauer and Dumais 1997) and word association spaces (WAS; Steyvers et al. 2004).

In the domain of free recall, computational models of memory are typically evaluated through a generative process: The model is used to generate a large number of synthetic recall sequences, and a number of summary statistics are calculated, for example, the probability of recall by serial position, or a semantic organization score. These summary statistics are then compared to the same summary statistics calculated from the recall sequences collected in the actual experiment. The fitness of the model is then quantified in terms of how well the model’s summary statistics match the observed summary statistics (e.g. Raaijmakers and Shiffrin 1980; Sederberg et al. 2008; Brown et al. 2007). However, a difficulty arises when one wishes to assess the model’s predictions regarding semantic organization: The same semantic model can be used to create the semantic associative structures in the model, and to calculate the degree of semantic organization in the recall sequences generated by the model. This leads to a circularity that can complicate the evaluation of the validity of the model (as examined by Manning and Kahana 2012 and Polyn et al. 2009).

A predictive framework for evaluating models of recall organization

We present a computational modeling framework based on the context maintenance and retrieval (CMR) model. CMR is well-suited to examine the nature of temporal and semantic interactions in free recall, as it makes detailed predictions regarding behavior in this paradigm (Polyn et al., 2009; Healey and Kahana, 2014; Lohnas et al., 2015), including higher-order effects of compound temporal cuing (Lohnas and Kahana, 2014). We used a recently developed variant of CMR that allows direct calculation of the probability of entire recall sequences (Kragel et al., 2015), allowing for the exact calculation of the likelihood of observing a set of free-recall data according to the model. Within our modeling framework, we constructed competing model variants by combining one of three different models of semantic similarity with one of three different models of how temporal and semantic information interact. Along with a baseline model with no semantic structure, this yields ten model variants, which are described in more detail below. We examine the behavior of these model variants in three free-recall experiments which vary on a number of methodological characteristics.

To contrast different model variants, we used a maximum likelihood statistic to determine how well a given model variant can predict the behavior of the participants in an experiment. For each model variant, we first optimized a set of parameters to fit each participant in an experiment. These parameters determine the behavior and predictions of the model, allowing us to calculate the likelihood of each recall event, conditional on both the structure of the study list, and the specific sequence of recalls leading up to that event. The maximum likelihood then provides an unbiased measure for evaluating competing models of memory search. While evaluating models based on maximum likelihood provides important benefits such as high consistency and efficiency in parameter estimation (Myung, 2003), little work has used this technique with models of free recall (Farrell and Lewandowsky, 2008; Socher et al., 2009). The dearth of likelihood-based fitting in models of free recall may stem from the historical emphasis on fitting certain summary statistics such as the serial position curve (e.g. Sederberg et al. 2008), as well as the common use of simulation models for which exact likelihoods cannot easily be calculated (e.g. Raaijmakers and Shiffrin 1980; Sederberg et al. 2008; Polyn et al. 2009; Davelaar et al. 2005; Farrell 2012). In addition to comparing models based on maximum likelihood, we also examined summary statistics that focus on specific aspects of recall behavior. Using the best-fitting parameters for each participant, we used the model to generate recall sequences. We then calculated the same set of summary statistics for the observed data and model-generated data, to determine whether model variants can account for specific theoretically important empirical phenomena observed in the experiment.

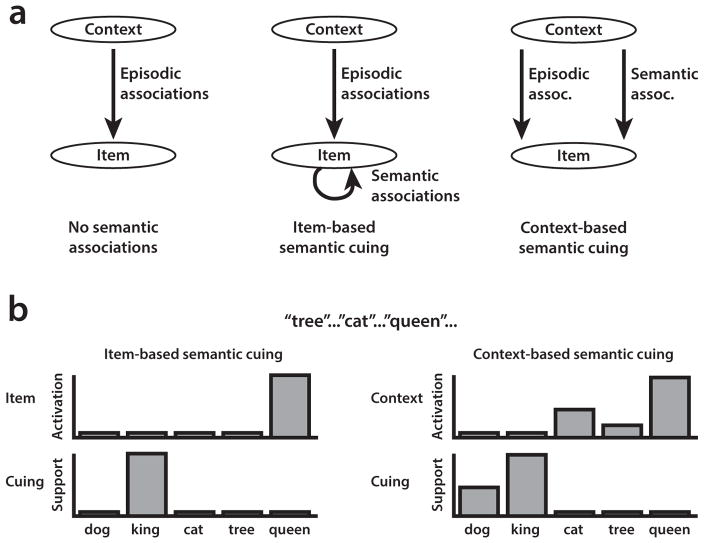
The CMR model is one of a class of retrieved-context models, which propose that a feature-based representation of each studied item causes item-specific information to be integrated into a gradually changing representation of temporal context (Kahana et al., 2008; Polyn and Kahana, 2008). When an item is recalled, the context associated with it is reactivated, providing a good cue for items studied nearby in the list and resulting in temporal organization. We use our framework to examine how temporal and semantic information interact during memory search. While each model variant we examined used temporal context as a cue, we examined the possibility that item cues might also be involved in probing semantic associations. The first type of cuing model we examined is the version of CMR described by Polyn et al. (2009). This model uses context-based semantic cuing: The item-specific information integrated into temporal context activates a set of pre-experimental semantic associations, such that the same contextual representation guides both temporal and semantic organization (Figure 2a, right side). We contrasted this with a version of CMR in which temporal and semantic organization are more independent. This second model variant uses item-based semantic cuing, in which the feature-based representation of the retrieved item directly activates pre-experimental semantic associations, resulting in semantic organization during memory search (Figure 2a, center). In the item-based semantic cuing model, temporal organization is guided by the temporal context representation, but semantic organization is guided by the reactivated representation of the remembered item. The predictive power of these two model variants were compared with that of a third, in which both item-based and context-based semantic cuing mechanisms operate simultaneously. Each model variant simply changes the locus of semantic influences. For all three variants, temporal organization is guided by the temporal context representation.

Each of the three cuing models are combined with each of three distinct vector space models of semantic similarity: Latent Semantic Analysis (LSA), Word Association Spaces (WAS), and Global Vectors (GloVe). Each vector space model constructs a representational vector for each word in a corpus. The representational similarity of any two vectors (calculated by the cosine operation) determines the strength of semantic association between the two corresponding items.

LSA is a well-established vector space model of semantic similarity that is based on the co-occurrence statistics of words in a large text corpus (Landauer and Dumais, 1997). The corpus is partitioned into distinct documents, and each word is assigned a representational vector specifying the set of documents in which it occurs. The dimensionality of this vector is reduced using singular value decomposition (SVD), which helps the model infer indirect relationships between words. If two words appear alongside similar sets of words across many documents, they are assigned similar representational vectors. LSA has been shown to account for some aspects of semantic organization in free recall (Sirotin et al., 2005; Polyn et al., 2009).

WAS is another well-established vector space model based on data from a large set of free-association norms (Steyvers et al., 2004). Representational vectors specify which words were associated with one another in the original free-association study (Nelson et al., 2004), and like LSA, SVD is used to reduce the dimensionality of those vectors. Prior work suggests that WAS can predict category clustering (Sirotin et al., 2005) and intrusions (Steyvers et al., 2004) more accurately than LSA, but comparing WAS and LSA using standard behavioral measures is difficult given differences in the distributions of similarity values in the two models (Howard et al., 2007; Manning and Kahana, 2012).

GloVe is a recently developed vector space model that, like LSA, is based on co-occurrence statistics in a text corpus, but which also contains characteristics of prediction-based semantic models (Pennington et al., 2014). GloVe has been shown to outperform LSA (and a number of other semantic models) on several validation tests, including word similarity, named entity recognition, and word analogies (Pennington et al., 2014).

Each of the model variants (combining each cuing model with each semantic similarity model) is assessed using the complementary measures of fit to a set of summary statistics and overall maximum likelihood. The summary statistics show whether a given model variant produces the relevant empirical phenomena observed in the experiments. However, the summary statistics that measure semantic organization are often calculated in terms of the same vector space models used to define semantic structure in the cognitive model. The likelihood statistic avoids this circularity by quantifying model performance in terms of the model’s ability to predict the specific sequence of recalls made on every trial.

Methods

We tested competing models of temporal and semantic organization based on their ability to predict recall behavior in three free-recall experiments. These experiments differed in a number of characteristics, including stimulus pool, presentation time, encoding task, and delay before recall, allowing us to assess the generality of our conclusions across a range of experimental procedures.

Experiment 1

Participants

Participants included 41 people (14 female) between the ages of 18 and 30. Participants were recruited as part of a series of studies designed to examine electrophysiological correlates of encoding and retrieval in free recall. We focus on the first study of the series, which included 4 sessions for each participant. Analyses on the data from these participants appear in Lohnas et al. (2011), Lohnas and Kahana (2014), and Lohnas et al. (2015).

Stimuli and Procedure

A pool of 1655 nouns were selected from a larger pool of 5018 words that formed the corpus for the word association spaces (WAS) model (Steyvers et al., 2004). These words were identified as nouns using the CELEX2 English database (Baayen et al., 1995), and were identified (by three raters) as being appropriate for the binary classification tasks used in the free-recall experiment (size and animacy judgments, described below). Words were excluded if they were abstract or were highly ambiguous for either of the judgment tasks. Three additional raters performed the size and animacy judgments on the set of 1655 nouns; these ratings were used to balance the lists with regard to the classification responses, as described below. During the course of the study, an additional 17 words were excluded because they sounded similar to other words in the pool. This final set of 1638 words was the same as those used in Expt. 3, described below.

Each participant performed 4 experimental sessions (held on separate days), each of which contained 12 trials. Each trial consisted of a study period, followed by a free-recall period. There were two types of trials: control trials and task-shift trials. On control trials, every word in the list was studied with the same encoding task. On task-shift trials, half of the items were studied with each encoding task. Within each session, a participant performed 6 control trials, for a total of 24 trials across the four sessions. Here, we focus on these control trials, and all analyses are carried out without regard to encoding task.

During the study period, a series of 24 words was presented, one word at a time. Each word remained on the screen for 3 s, and was followed by a blank 0.8–1.2 s inter-stimulus interval. Each word was presented with a task cue above it, indicating the judgment that the participant should make for that word (either judging whether the item would fit in a shoebox, or whether the item was living or nonliving). Participants indicated their judgment for each word by pressing a key.

After the final item was presented, a row of asterisks and a beep indicated the start of the recall period. Participants were given 90 seconds to vocally recall as many words as they could remember from the most recent list, in whatever order they came to mind.

The binary judgments from the three raters (described above) were averaged together to assign each word an average response for each encoding task. These average responses were used to ensure that the study lists were well balanced in terms of the judgments, making sure that no particular list was dominated by a particular class of response. Items judged big or living were assigned a value of 1, small or nonliving items were assigned a value of 0. As such, a word that was judged big by two of the three raters was assigned a value of 0.66 for the size judgment; if all three raters judged the word to be nonliving, it would be assigned a value of 0 for the animacy judgment. The words on a given list were chosen such that the average value of the words judged with a given task fell between 0.3 and 0.7.

LSA similarity values were not available for two words that were used in Experiment 1. Therefore, we excluded from all analyses 27 lists that included either of those words, leaving 957 trials considered here.

Experiment 2

Participants

Participants included 48 people between the ages of 18 and 30. Scalp EEG was recorded in a subset of these participants; results from those participants were previously reported by Sederberg et al. (2006).

Stimuli and Procedure

The experimental procedure was described in detail by Sederberg et al. (2006). Stimuli consisted of 308 common nouns (Friendly et al., 1982). Participants studied and recalled 48 lists which each contained 15 words drawn from the stimulus pool. Words did not appear more than once in a given list, but appeared in 1–3 lists for a given participant. Each word appeared for 1.6 seconds, followed by an inter-stimulus interval of 0.8–1.2 s. Participants were instructed to visualize each word as it was presented. Immediately following each list presentation, participants performed an arithmetic distraction task for 20 s. After the distraction period, participants were given 45 s to vocally recall items from the previous list in any order they wished.

WAS similarity values were not available for 11 words that were used in Experiment 2. Therefore, we excluded from all analyses 992 trials that included any of these words, leaving 1312 trials considered here.

Experiment 3

Participants

Participants included 126 people between the ages of 17 and 30, from the Penn Electrophysiology of Encoding and Retrieval Study (PEERS). Scalp EEG was recorded in these participants, and results from these participants were previously reported by Healey and Kahana (2014).

Stimuli and Procedure

The experimental procedure was described in detail by Healey and Kahana (2014); we describe the relevant details here. Stimuli were the 1,638 nouns described above (Expt. 1). Participants studied and recalled 112 lists which each contained 16 words drawn from the stimulus pool. Different lists had different encoding task conditions; here, we focus on the 28 lists for each subject that were studied with no explicit encoding task. Word association spaces similarity values (Steyvers et al., 2004) were used to group words into four similarity bins (high similarity: cos(θ) > 0.7; medium-high similarity: 0.4 < cos(θ) < 0.7; medium-low similarity: 0.14 < cos(θ) < 0.4; low similarity: cos(θ) < 0.14). In each list, two pairs of items from each of the groups were arranged such that one pair occurred at adjacent serial positions and the other pair was separated by at least two other items. Each word appeared for 3 seconds, followed by an inter-stimulus interval of 0.8–1.2 s.

After the final item was presented in each trial, there was a 1.2–1.4 s delay, followed by the presentation of a row of asterisks and a beep indicating the start of the recall period. Participants were given 75 seconds to vocally recall as many words as they could remember from the most recent list, in whatever order they came to mind.

LSA similarity values were not available for two words that were used in Experiment 3. Therefore, we excluded from all analyses 47 lists that included either of those words, leaving 2725 trials considered here.

Models of semantic associations

The word association spaces (WAS) algorithm (Steyvers et al., 2004) provides similarity scores for all word pairs in a corpus of 5018 words, a subset of which were used to create the study lists in Experiments 1 & 3. These similarity scores are derived from the University of South Florida free-association norms (Nelson et al., 2004). We used the 400-dimension singular value decomposition of the $S_{ij}^{(2)}$ measure described by Steyvers et al. (2004), which is freely available online¹. We defined the WAS similarity between two words as the cosine of the angle between their corresponding vectors.

The latent semantic analysis (LSA) algorithm (Landauer and Dumais, 1997) was used to derive similarity scores for all word pairs in the Touchstone Applied Science Associates, Inc. (TASA) corpus. This technique produces a 400 dimensional vector for each word. We defined the LSA similarity between two words as the cosine of the angle between their corresponding vectors.

We used publicly available 300 dimensional GloVe vectors² that were trained on a combination of the Gigaword 5 corpus (Parker et al., 2011) and a dump of Wikipedia article text from 2014. The corpus was tokenized and converted to lowercase, and a vocabulary was created with the 400,000 most frequent words. Co-occurrence was based on a decreasing weighting function, where words that are d words apart contribute 1/d to the co-occurrence count. As with WAS and LSA, we calculated similarity between each pair of words based on the cosine similarity of their vectors.

Figure 1 provides a visualization of the semantic similarity values for the different semantic models that we considered³. The circle of words represents a sample study list from Experiment 1. The weight of the line connecting two words indicates how strongly associated the two words are. These schematic figures highlight a difference between the co-occurrence based models (LSA and GloVe) and WAS: While WAS has relatively sparse connectivity, LSA and GloVe have many connections of moderate strength (see also Manning and Kahana 2012). We examined the degree to which the different semantic models captured similar relations between items by calculating rank correlations between the similarity values from each model. For the 1655 words included in Experiments 1 and 3, each pair of models demonstrated a significant but small Spearman’s correlation (LSA-GloVe: ρ = 0.366, p < 0.0001; GloVe-WAS: ρ = 0.232, p < 0.0001; LSA-WAS: ρ = 0.199, p < 0.0001), demonstrating that the interitem similarities predicted by the different models were largely distinct.

Figure 1.

Cosine similarity between pairs of items in a sample study list from experiment 1, for different models of semantic similarity. Greater line saturation and thickness indicate greater estimated similarity. Similarity values for different models were scaled to be on the same range. (a) Similarity based on latent semantic analysis (LSA). (b) Similarity based on the global vectors (GloVe) model. (c) Similarity based on word association spaces (WAS).

Model of memory search

We used a modified version of the context maintenance and retrieval model (CMR) as a framework to evaluate the impact of different models of semantic associations and different semantic cuing mechanisms on behavior in free recall. CMR consists of two interacting representations: a context layer and a feature layer. Two associative matrices (feature-to-context, and context-to-feature) allow these representations to influence one another. When an item is studied, a representation of it becomes active on the feature layer. This representation is projected through the feature-to-context associative connections, which causes contextual information associated with the item to be retrieved and integrated into the context representation. This contextual integration mechanism causes the contextual representation to change slowly over time. Thus, at any moment, context reflects a recency-weighted average of information related to recently presented stimuli. Studied items become associated to the context that was active when they were presented, so that context can serve as a cue to retrieve items, and recalled items can retrieve the context that is associated with them. When an item is recalled, its feature representation is reactivated, which allows the system to reinstate the context representation associated with the item. This reinstated context can then be used to cue for another item on the list. Items that are associated with similar states of context (such as adjacent items in a list) tend to be good cues for one another. See Formal description of the model for further details about model mechanisms. The mechanisms of item-context association, contextual cuing, and context reinstatement allow the model to account for a number of behavioral effects in free recall, including recency and temporal contiguity effects (Howard and Kahana, 2002a; Howard, 2004; Howard et al., 2005; Sederberg et al., 2008; Polyn et al., 2009).

Polyn et al. (2009) introduced CMR, which is based on the temporal context model (TCM; Howard and Kahana 2002a). CMR added, among other things, a mechanism to explain how semantic associations influence recall. Under this framework, the model is initialized with pre-experimental associations representing a person’s prior experience with an item. When an item is studied or recalled, these associations cause the system to retrieve the item’s pre-experimental context. This pre-experimental context is associated with the item’s semantic associates. As such, when this pre-experimental context is used as part of a retrieval cue, the item’s semantic associates are likely to be retrieved next, giving rise to semantic organization. We refer to this mechanism as context-based semantic cuing (Fig. 2); when this mechanism is in operation, the context representation is responsible for both temporal and semantic organization.

Figure 2.

Illustration of cuing mechanisms used by the different model variants. (a) Schematic of model variants. Left: Model with no semantic associations. Recall is driven solely by episodic associations between items and context. Center: Temporal context influences recall through episodic cuing as before, but retrieved items also will cue for other semantically related items, providing additional support for those items. Right: Only context is used as a cue to retrieve items; context projects through both episodic and semantic associations. (b) Schematic of predictions for item-based semantic cuing and context-based semantic cuing, after learning a sample list and recalling the sequence “tree”, “cat”, “queen”. In the item-based semantic cuing model, only the last recalled item, “queen,” is used as a semantic cue, resulting in stronger support for the related item “king.” In the context-based semantic cuing model, the entire current state of context is used as a semantic cue. Since “cat” is still somewhat active in context, it provides additional support for the related item “dog.”

Context-based semantic cuing can be contrasted with an alternative mechanism, which we refer to as item-based semantic cuing. Using this mechanism, semantic associations link item representations directly to one another (without using the context representation as a mediator). During free recall, when an item is recalled, its reactivated representation serves as a direct cue for semantically related items. The item-based semantic cuing mechanism has been used as part of several versions of the search of associative memory (SAM) model (Raaijmakers and Shiffrin, 1980; Sirotin et al., 2005; Kimball et al., 2008; Kahana, 2012). In the item-based semantic cuing models we examine here, although item representations are used to probe semantic associations, the context representation still projects through episodic associations as in other versions of CMR.

With item-based semantic cuing, semantic organization is only influenced by the just-recalled item, as depicted in Figure 2b. In contrast, with context-based semantic cuing, any items whose pre-experimental context is part of the context representation will influence semantic organization, because the context retrieved with each recalled item only partially updates the context representation (Lohnas and Kahana, 2014). Thus, semantic organization will be influenced by the set of items recalled prior to the current recalled item, though the semantic identity of the most recently retrieved item will have the most influence. In addition to examining the item-based semantic cuing and context-based semantic cuing models, we also evaluated whether semantic cuing might involve a weighted combination of item and context information. Note that while these different model variants used different types of semantic cuing, each of them used context-based episodic cuing (Fig. 2), allowing each variant to account for the temporal organization observed in free recall (Kahana, 1996).

The version of CMR described by Polyn et al. (2009) used context-based semantic cuing. Under this mechanism, semantic organization after recall of a given item should be sensitive to the items that were recalled prior to that item. Polyn et al. (2009) showed that this version of CMR can produce a reasonable overall amount of semantic organization while simultaneously accounting for temporal and source organization. However, that study focused on semantic organization conditional only on the just-recalled item; the more nuanced predictions of the model have not been evaluated.

Here, we use the CMR framework to assess the relative validity of the LSA, GloVe, and WAS models of semantic association, and to contrast the item-based, context-based, and item+context semantic cuing mechanisms described above. To accomplish this, each of the cuing mechanisms was paired with each model of semantic association. For each of the three experiments reported here, we evaluated a base model with no semantics, and every combination of semantic association model and cuing mechanism. We first compared these models based on their ability to predict the sequences of individual recalls that were observed in the experiment.

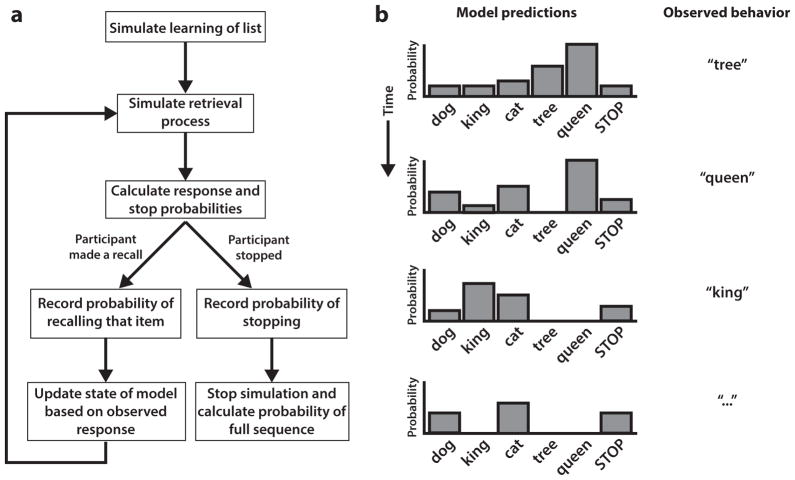
Likelihood calculation

During each recall period, the participant produces a sequence of responses. This recall sequence is described as a series of recall events, followed by a recall termination event. For simplicity, we excluded repeated items and intrusions from the set of recall events, so that the remaining recall events corresponded to correct recalls. We discuss the impact of excluding repeats and intrusions below in Exclusion of recall errors. For each recall event, the model is used to calculate each individual item’s probability of being recalled from the list, as well as the probability of recall termination (Fig. 3). From this set of probabilities, we record the probability of whatever recall event actually took place (for example, recalling item 24 in the list), and take the logarithm of this probability (to avoid precision issues caused by very low probabilities). Thus, if the participant recalled item 24, the model simulates recall of item 24, which involves reactivation of the item representation, and updating of the context representation. The updated model is then used to predict the next event in the recall sequence (either another successful recall, or termination), and the logarithm of this probability is recorded. This process is repeated until we reach the end of the recall sequence being examined. At this point the model is re-initialized and applied to the next list of the experiment. The log-transformed probabilities of all recall and termination events in the experiment are summed to obtain the log-likelihood of the entire dataset, given a specific model and a specific set of parameters.

Figure 3.

(a) Schematic of recall prediction for one list, in our modeling framework. First, the study period is simulated and the model learns the list. Then retrieval is simulated, and the model calculates the probability of recalling each of the items, as well as the probability of stopping recall. We then record the predicted probability of the observed behavior. If an item was recalled, we update the state of the model conditional on that recall. This process is repeated until the entire observed recall sequence has been simulated. (b) Schematic example of one list with five words. At each step of the recall process, the model makes predictions conditional on the observed behavior up to that point.

Model comparison

For each model variant, we used a parameter optimization technique known as differential evolution to find the parameter set that maximized the likelihood of the observed data (Storn, 2008). We optimized the parameters separately for each individual participant. We used a MATLAB-based implementation of differential evolution, based on code developed by Price et al. (2005). We used a variant of the DE/best/1/bin method described by Storn (2008), with some modifications to make search more robust. For each search through parameter space, we began with 1000 parameter sets at randomly chosen points in the parameter space. For each iteration of the search, the likelihood of the data given the current parameters was evaluated at each point. Then candidate vectors were evaluated to determine the composition of the next generation of the individuals.

First, mutated vectors for generation g, v_i,g, were created from the current population vectors x_i,g according to

$$v_{j,i,g}=x_{j,\mathit{best},g}+({\eta }_{j,i,g}+F)(x_{j,r1,g}-x_{j,r2,g}),$$ (1)

where v_j,i,g is an element j of the mutated vector i for generation g, x_best,g is a vector randomly sampled with replacement from the top 5% of points, F is a scaling factor that we set to 0.85, η_j,i,g is uniformly distributed random jitter between 0 and 0.001, and x_r1,g and x_r2,g are vectors randomly sampled from the original population. To enhance diversity, candidate vectors u_i,g were created using a crossover step, where each element of each candidate vector, u_j,i,g, was set according to

$$u_{j,i,g}=\{\begin{array}{ll}{v}_{j,i,g},\hfill & \text{if}\text{rand}[0,1]\le Cr\hfill \\ x_{j,i,g},\hfill & \text{otherwise},\hfill \end{array}$$ (2)

where the crossover probability Cr was set to 0.9.

To prevent premature convergence, candidate vectors were sometimes selected even when they had a lower likelihood. The candidate vector was accepted with probability α, defined as

$$\alpha =min\left(1,\frac{L({\mathbf{u}}_{i,g})}{L({\mathbf{x}}_{i,g})}\right),$$ (3)

where L(u_i,g) and L(x_i,g) are the likelihoods of the candidate and original vectors, respectively.

Iterations of the algorithm were run until the maximum log likelihood over all parameter sets examined so far had not changed more than 0.0001 over the last 100 generations. Each search was repeated 15 times for each subject with different random starting points, and the parameter set with the maximum log likelihood over all the searches was selected. If, for a given subject, the searches failed to find a greater or equal likelihood for a more complex model compared to a simpler model (e.g. a semantic model compared to the base model), the best parameter set for the complex model was set to the best-fitting parameter set for the simpler model.

Model performance was quantified using the Aikake Information Criterion (AIC; Wagenmakers and Farrell 2004) and the Bayesian Information Criterion (BIC; Schwarz 1978). For each model, we calculated AIC with a correction for finite samples:

$${\mathit{AIC}}_c=-2logL+2V+\frac{2V(V+1)}{(n-V-1)},$$ (4)

where L is the maximum likelihood value for the candidate model, V is the number of free parameters, and n is the number of estimated data points.

We also calculated BIC according to:

$$\mathit{BIC}=-2logL+\mathit{V}logn$$ (5)

We compared model performance using AIC weights, which indicate the probability that each model (of K competing models) generated the observed data, under the assumption that one of the models generated the data. The AIC weight for a given model i, w_iAIC, is defined as:

$$w_i\mathit{AIC}=\frac{\mathit{exp}(-\frac{1}{2}{\mathrm{\Delta }}_i\mathit{AIC})}{{\sum }_{k=1}^K\mathit{exp}(-\frac{1}{2}{\mathrm{\Delta }}_k\mathit{AIC})},$$ (6)

where Δ_iAIC is the difference in AIC_c between a given candidate model and the best-fitting model in the set. BIC weights were calculated in the same manner, substituting BIC for AIC (Wagenmakers and Farrell, 2004).

Analysis of recall behavior

We used a set of summary statistics to characterize the recall performance of the participants, and to further characterize the performance of each optimized model variant. In order to calculate these summary statistics on an optimized model variant, we first used the model to generate simulated recall sequences, as follows. For each recall attempt, we calculated the probabilities of each recall event (recalling an item or stopping recall), using the same procedure described in Likelihood calculation. We then sampled an event at random using this probability distribution, and updated the state of the model accordingly. Each recall period was simulated in this manner until a stop event was chosen. To calculate summary statistics for each model, we simulated each list in the experiment 100 times, and calculated each statistic averaged over the 100 simulated replications of the experiment.

Behavior in free recall can be described in terms of three stages: initiation, transitions, and termination (Kahana, 2012). We measured recall initiation by calculating the probability of first recalling an item as a function of the serial position in which it was presented in the list. After the first recall, transitions between recalled items exhibit two major forms of organization: temporal clustering and semantic clustering.

Temporal clustering is the tendency of participants to successively recall items that were presented adjacent to one another in the list (Kahana, 1996). We used a lag-based conditional response probability (lag-CRP; Kahana 1996) analysis to characterize temporal clustering (where lag indicates the difference between the position of two items in the study list). The lag-CRP analysis provides the probability of making recall transitions of a particular lag, conditional on that lag being available for recall (an item was considered unavailable if there was no item presented at that serial position, or if that item had already been recalled previously). The first three output positions were excluded from this analysis. In this analysis and the other transition-based analyses described below, when analyzing the observed data, transitions to or from intrusions or repeats of already-recalled words were excluded.

We measured semantic clustering using a related measure, the semantic-CRP (Howard and Kahana, 2002b; Sederberg et al., 2010). Rather than partitioning recall transitions on the basis of lag, this analysis partitions transitions on the basis of the semantic identities of the items themselves. First, we tallied the number of times each participant made a transition from item i to item j, for each item in the stimulus pool. We also tallied a separate count of the number of times that each participant could have made each possible transition between words, given the words that were still available at each point in recall. A given transition between items i and j was not counted as possible if item i was never recalled. We then determined a set of semantic similarity bins that we used to group together inter-item transitions (details on how the bins were determined are specified below). Within each bin, we calculated the number of actual transitions in that bin, and divided by the number of possible transitions.

In a set of preliminary analyses, we contrasted a version of the semantic-CRP analysis described by Howard and Kahana 2002b with a slightly different version described by Sederberg et al. 2010. We found that the semantic-CRPs for the Base model, which had no semantic associations and therefore could not produce semantic organization, showed an increased probability of very low- or high-similarity transitions when the semantic-CRPs were calculated as described by (Howard and Kahana, 2002b). This led us to implement a version of the analysis more similar to that described by Sederberg et al. (2010), which did not demonstrate this distortion.

Prior implementations of the semantic-CRP analysis have generally used bins that contain deciles (Healey and Kahana, 2014) or percentiles (Howard and Kahana, 2002b; Howard et al., 2007). However, because semantic similarity values based on WAS and LSA are highly positively skewed (Manning and Kahana, 2012), this results in many bins at low similarity values, and very few bins at higher similarity values. To better estimate CRPs for the full range of similarity values, we took a different strategy of determining bin sizes so that we obtain a minimal sample size at each bin (see Sederberg et al. 2010 for another example of unequal bin sizes used for this analysis). First, we obtained the semantic similarities for each inter-item transition that was possible at least once over all recall sequences in the study, based on the semantic similarity measure of interest (LSA, GloVe, or WAS). Starting from the highest similarity value, we decreased the lower limit of the bin by increments of 0.05 until there were at least 10 possible transitions per subject on average. After defining a bin, the lower limit of that bin became the upper limit of the next bin, and the process was repeated. The center of each bin was defined as the mean similarity value over all possible transitions within that bin. We determined the bins from the actual data, then applied these bins to the simulated data from our model variants.

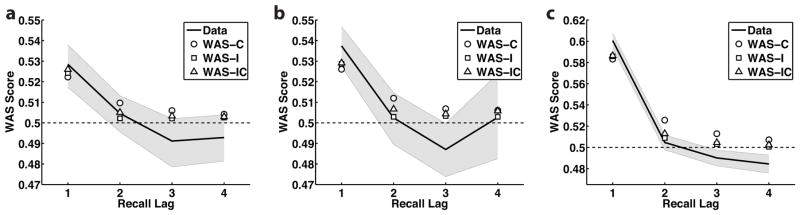
In order to examine the specific predictions of the context-based semantic cuing mechanism, we developed a novel measure to determine whether the context in which a word appears in the recall sequence predicts subsequent semantic organization. We used the semantic score metric introduced by Polyn et al. (2009) to characterize the percentile of semantic relatedness of each transition during recall. For each transition between recalled words, first the items that are still available for recall (i.e. that have not been recalled previously) are determined. These available words are ranked on their semantic similarity to the just-recalled item. The percentile of the transition the participant actually made is noted, and this percentile is averaged over all transitions to obtain a semantic score that reflects the overall amount of semantic organization. We calculated semantic score by ranking available items based on similarity to items of recall lag n, where n is the number of output positions separating the previously recalled item at output position i–n from the next item i in the recall sequence. When n = 1, the two recall events are adjacent; this corresponds to a standard semantic score as described by Polyn et al. (2009). For example, say a participant studied the list dog king cat tree queen, then recalled “tree”, “cat”, “queen”, “dog”. After the participant recalled “queen”, there were two possible words that could have been recalled next: dog and king. For recall lag 1, these items would be ranked based on their similarity to the just-recalled item queen, so that king would be ranked highest and the semantic score for that transition would be 0 (since the participant next recalled dog instead). In contrast, for recall lag 2, the remaining items would be ranked based on their similarity to cat, so that dog would be ranked highest and the semantic score for that transition would be 1.

For each participant, we calculated the semantic score for each recall lag from 1 to 4, averaging over all valid transitions. For a given recall lag, a transition was excluded from the analysis if either item i or item i–n was a repeat or an intrusion. The first three recalled items were excluded from the analysis, so that the same output positions would be included for recall lags 1–4. Semantic score is expected to be 0.5 by chance, indicating recall without regard to semantic similarity. If semantic score is greater than 0.5 for n > 0, we take this as evidence that semantic cuing is influenced by prior items in the recall sequences, consistent with context-based semantic cuing.

We calculated the probability of recall termination as a function of output position. We excluded repeats and intrusions when calculating output position, so that the probability of stopping at output position list length +1 is unity. Finally, we calculated the serial position curve, which shows the probability of recalling each item as a function of its serial position in the list.

For each measure of recall behavior, we calculated confidence intervals using a bootstrap procedure. For each of 5000 samples, we sampled subject means with replacement, and calculated a simulated group mean. We set the confidence interval to include the middle 95% of the simulated group means.

Formal description of the CMR model

Here, we give a formal description of the equations that define CMR’s structure and behavior. Table 1 provides an overview of the parameters that control the behavior of the model.

Table 1.

List of model parameters, with a brief description of each.

Parameter Type	Parameter	Description
Context Updating	βenc	Rate of context drift during encoding
	βdelay	Rate of context drift during end-of-list distraction
	βstart	Amount of start-list context retrieved at start of recall
	βrec	Rate of context drift during recall
Associative Structure	α	Initial strength of context-to-item connections
	δ	Initial strength of the diagonal of MCF
	s	Scaling of semantic association strengths
	γ	Amount of experimental context retrieved by a recalled item
	ϕs	Scaling of primacy gradient in learning rate on MCF
	ϕd	Rate of decay of primacy gradient
Recall Dynamics	τ	Sensitivity parameter of the Luce choice rule
	θs	Scaling of the stop probability over output position
	θr	Rate of increase in stop probability over output position

CMR takes the form of a simplified neural network with two interacting representations, a feature-based representation of the studied item (the item layer, F) and a contextual representation (the context layer, C). The two layers communicate with one another through two sets of associative connections represented by matrices M^FC and M^CF. Each of these weight matrices contains both pre-experimental associations and new associations learned during the experiment. Pre-experimental weights are designated ${\mathbf{M}}_{\text{pre}}^{FC}$ and ${\mathbf{M}}_{\text{pre}}^{CF}$; the experimental weights are ${\mathbf{M}}_{exp}^{FC}$ and ${\mathbf{M}}_{exp}^{CF}$.

In the present simulations, we are particularly interested in structure of the pre-experimental weights. For all model variants, we set the pre-experimental item-to-context associations according to

$${\mathbf{M}}_{\text{pre}(i,j)}^{FC}=\{\begin{array}{ll}1-\gamma ,\hfill & \text{if}i=j\hfill \\ 0,\hfill & \text{if}i\ne j.\hfill \end{array}$$ (7)

This connects each unit on F to the corresponding unit on C. The γ parameter controls the strength of these pre-experimental associations relative to the experimental associations described below.

For the base model, which does not contain any semantic associations, we set the pre-experimental context-to-item associations according to

$${\mathbf{M}}_{\text{pre}(i,j)}^{CF}=\{\begin{array}{ll}\delta ,\hfill & \text{if}i=j\hfill \\ \alpha ,\hfill & \text{if}i\ne j.\hfill \end{array}$$ (8)

Here, the α parameter allows all the items to support one another in the recall competition in a uniform manner. Our δ parameter is similar to the γ^CF parameter described by Sederberg et al. (2008). Our implementation is different from theirs in that α is free to be non-zero, and some model variants also include the addition of semantic similarity strengths. In a set of preliminary simulations, we tested a form of the model where ${\mathbf{M}}_{\text{pre}}^{CF}$ was set to 0. Through a series of model comparison analyses (not reported here), we found that freeing both the δ and α parameters substantially improved the fit, based on AIC.

For the set of model variants which used context-based semantic cuing, the context-to-item associations were set according to

$${\mathbf{M}}_{\text{pre}(i,j)}^{CF}=\{\begin{array}{ll}\delta ,\hfill & \text{if}i=j\hfill \\ \alpha +s{\mathbf{M}}_{i,j}^{\text{sem}},\hfill & \text{if}i\ne j,\hfill \end{array}$$ (9)

where ${\mathbf{M}}_{i,j}^{\text{sem}}$ gives the semantic similarity between items i and j according to WAS, GloVe, or LSA, and s is a scaling parameter (cf. Polyn et al. 2009). In other words, we used a linear transform to map semantic cosine similarity values based on WAS, GloVe, or LSA to semantic strengths in the model, where α serves as an intercept parameter, and s is a slope parameter. The diagonal of M^sem is set to 0, so that self-strengths are solely determined by the δ parameter.

At the start of the list, context is initialized with a state that is orthogonal to the pre-experimental context associated with the set of items. Similarly, item representations are assumed to be orthonormal to each other; each unit of F corresponds to one item. When an item i is presented during the study period, its representation on F, f_i, is activated. Pre-experimental context ${\mathbf{c}}_i^{\text{IN}}$ is retrieved and is input to the context layer to update the current state of context. The input to context is

$${\mathbf{c}}_i^{\text{IN}}={\mathbf{M}}^{FC}{\mathbf{f}}_i={\mathbf{M}}_{\text{pre}}^{FC}{\mathbf{f}}_i,$$ (10)

since ${\mathbf{M}}_{exp}^{FC}$ is assumed to be zero at the start of the list. The retrieved pre-experimental context ${\mathbf{c}}_i^{\text{IN}}$ is then normalized to have length 1.

After retrieval of pre-experimental context ${\mathbf{c}}_i^{\text{IN}}$, the current state of context is updated according to

$${\mathbf{c}}_i={\rho }_i{\mathbf{c}}_{i-1}+\beta {\mathbf{c}}_i^{\text{IN}},$$ (11)

where β is set to β_enc, a free parameter of the model, and ρ_i is set so that the length of c_i is 1, according to

$${\rho }_i=\sqrt{1+{\beta }^2[{({\mathbf{c}}_{i-1}·{\mathbf{c}}_i^{\text{IN}})}^2-1]}-\beta ({\mathbf{c}}_{i-1}·{\mathbf{c}}_i^{\text{IN}}).$$ (12)

After context is updated, the current item f_i and the current state of context c_i become associated, through simple Hebbian learning. After each item presentation, the experimental associations are updated according to

$$\mathrm{\Delta }{\mathbf{M}}_{exp}^{FC}=\gamma {\mathbf{c}}_i{\mathbf{f}}_i^{\prime }.$$ (13)

When an item is presented, the network also learns associations from the current state of context to the current item, according to

$$\mathrm{\Delta }{\mathbf{M}}_{exp}^{CF}={\varphi }_i{\mathbf{f}}_i{\mathbf{c}}_i^{\prime },$$ (14)

where ϕ_i scales the amount of learning, simulating the increased attention to initial items in a list that has been proposed to explain the primacy effect (Sederberg et al., 2008). ϕ_i depends on the serial position i of the studied item:

$${\varphi }_i={\varphi }_s{e}^{-{\varphi }_d(i-1)}+1.$$ (15)

The free parameters ϕ_s and ϕ_d control the magnitude and decay of this learning-rate gradient, respectively.

To simulate the end-of-list distraction in Experiment 2, we assumed that distraction during the retention interval causes a change in context (Sederberg et al., 2008). Context is updated according to Equation 12, where β is set to β_RI, and ${\mathbf{c}}_i^{\text{IN}}$ is a vector that is orthogonal to the pre-experimental contexts of the studied items.

Before initiating recall, we assume that some amount of the pre-list context is reinstated. We assume that context is updated according to

$${\mathbf{c}}_{\text{start}}={\rho }_{N+1}{\mathbf{c}}_N+{\beta }_{\text{start}}{\mathbf{c}}_0,$$ (16)

where c_start is the state of context at the start of free recall, N is the number of items in the list, c₀ is the state of context at the start of the list before any items have been presented, and ρ_N+1 is calculated according to Equation 12. This mechanism is consistent with evidence that participants sometimes recall the start of the list and use that event as a cue (Laming, 1999). In preliminary simulations we found that models including this start-list context reinstatement demonstrated a better fit to the primacy effect than models containing the learning-rate gradient alone (see also Kragel et al. 2015).

At each recall attempt, the current state of context is used as a retrieval cue to attempt retrieval of a studied item. First, the activation of each item a is determined according to

$$\mathbf{a}={\mathbf{M}}^{CF}\mathbf{c}.$$ (17)

In order to avoid the possibility of the model assigning a probability of 0 to any possible recall, we set a minimal activation for each item of 10⁻⁷.

At each recall attempt, we calculated the probability of stopping recall (in which case no item was recalled, and search terminated). Probability of stopping recall varies as a function of output position j (where j = 0 for the first attempt), according to

$$P(\text{stop},j)={\theta }_s{e}^{j{\theta }_r},$$ (18)

where θ_s and θ_r are free parameters that determine the scaling and rate of increase, respectively, of the exponential function. The stopping mechanism does not interact with any model mechanism, and is simply intended to capture the average probability of stopping as a function of output position.

The probability P(i) of recalling a given item i is defined conditional on recall not stopping at that position, and varies with activation strength, according to

$$P(i)=(1-P(\text{stop}))\frac{{\mathbf{a}}_i^{\tau }}{{\displaystyle \sum _k^N}{\mathbf{a}}_k^{\tau }},$$ (19)

where τ is a sensitivity parameter that determines the contrast between well-supported and poorly supported items. High values of τ will cause a greater influence of differences in support, while low values will cause relatively uniform probabilities of recalling each item.

If an item is recalled, then that item is reactivated on F. The reactivated item is then used to retrieve both experimental and pre-experimental context, according to

$${\mathbf{c}}_i^{\text{IN}}={\mathbf{M}}^{FC}{\mathbf{f}}_i.$$ (20)

Context is then updated using Equation 11, and is used to cue for another recall attempt. The process continues until the model reaches the end of the recall sequence.

Item-based semantic cuing

We also examined an item-based semantic cuing model that used separate context and item cues for episodic and semantic associations. In this model, contextual cuing worked as before, but semantic associations were not included in M^CF. Recall initiation was driven by projecting context through episodic associations on M^CF. For each following recall attempt, the feature-layer vector corresponding to the last recalled item, f_i, was projected through the scaled semantic similarity matrix (the diagonal, representing item self-strengths, was set to 0). The item activations corresponding to contextual cuing and item cuing were added to obtain the total item activation:

$$\mathbf{a}=s{\mathbf{M}}^{\mathit{sem}}{\mathbf{f}}_i+{\mathbf{M}}^{CF}\mathbf{c}$$ (21)

The activation values a were then used with Equation 19 to determine recall probabilities.

We also examined a model that combined context- and item-based semantic cuing. This was the same as the item-based semantic cuing model, but rather than cuing semantics using just the item vector, we used a weighted combination of context and item:

$$\mathbf{a}=s{\mathbf{M}}^{\mathit{sem}}(\lambda {\mathbf{f}}_i+(1-\lambda )\mathbf{c})+{\mathbf{M}}^{CF}\mathbf{c},$$ (22)

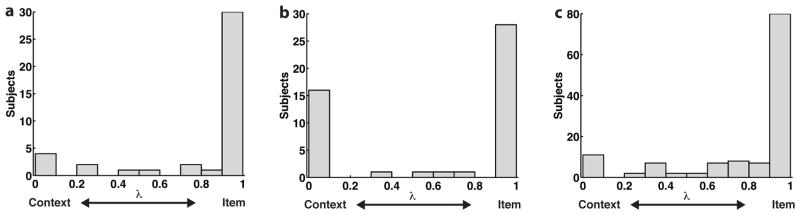
where λ is a parameter controlling the relative weighting of the item cue compared to the context cue. Note that this model is equivalent to the item-based semantic cuing model when λ = 1, and the context-based semantic cuing model when λ = 0. Note also that each model variant, regardless of the value of λ, used a context cue to probe the episodic associations stored in M^CF.

Results

The modeling framework used here is designed to account for the simultaneous influence of temporal and semantic information on memory search in three free-recall experiments which differed on a number of methodological characteristics. We consider three models of semantic relatedness (LSA, GloVE, and WAS), which provide similarity scores specifying the semantic associations between the studied words. We also consider three models of semantic cuing (item-based semantic cuing [I], context-based semantic cuing [C], and hybrid semantic cuing [IC]), which specify how this semantic information is used during memory search. The hybrid semantic cuing model includes both forms of semantic cuing; a mixing parameter λ determines the relative strength of each cuing mechanism. For each experiment we construct a baseline model without semantic structure, and 9 models with semantic structure (crossing the three models of semantic relatedness with the three models of semantic cuing). Note that, while these models varied in the specifics of semantic organization, each of them used the same contextual cuing mechanism to guide temporal organization. We compare the set of 10 models in terms of their overall fit to the recall sequences (i.e., the likelihood statistic; what is the probability that the observed data was generated by this model?). Each model is also used to generate recall sequences, which allows us to compare the models in terms of their fit to a number of important summary statistics which characterize recall performance, temporal organization, and semantic organization.

Serial position effects and temporal organization

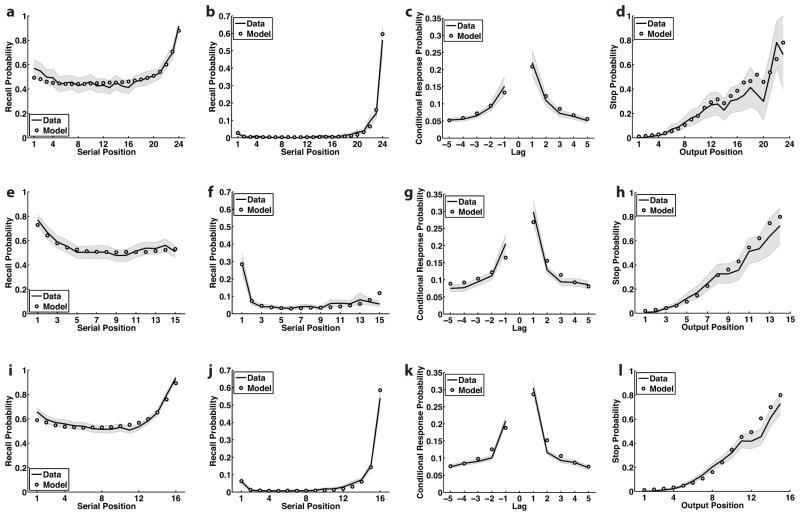
Table 2 reports the overall fitness of each of the 10 model variants in each experiment, in terms of AIC weights. AIC weights indicate, for a given set of competing models, the probability of each model generating the observed data, under the assumption that one of them did. It should be noted that while the base model had the lowest AIC weight for both experiments (i.e., it had the worst fit to the recall sequences), it still provided an excellent fit to a number of important summary statistics, including the recency, primacy, and contiguity effects. The generative version of the Base model provided a good qualitative fit of recall as a function of serial position (Fig. 4a,e,i), including the widely varying magnitudes of the recency and primacy effects in the different experiments. Primacy was slightly under-predicted in Experiments 1 and 3, which was an issue with each model variant examined in this study. Given that retrieved-context models have successfully accounted for the magnitude of primacy in prior work (e.g. Polyn et al. 2009), it appears that this under-prediction of primacy is caused by our different emphasis on fitting entire recall sequences, rather than traditional summary statistics such as the serial position curve (as in prior work with retrieved-context models). The model also provides a qualitative account of the probability of initiating recall at each serial position (Fig. 4b,f,j). The model accounts for the temporal organization observed in the data, and captures the tendency for participants to make forward transitions more often than backward transitions (Fig. 4c,g,k). Finally, the model accounts for the finding of a positively accelerated increase in stop probability with output position (Fig. 4d,h,l). The nine model variants with semantic associations also accounted for each of these summary statistics for each experiment, with fits that were very similar to the Base model. RMSD for each model variant, pooled over the non-semantic summary statistics, is presented in Tables 3, 4, and 5. RMSD was not significantly different from the Base model for any of the models with semantic associations (p > 0.05, Bonferroni corrected), with one exception: In Experiment 3, the GloVe-C model had a significantly higher RMSD across subjects compared to the Base model (t(125) = 3.34, p = 0.01, Bonferroni corrected), due to a slightly worse fit of the lag-CRP. This may reflect a compromise in the fit between temporal and semantic organization (which are most strongly related in the context-based semantic cuing models).

Table 2.

AIC weights for models with semantic similarity. Models with wAIC > 0.1 are displayed in bold. Weights for the base model not shown (Experiment 1: 6.404e-48; Experiment 2: 1.93e-90; Experiment 3: 1.14e-89). LSA: latent semantic analysis; GloVe: global vectors model; WAS: word association spaces. C: context-based semantic cuing; I: item-based semantic cuing; IC: combined item and context-based semantic cuing.

	Experiment 1			Experiment 2			Experiment 3
	C	I	IC	C	I	IC	C	I	IC
LSA	3.37e-40	2.22e-28	8.39e-42	1.95e-52	5.30e-34	4.20e-44	0	0	0
GloVe	2.75e-21	2.78e-6	7.38e-18	3.15e-11	7.78e-9	2.41e-11	0	1.33e-294	2.68e-314
WAS	6.72e-7	0.9999	6.16e-12	3.87e-6	0.9999	4.10e-7	3.90e-74	1	4.01e-8

Figure 4.

Measures of recall behavior, for the observed data and for model simulations. Top row: Experiment 1; middle row: Experiment 2; bottom row: Experiment 3. (a) Recall probability as a function of serial position, for the data from Experiment 1 and the best-fitting model with no semantic associations. (b) Probability of starting recall with each serial position. (c) Conditional response probability as a function of lag. (d) Stop probability by output position. (e–h) Same measures as above, for Experiment 2. (i–l) Experiment 3. Shaded areas indicate 95% confidence intervals for the observed data.

Table 3.

Best-fitting parameters for Experiment 1. Reported values indicate averages over subjects; values in parentheses indicate standard error of the mean. RMSD is reported for the summary statistics shown in Figure 4. LSA: latent semantic analysis; GloVe: global vectors; WAS: word association spaces. C: context-based semantic cuing; I: item-based semantic cuing; IC: combined item and context-based semantic cuing.

	Base	LSA-C	LSA-I	LSA-IC	GloVe-C	GloVe-I	GloVe-IC	WAS-C	WAS-I	WAS-IC
βenc	0.72 (0.02)	0.72 (0.02)	0.71 (0.02)	0.72 (0.02)	0.71 (0.02)	0.69 (0.02)	0.70 (0.02)	0.72 (0.02)	0.70 (0.02)	0.71 (0.02)
βrec	0.87 (0.02)	0.88 (0.02)	0.86 (0.02)	0.87 (0.01)	0.89 (0.01)	0.84 (0.02)	0.85 (0.02)	0.89 (0.01)	0.86 (0.02)	0.87 (0.02)
βstart	0.18 (0.04)	0.19 (0.04)	0.18 (0.04)	0.18 (0.04)	0.20 (0.04)	0.22 (0.05)	0.22 (0.05)	0.19 (0.04)	0.19 (0.04)	0.19 (0.04)
α	7.69 (2.66)	6.57 (2.58)	9.09 (2.75)	8.16 (2.68)	6.34 (2.41)	10.33 (2.72)	9.08 (2.70)	5.86 (2.37)	9.79 (2.96)	8.61 (2.90)
δ	33.60 (5.96)	34.90 (6.34)	34.36 (6.05)	33.59 (6.05)	33.94 (6.25)	33.79 (5.93)	33.47 (5.98)	33.77 (6.27)	34.87 (6.31)	33.64 (6.32)
γ	0.17 (0.04)	0.16 (0.03)	0.20 (0.04)	0.18 (0.04)	0.15 (0.03)	0.22 (0.04)	0.18 (0.04)	0.16 (0.03)	0.21 (0.04)	0.18 (0.03)
λ	–	–	–	0.84 (0.06)	–	–	0.91 (0.04)	–	–	0.83 (0.05)
ϕs	30.84 (6.37)	29.82 (6.17)	27.85 (6.08)	27.81 (6.03)	27.82 (5.93)	20.33 (5.16)	22.67 (5.49)	30.53 (6.23)	27.35 (6.07)	27.06 (6.06)
ϕd	14.48 (4.96)	13.34 (4.65)	15.06 (5.19)	14.39 (4.66)	13.51 (4.77)	13.61 (4.64)	16.76 (5.36)	16.12 (5.22)	16.00 (5.14)	15.13 (5.05)
s	–	0.49 (0.12)	0.80 (0.20)	0.81 (0.19)	0.77 (0.20)	1.05 (0.19)	1.12 (0.22)	1.60 (0.31)	1.79 (0.35)	2.05 (0.42)
τ	20.86 (5.11)	16.89 (4.60)	27.56 (5.90)	22.67 (5.33)	17.27 (4.35)	37.92 (6.51)	30.18 (6.15)	16.10 (4.16)	26.85 (5.70)	22.44 (5.08)
θs	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)
θr	0.32 (0.01)	0.32 (0.01)	0.32 (0.01)	0.32 (0.01)	0.32 (0.01)	0.32 (0.01)	0.32 (0.01)	0.32 (0.01)	0.32 (0.01)	0.32 (0.01)
ln(L)	−28664.34	−28600.32	−28573.11	−28558.88	−28556.78	−28522.23	−28503.75	−28523.65	−28509.44	−28490.12
AIC	58271.28	58232.82	58178.40	58240.21	58145.73	58076.63	58129.94	58079.47	58051.04	58102.67
BIC	59889.35	59994.10	59939.68	60144.01	59907.01	59837.91	60033.75	59840.75	59812.33	60006.48
wAIC	1.50493e-48	3.37118e-40	2.21533e-28	8.39428e-42	2.75331e-21	2.77987e-06	7.37794e-18	6.72363e-07	0.999997	6.15624e-12
wBIC	1.88246e-17	3.37118e-40	2.21533e-28	9.44576e-73	2.75331e-21	2.77987e-06	8.30211e-49	6.72363e-07	0.999997	6.92738e-43
RMSD	0.1093	0.1082	0.1095	0.1097	0.1096	0.1088	0.1076	0.1086	0.1084	0.1086

Table 4.

Best-fitting parameters for Experiment 2. Reported values indicate averages over subjects; values in parentheses indicate standard error of the mean. RMSD is reported for the summary statistics shown in Figure 4. LSA: latent semantic analysis; GloVe: global vectors model; WAS: word association spaces. C: context-based semantic cuing; I: item-based semantic cuing; IC: combined item and context-based semantic cuing.

	Base	LSA-C	LSA-I	LSA-IC	GloVe-C	GloVe-I	GloVe-IC	WAS-C	WAS-I	WAS-IC
βenc	0.76 (0.04)	0.70 (0.04)	0.64 (0.04)	0.66 (0.04)	0.66 (0.05)	0.60 (0.05)	0.64 (0.04)	0.63 (0.05)	0.62 (0.04)	0.63 (0.04)
βrec	0.84 (0.04)	0.86 (0.03)	0.81 (0.03)	0.81 (0.03)	0.88 (0.03)	0.81 (0.04)	0.80 (0.04)	0.86 (0.03)	0.83 (0.03)	0.82 (0.03)
βdelay	0.63 (0.07)	0.63 (0.07)	0.63 (0.07)	0.70 (0.07)	0.67 (0.07)	0.65 (0.07)	0.75 (0.06)	0.72 (0.06)	0.64 (0.07)	0.73 (0.06)
βstart	0.20 (0.05)	0.18 (0.04)	0.18 (0.04)	0.14 (0.03)	0.17 (0.04)	0.16 (0.03)	0.13 (0.03)	0.19 (0.04)	0.23 (0.05)	0.16 (0.04)
α	4.17 (1.51)	5.74 (2.30)	7.23 (2.36)	7.65 (2.53)	6.20 (2.28)	10.95 (3.60)	7.77 (2.36)	8.08 (3.14)	7.15 (2.55)	7.30 (2.92)
δ	3.29 (1.33)	9.60 (3.45)	6.50 (2.21)	7.69 (2.47)	9.49 (3.31)	14.33 (4.11)	11.58 (3.39)	14.22 (4.16)	10.87 (3.27)	8.72 (3.16)
γ	0.45 (0.05)	0.40 (0.05)	0.47 (0.05)	0.50 (0.05)	0.41 (0.05)	0.42 (0.05)	0.44 (0.05)	0.41 (0.05)	0.49 (0.06)	0.50 (0.05)
λ	–	–	–	0.84 (0.05)	–	–	0.77 (0.05)	–	–	0.64 (0.07)
ϕs	46.72 (6.50)	31.08 (5.78)	26.31 (5.76)	20.24 (5.25)	29.71 (5.70)	25.11 (5.53)	18.31 (4.80)	26.07 (5.35)	23.20 (5.44)	23.24 (5.35)
ϕd	13.57 (4.46)	15.27 (4.74)	12.58 (4.40)	12.84 (4.48)	13.17 (4.43)	11.78 (4.38)	11.46 (4.09)	8.87 (3.42)	13.26 (4.50)	9.77 (3.50)
s	–	1.34 (0.57)	1.69 (0.66)	1.22 (0.40)	2.38 (1.07)	2.05 (0.89)	1.35 (0.45)	5.21 (2.42)	2.96 (1.31)	5.19 (2.49)
τ	16.62 (4.79)	25.53 (5.75)	33.00 (5.85)	36.48 (6.18)	32.89 (6.14)	38.93 (6.05)	41.82 (6.30)	26.65 (5.50)	29.50 (5.62)	27.86 (5.68)
θs	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)
θr	0.42 (0.02)	0.42 (0.02)	0.42 (0.02)	0.42 (0.02)	0.42 (0.02)	0.42 (0.02)	0.42 (0.02)	0.42 (0.02)	0.42 (0.02)	0.42 (0.02)
ln(L)	−24490.10	−24348.81	−24306.36	−24275.35	−24253.93	−24248.42	−24199.92	−24242.21	−24229.74	−24190.18
AIC	50199.31	50024.30	49939.40	49985.92	49834.52	49823.51	49835.06	49811.08	49786.16	49815.57
BIC	52147.08	52128.42	52043.52	52245.40	51938.64	51927.62	52094.54	51915.20	51890.28	52075.05
wAIC	1.92945e-90	1.94524e-52	5.30204e-34	4.20467e-44	3.14943e-11	7.77679e-09	2.41321e-11	3.87335e-06	0.999996	4.10211e-07
wBIC	1.71817e-56	1.94524e-52	5.30204e-34	7.7123e-78	3.14943e-11	7.77679e-09	4.42636e-45	3.87335e-06	0.999996	7.52418e-41
RMSD	0.0982	0.0991	0.0984	0.0982	0.0988	0.0974	0.0984	0.0978	0.0981	0.0978

Table 5.

Best-fitting parameters for Experiment 3. Reported values indicate averages over subjects; values in parentheses indicate standard error of the mean. RMSD is reported for the summary statistics shown in Figure 4. LSA: latent semantic analysis; GloVe: global vectors model; WAS: word association spaces. C: context-based semantic cuing; I: item-based semantic cuing; IC: combined item and context-based semantic cuing.

	Base	LSA-C	LSA-I	LSA-IC	GloVe-C	GloVe-I	GloVe-IC	WAS-C	WAS-I	WAS-IC
βenc	0.83 (0.01)	0.72 (0.02)	0.70 (0.02)	0.71 (0.02)	0.70 (0.02)	0.67 (0.02)	0.70 (0.02)	0.69 (0.02)	0.69 (0.02)	0.71 (0.02)
βrec	0.86 (0.01)	0.90 (0.01)	0.80 (0.01)	0.81 (0.01)	0.91 (0.01)	0.79 (0.02)	0.81 (0.01)	0.91 (0.01)	0.80 (0.02)	0.80 (0.01)
βstart	0.23 (0.03)	0.28 (0.03)	0.27 (0.03)	0.26 (0.03)	0.30 (0.03)	0.26 (0.03)	0.26 (0.03)	0.32 (0.03)	0.28 (0.03)	0.28 (0.03)
α	3.90 (0.75)	3.63 (0.58)	9.30 (1.27)	7.76 (1.26)	4.98 (0.72)	13.94 (1.57)	10.46 (1.10)	3.83 (0.53)	7.24 (1.06)	6.35 (0.93)
δ	34.88 (3.53)	37.65 (3.47)	32.31 (3.30)	30.74 (3.32)	40.03 (3.63)	33.95 (3.16)	31.98 (3.19)	40.02 (3.66)	32.79 (3.37)	32.00 (3.33)
γ	0.22 (0.03)	0.19 (0.03)	0.28 (0.03)	0.26 (0.03)	0.18 (0.02)	0.29 (0.03)	0.27 (0.03)	0.18 (0.02)	0.25 (0.03)	0.24 (0.03)
λ	–	–	–	0.91 (0.02)	–	–	0.95 (0.02)	–	–	0.81 (0.03)
ϕs	37.24 (3.74)	25.92 (3.29)	19.94 (2.90)	20.10 (2.90)	23.19 (3.14)	18.48 (2.84)	19.65 (2.95)	22.22 (3.07)	22.02 (3.01)	22.68 (3.08)
ϕd	14.69 (2.82)	14.21 (2.85)	10.91 (2.51)	8.07 (2.06)	12.98 (2.68)	11.16 (2.52)	10.70 (2.45)	15.41 (2.99)	14.63 (2.95)	13.02 (2.73)
s	–	1.00 (0.08)	1.95 (0.28)	1.80 (0.20)	1.77 (0.42)	2.52 (0.37)	3.25 (0.87)	1.27 (0.11)	2.27 (0.61)	2.03 (0.30)
τ	21.50 (3.32)	29.32 (3.62)	51.39 (4.04)	43.55 (3.98)	34.67 (3.78)	68.11 (3.84)	57.02 (3.96)	27.83 (3.43)	36.62 (3.76)	34.18 (3.68)
θs	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)	0.01 (0.00)
θr	0.42 (0.01)	0.42 (0.01)	0.42 (0.01)	0.42 (0.01)	0.42 (0.01)	0.42 (0.01)	0.42 (0.01)	0.42 (0.01)	0.42 (0.01)	0.42 (0.01)
ln(L)	−55608.13	−54659.31	−54394.66	−54300.50	−54335.26	−53999.59	−53902.58	−53491.95	−53322.92	−53197.59
AIC	114147.96	112532.31	112003.01	112099.41	111884.21	111212.87	111303.58	110197.58	109859.52	109893.59
BIC	118720.53	117505.10	116975.80	117469.68	116856.99	116185.66	116673.84	115170.37	114832.31	115263.85
wAIC	0	0	0	0	0	1.3319e-294	2.67743e-314	3.90117e-74	1	4.00501e-08
wBIC	0	0	0	0	0	1.3319e-294	0	3.90117e-74	1	1.95914e-94
RMSD	0.0959	0.0972	0.0971	0.0978	0.0981	0.0967	0.0972	0.0968	0.0967	0.0958

Model comparison

Given that our Base model with no semantic associations was able to account for benchmark phenomena in free recall, we examined whether the predictive power of the model could be improved by the addition of semantic structure. The addition of associative structure based on LSA, GloVe, or WAS led to a substantially better fit, regardless of the cuing mechanism used: For each experiment, wAIC and wBIC for the set of semantic models (aggregating over cuing mechanisms and semantic models) was virtually 1. For all experiments and semantic models, AIC was lower (i.e., fitness was improved) when an item-based, rather than context-based, semantic cuing mechanism was used. Similarly, for a given semantic cuing mechanism, WAS always provided the best fit, followed by GloVe, then LSA. The WAS-I model provided the best fit overall for all three experiments, with AIC weights approaching 1. Critically, our measure of model fitness is based on the likelihood of the recall sequences under that model; it makes no assumptions about the actual structure of our participants’ semantic knowledge, and therefore avoids complications that arise when a semantic model is used to both generate and evaluate model predictions (Polyn et al., 2009; Manning et al., 2012). This analysis of AIC weights aggregates over multiple participants, assuming that they all use similar semantic cuing mechanisms. In the Semantic organization section, we examine the possibility that people may use different cues to probe semantic memory.

Exclusion of recall errors

In this study, we focus on the processes giving rise to correct responses during free recall. While participants make error responses in the form of repeats and intrusions, they are relatively rare. Of the original set of recall attempts in Experiment 1, 4.52% were repeats, 1.34% were prior-list intrusions, and 3.73% were extra-list intrusions. In Experiment 2, 3.30% of recall attempts were repeats, 3.14% were prior-list intrusions, and 2.39% were extra-list intrusions. In Experiment 3, 2.97% of recall attempts were repeats, 0.56% were prior-list intrusions, and 2.33% were extra-list intrusions. The version of CMR used here was not designed to simulate these error responses; as such, we excluded repeats and intrusions by removing them from the recall sequences and simulating recall as if they had not occurred. A potential issue with this approach is that by excising these error responses, we introduce a discontinuity in the recall sequence, which might hurt a model’s ability to predict a correct recall response following an error response. This was indeed the case: Across all model variants, log likelihood was, on average, lower for the correct recall events following an excluded repeat or intrusion, indicating that these events had lower prediction accuracy (Experiment 1: following repeat or intrusion −2.890; other recalls −2.378; Experiment 2: following repeat or intrusion −2.463; other recalls −2.112; Experiment 3: following repeat or intrusion −2.413; other recalls −1.935).

In order to test whether these differences in log likelihood following repeats and intrusions affected our model comparison analysis, we calculated AIC weights with recall events immediately following a repeat or intrusion excluded. AIC weights for this restricted set of recall events were comparable to when all recall events were included (wAIC for WAS-I model, Experiment 1: 0.9958; Experiment 2: 0.9999; Experiment 3: 1.0000). Similar AIC weights were also obtained when the two recall events following a repeat or intrusion were excluded (wAIC for WAS-I model, Experiment 1: 0.9513; Experiment 2: 0.9996; Experiment 3: 1.0000)

Semantic organization

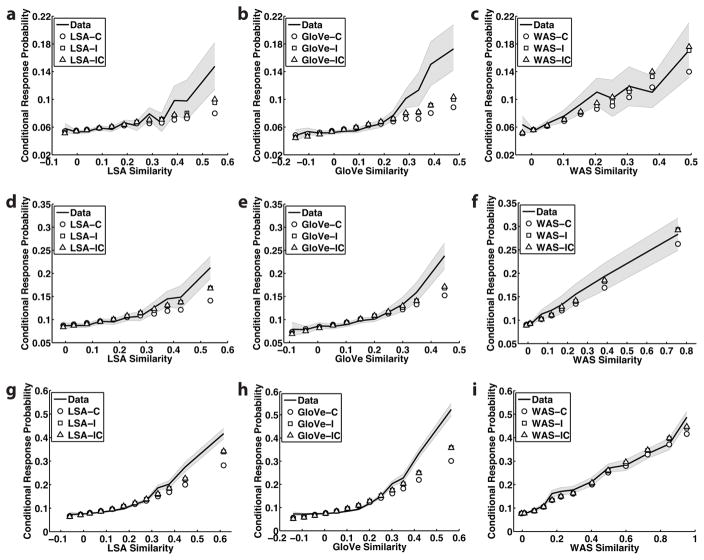
In order to characterize how the model of semantic associations (WAS, GloVe, or LSA) and the type of semantic cuing mechanism (item, context, or item+context) influenced the behavior of the models, we carried out a set of semantic-CRP analyses (Fig. 5). The semantic-CRP shows how the likelihood of two items being recalled in adjacent output positions increases as a function of the semantic similarity of the two items. We examined three versions of the semantic-CRP, using each of the different semantic similarity models.

Figure 5.

Measures of semantic organization, for the observed data and for model simulations. Top row: Experiment 1; middle row: Experiment 2; bottom row: Experiment 3. (a) Conditional response probability as a function of latent semantic analysis (LSA) semantic similarity bin. The line indicates the mean value in the data, and the shaded region represents the 95% confidence interval. Also shown is the performance of the LSA-based models. C: context-based semantic cuing; I: item-based semantic cuing; IC: combined item and context-based semantic cuing. (b) Conditional response probability as a function of global vectors (GloVe) semantic similarity bin. (c) Conditional response probability as a function word association spaces (WAS) semantic similarity bin. (d–f) Conditional response probability by semantic similarity bin for Experiment 2. (g–i) Experiment 3.

Qualitatively, for each combination of model and semantic-CRP analysis, the context-based semantic cuing models predicted a more shallow slope for the semantic-CRP than the item-based cuing models. This suggests that an increase in the strength of semantic associations in the context-based cuing models would have impaired the ability of these models to account for other aspects of the recall sequences. We examined whether these differences in fit were significant, focusing on the WAS-based models, which had the best predictive power overall. We calculated RMSD, a measure of error in the model fit, for each model and subject, and examined whether RMSD was significantly different between the item, context, and item+context models for a given semantic model. There were no significant differences between any pair of models in Experiments 1 or 2, but in Experiment 3 RMSD was significantly greater for the WAS-C model when compared to the WAS-I model (t(125) = 3.58, p = 0.00049) and the WAS-IC model (t(125) = 4.61, p = 9.9e − 6), suggesting that adding an item-based semantic cuing mechanism to the standard CMR model allowed a better fit to the data.

Testing for persistence of semantic influence

While the item-based and context-based semantic cuing models make similar predictions for the strength of temporal organization, they make a divergent prediction regarding how long semantic information should exert an influence during the recall period. The item-based model suggests that the semantic organizational influence of a given recalled item should be short-lived, only directly affecting the immediately following recall event. In contrast, the context-based model suggests that this influence is longer lived, given that the contextual information associated with that remembered item fades gradually. We designed a novel analysis of semantic organization to distinguish between these two accounts; this analysis is described in detail in the methods section (Analysis of recall behavior ). While the semantic CRP analysis focuses on adjacent items in the recall sequence, this analysis examines whether more distant items in the recall sequence can exert a semantic influence on one another. (Polyn et al., 2009) presented a semantic organization score that focused on the relatedness of items in adjacent output positions (i.e., recall events with a lag of 1). Here, we extend that analysis to quantify the influence of a recalled item on more distant recall events (i.e., recall events of lag 2–4). The context-based semantic cuing mechanism predicts that the semantic organization score should decrease as a function of recall lag, but should be greater than chance (0.5) for recall lags greater than 1.

As shown in Figure 6, the best-fitting WAS-C models predicted an above-chance WAS score for recall lag 2 in each experiment. In contrast to this prediction, we found that WAS factor for the observed data was not significantly greater than 0.5 at any recall lag greater than 1 (Fig. 6; p > 0.05 for recall lags 2–4 in each experiment). Critically, we found that the predictions of the WAS-I model for semantic organization score as a function of recall lag were significantly more accurate than the WAS-C model. The RMSD for the WAS-C model was significantly greater across subjects than the WAS-I model in Experiment 2 (WAS-C RMSD: 0.0466, SEM 0.0037; WAS-I RMSD: 0.0453, SEM 0.0036; t(47) = 2.15, p = 0.037) and Experiment 3 (WAS-C RMSD: 0.0421, SEM 0.0017; WAS-I RMSD: 0.0395, SEM 0.0016; t(125) = 4.41, p = 0.00002). A similar but non-significant trend was observed in Experiment 1 (WAS-C RMSD: 0.0307, SEM 0.0028; WAS-I RMSD: 0.0304, SEM 0.0027; p > 0.05).

Figure 6.

Examination of persistent effects of semantic information, for the observed data and model simulations. (a) Effects of semantic recall context in Experiment 1. Plot shows WAS factor calculated based on lag during recall (e.g. WAS score for recall lag of 1 is based on similarity to the last recalled item). The models with context-based semantic cuing predict that WAS factor will be greater than chance (0.5; indicated by the dotted line) for lags greater than 1; however, we did not observe this in the data. (b) Data and model simulations for Experiment 2. (c) Experiment 3. Shaded areas indicate 95% confidence intervals for the observed data.

Interestingly, the observed semantic organization score for recall lags 3 and 4 was significantly below the chance level of 0.5 in Experiment 3 (lag 3: t(125) = 2.61, p = 0.011; lag 4: t(125) = 3.58, p = 0.0005). In contrast, none of the models dropped below 0.5 at any recall lag. Therefore, this effect in the observed data is unlikely to be a product of some bias in the analysis, and instead might reflect a mechanism not implemented in the model. One possibility is that participants sometimes strategically shift between targeting different clusters of semantically related items; if this were the case, then after a transition to a new cluster of related items, items from earlier clusters would be less likely to be recalled, resulting in a below-chance distance factor to those items. Evidence for strategic targeting of groups of related items has previously been observed in free recall of items from categorized lists (Pollio et al., 1969). Although the context-based semantic cuing model predicts that semantic cues will persist over time, it predicts that this change will be gradual, while in practice participants may sometimes exhibit sharper changes (e.g. shifting from targeting words related to animals to targeting words related to musical instruments).

Individual differences in semantic cuing

In terms of the AIC weights, which aggregate across participants, there is overwhelming support for the item-based semantic cuing model in each of the three experiments (Table 2). However, the modeling framework was designed to find the optimal parameter settings for each individual in each experiment, which allows us to examine whether there were individual differences in cuing strategy across participants. Given that WAS provided the best overall description of behavior relative to the other models of semantic associations (and regardless of the type of cuing used), we focus our examination on the hybrid WAS-IC model. This model contains the the free parameter λ, which specifies for each participant the relative weighting of item-based and context-based semantic cuing (where λ = 0 indicates pure context-based semantic cuing, and λ = 1 indicates pure item-based semantic cuing). Regardless of the value of λ, all models used context-based episodic cuing to guide temporal organization.

Figure 7 presents a histogram for each experiment, with the best-fitting values of λ for each participant. In each experiment, we find that the modal value of λ is 1, indicating that the majority of participants in each experiment were best fit by a pure item-based semantic cuing model. However, we also find that in each experiment there are a subset of participants whose behavior is better described by a model with λ < 1, indicating some evidence for context-based semantic cuing. This pattern is most striking in Experiment 2, where 16 participants were best fit by a pure context-based semantic cuing model. This result suggests that while there are many similarities in recall performance across participants (Healey and Kahana, 2014), there are differences in how semantic structure affects recall organization across different participants. The difference in the distribution of λ across participants may be related to procedural differences in the experimental paradigms. For example, the faster presentation time or the type of encoding task (visualization) in Experiment 2 may have encouraged a different type of encoding that led to semantic information being integrated into temporal context for a subset of participants, yielding behavior consistent with the context-based cuing model. This point receives more attention in the discussion.

Figure 7.

Value of the λ parameter for the best-fitting WAS with combined item and context-based semantic cuing, for each experiment. (a) In Experiment 1, most participants had values of λ of very near to 1, indicating that their recall behavior was more consistent with the item-based semantic cuing mechanism. (b) In Experiment 2, a substantial subset of participants had values of λ that were near to 0, consistent with the context-based semantic cuing mechanism. (c) Most participants in Experiment 3 had behavior that was most consistent with item-based semantic cuing.

Discussion

We developed a likelihood-based modeling framework where a model of semantic associations is embedded in the context maintenance and retrieval model (CMR); this framework allowed us to assess the relative validity of competing models of semantic organization in free recall while accounting for many of the complexities of memory search. CMR proposes that studied items become associated with a representation of temporal context, which provides an important cue during memory search. This context-based episodic cuing mechanism has been shown to explain several important aspects of temporal organization in free recall (Howard and Kahana, 2002a; Sederberg et al., 2008; Howard et al., 2009); however, it is less clear whether temporal context also influences semantic organization. We contrasted two mechanisms by which semantic associations have been proposed to influence free recall: an item-based mechanism where retrieved items cue for semantic associates, and a context-based mechanism where retrieved context serves as a semantic cue. While temporal organization in free recall is consistent with a context-based cuing mechanism (Howard and Kahana, 2002a; Lohnas and Kahana, 2014), we found that semantic organization in free recall is more consistent with an item-based semantic cuing mechanism, suggesting that semantic and episodic associations are probed using distinct cues during memory search. Furthermore, we found that models using word-association spaces (WAS) to determine semantic structure outperformed models using latent semantic analysis (LSA) or global vectors (GloVe) to determine semantic structure, in terms of the models’ ability to predict the identities of a sequence of recalled items. We propose that our modeling framework provides specific advantages in the evaluation of computational models of semantic and episodic memory, and may provide the basis for developing better measurements of semantic organization in recall sequences.

Models of semantic association strength

Both WAS and LSA have been used to characterize behavior in free recall (Howard and Kahana, 2002b; Howard et al., 2007; Manning and Kahana, 2012) and have been used as components of models of memory search (Sirotin et al., 2005; Polyn et al., 2009). The present results suggest that WAS is better able than both LSA and a more recently developed technique, GloVe, to predict behavior in recall of lists of words with no obvious semantic structure. Our results complement those of Sirotin et al. (2005), who compared the ability of WAS and LSA to explain behavior in free recall of categorized materials. They developed a version of the search of associative memory (SAM) model (Raaijmakers and Shiffrin, 1980) that included semantic associations between items. Sirotin et al. (2005) assumed that search of long-term memory is driven by both episodic and semantic inter-item associations. They compared a model with semantic structure based on WAS to a model with semantic structure based on LSA, and found that the WAS-based model was better able to account for category clustering in a multi-trial free recall study (Kahana and Wingfield, 2000). Their analysis of recall behavior focused on only one aspect of semantic organization, namely clustering by taxonomic category. In contrast, our likelihood-based framework does not require choosing a particular summary statistic to evaluate the fitness of a model. As such, this framework can be applied to experiments where the studied items do not have a systematic category structure. Furthermore, the framework is flexible enough that it can be used to evaluate any model of semantic structure, as long as that model provides estimates of the associative strengths between items. While the vector-space models (WAS, GloVe, and LSA) evaluated here contain symmetric associative strengths, this characteristic is not necessary–the framework can evaluate semantic models in which the associative strength from item i to item j is not the same as the associative strength of item j to item i.

We are interested in determining which model contains semantic relatedness scores that best correspond to those in the human memory system. In terms of predictive power and fit to summary statistics, WAS is the clear winner in this regard. However, the conclusions we can draw regarding the processes giving rise to these semantic structures are limited. The superior performance of the WAS model is not surprising, in that its representations are constructed from the results of a behavioral free-association experiment, while LSA and GloVe are trained on large text corpora. In other words, WAS incorporates behavioral results from a similar cognitive task into its structure (i.e., free association vs. free recall), sidestepping the need to describe the processes by which this structure develops (Jones et al., 2015).

Nonetheless, by contrasting WAS with the other models of semantic association, we may gain insight into how these other models can be modified to increase their utility as cognitive models of semantic similarity. In our examination of the semantic CRP (Figure 5), only the WAS-CRP showed a linear relationship between semantic similarity and likelihood of semantic clustering in the observed data. In contrast, the LSA-CRP and GloVe-CRP showed positively accelerated curves describing this relationship. One interpretation of this difference is that WAS does a better job estimating the global structure of the semantic space containing these word representations. All three models seem to do a good job describing the local structure of semantic space, in that all three semantic-CRP curves capture the increased likelihood of clustering associated with highly related word pairs (i.e., words that are nearby in semantic space). However, only WAS seems to capture the behavioral consequences of small changes in semantic relatedness for less related word pairs (i.e., words that are more distant in semantic space). This interpretation is supported by our modeling results, in which only the WAS models are able to fit the full extent of the semantic-CRP, consistent with the idea that WAS provides a good match to the associations guiding recall. By this logic, the failure of the LSA and GloVe models to fit their corresponding semantic-CRP curves is likely due to the presence of semantic associations that don’t match the ones guiding behavior. If the strength of these semantic associations were increased, it would be at the cost of predicting semantic clustering that mismatches the observed data.

In future work, it may be possible to identify transformations on the LSA or GloVe representations that improve their predictive power in free recall. This would be of utility to many cognitive researchers interested in estimating semantic similarity, as the semantic similarity estimates in WAS are limited to the 5018 words that were part of the original free-association study (Nelson et al., 2004). Such an endeavor might also inform the development of process-based models attempting to describe the emergence of semantic structure with experience (Rogers and McClelland, 2004; Jones and Mewhort, 2007; Rao and Howard, 2008).

Mechanisms of semantic cuing

Polyn et al. (2009) developed CMR, which extended the temporal context model (TCM) to account for multiple influences on recall organization, including source context and semantic similarity. CMR is a retrieved-context model, wherein retrieval of a particular item causes the system to reactivate the temporal context representation associated with that item. This retrieved context contains a weighted average of information related to the items preceding the just-recalled item in the study list. The version of CMR presented by Polyn et al. (2009) used a context-based semantic cuing mechanism, where retrieved temporal context projects through a set of semantic associations, providing support for any items that are semantically related to any of the items represented in the context cue. We constructed an alternative model in which semantic cuing was driven by semantic associations attached to a feature-based representation of the studied item. This item-based semantic cuing mechanism is similar to the semantic cuing mechanism in the eSAM model (Sirotin et al., 2005), in which only the most recently recalled studied item is used to cue its semantic associates. In both variants of the model, recall organization is simultaneously determined by temporal and semantic information, but the nature of temporal/semantic interactions differs between the two versions.

Across three experiments with widely varying methodological characteristics, we found that the context-based semantic cuing mechanism described by Polyn et al. (2009) was inferior to the item-based semantic cuing mechanism. While the context-based semantic cuing mechanism performed substantially better than a model without any semantic structure, models with an item-based semantic cuing mechanism were overall best at predicting behavior. Under this item-based mechanism, although temporal context is still used as an episodic cue, only the most recently recalled item is used as a semantic cue. We developed a novel analysis of semantic organization to examine a divergent prediction of the two models: While context-based semantic cuing predicts that an item will have a gradually fading influence on semantic organization, the item-based mechanism predicts that the semantic influence of a given item will be limited to the immediately following response. As shown in the results of the recall-lag analysis presented in Figure 6, the predictions of the item-based model provided a better fit to the observed data.

An examination of individual differences in recall behavior revealed limited evidence for the engagement of a context-based cuing mechanism in some subjects. This evidence was most obvious in Experiment 2, where a substantial minority of the participants were best described by the context-based semantic cuing mechanism. It is possible that methodological differences between the experiments underlie this observation. Experiment 2 had a faster presentation time than Experiments 1 & 3, and it included an end-of-list distraction period. Participants in Experiment 2 were encouraged to visualize the items, whereas in Experiment 1 they performed one of two binary classification tasks. In Experiment 3, we examined trials without an explicit encoding task, but these were surrounded by trials in which participants performed the same binary classification tasks as in Experiment 1, which may have influenced their encoding strategy. More work is needed to determine what circumstances determine whether recall behavior is more consistent with item- or context-based semantic cuing.

One methodological characteristic common to the three experiments was that there was no obvious semantic structure to the study lists. Words were randomly chosen from a large pool. It may be that context-based semantic cuing is more likely to be engaged when study lists have explicit semantic structure, as in blocked categorized free recall paradigms (e.g. Puff 1966). Recent scalp EEG evidence is consistent with this idea. Using scalp EEG during encoding of categorized materials, Morton et al. (2013) found evidence of persistent category-specific activity, which became stronger when multiple items from the same category were presented in sequence. The rate at which this category-specific signal increased predicted individual differences in organization by stimulus category during recall. Morton et al. (2013) proposed that this integrative category-specific signal is consistent with the operation of a temporal context mechanism. If each studied item caused category-specific information to be integrated into context, this would explain both why the category-specific signal gets progressively stronger, and why this rate of increase is related to individual differences in category clustering. To test this account, Morton and Polyn (in preparation) created a modified version of CMR in which each item is associated with a distributed pre-experimental contextual representation containing semantic information. As in the context-based semantic cuing models examined in the present work, their distributed-CMR model assumed that both temporal and semantic organization are driven by contextual cues. They simulated the Morton et al. (2013) experiment, and found that the distributed-CMR model correctly accounts for the relationship between category-specific neural activity during encoding and individual differences in semantic organization. In future work, we plan to adapt the distributed-CMR model to work within the likelihood-based framework presented in this article. This will allow us to directly contrast the semantic cuing models evaluated here, in which semantic associations only have an influence during retrieval, with the distributed-CMR model, where semantic information is integrated into context during encoding.

One clear prediction of the context-based semantic cuing mechanism is that a weighted combination of the prior recalls determines the semantic influences for the current recall event, causing a form of compound cuing. Temporal organization shows clear compound cuing effects, in a way that is consistent with the CMR model (Lohnas and Kahana, 2014). While we observed similar temporal organization effects as in previous studies (Fig. 4), we found no evidence for compound semantic cuing (Fig. 6). However, it is possible that other types of free-recall paradigms may show evidence for compound semantic cuing. Kimball et al. (2007) examined behavior in the false memory paradigm, in which participants have a strong tendency to falsely recall critical items that are semantically related to the items from the study list (Deese, 1959; Roediger and McDermott, 1995). They proposed a modified version of the SAM model in which a compound cuing mechanism (in which multiple remembered items exerted semantic influences during recall) was necessary to fully account for data in false memory experiments. It may be that the strong semantic structure of study lists in the false memory paradigm leads to the engagement of a context-based cuing mechanism. However, more work is needed to determine whether the CMR model can account for the major empirical phenomena from false memory paradigms.

Measurement of semantic organization

In the current work, the influence of semantic information is reflected in the magnitude of the s parameter, which scales the influence of semantic associations on memory search. Because the model contains other parameters which account for behavioral variance due to temporal structure, the best-fitting value of the s parameter may provide a good estimate of the magnitude of semantic organization in a given experiment. As such, the computational modeling framework used here may be useful for measuring semantic organization while accounting for other influences on recall behavior. Properly accounting for temporal organization is critical when considering experimental manipulations that alter the temporal organization of semantically related stimuli, as in experiments that contrast study lists with blocked vs. random presentation of categorized stimuli (Puff, 1966). However, most of the prior work on blocked-random effects has not accounted for this influence (e.g. Cofer et al. 1966; D’Agostino 1969; Borges and Mandler 1972). Through bootstrapping techniques, it is possible to estimate the amount of semantic organization due to temporal clustering (Morton et al., 2013). However, this technique requires collecting data from baseline lists with no category structure, and involves the assumption that other aspects of recall behavior are unaffected by the manipulation of the temporal structure of the categorized materials. To avoid these issues, CMR could be fit separately to blocked and random lists. The semantic scaling parameter would then provide an estimate of the strength of semantic organization, while the other parameters (as well as the structure of the model itself) could account for alterations in temporal organization and other influences that might vary between conditions. While further work is necessary to determine whether CMR will provide reliable estimates of semantic organization in these experiments, the current work establishes the plausibility of such an approach, which may prove useful for investigating interactions between temporal and semantic structure during memory search.

Conclusions

While prior research has found that semantic knowledge exerts an important influence on the search of episodic memory, many questions remain about the cognitive mechanisms that mediate this influence. We developed a modeling framework that allows one to both evaluate the relative utility of different models of semantic associations, and to compare different mechanisms by which semantic information affects memory search. In order to be able to calculate the exact likelihood of recall sequences under a given model, we used a simplified version of CMR, which did not contain mechanisms to determine response latency, to produce recall errors, or to produce organizational effects related to source characteristics (Polyn et al., 2009; Lohnas et al., 2015). However, we believe it will be possible to develop this framework to incorporate these mechanisms, allowing one to examine different models of how semantic information influences inter-response times, recall errors, and other organizational effects. More generally, we hope that the computational modeling framework presented here will continue to help shed light on how prior semantic knowledge shapes the formation and utilization of episodic memories.

Appendix

Maximum-likelihood parameter estimates, as well as log likelihood, AIC, BIC, AIC weights, BIC weights, and RMSD are shown in Tables 3–5. Although all parameters were allowed to vary freely for each of the model variants, many of the best-fitting parameters were quite similar across all models. Parameters controlling the rate of context evolution (β_enc, β_delay, and β_rec), parameters involved in the primacy effect (ϕ_s, ϕ_d, and β_start), and stopping parameters (θ_s and θ_r) were all comparable across the 10 model variants within each experiment. The semantic scaling parameter, s, was generally greater for better-fitting models, suggesting that the influence of semantics is increased when the model of semantic cuing is improved. For a given semantic model, α was increased for item-based semantic cuing models. Increasing α causes recall to become more stochastic (less dependent on the particular context cue used). This may help the item-based semantic cuing models to mimic the tendency of context-based semantic cuing models to predict more diffuse cuing of multiple items in the list (see Fig. 2d for an illustration).