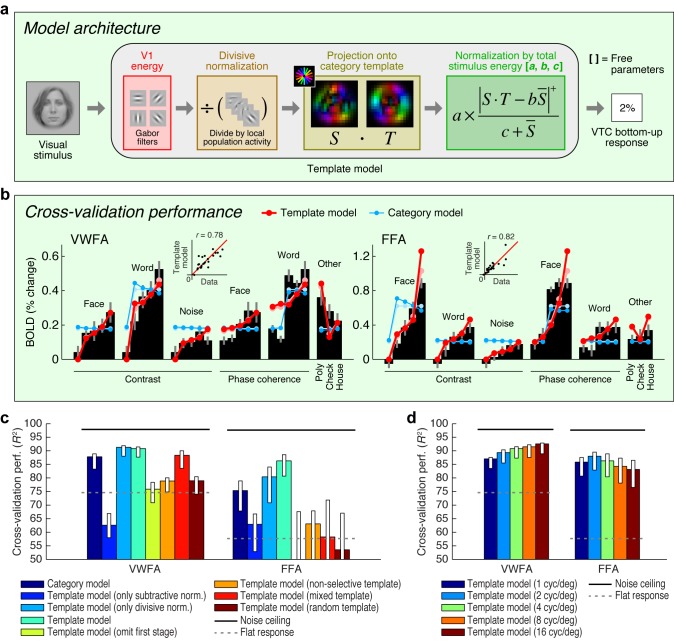
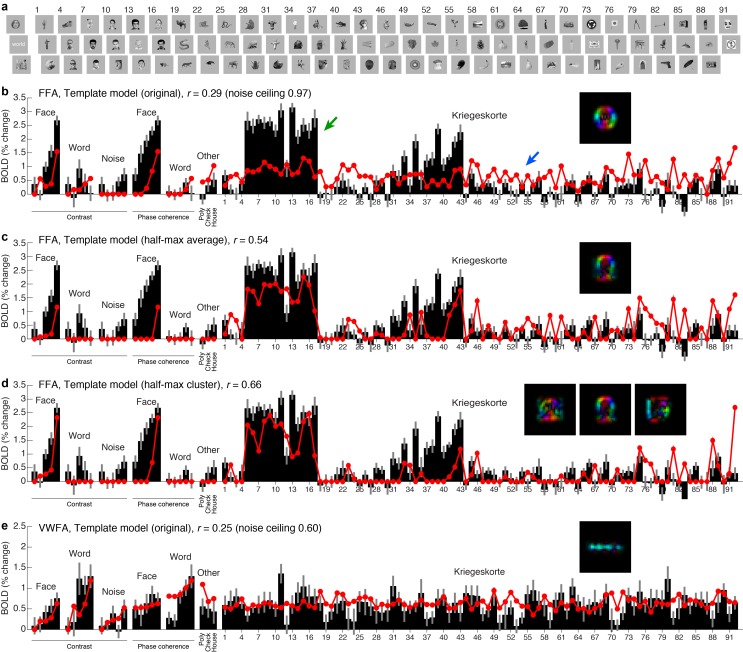
Figure 2. Model of bottom-up computations in VTC.

(a) Model architecture. The predicted response of the Template model is given by a series of image computations (see Materials and methods). (b) Cross-validation performance. Black bars indicate bottom-up stimulus-driven responses measured during the fixation task, dark lines and dark dots indicate model predictions (leave-one-stimulus-out cross-validation), and light lines and light dots indicate model fits (no cross-validation). Scatter plots in the inset compare model predictions against the data. The Template model is compared to the Category model which simply predicts a fixed response level for stimuli from the preferred stimulus category and a different response level for all other stimuli (the slight decrease in response as a function of contrast is a result of the cross-validation process). (c) Comparison of performance against control models. Bars indicate leave-one-stimulus-out cross-validation performance. Error bars indicate 68% CIs, obtained by bootstrapping (resampling subjects with replacement). Solid horizontal lines indicate the noise ceiling, that is, the maximum possible performance given measurement variability in the data. Dotted horizontal lines indicate the cross-validation performance of a model that predicts the same response level for each data point (this corresponds to R² = 0 in the conventional definition of R² where variance is computed relative to the mean). The performance of the Template model degrades if the second stage of nonlinearities is omitted (Template model (only subtractive normalization)) or if the first stage of the model involving V1-like filtering is omitted (Template model (omit first stage)). The plot also shows that the precise configuration of the template is important for achieving high model performance (Template model (non-selective, mixed, random templates)). (d) Performance as a function of spatial frequency tuning. Here we manipulate the spatial frequency tuning of the filters in the Template model (while fixing spatial frequency bandwidth at one octave). The Template model uses a single set of filters at a spatial frequency tuning of 4 cycles/degree.

DOI: http://dx.doi.org/10.7554/eLife.22341.005

Figure 2—figure supplement 1. Testing the Template model on a wide range of stimuli.

(a) Stimuli. We collected an additional dataset consisting of 92 images from a previous study by Kriegeskorte et al. (2008) (all images shown), along with 22 images from the original experiment (three images shown). We assessed model accuracy using 20-fold cross-validation across stimuli (see Materials and methods for details). (b) Performance of Template model (original). Black bars indicate data from FFA, with error bars indicating 68% CIs (error across trials). Red lines and red dots indicate model predictions. Inset shows the category template used in the model. The model performs poorly. (c) Performance of Template model (half-max average). This model derives the category template by computing (in the V1-like representation) the centroid of all stimuli in the training set that evoke at least half of the maximum response. Performance improves. (d) Performance of Template model (half-max cluster). This model derives multiple category templates by performing k-means clustering (in the V1-like representation) on all stimuli in the training set that evoke at least half of the maximum response. Performance further improves, resolving both underprediction of responses (for example, green arrow in panel b) and overprediction of responses (for example, blue arrow in panel (b). (e) Results for VWFA. Similar responses are observed across the 92 Kriegeskorte images. Responses are well predicted by the original Template model, up to the level of measurement noise in this region.

DOI: http://dx.doi.org/10.7554/eLife.22341.006