Mathematical Model of Cardiovascular and Metabolic Responses to Umbilical Cord Occlusions in Fetal Sheep

Abstract

Fetal acidemia during labor is associated with an increased risk of brain injury and lasting neurological deficits. This is in part due to the repetitive occlusions of the umbilical cord (UCO) induced by uterine contractions. Whereas fetal heart rate (FHR) monitoring is widely used clinically, it fails to detect fetal acidemia. Hence, new approaches are needed for early detection of fetal acidemia during labor. We built a mathematical model of the UCO effects on FHR, mean arterial blood pressure (MABP), oxygenation and metabolism. Mimicking fetal experiments, our in silico model reproduces salient features of experimentally observed fetal cardiovascular and metabolic behavior including FHR overshoot, gradual MABP decrease and mixed metabolic and respiratory acidemia during UCO. Combined with statistical analysis, our model provides valuable insight into the labor-like fetal distress and guidance for refining FHR monitoring algorithms to improve detection of fetal acidemia and cardiovascular decompensation.

1 Introduction

One of the main issues during childbirth is the possibility of developing severe fetal acidemia (pH < 7.0) caused by umbilical cord occlusions (UCO) due to repetitive uterine contractions. The resulting increased risk of ischemic brain injury can be associated with acidemia (Liston et al. 2007). The sudden compression of the umbilical cord leads to fetal hypertension and fetal heart rate (FHR) decelerations, which are mediated through chemoreflex and sympathetic stimulation (Low et al. 1995; Westgate et al. 1999; Bennet et al. 2005). Fetal oxygen delivery via the umbilical cord is interrupted and leads to hypoxemia and acute cerebral hypoxia (Mallard et al. 1995; Koos et al. 1995; Bishai et al. 2003; Hunter et al. 2003; Westgate et al. 2007; Thakor and Giussani 2008). In addition, FHR reduction and oxygen deficiency also activate sympathetic and parasympathetic brainstem centers resulting in changes of afferent and threshold efferent firing rates (Frasch et al. 2009a, 2012). These activities, in turn, via efferent signaling, regulate FHR and systemic arterial blood pressure. Furthermore, prolonged cord compression and/or repeated cord compressions may cause accumulation of metabolites, such as CO₂ and lactate, in the fetus, which contributes to acidemia (Bennet et al. 2005; Frasch et al. 2009b), as well as prolonged cerebral hypoperfusion (Yan et al. 2009). A comprehensive discussion on the dynamic changes of the fetal circulation and blood flow distribution during hypoxia and asphyxia due to different experimental disturbances can be found in the review paper (Jensen et al. 1999).

Beyond the physiological understanding of the general process, a clinically relevant question is how to monitor and predict the levels of fetal acidemia based on the available clinical data so that the fetal brain can be protected by medical intervention. Since direct continuous measurements of acidemia from fetal blood are not possible clinically and measurements can only be done intermittently in an animal model, an attempt has been made to use statistical approaches to make prediction of acidemia based on FHR (Agrawal et al. 2003). However, current FHR-based clinical algorithms do not provide an accurate prediction of acidemia (de Haan et al. 1997). This is because there is no a priori knowledge of which FHR properties best reflect acidemia. Therefore, a mechanistic modeling approach that can identify FHR properties related to acidemia will provide valuable insights that are useful for developing more effective diagnostic tools.

Mathematical modeling and simulation are useful alternatives to experiments, especially when they are too difficult or too expensive. One of the advantages of mathematical models is that they allow us to conduct parametric studies easily—the physical quantities can be easily tracked. A popular mathematical model in describing the cardiovascular system coupled with the central nervous system has been proposed by Ursino (1998), followed by many related studies that can reproduce and predict the cardiovascular responses in various systems successfully (Ursino and Magosso 2000, 2003; Liang and Liu 2006; Liang et al. 2009; van der Hout-van der Jagt et al. 2013). The drawback is that usually the biological system has a large number of parameters, some of which are difficult or impossible to measure. This makes analysis difficult and can easily introduce uncertainties and errors in the model. A similar cardiovascular mathematical model was used to explore physiological mechanisms in postural change and related physiology problems (Olufsen et al. 2004, 2005; Ellwein et al. 2008). These models are based on electric circuit analogs. In addition, Olufsen’s group (Ellwein et al. 2008) also performed a sensitivity analysis to better understand the model’s dynamics and the impact of the parameters on outputs. A recent review of various models can be found in Shi et al. (2011).

The metabolic dynamics formulated using a deterministic approach are based on the cardiovascular model by Olufsen’s group and a similar (local) sensitivity analysis. A regulation model is incorporated to provide cardiovascular feedback with respect to the arterial pressure and substrate (oxygen, lactate, glucose) concentrations via central neural system, following the works in Ursino (1998), Liang and Liu (2006), van der Hout-van der Jagt et al. (2012, 2013). Details are revealed in Sect. 2. Furthermore, the current model incorporates biochemical processes with proper substrate transfer between blood and organs. As indicated by experiments (Westgate et al. 2001; Frasch et al. 2009b), metabolic dynamics are closely related to the development of acidemia in fetal sheep and accumulation of waste, such as CO₂ and lactate, contribute to the decline in pH. A mathematical model can continuously display in both time and space, the evolution of implicated molecular concentrations, unlike experimental measurements.

The present mathematical model consists of three elements: a lumped parameter model for the cardiovascular circuit coupled with nervous regulation and reciprocal perfusion–metabolism influences. This model is used to investigate the effect of UCOs on FHR, MABP pattern and acidemia development. Our model reproduces some of the patterns observed in animal experiments such as FHR overshoot, deceleration, MABP and pH decline, lactate and CO₂ increase. More importantly, we have confirmed correlation between root-mean-square of the successive differences (RMSSD), a statistical measure of FHR variability and critical levels of lactate and pH (Frasch et al. 2009c). On the other hand, we have also shown that one has to be careful when applying RMSSD as a predictive index. In particular, a variable window size should be used to compute RMSSD when the occlusion duration varies instead of blindly applying standard signal processing techniques.

The rest of the paper is organized as follows. The model equations are given in Sect. 2 for different components. In Sect. 3, model calibration is discussed and a sensitivity analysis is carried out to identify the most sensitive parameters in the mathematical model. Numerical results motivated by different fetal experiments are presented in cardiovascular responses in Sect. 3.2 and metabolic dynamics in Sect. 3.3. Statistical analysis based on contingency tables and RMSSD are discussed in Sect. 3.4. Finally, a summary and conclusions are given in Sect. 4.

2 Mathematical Formulation

2.1 Cardiovascular System

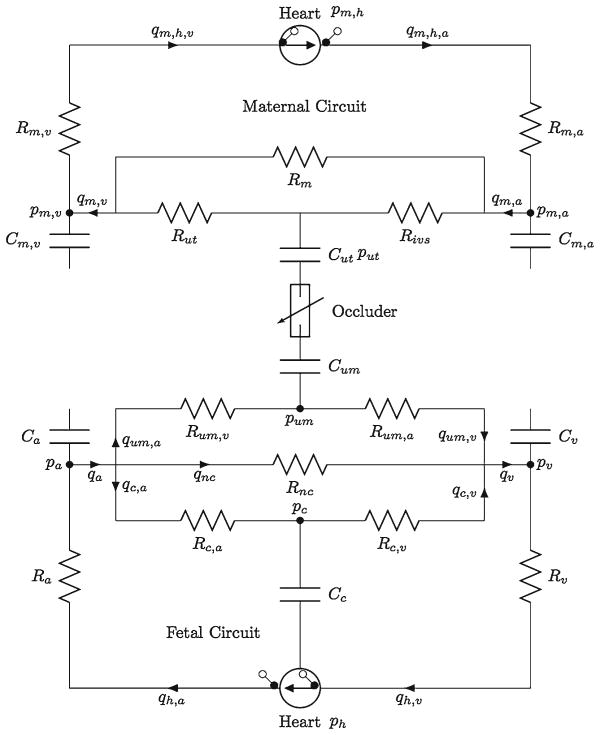
Our model includes both maternal and fetal circulations. Similar to previous studies (Olufsen et al. 2004; van der Hout-van der Jagt et al. 2012), we use an electrical circuit analog, where pressure p(t) is analogous to voltage, volumetric flow rate q(t) to the current and compliance C to capacitance. In addition, the resistance R accounts for the pressure drop due to blood viscosity in each element of the circuit. A schematics of the model with individual components is given in Fig. 1. We model the heart (in both maternal and fetal circulation) as an effective left ventricle (Olufsen et al. 2004), which has two ideal valves on two sides. Two compartments are used to model the branching flow before and after the ventricle, where p_a and p_v are computed (Olufsen et al. 2004). Our model hearts are effective pumps that produce the desirable cardiovascular outputs to maintain both maternal and fetal blood circulations. The fetal systemic circulation is modeled as one compartment with subscript ‘nc’ (Fig. 1). Whereas the remaining fetal circulation is considered as one compartment, the umbilical cord and cerebral circulation are modeled separately with arteries and veins (van der Hout-van der Jagt et al. 2012). The maternal circulation system is coupled with the fetal circulation system through partial oxygen pressure in intervillous space of the placenta connected to the umbilical cord. We adopt an oxygen transport model (Couto et al. 2002) where the oxygen distribution in the circulatory systems is given by conservation of mass (van der Hout-van der Jagt et al. 2012) including convection, diffusion and reaction (metabolic uptake and consumption) in the circuit. The blood pressure and oxygen content are coupled through a regulatory model on heart rate by the vagal-sympathetic control (Ursino 1998; van der Hout-van der Jagt et al. 2012).

Fig. 1.

Illustration of model setup. Our model includes two circulatory networks: maternal circulation (top) and fetal (bottom) circulations. Resistors R and compliances C are indicated, arrows giving blood flow direction, similar to van der Hout-van der Jagt et al. (2012). In this sketch, ‘a’ stands for artery, ‘v’ for vein, ‘um’ for umbilical cord, ‘m’ for mother systemic part, ‘nc’ for fetal systemic part, c’ for cerebral part, ‘ut’ for uterine and ‘ivs’ for intervillous space

The basic equations predicting blood pressure and flow can be obtained by computing the volume of each compartment V_i = C_i p_i, where C_i and p_i are the corresponding compliance and pressure, respectively, and the change of volume in each compartment is then given by

$$\frac{\mathrm{d}{V}_i}{\mathrm{d}t}=q_{\text{in}}-q_{\text{out}}.$$ (1)

where the subscript i stands for a (artery), v (vein), um (umbilical) and c (cerebral; Fig. 1). An analogy to Ohm’s law provides a linear relation between pressure p and flow rates q

$$q_i=\frac{p_{\text{in}}-p_{\text{out}}}{R_i}.$$ (2)

In this study, only the resistance in the system is modeled, whereas inertia is neglected (Olufsen et al. 2004). With compliances kept as constants, the equations for pressure change are given by

$$C_i\frac{\mathrm{d}{p}_i}{\mathrm{d}t}=q_{\text{in}}-q_{\text{out}}.$$ (3)

The fetal heart is modeled similarly as the left ventricle used in the study (Olufsen et al. 2004) (a combined ventricle) where the details in pulmonary circulation and the ductus arteriosus are ignored. The rate of volume change and pressure–volume relationship (Olufsen et al. 2004) are given by

$$\frac{\mathrm{d}{V}_h}{\mathrm{d}t}={\mathbb{1}}_{(p_h<p_v)}{q}_v-{\mathbb{1}}_{(p_h>p_a)}{q}_a,$$ (4)

$$p_h=a_h{(V_h-b_h)}^2+(c_h(t)V_h-d_h)g_h(t).$$ (5)

In Eq. 4, 𝟙 _(ph <_pv) and 𝟙 _(ph >_pa) are the indicator functions for valves with zero and one for a closed and open valve, respectively. Conservation of the total volume of the system requires that $\frac{\mathrm{d}}{{\mathrm{d}}_t}{\sum }_{i\in [\mathrm{a},\mathrm{v},\text{um},\mathrm{c},\mathrm{h}]}{V}_i=0$ in fetus and $\frac{\mathrm{d}}{{\mathrm{d}}_t}{\sum }_{i\in [\mathrm{a},\mathrm{v},\text{ut},\mathrm{h}]}{V}_i=0$ in mother (Olufsen et al. 2004), where V_i = C_i p_i. To model the branching before and after the ventricle, the flow rate satisfies the law of mass conservation (Olufsen et al. 2004, 2005; van der Hout-van der Jagt et al. 2012), given by

$$q_a=q_{c,a}+q_{\text{nc}}+q_{\text{um},a},$$ (6)

$$q_v=q_{c,v}+q_{\text{nc}}+q_{\text{um},v}.$$ (7)

In Eq. 5, V_h, p_h and c_h(t) are the heart volume, pressure and contractility, respectively. The parameters a_h and b_h are related to the ventricular elastance during relaxation and the ventricular volume for zero diastolic pressure, respectively, whereas c_h and d_h are related to the volume-dependent and volume-independent components of the developed pressure, respectively (Olufsen et al. 2004). Here g_h(t) = f_h(t)/f_h(t_p) is an activation function that controls periodic oscillation. In maternal circulation, c_h,m(t) = c_m is assumed to be a constant, whereas in fetal circulation c_h(t) is regulated by β sympathetic activity (see Eq. 34 below) and f_h(t) is given by Olufsen et al. (2004),

$$f_h(t)=\{\begin{array}{ll}{p}_p(G)\frac{t^n{(\beta (H)-t)}^m}{n^n{m}^m{({\beta }_h(H)/(m+n))}^{m+n}},\hfill & 0\le t\le {\beta }_h(H),\hfill \\ 0,\hfill & {\beta }_h(H)<t\le T\hfill \end{array}$$

where H is the heart rate controlled by the nervous system (Sect. 2.4), n and m characterize the contraction and relaxation phases, t_p and p_p are the peak time and peak value of the activation and β_h(H) is the valve closure time. According to Olufsen et al. (2004), the expressions for t_p, p_p and β_h(H) are given by

$$t_p=t_{min}+\frac{{\theta }^{\nu }}{H^{\nu }+{\theta }^{\nu }}(t_{max}-t_{min}),$$ (8)

$$p_p=p_{min}+\frac{H^{\eta }}{H^{\eta }+{\varphi }^{\eta }}(p_{max}-p_{min}),$$ (9)

$${\beta }_h(H)=\frac{n+m}{n}{t}_p(H)$$ (10)

where ν and η are parameters that control the steepness of the sigmoidal change. Blood is pumped out from heart into arterial system and flows through each individual compartment such as the umbilical cord, cerebral and systemic compartments in the fetal circulation system, and returns to the heart via the vein (Fig. 1).

2.2 Metabolic Model

The model for oxygen distribution is based on mass conservation (Couto et al. 2002; van der Hout-van der Jagt et al. 2012). Oxygen concentration [O₂] in each compartment is given by the following equations

$$\frac{\mathrm{d}({[{\mathrm{O}}_2]}_{\text{ivs}}{V}_{\text{ivs}})}{\mathrm{d}t}=q_{\text{ivs}}({[{\mathrm{O}}_2]}_{m,a}-{[{\mathrm{O}}_2]}_{\text{ivs}})-S_{{\mathrm{O}}_2,d},$$ (11)

$$\frac{\mathrm{d}({[{\mathrm{O}}_2]}_{\text{um}}{V}_{\text{um}})}{\mathrm{d}t}=q_{\text{um},a}({[{\mathrm{O}}_2]}_a-{[{\mathrm{O}}_2]}_{\text{um}})+S_{{\mathrm{O}}_2,d},$$ (12)

$$\frac{\mathrm{d}({[{\mathrm{O}}_2]}_c{V}_c)}{\mathrm{d}t}=q_{c,a}({[{\mathrm{O}}_2]}_a-{[{\mathrm{O}}_2]}_c)-{\mathrm{O}}_{\text{met},c},$$ (13)

$$\frac{\mathrm{d}({[{\mathrm{O}}_2]}_{\text{nc}}{V}_{\text{nc}})}{\mathrm{d}t}=q_{\text{nc}}({[{\mathrm{O}}_2]}_a-{[{\mathrm{O}}_2]}_{\text{nc}})-{\mathrm{O}}_{\text{met},\text{nc}},$$ (14)

where the subscript ivs stands for the intervillious space. The feeding oxygen concentration in fetus is given by

$${[{\mathrm{O}}_2]}_a=\frac{{[{\mathrm{O}}_2]}_{\text{um}}{q}_{\text{um},a}+{[{\mathrm{O}}_2]}_{\text{nc}}{q}_{\text{nc}}+{[{\mathrm{O}}_2]}_c{q}_{c,a}}{q_a},$$ (15)

whereas [O₂]_m,a = 0.2 is fixed in the maternal part (Couto et al. 2002). S_O2,_d and O_met,i account for diffusion and metabolic uptake, respectively (Couto et al. 2002; van der Hout-van der Jagt et al. 2012). The oxygen diffusion in the placenta is determined by the oxygen partial pressure difference between the intervillous space and the umbilical cord (or umbilical microcirculation),

$$S_{{\mathrm{O}}_2,d}=D({\mathrm{P}}_{{\mathrm{O}}_2,\text{ivs}}-{\mathrm{P}}_{{\mathrm{O}}_2,\text{um}})$$ (16)

where P_O2 is the partial oxygen pressure and D is the mass transfer coefficient. Oxygen concentration is related to oxygen partial pressure by the following relation (subscripts um, c, nc, ivs are omitted)

$$[{\mathrm{O}}_2]=\frac{{\alpha }_b{\text{Hb}}_i}{1+c_{1,i}{({\mathrm{P}}_{{\mathrm{O}}_2}^3+c_{2,i}{\mathrm{P}}_{{\mathrm{O}}_2})}^{-1}}+{\beta }_d{\mathrm{P}}_{{\mathrm{O}}_2},$$ (17)

where constant α_b represents the maximum binding capacity of hemoglobin, Hb_i (i = f, m) is the hemoglobin concentration for fetus and mother, and constant β_d is the content of dissolved oxygen, and c_1,i and c_2,i (i = f,m) are scaling constants. The metabolic uptake in Eqs. 13 and 14 is constant when the oxygen supply is sufficient. When oxygen concentration drops below a threshold concentration, [O₂]_th, it is assumed to be a linear function of the oxygen concentration. Combining the two, we have

$$O_{\text{met}}=\{\begin{array}{ll}{\mathrm{O}}_{\text{met},0},\hfill & [{\mathrm{O}}_2]\ge {[{\mathrm{O}}_2]}_{\text{th}},\hfill \\ {\mathrm{O}}_{\text{met},0}+K_{\text{th}}([{\mathrm{O}}_2]-{[{\mathrm{O}}_2]}_{\text{th}}),\hfill & [{\mathrm{O}}_2]<{[{\mathrm{O}}_2]}_{\text{th}}\hfill \end{array}$$

for all fetal compartments (van der Hout-van der Jagt et al. 2012). In maternal circulation, we assume that oxygen supply is sufficient (Couto et al. 2002; van der Hout-van der Jagt et al. 2012).

As an indicator for asphyxia (due to prolonged UCO typically), we model the CO₂ distribution, using the equation for the law of mass conservation for CO₂, in each fetal compartment as follows

$$\frac{\mathrm{d}({[{\text{CO}}_2]}_{\text{um}}{V}_{\text{um}})}{\mathrm{d}t}=q_{\text{um},a}({[{\text{CO}}_2]}_a-{[{\text{CO}}_2]}_{\text{um}})+D_{{\text{CO}}_2}({\mathrm{P}}_{{\text{CO}}_2,\text{ivs}}-{\mathrm{P}}_{{\text{CO}}_2,\text{um}}),$$ (18)

$$\frac{\mathrm{d}({[{\text{CO}}_2]}_c{V}_c)}{\mathrm{d}t}=q_{c,a}({[{\text{CO}}_2]}_a-{[{\text{CO}}_2]}_c)+M_c,$$ (19)

$$\frac{\mathrm{d}({[{\text{CO}}_2]}_{\text{nc}}{V}_{\text{nc}})}{\mathrm{d}t}=q_{\text{nc}}({[{\text{CO}}_2]}_a-{[{\text{CO}}_2]}_{\text{nc}})+M_{\text{nc}}+M_{\text{pH}},$$ (20)

where [CO₂]_a is given by

$${[{\text{CO}}_2]}_a=\frac{{[{\text{CO}}_2]}_{\text{um}}{q}_{\text{um},a}+{[{\text{CO}}_2]}_{\text{nc}}{q}_{\text{nc}}+{[{\text{CO}}_2]}_c{q}_{c,a}}{q_a}.$$ (21)

D_CO2 is the diffusion coefficient, P_CO2 is the partial pressure of carbon dioxide, M_i is the production rate of [CO₂]_i and M_pH is given by

$$M_{\text{pH}}=0.1\frac{{\left([{\mathrm{H}}^{+}]-40\right)}^2}{1+{\left([{\mathrm{H}}^{+}]-40\right)}^2}.$$ (22)

We assume that CO₂ is cleared in the placenta by fixing P_CO2,ivs = 40 mmHg. In addition, we assume that the production of carbon dioxide is related to the metabolic rate of oxygen and M_c(nc) = K_M O_met,c(nc) (Khoo et al. 1991) with a constant K_M (taken to be 0.2 in this study). The partial pressure of carbon dioxide relates to the concentration linearly as Khoo et al. (1982)

$$[{\text{CO}}_2]=K_{{\text{CO}}_2}{\mathrm{P}}_{{\text{CO}}_2}+k_{{\text{CO}}_2},$$ (23)

where K_CO2 and k_CO2 are scaling constants.

To assess the acidity level (de Haan et al. 1997; Frasch et al. 2009b; Ross et al. 2013), lactate and pH values usually measured in fetal animal experiments are included in our model (Fig. 2). Following Cabrera et al. (1998) and D’Angelo and Papelier (2005), we consider pyruvate-, glucose- and lactate-related metabolic pathways in the fetal body or systemic compartment, in particular, anaerobic glycolysis, pyruvate reduction, gluconeogenesis, glycogen synthesis and breakdown, lactate oxidation, lactate buffering. The equations for glucose (GL), lactate (LA) and pyruvate (PY), from the literature (D’Angelo and Papelier 2005) which solves a coupling between cardiovascular response and metabolism for excises, are

$$\frac{\mathrm{d}V[\text{GL}]}{\mathrm{d}t}=q({[\text{GL}]}_a-[\text{GL}])+m{\varphi }_{\text{GY},b}\frac{\text{PS}}{\text{PS}+k_{\text{GY},b}}[\text{GY}]-{\varphi }_{GL,b}\frac{\text{PS}}{\text{PS}+k_{\text{GL},b}^{\text{PS}}}\frac{[\text{GL}]}{\text{RS}/k_{\text{GL},b}^{\text{RS}}+1}-{\varphi }_{GY,s}\frac{[\text{GL}]}{\text{PS}/k_{\text{GY},s}+1}$$ (24)

$$\begin{array}{l}\frac{\mathrm{d}V[\text{PY}]}{\mathrm{d}t}=q({[\text{PY}]}_a-[\text{PY}])+2{\varphi }_{GL,b}\frac{\text{PS}}{\text{PS}+k_{\text{GL},b}^{\text{PS}}}\frac{[\text{GL}]}{\text{RS}/k_{\text{GL},b}^{RS}+1}\\ -{\varphi }_{\text{PY},r}\frac{\text{RS}}{\text{RS}/k_{\text{PY},r}+1}[\text{PY}]-{\varphi }_{\text{PY},o}\frac{\text{RS}}{\text{RS}/k_{\text{PY},o}+1}[\text{PY}]\\ +{\varphi }_{LA}\frac{1}{\text{RS}/k_{\text{LA},o}+1}[\text{LA}]\end{array}$$ (25)

$$\frac{\mathrm{d}V[\text{LA}]}{\mathrm{d}t}=q({[\text{LA}]}_a-[\text{LA}])+{\varphi }_{\text{PY},r}\frac{\text{RS}}{\text{RS}/k_{\text{PY},r}+1}[\text{PY}]-{\varphi }_{\text{LA}}\frac{1}{RS/k_{\text{LA},o}+1}[\text{LA}],$$ (26)

where V is the compartment volume, whereas q is the corresponding flow rate (subscripts nc, c, um are omitted), the first term on the right-hand side of the equations models convective exchange, [*]_in is the arterial concentration given by Eq. 15, PS = [ADP]/[ATP] and RS = [NADH]/[NAD] are set to 0.13 and 0.11, respectively (Cabrera et al. 1998), [GY] is glycogen concentration, which is much greater than that of the others (Table 2 in Cabrera et al. 1998) and hence is treated as a constant in the current model, ϕ_i are the reaction rates and k_i are constants in compartment denoted by i. The subscripts are short names for different stoichiometry GY, b (GY → mGL), GY, s (mGL → GY), GL, b (GL → 2PY), LA, o (LA → PY) and PY, r (PY → LA).

Fig. 2.

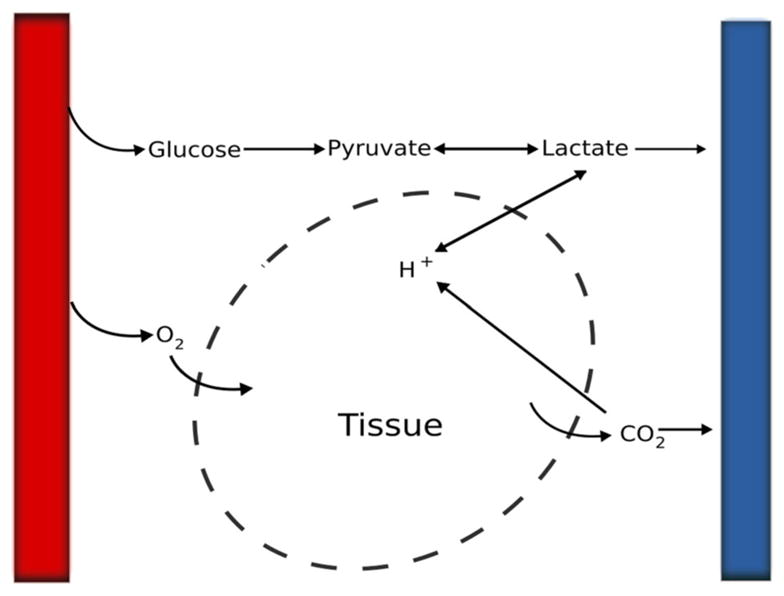
Illustration of the simplified metabolic process in certain compartment in the model. Left (right) column stands for artery (vein)

Close inspection reveals that the kinetic coefficients in front of the substrates are effectively (unknown) constants and we tune them to fit the experimental measurements. Using simplifying notation, we obtain

$$\frac{\mathrm{d}V[\text{GL}]}{\mathrm{d}t}=q({[\text{GL}]}_a-[\text{GL}])+K_1-K_2[\text{GL}],$$ (27)

$$\frac{\mathrm{d}V[\text{PY}]}{\mathrm{d}t}=q({[\text{PY}]}_a-[\text{PY}])+K_3[\text{GL}]-K_4[\text{PY}]+K_5[\text{LA}],$$ (28)

$$\frac{\mathrm{d}V[\text{LA}]}{\mathrm{d}t}=q({[\text{LA}]}_a-[\text{LA}])+K_6[\text{PY}]-K_5[\text{LA}],$$ (29)

where K_i are constants. Constant concentrations for GL, PY, LA are imposed in cerebral and umbilical cord compartments (Table 3). This needs to be modified when asphyxia is fully developed (Yan et al. 2009), which is beyond of the scope of the current paper.

Table 3.

Parameter values for metabolic model

Parameter	Value	Parameter	Value
αb (ml O2/g Hb)	1.34	βd (ml O2/ml blood/mmHg)	0.0031
Hbm (g Hb/ml blood)	12 × 104	Hbf (g Hb/ml blood)	17 × 104
c1,m (mmHg3)	23,400	c2,m (mmHg2)	150
c1,f (mmHg3)	10,400	c2,f (mmHg2)	150
[O2]a,n (ml O2/ml blood)	0.04	PCO2,n (mmHg)	44
PO2,0,c (mmHg)	7	[O2]th (ml O2/ml blood)	0.068
PO2,a,n (mmHg)	7.5	Kth (ml blood/s)	9.33
KCO2 (ml CO2/ml blood/mmHg)	0.244	kCO2 (ml CO2/ml blood)	0.007
DCO2 (ml CO2/s/mmHg)	0.1	D (ml O2/s/mmHg)	0.0283
[GL]a (mM)	1	[LA]a (mM)	0.8
[Py]a (mM)	0.12	[H+]a (nM)	40
K1 (mmol/s)	100	K2 (ml/s)	40
K3 (ml/s)	0.4	K4 (ml/s)	4
K5 (ml/s)	0.5	K6 (ml/s)	10
K7 (10−6 ml/s)	55	K8 (nmol/s)	10
K9 (nmol/s)	15	K10 (106 ml/s)	0.2

The effect of pH is not included in the lactate Eq. 29, which is modified by adding the production due to deprotonation of lactic acid,

$$\frac{\mathrm{d}V[\text{LA}]}{\mathrm{d}t}=q({[\text{LA}]}_a-[\text{LA}])+K_6[\text{PY}]-K_5[\text{LA}]+K_{10}[{\mathrm{H}}^{+}].$$ (30)

In addition, we add an equation for [H⁺] which takes into account two sources of acidity: lactate dehydrogenase and CO₂ accumulation. Under umbilical cord occlusion, experimental evidence shows significant waste accumulation (especially CO₂). We use the following equation in Orlowski et al. (2011)

$$\frac{\mathrm{d}V[{\mathrm{H}}^{+}]}{\mathrm{d}t}=q\left({[{\mathrm{H}}^{+}]}_a-[{\mathrm{H}}^{+}]\right)+K_7[\text{LA}]+K_8[{\text{CO}}_2]-K_9,$$ (31)

where K₇ and K₈ are coefficients for [H⁺] accumulation due to increased level of lactate and CO₂; K₉ accounts for the ATP consumption among other effects, which is assumed to be an effective constant that helps to restore normal [H⁺] level.

2.3 Effectors

Following Ursino (1998) and van der Hout-van der Jagt et al. (2013), there are a few effectors in the model. For autoregulation (van der Hout-van der Jagt et al. 2013) in the fetal brain, we use the following equation,

$$\frac{\mathrm{d}{R}_{c,a}}{\mathrm{d}t}=\frac{R_{c,a}^{\ast }-R_{c,a}}{{\tau }_{\text{Rc}}}$$ (32)

where

$$R_{c,a}^{\ast }=\frac{R_{c,a,min}+R_{c,a,max}exp\left(\frac{{[{\mathrm{O}}_2]}_a-{[{\mathrm{O}}_2]}_{a,n}}{k_c}\right)}{1+exp\left(\frac{{[{\mathrm{O}}_2]}_a-{[{\mathrm{O}}_2]}_{a,n}}{k_c}\right)}$$ (33)

where R_c,a,min = 0.1R_c,a,0 and R_c,a,max = R_c,a,0. Once oxygen is low, the reduced resistance will allow more flow to the brain. This acts in the opposite direction as the one in systemic circulation (Eq. 36).

The fetal heart contractility c_h (t) in Eq. 5 is regulated by sympathetic nervous control that targets mainly β-adrenergic receptors with a firing rate f_sβ (Sect. 2.4).

$$\mathrm{\Delta }c=G_{c}ln\left(\frac{f_{\mathrm{s}\beta }-f_{\mathrm{s},min}+f_{\mathrm{s},1}}{f_{\mathrm{s},1}}\right)$$ (34)

which is set to zero if f_sβ < f_s,min.

The venous compliance C_v and resistance R_nc (van der Hout-van der Jagt et al. 2013) are regulated by sympathetic nervous system that targets mainly α-adrenergic receptors with a firing rate f_sα,

$$\mathrm{\Delta }{C}_v=G_{v}ln\left(\frac{f_{\mathrm{s}\alpha }-f_{\mathrm{s},min}+f_{\mathrm{s},1}}{f_{\mathrm{s},1}}\right),$$ (35)

$$\mathrm{\Delta }{R}_{nc}=\frac{R_{\text{nc},min}+R_{\text{nc},max}exp\left(\frac{f_{\mathrm{s}\alpha }-f_{\mathrm{s}\alpha ,n}}{k_{R_{\text{nc}}}}\right)}{1+exp\left(\frac{f_{\mathrm{s}\alpha }-f_{\mathrm{s}\alpha ,n}}{k_{R_{\text{nc}}}}\right)}.$$ (36)

2.4 Afferent/Efferent Pathways

Changes in blood and oxygen partial pressures trigger nervous responses via baro- and chemoreceptors. Their effects on heart rate have been described (Ursino 1998; Liang and Liu 2006; van der Hout-van der Jagt et al. 2013), modified in the present work and incorporated in the model. In particular, the period of heart pumping motion T is given by T = T₀ + ΔT_s + ΔT_va, where T₀ = τ₀ + T_s,0 + T_va,0 with τ₀ an offset term, T_s/va,0 the baseline values of sympathetic/vagal contribution and ΔT_v, ΔT_s are determined by

$$\frac{\mathrm{d}\mathrm{\Delta }{T}_{\text{va}}(t)}{\mathrm{d}t}=\frac{1}{{\tau }_{T,\text{va}}}\left(-\mathrm{\Delta }{T}_{\text{va}}(t)+G_{T,\text{va}}{f}_{\text{va}}(t-D_{T,\text{va}})-T_{\text{va},0}\right),$$ (37)

$$\frac{\mathrm{d}\mathrm{\Delta }{T}_s(t)}{\mathrm{d}t}=\frac{1}{{\tau }_{T,s}}\left(-\mathrm{\Delta }{T}_s(t)+{\overline{G}}_{T,s}{f}_s(t-D_{T,s})+G_{T,s}^{\prime }\left(f_s-f_{\mathrm{s},0}\right)\right).$$ (38)

Here τ_T,va and τ_T,s are the respective time constant, G_T,va and Ḡ_T,s, $G_{T,s}^{\prime }$ the gains, D_T,va and D_T,s the delay of the vagal and sympathetic responses. In the results presented in this paper, they are set to zero. At equilibrium state, the second and third terms in the right-hand side of Eqs. 37 and 38 vanish, which leads to ΔT_va → 0 and ΔT_s → 0, so that the baseline period is recovered at T = T₀. Finally, f_va and f_s are given by

$$f_{\text{va}}=W_{\text{br},\text{va}}\frac{f_{\text{va},min}+f_{\text{va},max}exp\frac{f_{\text{br}}-f_{\text{br},n}}{k_v}}{1+exp\frac{f_{\text{br}}-f_{\text{br},n}}{k_v}}+W_{\text{cr},\text{va}}{f}_{\text{cr}}+f_{\text{hy}},$$ (39)

$$f_s=ln\left(\frac{f_{\mathrm{s}\beta }-f_{\mathrm{s},min}+f_{\mathrm{s},1}}{f_{\mathrm{s},1}}\right),$$ (40)

with

$$f_{\text{hy}}=\frac{f_{\text{hy},min}+f_{\text{hy},max}exp\frac{{\mathrm{P}}_{{\mathrm{O}}_2,\mathrm{c}}-{\mathrm{P}}_{{\mathrm{O}}_2,\mathrm{c},0}}{k_{\text{hy}}}}{1+exp\frac{{\mathrm{P}}_{{\mathrm{O}}_2,\mathrm{c}}-{\mathrm{P}}_{{\mathrm{O}}_2,\mathrm{c},0}}{k_{\text{hy}}}}-f_{\text{va},o},$$ (41)

$$f_{\mathrm{s}\alpha (s\beta )}=f_{\mathrm{s},\infty }+(f_{\mathrm{s},0}-f_{\mathrm{s},\infty })exp{k}_{\mathrm{s}}\left(-W_{\text{br},s\alpha (s\beta )}{f}_{\text{br}}+W_{\text{cr},s\alpha (s\beta )}{f}_{\text{cr}}-f_{\mathrm{s}\alpha (s\beta ),o}\right),$$ (42)

where f_br and f_cr are the afferent baro- and chemoreceptor firing rates, respectively, and f_sα(sβ),o is the hypoxia offset that creates a threshold for sympathetic response. In addition, f_s = 0 when f_sβ/sα < f_es,min, and f_s = f_s,max when f_sα(sβ) exceeds a threshold value f_s,max. Furthermore, the baro- and chemoreceptors afferent firing rates f_br and f_cr are governed by the following first-order ODE (van der Hout-van der Jagt et al. 2013)

$$\frac{\mathrm{d}{f}_{\text{br}}}{\mathrm{d}t}=\frac{f_{\text{br}}^{\ast }-f_{\text{br}}}{{\tau }_{\text{br}}},\frac{\mathrm{d}{f}_{\text{cr}}}{\mathrm{d}t}=\frac{f_{\text{cr}}^{\ast }-f_{\text{cr}}}{{\tau }_{\text{cr}}},\frac{\mathrm{d}{\overline{p}}_a}{\mathrm{d}t}=\frac{p_a-{\overline{p}}_a}{N_p}$$ (43)

where according to Magosso and Ursino (2001)

$$f_{\text{br}}^{\ast }=\frac{f_{br,\mathit{min}}+f_{\text{br},max}exp\frac{\overline{p}-p_n}{{\tau }_{\text{pr},\text{br}}}}{1+exp\frac{{\overline{p}}_a-p_n}{{\tau }_{\text{pr},\text{br}}}},$$ (44)

$$f_{\text{cr}}^{\ast }=\frac{f_{\text{cr},max}+f_{\text{cr},min}exp\frac{{\mathrm{P}}_{{\mathrm{O}}_2,a}-{\mathrm{P}}_{{\mathrm{O}}_2,\mathrm{n}}}{{\tau }_{\text{pr},\text{cr}}}}{1+exp\frac{{\mathrm{P}}_{{\mathrm{O}}_2,a}-{\mathrm{P}}_{{\mathrm{O}}_2,\mathrm{n}}}{{\tau }_{\text{pr},\text{cr}}}}\left(\overline{K}ln\left(\frac{{\mathrm{P}}_{{\text{CO}}_2,\text{nc}}}{{\mathrm{P}}_{{\text{CO}}_2,\text{nc},\mathrm{n}}}\right)+1\right),$$ (45)

$${\overline{p}}_a=\frac{1}{N_p}{\int }_0^t{p}_a(s)exp(-\psi (t-s))\mathrm{d}s,$$ (46)

where p̄_a is the mean arterial blood pressure (MABP) and f_br,max, f_br,min, f_cr,max, f_cr,min, K̄, p_n, P_CO2,n,nc, P_O2,n, τ_pr,br, τ_pr,cr, ψ are constants. The formula used in van der Hout-van der Jagt et al. (2013) is recovered when P_CO2,nc is in the normal range and f_cr rises when P_CO2, nc increases. Unless otherwise stated, K̄ = 1.

The normalization factor N_p is introduced to ensure that the correct mean arterial blood pressure is calculated (Olufsen et al. 2004),

$$N_p={\int }_0^{t}exp(-\psi (t-s))\mathrm{d}s=\frac{1-exp(-\psi t)}{\psi }.$$ (47)

The offset value f_sβ/sα,o in Eq. 42 is determined by

$$\frac{\mathrm{d}{f}_{\mathrm{s}\alpha (s\beta ),o}}{\mathrm{d}t}=\frac{f_{\mathrm{s}\alpha (\mathrm{s}\beta ),o}^{\ast }-f_{\mathrm{s}\alpha (\mathrm{s}\beta ),o}}{{\tau }_s}$$ (48)

where

$$f_{\mathrm{s}\alpha (\mathrm{s}\beta ),o}^{\ast }=\frac{f_{\mathrm{s}\alpha (\mathrm{s}\beta ),min}+f_{\mathrm{s}\alpha (\mathrm{s}\beta ),max}exp\left(\frac{{\mathrm{P}}_{{\mathrm{O}}_2,a}-{\mathrm{P}}_{{\mathrm{O}}_2,a,n}}{k_{\text{pr},s}}\right)}{1+exp\left(\frac{{\mathrm{P}}_{{\mathrm{O}}_2,a}-{\mathrm{P}}_{{\mathrm{O}}_2,a,n}}{k_{\text{pr},s}}\right)}.$$ (49)

Due to hypoxemia in fetal circulation, the vagal firing rate increases, hence decreasing FHR. The sympathetic response has the opposite effects (Frasch et al. 2009a, c).

To take into account the apparent mutual inhibition of sympathetic and vagal nerves, we model the sympathetic gain Ḡ_T,s as a sigmoidal function of vagal firing rate f_va,

$${\overline{G}}_{T,s}=\frac{\delta G_{T}exp\frac{f_{\text{va}}-f_{\text{va},n}}{{\tau }_{\text{gs}}}}{1+exp\frac{f_{\text{va}}-f_{\text{va},n}}{{\tau }_{\text{gs}}}},$$ (50)

which shows the sympathetic gain tends to the minimal value as the vagal firing rate increases due to the inhibition effect as mentioned. Similarly, we introduce the following for the vagal gain G_T,va

$$G_{T,\text{va}}=G_{T,\text{va},0}+\frac{G_{T,\text{va},min}exp\frac{f_{\mathrm{s}\beta }-f_{\mathrm{s}\beta ,n}}{{\tau }_{\text{gv}}}}{1+exp\frac{f_{\mathrm{s}\beta }-f_{\mathrm{s}\beta ,n}}{{\tau }_{\text{gv}}}},$$ (51)

where G_T,va,min = 0.1G_T,va,0. It was pointed out (Kubota et al. 1992a, b; Levy and Zieske 1969) that the gains may depend on pressure and other dynamic variables. For simplicity, they are chosen as constants in the current model. We assume that the sympathetic and vagal activities in system are mutually inhibitory and mediated via the chemoreceptors and baroreceptors (see Eqs. 50 and 51), which is consistent with physiological explanations (Westgate et al. 2007).

In summary, the above set of 30 ordinary differential equations form a coupled system. Due to the nonlinear nature of the equations, they are solved numerically using MATLAB solver ode15s and subroutines sens_sys and sens_ind, which are given in Breit (2004), for sensitivity analysis. Because of the stiffness of the system, ode15s is chosen over other solvers.

3 Results and Discussion

Two control parameters are used to measure UCO severity: 1) the ratio between the occlusion and the recovery durations and 2) the occlusion degree (partial or complete). As we show below, the effects of these parameters on FHR are significant.

3.1 Model Calibration: Baseline Values and Sensitivity Analysis

As in many cardiovascular models (Ursino 1998; Olufsen et al. 2004; van der Hout-van der Jagt et al. 2012), the parameter space is large. Most of the parameter values are obtained from the literature and the remaining ones are calibrated by comparing our model outputs with available experiments. For example, G_T,va,0 ~ 0.04 is taken instead of 0.09 used for the adult model (Ursino 1998; van der Hout-van der Jagt et al. 2012) to reflect the fact that the vagal control in fetus is not as mature. $G_{T,s}^{\prime }$ and δG_T are tuned to achieve a reasonable reduction in FHR for fetus. The values of adjusted parameters are given in Tables 1, 2 and 3.

Table 1.

Parameter values for cardiovascular model

Parameter	Value	Parameter	Value
ah (mmHg/ml2)	0.0003	bh (ml)	6.3041
ch (mmHg/ml)	0.9	ch,m (mmHg/ml)	1.5
dh,m (mmHg)	1.1264	dh (mmHg)	5
ψ (1/s)	0.05	Hm (1/s)	0.9
n	5.9717	m	4.0917
pmax (mmHg)	1.2028	pmin (mmHg)	1.0994
tmax (s)	0.2653	tmin (s)	0.0801
η	19.0681	ϕ (1/s)	1.3296
θ (1/s)	1.1364	ν	9.1682
Cm,a (ml/mmHg)	5.6	Cm,v (mmHg s/ml)	112
Ca (ml/mmHg)	0.8	Cv (mmHg s/ml)	3.5
Cum (ml/mmHg)	1.1	Cc (mmHg s/ml)	0.057
Rm,a (mmHg s/ml)	0.05	Rm,v (mmHg s/ml)	0.025
Rivs (mmHg s/ml)	3.38	Rutv (mmHg s/ml)	0.675
Ra (mmHg s/ml)	0.045	Rv (mmHg s/ml)	0.27
Rum,a (mmHg s/ml)	5.236	Rum,v (mmHg s/ml)	0.015
Rm (mmHg s/ml)	0.45	Rnc,0 (mmHg s/ml)	1.5
Rc,v (mmHg s/ml)	0.015	Rc,a,0 (mmHg s/ml)	10.485

Table 2.

Parameter values for regulation model

Parameter	Value	Parameter	Value
Rnc,min (mmHg s/ml)	0	Rnc,max (mmHg s/ml)	11.25
Rc,min (mmHg s/ml)	10.485	Rc,max (mmHg s/ml)	1.0485
T0 (s)	0.406	Tva,0 (s)	0.373
Ts,0 (s)	−0.177	τ0 (s)	0.21
fbr,min (1/s)	2.52	fbr,max (1/s)	47.78
fcr,min (1/s)	1.16	fcr,max (1/s)	17.07
fhy,min (1/s)	0	fhy,max (1/s)	2.5
fva,min (1/s)	3.2	fva,max (1/s)	6.3
fs,min (1/s)	2.66	fs,max (1/s)	60
fs,0 (1/s)	16.11	fs,∞ (1/s)	2.1
fcr,n (1/s)	11	fbr,n (1/s)	25
fs,1 (1/s)	1	fsα,n (1/s)	9
fva,n (1/s)	10	fsβ,n (1/s)	5.5
fva,o (1/s)	−0.68	τpr,br (mmHg)	4.09
τpr,cr (mmHg)	7.24	τRc (mmHg s/ml)	10
τgs (1/s)	0.05	τgv (1/s)	0.04
τbr(cr) (s)	2	τT,v (s)	1.5
τT,s (s)	6	τs (s)	30
kRnc (1/s)	1.44	kpr,s (mmHg)	2
kc	0.018	khy (mmHg)	1.7
kbr (1/s)	4.09	kcr (1/s)	7.24
ks (1/s)	0.0675	kv (1/s)	7.06
Wcr,va	0.2	Wbr,va	1
Wbr,sβ	1	Wcr,sβ	1
Wbr,sα	1	Wcr,sα	1
GT,s (s2)	−0.13	GT,va,0 (s2)	0.04
$G_{T,s}^{\prime }({\mathrm{s}}^2)$	0.046	δGT (s2)	0.1235
Gc (mmHg s/ml)	0.27	Gva (mmHg s/ml)	−0.17

3.1.1 Baseline Case

Several important and clinically relevant quantities are listed in Table 4, which is the baseline case used for model calibration. The predicted values from our model are consistent with experimental data. At the onset of a complete UCO, the flow rate in umbilical cord q_fs,a = q_fs,va = 0 and O₂ exchange S_O2,d = 0 in the corresponding transport equations (Sect. 2). The flow is stopped in the umbilical cord compartment and O₂ and CO₂ cannot be delivered continuously between placental and fetal circulations. Mild and moderate UCOs represent partial occlusions, where the passed flow is set to be 50 and 25 % of the normal case, respectively (Ross et al. 2013). The severe case is referred to as the complete occlusion regarding the degree of occluder.

Table 4.

Clinically relevant quantities for the baseline case in feuts

Physical quantity	Reference/target value	Model output
FHR (bpm)	135 (van der Hout-van der Jagt et al. 2012), 163 ± 5 (Frasch et al. 2011)	148
Mean fetal arterial p̄a (mmHg)	55 ± 5 (Bennet et al. 2005), 46 ± 2 (Hunter et al. 2003)	52.5
Umbilical PO2 (mmHg)	18 (van der Hout-van der Jagt et al. 2012)	17.6
Cerebral PO2 (mmHg)	10 ± 1 (Bishai et al. 2003)	12.3
Systemic PCO2 (mmHg)	45.5 ± 2 (Bennet et al. 2005) 52.7 ± 0.9 (Frasch et al. 2009c, 2011)	47.5
Intervillous space PO2 (mmHg)	23.3 (van der Hout-van der Jagt et al. 2012; Quilligan et al. 1960)	23.2
Systemic lactate (mM)	1.6 ± 0.2 (Frasch et al. 2009c)	2.1
Systemic pH	7.36 ± 0.1 (Frasch et al. 2009c), 7.4 ± 0.01 (Bennet et al. 2005)	7.25

From an experimental point of view, FHR and MABP are two important quantities often used in modeling and monitoring fetal acidemia, with FHR being the single quantity available clinically. One important feature of FHR in experiments with repetitive UCOs is its significant drop during occlusions. In our model, it is assumed that the sympathetic and vagal activities are mutually inhibitory and mediated via baro- and chemoreceptors (Eqs. 50, 51) (Westgate et al. 2007). FHR does not change markedly when these mechanisms are blocked (van der Hout-van der Jagt et al. 2013).

FHR overshoot and MABP decline are determined by systemic vascular resistance, myocardial contractility and venous compliance under the central nervous control as proposed in the literature (van der Hout-van der Jagt et al. 2013). We tune the parameters G_c and G_va in Eqs. 34 and 35 for the myocardial contractility and venous compliance, respectively, to achieve FHR overshoot and MABP decline comparable to experimental data. In most cases, sufficient control is achieved with G_va = 0; namely, the venous compliance is chosen as a constant (Olufsen et al. 2004). However, for 1:5 UCO, a nonzero G_va is used to reproduce experimental data (Westgate et al. 1999, 2001).

3.1.2 Sensitivity Analysis

We carry out a local sensitivity analysis on model parameters according to Ellwein et al. (2008), using MATLAB subroutines, sens_sysand sens_ind (Breit 2004).

Suppose the system of equations can be written as

$$\frac{\mathrm{d}\mathit{X}}{\mathrm{d}t}=F(\mathit{X},t,\mathit{p}),$$ (52)

where X denotes the state variables and p = [p₁, p₂, … p_n] stands for the parameters. Then the relative sensitivity matrix is defined as

$$S_{ij}{(t,\mathit{p})\mid }_{\mathit{p}={\mathit{p}}_0}=\frac{\partial {\mathit{X}}_i(t,p)}{\partial p_j}{\frac{p_j}{X_i(t,p)}\mid }_{p=p_0},p_j,X_i\ne 0.$$ (53)

We compute a maximum relative sensitivity

$${\mathit{S}}_j=\underset{i}{max}{\left(\underset{t}{max}{S}_{ij}(t,p)\right)\mid }_{\mathit{p}={\mathit{p}}_0}.$$ (54)

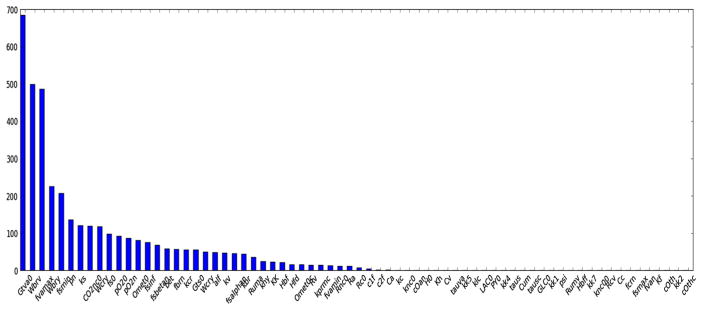
We conduct simulations over a period of 500 s without occlusion during which data were recorded. A representative ranking of parameter sensitivity (Fig. 3) illustrates the distribution of most to least sensitive parameters for a numerical test with 70 selected parameters. Unique identification of a full set of parameters appears to be time-consuming and difficult (Ellwein et al. 2008). Some parameters appearing in the regulation model are most sensitive. Many kinetic coefficients appear to be less sensitive (Gui et al. 2015Table 5 with their effects.

Fig. 3.

Results of sensitivity for 70 selected parameters used in the model. The vertical axis is calculated based on Eq. 54

Table 5.

Descriptions of the top 10 most sensitive parameters in the model in decreasing order

Parameter	Role	Effect
GT,va,0	Vagal gain	Increase the contribution to heart period by vagal activity
Wbr,va	Weight factor in fva in (39)	Increase the contribution due to baroreflex in vagal firing rate
fva,max	Maximum in sigmoid curve due to baroreflex	Increase fva in (39)
Wbr,sβ	Factor in front of fbr in (42)	Decrease fsβ
fs,min	Threshold in (40)	Increase the inactive range fs
Pn	Threshold to trigger baroreceptor in (44)	Reduce the time to obtain the FHR overshoot
ks	Factor in the exponent of (42)	Increase the steepness of sigmoid curve in (42)
Wcr,va	Weight factor in front of fcr in (39)	Increase fva
fs,0	Factor in (42)	Increase fsα(sβ)
PO2,c,0	Threshold to trigger chemoreceptor in (41)	Promote the chemoreflex

Our simulation approach differs from that of Ellwein et al. (2008), in which high-quality data were available. In that case, an optimization procedure is used to fit model output to experimental data. The sensitivity analysis further helps to reduce the computational cost as optimizing the most sensitive parameters suffices to obtain robust results. Unfortunately, we do not have high-quality experimental data as in Olufsen et al. (2004) at this stage. Our sensitivity analysis can only point out the most important controlling parameters that can guide potential future experiments.

3.2 Cardiovascular Dynamics: FHR and MABP Behavior

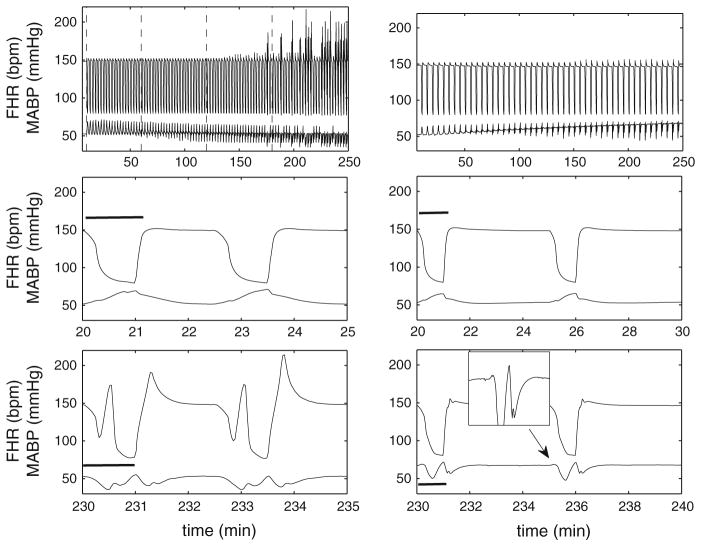
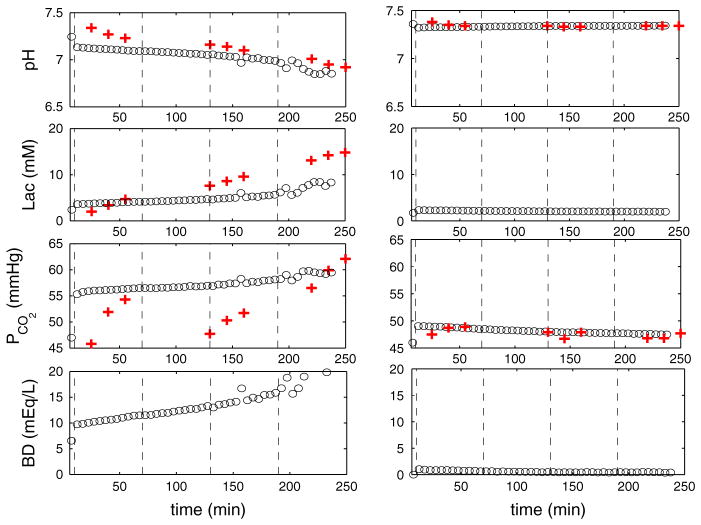
We studied the 1-min occlusion scenario, a clinically relevant case. The recovery time for 1-min complete occlusion, that is, the UCO frequency, influences the system behavior significantly. Based on our in silico experiments, for 1:2.5 UCO, FHR overshoot appears after about two and half hours with developing acidosis, as demonstrated in vivo (Westgate et al. 1999, 2001; Bennet et al. 2005). In contrast, 1:5 UCO scenario does not show any significant FHR overshoots and acidosis, as shown in the literature (Westgate et al. 2001). The numerical results displayed in Fig. 4 show the typical time variations of FHR and MABP at the early and late stages of occlusion, respectively. For 1:2.5 UCO, FHR deceleration appears once the occlusion begins. The pronounced FHR overshoot occurs only after a delay of approximately 3 h, in agreement with experiments (Westgate et al. 2001). This is accompanied by an eventual decline in MABP after approximately 2 h. At the early stage of the occlusions, MABP rises as soon as the occlusion starts (de Haan et al. 1997; Bennet et al. 2005). The inset in the bottom panel of Fig. 4 (for 1:5 UCO) shows that MABP rises during each occlusion period, even after numerous repetitive occlusions, as expected, but this initial rise tends to disappear in 1:2.5 UCO (left bottom panel). This is again in agreement with experiments (Frasch et al. 2011), as hypotension is expected when pH drops below 7.2. The difference in 1:5 and 1:2.5 UCOs indicates that with sufficient time for recovery, the regulation of effectors is able to maintain the blood pressure level and avoid instability. The detailed mechanism is still unknown and in the real situation, the regulatory functions represented by Eqs. 34 and 35 may depend on time-dependent or memory-related factors. Overall, the results in Fig. 4 demonstrate a reasonable agreement between experimental and numerical data. We will compute the correlation of FHR, MABP and acidosis in Sect. 3.4, as well as the output of the metabolic model.

Fig. 4.

Numerical results of FHR and MABP for 1:2.5 and 1:5 UCO. Numerical results for 4 h of occlusions with 1:2.5 UCO (left) and 1:5 UCO (right). G_c = 0.27 and G_va = −0.67 are used in simulation with 1:5 UCO. The dashed lines in the upper left panel divide the time periods into four one-hour windows. The first dashed line marks the beginning of the occlusions. The middle row displays a zoom of 5- (left) and 10-min (right) windows for each case at the beginning of the occlusion, and the bottom row 5- (left) and 10-min (right) windows near the end of occlusions. The black bar indicates the occlusion duration. The inset of the right bottom panel shows that MABP rises slightly at the beginning of each occlusion and then declines

In addition, intermediate rise occurs typically in FHR and MABP in each occlusion for 1:2.5 UCO, when the FHR overshoot is pronounced. Similar intermediate rise was reported in Westgate et al. (1999), where in the UCO 1:2.5 group, FHR initially recovers after the occlusion, but rapidly falls again before returning to the baseline value eventually. In our case, the trend is similar, but it appears earlier than experiments, with a relatively larger magnitude. We suspect this is caused by some system delay factor. Eqs. 37 and 38 contain delay variables D_T,va and D_T,s. These are set to zero here because: 1. the delay model in the literature was developed for adults and the correct parameter values are unknown for fetuses; 2. computational cost is much higher for a delayed differential equation system for 4-h simulations than a few minutes as in Olufsen et al. (2004). In addition, this transient growth due to delay does not seem to affect the general feature of our model outcome including the metabolic dynamics (reported below).

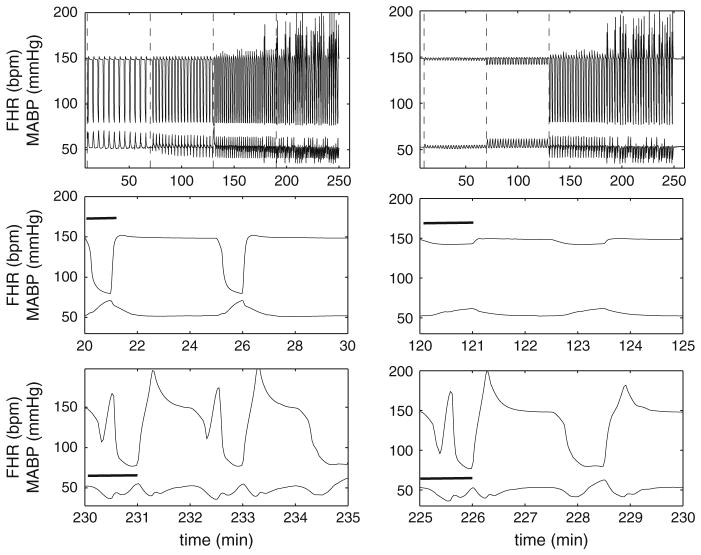
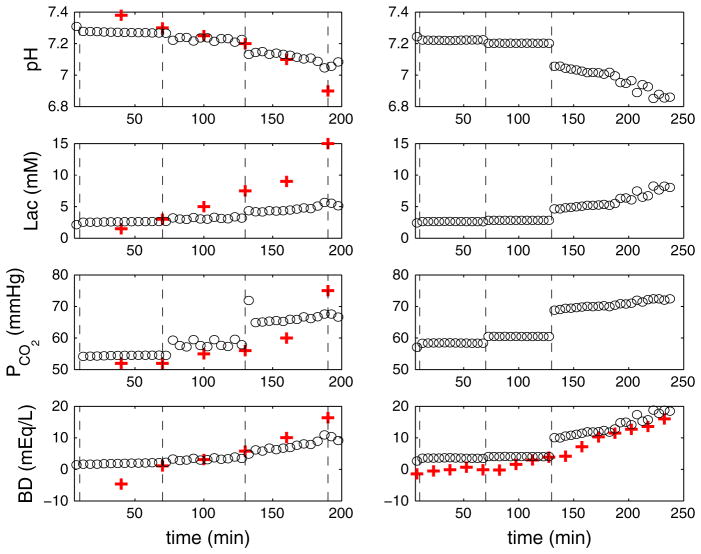
Figure 5 displays the numerical results of FHR and MABP for variable UCOs. Complete UCO with varying frequency was motivated by experiments carried out in Frasch et al. (2009b). The FHR overshoot occurs only after a delay of more than 2 h for the 1:2 UCOs, and MABP declines from the second hour for 1:3 UCOs. This is consistent with Fig. 4, in that relatively small frequency UCOs promote the MABP decline and FHR overshoot. Constant frequency UCOs with varying degrees mimic experiments in Frasch et al. (2009c). Mild occlusion has little effect, but moderate occlusion decreases FHR (~10 mmHg) to a lesser extent to complete UCOs (~70 mmHg). As in Frasch et al. (2009c), after 2 h of severe UCOs, pH drops below 7.0. Therefore, the FHR overshoot instability may be correlated with the worsening acidemia.

Fig. 5.

Numerical results of FHR and MABP for variable UCO. Left panel Complete UCO with varying occlusion frequency (1:5 UCO for the first, 1:3 for second and 1:2 for the third and fourth hours). Right panel Constant frequency UCOs with varying occlusion degree (mild occlusion during the first, moderate during the second and severe during the third and fourth hours). Dashed lines are inserted to divide the periods into four windows, each representing 1 h. The left dashed line marks the beginning of occlusions. The middle row represents 5-min windows at the beginning of the occlusion, and the bottom row 5-min windows near the end of occlusions. The black bar indicates the occlusion duration

3.3 Metabolic Dynamics

To assess the fetal acidemia, a simplified metabolic model is coupled with the cardiovascular model to evaluate pH as well as BD defined by Eq. 55 (see also Frasch et al. 2009b)

$$\text{BD}=-\left(0.02786{\mathrm{P}}_{{\text{CO}}_2}{10}^{\text{pH}-6.1}+13.77\text{pH}-124.58\right).$$ (55)

In particular, we computed the variations of lactate, [H⁺] and P_CO2 in the systemic compartment to compare with the experimental data.

Figure 6 shows several experimentally measurable quantities over 4-h occlusions. Agreement is shown when comparing with the data extracted from Bennet et al. (2005). Corresponding to the FHR overshoot instability for 1:2.5 UCO in Fig. 4, we find that pH drops below 7.00 and lactate accumulates beyond 10 mM. On the other hand, pH remains in the normal range for 1:5 UCOs, even after four hours of repeated occlusions (Westgate et al. 2001; Bennet et al. 2005). pH, lactate and P_CO2 remain close to baseline values. The results depicted in Fig. 7 for variable UCOs captured the experimental data trend. Relatively low-frequency UCOs and completely occluded UCOs have greater influence than those with higher frequency or partially occluded UCOs. Fetal acidosis occurs for severe UCOs, indicated by the BD values and FHR overshoot instability. In an attempt to quantify the relationship of these variables, we compute the correlations between relevant quantities in Sect. 3.4.

Fig. 6.

(Color figure online) Numerical results of pH, lactate, P_CO2 and BD for 1:2.5 and 1:5 UCO. Time variations of pH, lactate, P_CO2 in the systemic compartment and BD for 1:2.5 UCOs (left) and 1:5 UCO (right). The circle symbol represents the mean values over 5 min after occlusion begins. The plus symbol represents experimental data (Table 1 in Bennet et al. 2005)

Fig. 7.

(Color online) Numerical results of pH, lactate, P_CO2 and BD for variable UCOs. Time variations of pH, lactate, P_CO2 and BD in the systemic compartment for complete UCO with varying frequency (left column 1:5 UCO for the first, 1:3 for second and 1:2 for the third and fourth hours) and UCO of varying degree with constant frequency (right column mild occlusion during the first, moderate during the second and severe during the third and fourth hours). In the simulations displayed by the left column, K₇ = 35 × 10⁻⁶ s⁻¹ in Eq. 31 and K₆ = 5 s⁻¹ are chosen to match with the experimental pH variation; k_CO2 = 0.008 in Eq. 23 is chosen to match the baseline value of P_CO2 = 52.7 ± 0.9 mmHg in the experiments (Frasch et al. 2009b). The remaining parameters are given in Tables 1, 2 and 3

3.4 Statistical Analysis

We begin this section by computing a contingency table for each case discussed earlier. In order to make a direct comparison with experimental data, we also present some analysis on RMSSD, an index of vagal modulation of heart rate variability.

We examined correlations between acidemia quantified by BD and lactate on one hand and FHR and MABP on the other. Due to the cyclical nature and time dependency, classical Pearson correlation is not applicable to the data considered here. Therefore, we discretize the original signal into binary time sequences with 1 indicating the occurrence of an anomaly and 0 otherwise. An anomaly is defined as an event when an observation occurs outside an estimated confidence interval of long-term average. We use the mean μ̃ and standard deviation σ̃ to set a threshold value, μ̃ ± 2σ̃, in order to sort out the relevant quantities. For example, when the FHR (or BD or lactate) is larger than the upper bound threshold value μ̃ + 2σ̃, these quantities are set to 1, otherwise to zero. Similarly, when MABP is smaller than the lower bound of the threshold value μ̃ − 2σ̃, the MABP is set to 1, otherwise to zero. Contingency tables are then constructed for each pair based on the simultaneous occurrence of 1s and 0s.

For 1:2.5 UCOs, representative tables are constructed by taking the last two hours of simulation data, given in Table 6. The counts in each cell record the total number of occurrence for one combination between two discretized time sequences. For example, the first cell in each table records the total numbers of normal occurrence in both time series.

Table 6.

Contingency tables for 1:2.5 UCO

	Y = 0	Y = 1	Y = 0	Y = 1	Y = 0	Y = 1
X = 0	3303	266	3167	251	3204	31
X = 1	4	27	140	42	103	262

X stands for the binary series for FHR, MABP and lactate from left to right, whereas Y stands for BD

To search possible correlations among FHR, MABP, lactate and BD, two statistical tests are carried out. The first is the traditional Chi-square test, and the second is on the odds ratio derived from each contingency table. Both tests reject the hypothesis that these variables are independent with very small p values (p < 0.0001). Therefore, we conclude that the anomalies in these sequences are indeed correlated with each other. The same conclusion can be drawn for UCOs with varying frequencies (Table 7). These findings are consistent with our results in Sects. 3.2 and 3.3, as FHR overshoot, MABP decline and lactate level increase becomes significant when large BD value appears near the end of the occlusions.

Table 7.

Contingency tables for UCO with various frequencies

	Y = 0	Y = 1	Y = 0	Y = 1	Y = 0	Y = 1
X = 0	3250	324	3137	304	3151	74
X = 1	4	22	117	42	103	272

X stands for the binary series for FHR, MABP and lactate from left to right, whereas Y stands for BD

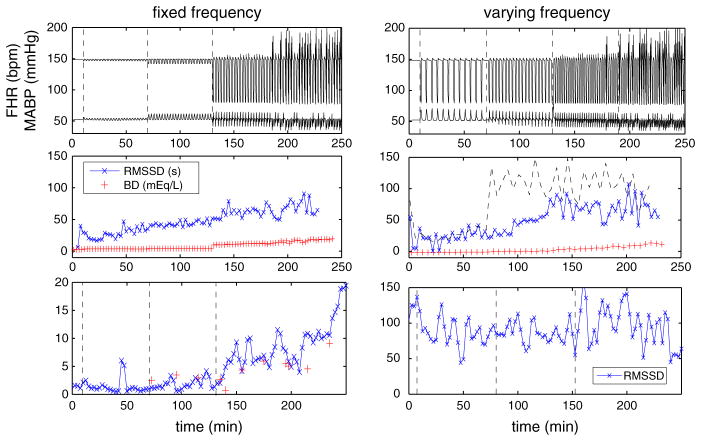
However, our results from Table 8 for UCOs with variable occlusion degrees suggest that contingency tables alone may not be sufficient to reveal the subtle relationship among FHR, MABP and BD. Following Frasch et al. (2009a, c), Durosier et al. (2014) via Eq. 56, we compute RMSSD based on our FHR output

$$\text{RMSSD}=\sqrt{\frac{1}{N-1}\left({\sum }_i{D}_i\right)},$$ (56)

where D_i = |P_i+1 − P_i|² with P_i the period between two maximum peaks and N is the number of intervals within a certain window. For the case in the left column of Fig. 8, where the frequency is varying, the computed RMSSD qualitatively captures the trend of experimental data, which is displayed in the bottom panel (the discrepancy in magnitude is due to sampling frequency). As the occlusion proceed, RMSSD increases monotonically. The contingency tables do not exhibit significant correlation for this case. However, based on our pH and BD results, we obtain significant increase in RMSSD when acidosis occurs, compared to the baseline values.

Table 8.

Contingency tables for UCO with various degrees

	Y = 0	Y = 1	Y = 0	Y = 1	Y = 0	Y = 1
X = 0	3220	376	3135	372	3118	92
X = 1	2	2	87	6	104	286

X stands for the binary series for FHR, MABP and lactate from left to right, whereas Y stands for BD

Fig. 8.

(Color figure online) Computed RMSSD with a sampling frequency of 4 Hz and BD for UCOs with varying occlusion degrees (left) and varying frequencies (right). Patterns of FHR (top), RMSSD and BD (middle), and the corresponding representative experimental results (Gold et al. 2015; Wang et al. 2014) (bottom). In the middle row, RMSSD is computed using 5-min windows for the left column. For the right column, RMSSD is computed using both 3- (cross-symbol) and 5-min (dashed line) windows

In contrast, RMSSD is overestimated for moderate occluded UCOs as soon as occlusion occurs (middle right panel using 5-min window as indicated by the dashed line), whereas no obvious increase is observed afterward. This is similar to a representative set of experimental data (Wang et al. 2014) (bottom right panel).

Interestingly, if we reduce the window size, the computed RMSSD evolves very differently. For example, RMSSD using a 3-min window (cross-symbols, middle right panel of Fig. 8) gradually increases as UCOs proceed and acidosis develops. This suggests that, in addition to the importance of sampling frequency (Durosier et al. 2014), a proper window size is also important.

4 Concluding Remarks

We have investigated the cardiovascular and metabolic responses to UCOs in a fetal sheep circulation system using a mathematical model. Our model comprises a cardiovascular circuit, a simplified metabolic model, and neural control of blood pressure and oxygen content by baro- and chemoreceptors (Ursino 1998; van der Hout-van der Jagt et al. 2012, 2013). Waste accumulation in the systemic compartment, such as CO₂ and lactate, is solved simultaneously with the cardiovascular response.

Our mathematical model produces the pattern observed in animal experiments, including FHR decrease and overshoot, MABP and pH decline, and increased levels of lactate and CO₂. In particular, the development of the cardiovascular and metabolic responses in our model are the result of sufficiently long-lasting repetitive occlusions. In other words, acidosis depends on the total duration of occlusion rather than on an individual event, as in de Haan et al. (1997). In addition, the FHR decrease, FHR overshoot and MABP response evolve accordingly to observations obtained using various experimental scenarios. In particular, our results from 1:5 and 1:2.5 UCO demonstrate the possibility that properly functioning effectors (cardiac contractility, systemic resistance and venous compliance) are able to main the blood pressure level and avoid instabilities in FHR. Our simplified metabolic model reproduces measured changes in pH, lactate and glucose. Although expected correlation between FHR overshoot, MABP decline and acidosis (quantified by BD) can be obtained when the occlusion is complete, our results suggest that the correlation analysis may fail when the UCO degree varies significantly. In that case, we show RMSSD is able to qualitatively predict acidemia.

The choice of window size is important in computing RMSSD when UCO frequency varies. Uterine contractions during labor vary in frequency and degree. Therefore, the usual choice of fixed window size may affect the results obtained in Durosier et al. (2014), in addition to the sampling frequency. A proper combination of FHR monitoring and RMSSD computation may then be used to detect acidemia.

One limitation of our model is that, as other mathematical biology models in the literature, the parameter space is large, despite our effort to keep the model simple. Although sensitivity analysis has been carried out, physiological parameters are difficulty to estimate accurately. We plan to use statistical modeling to control the uncertainty in parameters in future work (Ramsay et al. 2007). Another limitation pertains to the simplified metabolic process. A more detailed model will potentially improve predictions of impaired nutrient supply (Cloutier et al. 2009). The transport equations are used with relatively simple kinetic reaction terms involving only O₂, CO₂, pyruvate, lactate, glucose and [H⁺] in the systemic compartment. Nevertheless, more experimental data will be needed to properly model the kinetics and regulation.

Abbreviations

FHR

Fetal heart rate

MABP

Mean arterial blood pressure

UCO

Umbilical cord occlusions

BD

Base deficit

RMSSD

Root-mean-square of the successive differences

List of Symbols

a_h

Coefficient related to ventricular elastance during relaxation (mmHg/ml²)

α_b

Maximum binding capacity of hemoglobin (ml O₂/g Hb)

b

Parameter related to ventricular volume for zero diastolic pressure (ml)

β_d

Scaling factor on dissolved oxygen (1/mmHg)

β_h (H)

Time for the onset of ventricular relaxation (s)

η

Parameter controlling the steepness of the relation for heart pressure

θ

Median value of time for peak pressure in heart model (1/s)

ϕ

Median value of heart pressure in heart model (1/s)

ψ

Scaling factor in mean arterial pressure (1/s)

[CO₂]_i

Carbon dioxide concentration in compartment i = nc, c, um (ml CO₂/ml blood)

[CO₂]_a

Feeding Carbon dioxide concentration in fetus (ml CO₂/ml blood)

c_f, c_m

Heart contractility for fetus/mother (mmHg/ml)

c_1,m, c_1,f

Scaling constant in the relation between Oxygen content and its partial pressure for mother and fetus (mmHg³)

c_2,m, c_2,f

Scaling constant in the relation between Oxygen content and its partial pressure for mother and fetus (mmHg²)

C_i

Compliance in compartment i = nc, c, um, ut (ml/mmHg)

d_f, d_m

Parameter related to the volume-dependent and volume-independent components of the developed pressure (mmHg)

δG_T

Scaling factor for sympathetic gain (s²)

D

Mass transfer coefficient in Oxygen model (ml O₂/s/mmHg)

D_CO2

Mass transfer coefficient in Carbon dioxide model (ml CO₂/s/mmHg)

ΔC_v

Effector in venous compliance (ml/mmHg)

Δc

Effector in heart contractility (mmHg/ml)

f_br, f_cr

Afferent firing rate via stimulation of baro/chemoreceptor (1/s)

f_i,o

Offset values that create a threshold for vagal or sympathetic response i = va, sβ, sα (1/s)

f_i,min, f_i,max

Control constants in sigmoid functions i = s, va, hy, br, cr (1/s)

f_i,n

A normal value for corresponding afferent or efferent firing rate i = br, cr, va, sβ, sα (1/s)

f_s,0, f_s,∞

Constants in sympathetic firing rate function (1/s)

f_sβ, f_sα

Efferent α- and β- sympathetic firing rate (1/s)

f_s,1

Control parameter in sympathetic firing rate function (1/s)

f_va

Efferent vagal firing rate (1/s)

G_i

Gain constants i = T_va, T_s (s²)

G_c, G_va

Constants in effectors (mmHg s/ml)

[GL]_a

Arterial glucose concentration (mM)

[GL]_i

Glucose concentration in compartment i = nc, c, um (mM)

g(t)

Activation function in heart model

H (FHR)

Heart rate (1/s)

[H⁺]_a

Arterial proton concentration (nM)

[H⁺]_i

Proton concentration in compartment i = nc, c, um (nM)

Hb_f, Hb_m

Hemoglobin concentration in fetus or mother (g Hb/ml blood)

K_f

Constant in Oxygen metabolic model (ml blood/s)

K₁

Kinetic constant (mmol/s)

K_i

Kinetic constant i = 2, 3, 4, 5, 6 (ml/s)

K₇

Kinetic constant (10⁻⁶ ml/s)

K₈, K₉

Kinetic constant (nmol/s)

K₁₀

Kinetic constant (10⁶ ml/s)

K_CO2

Scaling constants (ml CO₂/ml blood/mmHg)

k_CO2

Scaling constants ml (CO₂/ml blood)

k_c

Control constant

k_hy, k_pr,s

Control constant (mmHg)

k_i

Constant i = R_nc, br, cr, s, va (1/s)

[LA]_a

Arterial lactate concentration (mM)

[LA]_i

Lactate concentration in compartment i = nc, c, um (mM)

M_i

Production rate of [CO₂]_i with i = nc, c, um (ml/s)

M_pH

Production rate due to [H⁺] accumulation (ml/s)

N_p

Normalization factor (s)

ν

Parameter related to steepness of the time for peak pressure in heart model

m, n

Parameters related to the onset time of ventricular relaxation in heart model

[O₂]_th

Threshold value to control Oxygen metabolic uptake (ml O₂/ml blood)

[O₂]_a, [O₂]_m,a

Feeding Oxygen concentration in fetus and mother (ml O₂/ml blood)

[O₂]_a,n

A normal value to control the sigmoid function in systemic resistance (ml O₂/ml blood)

[O₂]_i

Oxygen concentration in compartment i = nc, c, um, ivs (ml O₂/ml blood)

O_met,i

Metabolic Oxygen uptake in compartment i = nc, c (ml O₂/s)

p_min, p_max

Control constants in heart model (mmHg)

p_i

Blood pressure in compartment i = nc, c, um, h, ut, ivs (mmHg)

p̄_a (MABP)

Mean arterial blood pressure (mmHg)

P_O2,_i

Oxygen partial pressure in compartment i = nc, c, um, ivs (mmHg)

P_CO2,_i

Carbon dioxide partial pressure in compartment i = nc, c, um (mmHg)

P_CO2,nc, n

A normal value for Carbon dioxide partial pressure in systemic compartment (mmHg)

P_O2, _c,0

Threshold value for cerebral Oxygen partial pressure to control the sigmoid function in firing rate function f_hy (mmHg)

[PY]_a

Arterial pyruvate concentration (mM)

[PY]_i

Pyruvate concentration in compartment i = nc, c, um (mM)

q_i,a

Arterial flow rate into compartment i = nc, c, um (ml/s)

q_i,v

Venous flow rate out of compartment i = nc, c, um (ml/s)

q_in, q_out

Flow rate in/out of corresponding compartment by summing over flow rate from local branches (ml/s)

R_i

Resistance in compartment i = nc, c, um, ut, ivs, m (mmHg s/ml)

R_c,a,0, R_cn,0

Baseline values for cerebral and systemic resistance (mmHg s/ml)

R_c,min, R_c,max

Constants in cerebral autoregulation model (mmHg s/ml)

R_nc,min, R_nc,max

Constants in systemic resistance model (mmHg s/ml)

ΔR_nc

Effector in systemic resistance (mmHg s/ml)

S_{i j}

Relative sensitivity matrix

S_[O2],_d

Oxygen diffusion (ml O₂/s)

S_P[O2]

Scaling function to relate Oxygen content and its partial pressure

s_mv, s_av

Indicator function of mitral/aortic valve

t_p

Peak time (s)

t_min, t_max

Control constants in heart model (s)

T₀

Base line value for heart period (s)

T_v,0, T_s,0

Contributions from vagal and sympathetic activities on the base heart period (s)

τ_i

Control constant i = gs, gv (1/s)

τ₀

Offset constant in heart period (s)

τ_pr,br, τ_pr,cr

Control constant (mmHg)

τ_br, τ_cr, τ_s, τ_Rc

Time constant (s)

τ_T,s, τ_T,v

Time constant (s)

ΔT_s, ΔT_va

Contribution to heart period from sympathetic/vagal activity (s)

V_i

Volume in compartment i = nc, c, um, h, ut (ml)

V_total

Total volume of all compartments in the circulation system (ml)

W_br,i, W_cr,i

Weight factor i = sα, sβ