SVM-Based System for Prediction of Epileptic Seizures from iEEG Signal

Abstract

Objective

This paper describes a data-analytic modeling approach for prediction of epileptic seizures from intracranial electroencephalogram (iEEG) recording of brain activity. Even though it is widely accepted that statistical characteristics of iEEG signal change prior to seizures, robust seizure prediction remains a challenging problem due to subject-specific nature of data-analytic modeling.

Methods

Our work emphasizes understanding of clinical considerations important for iEEG-based seizure prediction, and proper translation of these clinical considerations into data-analytic modeling assumptions. Several design choices during pre-processing and post-processing are considered and investigated for their effect on seizure prediction accuracy.

Results

Our empirical results show that the proposed SVM-based seizure prediction system can achieve robust prediction of preictal and interictal iEEG segments from dogs with epilepsy. The sensitivity is about 90–100%, and the false-positive rate is about 0–0.3 times per day. The results also suggest good prediction is subject-specific (dog or human), in agreement with earlier studies.

Conclusion

Good prediction performance is possible only if the training data contain sufficiently many seizure episodes, i.e., at least 5–7 seizures.

Significance

The proposed system uses subject-specific modeling and unbalanced training data. This system also utilizes three different time scales during training and testing stages.

I. Introduction

There is a growing interest in data-analytic modeling for detection and prediction of epileptic seizures from intracranial electroencephalogram (iEEG) recording of brain activity [1]–[11]. Seizure prediction has the potential to transform the management of patients with epilepsy by administering preemptive clinical therapies (such as neuromodulation, drugs) and patient warnings [12]. It is commonly accepted that statistical characteristics of iEEG signal change prior to seizures. However, robust seizure prediction remains a challenging problem, due to the absence of long-term iEEG data recordings containing adequate seizures for training and testing [11] and patient-specific nature of seizure prediction models [1]. The main challenge for successful development of seizure forecasting models is a mismatch between clinical considerations and standard data-analytic modeling assumptions underlying most machine learning algorithms. Hence, we propose an SVM-based system for seizure prediction, where the design choices and performance metrics are closely correlated with clinical objectives. Furthermore, we apply this system to several data sets with adequate preictal and interictal segments to rigorously validate its performance.

This paper describes a data-analytic modeling approach for seizure prediction from canine iEEG recordings. Using canine data (from dogs with epilepsy) is important due to the biological similarity of canine and human seizures, and the availability of high-quality canine iEEG data [2], [13]–[15]. Previous research strongly suggests that a successful seizure forecasting should be subject-specific [8], [9], [16]–[18]. That is, a separate data-analytic model should be estimated for each dog (or for each human subject), using only that dog’s past iEEG recordings as training data. The subject-specific or patient-specific nature of data-analytic modeling implies the need for long recordings of iEEG used as labeled training data. This provides additional motivation for using available canine data sets with months of recorded iEEG data.

Most seizure prediction studies assume that there are three distinct ‘states’ of brain activity in subjects with epilepsy (e.g., interictal, preictal and ictal), and that such states can be detected from iEEG signal. In fact, the ictal state can be easily detected from iEEG signal. However, the task of seizure forecasting (or prediction) is quite challenging, as it requires discrimination between interictal vs. preictal states. This clinical hypothesis (about discrimination between interictal and preictal states) can be empirically validated using previously recorded iEEG segments classified (or labeled by a human expert) as interictal or preictal. Using these past labeled data (aka training data), we estimate a data-analytic model for discriminating between interictal and preictal iEEG segments, in order to apply it for prediction of future inputs (or test inputs). Then accurate prediction of test inputs (aka out-of-sample data) may be used as the evidence for preictal state. Note that all data-analytic models discussed in this paper are subject-specific, and a separate prediction model is estimated for each dog.

The task of discriminating between preictal and interictal states is called seizure prediction or seizure forecasting (from iEEG signal). Thus, we adopt a binary classification setting, where a classifier is estimated using training data, and then its prediction performance is evaluated using out-of-sample test data. Support Vector Machine (SVM) classifiers are adopted in our seizure prediction system, due to their robustness for modeling high dimensional data.

Next, we discuss iEEG data preparation preceding data-analytic modeling. The training data represents 4hr segments obtained from a continuous stream of iEEG recording, and these 4hr segments are labeled as either preictal or interictal by human experts. That is, preictal segments correspond to lead seizures (defined as seizures preceded by a minimum of 4-hour period with no seizures), and interictal segments were chosen randomly from iEEG stream (but restricted to be at least one week away from any seizure). Note that the available iEEG data within one week of recorded seizures but not preceding a lead seizure has been discarded (i.e., not used for modeling). This labeled data set is appropriate for many statistical and machine learning techniques developed for binary classification. Since seizures are very rare events (for most patients and canines), there are plenty of available interictal data, but very few preictal data. Hence, it is common to preselect a ratio of interictal to preictal training data. This asymmetric nature of seizure data is usually known as an ‘unbalanced setting’ or ‘unbalanced classification’ in data-analytic studies [19], [20]. Unbalanced data modeling affects both training and testing stages, as well as the choice of proper performance metrics. For example, wide availability of interictal data implies that classification of interictal segments is intrinsically easier than classification of preictal segments. This consideration may motivate certain modifications of SVM classifiers and may also suggest using appropriate metrics for prediction performance.

This paper shows how the understanding of clinical assumptions and characteristics of available data directly affects the design choices for our SVM-based seizure prediction system. The paper is organized as follows. Section II presents important clinical considerations (for seizure prediction) leading to proper formalization of seizure prediction under predictive classification setting. Section III describes various design choices for the proposed seizure prediction system, including data representation and feature engineering. Section IV describes experimental design and post-processing steps important for robust prediction performance. Section V presents empirical performance evaluation using several canine data sets. Discussion and conclusions are presented in Section VI and Section VII. A preliminary version of this work has been reported in [21].

II. Problem Formalization for Seizure Prediction

There are several important design considerations for data preparation and data encoding (preceding data-analytic modeling), leading to proper formalization of seizure prediction under classification setting as discussed next.

A. Available iEEG Data and Clinical Considerations

The available data are taken from a continuous stream of iEEG recording, then segmented and labeled as either ‘preictal’ or ‘interictal’ by human experts (Data are available at ftp://msel.mayo.edu). The preictal segment is defined as the segment preceding an ictal (or seizure) period that can be clearly identified from the iEEG signal. However, the length of preictal segments is defined differently between studies, ranging from 10 to 60 minutes without much or any justification [2]–[6]. In addition, the interictal segments are chosen as any other available continuous iEEG data sufficiently far away from a seizure. There is clearly an overabundance of available interictal data, so it is typical to preselect an ‘imbalance ratio’ of interictal to preictal training data. The imbalance ratios used in our study typically range from 8:1 to 10:1 (for different dog-specific models).

The problem of seizure prediction corresponds to classification of continuous iEEG segments (about 0.5–1hr long) extracted from iEEG signal recording. Yet in many studies this problem has been formalized as classification of short moving windows of iEEG signal (typically, 20s long). This formalization is adopted mainly due to data-analytic reasons, since a single 1hr segment contains 180 samples (corresponding to 20s windows). Such a significant increase in the number of training samples makes the classifier estimation/training possible. However, it is not clear how accurate prediction of short windows is relevant to the clinical objective of predicting 1hr segments. In particular, during the operation or test stage, a prediction is made for each new moving window. This results in a large number of isolated mispredictions for 20s windows. Typically, these mispredictions adversely affect the prediction accuracy. In order to address this problem, several previous studies adopted simple post-processing, such as 3- out-of-5 majority voting (over five consecutive predictions for 20s windows), or a Kalman filter to smooth out the classifier outputs during testing [4]. In the proposed system, we differentiate between the time scales for SVM classification (20s windows) vs. clinical prediction (1hr segments). Hence, iEEG data is represented in two time scales:

• feature vectors extracted from 20s windows are used as inputs to SVM classifier,

• 1 hr segments (180 consecutive 20s windows) are used for prediction (or testing stage).

Thus prediction of 1hr segments involves some extensive post-processing, or majority voting over 180 consecutive predictions for 20s windows. These post-processing rules should reflect statistical properties of iEEG signals and also reflect the understanding of SVM classifiers (for unbalanced data), as explained in Section IV-B.

Two additional design considerations important for seizure prediction include:

• Preictal period (PP), or preictal zone, preceding a seizure. The duration of preictal period is clinically unknown, however it is implicitly defined by the duration/size of labeled segments in the training data.

• Prediction horizon (PH) defined as time interval after a seizure prediction/warning is made, within which a leading seizure is expected to occur. The prediction horizon is also unknown but it cannot be shorter than the preictal period. Also note that it is much easier to make predictions with very long prediction horizon. For example, one can predict reliably that the next seizure will occur sometime within the next year, but it is much harder to predict that a seizure will occur within the next two hours.

These two design parameters, PP and PH, are clearly important for a successful seizure prediction. Due to subject-specific nature of seizure prediction, there have been multiple attempts to ‘optimize’ these parameters. Past research in this area reflects two extreme views:

1. It may be possible to find good/optimal values of PP and PH for all patients [8], [9], [16]. Typically, good values for PP range between ten minutes to one hour. Sometimes, the selection of PH is performed independently of the chosen PP (subject to natural constraint PH > PP).

2. An optimal choice of PP should be always seizure-dependent. For example, Bandarabadi et al. [17] present a statistical analysis for the optimal choice of PP and conclude that optimal PP is seizure-specific, i.e., it is not possible to select a single good PP for future data.

Our approach to this dilemma is that inherent variability of seizure prediction should be captured via subject-specific modeling. So we adopt the view (1) by selecting fixed values of PP and PH for all patients/dogs. Specifically, we use 1hr preictal period—which effectively assumes that there is a ‘warning signal’ somewhere within 1hr before a lead seizure. Note that using 1hr PP is consistent with earlier studies using shorter PP (say, 10min or 20min), as long as the value of PH is at least 1hr. With regard to PH, our modeling approach uses two possibilities (1hr and 4hrs) during testing (or seizure prediction), reflecting the intrinsic statistical variability of seizure data.

Finally, we point out that a good choice of PP and PH reflects a number of clinical and data-analytic constraints. Moreover, this choice is meaningful only in the context of a particular seizure prediction system (which uses other design parameters). For example, using 10min preictal period will result in 6-fold reduction of preictal training data. This would prevent an accurate model estimation (SVM training) due to high-dimensionality of input data samples (20s windows). In summary, our selection of 1hr preictal period can be empirically justified only by the empirical results (seizure prediction performance) presented later in the paper.

B. Summary of Available Data

The available data for each dog are continuously recorded from 16 channels of raw iEEG data sampled at 400Hz. Expert review of the recorded iEEG suggested multifocal seizure onset for all dogs, but propagation of seizures from a single focal onset region distant from the implanted electrodes cannot be excluded. After pre-processing to remove discontinuities and large artifacts, each 4hr segment of iEEG data is labeled as ‘interictal’ or ‘preictal’ by human experts. Here a typical canine data set may contain several leading seizures (4hr preictal segments) and about eight times more interictal segments. Table I summarizes the number of interictal and preictal segments for the six dogs in our analysis. All dogs recorded at least seven seizure episodes (preictal segments corresponding to leading seizures), except for Dog-M3 (having just three leading seizures). Note that Table I represents a global view of the data as a collection of 4hr segments. However, data-analytic modeling is performed at several time scales. That is, 20s windows of iEEG signal are used for classifier training (SVM model estimation), whereas prediction/ testing is performed for 1hr segments (represented as a group of 180 windows). Optionally, SVM system’s predictions for four consecutive 1hr segments may be aggregated to form a prediction for each 4hr segment.

TABLE I.

The number of interictal/preictal 4hr segments for each dog.

Dog	interictal	preictal
L2	152	19
L7	88	11
M3	15	3
P2	64	8
L4	56	7
P1	232	29

III. Feature Engineering and SVM System Design

For data-analytic modeling, each moving window is represented as a set of input features. A common set of input features for SVM classification is a set of spectral features calculated from the iEEG signals. Standard Delta (0–4Hz), Theta (4–8Hz), Alpha (8–12Hz), Beta (12–30Hz), and Gamma (30–100Hz) spectral bands are the most common frequency ranges used, with some studies splitting the Gamma band into 3–4 sub-bands [2], [4]. Some studies also use additional features such as autoregressive errors, decorrelation time, wavelet coefficients, etc [3]. However, these studies have not had the same level of classification accuracy as studies that used only spectral features. Calculation of spectral features requires a predefined time window, with each window resulting in one data sample representing spectral features (for this window). The time window sizes vary from study to study, and the common window size is 20 seconds (also used in our system). Note that using 20s windows as training samples for model estimation is also clinically plausible, since seizure warning signals are often manifested as auras that last just a few seconds.

A. Feature Engineering

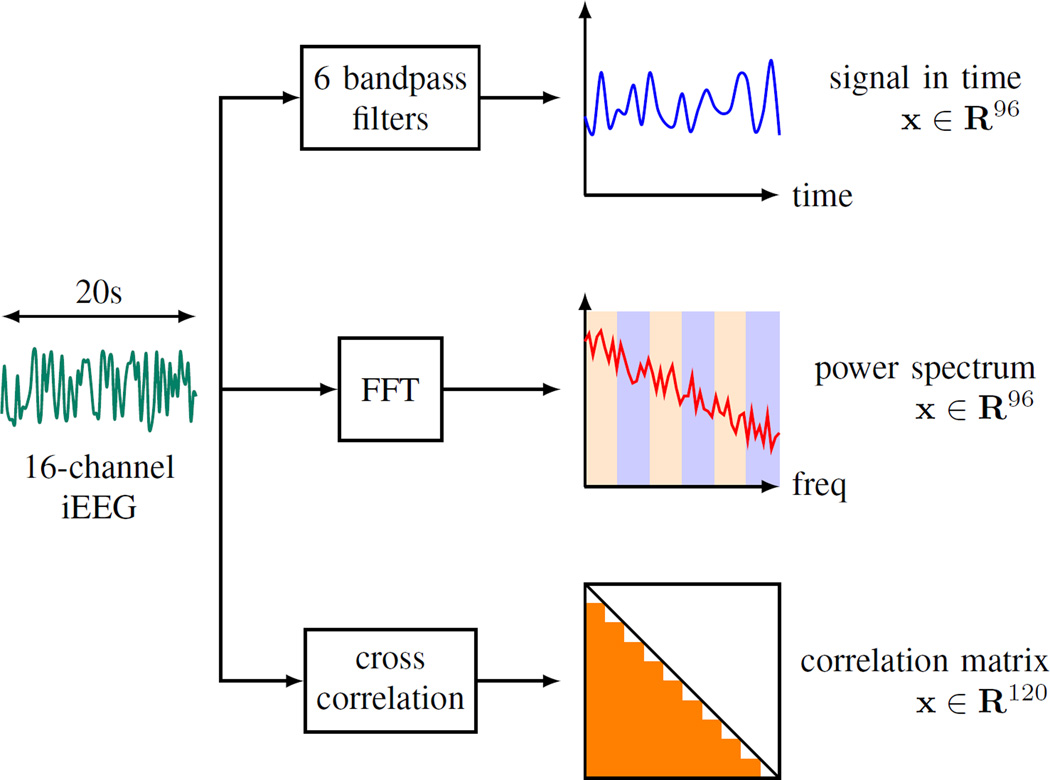
We represent each 1hr iEEG segment as a group of 20s non-overlapping windows. Further, we utilize three approaches to extract features from 20s windows, as illustrated in Fig. 1:

1. The iEEG signal within a 20s window is first passed through six Butterworth bandpass filters corresponding to 6 standard Berger frequency bands (0.1–4Hz, 4–8Hz, 8–12Hz, 12–30Hz, 30–80Hz and 80–180Hz). Then the output signals from the filters are squared to obtain the estimates of power in six bands. This procedure is repeated for 16 iEEG channels and yields a 96-dimensional feature vector. This feature encoding will be referred to as BFB throughout this paper.

2. The frequency spectrum of the iEEG signal is obtained by applying Fast Fourier Transform (FFT) to each 20s window. Next, the power in each Berger frequency band is approximated by summing up the magnitudes of the spectrum in the corresponding band. This procedure, indicated as FFT in this paper, also encodes the spectral contents in 16 iEEG channels as a 96-dimensional feature vector. Note that both BFB and FFT methods perform signal encoding through power estimation. But the former method utilizes signal representation in time domain, while the latter in frequency domain.

3. The third feature extraction, XCORR, calculates the cross-channel correlation of signals from two different channels in order to measure their similarity. Given 16 iEEG channels, there are 120 different pairs. Calculating the cross-channel correlations for all 120 pairs results in a 120-dimensional feature vector.

Fig. 1.

Three feature encodings for iEEG data: BFB, FFT, and XCORR.

Note that all three feature representation methods have the same or similar number of features. This observation may be important for interpretation of SVM modeling results reported later in Section V, because all three feature encoding methods yield similar dimensionality of the input space for SVM classifier. That is, comparison of prediction performance results for these feature encoding methods (reported in Section V) can indeed suggest possible advantages of a particular feature encoding method.

B. Proposed System

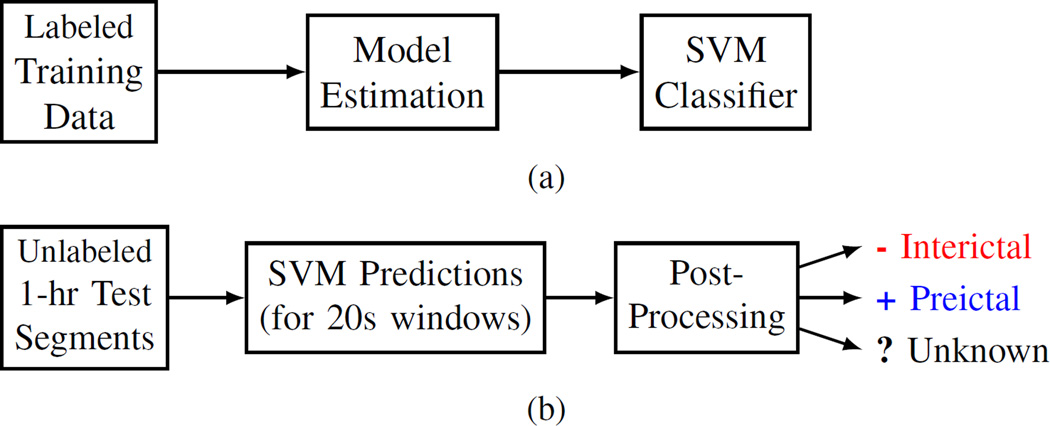
Next, we describe an SVM-based system for seizure prediction from iEEG data. The available iEEG data include pre-processed 4hr segments labeled as interictal or preictal. The data-analytic model should predict future (out-of-sample) 1hr test segments that were never used for model estimation. Hence, the proposed system assumes 1hr preictal period and 4hr prediction horizon [21].

In our system, an SVM classifier is trained using 20s labeled windows and then used to predict 1hr unlabeled test segments, as shown in Fig. 2. Many earlier SVM-based prediction systems used the same implementation for the training stage, i.e., training an SVM classifier using labeled samples corresponding to features extracted from short moving windows [2], [4], [6]. However, all these earlier efforts aimed at achieving good prediction for 20s windows, according to standard classification setting adopted in machine learning [19], [20]. In contrast, our system aims to make predictions for 1hr test segments. Hence, during the operation stage shown in Fig. 2(b), the system should assign the same class label to all 20s windows of an 1hr test segment. This involves some form of post-processing as explained later in Section IV-B.

Fig. 2.

Proposed system design for (a) training stage, and (b) prediction/operation stage.

The design of our system for seizure prediction is driven mainly by scarcity and poor quality of preictal data. That is, scarcity refers to very limited amount of preictal data (about 3–11 seizure episodes), and ‘poor quality’ denotes the fact that a ‘seizure warning signal’ may occur somewhere within the 4hr training segment labeled as ‘preictal.’ We can reasonably assume that preictal signal is more likely to occur right before seizure onset; so only the last hour of a 4hr segment is used for training. Hence, the training data for model estimation include 1hr segments labeled as interictal or preictal. The limited amount and poor quality of preictal data contribute to the difficulty of reliable seizure prediction. In our system, these negative factors are partially alleviated by [21]:

• Large amount of interictal data, leading to highly imbalanced ratio of interictal vs. preictal data (typically, 8:1 to 10:1) during model estimation or training stage.

• Proper specification of training (model estimation) and ‘successful prediction’ (or testing). This includes using different time scales for training and operation stages (shown in Fig. 2), and also additional post-processing steps critical for robust prediction, as discussed next.

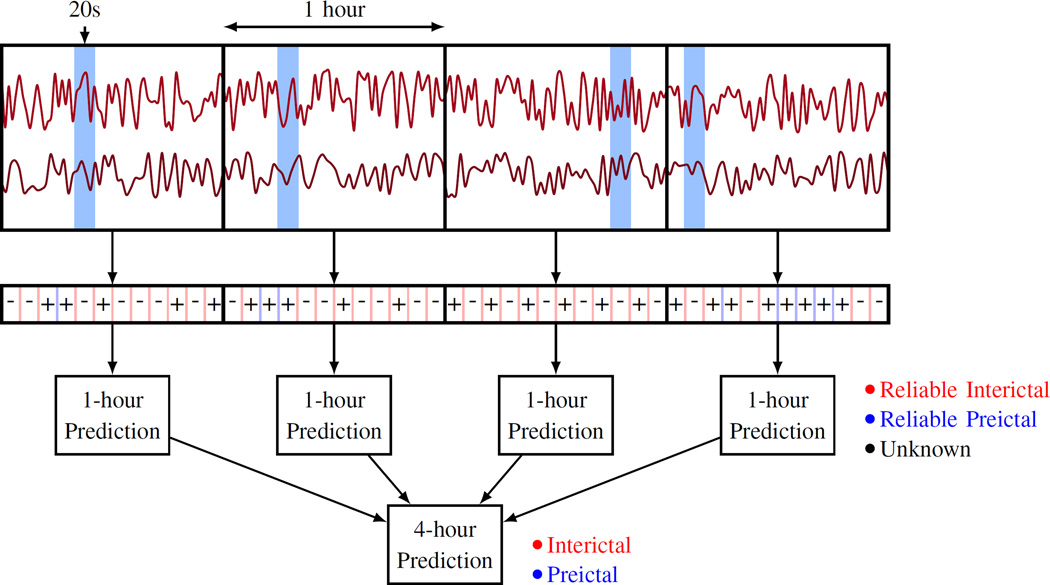
From the clinical perspective, the problem of seizure prediction can be formalized as predictive classification of 1hr iEEG segments assuming 4hr prediction horizon. Consequently, the training data for model estimation includes 1hr segments labeled as preictal or interictal. The system is designed to predict/classify continuous 1hr test segments (as preictal or interictal), signaling that a seizure will or won’t occur in the next 4-hour period [21]. Hence, the test data consist of 4hr test segments that should be classified (predicted) as preictal or interictal. The system makes actual predictions for 1hr test segments, and further a 4hr segment is predicted as

• preictal, if at least one of the four consecutive 1hr test segments is classified as preictal; or

• interictal, if all four 1hr test segments are classified as interictals.

Our system’s predictions are made in three time scales (20s, 1hr, and 4hr) as shown in Fig. 3. The system makes predictions for 20s windows, which are then aggregated into predictions for 1hr segments. Finally, predictions for four consecutive, non-overlapping 1hr test segments are combined into predictions for 4hr segments.

Fig. 3.

Predictive modeling in three time scales: 20s, 1hr, and 4hr.

C. Prediction Performance Indices

The most common prediction performance metrics in machine learning are False Positive (FP) and False Negative (FN) error rates. A FP error corresponds to incorrect prediction for a preictal segment. A FN error is made when a system mispredicts a preictal test segment as ‘interictal.’ It is important to note that all performance metrics for seizure prediction are contingent upon the pre-defined length of preictal period and prediction horizon. However, many earlier studies report FP/FN error rates without clearly defined preictal period and/or prediction horizon. Empirical results for our system’s prediction performance (shown in Section V) present FP and FN error rates for:

• 1hr test segments, and

• 4hr test segments (formed by combining predictions for four 1hr segments).

Note that reporting FP and FN error rates is identical to reporting errors for interictal test segments (FP) and for preictal test segments (FN). Further, we also report Sensitivity (SS) and False-Positive Rate (FPR) per day, as both are commonly used in seizure prediction research. The two sets of performance indices are in fact equivalent.

IV. Experimental Design and Post-processing

A. Experimental Design

This section describes experimental settings for data-analytic modeling (for the system shown in Fig. 2), using the Dog-L4 data set as an example. This data set has seven recorded leading seizures, i.e., seven 4hr segments labeled as preictal, and about eight times more interictal segments. The experimental design reflects both the clinical objectives (prediction of 1hr test segments) and data-analytic constraints (very small number of preictal segments in the training data).

Based on these considerations, we adopted an unbalanced setting for training data (over a balanced one). Under unbalanced setting, the amount of interictal (negative) segments is about eight times more than that of preictal (positive) data. Since Dog-L4 data set has seven seizures, 6 preictal along with 55 interictal 1hr segments are used for training (model estimation), and two unlabeled 1hr segments are used for testing. Under this experimental setting, testing is always performed using out-of-sample data. This unbalanced modeling set up is summarized in Table II, which shows the labels of iEEG segments used for training and testing in each modeling experiment.

TABLE II.

Experimental design for Dog-L4 under the unbalanced Setting. The decimal labels encode 1hr segments.

Experiment	Training set		Test set
	interictal	preictal	interictal	preictal
1	2–56	2, 3, 4, 5, 6, 7	1	1
2	1, 3–56	1, 3, 4, 5, 6, 7	2	2
3	1, 2, 4–56	1, 2, 4, 5, 6, 7	3	3
4	1–3, 5–56	1, 2, 3, 5, 6, 7	4	4
5	1–4, 6–56	1, 2, 3, 4, 6, 7	5	5
6	1–5, 7–56	1, 2, 3, 4, 5, 7	6	6
7	1–6, 8–56	1, 2, 3, 4, 5, 6	7	7

According to this experimental setting, we estimate seven different models and each model is tested on its own test set. The final performance index is the prediction accuracy, i.e., the number (or fraction) of accurately predicted test segments (in all seven experiments). Reporting prediction accuracy separately for interictal and preictal test segments reflects a requirement that a good system should classify each iEEG segment well, rather than many segments over a long observation period. This is because seizures occur very infrequently, so a trivial decision rule ‘label every segment as interictal’ will yield quite high prediction accuracy (over long observation period), but it is clinically useless [21].

Further, we discuss details of training the SVM model shown in Fig. 2(a). The SVM complexity parameter C is estimated via 6-fold cross-validation on the training set [19]–[21], so that balanced validation data always include samples from one interictal and one preictal segment. Note that 6-fold cross-validation is used because Dog-L4 training data have six preictal segments. For other data sets, M-fold cross-validation is used if the training data contain M preictal segments. All SVM training and cross-validation are performed using equal misclassification costs. There are three important points related to SVM modeling under unbalanced setting [21]:

1. Linear SVM parameterization is adopted, even though available training data may not be linearly separable. Yet, introducing nonlinear kernels is avoided, as it may result in overfitting, due to high variability of (very limited) preictal training data.

2. Balanced validation data set was used for model selection (e.g., tuning C parameter). The decision to use balanced validation data reflects the clinical objective that the system should accurately predict each test segment.

3. Although SVM training is performed using equal misclassification costs, the combination of using unbalanced training data and balanced validation data is formally equivalent to using unequal misclassification costs [19].

B. Post-processing

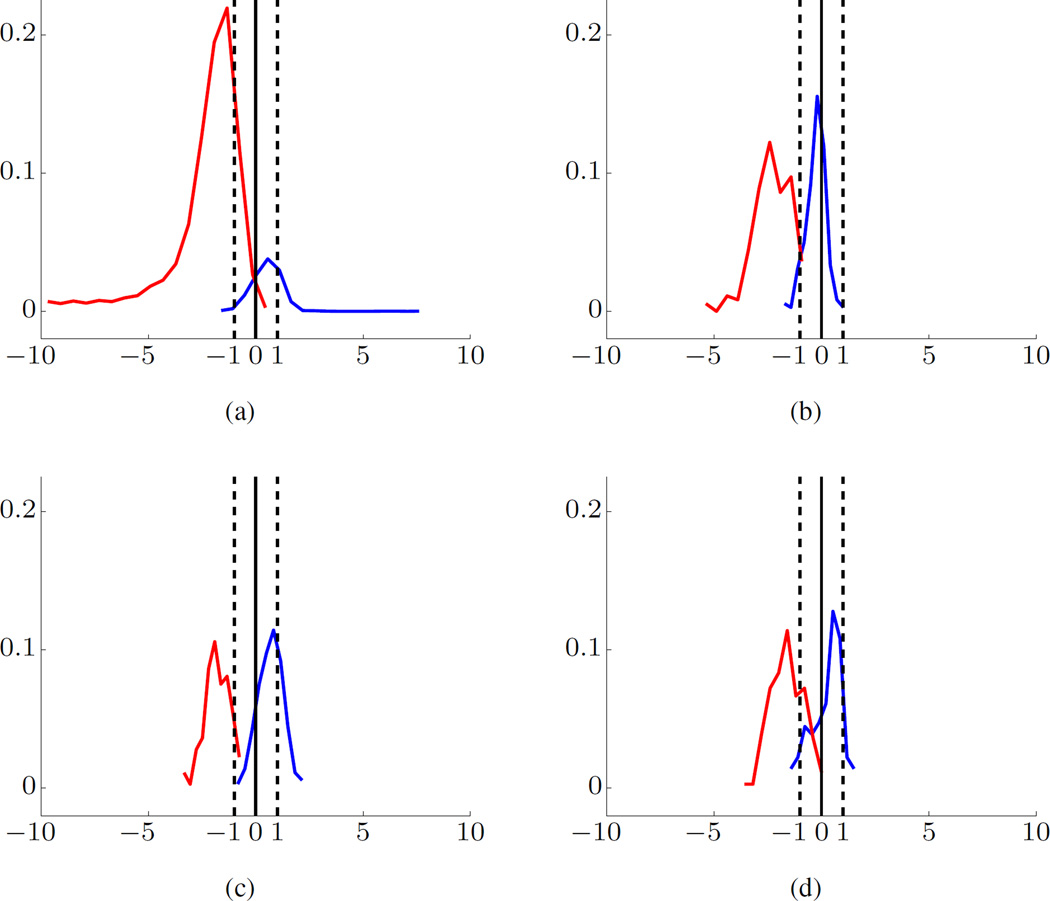
During the test stage shown in Fig. 2(b), the prediction of a test segment involves some kind of post-processing or majority voting over all 180 windows (comprising this 1hr test segment). This post-processing should be related to the properties of binary SVM classifiers, conveniently represented using the histogram-of-projections technique for visual representation of the trained SVM model [19]–[22]. This technique displays the empirical distribution of distances between (high-dimensional) samples and the SVM decision boundary (of a trained SVM model).

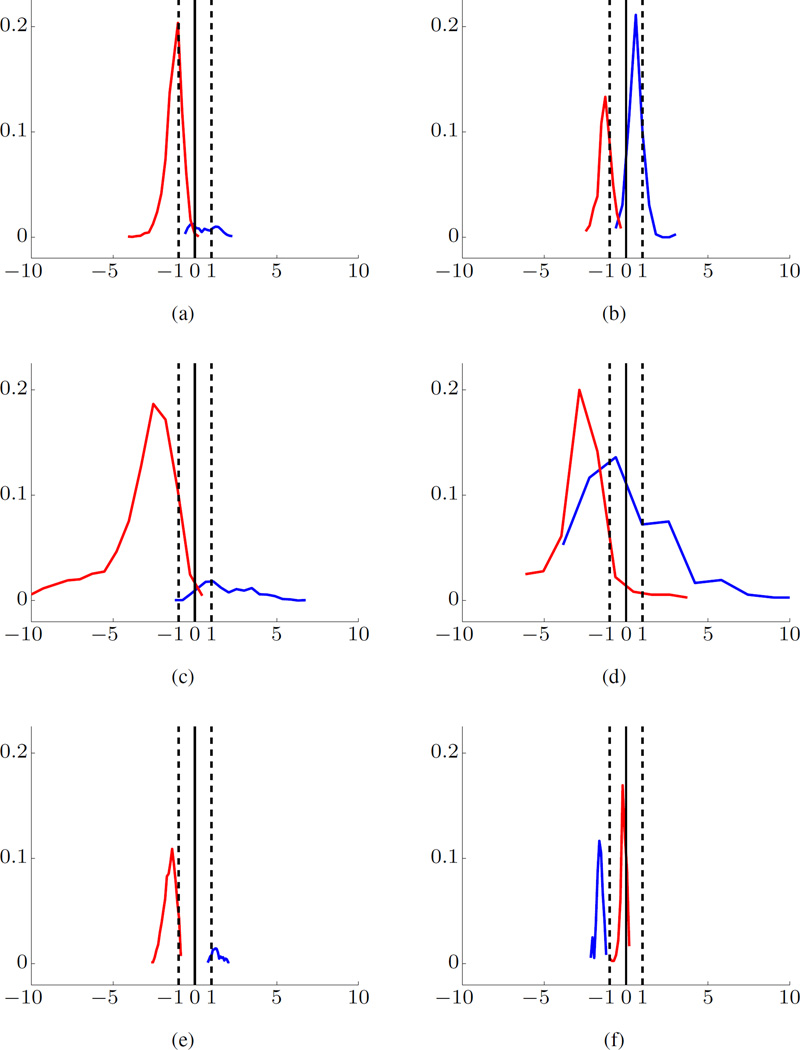
A typical histogram of projections of SVM model estimated using Dog-L4 training data is shown in Fig. 4(a). In the figure, the empirical distribution is represented in the form of a univariate histogram of distances for training samples (or test samples), along with SVM decision boundary (marked as ‘0’ distance on x-axis) and SVM margin borders for negative and positive classes (marked as ‘−1/+1’). Further, the x-axis of a histogram represents a scaled distance between a high-dimensional feature vector and SVM decision boundary. The y-axis represents the fraction of samples. The distance to the decision boundary is scaled so that the margin borders always have values −1 or +1.

Fig. 4.

SVM modeling for Dog-L4 data set using BFB feature encoding. Histograms of Projections for training data (a), and for test data (b)–(d). The preictal data are shown in blue and interictal data in red. Margin borders correspond to −1/+1 (marked by dashed vertical lines). The x-axis is the scaled distance and y-axis the fraction of samples.

The training data correspond to high-dimensional feature vectors for 20s windows. As shown in Table I and II, the training data include 55 interictal and 6 preictal 1hr segments; so it is very imbalanced. Note that a small portion of the training interictal segment (in red) falls on the wrong side of the decision boundary, indicating very small error rate (for 20s windows). A larger portion of the training preictal data (in blue) falls on the wrong side of SVM model, suggesting higher FN error rate. However, the histogram in Fig. 4(a) indicates that interictal (red, negative) and preictal (blue, positive) training samples are generally well-separated by the SVM model.

The test data consist of one preictal and one interictal segment, and typical histograms for such balanced test data are shown in Fig. 4(b)–(d). The majority of samples for interictal test segment fall on the correct side of the decision boundary ‘0.’ Yet the histogram for preictal test samples is very unstable, i.e., it can be right-skewed or, left-skewed with respect to decision boundary, or even may fall within the margin borders, as shown in Fig. 4(b), 4(c), and 4(d), respectively. These observations can be used to implement meaningful post-processing rules for classifying 1hr test segments, e.g., majority voting over 180 predictions for all 20s windows comprising 1hr test segment.

In our system, we adopted the 70% majority threshold [21]. That is, if at least 70% of all SVM predictions (for a given 1hr test segment) fall on one side of SVM decision boundary, this segment is classified as Reliable Interictal or Reliable Preictal; otherwise, it is classified as Unknown. As shown in Fig. 2(b), our system can make three different predictions. For example, the histograms of the preictal test segments (blue) in Fig. 4(b), 4(c), and 4(d) will be classified as reliable interictal (an error), reliable preictal, and unknown, respectively. On the other hand, all three interictal test segments (red) in Fig. 4(b)– (d) will be correctly predicted as reliable interictal.

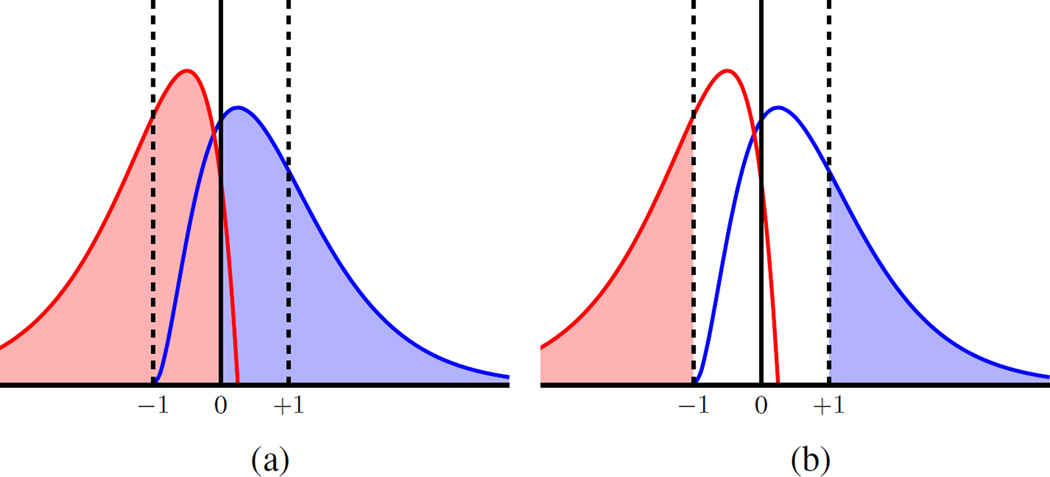
The notion of reliable predictions for 1hr test segments in our system is quantified as the percentage of test inputs (20s windows) falling on one side of the decision boundary, as illustrated in Fig. 5(a). Three important points about ‘reliable’ predictions should be highlighted:

1. The reliability of interictal predictions is expected to be higher than that of preictal predictions, since the histograms of projections for training interictal samples are much more stable than those for preictal samples.

2. Due to high confidence in interictal predictions (and low confidence in preictal predictions), segments that cannot be predicted reliably as interictal should be regarded as preictal. That is, 1hr test segments classified as ‘unknown’ in our system (see Fig. 2(b)) will be always regarded as ‘preictal,’ such as the segment (in blue) shown in Fig. 4(d). Hence, the post-processing decision rules for test segments can be summarized as follows:

   • An 1hr test segment is classified as ‘interictal’ if at least 70% of its 20s windows are predicted as interictal; otherwise this segment is classified as ‘preictal.’

3. The confidence of predictions can be also controlled by the threshold for making prediction decision. In particular, instead of using SVM decision boundary (marked as ‘0’) for classification decision, we can use the margin borders ‘−1/+1,’ as illustrated in Fig. 5(b). That is, reliable predictions correspond to test input samples falling on the correct side of SVM margin borders; whereas predictions falling between the margin borders are regarded as ‘unreliable.’ These choices for threshold level are discussed in Section V-D.

Fig. 5.

Univariate histogram of projections for test samples: (a) decision threshold for majority voting is taken relative to decision boundary ‘0’; (b) decision threshold is taken relative to margin borders (‘−1’ or ‘+1’).

V. Empirical Evaluation

This section describes prediction performance results for the proposed system using experimental setup outlined in Section IV. These results illustrate the effect of system’s design choices on its prediction performance. These design choices include both pre-processing (e.g., three feature representations) and post-processing (e.g., making predictions for 1hr vs. 4hr test segments). As noted earlier in Section III-B, seizure prediction using 4hr prediction horizon can be technically implemented by combining SVM predictions for four consecutive 1hr test segments. That is, a 4hr prediction horizon is modeled via 4hr test segment, which is classified as preictal only if at least one of the four consecutive 1hr test segments is predicted as preictal.

A. One-Hour vs. Four-Hour Test Segment

Prediction results for Dog-L4 (using the experimental design shown in Table II) are summarized in Table III. Specifically, Table III shows the prediction results for test segments under three different feature representations. This table presents predictions for four consecutive 1hr test segments, treated independently, under ‘1hr’ column. Combining these 1hr predictions into a single prediction is shown under ‘4hr’ column. Symbols -, +, and ? denote ‘reliable interictal,’ ‘reliable preictal,’ and ‘unknown’ predictions, respectively.

TABLE III.

Predictions for 1hr and 4hr segments via different feature encodings for Dog-L4. Symbols −, +, and ? denote reliable interictal, reliable preictal, and unknown, respectively.

Features	BFB				FFT				XCORR
Segments	interictal		preictal		interictal		preictal		interictal		preictal
Exp	1hr	4hr	1hr	4hr	1hr	4hr	1hr	4hr	1hr	4hr	1hr	4hr
1	−−−−	−	−?+?	+	−−−−	−	−+++	+	−−−−	−	−++?	+
2	−−−−	−	−+??	+	−−?−	+	++++	+	−−−−	−	?+??	+
3	−−−−	−	??++	+	−−−−	−	?+++	+	−−−−	−	−???	+
4	−−−−	−	++++	+	−−−−	−	++++	+	−−−?	+	?+++	+
5	−−−−	−	+?+?	+	−−−−	−	???−	+	−−−−	−	−?−?	+
6	−−−−	−	−−??	+	−−−−	−	−?++	+	−−−−	−	−−−−	−
7	−−−−	−	−−−−	−	−−−−	−	−++?	+	−−−−	−	−?−−	+
Error %	0	0	29	14	4	14	14	0	4	14	39	14

These results indicate very good (stable) predictions for interictal test segments, and rather unstable performance for preictal segments. In particular, the patterns of 1hr predictions for preictal segments vary significantly under three feature encodings. However, most preictal test segments are correctly classified when four 1hr predictions are combined together. For example, results under the FFT feature encoding indicate 100% prediction accuracy for 4hr preictal segments. Further the prediction errors for 4hr preictal segments are smaller than those for 1hr segments, for all feature representations. This observation underscores the significance of ‘4hr prediction horizon’ aspect in our system, discussed in Section III-B.

Next, we present prediction performance results for several representative data sets, under three feature encodings. All modeling results follow the same methodology as presented in Section IV for Dog-L4 data set. That is, for each data set we estimate several SVM models, so that the number of experiments equals the number of seizures in the available data. Table IV summarizes the prediction performance results. These results show error rates for 4hr test segments, obtained by combining predictions for four consecutive 1hr segments made by the system.

TABLE IV.

Summary of prediction performances for 4hr test segments.

(a) FP and FN error rates (%).
Dog	BFB		FFT		XCORR		Combo
	FP	FN	FP	FN	FP	FN	FP	FN
L2	5	21	10	21	11	42	5	21
L7	9	9	0	27	9	9	0	9
M3	0	33	33	33	0	33	0	33
P2	0	0	0	0	0	25	0	0
L4	0	14	14	0	14	14	0	0
P1	7	17	14	21	7	31	3	10

(b) SS (%) and FPR per day.
Dog	BFB		FFT		XCORR		Combo
	SS	FPR	SS	FPR	SS	FPR	SS	FPR
L2	79	0.32	79	0.63	58	0.63	79	0.32
L7	91	0.55	73	0.00	91	0.55	91	0.00
M3	67	0.00	67	2.00	67	0.00	67	0.00
P2	100	0.00	100	0.00	75	0.00	100	0.00
L4	86	0.00	100	0.86	86	0.86	100	0.00
P1	83	0.41	79	0.83	69	0.41	90	0.21

Due to asymmetric nature of the data, we report the FP and FN error rates separately, where FP and FN errors correspond to interictal and preictal errors, respectively. All prediction performance results are presented using two equivalent performance indices, i.e., FP and FN test error rates, and SS and FPR per day. Empirical results in Tables III and IV suggest that no single feature encoding is consistently superior to others. As expected, results in Table IV(a) indicate high FN error rate and much lower FP error rate. This is due to scarcity and poor quality of preictal training data, as noted in Section III-B.

B. Combining Predictions

Comparing the predictions for 1hr test segments under three different feature encodings in Table III suggests that some errors can be eliminated if the three predictions were combined. For example, an 1hr interictal segment in Experiment 2 of Dog-L4 is classified as unknown ‘?’ under FFT, but is reliably predicted as interictal under BFB and XCORR encodings, as shown in Table III. Similarly, the last 1hr interictal segment in Experiment 4 is predicted as ‘unknown’ under XCORR, but is classified correctly under BFB or FFT.

Therefore, we suggest combining the 1hr-segment predictions under BFB, FFT, and XCORR encodings before making the decisions for the 4hr segments. The combining rule is a simple majority voting (2-out-of-3). The corresponding error rates are shown in Table IV(a) under the ‘Combo’ column. Using this combining rule, both FP and FN error rates are reduced relative to error rates achieved by each feature representation. Equivalently, this combining rule results in improved sensitivity and reduced false-positive rate per day for all data sets, as shown in Table IV(b). Note that using such rule, system’s predictions could be better (but never worse) than predictions obtained by each component classifier (using its own feature encoding).

C. Insufficient Preictal Data

Prediction results shown in Table IV suggest rather poor prediction accuracy for Dog-M3. For instance, under FFT, 33% FP error rate translates to one false seizure prediction every 12 hours, and 33% FN error rate means that one seizure (out of three) is mispredicted. Such a poor prediction performance can be anticipated/explained by noting that the available data set contains only three preictal segments (see Table I). These results suggest that good predictions using the proposed system may be possible only if available data have sufficiently many (say, at least six) preictal segments.

Typical histograms of projections for Dog-M3 are shown in Fig. 6. Since Dog-M3 data set has only three seizures, SVM modeling requires three experiments, so that each experiment uses two preictal segments for training and one for testing. The histograms shown in Fig. 6 clearly indicate that an SVM model (estimated using just two preictal training segments) cannot consistently predict preictal test segments [21].

Fig. 6.

SVM modeling for Dog-M3 data set using BFB feature encoding. Histograms of Projections (for three experiments) for training and test data are shown on the left and right side, respectively. The preictal data are shown in blue and interictal data in red.

This phenomenon may have a simple clinical explanation: all subject-specific seizures have two to three different modalities, e.g., seizures occurring during sleep, or during awake state, or seizures caused by stress. Clearly, data-analytic models should include all subject-specific modalities in the training data, in order to achieve clinically acceptable prediction performance. When the available data contain just a few seizures, this condition is not likely to be satisfied. For example, assume that for Dog-M3 two seizures (used as training data) occurred during awake state, and one seizure (used for testing) occurred during sleep. Then, of course, the data-analytic model (estimated using preictal segments during awake state) would not reliably predict seizures during sleep. Hence, we suggest excluding modeling results for Dog-M3 from our performance comparisons.

D. Decision Threshold Adjustments

Note that all prediction results presented in Tables III and IV used SVM decision boundary for making classification decisions. This SVM boundary is marked as ‘0’ in the histograms in Figs. 4–6. Using this standard threshold at ‘0,’ the proposed system achieves low FP and high FN test error rates. Clinically, it may be desirable to reduce FN error rate (at the expense of raising FP error rate). In our system, this can be achieved by moving the decision threshold from ‘0’ to margin borders ‘−1/+1’ (as illustrated in Fig. 5), and by varying the value of majority threshold. Table V shows the test error rates for three threshold values with respect to margin borders ‘−1/+1.’ Performance results using standard threshold at ‘0’ (as in our earlier experiments) are listed in the right column for comparisons. A few comments regarding the selection of threshold values:

• By moving the decision threshold from ‘0’ to margin borders ‘−1/+1,’ we should select a lower threshold value. Otherwise, most test segments would be predicted as ‘unknown’ in our system, and ultimately classified as preictal. This will result in very low FN but high FP error rate.

• Choosing decision threshold at margin borders ‘−1/+1’ generally tends to decrease FN error rate but increase FP rate, relative to using decision threshold at ‘0,’ as evident from Table V. In practice, selection of a good decision threshold may be subject-specific, and should be made by a neurologist.

• Arguably, it may be possible to select an optimal threshold value for each data set (or patient), provided that the available data contain sufficiently many seizure episodes [21].

TABLE V.

Effect of choosing decision threshold at margin borders ‘−1/+1’ on system prediction performance.

(a) FP and FN error rates (%).
Dog	±1, 30%		±1, 40%		±1, 50%		0, 70%
	FP	FN	FP	FN	FP	FN	FP	FN
L2	21	11	26	11	26	5	5	21
L7	9	9	18	9	18	9	9	9
P2	0	0	0	0	0	0	0	0
L4	0	0	0	0	14	0	0	14
P1	17	3	21	0	28	0	7	17

(b) SS (%) and FPR per day.
Dog	±1, 30%		±1, 40%		±1, 50%		0, 70%
	SS	FPR	SS	FPR	SS	FPR	SS	FPR
L2	89	1.26	89	1.58	95	1.58	79	0.32
L7	91	0.55	91	1.09	91	1.09	91	0.55
P2	100	0.00	100	0.00	100	0.00	100	0.00
L4	100	0.00	100	0.00	100	0.86	86	0.00
P1	97	1.03	100	1.24	100	1.66	83	0.41

E. Using Nonlinear SVM Parameterization

Note that all prediction results presented in Tables III, IV, and V used linear SVM, due to very small number of preictal training samples. In contrast, all previous seizure prediction studies employed nonlinear SVM classifiers, such as radial basis function (RBF) SVM [4], [14], [18]. These earlier studies provide no justification for using nonlinear SVM and/or for choosing RBF kernel.

Arguably, nonlinear (RBF) kernel parameterization is more flexible and it certainly includes linear SVM (as a special case). However, this additional flexibility results in a more difficult and potentially unstable model selection. That is, modeling using RBF SVM requires tuning two complexity parameters (regularization parameter C and the kernel width parameter γ) vs. tuning a single parameter C for linear SVM.

These arguments are quantified next using empirical comparisons between RBF SVM and linear SVM for Dog-L4 data set with BFB feature encoding. For both approaches, we use the same cross-validation procedure for model selection (as described in Section IV). Table VI shows the optimized values of the tuning parameters and the corresponding resampling error rates, for both approaches. As evident from this table:

• the chosen RBF width parameter is rather unstable;

• the cross-validation error rate for RBF SVM is much lower than for linear SVM.

These observations suggest that the RBF SVM tends to overfit available data, in the sense that it always achieves (almost) perfect separation between the two classes. Yet the prediction (test) errors for both methods are virtually the same, i.e., using 1hr prediction horizon the linear SVM yields zero FP and 29% FN test error rates, whereas RBF SVM yields zero FP and 25% FN error rates. Note that FN error rates shown in Table VI for linear SVM are in the 10–25% range which is quite close to ‘true’ 29% FN test error. In contrast, FN error rate estimated from training data using RBF SVM is mostly in 0–5% range (see Table VI), indicating overfitting. Overall, these results suggest that seizure prediction using SVM modeling should adopt linear SVM, assuming realistic (small) amount of preictal data, such as 7–20 seizures.

TABLE VI.

Cross-validation training errors (%) and selected tuning parameters for Dog-L4 data set using RBF SVM.

Exp	Linear			RBF
	FP	FN	C	FP	FN	C	γ
1	0.37	22.7	105	0.06	1.67	106	24
2	0.44	20.7	105	0.06	0.74	106	24
3	0.45	23.8	105	0.03	0.74	106	26
4	0.45	22.5	105	0.12	1.39	106	24
5	0.47	21.9	105	0.01	0.09	106	26
6	0.54	20.5	105	0.30	8.24	106	2−4
7	0.37	11.3	105	0.03	0.83	106	22

VI. Discussion

Modeling results presented in this paper suggest that reliable seizure prediction from iEEG signal is indeed possible. Since our SVM-based seizure prediction system used only iEEG input, its performance can be certainly improved by incorporating other physiological inputs (e.g., heart rate). Furthermore, it may be possible to include information about different seizure modalities, e.g. seizures during sleep vs. awake state— such additional information may improve the prediction accuracy. Several important findings and limitations based on our modeling experience are summarized next:

1. Quantity of preictal data. Successful data-analytic seizure prediction models can be estimated (using our system in Fig. 2) only if the training data contain sufficient amount of preictal data, e.g., at least 5–7 seizure episodes. For example, it is not possible to achieve good prediction performance using data sets containing just three seizures. This is well-defined quantifiable limitation of the proposed data-analytic approach. This limitation is also supported by recent findings reported in human focal epilepsy [23].

2. Subject-specific modeling. An important property of our seizure prediction system is subject-specific (or patient-specific) aspect of data-analytic modeling. Hence, we expect that prediction quality varies for different subjects, due to varying quality of preictal data for different subjects. For example, prediction results for Dog-L2 were consistently worse than for Dog-L4, even though the Dog-L2 data set had more data segments (both preictal and interictal).

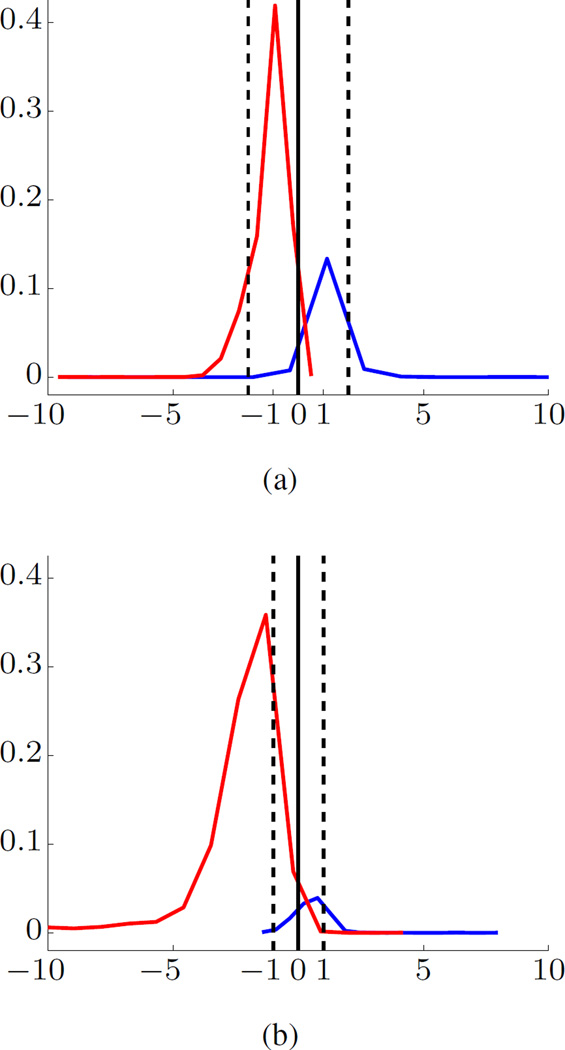
3. Seizure prediction for human data. Even though we have only limited experience in modeling human iEEG data, we can reasonably expect that the proposed system can be successfully used for human seizure prediction. This expectation is based on visual similarity of the histograms of projections for canine and human data. Figure 7 shows histograms of projections for trained SVM model (under unbalanced setting) for human and canine data sets from Kaggle competition. There is an apparent visual similarity, even though human and dogs’ iEEG data in Kaggle competition were obtained using different frequencies and different number of channels. This similarity (between human and canine histograms of projections) may suggest that our data-analytic seizure prediction system would provide similar prediction accuracy for human iEEG data.

Fig. 7.

Histograms of projections of trained SVM models for (a) human and (b) canine iEEG data.

While there exist human EEG recordings/databases such as EPILEPSIAE, these data are fundamentally different from canine iEEG data used in our study. That is, human EEG data represent the recordings from epilepsy patients undergoing pre-surgical intracranial EEG monitoring. These human EEG recordings are rarely more than 7–14 days in duration, and are typically taken while a patient’s medications are tapered to promote seizures, causing corresponding changes in baseline EEG signal characteristics. In contrast, the canine data used in our paper reflect continuous long-term (multiple months) recordings of dogs with naturally occurring epilepsy. No similar human EEG data are yet available, but canine epilepsy is an excellent analog for human epilepsy [13]. The data used in our paper are an order of magnitude longer per subject than the EPILEPSIAE and comparable databases.

We also briefly comment on the difference between earlier SVM-based seizure prediction studies and our approach. All earlier studies tried to optimize the classifier performance for 20s windows [4], [24], [25], reflecting an assumption that good classification performance for 20s windows would result in accurate seizure prediction. This approach has two methodological flaws. First, the class labels for training data are known only for 1hr segments rather than for each 20s window. In fact, many 20s windows within a 1hr preictal segment may be statistically more similar to 20s interictal windows. Second, the clinical objective is to predict 1hr segments rather than individual 20s windows. The proposed SVM-based system reflects this clinical knowledge and makes predictions for 1hr segments.

An important distinction of our system lies in its new approach to handling heavily unbalanced data. In this respect, we point out several earlier attempts to apply SVM classifiers to unbalanced seizure prediction data. One approach is to specify different misclassification costs during SVM training [4]. Under this approach, it is not clear how to define the proper ratio of misclassification costs. Also, during testing stage, prediction is performed for individual 20s windows, leading to high FN error rate (equivalent to low sensitivity). Another approach is to use standard SVM classifier (under balanced setting with equal misclassification costs). According to this approach [18], using balanced SVM training is accomplished by removing the majority of interictal samples from the training set. This results in effectively discarding useful statistical information. Not surprisingly, our system’s prediction performance results (in terms of both sensitivity and FPR per day) are better than results reported in both studies [4], [18].

Finally, we summarize several important methodological aspects of seizure prediction. Sound application of machine learning methods for estimating predictive models requires clear understanding of application-specific objectives in the context of statistical assumptions underlying machine learning algorithms. This step is important and should always precede actual data modeling, i.e., application of a learning algorithm to available data. This step is called problem formalization [19], and it results in:

• Learning problem setting appropriate for a given application,

• Specific metrics used to evaluate prediction performance.

In many real-life applications, this formalization step is missing, and it leads to considerable confusion, e.g., exaggerated performance claims, non-reproducible results, etc. Notably, most widely used machine learning methods (such as neural networks, SVM, decision trees, LASSO, and so on) implement standard inductive learning setting [19], [20], where training and test inputs represent i.i.d. data samples from the same (unknown) distribution. The proposed seizure prediction system (shown in Fig. 2) has several novel data-analytic interpretations and improvements:

• During training stage, a binary classifier is estimated from labeled training samples (20s windows), as under standard classification setting. Further, we use unbalanced training data set, that includes 20s samples from many interictal segments, in addition to few available preictal segments. However, we use balanced validation data set (for model selection), to reflect the clinical requirement that the goal is to classify each 1hr test segment (as interictal or preictal).

• During testing stage, the goal is to predict a group of 180 unlabeled test samples (20s windows), under the assumption that all test samples (in this group) belong to the same class. This is clearly different from standard inductive setting. Further, the system can make three possible predictions for each 1hr test segment (e.g., reliable interictal, reliable preictal and unknown).

• Additional post-processing during testing stage is applied to ‘unknown’ predictions which are all regarded as preictals. This post-processing scheme assumes that (a) the seizure prediction system can predict interictal 1hr test segments very reliably, and (b) the system can predict preictal test segments either correctly or as ‘unreliable.’ This reflects clinical knowledge that interictal segments are inherently much easier to predict (than preictal).

VII. Conclusions

This paper presents an SVM-based system for seizure prediction using iEEG signals. The system is designed based on proper understanding of clinical considerations and their formalization into data-analytic modeling assumptions. Two important properties of our seizure prediction system are subject-specific modeling and using heavily unbalanced training data. This system also has several novel data-analytic interpretations and improvements. During the training stage, a binary classifier is estimated using unbalanced interictal and preictal data. However, a balanced validation data set is used for model selection. In addition, different time scales are utilized for the training and testing stages. The system is trained using 20s labeled windows; however, predictions are made for 1hr test segments (corresponding to a group of 180 consecutive 20s windows). Our results show that this system can achieve robust prediction of preictal and interictal iEEG segments from dogs with epilepsy.