Automatic Estimation of Volumetric Breast Density Using Artificial Neural Network-Based Calibration of Full-Field Digital Mammography: Feasibility on Japanese Women With and Without Breast Cancer

Abstract

Breast cancer is the most common invasive cancer among women and its incidence is increasing. Risk assessment is valuable and recent methods are incorporating novel biomarkers such as mammographic density. Artificial neural networks (ANN) are adaptive algorithms capable of performing pattern-to-pattern learning and are well suited for medical applications. They are potentially useful for calibrating full-field digital mammography (FFDM) for quantitative analysis. This study uses ANN modeling to estimate volumetric breast density (VBD) from FFDM on Japanese women with and without breast cancer. ANN calibration of VBD was performed using phantom data for one FFDM system. Mammograms of 46 Japanese women diagnosed with invasive carcinoma and 53 with negative findings were analyzed using ANN models learned. ANN-estimated VBD was validated against phantom data, compared intra-patient, with qualitative composition scoring, with MRI VBD, and inter-patient with classical risk factors of breast cancer as well as cancer status. Phantom validations reached an R ² of 0.993. Intra-patient validations ranged from R ² of 0.789 with VBD to 0.908 with breast volume. ANN VBD agreed well with BI-RADS scoring and MRI VBD with R ² ranging from 0.665 with VBD to 0.852 with breast volume. VBD was significantly higher in women with cancer. Associations with age, BMI, menopause, and cancer status previously reported were also confirmed. ANN modeling appears to produce reasonable measures of mammographic density validated with phantoms, with existing measures of breast density, and with classical biomarkers of breast cancer. FFDM VBD is significantly higher in Japanese women with cancer.

Introduction

Breast cancer is the most frequently diagnosed invasive cancer and the most common cause of cancer death among women globally [1]. Though incidence and mortality rates vary greatly around the world, an increase of cases worldwide has been observed in both less and more developed countries [2].

In Japan, an increase of breast cancer incidence in recent years has been found to be the predominant contributor to the overall rise of cancer incidence in women. Despite a decrease in cancer mortality overall, breast cancer mortality in Japan has only recently seen a plateau after a gradual increase since the 1960s. A closer look with respect to age reveals that while this rate has been decreasing among women aged 30–54, this is not the case among older groups [3].

Recent improvements in breast cancer prognosis can be largely attributed to the ability to detect cancers earlier while tumors are small in size and have not spread to lymph nodes or further, aided by advances in technology and efforts toward personalization of medicine. Screening X-ray mammography remains the most common and effective method for early detection of breast cancer and several randomized and controlled trials worldwide [4–6] and meta-analyses/reviews of trials [7, 8] have shown evidence of its benefits. Additionally, the ability to stratify women based on risk of developing cancer with genetic, hormonal, and lifestyle markers has proved to be of great value [9, 10]. Though breast cancer risk assessment models using multidisciplinary approaches have been in development for many years and are promising, there still appears to be much room for improvement in terms of positive predictive values of those available thus far [11]. Extracting and incorporating quantitative biomarkers from routine radiographic imaging, such as mammographic breast density, is a relatively recent trend seen likely to enhance existing risk models [12–14].

Breast density, as measured by mammography, is the amount and appearance of glandular and fibrous (more generally, fibroglandular) tissue in the breast. High breast density is a strong risk factor for developing breast cancer [15–19]. It also has significant influence over radiologist screening sensitivity [20] as well as computer-aided detection (CAD) sensitivity and specificity [21, 22] due to dense tissue and cancer having similar appearances on mammograms. On the other hand, having low breast density has recently been shown as related to worse prognosis irrespective of patient age, BMI, or menopausal status [23]. There is also some evidence indicating that density may be a correlate of the rate of breast tissue aging [24, 25]. Since these associations have been shown in both pre- and post-menopausal women [16] and the measure itself is one of the few modifiable risk factors for breast cancer [26], it is currently a major focus for breast cancer imaging and many are undertaking its research.

Standard in the industry are breast density metrics typically estimated using categorical methods [27] or measuring the area occupied by dense tissue on a mammogram using threshold segmentation [28]. Such methods tend to be subjective and can be cumbersome as well as costly since they usually need manual operation by experts with special training. As a product of this, these measurements may suffer limitations in distinguishing all dense parts of the breast, thereby not sufficiently reflecting tissue composition and their associations with cancer risk may be weakened. More recently, with the emergence and growth of digital mammography technology in parallel with spread of computerized algorithms for image interpretation and diagnosis [29], interest in measuring breast density in a fully automatic, quantitative, as well as volumetric manner has grown [18, 30–33]. Noticeably, due to the rise in information processing power and growing amounts of data being created, machine learning algorithms have also seen an increased presence in such computer-aided analyses in breast imaging and radiology as a whole [33–37].

Artificial neural networks (ANN) are a family of statistical learning algorithms that simulate the structure of biological neural networks for approximating mathematical functions and are well suited for medical applications [38]. In brief, they are made up of interlinked synthetic neurons that process information using a connectionist approach of computation and allow for machine learning due to their adaptive ability to change structure based on information processed [39]. As a product of this, ANN are capable of learning complicated patterns from data and are able to provide accurate predictions despite vague or even missing data [40]. The multilayer feedforward perceptron specifically, a popular ANN architecture, has been shown as capable of approximating any measurable function to any desired degree of accuracy [39].

As of this writing, 26 of the 50 states in the USA have enacted bills that mandate informing patients of their breast density. Several other states have proposed legislation of the same nature. Furthermore, federal legislation has been introduced that would require national reporting of whether or not the patient has dense tissue. Such efforts have also stirred up interest in other countries, including Japan [41–44]. Despite existing work reporting on mammographic breast density worldwide however, it does not appear that an automatic method of measuring quantitative volumetric breast density (VBD) on full-field digital mammography (FFDM) has yet been accepted into routine practice. Moreover, to the best of our knowledge, works using ANN to model VBD do not exist so far.

It appears a breast cancer risk predictor with high discriminatory power that would enable an increase in efficiency, efficacy, and cost-effectiveness of breast screening programs is a global objective and the effort may be facilitated by considering quantitative imaging biomarkers. The purpose of this study was to develop an innovative method to automatically quantify VBD from FFDM using a statistical machine learning approach. Specifically we modeled VBD phantom calibration data with a feedforward multilayer ANN given its universal approximation ability and evaluated our method on phantom data, against a qualitative standard of scoring breast composition, against quantitative VBD estimated from MRI, and on a population of Japanese women with and without breast cancer.

Materials and Methods

Study Population

This retrospective study was approved by the Institutional Review Board of the recruitment hospital and informed consent was waived. Mammograms acquired between February 2012 and June 2013 on one Amulet f FFDM system (Fujifilm Medical, Tokyo, Japan) in Hokkaido University Hospital (Sapporo, Japan) of 46 women, subsequently diagnosed with unilateral invasive carcinoma, were included in the study and their cranial-caudal (CC) images contralateral to the tumor were used in the analysis. MRI studies of these 46 women were also collected from the same period (3D T1-weighted images, Achieva 3.0 T system, Philips Healthcare, Best, Netherlands). Additionally, screening CC mammograms acquired on the same system in June 2013 of 53 women with negative findings were also included in the analysis. Patient demographics are summarized in Table 1. In addition, age at menarche (12.8 ± 1.5 years), post-menopausal status (n = 33), and status as nulliparous (n = 12) were available for women with cancer.

Table 1.

Study population health demographics

Parameter	Cancer	Non-cancer	p value, by t or X 2 test
Patients, n	46	53
BMI, kg/m2a	23.6 (3.9)	22.5 (4.1)	0.189
Age, yearsa	58.8 (11.0)	60.3 (11.9)	0.516
Age >50, n	30 (65 %)	40 (75 %)	0.264

^aParameters reported as mean (standard deviation)

Breast Density Modeling

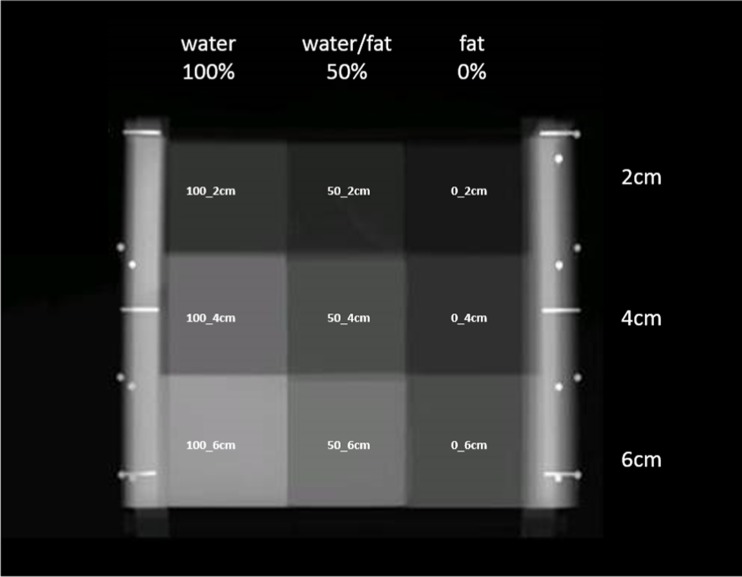
One “GEN III” VBD quality control (QC) phantom (University of California, San Francisco, CA, USA), consisting of radiographically breast tissue-equivalent materials at several fibroglandular densities and thicknesses (Computerized Imaging Reference Systems, Inc., Norfolk, VA, USA), served as the VBD reference for the ANN modeling performed in our study. In brief, the GEN III phantom was specially designed with features for calibrating parameters of FFDM systems to quantify VBD accurately and precisely [45]. It includes nine regions covering fat-equivalent 0 % VBD, 50/50 water/fat-equivalent 50 % VBD, and water-equivalent 100 % VBD compositions at 2, 4, and 6 cm thicknesses (Fig. 1), useful for our study’s calibration purposes.

Fig. 1.

GEN III phantom image. Example FFDM image of GEN III phantom, with nine breast tissue-equivalent regions used in the study as references annotated with their percent volumetric breast density (VBD, also at top) and thickness combinations (also at right)

A survey of all standard screening exams acquired on the FFDM system used in the study during June 2013 was performed to estimate expected ranges of clinical X-ray imaging parameters that affect appearance of mammograms. Table 2 briefly describes parameters included and their observed ranges: X-ray anode target and filter materials, tube voltage, current exposure time, relative image exposure sensitivity, and background detector signal. These five parameters, along with those two presented from the breast being imaged—tissue thickness and fibroglandular density, were considered primary determinants of signal intensity on FFDM for the purposes of our modeling. Next, repeated imaging of the GEN III phantom was performed across the ranges of imaging parameters seen in the survey of clinical images. In total, 300 images of the GEN II phantom were acquired. From this set of images, it would be possible to learn the relationship between the seven imaging and breast parameters with signal intensity. Conversely, fibroglandular density (VBD) could be modeled from signal intensity and six other parameters (Table 2). Before going forward with the latter however, virtual phantom data was generated from the set of physical phantom data in order to train the ANN model with a more robust calibration set than just that of the GEN III’s nine tissue composition regions. The nine VBD regions’ values of each calibration image acquired were fitted with empirical functions given thicknesses and observed signal intensity. An example of this fitting can be seen in Fig. 2 for one GEN III image. Each function was then used to compute sets of 100 interpolated points using random combinations of thickness and intensity values within expected limits given the particular image parameters used (300 images × 100 points = 30,000 virtual phantom data points total). Physical phantom data was ultimately not used directly to train the ANN model here, but instead used as one of two phantom datasets for validation of the ANN method as discussed below.

Table 2.

Imaging and breast parameter determinants of signal intensity on FFDM considered for ANN VBD calibrations

Parameter source	Parameter	Description	Ranges seen in survey of screening exams
FFDM system	Anode target and filter materials	Combination of X-ray anode target and filter materials used (molybdenum and rhodium)	Mo/Mo	Mo/Rh
	Tube voltage	Voltage of X-ray tube (kV)	26–28	28–30
	Current exposure time	Time of exposure at X-ray tube current (mAs)	26–84	40–78
	Relative image exposure sensitivity	Image exposure sensitivity optimization factor, based on median value of image histogram	33–71	31–53
	Background detector signal	Background signal intensity at location without breast tissue	680–1023	470–1023
Breast	Tissue thickness	Thickness of breast at pixel location (cm)
	Fibroglandular densitya	Volumetric density of breast at pixel location (%)

^aANN calibration of FFDM was ultimately performed so as to output fibroglandular density (VBD), taking the remaining seven parameters as input (signal intensity, in addition to the six other parameters listed)

Fig. 2.

An example of one GEN III phantom image’s nine tissue composition regions plotted with its fitted function for volumetric breast density (z-axis), given tissue thickness (x-axis) and signal intensity (y-axis). Each function was used to derive two separate sets of virtual phantom data using random combinations of thickness and intensity—the first for training the artificial neural network calibrations and the second for its validation

One three-layer (one input, one hidden, one output) ANN model was trained using all virtual calibration phantom data generated. The input layer consisted of seven nodes (one for each imaging and breast parameter considered, Table 2), the hidden layer consisted of three sigmoid nodes (approximately half the number of parameters) introducing non-linearity, and the output layer consisted of one un-thresholded linear node for numeric output (VBD). Training time was set to 500 epochs, with backpropagation weight updates set to a learning rate of 0.3 and a momentum of 0.2. ANN modeling, and VBD estimation was performed using the WEKA 3.6.12 framework (University of Waikato, Hamilton, New Zealand).

Breast Density Analysis

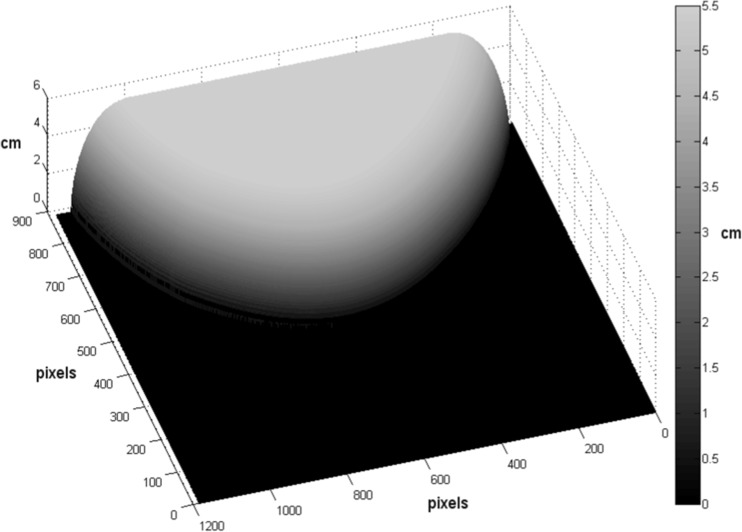
First, any protrusion of nipple at the breast image’s edge on the mammogram was removed by replacement with a smooth polynomial function fit to the surrounding edge. As only the small variant 18 × 24 cm compression paddle of the extremely rigid and non-tilting variety was in use at the study institution, the first approximation of patient breast thickness making contact with both top and bottom compression surfaces was obtained directly from the FFDM system’s digital compression thickness readout [46, 47]. The compressed portion of breast volume was treated as an even thickness plane making uniform contact with both surfaces. Remaining breast periphery volume was defined as tissue which did not make contact with either compression surface. This periphery portion of the breast volume was modeled as a half-circle cross-section whose circumference made contact with the top compression paddle, the bottom detector platform, and the breast boundary on the image at every point along the breast edge. An example thickness map can be seen in Fig. 3.

Fig. 3.

Breast thickness modeling. Example breast tissue thickness map, modeled using compression paddle thickness and breast edge as described in methods. Breast tissue thickness (in z-direction, per color bar) is projected atop the bottom detector platform (0 cm, represented as black). The sum of thicknesses at all pixels makes up total breast volume (TBV)

Total breast volume (TBV) was defined as the sum of volumes at each breast pixel (pixel area × breast thickness at pixel). Fibroglandular density (VBD) at each breast pixel was estimated with the ANN model learned using the pixel signal intensity, calculated breast thickness, and five imaging parameters described above read from the FFDM image meta-data (Table 2). Absolute dense volume (DV) of the entire breast was next calculated by totaling the product of breast thickness and VBD at each pixel of the breast. Subsequently, VBD of the entire breast was calculated as the ratio of DV to TBV.

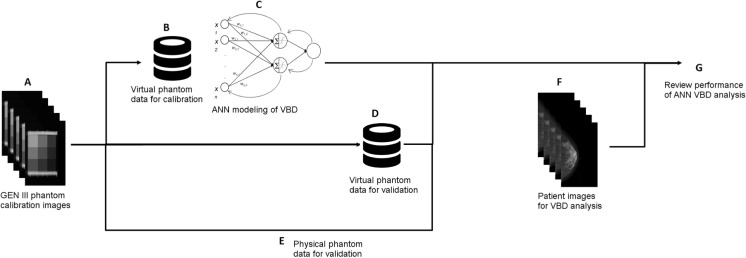
Figure 4 summarizes the study’s ANN VBD modeling and analysis as described above.

Fig. 4.

A–G Summary of mammographic breast density modeling and analysis performed in this study. Repeated imaging of a GEN III Volumetric Breast Density (VBD) phantom was performed on one FFDM system over a broad range of imaging parameters, determined by a survey of screening exams acquired as part of standard clinical practice (A). Physical phantom images were used to derive a set of virtual phantom data for the purposes of calibrating the FFDM system (B). This set of virtual calibration phantom data was used to train an artificial neural network (ANN), taking imaging parameters and data (anode and filter materials used, tube voltage, current exposure time, image exposure sensitivity, background detector signal, tissue thickness, and signal intensity) as input and outputting VBD (C). Physical phantom images were used to derive a second set of virtual phantom data for the purposes of validating the ANN calibrations of the FFDM system for calculating VBD (D). Furthermore, the original set of physical phantom images was used directly for validating the ANN calibrations (E). ANN VBD was calculated for a set of cancer and non-cancer patient’s FFDM images (F). Statistical analysis was performed fivefold: by reviewing performance on two sets of validation phantom data, intra-patient, against BI-RADS breast composition scoring, against MRI VBD, and inter-patient (G)

In addition to analysis of breast density by ANN, breast tissue composition scores were assigned to each mammogram of the patients using a standard for categorical breast density in the medical community. According to the current American College of Radiology (ACR) Breast Imaging-Reporting and Data System (BI-RADS) protocol, mammograms can be classified into four categories: a (almost entirely fatty), b (scattered fibroglandular densities), c (heterogeneously dense), and d (extremely dense) [27]. Consensus readings were performed by a radiologist specializing in breast imaging with 16 years of experience (F.K.) and a breast surgeon with 13 years of experience (M.B.) to visually estimate content of fibroglandular-density tissue within the breasts imaged.

VBD was also calculated quantitatively from MRI (as a standard of volumetric anatomical imaging) collected of the patients with cancer, using only the breast contralateral to the tumor. This was performed using a fuzzy c-means clustering technique, previously described [48]. An unsupervised algorithm assigned membership to each image voxel and automatically determined a threshold best to separate parenchyma and adipose tissue. MRI VBD was then calculated of the parenchyma (DV) as a percentage of TBV.

Mammograms used for quantitative density analysis were raw attenuation (“For Processing”) images normalized by the system’s image exposure sensitivity optimization algorithm, while those used for qualitative density assessment (BI-RADS scoring) were post-processed (“For Presentation”) images, as available clinically to radiologists. All image processing was performed using MATLAB R2012b (Mathworks, Inc., Natick, MA, USA).

Statistical Analysis

Validation of the ANN VBD modeling was performed fivefold: by reviewing performance on two sets of phantom data, intra-patient, against BI-RADS breast composition scoring, against MRI VBD, and inter-patient.

Phantom validation of ANN VBD was performed using a second set of virtual phantom data, randomly generated as the ANN training set was above, as well as that of the physical phantom itself. ANN-estimated VBD values were compared to their actual VBD values (derived in case of virtual phantom, known in case of physical phantom) using linear regression. Intensity-saturated regions on the physical phantom images, a small minority of values observed at limits of image bit depth were excluded. This saturation occurred due to some tissue-equivalent regions being at extremes of normal breast tissue composition by design (2 cm of 0 % VBD and 100 % VBD) having been exposed to broad ranges of imaging parameters extending beyond that seen from normal clinical use.

Intra-patient validation of VBD measures was performed using linear regression to determine the relationships between VBD measures calculated of non-cancer patients’ left and right breasts.

Comparisons of ANN VBD estimated of mammograms assigned in each of the four BI-RADS categories were performed using Tukey’s multiple comparisons test. Spearman’s correlation coefficient was also used to evaluate the correlation between the visual assessments and ANN VBD. Comparisons between ANN VBD measures and MRI VBD measures were performed using linear regression.

Inter-patient validations were conducted by reviewing VBD measures for their association with classical risk factors of breast cancer—age, age at menarche, BMI, menopause status, parity status, in addition to cancer status itself. Comparisons with risk factors were performed with the cancer patient data only. Linear regression was performed to determine the relationships between quantitative risk factors and values of VBD. X ² tests were used in comparing categorical risk factors, and Wilcoxon Mann–Whitney tests were used in comparing cancer status, with VBD measures. VBD measures used here of non-cancer patients were averages of left and right breasts.

Squared Pearson’s correlation coefficients (R ²) were calculated from associations of linear regression analyses performed. Root-mean-square errors (RMSE) were calculated to aggregate the magnitude of individual differences between compared values. Regression equation fit coefficients were also calculated for comparisons and their significance were tested with t tests. p values less than 0.05 were interpreted as significant. All statistical analyses were performed using JMP 11.0 (SAS Institute Inc., Cary, NC, USA).

Results

Phantom Validation

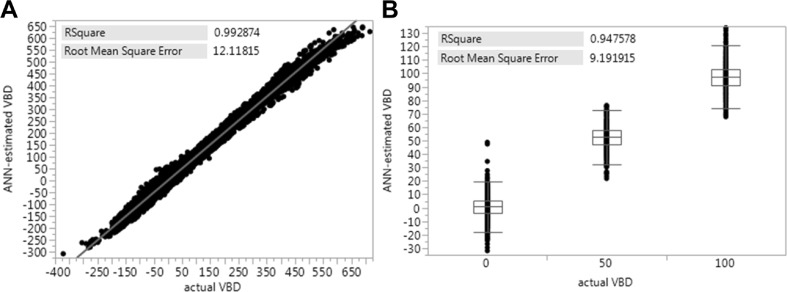
Results comparing ANN-estimated VBD against actual VBD values of the virtual and physical validation phantom data are shown in Fig. 5. Very strong correlations were achieved ranging from 0.948 estimating physical phantom VBD to 0.993 estimating virtual phantom VBD. RSME of estimated VBD ranging from 9.2 % with physical phantom data to 12.1 % with virtual phantom data were also apparent.

Fig. 5.

a, b Phantom validation of ANN VBD. Linear regression results comparing ANN-estimated VBD against actual VBD (derived with virtual phantom in a, known with physical phantom in b). In considering random combinations of imaging parameters within expected ranges seen clinically, virtual phantom data derivation produced VBD values beyond 0 and 100 % VBD (a). Comparison against physical phantom data shown as a boxplot since values quantized at 0, 50, and 100 % VBD (b). Plots are inlayed with squared Pearson’s correlation coefficients and root-mean-square errors

Patient Validation

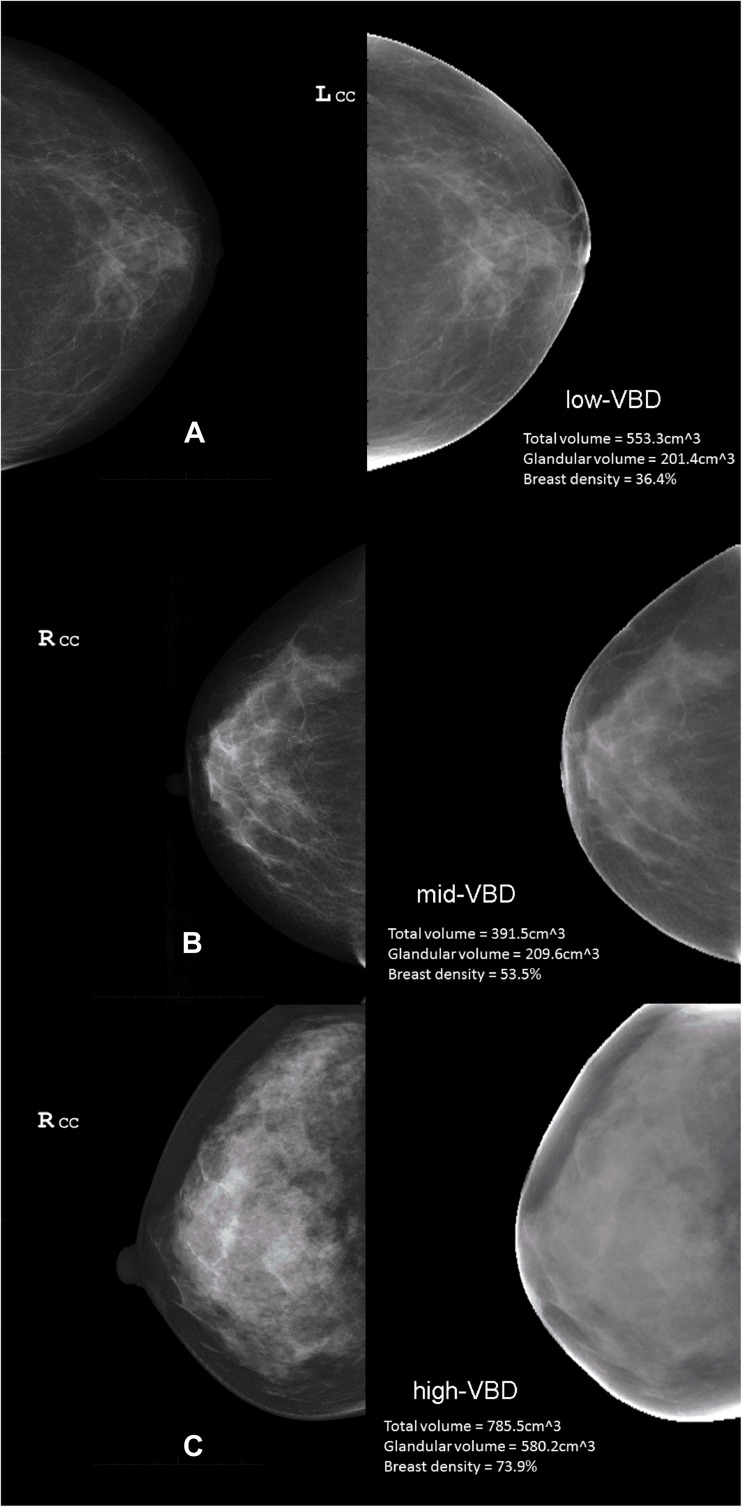
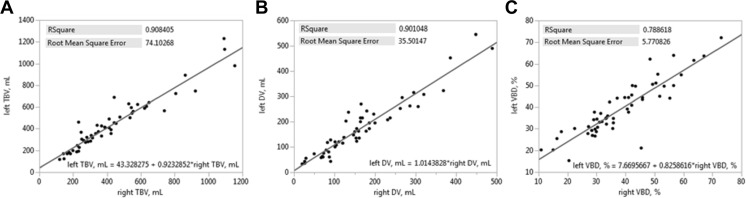
Example clinical images and ANN VBD maps of low-, mid-, and high-VBD breast are shown in Fig. 6. Comparisons of VBD results from non-cancer patients’ left and right breasts are summarized in Fig. 7. Excellent agreement between TBV values is seen with an R ² = 0.908 (Fig. 7a), as well as between DV values with R ² = 0.901 (Fig. 7b). Very good agreement between VBD values is also apparent with R ² = 0.789 (Fig. 7c). t tests reveal regression line intercepts to be significant with comparisons of TBV (43.3 ml, p = 0.040) and VBD (7.7 %, p < 0.001) between breasts.

Fig. 6.

a–c Clinical images and ANN VBD maps. Example images of low- (a), mid- (b), and high-VBD (c) breasts. In each panel, the vendor post-processed image used by radiologists for diagnostic reading is shown at left (not used in study, but shown here to illustrate images used clinically and commonly used to estimate mammographic density) and the ANN-calculated VBD map is shown at right

Fig. 7.

a–c Intra-patient validation of ANN VBD. Linear regression plots comparing ANN-estimated VBD measures of the left (y-axis) and right (x-axis) breast of non-cancer patients. Plots are inlayed with squared Pearson’s correlation coefficients, root-mean-square errors, and fit equations for comparisons of VBD (a), DV (b), and TBV (c)

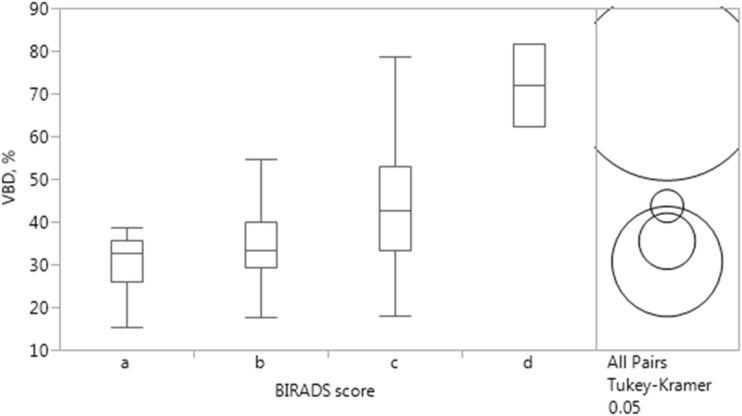
Comparison of ANN VBD against BI-RADS scoring is summarized in Fig. 8. Number of women falling into categories “a,” “b,” “c,” and “d” proved to be 6, 23, 68, and 2, respectively, with mean and standard deviation for ANN VBD distributions in each category being 30.7 % (8.0 %), 35.4 % (9.1 %), 43.7 % (13.1 %), and 71.9 % (13.6 %), respectively. Tukey’s multiple comparisons test revealed VBD in all categories as significantly different from each other (“a” and “d” p < 0.001, “b” and “c” p = 0.029, “b” and “d” p < 0.001, “c” and “d” p = 0.008), except between categories “a” and “b” (p = 0.825) as well as “a” and “c” (p = 0.062). ANN VBD and BI-RADS categories showed significant moderate association (r = 0.405, p < 0.001).

Fig. 8.

Comparison of BI-RADS breast tissue composition scoring and ANN VBD. Tukey’s multiple comparisons test reveal VBD in all categories as significantly different from each other, except between “a” and “b” as well as “a” and “c” (circles not overlapping at right, p values detailed in text)

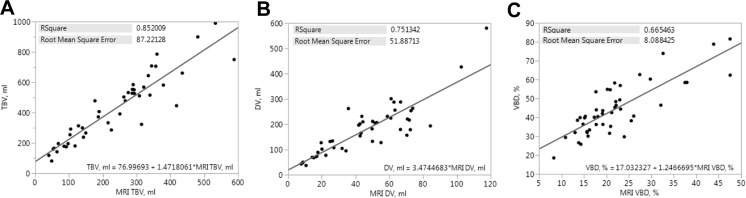
Comparison of ANN VBD results against MRI VBD is summarized in Fig. 9. Very good agreement between TBV is apparent with R ² = 0.852 (Fig. 9a), moderate agreement between DV is apparent with R ² = 0.751 (Fig. 9b), and good agreement between VBD is apparent with R ² = 0.665 (Fig. 9c).

Fig. 9.

a–c Linear regression plots comparing ANN-estimated measures of VBD (y-axis) with those measured on MRI (x-axis); total breast volume (a), dense volume (b), and volumetric breast density (c). Plots are inlayed with squared Pearson’s correlation coefficients, root-mean-square errors, and fit equations for comparisons

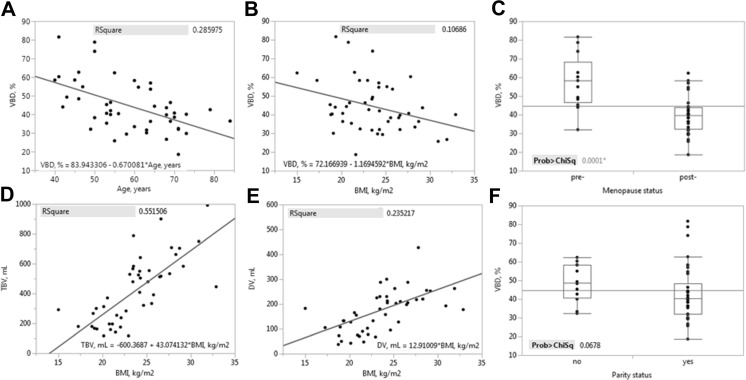
Comparisons of VBD results against classical risk factors of breast cancer that showed significant differences are summarized in Fig. 10. VBD shows a negative association with age, where slope of the regression line is significantly less than 0 with p < 0.001 (Fig. 10a). VBD also shows a negative association with BMI (Fig. 10b), where regression slope is significantly less than 0 with p = 0.027. The negative relationship of VBD with age seen above is also reflected in the comparison with respect to menopause status (Fig. 10c), where VBD in post-menopausal women is significantly lower than that of pre-menopausal women (p < 0.001). Comparing TBV and DV against the same risk factors revealed only that both are positively associated with BMI (p < 0.001, Fig. 10d and 8e). Though VBD was not significantly different given parity status in this population (p = 0.068), it is also shown in Fig. 10f and discussed below.

Fig. 10.

a–f Inter-patient validation of ANN VBD. Comparison plots of ANN-estimated measures of VBD with significant difference against classical risk factors of breast cancer; age (a), BMI (b, d, e), and menopause status (c). Though not reaching statistical significance, VBD compared with parity status (f) is also shown. Linear regression plots are inlayed with squared Pearson’s correlation coefficients and fit equations. Boxplots are inlayed with X ² test statistics

Comparisons of VBD results against cancer status are shown in Table 3. Though no significant difference was found of age, BMI (Table 1, p = 0.516 and 0.189, respectively), TBV, or DV (Table 3, p = 0.707 and 0.539, respectively) between the two groups, VBD was found to be significantly higher in the cancer group in relation with the non-cancer group (median of 41.3 vs 34.9 %, respectively, p = 0.046).

Table 3.

Comparisons of ANN-estimated measures of VBD between cancer and non-cancer patients

Parameter	Cancer			Non-cancer			p value, by Wilcoxon test
	Median (IQR)	Min	Max	Median (IQR)	Min	Max
TBV, mL	399.0 (361.0)	81.1	989.7	390.3 (290.8)	116.2	1161.0	0.707
DV, mL	178.8 (126.2)	36.7	580.2	115.8 (123.6)	26.9	497.0	0.539
VBD, %	41.3 (19.9)	18.6	81.5	34.9 (17.4)	15.5	72.5	0.046

Discussion

A novel automatic method of measuring mammographic density has been presented and evaluated in this work. Quantifying breast tissue density by ANN modeling of FFDM appears feasible, producing reasonable VBD estimates of breast tissue-equivalent phantoms, as well as of a patient population of Japanese women with and without cancer.

In our phantom validation studies of the method, excellent agreement of ANN-estimated VBD against actual values were seen reaching an R ² of 0.993 with virtual phantom data and an R ² of 0.948 with physical phantom data. In our intra-patient validation study, good to excellent agreement between VBD measures of left and right breasts of patient were apparent ranging from an R ² of 0.789 with VBD itself to an R ² of 0.908 with TBV. Comparisons of ANN VBD against two breast density metrics being used in the industry (one qualitative standard and one quantitative) also showed promising results. ANN VBD agreed and trended well with BI-RADS scoring, with categorizations having been shown as significantly different from each other (except between the lowest category with the adjacent two) and as significantly associated with ANN VBD. ANN VBD also agreed well with MRI VBD, where R ² ranging from 0.665 with VBD itself to an R ² of 0.852 with TBV were seen, in line with findings previously reported comparing mammographic VBD with MRI VBD [49]. In our inter-patient validation study, confirmations of relationships between mammographic density and several classical risk factors of breast cancer as previously reported were seen, with ANN VBD showing a negative association with age, BMI, and menopause status [15, 16, 50]. The reported association between mammographic density and cancer status [15–18] was also reflected in our findings. Despite there being no difference in age, BMI (Table 1, p = 0.516 and 0.189, respectively), or breast size (TBV, Table 3, p = 0.707) between the two groups of women, a significant difference in their VBD was seen. Women with cancer tended to have breasts higher in fibroglandular density than women without (median of 41.3 vs 34.9 %, respectively, p = 0.046), as expected.

It is our understanding that the clinical implementation of the methods developed in this study is attractive and feasible due to its ability, versatility, and simplicity. ANN, by their nature, can adapt to any measurable mathematical function with remarkable ease and we consider this study’s findings demonstrates ANN modeling has the potential to estimate VBD both accurately (against phantom references and existing metrics) and precisely (within patients). Contrasting with several other recently developed methods for quantifying breast density from mammography further highlights the uniqueness of our proposed method. It appears new works published still primarily take a 2D approach to either density- [51, 52] or parenchymal pattern-based segmentations [33, 37], though our method takes advantage of the third dimension. Other 3D approaches using mammography exist and also become more common, but are often proprietary [19, 53] or may require in-image phantoms [18]. Studies using 3D imaging modalities also continue, with MRI [54, 55] as well as 3D digital breast tomosynthesis [56], though neither of these modalities are standard for breast cancer screening. Furthermore, with the exception of Seo et al. and Japanese references mentioned in the introduction above, all aforementioned studies have looked at American, European, and Australian populations only, making our study distinctive in terms of population as well.

We note several limitations to the current study that highlight opportunities for future investigation. First, as summarized above, though previously reported relationships of mammographic density with clinical indicators of breast cancer and cancer status itself were largely confirmed with ANN VBD measures, such was not the case with parity. In both pre- and post-menopausal women, parity has been shown to strongly associated with breast cancer risk and inversely related to density [15, 16, 50]. Though it appears our comparison against parity trends in the same direction as that established (Fig. 10f), statistical significance was not reached with this population (p = 0.068). Sampling a larger population and further development of the ANN VBD method itself may allow for confirming the same relationship as well in the future, however.

Next, in looking more closely at patient analyses again, a few questions are raised. In intra-patient validation experiments, the correlation coefficient of comparing left and right measures of VBD was not as high as that of TBV and DV comparisons, though the reason for this is not completely clear. There also appears to be a trend where VBD of the left breast in non-cancer women were higher than that of their right breast, in general (+7.67 %, p = 0.003). This was also true of TBV, though less pronounced (+43.3 ml, p = 0.040). Clinical protocol at the study institution specifies mammograms be acquired to focus on glandular tissue, sometimes at the cost of dropped adipose tissue near the chest wall, though this does not explain these trends fully. Further investigation is needed as the method continues development and validation.

Furthermore, comparisons of ANN VBD with BI-RADS scoring did not show significant differences between categories “a” and the next two adjacent categories. We attribute this to there being a relatively small number of women categorized as “a” (n = 6), possibly due to the distribution of density in Japanese women being relatively high in general, which would be consistent with previous findings comparing Japanese women with others [57, 58]. Of course, the subjective nature of the manual assessment itself may have also had an effect.

Lastly, though measures were taken to exclude erroneous phantom data due to signal intensity saturation seen at imaging extremes, it was necessary to retain and use some saturated phantom regions in order to generate virtual phantom data. Inherently, calibration methods may have such limitations, and fitted functions ultimately may not agree exactly with experimental data. Further investigation is needed concerning these issues as well.

Though breast cancer incidence in Japan is only one third of that seen in Western countries, local numbers have doubled in all age groups over the past two decades. Moreover, incidence in women <50 in Japan appears similar to that in the USA and the UK, peaking at ∼45 years old [59]. Given the consistent findings in association of breast density to breast cancer risk and its potential to further personalize breast cancer care, it is very likely efforts toward capturing the measure quantitatively may permeate throughout Japan and elsewhere to identify those at high risk. We consider the conclusions of this research support the growing amount of compelling evidence that further investigation of methods to quantify VBD automatically are necessary with larger datasets and against outcomes such as performance of human and computerized screening, as well as risk of developing breast cancer.

Enabled by major advances in technology and necessitated by the rapid generation of large datasets, advances in statistical methods and machine learning are fundamentally changing the way biomedical research and image analysis is conducted. These methods have become essential not only in terms of confirmatory testing, but as well a data-driven computational knowledge discovery process. We demonstrate here the adaptability of ANN in estimating complex functions to quantify radiographic markers of VBD from FFDM.

The proposed ANN calibrated model appears to produce reasonable measures of mammographic density that are validated with breast tissue composition phantoms, associated with existing qualitative and quantitative measures of breast density, and associated with classical biomarkers of breast cancer as previously reported. VBD calculated from FFDM of Japanese women in this feasibility study appears to be significantly higher in those with cancer in comparison to those without. Further studies are warranted to confirm these findings and determine potential implications.

Compliance with Ethical Standards

Conflict of Interest

The authors declare that there is no conflict of interest that has an interest in the subject matter or materials discussed in the manuscript.