Abstract
In our previous studies, we demonstrated that repeated training on an approximate arithmetic task selectively improves symbolic arithmetic performance (Park & Brannon, 2013, 2014). We proposed that mental manipulation of quantity is the common cognitive component between approximate arithmetic and symbolic arithmetic, driving the causal relationship between the two. In a commentary to our work, Lindskog and Winman argue that there is no evidence of performance improvement during approximate arithmetic training and that this challenges the proposed causal relationship between approximate arithmetic and symbolic arithmetic. Here, we argue that causality in cognitive training experiments is interpreted from the selectivity of transfer effects and does not hinge upon improved performance in the training task. This is because changes in the unobservable cognitive elements underlying the transfer effect may not be observable from performance measures in the training task. We also question the validity of Lindskog and Winman’s simulation approach for testing for a training effect, given that simulations require a valid and sufficient model of a decision process, which is often difficult to achieve. Finally we provide an empirical approach to testing the training effects in adaptive training. Our analysis reveals new evidence that approximate arithmetic performance improved over the course of training in Park and Brannon (2014). We maintain that our data supports the conclusion that approximate arithmetic training leads to improvement in symbolic arithmetic driven by the common cognitive component of mental quantity manipulation.
Keywords: Cognitive training, Training effect, Transfer effect, Math intervention
1. Introduction
Imagine yourself in a six-day weight-training program. On the first day, you start squatting 80 lb. Then, you increase the weight adaptively on a daily basis until the last day when you squat 150 lb. Prior to this weight-training program, you could lift up to 200 lb; therefore, technically your weight-lifting performance did not improve. Nevertheless, after the six days of squatting, you find that you are able to sprint faster than you previously could! Whether your squatting performance improved or not has little to do with demonstrating the causal relationship between squatting and sprinting and its translational significance (Chelly et al., 2009; McBride et al., 2009). The essence of that causal relationship is not between squatting and sprinting but between strengthening leg muscles and sprinting.
Lindskog and Winman’s (2016) commentary on our previous paper (Park & Brannon, 2014) claim that there is no evidence of performance improvement1 in our non-symbolic approximate arithmetic condition and suggest that this undermines the conclusion that there is a causal relationship between approximate arithmetic training and symbolic arithmetic. Here we argue that regardless of whether there is evidence of improvement in a training task, evidence of selective transfer implicates a causal relationship between the training and transfer task. Furthermore we present new empirical evidence for improved performance in the approximate arithmetic training task. We maintain that our data supports the conclusion that approximate arithmetic training and symbolic arithmetic share a common cognitive element that is not shared by a host of other training tasks that we used as control conditions. We hypothesize that the cognitive element is the shared mental manipulation required by both approximate arithmetic and symbolic arithmetic.
2. Interpreting the effect of cognitive training does not require an improvement in the training task
L&W argue that there is no evidence that participants trained on solving approximate arithmetic in Park and Brannon (2013, 2014) learned to solve the task better over the course of training, and therefore that the proposed causal nature between approximate arithmetic and symbolic arithmetic should be questioned. We argue that (1) they conflate performance improvement in the observable measures with possible changes in an unobserved cognitive element that may actually explain transfer effects and (2) that transfer effects in cognitive training studies do not hinge upon evidence of improved performance in the training task.
A typical cognitive training study involves multiple sessions of a demanding training task, with a target task administered once prior to this training (pretest) and once after this training (posttest). The logic behind this paradigm is that if the cognitive elements of the training task are causally related to the cognitive elements of the target task, then repeated performance of the training task will improve the performance of the target task. Importantly, carefully designed control training task(s) and control target task(s) are critical in claiming the specificity of the causal relationship between the training and the target task. For instance, if a given training task not only improves performance in a hypothesized target task but also improves performance in other target tasks, then the causal relationship may be of less theoretical importance (albeit it may still be practically or educationally useful). Similarly, if performance in the hypothesized target task is improved not only by the hypothesized training task but also by other training tasks, then improved target task performance may be due to a test–retest effect.
One important aspect of this logic, for the purpose of present discussion, is that the interpretation of causality is between the unobserved cognitive elements of the training and the target tasks. As in our weight-training example above, if repeated squatting (training task) strengthens leg muscles (underlying element of the training task), then strengthened leg muscles (underlying element of the target task) could improve sprinting (target task). Thus, whether observable performance in the training task improves or not is not relevant for interpreting the cognitive training effect (i.e., improvement in the target task). Rather, it is the improvement, facilitation, strengthening, or growth of the unobservable cognitive elements that is important in the interpretation of cognitive training.2 Nevertheless, L&W conflate observable performance improvement in training tasks with possible changes in such an unobserved cognitive element. There may be many reasons why changes in the unobservable cognitive elements do not yield a change in the observable behavioral measure. As in the weight-training example, one scenario is that the adaptive progression of the training task does not push beyond individual capacity (i.e., over six days of weight training, you were only asked to lift up to 150 lb while your maximum capacity is in fact 200 lb). Another scenario may be that the changes in the unobservable cognitive elements do not directly enhance skills and strategies to perform the training task in short term.
Collectively in two papers we showed with three independent samples of participants that training approximate arithmetic improved symbolic math and did not improve a host of other target tasks (vocabulary, numerical-order judgment, approximate number comparison, and spatial 2-back; Park & Brannon, 2013, 2014). These three different samples were contrasted with a no-contact control condition, a condition for which participants were trained in answering multiple choice trivia questions, a spatial working memory condition, a numeral ordering condition, an approximate numerosity comparison condition, or an approximate numerosity matching condition. We found that approximate arithmetic training improved symbolic arithmetic performance in contrast to all of the other training conditions. We interpret these results to indicate that the unobservable cognitive element causally linking approximate arithmetic and symbolic arithmetic is something that is present in the approximate arithmetic task but not in the other control training tasks. Moreover, the fact that approximate arithmetic training improved symbolic arithmetic but did not improve performance on a variety of other cognitive tasks, suggests that this unobservable cognitive element selectively influenced symbolic arithmetic. We argued that these findings provide evidence for a causal link between approximate arithmetic and symbolic arithmetic driven by the facilitation in the manipulation of nonverbal numerical quantity.
Thus our first objection to the L&W commentary is that we disagree with their primary argument that no evidence of performance improvement over training nullifies the selective improvement we found in a cognitive training design. Instead, we argue that observable performance increases are not necessary to conclude that a training task has a selective benefit on a transfer task.
3. L&W’s alternative explanations are ad hoc
Our hypothesis that improvements in symbolic arithmetic are driven by the facilitation of nonverbal quantity manipulation is falsifiable and could indeed be incorrect. There may be other unobservable cognitive elements (that we are unaware of at this point) distinctively present in the approximate arithmetic but not in all other control training tasks, which may have led to improvements in symbolic arithmetic. However, L&W have not offered a hypothetical compelling alternative, and more importantly they have not offered any data in support of the ad hoc alternatives they propose.
3.1. The priming hypothesis
L&W argue that “priming” of the “approximate numeric processes [may have been] … transferred to the symbolic arithmetic test.” First, L&W’s use of the word priming is unclear. They raise an example from a perceptual priming study (e.g., when given a word-fragment completion task, it is faster and easier to complete [aa_d_a_k] after seeing the word aardvark) demonstrating that priming effects can last up to 17 years (Mitchell, 2006). However, approximate arithmetic involves nonverbal cognitive operations. Thus, it is unclear how the approximate arithmetic task is comparable to such a perceptual priming task or even a semantic priming task (e.g., the word bread primes butter). Second, regardless of the use of the word priming, their explanation of the priming effect directly contradicts with their argument that “the [approximate arithmetic training] results have causes that do not depend on a lasting improvement.” If symbolic arithmetic can be primed by approximate arithmetic for the next 17 years, why is that not a lasting improvement?
3.2. The general speed increase hypothesis
L&W argue that approximate arithmetic may “promote a nonspecific response speed increase” which is then “transferred to post-training tasks.” However, they offer unsatisfactory and ad hoc explanations for (1) why approximate arithmetic training and only that training promotes speeded response and (2) why symbolic arithmetic test and only that test is influenced by increased speed.
In one case, L&W argue that increased speed does not help responding faster in the numeral order judgment test because that test had a fixed number of trials and was self-paced, while increased speed helps responding faster in the symbolic arithmetic test because that test had a fixed time limit. However, it is just as reasonable to argue that participants would respond faster when there is a fixed number of trials in an effort to end the experiment earlier, and slower when there is fixed time because they know responding faster does not let them finish the experiment earlier.
In another case, L&W argue that the numerical symbol ordering training task (which in fact was the single training task that had the strongest emphasis on speed of response) does not induce the same sense of urgency that the approximate arithmetic task supposedly did, because numerical symbol ordering “does not involve discrete items, but a continuous stream of stimuli.” However, there is no satisfactory evidence to claim why a discrete item-to-item progression induces urgency but not the other. Furthermore it is unclear why the visuo-spatial short-term memory training (a.k.a. Corsi block training) would not have promoted a sense of urgency given that the longer you have to keep the block positions in memory the more likely that you will fail to reproduce the order.
Finally, if L&W’s argument that approximate arithmetic is the only training task that promotes non-specific response speed increase and urgency, then we should observe a reduction in response time (RT) over training in that task. To test this hypothesis, we computed the linear slope of the RT across all the blocks throughout the training sessions for each individual. Across participants, the slope of the RT in the approximate arithmetic training was very weakly negative (t(17) = −0.370, p = 0.716, Cohen’s d = −0.087). The slope of the RT in the approximate comparison training, however, was very strongly negative (t(17) = −4.233, p = 0.001, d = −0.998), suggesting participants tended to respond much faster in later sessions than in earlier sessions. Thus, if any condition promoted a sense of urgency, it appears it was the approximate numerosity comparison condition and yet that condition did not show transfer to symbolic arithmetic.
While we are not convinced by either of the ad hoc explanations offered by L&W for the selective transfer we obtained, we nevertheless believe that alternative hypotheses should be tested empirically. We welcome additional research that attempts to compare our shared quantity manipulation proposal with alternative proposals for the unobservable cognitive elements that are shared between approximate arithmetic and symbolic arithmetic.
4. Shortfalls of the simulation approach and new evidence for a training effect in the approximate arithmetic training task
L&W argue that the adaptive training procedure used in our study (Park & Brannon, 2013, 2014) is problematic in terms of assessing performance improvement in that training task. L&W offer simulations that suggest changes in the difficulty level, similar to what we report, would occur even in the absence of improved performance. We agree with this point and acknowledge that we did not present evidence of improved performance in our paper and therefore our conclusion that “performance improved significantly over six sessions in all four training conditions” was premature (Park & Brannon, 2014).3 In this section, however, we argue that there is a critical limitation to L&W’s simulation approach and introduce a novel empirical approach that tests a training effect in adaptive training task performance.
4.1. Shortfalls of the simulation approach
L&W’s simulation approach requires a formal model of internal decision-making process. To simulate an observer performing the approximate arithmetic task, L&W used a well-established model of the approximate number system (e.g., Barth et al., 2006; Pica, Lemer, Izard, & Dehaene, 2004) and represented the precision of numerosity representation (Gaussian noise, σ) as a single parameter that changed over training. However, this assumption is questionable because approximate arithmetic is hypothesized to involve at least three cognitive components (numerosity representation, visuo-spatial short-term memory, and mental operations) and that single parameter is insufficient to capture all those hypothetical cognitive processes. In other words, there is no guarantee that the internal decision model of the simulation is capable of capturing changes in the unobservable cognitive processes of interest, in which case the simulation results are likely to be invalid. To take this logic further, imagine a training task that has no known formal decision model. If one cannot formulate a decision model for a training task, no simulation can be performed, in which case there will be no (valid) results. For instance, numerical symbol ordering training employed in Park and Brannon (2013, 2014) likely has no known formal model to explain the decision process. Thus, simulation results of that training task (if there is any4) will likely be invalid. Again, because the decision model used in L&W’s simulation of approximate arithmetic is underspecified, the results are likely to be invalid as well. In sum, we argue that L&W’s simulation approach generally has little merit.
4.2. Empirical test of the training effects
As we describe in Section 2, we do not believe a failure to show performance improvements in a training task impacts our main conclusions. Nevertheless we were prompted by L&Ws simulations to reanalyze our data to test for improved performance in the training task. We describe here a new analysis that shows improved performance in the approximate arithmetic training data.
The problem with the adaptive training design is that difficulty increases over sessions, making it difficult to assess whether subjects improve at a given difficulty. Thus we conducted a new analysis that quantified the trend in accuracy under comparable or identical difficulty levels across time (Fig. 1). To do this we first identified the progression of the log-difference level across all 60 blocks for each participant (Park & Brannon, 2014). The log-difference levels were binned by deciles (e.g., 0–10th percentile, 10–20th percentile, … up to 90–100th percentile). Time (block number) and performance (block accuracy) data from four of the bins (30–40th, 40–50th, 50–60th, 60–70th percentiles) were extracted for further analysis. More extreme bins were excluded from the analysis because extreme bins (especially the high log-difference values) are likely to contain more variable log-difference levels and to represent a short time range, which may bias this trend analysis (see Fig. 1). A linear mixed-effects model was then used to predict the block accuracy with time (block) as a fixed-effects regressor and a random effect of bin. The fixed-effects parameter estimate for time enabled us to assess the linear slope of block accuracy within comparable log-difference levels across training.
Fig. 1.
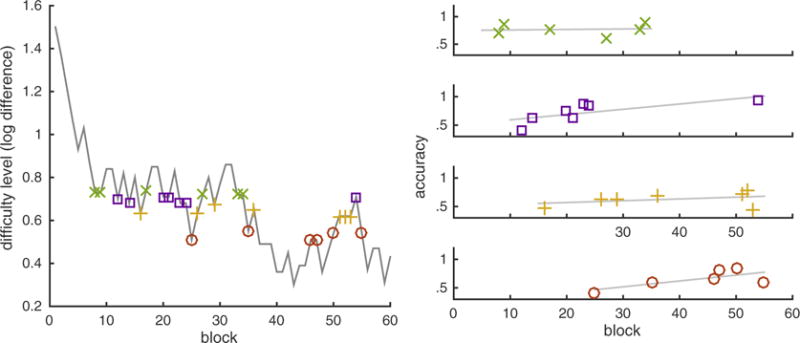
A graphical description of the empirical approach to test the training effects in an adaptive training paradigm. The left panel illustrates the progression of the difficulty level (log-difference) of the approximate arithmetic training in one representative participant. From this progression, we took samples of data where the difficulty ratios were identical or comparable across training blocks. Specifically, the log-difference levels were binned by deciles, and four decile bins (30–40th, 40–50th, 50–60th, 60–70th percentiles) were selected for further analysis. Each of the four bins is represented in different color. The graphs on the right panel illustrate the block accuracy of the approximate arithmetic task separated by the four bins, and the gray line represents the best linear fit. Using a linear mixed-effects model with block as a fixed-effects regressor and a random effect of bin, we tested whether or not accuracy increased as a function block. The logic is that if participants improved in solving the training task over the course of this adaptive training, then their accuracy for the identical/comparable difficulty level should increase over time. We found a positive linear slope across participants who performed approximate arithmetic training (t(17) = 1.965, p = 0.066 in match trials; t(17) = 2.219, p = 0.040 in compare trials), suggesting that participants’ performance improved over training. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The analysis was done separately for match and compare trials in approximate arithmetic. The linear slope from the linear mixed-effects model was marginally positive in the match trials (t(17) = 1.965, p = 0.066, d = 0.463) and significantly positive in the compare trials (t(17) = 2.219, p = 0.040, d = 0.523) across participants. It should be noted that while the p-values hovered around the p = 0.05 threshold, the effect size was moderate, providing confidence in the interpretation that accuracy measures from identical/comparable difficulty-level blocks improved over training. Thus, the empirical data suggest that approximate arithmetic performance improved over the course of training.
We conducted a similar analysis for participants in each of the other training conditions. For the approximate numerosity comparison training condition the linear slope showed no strong evidence for improvement in the accuracy both in the trials where the two dot arrays were intermixed (t(17) = 0.176, p = 0.862, d = 0.041) and in the trials where the two dot arrays were presented side-by-side (t(17) = 1.250, p = 0.228, d = 0.295).
In the case of numerical symbol ordering training, there was a small effect size in the slope for the linear mixed-effects model, although it did not reach statistical significance (t(16) = 1.222, p = 0.239, d = 0.296). This result is interesting because numerical symbol ordering training did result in near transfer—that is, participants trained with this task showed selectively improved numeral order judgment both in terms of accuracy (Park & Brannon, 2013) and RT (Park & Brannon, 2014). This pattern again illustrates that performance improvement of the training task is not needed to yield a transfer effect.
In the case of short-term memory training, the range of difficulty levels (span) was too small to create many bins. Thus, the accuracy measure from the median span across all blocks was regressed on time to estimate performance change under the same difficulty level over training. The slope of this regression model was significantly positive (t(17) = 4.449, p = 0.000, d = 1.049), demonstrating strong evidence for improved performance over training. Yet, this training did not yield selective improvement in symbolic arithmetic.
5. Supplementary information for Park and Brannon (2014)
We would like to thank L&W for giving us this opportunity to revisit our dataset, and we will take this opportunity to include a few details about the procedure in Park and Brannon (2014) that were inadvertently omitted.
First, in Experiment 1 of Park and Brannon (2014), the number of days between the pretest session and the first training session ranged between 1 and 4, except in one participant who received the first training session about 7 h after the pretest session. 81% of the participants received the first training session exactly 1 day after the pretests. The number of days between the last training session and the posttest session ranged between 0 and 3. 84% of the participants had 1 day in between sessions. 9% of the participants had no overnight break; however, they had on average of 3 h in between the sessions. One-way ANOVA showed no significant group differences in the number of hours between last training session and posttest session (F(4,88) = 1.02, p = 0.400).
Second, there were 36 numerical comparison trials in each block for approximate comparison training. This was in contrast to 20 trials per block in the approximate arithmetic training. We used a greater number of trials in approximate comparison to roughly equate time-on-task to that of approximate arithmetic, although approximate comparison still resulted in a slightly shorter time-on-task, so the rest period in between blocks was slightly increased to roughly match the start and end time of the training sessions.
6. Summary and conclusion
While L&W raise reasonable questions, there are significant shortfalls in their conclusions. In Section 2, we argue that an improvement in a target task does not need to be accompanied by improved performance measure of a training task, because the unobservable cognitive element that drives the transfer effect may be changed during training without directly improving performance in the training task. In Section 3 we take issue with L&Ws ad hoc alternative explanations for the selective transfer we obtained. In Section 4, we describe the shortfalls of L&W’s simulation approach and present a new empirical analysis that suggests there was in fact improvement in performance in the approximate arithmetic training.
We hope that our response (1) highlights the strength of our original conclusion that there is a causal relationship between approximate arithmetic and symbolic arithmetic, (2) emphasizes that cognitive training studies must include appropriate control transfer tasks and appropriate control training conditions to warrant conclusions of selective transfer, (3) demonstrates that improvement in the training task is not necessary for showing selective transfer, and (4) illustrates that although performance changes in adaptive training tasks are sometimes difficult to quantify they can be measured by approaches like the one we offer here. We thank L&W for giving us an opportunity to bring these discussion points to the table.
Acknowledgments
We thank Nick DeWind, Emily Szkudlarek, and Stephanie Bugden for helpful discussions. We also thank Martin Buschkuehl for his valuable comments to an earlier version of the manuscript. This work was supported by NIH 5R01HD079106 to EMB.
Footnotes
Note that Lindskog and Winman actually argue that there is “no evidence of learning.” However, they conflate performance improvement in the observable measures with possible changes in unobserved cognitive elements due to training (see Section 2). We suggest to reserve the term learning for the latter, and that it is more accurate to use the term performance improvement in this case.
In the case of working memory training, one study found that improvement in the target task was only observed in participants who showed an improvement in the training task (Jaeggi, Buschkuehl, Jonides, & Shah, 2011). Such a finding, however, does not argue against the idea that observable measures may not be directly driven by changes in an unobserved cognitive element.
The same criticism applies to other previous influential papers that use adaptive training procedures. For instance, Jaeggi, Buschkuehl, Jonides, and Perrig (2008) state that the “training groups improved in their performance on the working memory task.” Jaeggi et al. (2011) also interpreted changes in the difficulty level between the first two and the last two training sessions as a “significant improvement.” Likewise, Thorell, Lindqvist, Bergman Nutley, Bohlin, and Klingberg (2009) also quantified similar changes and interpreted that “children had improved significantly on all trained tasks.” Nevertheless, it should be noted that later work in n-back training revealed a significant improvement in n-back performance at posttest compared to pretest (Buschkuehl, Hernandez-Garcia, Jaeggi, Bernard, & Jonides, 2014; Jaeggi et al., 2010; Stepankova et al., 2014).
In fact, L&W did not provide a simulation for numerical symbol ordering training.
References
- Barth H, La Mont K, Lipton J, Dehaene S, Kanwisher N, Spelke E. Non-symbolic arithmetic in adults and young children. Cognition. 2006;98(3):199–222. doi: 10.1016/j.cognition.2004.09.011. [DOI] [PubMed] [Google Scholar]
- Buschkuehl M, Hernandez-Garcia L, Jaeggi SM, Bernard JA, Jonides J. Neural effects of short-term training on working memory. Cognitive, Affective, & Behavioral Neuroscience. 2014;14(1):147–160. doi: 10.3758/s13415-013-0244-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chelly MS, Fathloun M, Cherif N, Amar MB, Tabka Z, Van Praagh E. Effects of a back squat training program on leg power, jump, and sprint performances in junior soccer players. The Journal of Strength & Conditioning Research. 2009;23(8):2241–2249. doi: 10.1519/JSC.0b013e3181b86c40. [DOI] [PubMed] [Google Scholar]
- Jaeggi SM, Buschkuehl M, Jonides J, Perrig WJ. Improving fluid intelligence with training on working memory. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(19):6829–6833. doi: 10.1073/pnas.0801268105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeggi SM, Buschkuehl M, Jonides J, Shah P. Short- and long-term benefits of cognitive training. Proceedings of the National Academy of Sciences of the United States of America. 2011;108(25):10081–10086. doi: 10.1073/pnas.1103228108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeggi SM, Studer-Luethi B, Buschkuehl M, Su YF, Jonides J, Perrig WJ. The relationship between n-back performance and matrix reasoning—implications for training and transfer. Intelligence. 2010;38(6):625–635. [Google Scholar]
- Lindskog M, Winman A. No evidence of learning in non-symbolic numerical tasks – A comment on Park & Brannon (2014) Cognition. 2016;150:243–247. doi: 10.1016/j.cognition.2016.01.005. [DOI] [PubMed] [Google Scholar]
- McBride JM, Blow D, Kirby TJ, Haines TL, Dayne AM, Triplett NT. Relationship between maximal squat strength and five, ten, and forty yard sprint times. The Journal of Strength & Conditioning Research. 2009;23(6):1633–1636. doi: 10.1519/JSC.0b013e3181b2b8aa. [DOI] [PubMed] [Google Scholar]
- Mitchell DB. Nonconscious priming after 17 years invulnerable implicit memory? Psychological Science. 2006;17(11):925–929. doi: 10.1111/j.1467-9280.2006.01805.x. [DOI] [PubMed] [Google Scholar]
- Park J, Brannon EM. Training the approximate number system improves math proficiency. Psychological Science. 2013;24(10):2013–2019. doi: 10.1177/0956797613482944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Brannon EM. Improving arithmetic performance with number sense training: An investigation of underlying mechanism. Cognition. 2014;133(1):188–200. doi: 10.1016/j.cognition.2014.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306(5695):499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Stepankova H, Lukavsky J, Buschkuehl M, Kopecek M, Ripova D, Jaeggi SM. The malleability of working memory and visuospatial skills: A randomized controlled study in older adults. Developmental Psychology. 2014;50(4):1049–1059. doi: 10.1037/a0034913. [DOI] [PubMed] [Google Scholar]
- Thorell LB, Lindqvist S, Bergman Nutley S, Bohlin G, Klingberg T. Training and transfer effects of executive functions in preschool children. Developmental Psychology. 2009;12(1):106–113. doi: 10.1111/j.1467-7687.2008.00745.x. [DOI] [PubMed] [Google Scholar]


