General van der Waals potential for common organic molecules

Abstract

This work presents a systematic development of a new van der Waals potential (vdW2016) for common organic molecules based on symmetry-adapted perturbation theory (SAPT) energy decomposition. The Buf-14-7 function, as well as Cubic-mean and Waldman-Hagler mixing rules were chosen given their best performance among other popular potentials. A database containing 39 organic molecules and 108 dimers was utilized to derive a general set of vdW parameters, which were further validated on nucleobase stacking systems and testing organic dimers. The vdW2016 potential is anticipated to significantly improve the accuracy and transferability of new generations of force fields for organic molecules.

Graphical abstract

1. Introduction

Molecular recognition is central to biomolecular processes such as metabolism, signal transduction, and gene expression.¹ In drug discovery processes, one major goal is to identify small ligands that can selectively bind to a macromolecular target with a high affinities and favorable pharmacological properties.^{1b, 2} Computational modeling holds the promise of accelerating drug discovery and guiding molecular design by predicting ligand interactions with biomolecular targets.³ Although computational modeling and simulation can provide quantitative understanding of the mechanism underlying molecular recognition,^{2c, 4} effective sampling methods and accurate force fields continue to be the main challenges for reliable prediction of molecular interactions.

Classical force fields such as AMBER,⁵ CHARMM,⁶ OPLSAA,⁷ and GROMOS⁸ typically model the electrostatic interactions with fixed atomic point charges and treat van der Waals (vdW) interactions via simple functions, such as the Lennard-Jones (12-6) potential. As computationally efficient alternatives to quantum mechanical (QM) calculations, such classical point charge models have been widely used in molecular dynamic simulations of biological systems.^{5a, 7} Newer models that explicitly represent anisotropic atomic charge distributions and respond to surrounding changes via polarization⁹ can potentially lead to improved transferability between different chemical and physical environments. For example, the point charge model can be replaced by atomic multipole moments, such as dipole and quadrupole, to capture the anisotropic nature of the electronic structures.¹⁰ The polarization effects have been modeled by interactive atomic induced dipoles,¹¹ fluctuating charges¹² or Drude oscillators models.¹³ The AMOEBA force field, which employs atomic multipole moments and dipole polarizabilities, is one typical example of such newer models.

During the past decade, the AMOEBA polarizable force field¹⁴ has been extensively tested for water,¹⁵ various small molecules,¹⁶ ions,¹⁷ ionic liquids,¹⁸ and proteins systems.¹⁹ However, due to the missing treatment of charge penetration, atomic multipoles are unable to capture electrostatic interactions at very short range where the atomic electron clouds overlap. The current AMOEBA force field and most other widely used fixed-charge force fields address this issue by using a less repulsive van der Waals potential to compensate the charge penetration contribution in short range. The problem with this approach however, is that the resulting vdW parameters are less transferable.²⁰ Given the recent advances in computational chemistry and the computing power, the noncovalent interaction energy components can be computed using highly accurate quantum mechanical methods²¹ such as symmetry-adapted perturbation theory (SAPT).²² Recently, we have developed a general electrostatic model to incorporate the charge penetration effect based on the atomic multipole moments in AMOEBA.²³ This model significantly improves the agreement between point multipoles and quantum mechanical electrostatic energies from SAPT2+ decomposition even at short inter-molecular distances. This improvement leads to the need to revisit vdW potentials that are capable of capturing SAPT repulsion and dispersion energy.

Lennard-Jones (12-6) potential is one of the most common functions to describe the exchange-repulsion and dispersions interactions.²⁴ It has been adopted in a range of force fields²⁵ such as AMBER^5a and CHARMM⁶. This simple function contains only two parameters and it is faster to compute than exponential terms.²⁶ Other Lennard-Jones potential forms include the Lennard-Jones (9–6) function²⁷ and the Lennard-Jones (12–10) function^25f which is an alternative to the usual Lennard-Jones (12–6) function in AMBER^5a to model hydrogen bonds. As a special case of the Buckingham potential function,²⁸ the exponential-6 potential is widely used in force fields^{25c, 29} such as MM2,³⁰ MM3,³¹ and MM4.³² However, both Lennard-Jones and exponential-6 potentials account poorly for the high quality noble gas data while a simple buffered 14-7 (Buf-14-7) potential can accurately reproduce the noble gas potentials over a range of distances.³³ Besides the two interaction-specific parameters, the well depth and minimum-energy distance, the Buf-14-7 functional form is capable of adjusting the curvature of request depending on two shape parameters.

In addition to the functional forms, vdW interactions between unlike atoms (e.g. O and H) depend on the suitable combination of mixing rules to generate the well depth and distance parameters, unless pair-wise parameters are specified for all combinations. Current available force fields employ either geometric or arithmetic mean as the combining rules, which lead to large errors for mixed noble gas atom pairs.³⁴ More elaborate combination rules have been proposed, involving additional parameters such as polarizability, ionization potentials, or dispersion force coefficients.³⁵ Newly derived combining rules, Waldman-Hagler (W-H)³⁴ and Halgren (HHG),³³ require no additional parameters other than the well depth and distance, also well reproduce the experimental values of noble gas interactions.

In classical force fields, electrostatic parameters, such as atomic charges, are normally computed from ab initio quantum mechanics directly.³⁶ The so-called vdW interaction in a force field is actually less well-defined and is essentially utilized to capture everything beyond the charge-charge interactions, including the charge penetration, charge transfer and perhaps some of the many-body polarization effects in condensed-phase. Additional difficulty in force field parameterization lies in the limitations of ab initio methods. A “perfect” ab initio force field will not reproduce experimental condensed-phase thermodynamic properties without explicit quantum corrections such as zero-point energy. Thus deriving vdW parameters by fitting to gas-phase ab initio molecular interaction energy alone is insufficient if the resulting force fields were intended for condensed-phase systems, even with many-body polarization were explicitly accounted for. Given these limitations, the most effective approach, pioneered by Jorgensen and co-workers in developing OPLS and OPLSAA force fields,³⁷ has been to used derive vdW parameters directly against reliable and widely available liquid properties such as density and heat of vaporization.

This work presents the first systematic attempt to develop a new van der Waals potential, vdW2016, for common organic molecules based on SAPT energy decomposition. We first examined several common vdW functions to determine the best functional form based on noble gas interaction energy data. A general set of parameters (element based) was then determined by fitting to the exchange-repulsion and dispersion energies for 756 dimers made of 39 common organic molecules with different configurations and separation distances (S108x7 database). This new vdW potential was further validated on nucleobase stacking systems as well as on a testing set of small organic dimers (S36x7). Overall, the vdW2016 potential is expect to provide accurate prediction of vdW interaction energy for common organic molecules, including drug candidates.

2. Computational Methods

2.1. Van der Waals functions and mixing rules

The vdW functional form and mixing rules were determined from noble gas systems including helium (He), neon (Ne), argon (Ar), and krypton (Kr), where the non-bonded interactions were dominated by vdW interactions. Three typical vdW functional forms, Buf-14-7, Buckingham, and Lennard-Jones (12–6), were examined using the same sigma and epsilon extrapolated directly from the exchange-repulsion and dispersion energy of SAPT2+/aug-cc-pV5Z calculations (the dispersion energy has been scaled by 0.89 to match the CCSD(T)/CBS total interaction energy).²³ Different combinations of the vdW functions with three sets of mixing rules, Cubic-mean/HHG, W-H/W-H, Cubic-mean/W-H were examined against the SAPT2+/aug-cc-pV5Z potential surfaces. (See different functional forms, mixing rules and parameters in the SI, Table S1). According to the best fitting results with the perfect match with SAPT (Figure 1) and the lowest RMSE (Table 1, Table S2), we chose the Buf-14-7 (Eq. 1) as the functional form, and as mixing rules, Cubic-mean for σ (Eq. 2) and W-H for ε (Eq. 3). The parameter ε_ij is the potential well depth, and R_ij/σ_ij is the ratio between the actual separation of i-j atomic sites and the minimum-energy distance.³³ We also provided the results calculated using the same mixing rules, Cubic-mean/W-H, but the optimized delta and gamma and in the SI, where the Buf-14-7 is still the best choice.

Figure 1.

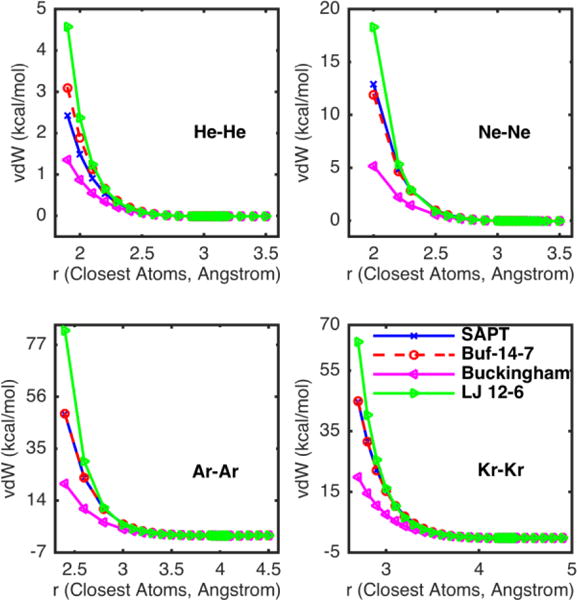
Plots of homodimer vdW energies in noble gas systems calculated by Buf-14-7 (red dash line with circle markers), Buckingham (magenta line with left-pointing triangle markers), and Lennard-Jones 12-6 (green line with left-pointing triangle markers) compared to QM reference SAPT2+ calculation (blue line with cross markers). Same sigma and epsilon parameters were used in all calculations: 3.11 Å and 0.014 kcal/mol for He; 3.31 Å and 0.048 kcal/mol for Ne; 4.07 Å and 0.160 kcal/mol for Ar; and 4.38 Å and 0.218 kcal/mol for Kr.

Table 1.

Differences between heterodimer vdW energies in noble gas system given by different combinations of vdW functional forms and mixing rules (ε_ij/σ_ij) compared to SAPT 2+ results. Same functional forms and parameters as above were used. Distances are ratios relative to the vdW minimum distances extrapolated from the SAPT2+ exchange-repulsion and dispersion energy.

RMSE	Distance	Buf-14-7	Buckingham	LJ (12-6)
Cubic-mean/HHG	0.6~0.9	0.540	4.245	3.731
	0.9~1.1	0.005	0.007	0.007
	1.1~2.0	0.004	0.009	0.008
W-H/W-H	0.6~0.9	0.256	4.369	3.392
	0.9~1.1	0.004	0.005	0.005
	1.1~2.0	0.002	0.008	0.006
Cubic-mean/W-H	0.6~0.9	0.238	4.439	3.060
	0.9~1.1	0.003	0.005	0.005
	1.1~2.0	0.001	0.007	0.006

$$E_{\mathit{vdw}}={\epsilon }_{\mathit{ij}}{\left(\frac{1+\delta }{\frac{R_{ij}}{{\sigma }_{ij}}+\delta }\right)}^7\left(\frac{1+y}{{\left(\frac{R_{ij}}{{\sigma }_{ij}}\right)}^7+y}-2\right)$$ (1)

$${\sigma }_{ij}=\frac{{\left({\sigma }_{ii}\right)}^3+{\left({\sigma }_{jj}\right)}^3}{{\left({\sigma }_{ii}\right)}^2+{\left({\sigma }_{jj}\right)}^2}$$ (2)

$${\epsilon }_{ij}={\left({\epsilon }_{ii}{\epsilon }_{jj}\right)}^{1/2}\frac{2{\left({\sigma }_{ii}\right)}^3{\left({\sigma }_{jj}\right)}^3}{{\left({\sigma }_{ii}\right)}^6+{\left({\sigma }_{jj}\right)}^6}$$ (3)

2.2. S108x7 fitting database

The interaction energies of seven heterodimers between methane, amine, ethene and water were added to the S101x7 database (39 molecules and 101 dimers)²³ to construct the S108x7 fitting database. (See newly added energy data in the SI, Table S4). The same structural optimization, distance generation and energy decomposition methods, including the extrapolation scheme and the scaling of dispersion energy, as in the S101x7 database construction were used to generate the energy profiles for newly added dimers. The parameters of the vdW model were optimized to match the sum of the dispersion and exchange energy in the S108x7 SAPT2+ database, which contains the total interaction energies as well as decomposed energy components for 108 pairwise interactions at seven distances (0.70, 0.80, 0.90, 0.95, 1.00, 1.05, 1.10 times of the equilibrium distances R). The mean unsigned error (MUE), mean signed error (MSE), and root-mean-square error (RMSE) were calculated to examine the performance of different models at all 7 distances for a total of 756 dimers. This set includes 216 dimers at 2 short distances (0.70R and 0.8R), and 540 dimers at 5 near equilibrium distances (0.9R, 0.95R, R, 1.05R and 1.10R).

2.3. Parameterization

The nonlinear least square optimization method, “lsqnonlin”, in Matlab³⁸ was applied to all fitting, including the optimization of delta and gamma parameters in the Buf-14-7 vdW function, σ and ε parameters for each vdW type. The inputs of the “lsqnonlin” program were the objective function, initial parameters, and parameter limits. The objective function is the mean squared difference between calculated vdW and SAPT values of all structures. Starting with the parameters of the 18 atom types listed in the previous charge penetration paper²³, we added ten types in order to better capture the vdW interactions. Detailed type assignments can be found in the results section. The parameter limits set higher and lower boundaries for each parameter, which were used to enforce the chemical trend for the σ parameters. The vdW energy for each model was calculated by using the SAPT geometry, vdW parameters, and mixing rules. An example is included in the SI.

2.4. S36x7 SAPT0 testing dataset

An S36x7 testing dataset was constructed containing newly generated non-aromatic heterodimer interaction energies between polar-nonpolar, polar-polar, and nonpolar-nonpolar molecules. Fifteen representative molecules were chosen, which covers 11 chemical types including alcohol, acid, amide, amine, sulfoxide, sulfide, alkane, alkene, alkyne, haloalkane, and phosphate ions in the S108x7 fitting database. Identical to the structural generation and optimization procedures used in the S108x7 database, the structures of the newly added pairs were optimized using MP2/cc-pVTZ method in Gaussian09 program.³⁹ Each dimer complex was studied for seven separation distances ranging from 0.70–1.10 times the equilibrium distance. For each of the resulting dimer configurations, the interaction energy was decomposed using SAPT0/jun-cc-pVDZ method⁴⁰ in PSI4 program.⁴¹ (See detailed energy data in the SI, TableS13). For aromatic systems, existing data for nucleicbases were utilized in the testing.⁴²

3. Results and Discussion

3.1. Parameters development

An iterative process was applied to determine the vdW types and parameters: the universal shape parameters delta and gamma for Buf-14-7, and the interaction parameters sigma and epsilon for each atom type. We first kept the shape parameters fixed to optimize sigma and epsilon. Then, the delta and gamma were optimized with the fixed the interaction parameters generated previously. New vdW types were added after analyzing the systematic errors of the model compared to SAPT. The final optimized delta and gamma parameters in the Buf-14-7 vdW function are 0.273 and 0.025, respectively. For comparison, the previous AMOEBA¹⁵ and MMFF94⁴³ force fields both used 0.07 and 0.12 for delta and gamma, respectively.

In Table 2, all atoms in the S108x7 system were clustered into 28 vdW types. In addition to the 18 atom types used in the charge penetration paper²³, ten more vdW types were added to better capture the vdW interactions. Polar H was divided into three types depending on whether it is connected to O, N or S. C in alkene (—C=C—) was separated from C in the carbonyl group. In aromatic rings, a separate type was used for C atoms bonded to non-carbon atoms (N and halogens). Both C and H in alkane molecules (sp3 C only bonded to other sp3 C or H) were separated from the general sp3 C and non-polar H to two new classes. Additional types were assigned to oxygen ion in acetate and phosphate as well as sp2 hybridized oxygen in phosphoric acid to capture their vdW interactions. S in sulfide and sulfoxide used different set of σ and ε, while P, F, Cl, and Br have only one set of parameters each.

Table 2.

VdW types and parameters (σ and ε) for H, C, N, O, P, S, F, Cl, and Br. Reduction factors for all Hs are 0.93, and are 1.00 for other molecules. Delta and gamma are 0.273 and 0.025, respectively. N represents for vdW type index.

N	vdW type	σ (Å)	ε (kcal/mol)	N	vdW type	σ (Å)	ε (kcal/mol)
1	H (nonpolar)	3.50 9	0.005	15	N (sp2)	3.81 6	0.109
2	H (nonpolar, Alkane)	3.47 5	0.005	16	N (aromatic)	3.69 1	0.131
3	H (polar, NH/N aromatic)	3.45 0	0.002	17	O (sp3, hydroxyl, water)	3.57 1	0.078
4	H (polar, OH)	3.54 1	0.002	18	O (sp2, carbonyl)	3.69 0	0.077
5	H (polar, SH)	3.55 0	0.005	19	O (O− in AcO−)	3.69 5	0.097
6	H (aromatic, CH)	3.38 5	0.003	20	O (O− in HPO42−)	3.69 3	0.097
7	C (sp3)	3.83 9	0.036	21	O (O− in H2 PO4−)	3.69 1	0.085
8	C (sp3, Alkane)	3.81 6	0.012	22	O (O in H3 PO4)	3.55 0	0.068
9	C (sp2, Ethene)	4.39 3	0.038	23	P (phosphate)	4.85 6	0.039
10	C (sp2, C=O)	4.12 9	0.012	24	S (sulfide, R−SH)	4.54 1	0.156
11	C (sp)	4.25 5	0.046	25	S (sulfur IV, DMSO)	4.41 3	0.130
12	C (aromatic, C-C)	4.42 0	0.025	26	F (organofluorine)	3.55 1	0.050
13	C (aromatic, C-X)	4.22 1	0.034	27	Cl (organochloride)	4.42 1	0.124
14	N (sp3)	3.75 3	0.141	28	Br (organobromine)	4.65 5	0.178

Good correlation has been found with a R² value of 0.955 between the average σ for each element and the atomic radius calculated via SCF minimal basis-set functions⁴⁴ (See detailed information in the SI, Figure S1 and Table S5). This trend confirms the physical meaning of the sigma parameters is in relevance to the atomic diameters. For simplicity, all H atoms use the same “reduction factor,” which translates the vdW center of hydrogen toward the heavy atom along the chemical bond.¹⁵ An optimal value of 0.93 was determined from the least-squared fit along with all other vdW parameters.

The van der Waals interactions calculated using the vdW2016 potential and the AMOEBA09⁴⁵ vdW component were compared to SAPT2+ results of the S108x7 dataset in Figure 2. By using a limited set of parameters, the new potential agrees with SAPT2+ with a correlation coefficient R² of 0.996 across all dimers and distances. Figure 3 shows the 108 dimers energy profiles from both the vdW2016 potential and SAPT. The errors (blue line) of the new vdW potential are rather even across all the dimers. As expected, the AMOEBA09 vdW parameters, based on the same Buf-14-7 function but with different shape parameters and mixing rules, underestimates the short-range vdW energy in comparison with SAPT, although displaying a very reasonable correlation with QM results (R² of 0.946). The AMOEBA09 vdW parameters were parameterized to capture the total interaction energy of molecule dimers and liquid thermodynamic properties. This underestimation of the repulsive energy was needed to compensate the missing charge penetration term in the original AMOEBA model. A similar trend is also seen for other fixed-charge force fields as discussed in later sections. In contrast, the vdW2016 potential has been specifically fitted to the sum of the dispersion and exchange-repulsion energy from SAPT.

Figure 2.

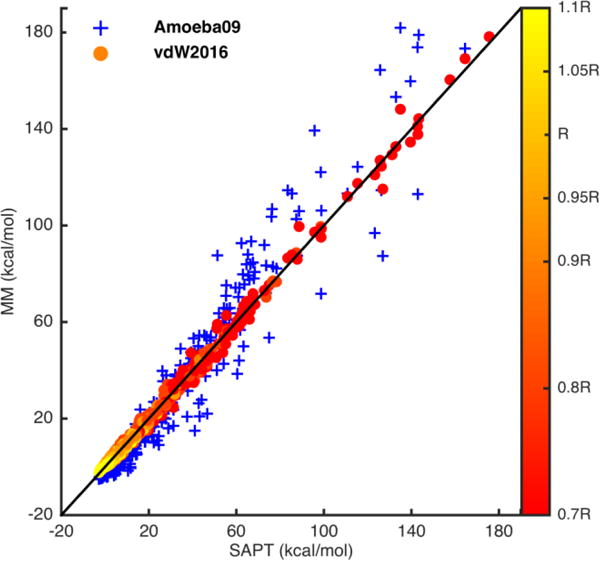
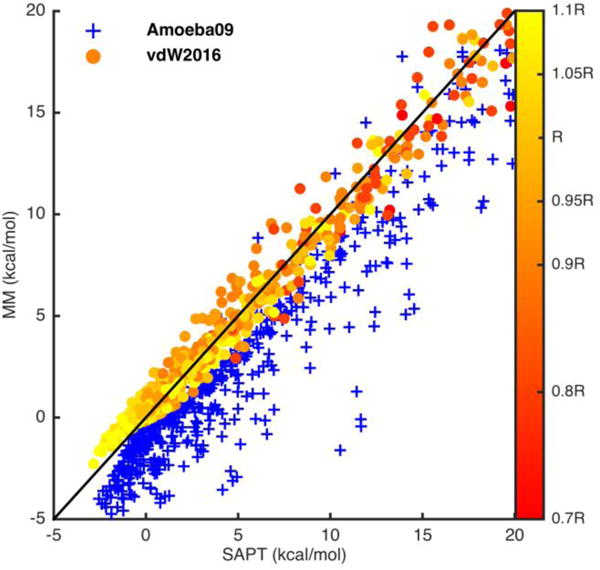
Plots of the vdW energy calculated by vdW2016 (circles filled with distances relative to the equilibrium distance R, red represents the short-range distances and yellow the long-range distances) and AMOEBA09 model (blue plus signs) compared to the SAPT2+/CBS/scaled results. The AMOEBA09 vdW parameters were derived to reproduce the total dimer interaction energies and liquid thermodynamic properties in a force field without charge penetration corrections. The top plot contains all the 7 distances complexes in the S108x7 data set. The bottom plot expanded the top one and contains complexes with energy from −5 kcal/mol to 20 kcal/mol.

Figure 3.

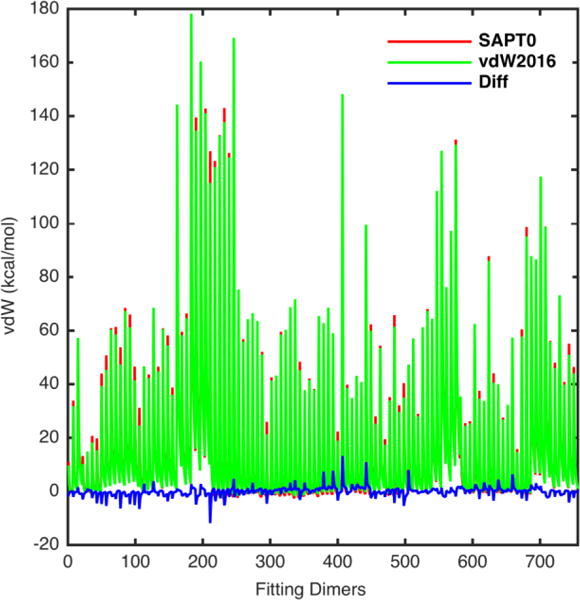
Plot of the fitting vdW energy calculated by vdW2016 model (green line) compared to the SAPT2+/CBS/scaled energy (red line). The blue line is the energy differences between the vdW2016 and QM results.

The statistical analysis of the vdW2016 model and the AMOEBA09 vdW component at different distances are listed in Table 3. For 108 dimers at all 7 distances, the vdW interaction energy values given by the vdW2016 potential and SAPT2+ are in excellent agreement, with a MUE of 1.054 kcal/mol, a RMSE of 1.680 kcal/mol, and a MSE of −0.006 kcal/mol. This agreement is remarkable given that some of the vdW energies at close distances are over a hundred kcal/mol (Figure 3), i.e. 56.5% of the complexes have the energy over 50kcal/mol and 14.8% are over 100 kcal/mol. For dimers in five distances near equilibrium, the MUE and the RMSE of the newly parameterized vdW potenial are 0.658 and 0.835 kcal/mol, respectively, a more than 3-fold reduction from the values of the previous AMOEBA model, 2.125 and 2.780 kcal/mol, respectively. The good agreement persists when including dimers at short separations (0.70, 0.80) where the absolute vdW interaction energy is rather high (44.3 kcal/mol averaged over 216 dimers). Overall, the vdW2016 potential tends to slightly underestimate both the exchange-repulsion energy (less repulsive) at short separations given a MSE value of −0.345 kcal/mol, and the attraction energy (less attractive) near equilibrium distances, with a MSE value of 0.130 kcal/mol.

Table 3.

Differences between vdW energies given by vdW2016 potential, AMOEBA09 parameters, compared to SAPT2+/CBS/scaled results in the S108×7 fitting dataset.

S108 fitting set	Statistics	New vdW model (kcal/mol)	AMOEBA09 vdW component (kcal/mol)
0.90R-1.10R (108x5 pairs)	MUE	0.658	2.125
	MSE	0.130	−1.970
	RMSE	0.835	2.780
0.70R-0.80R (108x2 pairs)	MUE	2.044	9.374
	MSE	−0.345	2.691
	RMSE	2.851	15.044
All distance 0.70R-1.10R (108x7 pairs)	MUE	1.054	4.196
	MSE	−0.006	−0.639
	RMSE	1.680	8.378

It should be noted that the target SAPT2+ attractive dispersion energies have been scaled by 0.89 in the S108x7 database.²³ This scaling was obtained by comparing the SAPT2+ total interaction energy with high-level ab initio data (CCSD(T)/CBS)). We have also derived a set of parameters by fitting to the non-scaled SAPT2+/CBS QM results with the same functional form, shape parameters as above. After optimization, the σ and ε parameters were increased slightly with similar overall quality. Detailed results and parameters are included in the SI (Table S6, Table S7 and Figure S2).

In addition, damping function (Eq. 4) constructed by Mooij et al.⁴⁶ with a simple c_damp = 3.54 used by Weitao Yang⁴⁷ was tested to further adjust the short-range dispersion. With the same vdW interaction parameters but slightly different delta and gamma shape parameters (0.272 and 0.026, respectively), a same RMSE value of 1.68 kcal/mol was obtained with a slightly better repulsion at short separations (RMSE 2.850 kcal/mol) but somewhat worse dispersion at the equilibrium distance (RMSE 0.837 kcal/mol). Thus, we argue that shape parameters, delta and gamma, in the Buf-14-7 are sufficient and the damping function is unnecessary for reproducing the vdW interaction energies of small organic molecules. See the detailed statistical analysis in the SI, TableS8.

$$f_d\left({\sigma }_{ij}\right)={\left(1-exp\left[-c_{\mathit{damp}}{\left(\frac{R_{ij}}{{\sigma }_{ij}}\right)}^3\right]\right)}^2$$ (4)

3.2. Validations

The transferability of the vdW2016 model and parameters has been further validated on molecular dimers that have not been included in the fitting process. Interaction energies between stacked nucleobase dimers were used to test aromatic parameters. The additional S36x7 heterodimer interaction energies were used to validate other polar and non-polar vdW types.

For aromatic systems, which are computationally expensive to obtain high level SAPT energy decomposition (e.g. SAPT2+), a previously published nucleobase stacking interaction energy database²¹ with SAPT0 data was used in the validations. The QM energy decomposition was obtained using the SAPT0/jun-cc-pVDZ method. We have only adopted dimers with total interaction energies less than 10 kcal/mol in the testing. The sum of the SAPT0 repulsion and dispersion energy was compared with the energy calculated by the vdW2016 model. The comparison with AMBER FF^145a and CHARMM 36⁴⁸ from the previous publication has also been included, however, it should be noted again that the vdW terms in these force fields were derived by fitting to QM total interaction energy and/or liquid properties and implicitly include contributions such as charge penetration etc. Overall, the vdW2016 potential yields an excellent correlation with the SAPT0 energy (R² = 0.983) for all base pairs in the translation and rotation configurations (Figure 4). It is also clear that the vdW energy from fixed-charge force fields systematically underestimates the vdW energy (too attractive) when compared to SAPT0 results, likely to compensate of the missing charge penetration contribution. The detailed statistical analysis of the different models and configurations are included in the SI (Table S9 and Table S10).

Figure 4.

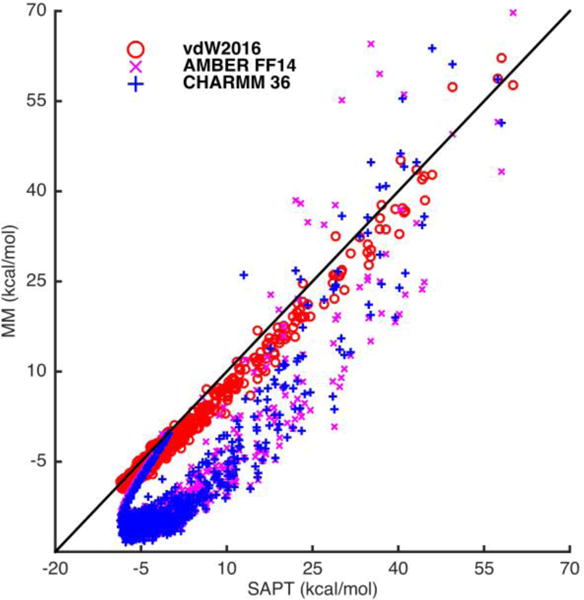
Plot of the vdW energy calculated using the vdW2016, AMBER FF14, and CHARM 36 models compared to the SAPT0/jun-cc-pVDZ QM results of ten stacked base pairs across their rotational (Twist, Roll, Tilt) and translational (Rise, Slide, Shift) configurations. The geometries were taken from Sherrill’s work.²¹

The AG and CT stacking pairs were examined in details in Figure 5. For some configurations, such as Shift, Slide, and Twist, a systematic shift was observed between the vdW2016 potential and the SAPT0, with the new vdW model predicting somewhat lower energy. This is due to the missing higher order terms in the SAPT0 level calculation while the vdW2016 potential was parameterized using SAPT2+ data. Although the SAPT0/jun-cc-pVDZ method performs qualitatively well for the mixed and dispersion dominated (MX/DD) complexes with a mean absolute error (MAE) of 0.32 kcal/mol compared to the CCSD(T)/CBS method,^{40b, 49} the SAPT0 interaction energy is systematically shifted upwards (less negative) compared to SAPT2+ and yields positive mean signed errors in several systems.^40b For example, it was shown that the MSE of SAPT0, compared to CCSD(T)/CBS,⁴⁹ is 0.11 kcal/mol for the Non-Bonded Curves (NBC10) systems,^49–50 0.47 kcal/mol for the HSG set,⁵¹ 0.08 and 0.05 kcal/mol for the mixed influenced and dispersion-dominated bound complexes in S22 set,⁵⁰ respectively. Thus, the errors would be reduced if the SAPT2+ method was used to conduct the comparison.

Figure 5.

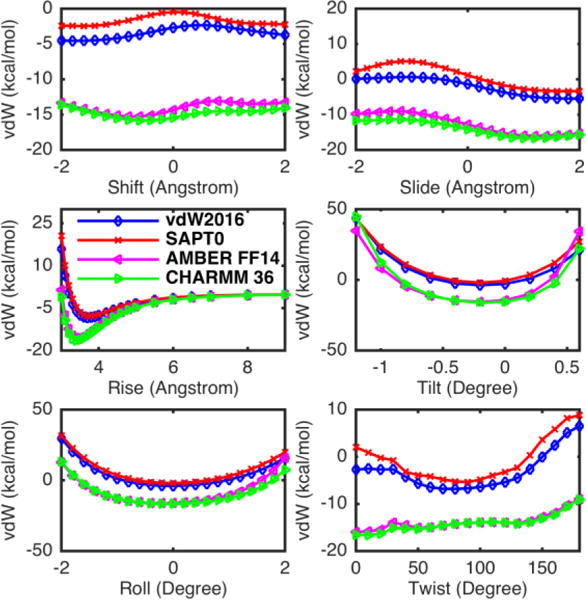
Plots of the AG:CT stacking vdW energy calculated using the vdW2016, AMBER FF14, and CHARMM models across rotational (Twist, Roll, Tilt) and translational (Rise, Slide, Shift) configurations.

Heterodimers of non-aromatic small organic molecules, which were not included in the fitting, were further examined to validate the transferability and accuracy of the vdW2016 potential. Fifteen representative molecules with 11 chemical types were chosen from the S108x7 database to construct the testing dataset (S36x7) covering interactions among alcohol, acid, amide, amine, sulfoxide, sulfide, alkane, alkene, alkyne, haloalkane, and phosphate ions. This dataset includes new cross interactions that were not covered in the original S108x7 database used for parameterization. Again, the vdW SAPT0 energy decomposition was obtained on these new dimers. Overall, a strong correlation, with R² value of 0.994 for 259 heterodimers, was found in this testing set. In contrast to the optimization process, where the new vdW potential tends to underestimate the dispersion attraction near equilibrium distance (MSE 0.13 kcal/mol), an overestimation was found (MSE of −0.11 kcal/mol) in the same distance range, which might due to the lower level SAPT0 reference energy is less attractive than the higher level SAPT2+ references used in S108x7 dataset. See more detailed data in the SI (Table S11, Table S12, Figure S3).

All the testing vdW energies predicted by the vdW2016 model are compared with the SAPT0 results in Figure 6. Larger errors, either overestimation or underestimation, are shown as the peaks and valleys in the blue line. Overall, the errors are rather even across all heterodimers and the shapes of the curve match the QM results well. Figure 7 shows the interaction energy surfaces of the selected pairs in details. Excellent agreement between the vdW model and SAPT0 can be observed for interactions between hydrogen bond donor (polar H) and acceptors (O, N or F), pairs made of alcohol, acid, amide, amine, haloalkane. For dimers with very short separation distances at around 1.3 angstrom, the vdW potential tended to overestimate the vdW energies in comparison with the SAPT0 results (See the plots of dimers DMSO-HPO₄²⁻, AcOH-Peptide, AcOH-DMSO, MeNH₂-CH₃SH, and CH₃SH-H₂PO₄⁻ in Figure 7). In addition, the T-shaped configuration of interactions between ethyne’s H and ethene’s double bond are the most problematic in both fitting and testing sets. Anisotropic vdW treatments, such as the Gay-Berne potential,⁵² may be necessary for C and H in unsaturated hydrocarbon.

Figure 6.

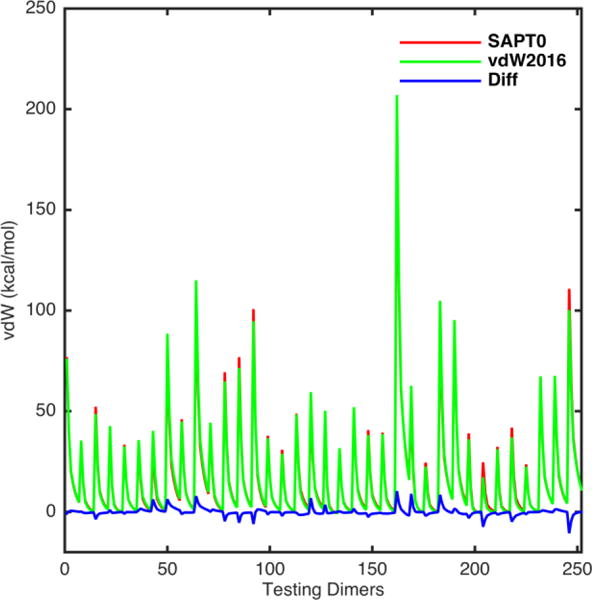
Plot of the vdW energy values of the testing set S36x7 calculated using the vdW2016 potential (green line) compared to the QM reference SAPT0/jun-cc-pVDZ (Red line). The blue line is the energy differences between the vdW2016 and SAPT0 results.

Figure 7.

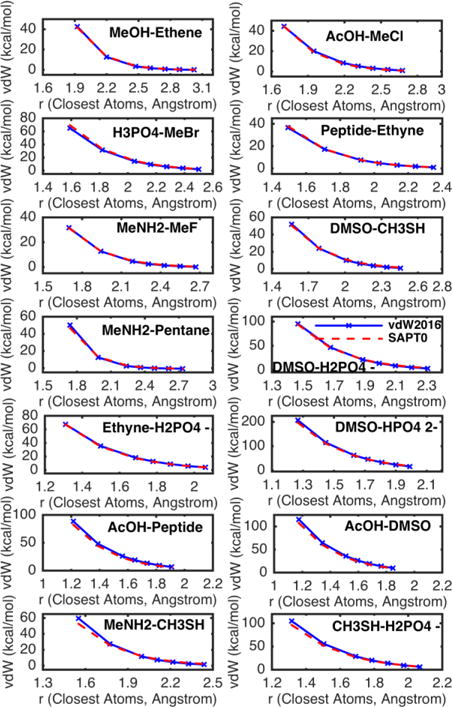
Plots of the vdW energy surfaces of selected pairs calculated using the new vdw2016 model (green line) and the reference SAPT0/jun-ccpVDZ (red line) in the S36x7 dataset.

4. Conclusions

The van der Waals interaction is one of the important fundamental noncovalent interactions in molecular systems. Accurate treatment of vdW interaction is crucial in molecular modeling. Based on investigations of noble gas molecular interactions, the soft-core Buf-14-7 was found to best reproduce the QM (SAPT2+) repulsion and dispersion energy. The most effective mixing rules were found to be Cubic-mean for sigma and W-H for epsilon. A quantum mechanics interaction energy database (S108x7) was used to calibrate the vdW model, which contains the detailed energy components for 756 pairwise interactions between 39 common organic molecules at various inter-molecular distances. The parameters of the vdW2016 model were derived by fitting to the sum of the SAPT2+/CBS/scaled exchange-repulsion and dispersion energy in the S108x7 database. With 28 pairs of vdW parameters for 9 chemical elements, we are able to reproduce vdW interaction energy for all dimers in this database with a RMSE of 1.68 kcal/mol (0.84 kcal/mol if within 90–110% of the equilibrium distances). Subsequently, the accuracy and transferability of the vdW2016 potential were validated by comparing to the SAPT0 energy of an additional set of stacked nucleobase⁴² and newly generated cross-interacting dimers (S36x7). As a result, the vdW2016 potential yields strong correlations with R² of 0.983 for all base pairs and 0.994 for 259 heterodimers compared to the SAPT0 energy.

Overall, the present systematic study shows that the accuracy and transferability of the new vdW2016 potential are excellent in comparison with the computationally rigorous SAPT data. However, it should be noted that the gas-phase dimer interaction energy data alone is insufficient for determining the vdW potential for condensed-phase applications. This new potential nonetheless serves as a starting point for future refinement using molecular dynamics simulations targeting liquid properties^{7, 53}. Recent advancement of decomposition of intermolecular forces has made it possible to construct molecular mechanics force fields more systematically and rigorously, which hopefully will lead to higher chemical accuracy and more general transferability.