Automatic car driving detection using raw accelerometry data

Abstract

Measuring physical activity using wearable devices has become increasingly popular. Raw data collected from such devices is usually summarized as “activity counts”, which combine information of human activity with environmental vibrations. Driving is a major sedentary activity that artificially increases the activity counts due to various car and body vibrations that are not connected to human movement. Thus, it has become increasingly important to identify periods of driving and quantify the bias induced by driving in activity counts. To address these problems, we propose a Detection Algorithm of Driving via Accelerometry (DADA), designed to detect time periods when an individual is driving a car. DADA is based on detection of vibrations generated by a moving vehicle and recorded by an accelerometer. The methodological approach is based on short-time Fourier transform (STFT) applied to the raw accelerometry data and identifies and focuses on frequency vibration ranges that are specific to car driving. We test the performance of DADA on data collected using wrist-worn ActiGraph devices in a controlled experiment conducted on 24 subjects. The median area under the receiver-operating characteristic curve (AUC) for predicting driving periods was 0.94, indicating an excellent performance of the algorithm. We also quantify the size of the bias induced by driving and obtain that per unit of time the activity counts generated by driving are, on average, 16% of the average activity counts generated during walking.

Introduction

The use of wearable accelerometry-based monitors of physical activity (PA) is becoming increasingly popular in large epidemiological studies. Objective PA measurements obtained from accelerometers are used to complement and calibrate the widely used self-reported questionnaires. In fact, the transformation of questionnaires is also profound and they are increasingly moving to wearable platforms such as smart phones or tablets and focus on a time range that is short enough to obtain reliable reports. Detailed quantification of the total PA volume as well as fractions that are attributable to specific types of daily activities is very challenging and has remained an elusive goal of PA monitoring research. Wearable accelerometers provide objective quantification of body acceleration, which is expected to be a good proxy for PA in the free-living environment. Objectively measured PA was shown to be significantly associated with age and health outcomes [1], while the total PA volume and amount of sedentary time are associated with demographic covariates [2].

Driving is a common sedentary activity that plays an important role in the day-to-day activities. Studies have shown that drivers in the United States spend on average 46 minutes per day driving a car [3]. The amount of daily driving has been shown to be associated with health outcomes, quality of life and obesity [4]. In addition, car driving is associated with physical and social functioning, especially among older adults [5]. Thus, objectively quantifying the amount and timing of daily driving for individuals is a crucial component of modern PA studies. An unfortunate consequence of the nature of accelerometer data is that acceleration produced during car driving is much higher than acceleration during typical sedentary behavior. If left unaccounted for this may result in overestimation of the daily PA, especially for individuals who drive more and walk less. The overestimation of PA by Fitbit® fitness trackers has been observed and reported before (see, e.g [6]). However, at this point no practical solution exists for addressing this problem.

In this paper, we propose an algorithm (Detection Algorithm of Driving via Accelerometry – DADA) for objective recognition and quantification of car driving. Our algorithm is based on the frequency domain analysis of the raw accelerometry signal within a short window of activity and provides an extension to previously developed algorithm for detection of sustained harmonic walking [7]. We apply DADA to the raw accelerometry data collected from the ActiGraph GT3X+ accelerometers worn on the left wrist in a controlled experiment undertaken at Indiana University on a group of 24 adults who performed walking and driving activities. We report the accuracy of DADA for driving detection using the area under the ROC curves (AUC) as well as the sensitivity and specificity at the universal optimal threshold. In addition, we quantify the overestimation of the PA recorded by the devices during the driving period as a proportion of walking activity per unit time.

Methods

Study Population

Twenty-four adults (8 men, 16 women) participated in a study to identify walking, stair walking and driving from raw accelerometry data. The study included a walking trial (approximately 0.66 miles) followed by a driving trial (approximately 12.8 miles). The walking trial included walking on a level ground, up and down stairs, and up and down inclined paths. Immediately after the walking period, participants were accompanied to their vehicle, which they drove on a predefined route that included both highway and city driving. The walking trial lasted between 10 and 14 minutes while the driving trial lasted between 18 and 30 minutes, depending on traffic. Participants wore four ActiGraph GT3X+ accelerometers—one on the left ankle, one on the right ankle, one on the left hip, and one on the left wrist. In this paper, only the data acquired from the left wrist were used for investigation. The accelerometers measured raw acceleration along three axes at a sampling rate of 100Hz. All four devices were synchronized to the same external clock providing parallel measurement for four body locations. A human observer recorded the start times, while the stop times were recorded and reported by the study participants. To ensure accuracy of the start and stop times, drivers were also asked to hit their steering wheels 3 times at the beginning and end of the driving trial to internally mark the raw accelerometry data with 3 consecutive spikes in the signal. The study was approved by the Institutional Review Board of the Indiana University; all participants provided written informed consent.

Driving detection algorithm - DADA

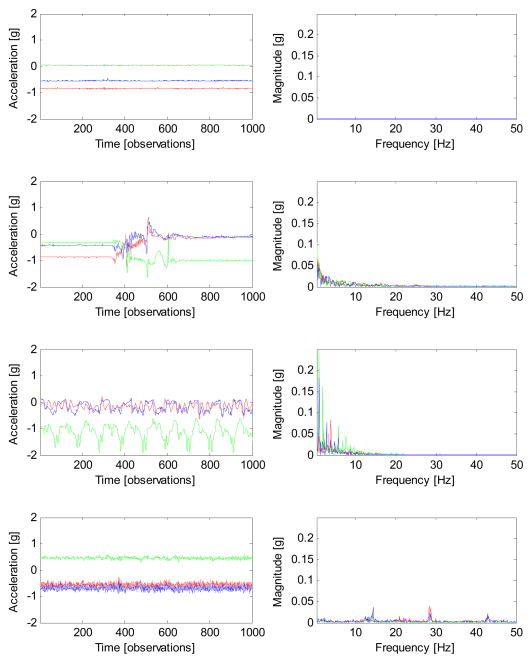
Figure 1 displays raw accelerometry data collected during four different activities: sitting still, standing up, walking and driving. The left panels show the raw acceleration signals, while the right panels their corresponding frequency spectra. The frequency spectrum is a standard technique in signal processing used to decompose the original signal in its fundamental frequencies, or vibrations. For sitting still (top plot) and standing up (top middle plot) the spectra do not have characteristic peaks, indicating that there is no dominant periodic movement of the device during these activities. For walking (middle bottom plot), there is an obvious group of frequencies that have a higher magnitude. As pointed out in [7], the range of “walking-related” frequencies is usually between 1 and 10 Hz, depending on the subject and the step frequency. These peaks have the highest magnitude in the range of 1 to 3 Hz and gradually fade out at higher harmonics. “Driving-related” frequencies (bottom set of plots) are typically above 8 Hz, accompanied by a set of harmonics. We believe that this is due to car vibrations induced by mechanical movements and road imperfections. The most remarkable part of these plots is that the dominating walking and driving frequencies are well separated, at least for this subject. This provides the intuition behind the algorithm: identify driving periods as those periods when the dominating frequency is higher than the maximum frequency of movement in humans.

Figure 1.

Sample of the data from the wrist-worn accelerometers. Raw signals (left column) and their corresponding frequency spectra (right column) for various activities: sitting still (top row), standing up (top middle row), walking (bottom middle row) and driving (bottom row).

The idea that vibrations from a running car affect a driver is not new. Several studies described this phenomenon [8] [9], but the focus was on reduction of vibrations that decrease comfort and may cause distraction or sleepiness. Our interest focuses on assessing whether accelerometers worn by individuals driving a car can provide sufficient information to detect driving. Hypothetically, this should be possible. Indeed, for a car with a 16in wheel diameter moving at 30mph, the rotational speed of a wheel is about 10.5Hz. Commonly used wearable accelerometers can capture signals up to 100Hz or more. Therefore, according to a Nyquist-Shannon theorem, vibrations up to 50Hz that are transmitted from the car to the human body should be detectable. In real-life experiments the wheel diameter and speed are unknown, while speed can change continuously during the experiment. Our algorithm overcomes these difficulties by scanning the entire high-frequency range of the spectrum that cannot be associated with any known periodic human activity, such as walking or running.

DADA algorithm

Let the measured signal be x(t) = {x₁(t), x₂(t), x₃(t)}, where x₁(t), x₂(t), x₃(t) denote the measurement along each of the orthogonal axis x, y and z of the wearable device at time t, respectively. We concentrate on the driving detection for a sensor placed on the left wrist of a driver. A subject may change a position of the device, which may affect the signal along each axis due to a change in the angle relative to earth’s gravity [10] [11] [12].

To alleviate the effect of hand movement we focus on the vector magnitude $VM(t)=\sqrt{x_1{(t)}^2+x_2{(t)}^2+x_3{(t)}^2}$. This form of the signal should be invariant to rotations and more robust to translations. The signal is then decomposed into its various frequencies using Fourier transformation in short non-overlapping time windows. The automatic time-sliding Fourier transform is referred to as the Short-time Fourier Transform (STFT) [13]. For a window of size τ centered at time t the STFT is a function of the frequency f and the time t and is expressed as

$$X(f,t)=\sum _{u=t-\tau /2}^{t+\tau /2}x(u)h(u)e^{-t2\pi f\frac{1}{T}}$$ (0.1)

Here h(u) is a weighting function that assigns more weight to observations that are closer to the middle of the interval centered at time t, and less weight to observations that are farther away.. We use the widely utilized Hanning window [14] defined as:

$$h(u)=0.5\{1-\mathit{cos}[2\pi u/(\tau -1)]\}$$ (0.2)

For every fundamental frequency, f₁, we calculate the area for a specific part of the spectrum corresponding to the three frequency intervals f_i ± B, i ∈ [1,2,3], where f₂ = 2 · f₁ and f₃ = 3 · f₁, which represent the harmonics of the fundamental frequency. The parameter B is the bandwidth and it is used to account for possible deviations from the frequency and its two harmonics. We then identify the frequency between f_min and f_max that maximizes the partial area under the spectrum, which corresponds to the frequency that maximizes the explained variability.

The last component of the algorithm is to calculate the ratio between the maximum partial area under the spectrum that corresponds to a particular frequency and area under the entire spectrum. If there are only driving-related peaks in the spectrum and there is no background noise, this ratio should be equal to 1. For non-driving-related signals, the spectrum would display random patterns between f_min and f_max and the ratio would be close to zero. A similar approach was used by Urbanek et al., 2015 [7] to identify periods of sustained harmonic walking by focusing on a range of fundamental frequencies between 1 and 2.4Hz.

Driving is a long-term duration activity as it rarely takes less than a few minutes. The periodic signal associated with wheel rotation is often combined with other signals due road imperfections, driver’s hand movements, and stop-and-go motions. Such distortions can be of higher amplitude (intensity) than the background signal characteristic of driving and can occur at random times during driving. To reduce the effect of these uncontrollable factors, we smooth the estimated ratios. Finally, the smoothed ratios are thresholded to estimate driving periods.

The full DADA algorithm is presented below.

DADA Algorithm

Inputs: x(t) – tri-axial acceleration signal, τ – window size, fmin – minimum frequency, fmax – maximum frequency, B – bandwidth, δ – threshold.

Output: y(t) – binary driving indicator.

Step 1: Obtain vector magnitude VM(t) from the raw accelerometry signal x(t). Step 2: Transform VM(t) to the frequency domain using STFT for all times t using the data from the time window [t − τ/2, t + τ/2] to obtain a frequency spectrum X(s). Step 3: Estimate the area under the spectrum X(s). Step 4: Compute the partial area under the spectrum for each value of f from fmin and fmax by integrating the spectrum over fi ± B, where j=1,2,3. Step 5: Find the frequency f for which IX(f) = ∫s∈(f,2f,3f) X(s) is maximized. Step 6: Compute the ratio, RX(f), of the partial area under the spectrum from Step 5 to the total area under the spectrum from Step 3. Step 7: Smooth the ratio RX(f) using kernel smoothing with a bandwidth equal to 10 seconds to obtain sRX(t). Step 8: Driving is predicted $\widehat{y(t)}=1$ at time t when sRX(t) > δ.

Tuning parameter selection

There are a number of tuning parameters that need to be selected or estimated; namely, the window length (τ), the bandwidth around the fundamental driving frequency (B), the minimum and maximum frequencies (f_min and f_max), and the threshold (δ). Window length (τ) is chosen to be sensitive to the “driving-related” frequencies which can change rapidly in time or vanish completely when a subject is not driving. We tested window sizes between 5 and 20 seconds, which provide good resolution for calculating the spectrum. The area of interest is centered at particular frequency f and covers a wider band, i.e. f ± B. The bandwidths tested were between 0.5 and 1.5Hz. Minimum and maximum frequencies (f_min and f_max) were based on the common wheel sizes and driving speeds. The frequency f_min was considered in the range of 8 and 12Hz and f_max in the range of 14 and 16Hz. The threshold parameter (δ) was estimated empirically to provide the best discrimination between the driving and non-driving periods.

Statistical analysis

We used receiver-operating characteristic curves (ROCs) to estimate the quality of the DADA algorithm. The area under the ROC curve (AUC) for each subject was estimated, and the optimal threshold was defined as a point at which the sum of sensitivity and specificity was maximized. A universal threshold was defined as the median of subject-specific thresholds. Subject-specific sensitivity and specificity was then estimated based on this universal threshold.

The acceleration levels were quantified using the vector magnitude count (VMC) defined as the mean absolute deviation of the acceleration signal as,

$$\mathit{VMC}=\frac{1}{T}\sum _{t=1}^T\left|{VM}_t-\frac{1}{T}\sum _{t=1}^T{VM}_t\right|,$$

where T denotes the total number of samples for the time period where VMC is computed and VM_t denotes the instantaneous vector magnitude of the tri-axial acceleration signal. We compute VMC for 10-second overlapping intervals with 90% overlap. To visualize the overlap between the VMC of walking and driving periods in a commonly used scale, we further summarized it in 1-minute non-overlapping intervals and displayed it in a histogram.

Results

There were 24 participants in the study, 16 women and 8 men. Their average age was 41.0 years (SD=8.7) and they had an average BMI of 25.4kg/m² (SD=5.8). 22 out of 24 participants were right-handed. The length of the non-driving period was on average 31.0min (SD=5.37min) and the length of the driving period was 23.3min (SD=4.12min).

Driving vs. non-driving (ROC/AUC)

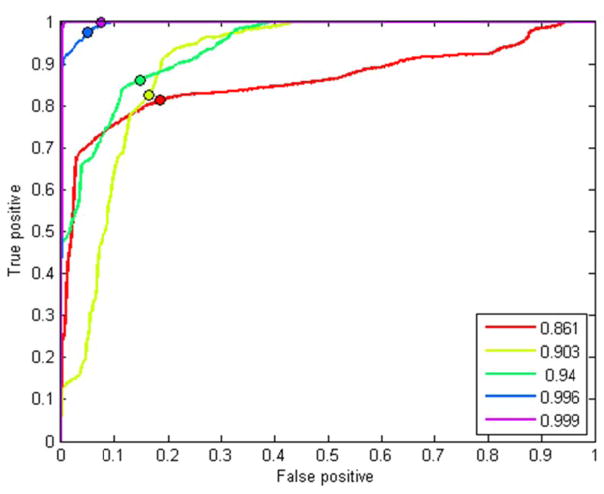
The main evaluation of the DADA algorithm was performed using the following tuning parameters: τ = 10s, f_min = 10Hz, f_max = 16Hz, and B = 1Hz. ROC curves were estimated for all 24 subjects. We present the ROC curves ranked by their AUC in Figure 2 for the 10^th, 25^th, 50^th, 75^th and 90^th percentiles. The median AUC estimated for the whole sample was equal to 0.940 (Q1=0.903, Q3=0.996).

Figure 2.

ROC curves for the subjects ranked by the AUC at 10^th percentile (red), 25^th percentile (light green), 50^th percentile (green), 75^th percentile (blue) and 90^th percentile (purple).

The median threshold value on the smooth ratio RX(f) used to define driving was estimated to be 0.093 (Q1=0.073, Q3=0.123). These thresholds were obtained by maximizing the sum between sensitivity and specificity. The subject-specific threshold exhibited limited variability, which allowed us to choose the universal threshold as the median threshold. With the universal threshold used for all study participants, the median true positive rate (sensitivity) was equal to 0.948 (Q1=0.869, Q3=0.966) and the median true negative rate (specificity) was equal to 0.881 (Q1=0.839, Q3=0.913) indicating an excellent performance of the DADA algorithm.

Sensitivity analysis

We conducted a sensitivity analysis to assess the change in performance of the DADA approach to the choice of tuning parameters. The cutoff point selection and the corresponding accuracy rates are shown in Table 1. For all combinations of tuning parameters considered the median AUC was above 0.85 indicating relatively low sensitivity to the tuning parameter selection. However, optimizing the tuning parameters can result in better prediction performance. For example, using the minimum frequency f_min≥10Hz, the window size τ=10s and the bandwidth B=1Hz, the estimated median AUC was above 0.93.

Table 1.

Influence of the four tuning parameters on the threshold selection and accuracy of the driving classification (f_min – minimum frequency, f_max – maximum frequency, τ – window size, B – bandwidth, AUC – area under the receiver operating characteristic curve, TPR – true positive rate, TNR – true negative rate).

fmin	fmax	τ	B	median AUC	median threshold	median TPR	median TNR
8	14	5	0.5	0.864	0.074	0.791	0.829
8	14	5	1	0.855	0.129	0.762	0.812
8	14	5	1.5	0.847	0.166	0.758	0.755
8	14	10	0.5	0.894	0.074	0.818	0.849
8	14	10	1	0.891	0.123	0.838	0.792
8	14	10	1.5	0.893	0.170	0.857	0.751
8	14	20	0.5	0.900	0.070	0.868	0.846
8	14	20	1	0.901	0.123	0.881	0.823
8	14	20	1.5	0.900	0.173	0.909	0.792
8	16	5	0.5	0.864	0.074	0.791	0.829
8	16	5	1	0.855	0.129	0.762	0.812
8	16	5	1.5	0.847	0.166	0.758	0.755
8	16	10	0.5	0.894	0.074	0.818	0.849
8	16	10	1	0.891	0.123	0.838	0.792
8	16	10	1.5	0.893	0.170	0.857	0.751
8	16	20	0.5	0.900	0.071	0.840	0.873
8	16	20	1	0.901	0.123	0.881	0.823
8	16	20	1.5	0.901	0.173	0.909	0.792
10	14	5	0.5	0.940	0.056	0.947	0.912
10	14	5	1	0.926	0.095	0.948	0.884
10	14	5	1.5	0.922	0.123	0.931	0.886
10	14	10	0.5	0.937	0.057	0.968	0.907
10	14	10	1	0.936	0.093	0.977	0.881
10	14	10	1.5	0.931	0.129	0.966	0.871
10	14	20	0.5	0.926	0.054	0.954	0.892
10	14	20	1	0.940	0.093	0.974	0.877
10	14	20	1.5	0.930	0.133	0.981	0.862
10	16	5	0.5	0.940	0.056	0.953	0.912
10	16	5	1	0.927	0.095	0.948	0.884
10	16	5	1.5	0.922	0.123	0.932	0.887
10	16	10	0.5	0.936	0.057	0.970	0.907
10	16	10	1	0.937	0.093	0.977	0.881
10	16	10	1.5	0.932	0.129	0.966	0.871
10	16	20	0.5	0.924	0.054	0.955	0.891
10	16	20	1	0.940	0.093	0.974	0.877
10	16	20	1.5	0.930	0.133	0.981	0.862
12	14	5	0.5	0.955	0.042	0.962	0.918
12	14	5	1	0.950	0.074	0.974	0.927
12	14	5	1.5	0.948	0.096	0.964	0.929
12	14	10	0.5	0.944	0.044	0.961	0.899
12	14	10	1	0.948	0.074	0.973	0.906
12	14	10	1.5	0.948	0.103	0.969	0.918
12	14	20	0.5	0.928	0.043	0.934	0.856
12	14	20	1	0.932	0.076	0.957	0.898
12	14	20	1.5	0.942	0.109	0.961	0.911
12	16	5	0.5	0.957	0.043	0.957	0.928
12	16	5	1	0.952	0.074	0.972	0.921
12	16	5	1.5	0.949	0.096	0.966	0.928
12	16	10	0.5	0.945	0.045	0.941	0.919
12	16	10	1	0.949	0.074	0.966	0.913
12	16	10	1.5	0.950	0.104	0.969	0.919
12	16	20	0.5	0.931	0.044	0.927	0.873
12	16	20	1	0.938	0.078	0.941	0.921
12	16	20	1.5	0.944	0.109	0.960	0.911

The universal threshold value depends primarily on the bandwidth B. This is because the numerator of the ratio RX(f), (Step 6 in the DADA Algorithm) increases with the size of the integration domain. The estimated sensitivity and specificity at the universal threshold is associated with f_min and is maximized for f_min = 10Hz or 12Hz. The window size τ has a smaller impact on prediction accuracy; part of this is probably due to the smoothing step of the algorithm.

Overestimation of PA

The information collected by accelerometers comes from a combination of vibrations generated by the activity of the individual and by their environment. Thus, in the absence of advanced algorithms that can identify car vibrations, all periods of driving will artificially increase the estimated human PA. To quantify this bias, we compare acceleration levels produced during driving and walking. We use walking as the reference because it is an important and recognizable activity that has been also shown to be associated with health outcomes [16].

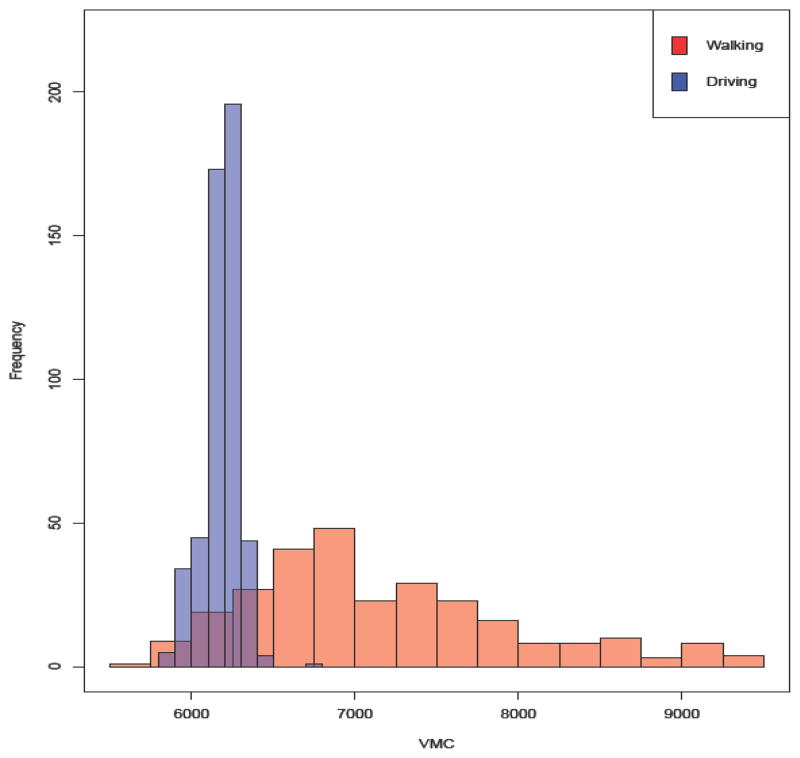
Figure 3 displays histogram plots of minute-by-minute VMC corresponding to driving (blue) and to walking (red) for all 24 subjects in the experiment. Acceleration levels for walking are larger than for driving. However, an overlap between the VMCs of the two activities can be observed. This suggests that acceleration produced during the sedentary driving might reach levels corresponding to walking. Specifically, range of the walking VMC is between 5727 and 9381, whereas the range for driving is between 5877 and 6731. Using the VMC cutoff of 6000, driving would be mis-classified as walking in 92.2% cases, while using a cutoff of 6200 it would be mis-classified in 48.8% of cases.

Figure 3.

Histogram of the minute-by-minute VMC corresponding to driving (blue) and to walking (red).

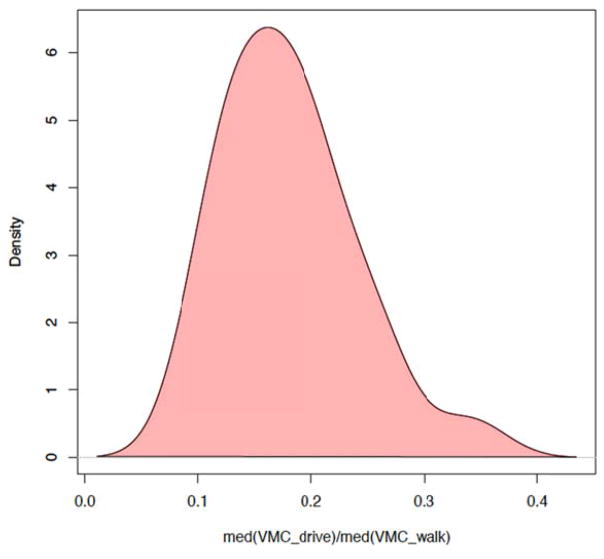
Figure 4 displays the density of ratios between the median driving and walking VMCs computed for each subject. On average, the VMC generated during driving is approximately 16% of the VMC generated during walking. Thus, the average time reported by adults in the United States of 46 minutes of driving [3] produces VMC equivalent to VMC for 7 minutes of walking. As the average self-reported time spent walking is equal to 13 minutes per day for adults in the United States [17], the overestimation of the walking-equivalent PA, when based solely on acceleration levels can be over 50%.

Figure 4.

Density of ratios between median driving and walking VMCs computed for each subject.

Discussion

We proposed and evaluated a driving detection algorithm (DADA) based on the raw accelerometry data obtained from wrist-worn accelerometers. The algorithm was shown to be highly accurate at distinguishing between driving and non-driving periods.

Public Health impact

Detecting car driving in the large observational studies is increasingly important. Indeed, objective estimation car driving periods can be used to complement, validate and calibrate subjective self-reported questionnaires on the driving time. This is important, as it has been reported [3] that car driving is one of the most common daily activities. Moreover, detecting car driving periods using raw accelerometry data can be used to better estimate PA, by reducing the extraneous environmental vibrations. Car driving, especially on highways, is a sedentary activity recorded by accelerometers as low-amplitude, high frequency accelerations. These accelerations result from a superposition of two sources: mechanical car vibrations transmitted through the steering system to the drivers’ hand [8] and arm movements related with steering the car [9]. The former source tends to dominate the amount of acceleration during driving and leads to overestimation of PA. In fact, even the manufacturers of the Fitbit fitness monitor admit that driving on a bumpy road might lead to overestimation of the daily step count [6]. The size of the bias induced by driving can be significant. We estimated that per unit of time the activity counts generated by driving are, on average, 16% of the average activity counts generated during walking. The daily volume of driving for many people in United States is much higher than walking. Average time of driving is 46 minutes per day [3], whereas self-reported walking is only 13 minutes per day [17]. Therefore, the average daily driving generates as much as 50% of the acceleration of the daily self-reported walking-equivalent PA. This suggests that driving can have serious effects on PA estimation if walking was a major activity performed.

One potential minor limitation of our approach is that we used the self-reported driving end times, which may be inaccurate. In the future analyses better marking of end times either using specific high-intensity hand movements or a pre-defined endpoint may improve the accuracy of estimating the driving endpoint. Another limitation is that the experiment was partially controlled and its performance in the free-living environment was not assessed. However, given our experience with walking detection in the free-living environment [7] and the clear separation of frequencies of the signal during driving, we expect that DADA will have a very good performance.

Conclusions

To the best of our knowledge, this is the first study using high frequency raw accelerometry data designed to identify driving activities. The basic idea is that vibrations produced by the rotation of the car wheel and transmitted to the wrist of the driver are of much higher frequency (>10Hz) than vibrations produced by other human activities. While signal processing approaches can be used to identify this discrepancy in frequency and thus identify periods of driving, summary measures, such as activity counts, will record driving periods as moderate intensity activity for long periods of time. The proposed algorithm, DADA, performs very well for a wide range of tuning parameters with AUC > 0.93.

Abbreviations

DADA

Detection Algorithm of Driving via Accelerometry

PA

Physical Activity

VM

Vector Magnitude

VMC

Vector Magnitude Count