Kinetics of low-temperature transitions and a reaction rate theory from non-equilibrium distributions

Abstract

This article surveys the empirical information which originated both by laboratory experiments and by computational simulations, and expands previous understanding of the rates of chemical processes in the low-temperature range, where deviations from linearity of Arrhenius plots were revealed. The phenomenological two-parameter Arrhenius equation requires improvement for applications where interpolation or extrapolations are demanded in various areas of modern science. Based on Tolman's theorem, the dependence of the reciprocal of the apparent activation energy as a function of reciprocal absolute temperature permits the introduction of a deviation parameter d covering uniformly a variety of rate processes, from those where quantum mechanical tunnelling is significant and d < 0, to those where d > 0, corresponding to the Pareto–Tsallis statistical weights: these generalize the Boltzmann–Gibbs weight, which is recovered for d = 0. It is shown here how the weights arise, relaxing the thermodynamic equilibrium limit, either for a binomial distribution if d > 0 or for a negative binomial distribution if d < 0, formally corresponding to Fermion-like or Boson-like statistics, respectively. The current status of the phenomenology is illustrated emphasizing case studies; specifically (i) the super-Arrhenius kinetics, where transport phenomena accelerate processes as the temperature increases; (ii) the sub-Arrhenius kinetics, where quantum mechanical tunnelling propitiates low-temperature reactivity; (iii) the anti-Arrhenius kinetics, where processes with no energetic obstacles are rate-limited by molecular reorientation requirements. Particular attention is given for case (i) to the treatment of diffusion and viscosity, for case (ii) to formulation of a transition rate theory for chemical kinetics including quantum mechanical tunnelling, and for case (iii) to the stereodirectional specificity of the dynamics of reactions strongly hindered by the increase of temperature.

This article is part of the themed issue ‘Theoretical and computational studies of non-equilibrium and non-statistical dynamics in the gas phase, in the condensed phase and at interfaces’.

1. Introduction

For understanding, monitoring and controlling the physical chemistry of materials and the biophysics of environments, information is needed on the kinetics of the involved elementary processes, specifically on their rates—often in a wide range of conditions and notably as a function of temperature. In the late nineteenth century, the increasing phenomenology started to be compacted, principally within the Arrhenius equation [1,2]; in the mid-1930s, the heuristic formulations of the transition-state theory (TST) were introduced ([3–6]; see also [7–14]); experimental progress in the age of nanotechnologies has been mainly extended in the low-temperature range: advances were propitiated to assist the new sciences of astrochemistry and astrobiology, demanding alternative paradigms. Computational progress has occurred by a variety of approaches, benchmarks being those aimed at exploring quantum mechanical advances (here the exemplary story is that of the F + H₂ reaction and its variants; see §4b): crucial progress came from time-independent methods, accompanied by those employing carefully checked time-dependent, classical trajectories or semi-classical techniques. The applications of the TST type of formulations benefit quantum mechanics ‘equilibrium’ calculations, where most degrees of freedom are frozen (or allowed to adiabatically adjust) except for a few, mostly one only, and specifically that corresponding motion along a reaction coordinate running through saddles in potential energy surfaces (PESs). Knowledge of PESs is thus crucial, and demands the enormous corpus of theories and computer information coming from quantum chemical calculations that make use of advanced electronic structure codes.

An early remarkable attempt at application to chemical kinetics of the then newly born science of statistical mechanics was initiated by Tolman in 1920 [15]: he concludes his later 1927 book [16, p. 323] saying

The problem of reaction velocities is probably nearer to the heart of most chemists than anything else in their whole range of activity. Rates of reaction are the factors that determine yields, and costs, and possibilities, and their theory must eventually succumb to scientific treatment

However, his optimism was soon frustrated. He subsequently abandoned the field and did not dedicate any attention to it in his monumental treatise [17], which from 1938 was the standard reference on the foundations of statistical mechanics. According to Laidler & King [18], both the use of old quantum theory and some assumptions on the role of radiation in activating chemical processes became obsolete; however, the relevance of what is now often referred to as the ‘Tolman theorem’ (see §2a) was definitely reformulated from a quantum-mechanical perspective by Fowler & Guggenheim [19]. They start a long chapter dedicated to chemical kinetics in their 1939 book on statistical thermodynamics by warning that

The subject of chemical kinetics strictly lies outside the province of this book. Equilibrium theory alone gives no information as to how equilibrium is attained. Nevertheless, equilibrium theory can be a useful tool for dealing with this problem, if combined with certain assumptions concerning the mechanisms involved. We therefore include a survey of such use of equilibrium theory, and shall lay particular stress on the assumptions involved, as these are too frequently ignored in discussions of reaction kinetics [19, p. 489].

We will do the same in this paper, where in order to illustrate the new results we will move directly to them from early motivations, paying only a little attention to some important intermediate developments.

The next section accounts for the basic theory, introducing the apparent activation energy (§2a) and its inverse, the transitivity, admitting an expansion in inverse absolute temperature (§2b), which leads directly to the deformed Arrhenius formula (§2c). Section 3 provides links to the rigorous statistical mechanics foundations, discussing the deviation from the thermodynamic limit (§3a) and introducing the non-equilibrium statistical distributions (§3b). A report on case studies, their treatment and an account of the state of the phenomenological progress is given in §4, which includes a presentation of the recently developed d-TST theory [20]. Final comments are given in the concluding §5.

2. The basic theory

(a). The apparent activation energy

The so-called Tolman's theorem was introduced in a 1920 paper [15], which provides a statistical-mechanics foundation to chemical kinetics, developing a formulation based on the kinetic theory of gases. Its interpretative and predictive power is controversial, but the attention paid by Tolman to the following function is remarkable:

2.1

which, as is well known, is now to be taken as the definition of the (apparent) activation energy E_a.

This function has been recommended by the International Union for Pure and Applied Chemistry (IUPAC) [21] as directly linked to the key experimental quantity, the reaction rate constant k(T) and obtainable by the familiar Arrhenius plots according to the practice of chemical kinetics. In (2.1), k is the Boltzmann constant and T is the absolute temperature. Formula (2.1) simplifies introducing, as is customary in statistical mechanics, the Lagrange parameter

2.2

to yield

2.3

The Tolman expression for E_a, as the difference between the average energy of chemically successful collisions and the total kinetic energy of the gas where the reaction occurs, attributes to this quantity the meaning of an energetic requirement for the reaction to occur. However, its often discussed identification with the Arrhenius activation energy turns out to be transparent only in particular cases [22–25], specifically in temperature ranges where it is a constant or varies slowly.

(b). The reciprocal temperature dependence of the reciprocal activation energy

In general, E_a is to be considered as temperature-dependent. In her comprehensive review ‘On the temperature dependence of E_a’, Berta Perlmutter–Hayman in 1976 [26] has examined in detail two power-series expansions for E_a, one directly in the temperature T and another in terms of its reciprocal (essentially our β, equation (2.2)). We have found it interesting to endorse as the basic expansion the reciprocal-activation–reciprocal-temperature relationship [27], for which we can provide a formal mathematical justification by extending the so-called Tolman theorem [15], following the quantum mechanical formulation in [19]. Tolman's function E_a, when written as the logarithmic derivative of the rate constants with respect to β (equation (2.3)), is indeed akin to the concept of an activation energy, in the sense that it represents a measure of an energetic obstacle to the progress of the reaction; therefore, its reciprocal can be interpreted as a measure of the propensity for the reaction to proceed and defined as the specific transitivity [20] of the process:

2.4

Our notation emphasizes the fact that in general the transitivity may not be constant but may take a gamma of values: it is assumed to be a smooth function of β in a sufficiently ample range of temperature, not including abrupt changes, e.g. in the mechanism or in the phases of reactants: in this range it will admit a Laurent expansion in a neighbourhood around a reference value denoted as β₀:

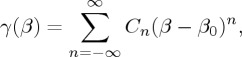2.5

where the coefficients C_n will contain n-order derivatives of γ(β) with respect to β and taken at β₀. The theory of chemical reaction kinetics is focused on the task of providing a set of such coefficients to connect to the experiment on k(T) via equations ((2.1)–(2.4)).

Since we require a description of the deviations of rates from their high-temperature behaviour, we now consider β₀ = 0 and look for a theory with a minimal number of parameters (Occam's razor), limited to only two terms of the Taylor–McLaurin series

2.6

where E is constant and represents an energetic obstacle at high temperatures and O(β²) indicates neglect of terms of order higher than one. In (2.6), d is the first-order coefficient (C₁) and is defined as the deformation parameter. The relationship was first given in [28,29] (see also [20]).

The expansion (2.6) in (2.3), as detailed previously [27,28], leads to a linear first-order differential equation for k(β) of the Bernoulli type that can be integrated by quadrature. It is immediate, but reassuring, to recover the Arrhenius equation within the validity of the first term, i.e. assuming E_a a constant. And it is simple, but remarkable, that inclusion of the second term leads directly to the deformed expression for the rate constant, which is to be considered next.

(c). The deformed Arrhenius rate formula

Further insight into the relationship (2.6) is gained by inserting it in the first equality in equation (2.3), considered as a differential equation for k(β). Equation (2.6) is of first order in the variable β and is easily integrated, specifying the lower limit of the integration range, β₀, as shown below:

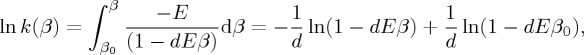2.7

yielding the deformed Arrhenius equation (d-Arrhenius)

2.8

when β₀, as remarked, can be taken to be zero at high temperature and the symbol A is introduced for the last term in (2.7) in view of its correspondence to the Arrhenius pre-exponential factor: indeed, it can be immediately realized that in the limit d → 0, the term (1 − dEβ)^1/d can be identified with the Arrhenius exponential law

2.9

where the apparent activation energy E_a becomes a constant identified with E, appearing as the first term in equation (2.6).

3. A statistical mechanics interlude

The key step of the previous section, which connects equations (2.8) and (2.9), is a well-known mathematical limit, which is due to Euler and is further under focus in the following developments (§3b).

For d < 0 in the equation (2.8) (sub-Arrhenius behaviour), the identification of d with features of the potential barrier permits entering the deformed exponential formula for describing quantum tunnelling [20,27]. For d > 0 (super-Arrhenius behaviour), one obtains a uniform generalization to classical statistical mechanics, where the Boltzmann–Gibbs distribution is deformed into that of the Pareto–Tsallis statistics (Here, the identification d = 1 − q must be made; see [30–33]). It is not difficult to show that the deformed distribution can be interpreted following lines of thought initiated by Maxwell and developed much later: it is obtained without taking the thermodynamic limit assumption of an infinite number of particles, a step clearly seen e.g. in [34–36] corresponding to an incomplete equipartition over available degrees of freedom (§3b).

(a). Deviation from the thermodynamic limit

Let's attempt to give a preliminary and perhaps more insightful schematic approach within the present context. In general, one can describe the deviation from the thermodynamic limit as due to the interruption of a discrete temporal sequence of events, which is equivalent to avoiding taking the assumption of a continuous time variable. We are inspired by Hinshelwood [37], who gave an illuminating elementary illustration of how exponential expressions come in throughout physical chemistry, and in particular determine the Arrhenius dependence of reaction rate constants upon temperature. The probability that a molecule possesses energy, E, in excess of the average is generally taken as proportional to e^−Eβ according to a Boltzmann distribution. One can understand this considering that to accumulate such an energy a molecule needs a fortunate sequence of favourable collisions and the exponential expression arises directly from the limit on probabilities of lucky runs, obtained by Euler in the eighteenth century and a mathematical milestone. That is the limit that we exploited in the previous section. We use it as in §3b.

Notoriously, Euler obtained the limit solving a problem posed by Jakob Bernoulli more than 100 years before: the problem is the important one on how to establish a connection between discrete and continuous computations of interest rates. (Incidentally, Eyring and co-workers [6] pointed out that a theory of reaction rates ‘is not merely a theory of the kinetics of chemical reactions; it is one that can, in principle, be applied to any rate process’). As remarked before, it has been known for a long time [26] that if one wants to keep the exponential form of the Arrhenius equation, there is an interdependence between the energy of activation and the pre-exponential factor, so that if E_a is temperature-dependent, the same must be true for A. The way out that is coherent with the IUPAC definition of E_a, given in equation (2.1), is to follow our procedure and to consider it as a differential equation for k, involving abandoning the exponential form in favour of its d-deformation, equation (2.8).

(b). Non-equilibrium statistical distributions

Let's elaborate further on the centrality of the road to the deformed exponential rate equation (2.8) via the remarkable discovery by Euler that the exponential function can be considered as the limit of succession, alternative to the previously known power-series:

3.1

The utilization of this expression, where for us the d parameter is the reciprocal of the continuous generalization of the integer N, marks a bifurcation between equilibrium and non-equilibrium treatments, leading to non-equilibrium statistical distribution when the number of microscopic ‘entities’ (particles, or in general sequences of events) is not considered to tend to infinity. When the assumption of the existence of the thermodynamic limit is relaxed, a deformed exponential distribution arises naturally to describe the probability distribution for fluctuations in many-particle systems. Invariably, all treatments (e.g. [38]) proceed directly to the limit.

The deformed exponential distribution arises naturally to account for probabilities attributed to the occurrence of long series of events generated randomly. Considering two mutually excluding events (A and B). For N trials (or for N particles in a microscopic description), let there be a pⁿ chance that the event A occurs and (1 − p)^N−n be the chance for event B. In more detail, n is the number of times which the trial experiment yields event A (for example, n can be the number of given particles on a specific configuration A in the microscopic description of the distribution). Then, the number of different ways to yield event A is given by the binomial coefficient

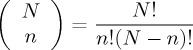3.2

and since the trials are independent, the Bernoulli probability distribution for n is the well-known binomial distribution

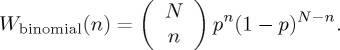3.3

Considering the mean of events 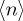 = pN, equation (3.3) can be conveniently rewritten as

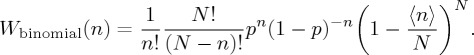3.4

If N → ∞, p → 0 in the binomial distribution (this step would amount to take the thermodynamic limit), the Poisson distribution is obtained

3.5

It can be shown that a modification of (3.4) accounts for the probability distribution of a specific event involving distinguishable (or Fermion) particles [39–43]:

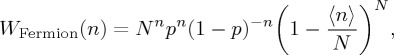3.6

which is the distribution that applies prior to the N → ∞ limit, leading to the Fermi–Dirac distribution.

In microscopic systems where quantum effects are operative and the indistinguishability of particles has to be taken into account separately, another physically significant case applies, wherein no limitation occurs on the number of particles per state (Boson particles):

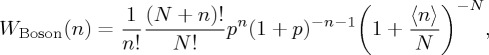3.7

recognized as a negative binomial distribution [40,44].

Proceeding as previously, the large N limit now leads to the Bose–Einstein distribution. In summary, the first case is the Fermi–Dirac distribution and the second case is the Bose–Einstein distribution [40,41,44] and appears that ‘tertium non datur’ [45]. The most probable distributions resulting for equations (3.4), (3.6) and (3.7) lead to Boltzmann, Fermi–Dirac and Bose–Einstein statistics [39,46], respectively, when the thermodynamic limit is taken. However, the presentation emphasizes that an intermediate step in the derivation of all the three statistical distributions in equations (3.4), (3.6) and (3.7) includes what we refer to as the Euler deformed exponential function, (1 − (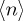/N))^N. This step is crucial here as well as to discuss the role of the Tsallis distribution in non-equilibrium statistics for finite heat baths: when finite size effects are negligible, we can establish the connection between the thermodynamic and the microscopic parameters: n = Eβ and d = 1/N [44,47–49]. See also important previous work on statistical distributions in the kinetics of rate processes [50–52].

4. Low-temperature behaviour in chemical kinetics and materials science

Modern experimental techniques and theoretical approaches are providing an ample phenomenology of deviations from the well-known Arrhenius behaviour, especially occurring at low temperatures. As a classification for the phenomenology of these processes, we illustrate the use of the deformed Arrhenius equation (equation (2.8)), permitting one to evaluate prototypical systems where the temperature dependence of the rate constant according to equation (2.8) is described by E > 0 and d > 0 or d < 0, corresponding to convex (super-Arrhenius), concave (sub-Arrhenius) in the semi-log plots against reciprocal temperature. A case for E < 0 will also be documented and indicated as anti-Arrhenius.

(a). Super-Arrhenius

The super-Arrhenius behaviour is one that deserves particular attention, and its occurrence is varied and demanding (figure 1). It often manifests because of collective phenomena, such as those amenable to treatment by the non-extensive thermodynamics of Tsallis, and covers an ample set of phenomena: rates of enzymatic catalysis-promoted processes [53–55], food preservation processes [56,57] and basic features of the dynamics of complex or glass-forming liquids and solids [58–63].

Figure 1.

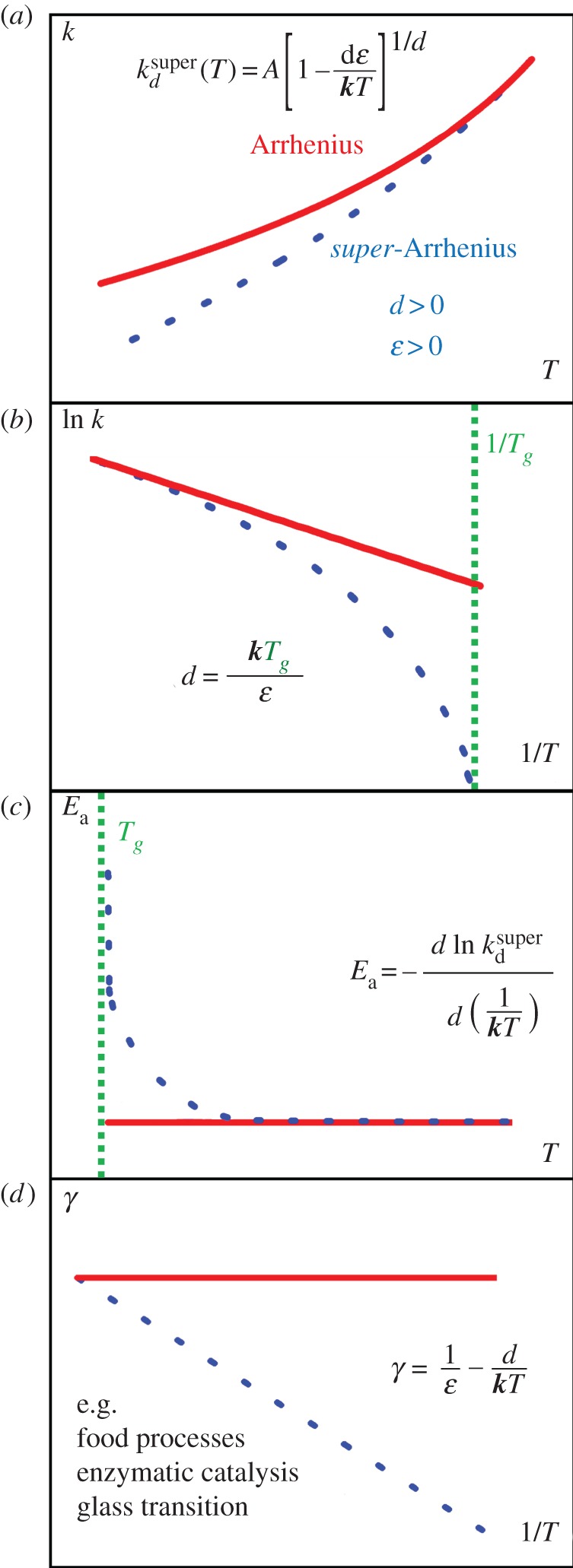
(a) The exponential dependence of reaction rates k(T) upon absolute temperature T. Deviations from linearity at low temperatures can be observed in the plot as showing a ‘convex’ curvature, i.e. lower than expected rates as temperature decreases. In (b), the super-Arrhenius behaviour is accentuaded in an Arrhenius plot view, where ln k(T) is reported against 1/T. In supercooled systems, an approximate relationship between the deformation parameter d and the glass transition temperature T_g illustrates the trend of this complicated phenomenon (see §4a). (c) Deviations from constancy of the apparent activation energy, expected from the Arrhenius Law, manifests for a super-Arrhenius behaviour the apparent activation energy increase with decreasing temperature. Panel (d) exhibits the linear relationship of the transitivity (equation (2.4)) with inverse temperature, basic to our derivation of the d-Arrhenius formula. Super-Arrhenius behaviour, often arising for collective phenomena, is amenable to a classical mechanics interpretation for the examples mentioned and discussed in §4a. (Online version in colour.)

A significant number of studies in the temperature dependence of rates of enzymatic catalysis reactions has inspired several formulations for the description of the mechanism involved in these processes [64–67]. Results in the kinetics of catalytic reactions of the dehydrogenase and oxidase enzymes have shown an undoubted super-Arrhenius behaviour [25,53,54,68].

The theory has interesting applications. A similar behaviour is found in the temperature dependence of food processes. We propose in [56] the use of equation (2.8) to describe the non-Arrhenius behaviour in these processes, showing that the d-Arrhenius formula is suitable for describing the effect of temperature on non-enzymatic browning of onion and on the rate of growth of several species of bacteria. The d-Arrhenius rate law provides a means to account for convex curvature. Such factors include particle diffusion and constraints on the proposed microscopic model, in particular requiring that any successful approach to super-Arrhenius processes should be consistent with the microcanonical rate constant (see §3a, [25,56]).

A most fundamental case of super-Arrhenius temperature dependence occurs for the diffusion in supercooled systems near the glass transition temperature T_g. The following discussion is a simplification for a didactic purpose of a very complicated and still controversial issue. The mechanism involved in convex curvature of Arrhenius plots in supercooled liquids is one of the less understood unsolved processes in condensed matter science [58,69,70]. An interesting example is the diffusion of krypton in methanol and ethanol mixtures at low temperature near their glass transition temperatures [71–73]. Since the diffusion coefficient D and viscosity η are connected (see e.g. the Stokes–Einstein formulation, D = kT/6πrη, where r is the range parameter [6,74]), a manifestation occurs for a super-Arrhenius behaviour of this property. A variety of liquids with different composition exhibit variations of the temperature-dependent viscosity [75]. Around T_g temperature, the Arrhenius-like formulation,

4.1

of course breaks down. In (4.1), η₀ is the viscosity when the temperature tends to infinity (β → 0) and the energy parameter E has to be substantiated by a proper microscopic model. It is no surprise that a variety of proposed non-Arrhenius equations provide options to tackle this problem: we mention those by William–Landel–Ferry [76], Bässler [77], Vogel–Tammann–Fulcher [78–80] and other variants [81,82]. The treatment leading us to equation (2.8) can inspire an option to describe the temperature-dependent viscosity, exploiting the flexibility and continuity of the deformed exponential function introduced owing again to the Euler limit, equation (3.1).

Let the deformed temperature rate law for viscosity be written as follows:

4.2

where the transitivity (see equation (2.6)) goes to zero, and T_g is identified as the temperature where the glass activation energy tends to infinity, so it is possible to propose a relationship with the deformation parameter d:

4.3

From the Kauzmann–Eyring [6,83] pre-exponential factor, where N_a is the Avogadro number and 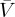is the molar volume and 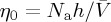, one can write, for the deformed viscosity rate law,

4.4

Several previous formulations described the dependence of T_g and E parameters from the intrinsic properties of the molecular system, and encourage us to give a heuristic interpretation for equation (4.4): from the Flory–Kauzmann hypothesis [83–85], T_g is proportional to the molecular mass (M) and the molecular dimensionality (L), T_g = M^1/2/L. According to Eyring and colleagues, the E parameter is connected to the energy of vapourization, ΔE_vap [6,86]: the work required to make a hole of molecular size is intuitively identified with the ΔE_vap, and so E may be estimated to correspond to a certain fraction of the ΔE_vap. This treatment of course does not provide further insight into these amply investigated issues, but points at a simple and perhaps useful parametrization of a long-standing intriguing rate phenomenon.

(b). Sub-Arrhenius cases

There are uncountable cases of concave deviation on the temperature rate constants for the elementary chemical reactions that can be classified as exhibiting a sub-Arrhenius behaviour (figure 2). In systems with no apparent changes in the chemical mechanism, this behaviour can be attributed in most cases to quantum mechanical tunnelling [28,29]. A number of investigations have provided examples of several chemical reactions within this regime. A series of experimental kinetic data and of benchmark quantum mechanical calculations [87–94] has established that, for example, the reaction of a fluorine atom with molecular hydrogen represents a prototypical case of sub-Arrhenius behaviour [95,96] has been experimentally confirmed [97].

Figure 2.

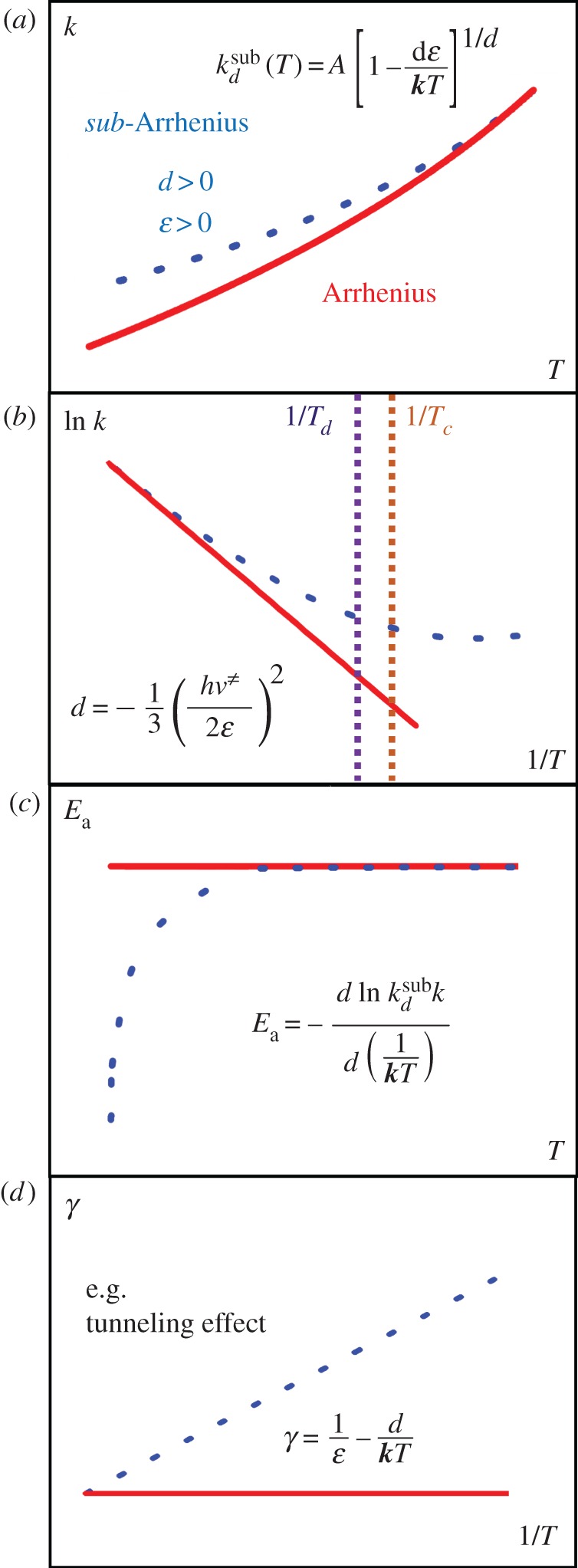
(a) The exponential dependence of reaction rates 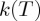upon absolute temperature 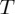. Deviations from linearity at low temperatures can be observed in the plot as showing a ‘concave’ curvature, i.e. higher than expected rates as temperature decreases. (b) The sub-Arrhenius behaviour is accentuaded in an Arrhenius plot view, where ln 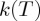is reported against 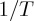. In elementary reactions at temperatures where quantum mechanical tunnelling is operative, there is a relation between the deformation parameter and features of (height and width) of the barrier (see 4b(i)). Panel (c) shows that deviations from constancy of the apparent activation energy, expected from the Arrhenius Law, for a sub-Arrhenius behaviour manifests as a decrease with decreasing temperature. Panel (d) exhibits the linear relationship of the transitivity (equation (2.4)) with inverse temperature, basic to our derivation of the 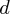-Arrhenius formula. Sub-Arrhenius behaviour, discussed as a manifestation of quantum mechanical tunnelling through a potential energy barrier as exemplified in the panel. (Online version in colour.)

Concerning atmospheric and industrial reactions, the direct H-atom abstraction from organic compounds by the hydroxyl radical often presents an evident concave curvature in the Arrhenius plot [98–101]. Within an entirely different chemical environment, experimental rate constants related to multiple proton transfer reactions in condensed matter also show strong sub-Arrhenius behaviour [102–104]. Also, sub-Arrhenius behaviour has been revealed for rates of processes promoted by enzymatic catalysis [55,68,105]. In the next sections, we address the TST and deform it to include the tunnelling correction as a simple tool to describe sub-Arrhenius behaviour.

(i). Transition state theory

The Eyring formulation [4,6] of chemical reaction rates provided chemists with the basic ingredients for understanding and even predicting both parameters A and E of the Arrhenius equation (equation (2.9)) [1] and is assumed as a paradigm for describing the temperature dependence of the rate coefficient of chemical reactions:

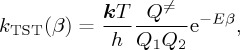4.5

(for simplicity, we consider a bimolecular process), where h is the Planck constant, Q₁ and Q₂ are the (translational, vibrational and rotational) partition functions of the two reactants, and Q^≠ is the partition function of the activated complex, from which the translational contribution along the reaction coordinate is excluded. A recent paper [20] exploits the fact that the parameters of equation (4.5) can be explicitly obtained from features of barriers on PESs, as generated from current codes for quantum chemistry calculations. The factor (kT/h) Q^≠/Q₁Q₂ has sometimes been called the collision number, but a more satisfactory term used is frequency factor. The quantity E is the energy of activation of the reaction, encountered before as representing the energy that the molecule in the initial state of the process must acquire before it can take part in the reaction.

Early concerns on possible deviations from Arrhenius behaviour because of quantum mechanical tunnelling (sub-Arrhenius behaviour) were circumvented ad hoc, e.g. by a multiplicative transmission coefficient κ evaluated according to recipes, such as those due to Eckart [106], Pelzer & Wigner [3] and Bell [107]. The tunnelling correction κ is introduced in the TST rate constant as a multiplicative factor, k = κ × k_TST and Henriksen & Hansen [7,108] have shown that indeed it is a natural extension of the original formulation. Recent attention has been focused on the role of non-equilibrium or deviation from assumed Maxwell–Boltzmann distributions in the reaction rate theory [109–111] and, in the next section, we show a proposal remarkably distinct from others (see [20]).

(ii). Deformed transition-state theory

What we call the sub-Arrhenius behaviour would be accounted for traditionally by introducing a tunnelling parameter κ, as discussed above. In the deformed transition-state theory (d-TST) formulation, we replace the κ × e^−Eβ factor in the TST rate constant, equation (4.5), by the deformed exponential function, yielding

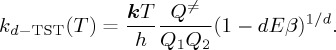4.6

The symbols are the same as in (4.5), to which (4.6) tends as d tends to zero, according to (3.1). In [27], the significance of the d parameter and an explicit procedure for its calculation were proposed comparing expansions for the apparent activation energies, E_a. It is shown that d is inversely proportional to the square of the barrier height (E) and directly proportional to the square of the frequency for crossing the barrier (ν^≠) at a maximum in the PES:

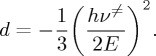4.7

The application of d-TST to several hydrogen transfer reactions has been showing promising results [20]. Temperature ranges for the validity of the approach are assessed with respect to features of the potential energy barrier to reaction [20,112], permitting comparison with experiments and tests against alternative formulations. Elementary reactions, widely investigated both experimentally and theoretically, which have been described successfully, are F + H₂ [28,96], F + HD [113], CH₄ + OH [20], CH₃Cl + OH [20], H₂ + CN [20], and also abstraction and dissociation in the nitrogen trifluoride channels [114], and proton rearrangement in curcumin [115] and methylhydroxycarbene [116]. The deformed formulation has also been found useful to describe other reactions not involving tunnelling but showing non-negligible sub-Arrhenius behaviour, such as the C + CH⁺ reaction [117], which is of relevance in cold interstellar clouds.

As discussed in [107,118], the degree of concavity in the Arrhenius plot can characterize the degree of tunnelling in chemical reactions. The crossover temperature, T_c = hν^≠/k, is the parameter that delimits the degree of tunnelling regimes. The ranges of tunnelling regimes are important to quantify how the tunnelling affects the rate constant in particular cases.

From a mathematical viewpoint, the d-TST formulation has clear limitations in the description of the deep tunnelling regime (Wigner limit) [119,120], since the Euler limit deformation of the exponential function fails to quantify the distributions of reactive particles with energy less than the height of the barrier. However, the flexibility of the distribution formula permits one to cover the sub-Arrhenius behaviour, specifically typical of quantum tunnelling, smoothly extending into the Boltzmann distribution [27] of the classical regime.

A definition of a validity temperature that delimits the applicability within the negligible or moderate tunnelling ranges can be obtained from the limit of the Bell equation [107,113,121]. In the case of the Wigner limit, when T tends to zero, k(T) tends to a constant. Assuming the Bell limit, 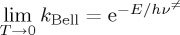in contrast with the d-TST limit, 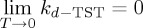, the temperature that marks the change of validity ranges can be found at the intersection of the two limiting behaviours:

4.8

where T_d is therefore the validity temperature of the d-TST formalism: at temperatures below T_d under deep tunnelling conditions, there is no guarantee of the accuracy of the d-TST description.

Although several other papers [109,110,122–125] have proposed ways to insert the Pareto–Tsallis distribution in the description of rate constants in chemical reaction theory, none gave a physical meaning and an explicitly tractable expression for the deformation parameter d as provided by (4.7).

(c). An anti-Arrhenius case

The rates of some processes increase as the temperature decreases according to an apparently negative activation energy. These processes can be classified as anti-Arrhenius. In a gas-phase reaction the anti-Arrhenius behaviour is frequently found in molecule–radical reactions [126–131]. Among these processes, the OH + HBr → H₂O + Br reaction is one of the most studied experimentally. Recently, salient features of the PES have been characterized and most kinetic aspects can be considered as satisfactorily reproduced by classical trajectory simulations [132,133]. An insightful illustration of the origin of this behaviour is concerned with the stereodirectional effect assessed by first-principles Born–Oppenheimer ‘canonical’ molecular dynamics [134,135]. The anti-Arrhenius behaviour is documented as being due to the adjustment of the reactants' mutual orientation in order to encounter the entrance into the ‘cone of acceptance’ for reactivity. The aperture angle of this cone is dictated by a range of directions of approach compatible with the formation of the specific HOH angle of the product water molecule; and consistently the adjustment is progressively less effective the higher the kinetic energy. Qualitatively, this emerging picture corroborates experiments on this reaction [136,137], involving collisions of aligned and oriented molecular beams, and covering a range of energies higher than the thermal ones. The rate constant from this molecular dynamic approach was estimated larger than expected and a calibration process was necessary for accounting of the limited dynamical sampling of the involved phase space.

Currently, there is ample activity investigating whether advances in molecular dynamics simulations can provide quantitative values for rate constants [138–140]. However, the methods have difficulty in estimating the rate constants, generally leading to overestimates, and the discrepancy with experimental data is larger for high temperatures, as documented for the OH + HBr reaction [134,135]. These uncertainties are often associated with inherent difficulties of possible direct evaluations from molecular dynamics simulation, and are ascribed to the statistical validity of samplings of the system phase space and the accurate characterization of transition state features [141–143]. These crucial issues in the applications of TST-type approaches to calculations of rates constitute hard problems in the extraction of rate constants from first-principles molecular dynamics experiments, preventing them from representing an at least semi-quantitative alternative to direct exact or approximate quantum mechanical methods, often prohibitive to be implemented.

As a final example on how the study of the anti-Arrhenius behaviour offers opportunities for fundamental research and can guide scientific progress in different areas, we note a recent paper where the stereodirectionality effect contributed to understanding the negative activation energy in addition reactions of arylchlorocarbenes to alkenes [144].

5. Concluding remarks

These notes were written to appear in a collection of papers presented on the occasion of a workshop on ‘Theoretical and Computational Studies of Non-Equilibrium and Non-Statistical Dynamics in Gas-Phase, Condensed-Phase, and Interfacial Reactions’ and the effort of organizers and the stimulus of the participants are acknowledged. The venue was the Institut Henri Poincaré in Paris in April 2016. To Poincaré we owe the observation that ‘mathematics is the art of giving the same name to different things'. Accordingly, we can interpret as a task for scientists that of providing samples of phenomena to be compacted within a common frame. In this presentation of progress on the kinetics of rate processes, the focus of our interest has been to emphasize the unifying role of the treatment of a different type of rate, mentioning the relationship with those occurring in the calculation of interest in bank accounts. The description of the rates of chemical changes is a subject where the main issue is to understand how systems depart from equilibrium states and how they approach new ones: the rates are typically exponentially influenced by the reciprocal of the temperature (Arrhenius behaviour). The description of deviations at low temperatures exploits Euler's solution of the problem posed by Jakob Bernoulli on the computation of compound rates. The key is the Euler formula, equation (3.1), established as a continuous limit of a discrete succession of events: in essence, our deformation formulas are based on the same now elementary mathematical tool.

Authors' contributions

Equal contributions by all authors.

Competing interests

We declare that we have no competing interests.

Funding

Financial support for the Italian Ministry for Education, University and Research, MIUR. Grant no. SIR2014(RBSI14U3VF).