Insights into the deactivation of 5-bromouracil after ultraviolet excitation

Abstract

5-Bromouracil is a nucleobase analogue that can replace thymine in DNA strands and acts as a strong radiosensitizer, with potential applications in molecular biology and cancer therapy. Here, the deactivation of 5-bromouracil after ultraviolet irradiation is investigated in the singlet and triplet manifold by accurate quantum chemistry calculations and non-adiabatic dynamics simulations. It is found that, after irradiation to the bright ππ* state, three main relaxation pathways are, in principle, possible: relaxation back to the ground state, intersystem crossing (ISC) and C–Br photodissociation. Based on accurate MS-CASPT2 optimizations, we propose that ground-state relaxation should be the predominant deactivation pathway in the gas phase. We then employ different electronic structure methods to assess their suitability to carry out excited-state dynamics simulations. MRCIS (multi-reference configuration interaction including single excitations) was used in surface hopping simulations to compute the ultrafast ISC dynamics, which mostly involves the ¹n_Oπ* and ³ππ* states.

This article is part of the themed issue ‘Theoretical and computational studies of non-equilibrium and non-statistical dynamics in the gas phase, in the condensed phase and at interfaces’.

1. Introduction

5-Bromouracil (5BU) can replace thymine (T) in DNA [1], causing strong mutagenic effects that have been explained by base mispairings due to 5BU’s tautomeric equilibrium [2,3]. The substitution of T by 5BU is also accompanied by an increased ultraviolet sensitivity of the affected DNA [4], where the presence of 5BU can cause single-strand breaks, alkali-labile bonds, double-strand breaks and DNA–protein cross-linking [5–7]. The occurrence of these lesions originates from the ability of 5BU to cleave the C–Br bond, leading to the formation of a uracilyl radical [8,9]. This radical in turn can abstract a hydrogen atom from a suitable donor (e.g. an adjacent sugar), thereby forming uracil (U); see figure 1 for the chemical structures of 5BU, T and U. Hence, the uracilyl radical is responsible for DNA damage and can be exploited for a variety of processes, such as DNA cross-linking [7], adenine elimination [6] or generation of reactive oxygen species for photodynamical therapy.

Figure 1.

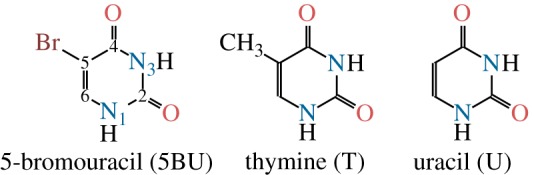
Chemical structures of 5-bromouracil (with ring atom numbering), thymine and uracil. (Online version in colour.)

Two different mechanisms have been proposed for the dissociation of the C–Br bond of 5BU [7,10,11]. The first route is initiated by an excited-state electron transfer from an adjacent nucleobase to 5BU, resulting in the formation of the 5BU^•− radical anion, which then undergoes C–Br cleavage, liberating a bromide ion and leaving behind the highly reactive uracilyl radical [12]. In the second one, isolated 5BU can also homolytically cleave the C–Br bond without any electron transfer involved [8,9]. These two routes differ in their selectivity for certain types of damage [7]. Moreover, it has been shown that the damage induced by 5BU depends on the DNA conformation [13], which could be used in tumour radiosensitization applications [14].

Given the potential applicability of 5BU, which has even been used in a clinical trial [14], a number of papers focused on the primary photochemical properties of 5BU. However, the molecular details of the deactivation of 5BU are still poorly understood. Based on experimental evidence, it has been suggested that C–Br homolysis occurs in the excited singlet state (starting from ¹ππ*) [10]. Intersystem crossing (ISC) to the triplet manifold has also been reported [7,10], but in these experiments, performed in 2-propanol, dissociation takes place involving electron transfer from the solvent. In this case, the associated quantum yields were reported to be 1.3% for homolysis from ¹ππ*, 3% for ISC and 0.6% for ISC followed by dissociation [7,10]. Excitation at lower energy apparently increases the ISC yield to 6% [7].

5BU has also been studied with femtosecond time-resolved pump–probe experiments in water [15,16], where it has been found that, after excitation, most of the signal decays with a 400 fs time constant, and the long-lived residual decays with a nanosecond time constant. Since the work reported in these studies [15,16] was focused on the dynamics of solvated electrons and the formation of 5BU^•−, no further interpretation was given regarding the time scales intrinsic to 5BU.

Mechanistically, static quantum chemical calculations on isolated 5BU have provided support for two pathways operating after 5BU is irradiated by UV light—one pathway is responsible for bromine elimination and the second leads back to the reactant through a conical intersection [17]. According to that study, there are two internal coordinates that are critical for the description of the deactivation processes of 5BU: the C₅–Br bond length and the out-of-plane angle of the bromine atom. The authors then proposed that reactivity is controlled by an extended S₀/ππ* near-degeneracy seam along a combination of these two internal coordinates. This seam can be accessed after small barriers are overcome. Depending on the particular point on the seam at which the system decays to the ground state, either dissociation or reactant recovery takes place.

In this paper, we study the gas-phase deactivation pathways of 5BU after UV irradiation using potential energy surface (PES) explorations and additionally using the Sharc (Surface Hopping with ARbitrary Couplings) dynamics method [18,19], in order to get additional insights, paying special attention to the role of triplet states. Previous Sharc simulations have shown that triplet states can be populated on ultrafast time scales in a number of nucleobases [20,21] and nucleobase analogues, such as those resulting from the substitution of the oxygen atom by the heavier sulfur atom [22–24]. Here, the presence of the heavy bromine atom might provide strong spin–orbit couplings, making the ISC to the triplet states a viable process, as proposed experimentally [7,10].

2. Computational methods

Two different strategies were employed here to study the deactivation pathways of 5BU: static quantum chemical calculations (single-point calculations, optimizations and linear interpolation scans) and non-adiabatic dynamics simulations. The methods employed in each case are detailed in the following.

(a). Quantum chemistry calculations

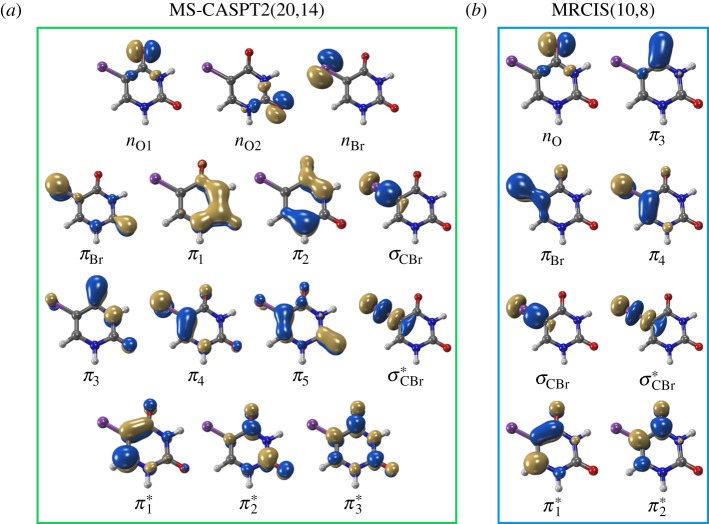
Vertical excitation calculations were performed, using the ground-state geometry reported in [17], which was optimized at the CASSCF(12,10)/6-311G* level of theory. First, the vertical excitation calculations were performed with Molcas v. 8.0 [25] at the MS-CASPT2(20,14) level of theory. We employed the ANO-RCC-VDZP [26] basis set, an IPEA (ionization potential–electron affinity) shift [27] of zero [28] and an imaginary level shift [29] of 0.2 atomic units to exclude intruder states. The employed active space orbitals (nine π/π* orbitals, three lone-pair orbitals, and the σ/σ* pair of the C–Br bond) are shown in figure 2a. Either nine singlet states or eight triplet states were included in the calculations, where this relatively large number of states was necessary to stabilize the active space.

Figure 2.

(a) Active space orbitals of the MS-CASPT2(20,14)/ANO-RCC-VDZP calculation. (b) Reference space orbitals of the MRCIS(10,8)/cc-pVDZ-DK calculations. (Online version in colour.)

In order to find a cheaper but still accurate alternative to MS-CASPT2(20,14), vertical excitation calculations were then performed with additional methods, using the same geometry. Here, we employed SA-CASSCF(14,11)/cc-pVDZ-DK [30] (using Molcas v. 8.0 [25]), ADC(2)/def2-TZVP (using Turbomole v. 7.0 [31]), TD-BP86/TZP, TD-B3LYP/TZP (both using ADF [32]) and MRCIS/cc-pVDZ-DK [30] (using Columbus v. 7 [33,34]).

The three main relaxation pathways possible in 5BU—ground-state relaxation, ISC and photodissociation—were investigated by means of optimizations of excited-state minima and crossing points. To this aim, we employed the external optimizer of ORCA [35], which was fed the appropriate gradients according to [36,37]. Owing to the high cost of MS-CASPT2(20,14) calculations, these optimizations used gradients from ADC(2) or numerical gradients from MS-CASPT2(12,9). Based on the optimized geometries, several linear-interpolation-in-internal-coordinates (LIIC) scans were performed at the MS-CASPT2(20,14) and ADC(2) levels of theory.

(b). Non-adiabatic dynamics simulations

Dynamics simulations were carried out with a local development version of the Sharc code [38]. Sharc is a generalization of the trajectory surface hopping method [39] that allows the simultaneous description of singlet and triplet states, coupled by non-adiabatic and spin–orbit couplings [18,19].

The initial conditions were sampled from a Wigner–Ville distribution [40] of the ground-state oscillator, based on MP2/ANO-RCC-VDZP harmonic frequencies. For a set of 1000 initial geometries, vertical excitation calculations provided the initial electronic state distribution [41]. This procedure yielded 93 admissible initial conditions in the 5.90±0.15 eV window around the absorption maximum of 5BU (at our MRCIS/cc-pVDZ-DK level of theory). Out of these, 82 trajectories were started in the S₂ and 11 in the S₃ state.

The trajectories were propagated for 400 fs, using a time step of 0.5 fs for the nuclear motion and 0.02 fs for the electronic wave function propagation. The local diabatization procedure [42] with wave function overlaps [43] was employed. Decoherence was treated with an energy gap-based scheme [44]. From the total 93 trajectories, 15 trajectories were discarded due to convergence problems.

For each nuclear time step, the involved energies, gradients, wave function overlaps [43] and spin–orbit couplings [45] were calculated at the multi-reference configuration interaction including single excitations (MRCIS) level of theory with the cc-pVDZ-DK basis set [46,47]. The Columbus v. 7.0 [33,34] program suite, employing integrals from Molcas [25,33], was used. The orbitals were optimized using SA-CASSCF(10,8) (orbitals in figure 2b), averaging simultaneously over four singlets and three triplet states. To keep the computations feasible, the MRCIS reference space employed a restricted active space scheme, where in the reference configuration state functions only up to two electrons were allowed in the three antibonding orbitals. This approach allowed retaining as many orbitals in the reference space as possible, to allow maximum flexibility in order to describe the three main deactivation pathways of this molecule. This is particularly important here, since valence excitations and excitations responsible for the dissociation of the C–Br bond need to be considered on the same footing.

3. Results and discussion

(a). Vertical excitation energies

Table 1 compares the available experimental excitation energies of 5BU in the gas phase [48] with the results of the vertical excitation calculations conducted here.

Table 1.

Comparison of experimental excitation energies (in electronvolts) with vertical excitation calculations at the MS-CASPT2, CASSCF, MRCIS, ADC(2) and TD-DFT levels of theory. For all calculations, the CASSCF geometry from [17] was used. Orbital labels refer (approximately) to figure 2a, except for MRCIS (those refer to figure 2b).

		MS-CASPT2a			CASSCFb			MRCISc			ADC(2)d			TD-BP86e			TD-B3LYPf
state	exp. [48]	E	fosc	char.	E	fosc	char.	E	fosc	char.	E	fosc	char.	E	fosc	char.	E	fosc	char.
S0		0.00	—	cs	0.00	—	cs	0.00	—	cs	0.00	—	cs	0.00	—	cs	0.00	—	cs
S1	4.66	4.60	0.30		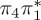5.02	0.00		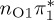5.09	0.00		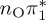4.75	0.00		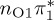4.10	0.00		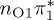4.66	0.12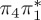
S2		4.92	0.00		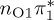6.17	0.00	π4σ*CBr	6.08	0.29		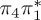4.95	0.21		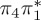4.23	0.08		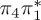4.78	0.00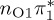
S3		5.47	0.00	π4σ*CBr	6.76	0.59		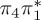6.21	0.00	π4σ*CBr	5.64	0.00	π4σ*CBr	4.69	0.00		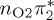4.98	0.00	π4σ*CBr
S4	6.12	6.01	0.03		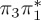7.61	0.01		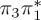7.74	0.11		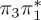6.04	0.00		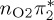4.73	0.00	π4σ*CBr	5.43	0.00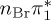
S5		6.23	0.00		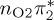7.99	0.00		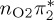8.13	0.01		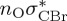6.20	0.04		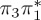4.87	0.00		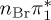5.79	0.00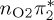
S6		6.55	0.00		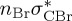8.52	0.00		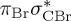8.36	0.00		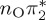6.42	0.00		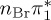5.01	0.00		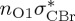5.88	0.06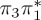
S7		6.61	0.00		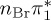8.66	0.03		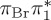8.59	0.14		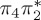6.64	0.26		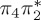5.20	0.05		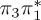5.90	0.00	π4Ryd
S8	7.20	7.08	0.00		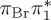8.83	0.00		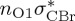8.64	0.00		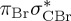6.74	0.00		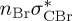5.45	0.09		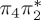6.08	0.12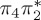
T1	3.35	3.51	—		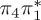3.81	—		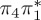3.92	—		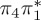3.63	—		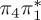3.23	—		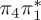3.20	—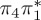
T2		4.78	—		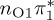4.88	—		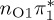4.82	—		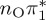4.55	—		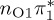3.89	—		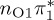4.43	—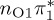
T3		5.01	—	π4σ*CBr	5.69	—		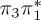5.68	—	π4σ*CBr	5.16	—	π4σ*CBr	4.35	—	π4σ*CBr	4.53	—	π4σ*CBr
T4		5.16	—		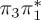5.93	—	π4σ*CBr	6.31	—		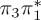5.36	—		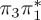4.51	—		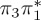4.75	—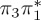
T5		5.91	—		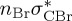6.83	—		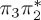7.87	—		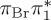5.90	—		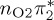4.64	—		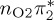5.20	—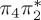
T6		6.05	—		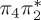7.80	—		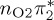8.00	—		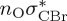6.00	—		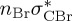4.73	—		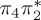5.37	—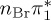
T7		6.24	—		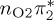8.02	—	π3σ*CBr	8.05	—		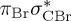6.03	—		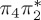4.76	—		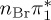5.56	—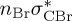
T8		6.99	—		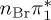8.34	—		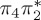8.24	—		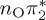6.38	—		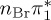4.94	—		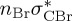5.58	—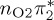
	RMSD	0.00			1.01			0.75			0.21			0.67			0.34

^aMS-CASPT2(20,14)/ANO-RCC-VDZP. S₀ energy: −3017.895007 atomic units. ^bCASSCF(14,11)/cc-pVDZ-DK. S₀ energy: −3016.429666 atomic units. ^cMRCIS(10,8)/cc-pVDZ-DK. S₀ energy: −3016.550517 atomic units.^dADC(2)/def2-TZVP. S₀ energy: −2986.073460 atomic units. ^eTD-BP86/TZP. S₀ binding energy: −2.845430 atomic units. ^fTD-B3LYP/TZP. S₀ binding energy: −3.361766 atomic units.

The singlet and triplet ππ* excitations were estimated experimentally to be 4.66 eV [48] and 3.35 eV [9,48], respectively. These excitations are accurately described by the S₁ and T₁ states of our MS-CASPT2 computations, with energies of 4.60 and 3.51 eV, respectively. The presence of the dark singlet n_O1π* (S₂) state (in the following, if not stated otherwise, ‘n_Oπ*’ refers to states involving the n_O1 orbital) energetically close to the spectroscopically active ¹ππ* state is reminiscent of the situation encountered in T and U [49–51]. The third excited state, S₃, is an excitation into the antibonding orbital of the C–Br bond (π₄σ*_CBr) and thus a state related to C–Br dissociation. The S₄ is another ππ* state, located at 6.01 eV. The order of the singlet states agrees with that obtained with previous calculations on 5BU [11,17]. The character of the triplet states mirror the singlet counterparts up to T₄, with the lowest triplet state being the ³ππ* state, followed by the ³n_Oπ* state (T₂).

Owing to their good agreement with the experimental values, the MS-CASPT2 values serve as reference data for the other levels of theory. As an estimator for the accuracy of the excited-state calculations, we computed root mean square deviations (RMSD, bottom of table 1), comparing states of matching characters against the MS-CASPT2 results. For the RMSD calculation, we only included the relevant, low-lying states with 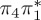, 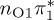or 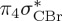characters—which are the S₁₋₃ or T₁₋₃ for MS-CASPT2 but might be different adiabatic states for the other methods. Among the five cheaper levels of theory, the worst result is obtained with CASSCF (1.01 eV RMSD) and the best result with ADC(2) (0.21 eV). Both the CASSCF and MRCIS methods significantly overestimate the energies of the ¹ππ* states, changing the order of singlet excited states; this observation is due to an imbalanced description of correlation energy in these methods. TD-BP86 systematically underestimates all excitation energies by about 1 eV on average, and alters the order of the states as well. On the other hand, TD-B3LYP describes the excitation energies fairly well, in particular the bright ¹ππ* state, and gives the correct order for the three lowest singlet states. In general, only the few lowest excited states in each multiplicity are consistently obtained with all methods, although the ordering can vary; for the higher states, different characters were obtained, and the energy deviations are larger than for the lower states.

(b). Potential energy surfaces

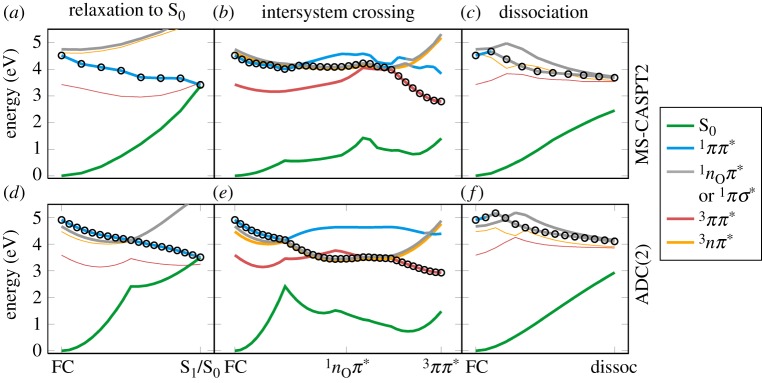
The calculated vertical excitations are only the first step in disentangling the actual photophysical relaxation pathways of 5BU. Hence, as a second step, we investigated the most important pathways—ground-state relaxation, ISC and photodissociation—in more detail. Because of the high cost of MS-CASPT2(20,14), the necessary optimizations were carried out with MS-CASPT2(12,9), which excludes the n_Br, π_Br, σ_CBr, σ_CBr and n_O2 orbitals. This reduced active space is only suitable to describe the lowest excitations (the ππ* and n_O1π* states), but allows optimizing the critical points for these states. As ADC(2) gave very promising results in the Franck–Condon region, we also performed these computations with ADC(2), to see whether its accuracy extends to the rest of the PESs.

The following minima were obtained at both levels of theory: the S₀ minimum, a minimum of the ¹n_Oπ* state (located on the S₁ adiabatic surface) and a ³ππ* minimum (T₁), shown in figure 3a–c. Additionally, crossing points between several electronic states (adiabatic surfaces in parenthesis) were found: a ¹ππ*/¹n_Oπ* (S₂/S₁) conical intersection (CoIn), a ¹ππ*/S₀ (S₁/S₀) CoIn, a 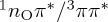(S₁/T₂) minimum-energy crossing (MXP) and a ³ππ*/³n_Oπ* (T₂/T₁) CoIn, which are presented in figure 3d–g. The attempted optimization of a ¹ππ* minimum ended in the ¹ππ*/S₀ CoIn. We also optimized the geometry of the uracilyl radical in the S₁ (¹πσ*) state (figure 3h); this optimization was constrained to r_CBr=2.8Å and α_C4C5Br=119°, in order to allow for sensible results with ADC(2). All optimized geometries can be found in the electronic supplementary material. Based on the geometries, the following three chains of LIIC scans were generated: (i) S₀ min – S₂/S₁ CoIn (only ADC(2)) – S₁/S₀ CoIn; (ii) S₀ min – S₂/S₁ CoIn – S₁ min – S₁/T₂ MXP – T₂/T₁ CoIn – T₁ min; and (iii) S₀ min – constrained S₁ min.

Figure 3.

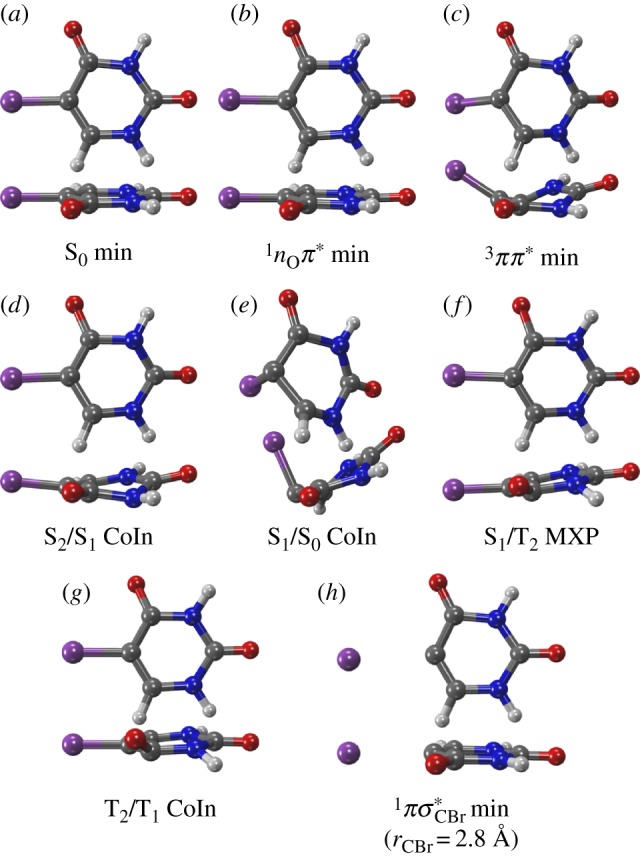
Geometries of the critical points optimized at the MS-CASPT2(12,9) level of theory. (Online version in colour.)

The energies along these LIIC paths were recomputed with MS-CASPT2(20,14) and ADC(2), yielding the curves presented in figure 4. At MS-CASPT2 level, ground-state relaxation (figure 4a) can be achieved by a barrierless descending path from the Franck–Condon region to the S₁/S₀ CoIn. This CoIn is related to a molecular geometry with strong ring puckering (depicted in figure 3e), as already reported for other pyrimidine nucleobases [51,52]. As the bright state is the S₁ at this level of theory, no other state crossing is involved, which should make ground-state relaxation an important and efficient relaxation route. Noteworthy, our calculations do not show the barrier reported by Kobyłecka et al. [17], probably because they employed CASSCF-based minimum-energy paths, whereas we performed optimizations at the higher MS-CASPT2 level of theory.

Figure 4.

Linear-interpolation-in-internal-coordinates (LIIC) scans for the most important photophysical paths in 5BU, using the MS-CASPT2(20,14)//MS-CASPT2(12,9) level of theory (a–c) and ADC(2) (d–f). (Online version in colour.)

In figure 4b, it can be seen that ISC in 5BU involves first switching from the bright ¹ππ* state to the ¹n_Oπ* state. Subsequently, close to the nearly planar ¹n_Oπ* minimum (figure 3b), a near-degeneracy region with the ³ππ* state can be reached through a slight pyramidalization at carbon atom C₄ (figure 3f,g). Note that, in this region, the lowest triplet states are exchanged, with ³ππ* being T₂, unlike at the Franck–Condon geometry. The spin–orbit coupling between the ¹n_Oπ* and ³ππ* states amounts to approximately 60 cm⁻¹ at this point, allowing for ISC. Decay to the lowest triplet minimum (³ππ*), which shows a boat-like ring conformation (figure 3c) like in uracil and thymine [53], is possible through the nearby T₂/T₁ CoIn. The energy of the ³ππ* minimum, 2.9 eV, fits very well with the 3.0 eV onset of the phosphorescence spectrum of 5BU [9]. The ISC route in 5BU is reminiscent of the one found in U [21] and T [24], where also the ¹n_Oπ* minimum is the gateway for population of the triplet manifold, due to the presence of the nearby S₁/T₂ MXP and T₂/T₁ CoIn (cf. figure 3b,f,g). Also of interest is the observation that from the ¹n_Oπ* minimum the system could easily cross back to the ¹ππ* state and subsequently deactivate to the ground state, as was already proposed in the literature for U and T [51,54].

We note that the spin–orbit couplings in 5BU are not much stronger than in U or T, although one might have expected this from the heavy-atom effect of the bromine atom. The relatively weak spin–orbit couplings can be explained by the fact that neither the ¹n_Oπ* nor the ³ππ* excitations involve the bromine orbitals significantly. Owing to the properties of the spin–orbit Hamiltonian, very large spin–orbit couplings could only be expected if the two involved states differ in one orbital localized at the heavy bromine atom. For example, the coupling between the ¹π₄σ*_CBr and 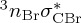states amounts to 860 cm⁻¹ at the Franck–Condon geometry. However, these strong interactions are only relevant at higher energies, but do not play a role after excitation to the S₁. Hence, in the low-energy range, ISC in 5BU should not be significantly different than ISC in U.

In figure 4c, the potential energy curves suggest that, in order to initiate photodissociation, the system would need to switch from the bright ¹ππ* state to the dissociative ¹πσ* state. At least in the shown scan, this involves a barrier of 0.2 eV. Moreover, the barrier might become larger after the molecule relaxes in the ¹ππ* state. In this regard, a transition-state search based on MS-CASPT2 potentials would be helpful. Unfortunately, the minimum-energy path presented in [17] is not, since this path was optimized using CASSCF(12,10), with an active space that excludes the n_O orbitals. This makes the dissociative πσ* state the lowest state in their optimization (according to our reproduction of their calculation), explaining why their minimum-energy path was dissociative. Instead, we expect that a minimum-energy path using the ¹ππ* gradients (e.g. at the MS-CASPT2 level) would not show dissociation, but rather approaches the S₁/S₀ CoIn.

Dissociation could in principle also happen from the ¹n_Oπ* minimum or via the triplet states, as experimentally observed in solution by Swanson et al. [10]. The ¹n_Oπ* minimum has a higher energy than the dissociation limit (according to figure 4c), but we expect that there exists some barrier due to the avoided crossing between ¹n_Oπ* and the dissociative states. Dissociation in the triplet state should be hampered by the low energy of the T₁ minimum (0.7 eV below the dissociation limit), and hence would need to occur from an unrelaxed triplet state.

Figure 4d–f presents the equivalent paths obtained from the ADC(2)/def2-TZVP calculations. For ground-state relaxation (figure 4d), the path involves the S₂/S₁ CoIn, because the bright state at ADC(2) level is wrongly the S₂. This state reordering could increase the probability to switch to the ¹n_Oπ* state during decay, but otherwise ADC(2) agrees with MS-CASPT2 in that the ground-state relaxation path is barrierless.

Regarding the ISC path (figure 4e), the most important feature of the ADC(2) curves is the low energy of the ¹n_Oπ* minimum relative to the S₂/S₁ crossing (in contrast to the MS-CASPT2 result, where the minimum is only 0.1 eV below the crossing). At the ADC(2) level, this would probably lead to population trapping in the ¹n_Oπ* minimum with subsequent ISC, whereas recrossing to the ¹ππ* state would be strongly suppressed. However, ISC itself seems to be well described at the ADC(2) level, with the 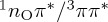crossing energetically close to the ¹n_Oπ* minimum.

Finally, figure 4f shows the potential curves for photodissociation at ADC(2) level of theory. Because ADC(2) is a single-reference method and cannot properly describe the full dissociation, we only present the energy scan for the C–Br bond length from 1.9 Å up to 2.8 Å (figure 3h). Despite the restricted scan, one can still study the barrier between the ¹ππ* and ¹πσ* states, and obtain an estimate of the dissociation energy. From the scan in figure 4f, it can be seen that ADC(2) qualitatively agrees with MS-CASPT2, giving a barrier of 0.2 eV, which is due to the avoided crossing between ¹ππ* and ¹πσ*. Because at the ADC(2) level the ¹n_Oπ* and triplet minima are quite low in energy, dissociation would be even less likely than at MS-CASPT2 level.

Based on the MS-CASPT2 results, we can therefore propose that ground-state relaxation should be the predominant relaxation route of 5BU in the gas phase. However, the close proximity of the bright ¹ππ* state to the ¹n_Oπ* state could lead to some population transfer into the latter state. Owing to the favourable location of the 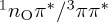crossing, it is then conceivable that some ISC occurs. Dissociation is disfavoured due to the barrier needed to be overcome before populating the dissociative ¹πσ* or n_Oσ* states. These findings do not fully agree with the conclusions drawn by Blancafort and co-workers [17], who proposed that in 5BU homolytic C–Br cleavage and relaxation to the ground state are in close competition, based on SA-CASSCF calculations.

(c). Choice of electronic structure method for dynamics

While the presented static quantum chemistry calculations reveal some new details on the excited-state behaviour of 5BU, it would also be advantageous to perform excited-state dynamics simulations, to obtain excited-state lifetimes or branching ratios between the relaxation channels.

Ideally, dynamics simulations in this case should be carried out with our reference method MS-CASPT2(20,14); however, this method is currently too expensive for dynamics. Even with the smaller active space CAS(12,9) employed for the optimizations, computing nuclear gradients for MS-CASPT2 remains very costly. Moreover, TD-DFT has been known to severely overestimate the energies of non-planar geometries in nucleobases [55]. For 5BU, we attempted to optimize the S₁/S₀ CoIn using the two TD-DFT methods from table 1, and found energy barriers of at least 2 eV from the Franck–Condon region to the CoIn, showing the inadequacy of these methods.

Currently, the only practicable choices to run Sharc simulations are CASSCF and MRCIS. The shared weakness of both methods is their significant overestimation of the ¹ππ* energies, which in this particular case can prevent ground-state relaxation and enhance dissociation. From table 1, it is clear that this overestimation is even more severe in CASSCF than in MRCIS. Although at CASSCF level, the bright ¹ππ* state is 0.6 eV above the dissociative ¹πσ* state, MRCIS predicts ¹ππ* to be 0.1 eV below ¹πσ*. Furthermore, as reviewed in [56], for U and T CASSCF predicts significant trapping in the ¹ππ* state, which is also not consistent with MS-CASPT2 calculations [51]. Hence, while both MRCIS and CASSCF do not fully agree with the MS-CASPT2 results, MRCIS is still clearly the preferred choice between those two options.

In order to investigate which parts of the PESs of 5BU can be described reasonably at the MRCIS level of theory, we also performed the LIIC calculations with this method. As expected, dissociation is not properly described (not shown), with a nearly barrierless path from the Franck–Condon region to the dissociation limit. Furthermore, owing to the high energy of the ¹ππ* state, the CoIn between S₀ and ¹ππ* is not as accessible as it should be, and relaxation to the ground state is hampered. The ISC pathway appears to be qualitatively correct. As can be seen in figure 5, the ISC pathway at MRCIS level is very similar to the one at ADC(2) level. In particular, after excitation to the bright ¹ππ* (S₂) state, the system first needs to cross from ¹ππ* to ¹n_Oπ* at the corresponding S₂/S₁ CoIn and then relax to the ¹n_Oπ* minimum. There, a barrier of 0.1 eV needs to be surmounted to reach a crossing with the ³ππ* (which is the adiabatic T₂ state at this point) with spin–orbit couplings of about 55 cm⁻¹, allowing ISC to take place. Once transferred to the T₂ state, the system can relax through the T₁/T₂ CoIn to the ³ππ* minimum, located on the adiabatic T₁. Hence, we conclude that trajectories at the MRCIS level of theory will be able to properly sample the ISC pathway of 5BU, although unfortunately they will only provide qualitative aspects of the deactivation mechanism, because the ground-state relaxation and dissociation pathways are under- and over-represented, respectively.

Figure 5.

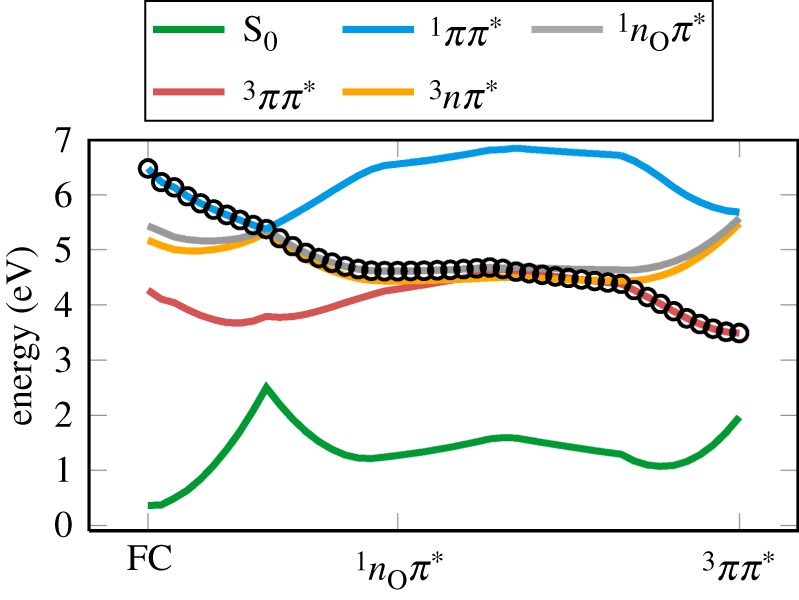
Linear-interpolation-in-internal-coordinates (LIIC) scans as in figure 4b,e, but for the MRCIS(10,8) level of theory. (Online version in colour.)

(d). Absorption spectrum

In order to prepare the initial conditions for the excited-state dynamics, we first simulated the absorption spectrum of 5BU, based on a distribution of geometries representing the ground-state vibrational state. In figure 6a,b, we show the simulated spectrum, as obtained with MS-CASPT2(20,14) and MRCIS, respectively. As expected from the single-point calculation at the equilibrium geometry, the MS-CASPT2 spectrum (depicted in figure 6a) shows an absorption band centred at approximately 4.3 eV, due to the bright ππ* (S₁) state. The character of the involved states, shown in figure 6c, was analysed by calculating wave function overlaps to the states at the equilibrium geometry; these overlaps allow one to compare states for hundreds of calculations without individually inspecting the orbital and expansion coefficients [57]. This analysis showed that, for the large majority of sampled geometries (figure 6c), S₁ has ππ* character and S₂ has n_Oπ* character, whereas for the higher states the character varies with geometry, e.g. the πσ* state, which is distributed between the S₂–S₅. Comparing the spectrum to experimental spectra, we find that the MS-CASPT2 calculations qualitatively reproduce the first absorption band of 5BU, but the sampling has shifted the peak to slightly lower energies than those predicted experimentally [7,15,48].

Figure 6.

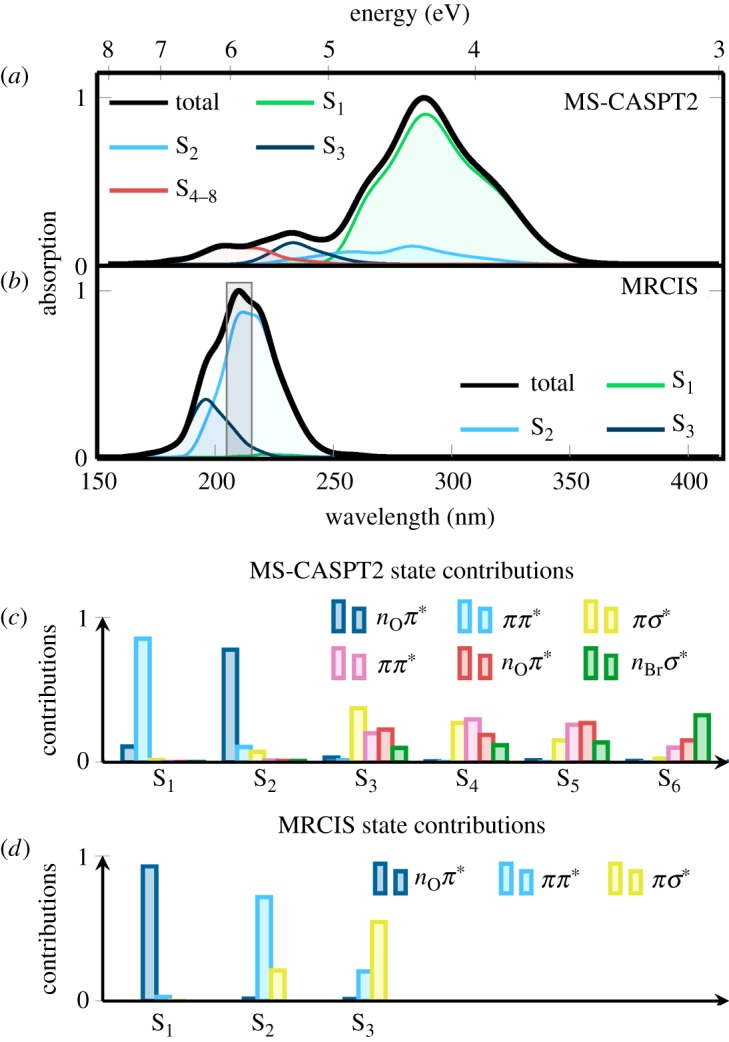
Calculated absorption spectrum of the keto tautomer of 5BU at the (a) MS-CASPT2(20,14)/ANO-RCC-VDZP and (b) MRCIS(10,8)/cc-pVDZ-DK levels of theory. The solid black lines show the total absorption spectrum; coloured lines indicate the contributions of the different singlet states, as indicated. Grey box in (b) denotes the excitation window employed in the dynamics simulations. In (c,d), the contributions of the state characters to the absorption bands in (a,b) are given. (Online version in colour.)

The MRCIS spectrum, shown in figure 6b, presents a peak centred at 5.9 eV, arising from the spectroscopically active ππ* state, which is either S₂ or S₃ depending on the initial geometry. This peak is shifted by 1.6 eV with respect to the MS-CASPT2 spectrum, as expected from the vertical excitation calculations (table 1). At almost all geometries, S₁ is the dark ¹n_Oπ* state (figure 6d), explaining why S₁ does not contribute to the spectrum. Instead, the absorption band is dominated by the bright ¹ππ* state, which is distributed between the S₂ and S₃ states. Contributions to the πσ* dissociative state can also be found in S₂ and S₃.

As with the vertical excitation energies, the comparison of the MRCIS spectrum with experimental data [7,15,48] suffers from the major drawback that the energy of the ππ* transition is blue-shifted at the MRCIS(10,8)/cc-pVDZ-DK level of theory. However, we note that, for the majority of initial conditions, the bright ¹ππ* state is below the dissociative ¹πσ* state. This should limit the amount of artificial dissociation so that still a number of trajectories can sample the other relaxation pathways, in particular ISC.

(e). Evolution of the trajectories

We shall start the discussion of the non-adiabatic dynamics data with the results obtained from an analysis of the kinetic constants. As a general finding, about a third of the propagated trajectories (23 of 78) undergo C–Br bond dissociation within 400 fs. Clearly, this dissociation quantum yield is far-fetched in comparison with the experimental few per cent yields [7,8,10], due to the level of theory employed in the dynamics. From the highly accurate MS-CASPT2 results, no ultrafast dissociation should be expected in the gas phase after ¹ππ* excitation. Therefore, we do not further discuss those trajectories that dissociated; only the 55 non-dissociating trajectories are included in the following analysis.

Figure 7 presents the temporal evolution of the excited-state populations and the results of the kinetic analysis. The populations were fitted to a sequential kinetic model with two parameters τ₁ and τ₂, which we identify as the internal conversion (IC) and ISC time constants, respectively. Errors for the parameters were obtained with the bootstrapping method [58], in order to judge whether the number of trajectories is sufficient to describe these processes.

Figure 7.

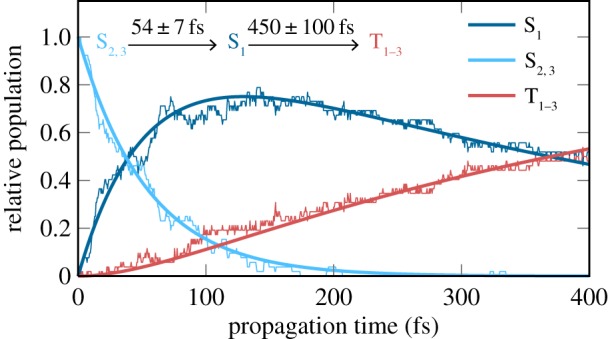
Temporal evolution of excited-state populations of the 55 non-dissociating trajectories, computed with Sharc and MRCIS(10,8)/cc-pVDZ-DK. (Online version in colour.)

We obtain τ₁=54±7 fs, meaning that the 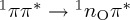population transfer is about 70% after 100 fs (see the S₁ line in figure 7). Note that this is substantially different from the results reported for uracil and thymine in previous SA-CASSCF-based dynamics simulations, where much less was transferred within 100 fs, because longer time constants were obtained for this pathway [21,24,59–62]. This difference is due to the fact that at SA-CASSCF level the ¹ππ* state is higher in energy than with MRCIS, and therefore population transfer from ¹ππ* to ¹n_Oπ* is slower at SA-CASSCF level.

The second time constant we obtain is τ₂=450±100 fs. That is, within 400 fs, 51% of the non-dissociating trajectories have moved to the triplet states and 49% are still in the singlet manifold. The calculated ISC time scale matches well with the 0.4 ps time constant reported in [16] for time-resolved pump–probe experiments (266 nm pump and 330 nm probe) on 5BU in water. In the same experiment, they also observe a nanosecond component, which could be assigned to the population trapped in the triplet states.

Interestingly, the time constant of 450 fs obtained for ISC in 5BU is smaller than those previously reported for U and T [21,24], which are approximately 800 fs and 900 fs, respectively. The factor of two in the ISC time constant is due to subtle differences in the excited-state PESs, due to the presence of the bromine atom, and ultimately because a different level of theory has been used in the previous simulations [21,24]. Otherwise, the general ISC mechanism in 5BU, T and U is the same and also the spin–orbit couplings have approximately the same size. However, while the ISC time constant appears to be reasonable, the overall triplet yield is clearly overestimated, because a large fraction of the trajectories should undergo relaxation to S₀ before ISC can occur. In our simulations, this relaxation is blocked by the large barrier to recross back to the ¹ππ* and to reach the ¹ππ*/S₀ CoIn. Consequently, for the simulated time, the MRCIS-based dynamics does not result in trajectories undergoing relaxation to the ground state, as was suspected from the static calculations.

These results show that a relevant deactivation pathway of 5BU should be ultrafast ISC. In particular, the results of the interpolation scans in figures 4 and 5 are reminiscent of the situation reported for U and T [21,53,63], where also from the bright ¹ππ* state the system can deactivate to the dark S₁ (n_Oπ*) state. This state is the doorway for ISC into the ³ππ* state, in accordance with the El-Sayed rules [64]. For 5BU, this ISC mechanism is in agreement with experimental data [7,10], which report ISC from a ¹n_Oπ* to a ³ππ* state. The involved geometries differ from the ground-state geometry by compressions and elongations along the C=O bonds and deformations of the ring.

4. Conclusion

We performed accurate vertical excitation calculations and potential energy surface explorations for 5-bromouracil (5BU), in order to investigate the excited-state dynamics of this molecule. The vertical excitation calculations showed that MS-CASPT2 with an active space of 20 electrons in 14 orbitals gives excitation energies in excellent agreement with experiment. In particular, the lowest excited states are the bright ¹ππ* state, a dark ¹n_Oπ* state and a dissociative ¹πσ* state at slightly higher energies. These three states are responsible for the three plausible photophysical reaction pathways of 5BU, according to MS-CASPT2. A barrierless pathway on the ¹ππ* state leads directly to a conical intersection with the S₀, allowing for efficient relaxation to the ground state. Alternatively, another conical intersection allows the interconversion of ¹ππ* into ¹n_O, from where ISC to the ³ππ* state can commence. Third, after surmounting a barrier of at least 0.2 eV, the molecule could switch from ¹ππ* to ¹πσ*_CBr, which would lead to the homolytic dissociation of the C–Br bond. Of these three pathways, MS-CASPT2 identifies relaxation to S₀ as the most probable pathway in the gas phase.

We also investigated the performance of different electronic structure methods in describing the deactivation of 5BU, including ADC(2), TD-BP886, TD-B3LYP, SA-CASSCF and MRCIS. All of these methods represent significantly lower cost alternatives to the expensive MS-CASPT2 computations performed. From the excitation energies and potential energy surfaces, ADC(2) seems to give the best results in agreement with the MS-CASPT2 reference calculations. The DFT-based methods fail especially in describing the ground-state relaxation pathway. SA-CASSCF and MRCIS, on the other hand, notably overestimate the energy of the ¹ππ* state, which makes dissociation more likely and ground-state relaxation less likely. For technical constraints, MRCIS was chosen to perform non-adiabatic dynamics simulations coupled to Sharc, a variant of the trajectory surface hopping method that can treat ISC. We found that ISC is mediated by the ¹n_Oπ* state and occurs with a time constant of 450±100 fs, showing that this process is ultrafast in 5BU, as already discussed in recent literature on pyrimidine bases [21,24,56,65]. Unfortunately, the trajectories do not allow one to obtain yields for the competitive photophysical pathways of 5BU, due to the shortcomings of MRCIS.

This study clearly shows that the proper description of the excited-state dynamics of 5BU is very challenging, and requires a multi-configurational electronic structure method with a large active space, in order to account for all the different, competing relaxation pathways. Moreover, previous experiments were conducted in the condensed phase, and the applications of 5BU involve the photoactive molecule in a complex biological environment, and the inclusion of such environments would add another level of complexity to future computations.

Authors' contributions

F.P. performed the CASSCF and MRCIS vertical excitations calculations, the Sharc dynamics simulations and drafted the manuscript. S.M. performed the rest of the quantum chemistry calculations, provided support for the dynamics simulations, performed the dynamics analysis and contributed to the draft. L.G. conceived and supervised the study and contributed to the writing of the manuscript. All authors discussed the results and approved the manuscript for publication.

Competing interests

The authors declare no competing interests.

Funding

This work is funded by the Austrian Science Fund (FWF) project P25827, the University of Vienna and the Universitat Autònoma de Barcelona. Part of the calculations have been performed at the Vienna Scientific Cluster (VSC).