Pedigree-based inbreeding coefficient explains more variation in fitness than heterozygosity at 160 microsatellites in a wild bird population

Abstract

Although the pedigree-based inbreeding coefficient F predicts the expected proportion of an individual's genome that is identical-by-descent (IBD), heterozygosity at genetic markers captures Mendelian sampling variation and thereby provides an estimate of realized IBD. Realized IBD should hence explain more variation in fitness than their pedigree-based expectations, but how many markers are required to achieve this in practice remains poorly understood. We use extensive pedigree and life-history data from an island population of song sparrows (Melospiza melodia) to show that the number of genetic markers and pedigree depth affected the explanatory power of heterozygosity and F, respectively, but that heterozygosity measured at 160 microsatellites did not explain more variation in fitness than F. This is in contrast with other studies that found heterozygosity based on far fewer markers to explain more variation in fitness than F. Thus, the relative performance of marker- and pedigree-based estimates of IBD depends on the quality of the pedigree, the number, variability and location of the markers employed, and the species-specific recombination landscape, and expectations based on detailed and deep pedigrees remain valuable until we can routinely afford genotyping hundreds of phenotyped wild individuals of genetic non-model species for thousands of genetic markers.

1. Introduction

Inbreeding depression, defined as reduced fitness of offspring resulting from matings among relatives, is commonplace, also in wild populations [1]. Inbreeding depression is widely hypothesized to explain the evolution of important biological phenomena such as dispersal [2], mating systems [3], mate recognition [4], extra-pair mating behaviour [5] and self-incompatibility [6]. Quantifying the magnitude of inbreeding depression is consequently fundamental to understanding and predicting evolutionary dynamics.

Inbreeding depression is caused by increased probabilities of identical-by-descent (IBD, i.e. the probability that two homologous alleles are descended from a common ancestor) in inbred individuals [7,8]. Because increased IBD translates into increased homozygosity [8], inbred individuals will on average have lower fitness, either because of increased expression of (partially) recessive deleterious alleles (i.e. directional dominance) or because homozygotes have inferior fitness compared with heterozygotes (i.e. overdominance effects) [9–11]. Traditionally, inbreeding depression is quantified as the relationship between fitness and pedigree-based inbreeding coefficient F. F estimates expected IBD due to known shared ancestors of parents relative to a specified base population ([12], ch. 7). Alternatively, because inbreeding reduces heterozygosity, inbreeding depression can be directly quantified from the relationship between fitness and heterozygosity (H) measured across genetic markers [13–15]. Until recently, marker-based estimates of IBD were mostly employed for populations without good pedigree data. The increased availability of high-density molecular markers has generated renewed interest in marker-based estimates of IBD, even in populations for which pedigree data are available (e.g. [16]). This is because, first, genetic markers allow testing for local effects, i.e. fitness effects caused by polymorphisms in gametic phase disequilibrium (i.e. linkage disequilibrium) with particular marker loci in physical proximity [13,17,18]. Second, although pedigrees measure the expected proportion of the genome that is IBD, markers estimate realized IBD [19,20]. Thereby they capture variation in IBD introduced by stochasticity inherent to Mendelian segregation and recombination [21–24]. For example, the standard deviation in realized IBD among offspring of full sibling matings (pedigree F = 0.25) is 0.044 in humans (Homo sapiens) [23] and 0.084 in zebra finches (Taeniopygia guttata) [25]. Third, markers can capture variation in inbreeding that is not captured because of shallow, incomplete or erroneous pedigree data (e.g. [26,27]). However, these advantages may be off-set by sampling variance in marker-based estimates, which will be large if the number of markers is small relative to the number of independently segregating units [28]. Furthermore, markers may be homozygous without sharing a recent common ancestor, i.e. identical-by-state (IBS) rather than IBD, and hence not predict the probability of IBD at adjacent chromosomal regions (i.e. IBD–IBS discrepancy) [25,29].

Assessing the influence of the above-mentioned species- and population-specific factors on the relative power that F and H possess to quantify inbreeding depression requires accurate fitness data, estimates of F based on a well-resolved pedigree, and estimates of H across many genetic markers, as well as theoretical or simulated expectations of the relationships among them. The correlations among the pedigree-based expectation of IBD (F), heterozygosity at a large number of physically unlinked selectively neutral loci (H), and fitness has been conceptualized in [18] as

1.1

Similarly, the relationship for regression slopes has been conceptualized in [18] as

1.2

In practice however, a finite number of chromosomes and reduced recombination among markers located on the same chromosome introduces Mendelian noise, which causes realized IBD at the marker loci to differ from its pedigree-based expectation, weakening the association between F and fitness ([25]; figure 1). Mendelian noise can be accounted for by dividing the right side of equation (1.1) by the squared correlation coefficient between F and realized IBD (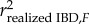), which following [25] leads to

1.3

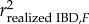can be quantified by simulating markers distributed on a genome with known recombination landscape and a specific pedigree [25].

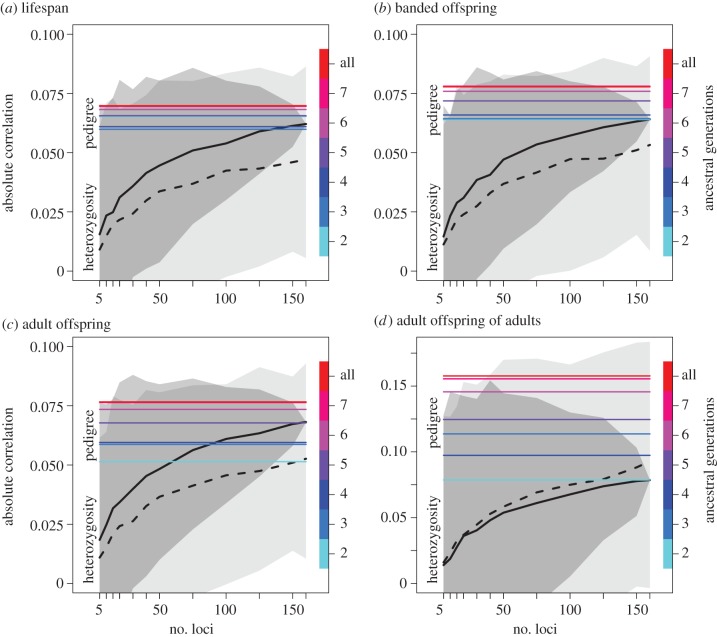
Figure 1.

The absolute correlation of heterozygosity (H) and pedigree-based inbreeding coefficients (F) with fitness increases with the number of microsatellites and pedigree depth, respectively. Fitness components: (a) lifespan, (b) lifetime number of banded offspring, (c) lifetime number of adult offspring and (d) lifetime number of adult offspring produced by adult individuals. The correlation between F and fitness increases with the number of ancestral generations available (horizontal coloured lines; legend along right axis). F calculated from seven ancestral generations explained as much variation as F calculated from the full pedigree. The correlation between H and fitness increased with the number of loci (solid black line; the dark grey area shows the central 95% of sampling variation), but is always weaker than the correlation with F based on the complete pedigree. The correlation with heterozygosity based on simulated neutral and unlinked loci (and thus with lower amounts of Mendelian noise) is indicated by the dashed black line, and the light grey area shows the central 95% of simulated values. Note that all correlations with H were positive, and all correlations with F were negative (electronic supplementary material, figures S2 and S3).

Expected values of r_F,H and β_F,H can be calculated following Szulkin et al. [18] as

1.4

and

1.5

where and σ²(H) are the observed mean and variance in H, and g₂ is a measure of the amount of identity disequilibrium, i.e. the correlation in H across loci measured as the excess of double homozygotes at two loci relative to the expectation under random association [30], which is expected to equal

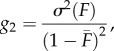1.6

where 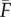and σ²(F) are the observed mean and variance in F. Note that in these equations, F is defined as the pedigree-based expectation of IBD [18] and that it is assumed that loci are physically unlinked [30]. Equations (1.4) and (1.5) remain valid (with F as pedigree-based inbreeding) when loci are linked because the reduction in r_F,H and β_F,H due to increased Mendelian noise is accounted for by dividing by the variance in H, which is higher for linked loci. Importantly however, when g₂ is estimated from linked markers, F in equations (1.4)–(1.6) has to be interpreted as a measure of realized IBD [31], and equation (1.4) will estimate r_{realized IBD,H}. Comparing the latter with r_{realized IBD,F} will reveal if H or F measures realized IBD better.

Precision of estimates of H, and hence its ability to capture variation in genome-wide IBD, improves with the number of markers [32,33]. Although a very large number of genetic markers is always expected to measure variation in realized IBD better than even a perfect (i.e. complete and error-free) pedigree [32], even a small number of markers might outperform an incomplete, short or error-ridden pedigree [25,29]. While simulations have yielded insights into the number of markers necessary to precisely estimate realized IBD in virtual populations [20,25,32], we still know relatively little about their applicability to real-world populations with fluctuating population sizes, overlapping generations and complex relatedness patterns. This is at least partly because there are few wild populations for which high-resolution pedigree, fitness and genetic marker data are simultaneously available [34,35].

To gain a better understanding of the relative power of marker- and pedigree-based estimates of inbreeding depression in real populations, we use high-quality pedigree and life-history data from a long-term study population of song sparrows (Melospiza melodia) on Mandarte Island, British Columbia, Canada [36]. We calculate F using a well-resolved pedigree and H using 160 microsatellites (also known as short tandem repeat loci, or STRs), and quantify the correlation between them. We subsequently analyse how well lifespan and reproductive success correlate with F or H, and compare these correlations to their theoretical predictions. Then, we test if H explains variation in fitness over and above what is explained by pedigree-based F. Finally, we investigate the effect of pedigree depth and marker number on the correlations of F and H with fitness.

2. Material and methods

(a). Inbreeding coefficients

All song sparrow individuals that lived on Mandarte Island have been colour-banded for individual identification at approximately 6 days after hatching since 1975, and are subject to detailed monitoring so that their lifespan and reproductive success are known [36]. Additionally, blood sampling of all individuals at approximately 6 days after hatching since 1993 allows correcting the pedigree for extra-pair paternities and determining the sex [37–41]. F was calculated using the R package pedigreemm [42] for individuals with at least two (and a mean of eight) genetically verified ancestral generations plus earlier genetically not verified generations. See the electronic supplementary material for details about the study system, pedigree reconstruction and selection of data used for analysis.

(b). Multilocus heterozygosity

We calculated mean H at 160 microsatellite loci (described in [37]), covering 35 linkage groups and a sex-averaged autosomal map length of 1731 centiMorgan [37], although the latter is likely an underestimate given the number of markers used [43]. Most of the 38–40 chromosomes typically found in birds [44] were covered by at least one and maximally 20 loci. See the electronic supplementary material for details about genotyping and error rates.

Here, we report analyses based on mean multilocus heterozygosity (H; i.e. the fraction of genotyped loci that is heterozygous), replacing any missing values at a given locus with the mean heterozygosity for this locus [14]. In our dataset, H is almost perfectly correlated with standardized multilocus heterozygosity (correlation coefficient r = 0.999) [45]. Because it can readily be interpreted as a probability or a proportion, we here use H as a measure of heterozygosity.

(c). Relationship between F and H, and identity disequilibrium

We estimated the correlation between F and H (r_F,H) and the slope of the regression of F on H (β_F,H) using 1966 individuals that hatched in the years 1993–2006 and had all four grandparents genetically verified. We calculated the theoretically expected values using equations (1.4) and (1.5). We derived the theoretically expected identity disequilibrium g₂ using equation (1.6), and estimated g₂ from marker data using approximations derived by Hoffman et al. [46]. These approximations allow for fast computation of g₂, which is important for large datasets. We estimated a 95% CI by bootstrapping 10 000 times across individuals.

(d). Fitness

To avoid complications arising from trade-offs among fitness components [47], we used measures of fitness that integrate over different life stages: lifespan (starting at banding), lifetime number of banded offspring, lifetime number of adult offspring for all individuals that hatched on Mandarte Island (which is zero for all individuals that died before breeding successfully), and the number of adult offspring produced during the lifetime of locally hatched individuals that survived to adulthood only (thereby reducing the large number of zeroes present in the other fitness measures). Our measures of fitness included extra-pair offspring sired by the focal individual and excluded offspring of which it was not the genetic parent.

Three of the fitness measures (lifespan, number of banded offspring, number of adult offspring) were calculated for all individuals that reached banding age (approx. 6 days) in our population, including those that died during their first year and hence did not produce any offspring. The inclusion of these individuals ensured that our measures of fitness captured this important source of variation (81% of banded nestlings died before the following spring). The number of banded offspring produced during the lifetime of an individual banded at approximately 6 days of age approaches the population genetic definition of fitness (i.e. number of zygotes produced by a zygote; [48]) as closely as is currently feasible in our study system.

(e). Observed relationships of F and H with fitness

All analyses used relative fitness, calculated by dividing by the mean fitness of the individuals that hatched in the same year, which removes environmentally induced variation in fitness componenents among cohorts, and results in estimates of inbreeding depression that can be interpreted as selection gradients measuring the strength of selection against inbred/homozygous individuals [49–51]. Results based on absolute fitness values, or based on F or H divided by their cohort means, were very similar.

Because our primary aim was to compare the strength of association between pedigree-based F and marker-based H with fitness, we quantified inbreeding depression as the correlation between F and each of the four relative fitness measures (following [29]), rather than as the slope of a regression of the logarithm of fitness on F (i.e. as lethal equivalents; [52]). Similarly, heterozygosity–fitness correlations were quantified as the correlation between H and each of the four relative fitness measures. See the supporting material for tests of the effects of sex, phenotype-dependent inbreeding, statistical testing and local effects. The number of individuals with known fitness, known H, and sufficiently well-known F data (see the electronic supplementary material) was 1432 for lifespan, 1426 for the number of banded or adult offspring, and 259 for the number of adult offspring produced by adults.

(f) Expected relationships of F and H with fitness

We calculated the expected relationship between H and fitness using equations (1.1) and (1.2). As discussed above, these equations do not account for Mendelian noise. Owing to the lack of knowledge on the recombination landscape of song sparrows, we cannot (yet) use simulations to quantify the amount of Mendelian noise. High r_{realized IBD,F} corresponds to little Mendelian noise. Mendelian noise for our song sparrow pedigree may lie near the estimates for humans (r_{realized IBD,F} = 0.91) and zebra finches (r_{realized IBD,F} = 0.75), but it depends also on the mean and variance in inbreeding in the population [25]. Rather than quantifying Mendelian noise directly, we instead calculated H from 160 unlinked and neutral microsatellites simulated across the song sparrow pedigree (electronic supplementary material). Although these microsatellites still contain variation introduced by sampling error and IBD–IBS discrepancy, they show reduced Mendelian noise because unlinked loci increase the correlation between F and realized IBD, and contrary to the real microsatellites they cannot be linked to genes affecting fitness. Hence, we expect the heterozygosity–fitness correlation based on simulated microsatellites to be closer to its expectation.

(g). Residual heterozygosity–fitness correlations

To test if H measures variation in realized IBD not captured by the pedigree-based expectation F (i.e. if H explains variation in fitness over and above the variation explained by F), we fitted linear models that simultaneously included both F and H as predictors.

(h). Role of marker number and pedigree depth

We investigated how much variation in fitness was explained by H and F as a function of both the depth of the pedigree and the number of microsatellites, both of which are known to influence the accuracy of estimates of IBD [32].

The effect of pedigree depth was investigated by calculating each individual's F after limiting the maximum number of ancestral generations used for pedigree calculations to 2–10. For example, if two ancestral generations were known, the pedigree consisted only of parents and grandparents. Note however that F for some individuals is based on fewer than this maximum number of ancestral generations, because of immigration or the limited length of the study period: for 24% of the individuals used in the analysis, 10 or more (maximally 12) ancestral generations were genetically verified, and 54% of individuals had eight or more genetically known ancestral generations. The explanatory power of F was measured as the absolute strength of the correlation r between F and each fitness measure [29].

To investigate the effect of the number of loci, we randomly sampled without replacement 500 times the following number of loci from all available 160 loci: 5, 10, 15, 20, 30, 40, 50, 75, 100, 125, 150 and 160 loci. Note that especially for the larger numbers of loci, the same loci will have been included in most of the replicate datasets, and that the full dataset with 160 loci was not resampled. For each dataset, we recalculated H across the sampled loci, and then calculated the correlation r between H and each of the fitness measures. Median r and the range of the central 95% of r values were extracted for each number of loci as an indication of the explanatory power of H and its uncertainty. Additionally, we simulated Mendelian inheritance at unlinked loci across the song sparrow pedigree (see the electronic supplementary material) to quantify the correlations between H and fitness in the absence of physical linkage and/or local effects.

3. Results

(a). Relationship between F and H

Mean H was 0.64 (i.e. on average 64% of the 160 loci were heterozygous) and mean F was 0.076 (i.e. the parents of the average individual were more closely related than (outbred) first cousins, whose offspring have F = 0.0625). Variances of H and F were 0.0028 and 0.0025, respectively. F was significantly correlated with H (electronic supplementary material, figure S1) and explained 43% of the variation in H. The expected (−0.662) and observed (−0.653) correlations of F and H were very similar, as were the expected (−0.635) and observed (−0.627) regression slopes of F on H (electronic supplementary material, table S1).

Identity disequilibrium g₂ as estimated from the mean and variance of F (following equation (1.6)) was 0.0030, and g₂ calculated using marker data was 0.0043 (95% CI = 0.0037 to 0.0050) across all 160 loci. As expected, mean g₂ based on marker data was not very sensitive to the number of loci included in its calculation, but the variation around this expectation increased considerably with a decreasing number of loci (electronic supplementary material, figure S5).

(b). Inbreeding depression in fitness

F was a significant predictor of all four fitness measures: lifespan (slope = −4.4, 95% CI = −7.2 to −2.0, p = 0.008, r = −0.07), lifetime number of banded offspring (slope = −6.2, 95% CI = −10.4 to −2.9, p = 0.005, r = −0.08), lifetime number of adult offspring (slope = −6.9, 95% CI = −11.9 to −3.0, p = 0.006, r = −0.08) and lifetime number of adult offspring of adults (slope = −6.4, 95% CI = −12.4 to −1.6, p = 0.014, r = −0.16) (electronic supplementary material, figure S2). F explained between 0.5% and 2.6% of variation in fitness.

(c). Heterozygosity–fitness correlations

H was a significant predictor of lifespan (slope = 3.6, 95% CI = 0.8 to 6.6, p = 0.02, r = 0.06), lifetime number of banded offspring (slope = 4.6, 95% CI = 1.0 to 9.3, p = 0.02, r = 0.06) and lifetime number of adult offspring (slope = 5.6, 95% CI = 1.0 to 10.8, p = 0.01, r = 0.07), but not of lifetime number of adult offspring of adults (slope = 2.5, 95% CI = −2.9 to 7.5, p = 0.21, r = 0.08) (electronic supplementary material, figure S3). H explained between 0.4% and 0.6% of variation in fitness. These values are comparable with those observed in other species [13].

(d). Predicted and observed relationships of F, H and fitness

Expected heterozygosity–fitness correlations and slopes were calculated as the product of the observed correlations and slopes of F versus H and fitness versus F ([18]; see equations (1.1) and (1.2) above). The expected correlations and slopes differed by 15–38% from those observed when using H calculated across all 160 microsatellites (electronic supplementary material, table S1): for all fitness measures except lifetime number of adult offspring of adults (where the pattern was opposite), observed heterozygosity–fitness correlations or slopes were stronger than expected. This is consistent with the fact that these expectations did not account for the presence of Mendelian noise. Doing so requires dividing the expectation by the (unknown) squared correlation coefficient between F and realized IBD (equation (3)), which would increase the expected strength of the association between H and fitness. In line with this, the simulated datasets based on 160 simulated unlinked and selectively neutral microsatellites yielded heterozygosity–fitness correlations and slopes that were on average very close to those expected, with a mean difference of 2–4% for lifespan, and lifetime number of banded or adult offspring (see below and figure 1). Only for lifetime number of adult offspring of adults was the mean difference between simulated and expected correlations higher (11%), but sample size was low.

(e). Residual heterozygosity–fitness correlations

For all fitness measures, H did not explain significant variation in fitness beyond what was already explained by F (electronic supplementary material, figure S4), as evidenced by regression models with both H and F as predictors (effect of H on lifespan: 95% CI = −1.2 to 3.9, p = 0.30; lifetime number of banded offspring: 95% CI = −1.8 to 5.1, p = 0.38; lifetime number of adult offspring: 95% CI = −2.2 to 6.4, p = 0.26; lifetime number of adult offspring of adults: 95% CI = −3.6 to 3.4, p = 0.89).

(f). Role of marker number and pedigree depth

As expected, the correlation of H and fitness increased with the number of loci used to measure H (figure 1). Although there is evidence that the rate of increase decreases as the number of loci increases, there is no evidence that an asymptotic maximum correlation had been reached at 160 loci. Greater pedigree depth increased the explanatory power of F. However, here there was evidence that an asymptotic maximum was reached, as seven ancestral generations provided equal explanatory power as the full pedigree.

H explained less variation in any of our fitness measures than the full pedigree (figure 1). Furthermore, H measured across loci simulated along the pedigree did on average not explain as much variation as H at the real genetic loci. This is noteworthy because the simulated loci are neutral and unlinked (i.e. not linked to genes affecting fitness), and correlations between heterozygosity and fitness can therefore only arise through identity disequilibrium (due to variance in inbreeding among individuals) with coding or regulatory loci. Real microsatellites on the other hand can additionally be directly linked to genes affecting fitness. However, many simulated datasets yielded correlations that were at least as strong as those in the real dataset, and therefore the data are consistent with our markers being selectively neutral.

4. Discussion

We used a detailed and well-resolved pedigree of genotyped song sparrows to quantify and compare observed and expected relationships between pedigree-derived inbreeding coefficients (F), heterozygosity (H) measured across 160 microsatellite loci, and four accurately measured components of fitness. We found that H based on a substantial number of markers distributed across most of the genome did not explain more variation in fitness than F, and hence that in this population F correlated better with realized IBD than H.

When investigated individually, both F and H explained a small but significant amount of variation in fitness. A small correlation coefficient does not imply a lack of biological meaning, especially when a trait is expected to be under the influence of many factors, including environmental noise [53]. The effect of F on fitness concurs with previous work showing inbreeding depression for many traits in this [54–60] and other populations [1]. Similarly, heterozygosity–fitness correlations of similar magnitude have been reported frequently [13–15]. Nevertheless, our study is among the few to test for evidence for inbreeding depression in lifetime reproductive success. Lifetime reproductive success captures the cumulative effects of most fitness components, and thereby avoids the possible complications introduced by trade-offs among fitness components [47].

The observed correlation between F and H closely matched the correlation predicted given the observed mean and variance in F and H. Conversely, the expected heterozygosity–fitness correlations calculated from the products of the correlations between F and H and fitness and F were smaller than those observed. However, when H was calculated across simulated unlinked and neutral microsatellites, heterozygosity–fitness correlations were closer to expectation. Although this is consistent with the presence of Mendelian noise in the real dataset that is not accounted for in the expectation [25], the discrepancy between observed and predicted heterozygosity–fitness correlations is not statistically significant because many simulated datasets yielded even stronger correlations than that observed (figure 1).

As expected based on the substantial variance in inbreeding in this population, H was correlated across loci (i.e. there was identity disequilibrium). The strength of identity disequilibrium based on marker data, estimated as g₂, was 0.0043. This estimate is significantly different from zero and similar to the average of 0.007 found across a range of populations of outbreeding vertebrates (including artificial breeding designs; [61], but several-fold lower than corresponding values from SNP datasets for harbour seals (g₂ = 0.028 across 14 585 SNPs) and oldfield mice (Peromyscus polionotus; g₂ = 0.035 across 13 198 SNPs) [46]. The high values of g₂ in these other populations may be due to a very high mean and variance in pedigree-based F, recombination landscapes where large parts of the genome are transmitted in blocks, or both. Furthermore, Nemo [62] simulations in the electronic supporting material show that gametic phase disequilibrium among linked markers increases identity disequilibrium, resulting in estimates of g₂ that are higher than expectations based on unlinked loci or a deep and error-free pedigree (equation (1.6)). Finally, while marker-based estimates of g₂ assume genotype errors to be uncorrelated across loci [46], variation in DNA quality or concentration may shape variation in allelic dropout rates, and hence apparent variation in homozygosity among individuals [63].

In line with linkage increasing g₂, g₂ estimated from our marker data (0.0043) was significantly and substantially higher than g₂ estimated from the mean and variance in F following equation (1.6) (0.0030). In theory, undetected relatedness among pedigree founders could also explain the discrepancy between marker- and pedigree-based estimates of g₂. However, simulation precluded this explanation for our dataset (electronic supplementary material, figures S6 and S7). Our conclusion that linkage affects g₂ contrasts with conclusions drawn by Stoffel et al. [31], where removing loci with a gametic phase disequilibrium r² ≥ 0.5 did not affect g₂. However, pairs of loci as little as 10 kb apart may yield r² values of only 0.27 to 0.3 on average [64]. Thus, Stoffel et al.'s pruned dataset must have still contained many linked loci. Furthermore, Stoffel et al. [31] explicitly redefined the inbreeding coefficient as used in, for example, Szulkin et al. [18], to represent a variable that explains all the variance in heterozygosity. This results in a version of g₂ that captures variation in realized IBD rather than variation in F. Although linkage effects should be incorporated in estimates of g₂ when the goal is to measure realized IBD [46], the quantification of pedigree properties, such as selfing rate, should be done using unlinked markers only [30].

Mean (0.076) and variance (0.0025) of F in our dataset were fairly high compared with estimates from other animal populations (e.g. [29]). However, such comparisons are hampered because F is the expectation of IBD relative to a specified base population assumed to consist of unrelated and outbred individuals. Consequently, mean and variance of F will initially increase with increasing pedigree depth, until an equilibrium, determined by the proportion of unrelated immigrants coming into the population each generation, has been reached (electronic supplementary material, figure S8). With increasing pedigree depth, the assumption of a base population of unrelated individuals becomes less important, because most inbreeding events are captured by the pedigree and any relatedness among founders becomes relatively less important. This suggests that in deep, well-resolved pedigrees, there is less undetected inbreeding (i.e. background F in Fig. 1 of [25]) for genetic markers to uncover. This is supported by our result that the explanatory power of F increased with pedigree depth (figure 1). By contrast, in the captive zebra finch population studied by Forstmeier et al. [29], 11 microsatellites explained more variation in fitness than pedigree-based F. Although their pedigree was mostly based on five ancestral generations (and up to seven in some cases), only 2.5 generations were known for an average individual, leading to an estimate of F = 0 for 90.9% of individuals. The song sparrow pedigree on the other hand had a mean number of 7.5 and a minimum number of 2 (except for offspring of immigrants) ancestral generations and only 7.5% of individuals with F = 0 (electronic supplementary material). Thus, the shallower zebra finch pedigree is likely to be partially responsible for the better performance of markers relative to the pedigree in that study [29]. Nevertheless, shortening the zebra finch pedigree had only moderate effects on its correlation with realized IBD [25], and other factors are hence likely important too.

Another contributor to the better performance of heterozygosity in [29] is the fact that about half of the autosomal genome of zebra finches lies on only six chromosomes, and these chromosomes experience little recombination in their central regions [65,66]. Hence the amount of Mendelian noise is high in this zebra finch population, and more Mendelian noise increases the variance of realized IBD around its expectation, and thereby the usefulness of markers relative to pedigrees for estimating IBD, as a lot of the variation in IBD can be measured with a few variable markers that lie within the large regions with little recombination [25,29]. Although recombination rates may also increase towards the telomeres in other bird species, this effect tends to be less strong than in zebra finches [43,67,68]. In contrast with birds, in humans and even more so in mice (Mus musculus) and rats (Rattus norvegicus), recombination rates are largely homogeneous across the chromosomes [69]. Such a regular recombination landscape reduces Mendelian noise in humans considerably as compared to that in zebra finches, despite humans having 17 fewer chromosomes than zebra finches [25].

Finally, the power of markers to estimate IBD is influenced by the IBD–IBS discrepancy, i.e. the extent to which markers are IBS but not IBD [25]. The 11 microsatellites employed by Forstmeier et al. [29] were more variable (mean number of alleles N_A = 11.4) than the markers used in our study (N_A = 8.9 [37]). This reduced marker variability led to higher IBD–IBS discrepancy of 31.2% in our song sparrow dataset (electronic supplementary material, figure S1), when compared with 13.3% in the zebra finch dataset [25]. High IBD–IBS discrepancy of individual markers can be accommodated for by genotyping many markers near chromosomal regions of interest [27].

5. Conclusion

We have shown that pedigree-based expectations of IBD are valuable predictors of variation in fitness, even in the presence of relatively extensive genetic data covering most of the genome. Compared with datasets of tens or hundreds of thousands of SNPs in some other systems, 160 microsatellites are few (e.g. [16,46]), but microsatellites are more polymorphic [70] and thus more informative about ancestry than SNPs [71]. We agree with previous authors (e.g. [23,29]) that realized IBD must explain more variation in fitness than expected IBD whenever there is inbreeding depression, and that extensive genetic data upwards of approximately 10 000 SNPs allows quantifying realized IBD better than most pedigrees [32,72]. With such large numbers of markers, it can be expected that heterozygosity at these markers would explain more variation in fitness than F [73]. However, such datasets are still rare and expensive to obtain, especially for thousands of individuals with fitness data from wild populations. Furthermore, realized IBD at the relevant fitness-coding loci may differ from estimates of IBD based on markers or pedigrees, for example if there are major genes explaining variation in fitness, fitness-coding genes are clustered, or not closely linked to the markers. Our study shows that the minimum number of loci required to outperform expectations of IBD from a high-quality pedigree may be quite high, at least compared with previously published results from a captive population of zebra finches [29].

Several factors influence how well markers estimate realized IBD compared with the expectation based on a well-resolved pedigree: sampling variance of the markers [28], Mendelian noise influenced by characteristics of the recombination landscape [25], and the fact that markers reveal IBS that may differ from IBD [29], leading to IBD–IBS discrepancy [25]. Marker-based estimates will perform better than pedigree-based estimates if the latter are based on low-resolution pedigree data covering few ancestral generations, e.g. due to short study duration, difficulty in locating individuals or high immigration rates. Thus, predictions about the number of loci needed to obtain accurate estimates of inbreeding from marker data must consider the specifics of the study population, such as pedigree depth and completeness, the recombination landscape, and marker variability and location. In the song sparrow population of Mandarte Island, H across a large number (160) of microsatellites explained variation in fitness, but pedigree-based F explained more of it. Thus at least in this case, H at 160 markers did not appear to measure realized IBD better than the predictions based on a good pedigree, but both measures of inbreeding on their own were significant predictors of variation in fitness.

Data accessibility

Data and simulation script are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.p9s04 [74].

Authors' contributions

P.N. conceived the study, contributed to data collection, analysed the data and drafted the manuscript. L.F.K. acquired funding and contributed to study design. G.C. contributed to data collection. F.G. wrote simulation software. P.A. coordinated the long-term project. J.M.R. contributed to data collection. E.P. conceived the study and contributed to writing. All authors reviewed, improved and approved the manuscript.

Competing interests

The authors declare no conflict of interest.

Funding

Our work was supported by Swiss National Science Foundation grants (31003A-116794 to L.F.K., PP00P3_144846 to F.G.), Natural Sciences and Engineering Research Council of Canada grants to P.A., and grants by the Forschungskredit of the University of Zurich (FK-15-104), Georges und Antoine Claraz-Schenkung and Dr Joachim de Giacomi foundation to P.N.