Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Mar 22;7:44690. doi: 10.1038/srep44690

Magnetic frustration of graphite oxide

Dongwook Lee 1,2,a, Jiwon Seo 1,3,b
PMCID: PMC5361081  PMID: 28327606

Abstract

Delocalized π electrons in aromatic ring structures generally induce diamagnetism. In graphite oxide, however, π electrons develop ferromagnetism due to the unique structure of the material. The π electrons are only mobile in the graphitic regions of graphite oxide, which are dispersed and surrounded by sp3-hybridized carbon atoms. The spin-glass behavior of graphite oxide is corroborated by the frequency dependence of its AC susceptibility. The magnetic susceptibility data exhibit a negative Curie temperature, field irreversibility, and slow relaxation. The overall results indicate that magnetic moments in graphite oxide slowly interact and develop magnetic frustration.

Carbon, one of the most abundant elements on earth, forms millions of chemical compounds. Among them, graphene-based carbon compounds such as graphite have been used in many industries, and they still hold the attention of physical and chemical engineers owing to their outstanding properties such as high specific surface area, lubricating ability, sorption, catalytic characteristics, and deaccelerating effects1,2,3. Aromatic rings in graphitic compounds, which are units of the graphitic structure, are considered diamagnetic units because a current along the ring produces diamagnetism when an external magnetic field is applied. Thus, graphitic materials generally exhibit diamagnetic properties. However, recent reports on the various ferromagnetic properties of graphitic compounds have sparked research on carbon magnetism. Their origins are as follows: proton-irradiated graphite4,5, graphite with zigzag edges6,7,8, defect-induced graphite9,10, hydrogen-mediated graphite11,12, and others13,14,15,16. These materials are conductors and have layered structures like graphite. Thus, the magnetic properties of ferromagnetic carbon systems have been considered together with their electrical properties. The emergence of nano-graphite has resulted in increased interest in nano-graphitic structures17,18,19,20,21. In nano-carbon structures, the electrical conductivities are less important. Rather, the edge condition and functional groups are more received22,23,24. However, no thorough research exists on the mixed structure of nano-graphite and non-graphitic compounds. Graphite oxide (GO)25,26,27 has attracted huge interest owing to its structural properties, which induce various properties such as optical, thermal, and dielectric properties, as well as mass production of graphene by reduction28,29,30,31. The graphitic regions in GO are dispersed among non-graphitic carbon atoms. The co-existence of graphitic and non-graphitic regions in GO results in an abundant surface area; hence, GO has been studied in the energy-storage industry and for application in sensors32,33,34,35.

The ferromagnetism in GO has been carefully investigated36,37,38,39,40. In our previous letter36, we showed that GO exhibits ferromagnetic behavior owing to the graphitic regions circulated by epoxy groups, and it has an S-shaped M-H curve. Here, we demonstrate the frequency dependence behavior of the AC susceptibility of GO and extract spin-glass parameters through scaling analysis. Its magnetic moment slowly changes with time at low temperature and GO illustrates glass-like behavior at these temperatures. This behavior is caused by interactions between the graphitic regions in GO.

To characterize materials using solid-state NMR, it would be better to compare the high-power decoupling (HPDEC) spectrum of samples with their cross-polarization magic angle spinning (CP/MAS) spectrum. In the HPDEC mode, the coupling between carbon and hydrogen atoms is broken, while in CP/MAS, the signal of carbon atoms is enhanced by the cross-polarization of carbon and hydrogen atoms. Thus, by comparing HPDEC data with CP/MAS data, we can determine which peaks come from carbon atoms near hydrogen atoms26,41.

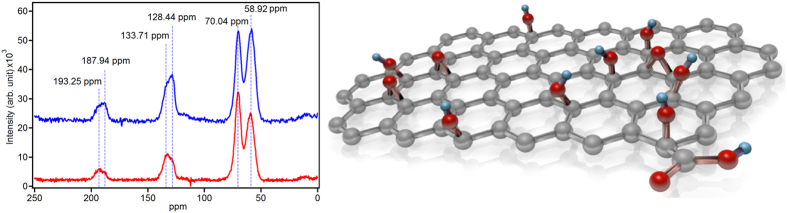
Figure 1 shows the experimental 13C MAS spectrum of GO acquired with HPDEC and CP/MAS with a 3550 μs contact time, during which the spectrum has a maximum value. There are peaks at roughly 60, 70, 120, 130, and 190 ppm. The intensity of the peak at 70.04 ppm is increased in the CP/MAS mode, while the peak intensity at 58.92 ppm does not differ between the HPDEC and CP/MAS modes26,41,42. The two small peaks at 187.94 and 193.25 ppm demonstrate similar behavior. The peak at 193.25 ppm does not change with the modes. However, the peak at 187.94 ppm increased in the CP/MAS mode. Therefore, we conclude that the peak at 58.92 ppm is due to the epoxy groups, the peak at 70.04 ppm is due to the hydroxyl groups, the peak at 130 ppm is due to the stable double bonds41, the peak at 193.25 ppm is due to the ketone groups26,43, and the peak at 187.94 ppm might be a result of the chemical groups containing carbon and hydrogen atoms such as -COOH. The broad peak around 130 ppm is due to graphitic rings. The NMR data indicate that GO is composed of graphitic and non-graphitic regions.

Figure 1.

Figure 1

Open in a new tab

(Left) Solid-state 13C NMR spectra of GO. High-power decoupling (red) and CP/MAS using 3550 μs contact time (blue). (Right) Schematic of GO. Red balls represent oxygen atoms and cyanide balls represent hydrogen atoms.

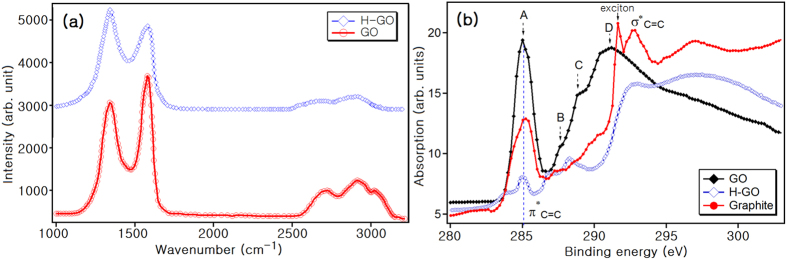
Figure 2(a) compares the Raman spectra of GO and H-GO. GO exhibits two high peaks at 1440 (D) and 1660 (G) cm−1. It also exhibits characteristic peaks at 2750 (2D), 2930 (D + G), and 3150 (2G) cm−1. After thermal treatment, the characteristic peaks of GO at the above positions were diminished. The diminished 2D peak indicates that the graphitic regions in GO were damaged. In addition, the D peak at 1440 cm−1 increased and grew broader, implying that more defects were produced during the heat treatment.

Figure 2.

Figure 2

Open in a new tab

(a) Raman spectra of GO and H-GO (b) C K-edge XANES spectra of GO, H-GO, and graphite at 298 K.

Figure 2(b) illustrates the C K-edge X-ray absorption near-edge structure (XANES) spectra of GO, H-GO, and polycrystalline graphite acquired in the total electron yield (TEY) mode at 298 K. The spectrum of graphite has two main peaks; the first peak at 285 eV is due to the π* state of C=C44,45,46 and the second at 292 eV is assigned to C=C σ* antibonding44,45,46. The spectrum also includes the peak from the core-exciton, a sharp peak at 291.6 eV. The spectrum of GO is different from that of graphite; peak A is due to unoccupied π* states44, peak B at 287 eV results from aliphatic C-OH47, peak C at 289 eV is due to C-O-C bonding, and peak D at 291.8 eV indicates unoccupied σ* states44. The peaks in the H-GO spectrum of H-GO differ from those in the other samples. Here, peak A (the π* state of C=C) is suppressed because the graphitic structure in GO was damaged during the heat treatment, which is consistent with the Raman results in Fig. 2(a). The height of peak B’ at 288 eV near peak B increases due to the generation of aliphatic C-H such as cyclohexane47. Peak C is nearly eliminated because epoxy groups decomposed during the thermal treatment and peak D shifts to 293 eV.

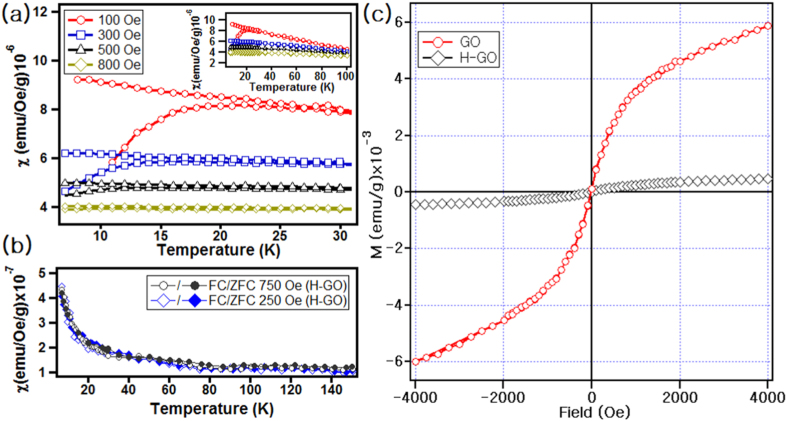
DC magnetic susceptibility measurements were performed using a superconducting quantum interference device (SQUID) magnetometer in zero-field-cooled (ZFC) and field-cooled (FC) modes with various applied magnetic fields. Figure 3(a) shows the susceptibilities of GO as a function of temperature. The susceptibility curves in ZFC mode exhibit a characteristic maximum and a thermal hysteresis (multiple paths) below it. As the temperature decreases, the FC curves become saturated. As the field increases from 100 to 800 Oe, the peaks become broader and shift from 25 to 15 K. This feature often appears in relaxors such as spin-glass materials48,49,50,51,52,53. The inset in Fig. 3(a) depicts the curves across a wide temperature range. The curves were fitted by the Curie-Weiss law, and the Curie temperatures θc at different magnetic fields are given in Table 1. A negative θc indicates the presence of antiferromagnetic interactions. H-GO does not show thermal hysteresis in Fig. 3(b). Instead, it exhibits a paramagnetic behavior. The Curie temperatures of H-GO are 0.56 and 0.51 K at 250 and 750 Oe, respectively.

Figure 3.

Figure 3

Open in a new tab

(a) Magnetic susceptibility of GO as a function of temperature at various field strengths. The inset shows the susceptibility of GO in the temperature range 6 ≤ T ≤ 180 K. (b) Magnetic susceptibilities of H-GO as a function of temperature at various field strengths. (c) Magnetization versus magnetic field curves of GO and H-GO.

Table 1. Curie temperature (θc) and effective Bohr magneton number (nB) of the samples obtained with different magnetic fields.

Sample GO GO GO GO H-GO H-GO
Field (Oe) 100 300 500 800 250 750
θc (K) −52.2 −40.2 −19.5 −12.0 0.56 0.51
nB 1.02 Inline graphic 10−3 1.23 Inline graphic 10−3 1.35 Inline graphic 10−3 1.32 Inline graphic 10−3 8.34 Inline graphic 10−5 1.43 Inline graphic 10−4
Open in a new tab

In the Curie-Weiss equation (χ = C/(T − θc)), C is the Curie constant and is described as follows: C = (nB)2(μB)2/3kB, where μB is the Bohr magneton and kB is the Boltzmann constant.

In H-GO, the Bohr magneton number nB is below the order of 10−4, i.e., negligible compared to that of GO. In addition, H-GO exhibits a linear curve in the M-H measurements in Fig. 3(c), unlike GO, which has an S-shaped curve. The above data indicate that there are ferromagnetic as well as antiferromagnetic interactions in GO and the magnetic properties of GO were destroyed during the heat treatment.

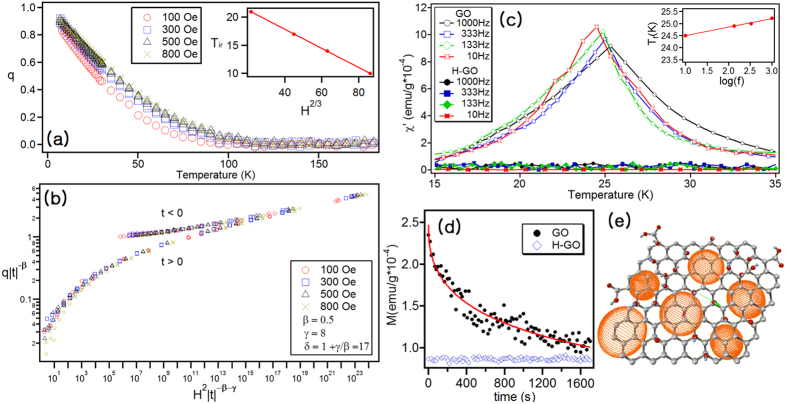
Further investigation of the magnetic behavior of GO was carried out using the Almeida-Thouless (AT) law and critical scaling analysis. The irreversibility temperatures (Tir) identified by the splitting of the ZFC and FC curves in Fig. 3(a) are plotted as a function of the applied field in Fig. 4(a), and they follow the AT line (H2/3) (Fig. 4(a) (inset))54. By extrapolating the AT line to H = 0, we determine a freezing temperature Tf = 24.5 ± 0.05 K. The order parameters of the spin glass were obtained using critical scaling analysis55. Normalized q(T) values, i.e., the deviation of the observed susceptibility from paramagnetic behavior, were extracted from both FC and ZFC data and plotted at various fields, as shown in Fig. 4(b). The FC data was fitted to q = |t|β as t → 0, yielding q = H2/(1+γ/β) near Tf52 with β = 0.5 ± 0.1 and γ = 9 ± 1. These parameters vary from those associated with a spin-glass in that β = 0.2 ± 0.1 and γ = 4.5 ± 0.5 in 2D spin-glass and β = 0.5 ± 0.2 and γ = 4.0 ± 0.4 in 3D spin-glass56. This variation implies that GO may exhibit both 2D and 3D spin-glass behavior, i.e., both 2D and 3D glass behaviors are present in GO.

Figure 4.

Figure 4

Open in a new tab

(a) Scaling analysis of data in Fig. 3(a). Spin-glass order parameter q as a function of temperature. The inset shows that irreversibility temperatures Tir is linearly dependent on 1/H2/3 and follows the Almeida-Thouless Law (H2/3). (b) Critical scaling for GO. (c) AC susceptibility curves of GO with different AC fields. Frequency ranges from 10 to 1000 Hz. The inset displays a graph of the freezing temperature (Tf) vs. frequency. (d) AC susceptibility curves of H-GO with different AC fields. (e) FC relaxation effect in GO and H-GO at 7 K. (f) Schematic for glass-like behavior of GO. Red balls are oxygen atoms and cyanide balls are hydrogen atoms. Orange spheres indicate the magnetic domain developed in the graphitic regions in GO.

Figure 4(c) shows the in-phase component χ’(T, ω) of the AC susceptibility of GO between 15 and 35 K in the frequency range 10 ≤ ω ≤ 1000 Hz. The measurements were taken in zero field cooling (ZFC) conditions with a 10 Oe AC field at different frequencies. The χ’(T, ω) curve exhibits a characteristic pronounced maximum with amplitude and position, depending on the frequency. As ω increases, the χ’ exhibits a maximum with amplitude and position, which is similar to the AC susceptibility behavior of glassy systems57,58,59. The AC susceptibility’s dependence on the frequency is a sign of slowing in the magnetization dynamics. The maximum of the peak shifts towards higher temperatures with increasing frequencies, which is a common feature for spin glasses57,58,60. The inset shows that the freezing temperature depends on the frequency. However, H-GO does not show any characteristic peak in the AC susceptibility curve (Fig. 4(d)).

To determine whether the GO sample has a slow relaxation, its FC relaxation effects were examined. First, a magnetic field of 100 Oe was applied to the samples at room temperature and then cooled to 7 K. The measurements were performed just after the magnetic field was removed. In Fig. 4(e), the magnetization of GO decreases exponentially with time, whereas H-GO magnetization exhibits no time dependence. The magnetization curve of GO was fitted as 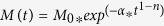Inline graphic, where n ~ 0.56 is similar to that of a dilute spin system52. Unlike GO, H-GO does not show slow relaxation.

In the previous letter, we demonstrated that the spin densities are mainly localized in the graphitic domains in GO, as shown in Fig. 4(f). When the distance between the graphitic domains becomes short enough, the spins in the domains can be coupled ferromagnetically and/or antiferromagnetically. According to our EDX analysis results, the C:O ratio of the sample is 6:2.3 and the ratio of sp2-carbon to sp3-carbon is 1.4. The graphitic domains are small because the oxygen coverage is so high. Thus, the interaction among the graphitic domains may be ferromagnetic and/or antiferromagnetic. However, the graphitic and non-graphitic regions in GO depends on the preparation method and the degree of oxidation27. The magnetic spin densities might be also influenced by the degree of oxidation and the preparation methods, which also determine the area and distribution of graphitic domains. In addition, the graphitic domains, which are hydrophobic, are different from hydrophilic reacted regions in GO. Thus, the amphiphilicity of GO might make the magnetic properties of GO more complex.

GO exhibits field irreversibility and slow relaxation. The DC susceptibility data show that the sample has a negative Curie temperature and exhibits field irreversibility in addition to slow relaxation. The frequency-dependence of AC susceptibility corroborates the spin-glass behavior. The destruction of epoxy groups gets rid of the magnetic properties of GO. Although the origin of this magnetism is not clear, it is apparent that the epoxy group plays a fundamental role in the observed magnetism. The overall results suggest that the magnetic moments in GO slowly interact and exhibit glass-like behavior.

Method

The GO samples were prepared by the Staudenmaier process27. GO was heated at 250 °C for 24 h (H-GO). The structural properties of the sample were characterized using solid-state nuclear magnetic resonance (NMR). The 13C spectra were obtained at 9.4 Tesla using a Bruker AVANCE 400 MHz spectrometer and 4 mm zirconia MAS rotors spun in air at 6 kHz. 13C MAS spectra with HPDEC were acquired at 100 MHz with 100-kHz, 90 °C pulses with a duration of 1.25 μs. 1H-13C CP/MAS spectra were recorded at different contact times (50–5050 μs) with increases of 500 μs. The peaks were most intense at 3550 μs. Raman spectra were collected at an excitation wavelength of 514 nm (Renishaw, RM-1000Invia, 2400 l/mm). X-ray absorption near edge structure (XANES) measurements were performed on the BACH beamline at ELLETRA in Italy. The magnetic properties of the samples were characterized with a Quantum Design MPMS 1802 magnetometer and a Lakeshore 7000 Series AC Susceptometer.

Additional Information

How to cite this article: Lee, D. and Seo, J. Magnetic frustration of graphite oxide. Sci. Rep. 7, 44690; doi: 10.1038/srep44690 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Acknowledgments

The authors acknowledge discussions with L. M. Brown and J. R. Cooper. They are also grateful for the help from the BACH beamline staff. This work was supported by the National Research Foundation of President Post-doctoral Fellowship Program (NRF-2013R1A6A3A060443).

Footnotes

The authors declare no competing financial interests.

Author Contributions J.S. managed the project and analyzed the data; D.L. prepared the samples, carried out experiments, and wrote the manuscript. All authors reviewed the manuscript.

References

  1. Broadbent K. A., Dollimore D. & Dollimore J. The surface area of graphite calculated from adsorption isotherms and heats of wetting experiments. Carbon 4, 281–287 (1966). [Google Scholar]
  2. Sliney H. E. Solid lubricant materials for high temperatures-a review. Tribology International 15, 303–315 (1982). [Google Scholar]
  3. Boersma M. A. M. Catalytic Properties of Alkali Metal-Graphite Intercalation Compounds. Catal. Rev. 10, 243–280 (1974). [Google Scholar]
  4. Han K.-H. et al. Ferromagnetic spots in graphite produced by proton irradiation. Adv. Mater. 15, 1719–1722 (2003) [Google Scholar]
  5. Esquinazi P. et al. Induced magnetic ordering by proton irradiation in graphite. Phys. Rev. Lett. 91, 227201 (2003). [DOI] [PubMed] [Google Scholar]
  6. Fujita M., Wakabayashi K., Nakada K. & Kusakabe K. Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Jpn. 65, 1920–1923 (1996). [Google Scholar]
  7. Yoshioka H. Spin excitation in nano graphite ribbons with zigzag edges. J. Phys. Soc. Jpn. 72, 2145–2148 (2003). [Google Scholar]
  8. Radovic L. R. & Bockrath B. On the Chemical Nature of Graphene Edges: Origin of Stability and Potential for Magnetism in Carbon Materials. J. Am. Chem. Soc. 127, 5917–5927 (2005). [DOI] [PubMed] [Google Scholar]
  9. Tyutyulkov N., Ivanov N., Müllen K., Staykov A. & Dietz F. Energy spectra of one dimensional stacks of polycyclic aromatic hydrocarbons without defects. J. Phys. Chem. B 108, 4275–4282 (2004). [Google Scholar]
  10. Vozmediano M. A. H., Lopez-Sancho M. P., Stauber T. & Guinea F. Local defects and ferromagnetism in graphene layers. Phys. Rev. B 72, 155121 (2005). [Google Scholar]
  11. Lehtinen P. O., Foster A. S., Ma Y., Krasheninnikov A. V. & Nieminen R. M. Irradiation-induced magnetism in graphite: A density functional study. Phys. Rev. Lett. 93, 187202 (2004). [DOI] [PubMed] [Google Scholar]
  12. Ruffieux P. et al. Hydrogen adsorption on sp2-bonded carbon: Influence of the local curvature. Phys. Rev. B 66, 245416 (2002). [Google Scholar]
  13. Klein D. J. & Bytautas L. Graphitic edges and unpaired π-electron spins. J. Phys. Chem. A 103, 5196–5210 (1999). [Google Scholar]
  14. Wang Y. et al. Room-temperature ferromagnetism of graphene. Nano. Lett. 9, 220–224 (2009). [DOI] [PubMed] [Google Scholar]
  15. Cervenka J., Katsnelson M. I. & Flipse C. F. J. Room-temperature ferromagnetism in graphite driven by two-dimensional networks of point defects. Nature Phys. 5, 840–844 (2009). [Google Scholar]
  16. Rao C. N. R., Matte H. R., Subrahmanyam K. S. & Maitra U. Unusual magnetic properties of graphene and related materials. Chemical Science 3, 45–52 (2012). [Google Scholar]
  17. Enoki T. et al. Magnetism of nano-graphite and its assembly. Polyhedron 20, 1311–1315 (2001). [Google Scholar]
  18. Enoki T. & Yousuke K. Magnetic nanographite: an approach to molecular magnetism. J. Mater. Chem. 15, 3999–4002 (2005). [Google Scholar]
  19. Matte H. S. S. R., Subrahmanyam K. S. & Rao C. N. R. Novel magnetic properties of graphene: presence of both ferromagnetic and antiferromagnetic features and other aspects. J. Phys. Chem. C 113, 9982–9985 (2009). [Google Scholar]
  20. Ito Y. et al. Tuning the Magnetic Properties of Carbon by Nitrogen Doping of Its Graphene Domains. J. Am. Chem. Soc. 137, 7678–7685 (2015). [DOI] [PubMed] [Google Scholar]
  21. Masrour R., Bahmad L., Benyoussef A., Hamedoun M. & Hlil E. K. Magnetism of Nano-Graphene with Defects: A Monte Carlo Study. J. Supercond. Nov. Magn. 26, 679–685 (2013). [Google Scholar]
  22. Wakabayashi K., Fujita M., Ajiki H. & Sigrist M. Electronic and magnetic properties of nanographite ribbons. Phys. Rev. B 59, 8271 (1999). [Google Scholar]
  23. Harigaya K. Tuning of magnetism in stacked nanographite with open shell electrons. Chem. Phys. Lett. 339, 23–28 (2001). [Google Scholar]
  24. Zhu L. Y. & Wang W. Z. Effects of intersite Coulomb interaction on ferromagnetism and dimerization in nanographite ribbons. J. Phys. Condens. Matter 18, 6273–6280 (2006). [Google Scholar]
  25. Brodie B. C. On the atomic weight of graphite. Phil. Trans. R. Soc. Lond. A 149, 249–259 (1859). [Google Scholar]
  26. Lee D. W. et al. The structure of graphite oxide: Investigation of its surface chemical groups. J. Phys. Chem. B 114, 5723–5728 (2010). [DOI] [PubMed] [Google Scholar]
  27. Lee D. W. & Seo J. W. sp2/sp3 carbon ratio in graphite oxide with different preparation times. J. Phys. Chem. C 115, 2705–2708 (2011). [Google Scholar]
  28. Lee D. W. et al. Transparent and flexible polymerized graphite oxide thin film with frequency-dependent dielectric constant. Appl. Phys. Lett. 95, 172901 (2009). [Google Scholar]
  29. Park S. & Ruoff R. S. Chemical methods for the production of graphenes. Nature Nanotech. 4, 217–224 (2009). [DOI] [PubMed] [Google Scholar]
  30. Lee D. et al. Ultrafast carrier phonon dynamics in NaOH-reacted graphite oxide film. Appl. Phys. Lett. 101, 021604 (2012), [Google Scholar]
  31. Lee D. et al. Quantum confinement-induced tunable exciton states in graphene oxide. Sci. Rep. 3, 2250 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Dua V. et al. All-organic vapor sensor using inkjet-printed reduced graphene oxide. Angew. Chem. Int. Ed. 49, 2154–2157 (2010). [DOI] [PubMed] [Google Scholar]
  33. Lee D. & Seo J. Three-dimensionally networked graphene hydroxide with giant pores and its application in supercapacitors. Sci. Rep. 4, 7419 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Xu S. et al. Fabrication of SnO2-Reduced Graphite Oxide Monolayer-Ordered Porous Film Gas Sensor with Tunable Sensitivity through Ultra-Violet Light Irradiation. Sci. Rep. 5, 8939 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Cassagneau T. & Fendler J. H. High density rechargeable lithium-ion batteries self-assembled from graphite oxide nanoplatelets and polyelectrolytes. Adv. Mater. 10, 877–881 (1998). [Google Scholar]
  36. Lee D., Seo J., Zhu X., Cole J. M. & Su H. Magnetism in graphene oxide induced by epoxy groups. Appl. Phys. Lett. 106, 172402 (2015). [Google Scholar]
  37. Wang M. & Li C. M. Magnetism in graphene oxide. New J. Phys. 12, 083040 (2010). [Google Scholar]
  38. Sarkar S. K., Raul K. K., Pradhan S. S., Basu S. & Nayak A. Magnetic properties of graphite oxide and reduced graphene oxide. Physica E 64, 78–82 (2014). [Google Scholar]
  39. Liu Y. et al. Realization of ferromagnetic graphene oxide with high magnetization by doping graphene oxide with nitrogen. Sci. Rep. 3, 2566 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tang T. et al. Identifying the magnetic properties of graphene oxide. Appl. Phys. Lett. 104, 123104 (2014). [Google Scholar]
  41. Lerf A., He H., Forster M. & Klinowski J. Structure of graphite oxide revisited. J. Phys. Chem. B 102, 4477–4482 (1998). [Google Scholar]
  42. Lee D. W. & Seo J. W. Formation of phenol groups in hydrated graphite oxide. J. Phys. Chem. C 115, 12483–12486 (2011). [Google Scholar]
  43. Pretsch E., Bühlmann P. & Affolter C. Structure determination of organic compounds: tables of spectral data (Springer-Verlag, Berlin, p. 64, 2000). [Google Scholar]
  44. Skytt P. et al. Angle-resolved soft x-ray fluorescence and absorption study of graphite. Phys. Rev. B 50, 10457–10461 (1994). [DOI] [PubMed] [Google Scholar]
  45. Stöhr J. NEXAFS Spectroscopy (Springer-Verlag, Berlin, p. 289, 1991). [Google Scholar]
  46. Coffman F. L. et al. Near-edge x-ray absorption of carbon materials for determining bond hybridization in mixed sp2/sp3 bonded materials. Appl. Phys. Lett. 69, 568–570 (1996). [Google Scholar]
  47. Stöhr J. NEXAFS Spectroscopy (Springer-Verlag, Berlin, p. 203, 1991). [Google Scholar]
  48. Hong C. S., Kim W. S., Chi E. O., Hur N. H. & Choi Y. N. Colossal magnetoresistance in La0.7Ca0.3MnO3−δ: Comparative study of single crystal and polycrystalline material. Chem. Mater. 14, 1832–1838 (2002). [Google Scholar]
  49. Zhou G. F. & Bakker H. Spin-glass behavior of amorphous Co2Ge synthesized by mechanical milling. Phys. Rev. Lett. 72, 2290–2293 (1994). [DOI] [PubMed] [Google Scholar]
  50. Peddis D., Cannas C., Musinu A. & Piccaluga G. Coexistence of superparamagnetism and spin-glass like magnetic ordering phenomena in a CoFe2O4 − SiO2 nanocomposite. J. Phys. Chem. C 112, 5141–5147 (2008). [Google Scholar]
  51. Falqui A., Lampis N., Lehmann A. G. & Pinna G. Low-temperature magnetic behavior of perovskite compounds PbFe0.5Ta0.5o3 and PbFe0.5Nb0.5o3. J. Phys. Chem. B 109, 22967–22970 (2005). [DOI] [PubMed] [Google Scholar]
  52. Chou F. C., Belk N. R., Kastner M. A., Birgeneau R. J. & Aharony A. Spin-glass behavior in La1.96Sr0.04CuO4. Phys. Rev. Lett. 75, 2204–2207 (1995). [DOI] [PubMed] [Google Scholar]
  53. Hanif K. M., Meulenberg R. W. & Strouse G. F. Magnetic ordering in doped Cd1−xCoxSe diluted magnetic quantum dots. J. Am. Chem. Soc. 124, 11495–11502 (2002). [DOI] [PubMed] [Google Scholar]
  54. De-almeida J. R. L. & Thouless D. J. Stability of the Sherrington-kirkpatrick solution of a spin-glass model. J. Phys. A 11, 983–990 (1978). [Google Scholar]
  55. Malozemoff A. P., Barnes S. E. & Barbara B. Non-mean-field interpretation of the irreversibility line in spin-glasses. Phys. Rev. Lett. 51, 1704–1707 (1983). [Google Scholar]
  56. Mydosh J. A. Spin glass: An Experimental Introduction (Taylor & Francis, London, 1993). [Google Scholar]
  57. Mulder C. A. M., Van Duyneveldt A. J. & Mydosh J. A. Susceptibility of the CuMn spin-glass: Frequency and field dependences. Phys. Rev. B 23, 1384 (1981). [Google Scholar]
  58. Mulder C. A. M., Van Duyneveldt A. J. & Mydosh J. A. Frequency and field dependence of the ac susceptibility of the AuMn spin-glass. Phys. Rev. B 25, 515 (1982). [Google Scholar]
  59. Bie X. et al. Observation of the second-order magnetic and reentrant spin-glass transitions in LiNi0.5Mn0.5o2. J. Alloy. Compd. 626, 150–153 (2015). [Google Scholar]
  60. Wang Y. T., Bai H. Y., Pan Mi. X., Zhao D. Q. & Wang W. H. Multiple spin-glass-like behaviors in a Pr-based bulk metallic glass. Phys. Rev. B 74, 064422 (2006). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES